идеальные и реальные растворы закон рауля и две формы его записи

1.1. Закон Рауля. Идеальные растворы.

Одним из важнейших свойств растворов является давление насыщенного пара, то есть пара, находящегося в равновесии с жидкостью. Парообразная фаза над раствором в общем случае содержит все летучие компоненты раствора.

Опытным путем Рауль установил (1887 г.), что парциальное давление насыщенного пара компонента раствора Рi пропорционально его мольной доле в растворе N_i:

, (1)

Большинство растворов отклоняется от закона Рауля, т.е. они являются неидеальными. Очень многие растворы подчиняются закону Рауля лишь при малых концентрациях.

Для газовой (паровой фазы) над идеальным раствором соблюдается закон Дальтона, в соответствии с которым:

, (2)

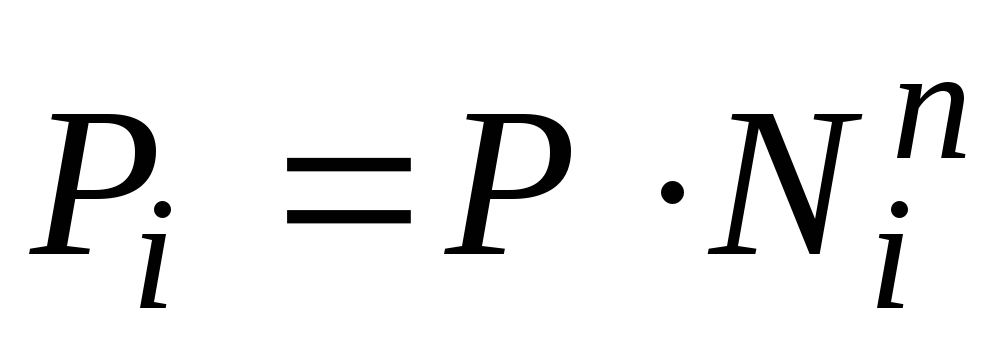
где Р— общее давление;

Общее давление насыщенного пара над раствором равно сумме парциальных давлений компонентов смеси: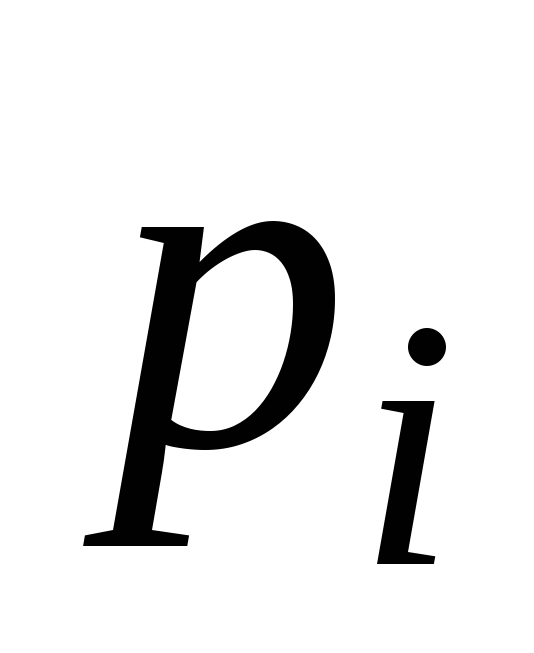

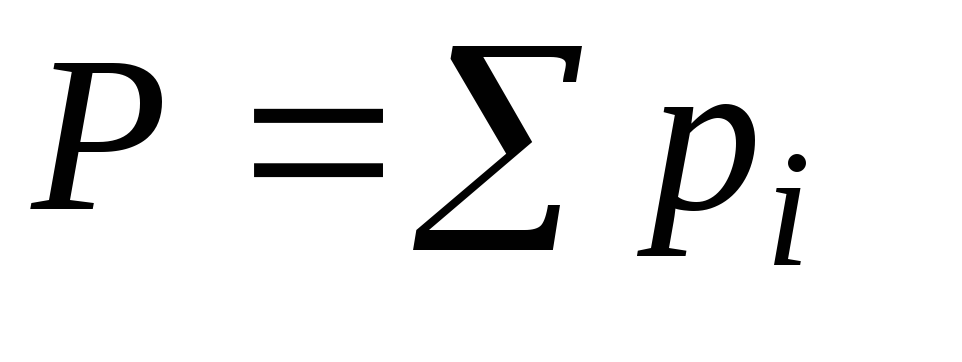
. (3)

Рассмотрим бинарный идеальный раствор, состоящий из компонентов А и В и находящийся в равновесии со своим паром. В соответствии с законом Рауля парциальное давление насыщенного пара каждого компонента при любой заданной температуре пропорционально его мольной доле в растворе:

Общее давление насыщенного пара над раствором равно:

Уравнения (4-6) показывают, что давление каждого компонента и общее давление пара над идеальным раствором линейно зависят от состава раствора.

Источник

Идеальные и реальные растворы закон рауля и две формы его записи

Кафедра физической и коллоидной химии ЮФУ

Материалы к лекциям для студентов химфака

Давление насыщенного пара растворов. Закон Рауля

Представим, что в равновесную систему жидкость А – пар введено некоторое вещество В. При образовании раствора мольная доля растворителя X_А становится меньше единицы; равновесие в соответствии с принципом Ле Шателье – Брауна смещается в сторону конденсации вещества А, т.е. в сторону уменьшения давления насыщенного пара Р_А. Очевидно, что, чем меньше мольная доля компонента А в растворе, тем меньше парциальное давление его насыщенных паров над раствором. Для некоторых растворов выполняется следующая закономерность, называемая первым законом Рауля :

Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причем коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.

(1)

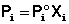
Поскольку сумма мольных долей всех компонентов раствора равна единице, для бинарного раствора, состоящего из компонентов А и В (компонент А считаем растворителем) легко получить следующее соотношение, также являющееся формулировкой первого закона Рауля:

(2)

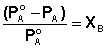
Относительное понижение парциального давления пара растворителя над раствором равно мольной доле растворенного вещества и не зависит от природы растворенного вещества.

(3)

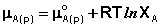
Химический потенциал растворителя в паре μ _А(п) можно выразить через парциальное давление пара растворителя Р_А:

(4)

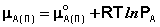
Химический потенциал чистого жидкого растворителя μ *_А равен химическому потенциалу равновесного пара:

(5)

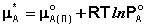
В состоянии равновесия μ _А(п) = μ _А(р). Комбинируя выражения (3-5), легко получить:

(6)

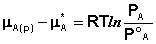
Принимая, что μ *_А = μ °_А(р), получаем следующее уравнение:

(7)

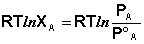
Отсюда легко получить выражение для первого закона Рауля:

=> => (8)

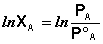
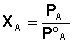
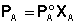
Если компоненты бинарного раствора летучи, то пар над раствором будет содержать оба компонента (относительное содержание компонентов в парах будет, как правило, отличаться от содержания их в растворе: пар относительно богаче компонентом, температура кипения которого ниже – см. следующий параграф). Рассмотрим идеальный бинарный раствор, состоящий из компонентов А и В, неограниченно растворимых друг в друге. Общее давление пара, согласно первому закону Рауля, равно

(9)

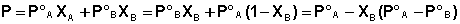
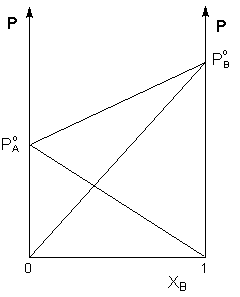
Таким образом, для идеальных бинарных растворов зависимость общего и парциального давления насыщенного пара от состава раствора, выраженного в мольных долях компонента В, является линейной при любых концентрациях (рисунок 1). К таким системам относятся, например, системы бензол – толуол, гексан – гептан, смеси других изомерных углеводородов. Для реальных растворов данные зависимости являются криволинейными (рисунок 2).

Рис. 1. Зависимость парциальных и общего давлений пара идеального раствора от концентрации.

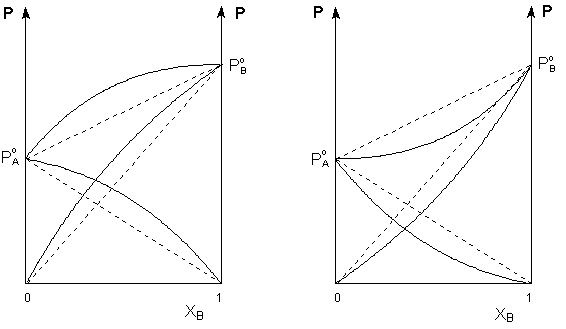
Рис. 2. Зависимость парциальных и общего давлений пара идеальных (штриховая линия) и реальных (сплошная линия) бинарных растворов от состава при положительных (слева) и отрицательных (справа) отклонениях от закона Рауля.

Если молекулы данного компонента взаимодействуют друг с другом сильнее, чем с молекулами другого компонента, то истинные парциальные давления паров над смесью будут больше, чем вычисленные по первому закону Рауля ( положительные отклонения ). Если же однородные частицы взаимодействуют друг с другом слабее, чем разнородные, парциальные давления паров компонентов будут меньше вычисленных ( отрицательные отклонения ).

Образование реальных растворов сопровождается тепловым и объёмным (т.н. контракция) эффектами. Реальные растворы с положительными отклонениями от закона Рауля образуются из чистых компонентов с поглощением теплоты (ΔН_раств > 0); объём раствора оказывается больше, чем сумма исходным объёмов компонентов (ΔV > 0). Растворы с отрицательными отклонениями от закона Рауля образуются с выделением теплоты (ΔН_раств

Copyright © С. И. Левченков, 2005.

Источник

22. Идеальные растворы. Закон Рауля и следствия из него. Фазовые диаграммы воды и водного раствора. Понятие об осмосе, уравнение Вант-Гоффа.

Существует несколько классификаций растворов. С точки зрения термодинамики целесообразно различать растворы идеальные и неидеальные или реальные. В идеальных растворах внутренняя энергия каждого компонента не зависит от концентрации, и молярный объем не изменяется при растворении. Компоненты при этом смешиваются как идеальные газы, и увеличение энтропии можно рассчитать по уравнениям, характерным для идеальных газов. Здесь сил взаимодействия между частицами нет, и вещества смешиваются без выделения или поглощения теплоты.

При исследовании растворов широко пользуются методом моделей. Простейшей моделью является идеальный раствор. Идеальные растворы делят обычно на две группы: разбавленные (более точно бесконечно разбавленные) и совершенные.

Образование идеального раствора не сопровождается изменением объема, тепловым эффектом, химическим взаимодействием. Такие растворы образуются в результате простого физического смешения

(ΔН_см = 0; ΔV_см = 0). Такие растворы получаются смешиванием неполярных жидкостей, характеризующихся близкими по силе молекулярными полями. В таких смесях отсутствуют явления сольватации, а отсюда нет и теплового эффекта растворения, нет и концентрации системы. Объем раствора равен сумме объемов смешиваемых компонентов. Это и есть идеальные или совершенные растворы.

Роль их в теории растворов аналогична роли идеальных газов (потому их и называют идеальными растворами).

Идеальные растворы довольно распространены. Пример: смешивание изомеров углеводорода (октаны и др.). Бензин, керосин, смесь бензола и толуола –идеальные растворы, представляют собой смесь различных углеводородов (жидких). Идеальные растворы имеют характер простых молекулярных смесей. К ним подходит «физическая» теория растворов. Физическая теория растворов предложена Вант-Гоффом и Аррениусом в 19 в. Согласно этой теории растворитель рассматривается как среда, в которой при растворении вещества его молекулы равномерно размещаются по всему объему раствора, межмолекулярные взаимодействия отсутствуют.

Законы Рауля. Важнейшей характеристикой вещества, находящегося в жидком состоянии или твердом является давление насыщенного пара, это давление – константа вещества, определяющая равновесие жидкость  пар, твердое вещество пар. Само равновесие достигается, когда процессы испарения компенсируется процессами конденсации. При нагревании давление пара возрастает.

Для разбавленных растворов относительное понижение давления пара растворителя (А) численно равно мольной доле растворенного вещества (В) (первый закон Рауля).

Так как для любого раствора сумма мольных долей Х _А + Х _В = 1, то формула будет

Таким образом, для разбавленных растворов давление пара растворителя пропорционально его мольной доле в растворе.

Из закона Рауля возникает два следствия. Согласно одному из них температура кипения раствора выше температуры кипения растворителя. Это обусловлено тем, что давление насыщенного пара растворителя над раствором становится равным атмосферному давлению (условие кипения жидкости) при более высокой температуре, чем в случае чистого растворителя. Повышение температуры кипения ΔТ_кип пропорционально моляльности раствора: с_m. ΔТ_кип= К_э с_m где К_э – эбулиоскопическая постоянная растворителя

Диаграмма состояния представляет собой графическое изображение зависимости между различными величинами, характеризующими состояние системы. Для однокомпонентных систем обычно используют диаграммы состояния, показывающие зависимость между давлением и температурой. Они называются фазовыми диаграммами состояния. Диаграмма показывает те состояния воды, которые термодинамически устойчивы при определенных значениях температуры и давления. Она состоит из трех кривых, разграничивающих все возможные температуры и давления на три области, отвечающие льду, жидкости и пару. Все три кривые пересекаются одной точке О. координаты этой точки – это единственная пара значений температуры и давления, при которых в равновесии могут находиться все три фазы: лед, жидкая вода и пар. Она носит название тройной точки.

Самопроизвольный переход растворителя через полупроницаемую мембрану, разделяющую раствор и растворитель или два раствора с различной концентрацией растворенного вещества, называется осмосом.

Источник

Коллигативные свойства растворов

Любому раствору характерны те или иные физические свойства, к которым относятся и коллигативные свойства растворов. Это такие свойства, на которые не оказывает влияние природа растворенного вещества, а зависят они исключительно от количества частиц этого растворенного вещества.

К коллигативным свойствам растворов относятся:

Рассмотрим подробнее каждое из перечисленных свойств.

Понижение давления паров

Давление насыщенного пара (т.е. пара, который пребывает в состоянии равновесия с жидкостью) над чистым растворителем называется давлением или упругостью насыщенного пара чистого растворителя.

Если в некотором растворителе растворить нелетучее вещество, то равновесное давление паров растворителя при этом понижается, т.к. присутствие какого – либо вещества, растворенного в этом растворителе, затрудняет переход частиц растворителя в паровую фазу.

Экспериментально доказано, что такое понижение давления паров напрямую зависит от количества растворенного вещества. В 1887 г. Ф.М. Рауль описал количественные закономерности коллигативных свойств растворов.

Первый закон Рауля

Первый закон Рауля заключается в следующем:

Давление пара раствора, содержащего нелетучее растворенное вещество, прямо пропорционально мольной доле растворителя в данном растворе:

p — давление пара над раствором, Па;

p₀ — давление пара над чистым растворителем, Па;

χ_р-ль — мольная доля растворителя.

n_в-ва и n_р-ля – соответственно количество растворенного вещества и растворителя, моль.

Иногда Первому закону Рауля дают другую формулировку:

относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества:

При этом принимаем, что χ_в-ва + χ_р-ль= 1

Изотонический коэффициент Вант-Гоффа

Для растворов электролитов данное уравнение приобретает несколько иной вид, в его состав входит изотонический коэффициент i:

Δp — изменение давления паров раствора по сравнению с чистым растворителем;

i – изотонический коэффициент.

Изотонический коэффициент (или фактор Вант-Гоффа) — это параметр, не имеющий размерности, который характеризует поведение какого – либо вещества в растворе.

То есть, изотонический коэффициент показывает, разницу содержания частиц в растворе электролита по сравнению с раствором неэлектролита такой же концентрации. Он тесно связан связан с процессом диссоциации, точнее, со степенью диссоциации и выражается следующим выражением:

n – количество ионов, на которые диссоциирует вещество.

α – степень диссоциации.

Повышение температуры кипения или понижение температуры затвердевания (кристаллизации). Второй закон Рауля

Равновесное давление паров жидкости имеет тенденцию к увеличению с ростом температуры, жидкость начинает кипеть, при уравнивании давления ее паров и внешнего давления.

При наличии нелетучего вещества, давление паров раствора снижается, и раствор будет закипать при более высокой температуре, по сравнению с температурой кипения чистого растворителя.

Температура замерзания жидкости также определяется той температурой, при которой давления паров жидкой и твердой фаз уравниваются.

Ф.М. Рауль доказал, что повышение температуры кипения, так же как и понижение температуры замерзания разбавленных растворов нелетучих веществ, прямо пропорционально моляльной концентрации раствора и не зависит от природы растворённого вещества. Это правило известно как Второй закон Рауля:

K — криоскопическая константа,

m_в-ва — моляльность вещества в растворе.

Растворы электролитов не подчиняются Законам Рауля. Но для учёта всех несоответствий Вант-Гофф предложил ввести в приведённые уравнения поправку в виде изотонического коэффициента i, учитывающего процесс распада на ионы молекул растворённого вещества:

Осмотическое давление раствора

Некоторые материалы имеют способность к полупроницаемости, т.е. им свойственно пропускать частицы определенного вида и не пропускать частицы другого вида.

Перемещение молекул растворителя (но не растворенного, в нем вещества), через полупроницаемую мембрану в раствор с большей концентрацией из более разбавленного представляет собой такое явление как осмос.

Представим два таких раствора, которые разделены полупроницаемой мембраной, как показано на рисунке выше. Растворы стремятся к выравниванию концентраций, поэтому вода будет проникать в раствор, тем самым уменьшая его концентрацию.

Для того, чтобы осмос приостановить, необходимо приложить внешнее давление к раствору. Такое давление, которое требуется приложить, называется осмотическим давлением.

Осмотическое давление и концентрацию раствора неэлектролита позволяет связать уравнение Вант — Гоффа, которое напоминает уравнение идеального газа Клапейрона – Менделеева:

R — универсальная газовая постоянная (8,314 Дж/моль·К);

T — абсолютная температура раствора.

Преобразуем уравнение следующим образом:

C = n/V = m/(M·V)

π = т·R·T / M·V или

Для растворов электролитов осмотическое давление определяется уравнением, в которое входит изотонический коэффициент:

где i — изотонический коэффициент раствора.

Для растворов электролитов i > 1, а для растворов неэлектролитов i = 1.

Если полупроницаемой перегородкой разделены два раствора, имеющие одинаковое осмотическое давление, то перемещение растворителя через перегородку отсутствует. Такие растворы называются изотоническими.

Раствор, с меньшим осмотическим давлением, по сравнению с более концентрированным раствором, называют гипотоническим, а раствор с большей концентрацией – гипертоническим.

Источник

Закон Рауля

Изменение термодинамических функций при образовании растворов.

2) разрушение кристаллической решётки (DН₂ > 0);

1) тепловой эффект смешения равен нулю (теплота не выделяется и не поглощается), т.е. DН_смеш. = 0;

2) объем системы не изменяется, т.е. DV_смеш. = 0;

3) изменение энтропии при образовании идеального раствора совпадает (равно) с изменением энтропии при смешении идеальных газов (для 1 моль смеси DS_смеш. = – R(х_Alnx_A + x_Blnx_B).

Здесь х_A и x_B – молярные доли компонентов A и B, соответственно. При этом идеальные растворы образуются самопроизвольно за счет увеличения энтропии (DS_смеш. > 0), поскольку DН_смеш. = 0. Кроме того, идеальные растворы подчиняются закону Рауля (р_i = p_0,i x_i) для всех компонентов при всех температурах и концентрациях.

Закон Рауля. Рассмотрим двухкомпонентную систему А–В, компоненты которой неограниченно растворимы друг в друге в жидком состоянии и при любых соотношениях образуют идеальный раствор. При нагревании таких растворов в пар переходят оба компонента, поэтому пар состоит из двух веществ. Общее давление насыщенного пара над раствором равно р_общ = р_А + р_В, где р_А и р_В – парциальные давления компонентов А и В соответственно. При этом молярные доли компонентов в паре (y_А, у_В), в соответствии с законом Дальтона, будут равны: ; .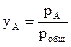

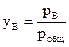
х_А, х_В – молярные доли компонентов А и В в жидкой фазе (растворе);

В 1887 г. Рауль экспериментально установил, что при любой заданной температуре парциальное давление насыщенного пара любого компонента над жидким идеальным раствором прямо пропорционально его молярной доле в растворе.

р_0,А, р_0,В – давление насыщенного пара над чистыми жидкими компонентами А и В при данной температуре.

В общем виде математическое выражение закона Рауля можно записать следующим образом:

Изобразим графически данные зависимости (это будут уравнения прямых линий):

Реальные (неидеальные) раcтворы не подчиняются законам идеальных растворов Рауля в форме p_i = p_0i×x_i. Отношение p_i / p_0i для реальных растворов равно уже не мольной доле, а некоторой функции от температуры и состава раствора: a_i = f(T, x_i), которую Дж. Льюис назвал термодинамической активностью i-ого компонента в растворе. В связи с этим для реальных растворов будут иметь место два равенства:

,(12)

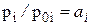
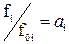
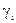
если пар подчиняется законам идеальных газов и если пар подчиняется законам реальных газов. Активность связана с мольной долей компонента через коэффициент активности :

a_i

Величина коэффициента активности указывает на степень отклонения реальных растворов от идеальности (законов идеальных растворов).

Если давление насыщенного пара над реальным раствором больше, чем над идеальным раствором того же состава (g_i > 1), то отклонения от идеальности называются положительными.

При этом, силы взаимодействия (F) между однородными молекулами компонентов раствора больше сил взаимодействия между разнородными молекулами компонентов раствора (т.е. F_А—А > F_А—В или F_В—В > F_А—В), и переход компонентов в пар будет энергетически более выгодным. Растворы с положительным отклонением от закона Рауля образуются обычно с поглощением теплоты (DH > 0) и увеличением объема (DV > 0).

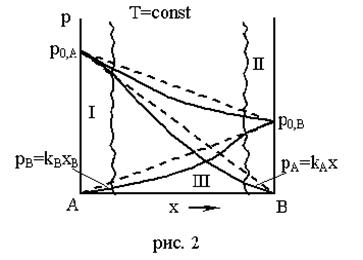
Если давление насыщенного пара над реальным раствором меньше, чем над идеальным раствором того же состава (g_i Положительные отклонения.

Пунктирная линия – для идеального раствора.

Рассмотрим три области: I, II, III.

Область I – это разбавленный раствор компонента В в А (здесь А – растворитель). В области I давление насыщенного пара растворителя (компонента А) подчиняется закону Рауля (сплошная линия совпадает с пунктирной), а для растворенного вещества В – не подчиняется закону Рауля.

Область II – здесь растворителем является компонент В, а компонент А является растворенным веществом. В этой области давление насыщенного пара компонента В подчиняется закону Рауля, а компонента А – не подчиняется.

Области I и II – это области предельно разбавленных растворов.

Закон Генри.

Предельно разбавленными называются такие растворы, в которых молярная доля растворенного вещества x₂ закон Генри:

Таким образом, в предельно разбавленных реальных растворах растворитель подчиняется закону Рауля, а растворенное вещество – закону Генри.

Источник