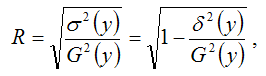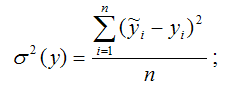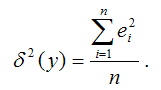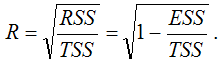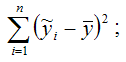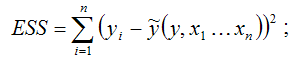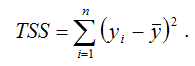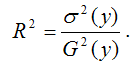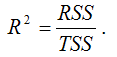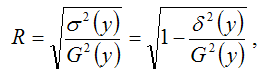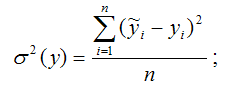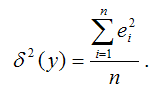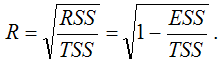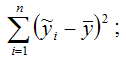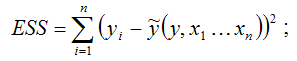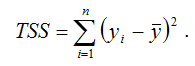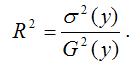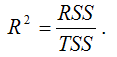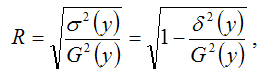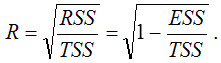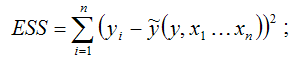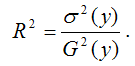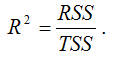индекс детерминации для нелинейных форм связи формула
Индекс детерминации для нелинейных форм связи формула
45. Показатели корреляции и детерминации для нелинейных моделей регрессии
Индексом корреляции для нелинейных форм связи называется коэффициент корреляции, который вычисляется для оценки качества построенной нелинейной модели регрессии.
Индекс корреляции для нелинейных форм вычисляется с помощью теоремы о разложении дисперсий по формуле:
где G2(y) – это общая дисперсия зависимой переменной;
?2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:
?2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:
Также индекс корреляции для нелинейных форм можно рассчитать с помощью теоремы о разложении сумм квадратов по формуле:
где RSS (Regression Sum Square) – сумма квадратов объяснённой регрессии:
ESS (Error Sum Square) – сумма квадратов остатков модели множественной регрессии с n независимыми переменными:
TSS (TotalSumSquare) – общая сумма квадратов модели множественной регрессии с n независимыми переменными:
Индекс корреляции для нелинейных форм связи изменяется в пределах от нуля до единицы. С его помощью нельзя охарактеризовать направление связи между результативной и факторными переменными. Чем ближе значение индекса корреляции для нелинейных форм связи к единице, тем сильнее взаимосвязь между результативной и независимыми переменными, и наоборот, чем ближе значение индекса корреляции для нелинейных форм связи к нулю, тем слабее взаимосвязь между результативной и независимыми переменными.
Индексом детерминации называется квадрат индекса корреляции для нелинейных форм связи.
Расчёт индекса детерминации с помощью теоремы о разложении дисперсий:
Расчёт индекса детерминации с помощью теоремы о разложении сумм квадратов:
Индекс детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.
Коэффициент множественной детерминации также называется количественной характеристикой объяснённой построенной моделью регрессии дисперсии результативной переменной. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.
Ответы на экзаменационные билеты по эконометрике (26 стр.)
Также индекс корреляции для нелинейных форм можно рассчитать с помощью теоремы о разложении сумм квадратов по формуле:
где RSS (Regression Sum Square) – сумма квадратов объяснённой регрессии:
ESS (Error Sum Square) – сумма квадратов остатков модели множественной регрессии с n независимыми переменными:
TSS (TotalSumSquare) – общая сумма квадратов модели множественной регрессии с n независимыми переменными:
Индекс корреляции для нелинейных форм связи изменяется в пределах от нуля до единицы. С его помощью нельзя охарактеризовать направление связи между результативной и факторными переменными. Чем ближе значение индекса корреляции для нелинейных форм связи к единице, тем сильнее взаимосвязь между результативной и независимыми переменными, и наоборот, чем ближе значение индекса корреляции для нелинейных форм связи к нулю, тем слабее взаимосвязь между результативной и независимыми переменными.
Индексом детерминации называется квадрат индекса корреляции для нелинейных форм связи.
Расчёт индекса детерминации с помощью теоремы о разложении дисперсий:
Расчёт индекса детерминации с помощью теоремы о разложении сумм квадратов:
Индекс детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.
Коэффициент множественной детерминации также называется количественной характеристикой объяснённой построенной моделью регрессии дисперсии результативной переменной. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все методы проверки гипотез, используемые для классических линейных моделей регрессии.
Таким образом, если внутренне линейную модель регрессии можно свести к линейной модели парной регрессии, то на эту модель будут распространяться все методы проверки гипотез, используемые для парной линейной зависимости.
Проверка гипотезы о значимости линейной модели множественной регрессии состоит в проверке гипотезы значимости индекса детерминации R2.
Рассмотрим процесс проверки гипотезы о значимости индекса детерминации.
Основная гипотеза состоит в предположении о незначимости индекса детерминации, т. е.
Обратная или конкурирующая гипотеза состоит в предположении о значимости индекса детерминации, т. е.
Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора.
Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают со значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора, и называется критическим.
При проверке значимости индекса детерминации критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=l-1 и k2=n-l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров.
При проверке основной гипотезы вида Н0:R2=0 наблюдаемое значение F-критерия Фишера-Снедекора рассчитывается по формуле:
При проверке основной гипотезы возможны следующие ситуации.
Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то с вероятностью а основная гипотеза о незначимости индекса детерминации отвергается, и он признаётся значимым. Следовательно, полученная модель регрессии также признаётся значимой.
Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл=Fкрит, то основная гипотеза о незначимости индекса детерминации принимается, и он признаётся незначимым. Полученная модель регрессии является незначимой и нуждается в дальнейшей доработке.
Если в начале эконометрического моделирования перед исследователем стоит выбор между моделью регрессии, внутренне нелинейной и линейной моделью регрессии (или сводящейся к линейному виду), то предпочтение отдаётся линейным формам моделей.
Проверка предположения о возможной линейной зависимости между исследуемыми переменными осуществляется с помощью коэффициента детерминации r2 и индекса детерминации R2.
Выдвигается основная гипотеза Н0о наличии линейной зависимости между переменными. Альтернативной является гипотеза Н1 о нелинейной зависимости между переменными.
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.
При проверке гипотезы о линейной зависимости между переменными критическое значение t-критерия определяется как tкрит(а;n-l-1), где а – уровень значимости, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров, (n-l-1) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.
При проверке основной гипотезы Н0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
где νR-r – величина ошибки разности (R2-r2), которая определяется по формуле:
Показатели корреляции и детерминации для нелинейных моделей регрессии
Индексом корреляции для нелинейных форм связи называется коэффициент корреляции, который вычисляется для оценки качества построенной нелинейной модели регрессии.
Индекс корреляции для нелинейных форм вычисляется с помощью теоремы о разложении дисперсий по формуле:
где G 2 (y) – это общая дисперсия зависимой переменной;
σ 2 (y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:
δ 2 (y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:
Также индекс корреляции для нелинейных форм можно рассчитать с помощью теоремы о разложении сумм квадратов по формуле:
где RSS (Regression Sum Square) – сумма квадратов объяснённой регрессии:
ESS (Error Sum Square) – сумма квадратов остатков модели множественной регрессии с n независимыми переменными:
TSS (TotalSumSquare) – общая сумма квадратов модели множественной регрессии с n независимыми переменными:
Индекс корреляции для нелинейных форм связи изменяется в пределах от нуля до единицы. С его помощью нельзя охарактеризовать направление связи между результативной и факторными переменными. Чем ближе значение индекса корреляции для нелинейных форм связи к единице, тем сильнее взаимосвязь между результативной и независимыми переменными, и наоборот, чем ближе значение индекса корреляции для нелинейных форм связи к нулю, тем слабее взаимосвязь между результативной и независимыми переменными.
Индексом детерминации называется квадрат индекса корреляции для нелинейных форм связи.
Расчёт индекса детерминации с помощью теоремы о разложении дисперсий:
Расчёт индекса детерминации с помощью теоремы о разложении сумм квадратов:
Индекс детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.
Коэффициент множественной детерминации также называется количественной характеристикой объяснённой построенной моделью регрессии дисперсии результативной переменной. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.
45. Показатели корреляции и детерминации для нелинейных моделей регрессии
45. Показатели корреляции и детерминации для нелинейных моделей регрессии
Индексом корреляции для нелинейных форм связи называется коэффициент корреляции, который вычисляется для оценки качества построенной нелинейной модели регрессии.
Индекс корреляции для нелинейных форм вычисляется с помощью теоремы о разложении дисперсий по формуле:
где G2(y) – это общая дисперсия зависимой переменной;
?2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:
?2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:
Также индекс корреляции для нелинейных форм можно рассчитать с помощью теоремы о разложении сумм квадратов по формуле:
где RSS (Regression Sum Square) – сумма квадратов объяснённой регрессии:
ESS (Error Sum Square) – сумма квадратов остатков модели множественной регрессии с n независимыми переменными:
TSS (TotalSumSquare) – общая сумма квадратов модели множественной регрессии с n независимыми переменными:
Индекс корреляции для нелинейных форм связи изменяется в пределах от нуля до единицы. С его помощью нельзя охарактеризовать направление связи между результативной и факторными переменными. Чем ближе значение индекса корреляции для нелинейных форм связи к единице, тем сильнее взаимосвязь между результативной и независимыми переменными, и наоборот, чем ближе значение индекса корреляции для нелинейных форм связи к нулю, тем слабее взаимосвязь между результативной и независимыми переменными.
Индексом детерминации называется квадрат индекса корреляции для нелинейных форм связи.
Расчёт индекса детерминации с помощью теоремы о разложении дисперсий:
Расчёт индекса детерминации с помощью теоремы о разложении сумм квадратов:
Индекс детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.
Коэффициент множественной детерминации также называется количественной характеристикой объяснённой построенной моделью регрессии дисперсии результативной переменной. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Схемы психологической детерминации
Схемы психологической детерминации индивидуальные или обобщенные представления в графической форме о причинно-следственных отношениях между особенностями в поведении субъекта и психологическими факторами, которые могли бы обусловить их появление. Содержание
СЪЕМКА МОДЕЛЕЙ
СЪЕМКА МОДЕЛЕЙ При съемке женской фигуры в подавляющем большинстве случаев модель должна выбрать в качестве опоры только одну ногу.У женской фигуры модели не должно быть прямых линий и углов. Нежелательно, чтобы модель стояла прямо, строго вертикально держа
35. Комплексные показатели и показатели рыночной активности
35. Комплексные показатели и показатели рыночной активности Одной из версий комплексных показателей являются «Z счета», метод расчета которых впервые был предложен Э. Альтманом. «Z счета» используются для измерения вероятности банкротства фирмы. При вычислении «Z
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
23. Проверка гипотезы о значимости парного коэффициента корреляции
23. Проверка гипотезы о значимости парного коэффициента корреляции Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости парного коэффициента корреляции между результативной
30. Частные коэффициенты корреляции для линейной модели регрессии с двумя факторными переменными
30. Частные коэффициенты корреляции для линейной модели регрессии с двумя факторными переменными Частные коэффициенты корреляции используются для оценки зависимости между результативной переменной и одной из факторных переменных при условии постоянства всех
31. Частные коэффициенты корреляции для модели множественной регрессии с тремя и более факторными переменными
31. Частные коэффициенты корреляции для модели множественной регрессии с тремя и более факторными переменными Частные коэффициенты корреляции для модели множественной регрессии с тремя и более факторными переменными позволяют определить степень зависимости между
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
33. Коэффициент множественной корреляции. Коэффициент множественной детерминации
33. Коэффициент множественной корреляции. Коэффициент множественной детерминации Если частные коэффициенты корреляции модели множественной регрессии оказались значимыми, т. е. между результативной переменной и факторными модельными переменными действительно
34. Проверка гипотезы о значимости частного и множественного коэффициентов корреляции
34. Проверка гипотезы о значимости частного и множественного коэффициентов корреляции Предположим, что по данным выборочной совокупности была построена линейная модель множественной регрессии. Задача состоит в проверке значимости частных и множественного
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
42. Метод наименьших квадратов для моделей регрессии, нелинейных по факторным переменным
42. Метод наименьших квадратов для моделей регрессии, нелинейных по факторным переменным Если модель регрессии является нелинейной по факторным переменным или нелинейной по оцениваемым коэффициентам, но внутренне линейной, то неизвестные коэффициенты данных моделей
43. Метод наименьших квадратов для моделей регрессии, нелинейных по оцениваемым коэффициентам
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
37. Метод корреляции трендов
37. Метод корреляции трендов В прогнозировании методы экстраполяционных трендов дополняются методами корреляции трендов, в рамках которых исследуется связь между различными тенденциями в целях установления их взаимного влияния и, следовательно, повышения качества
Коэффициент детерминации что измеряет — формула
Суть состоит в следующем: этот показатель измеряет меру зависимости вариации одной величины от многих других. Он применяется для оценки качества линейной регрессии.
Формула расчета:
Детерминация, что это такое — определение
Коэффициент детерминации – часть дисперсии переменной (зависимой), которая обуславливается конкретной моделью зависимости. Так эта единица поможет вычесть долю необъясненной дисперсии в дисперсии зависимой переменной.
Данный показатель может принимать значения в пределах от 0 до 1. Чем его значение ближе к 1, тем связаннее результативный признак с исследуемыми факторами.
Т.к. преступление является результатом связи поведения и личностных качеств, этот показатель в деятельности заинтересованных органов рассчитывается для оценки качества преступного поведения, дает представление, что послужило вероятностной причиной преступления, что является мотивацией, какие этому были причины и условия.
Коэффициент детерминации, что показывает?
Этот коэффициент показывает варианты результативного признака от влияния факторного признака, он тесно связан с числом корреляции. Если связь отсутствует, то показатель равняется нулю, при ее наличии – единице.
Есть определение детерминизма как принципа устройства мира. Основой этого представления является взаимосвязанность всех явления. Это учение отрицает существование вещей вне взаимосвязи с миром.
Противоположностью является индетерминизм, он связан с отрицанием объективных отношений детерминации, или отрицанием причинности.
Генетический детерминизм – вера в то, что любой организм развивается под генетическим контролем.
Под детерминантами преступности в криминологии понимают социальные явления, действия которых могут вызвать преступность.
С помощью расчетов такого рода можно оценить вероятностное социокультурное влияние различных факторов на развитие личности и предположить, как себя будет вести человек, например, в деловом общении, объективно оценить, подходит ли он для государственного управления, или воинской службы.
Так же коэффициент определяет, правильно ли выбран индекс для подсчета коэффициентов бета и альфа. Если в % цифра ниже 75 к определенному индексу, значения бета и альфа к нему будут некорректны.
Индекс детерминации
Индекс детерминации – это квадрат инд. корреляции нелинейных связей. Этим значением характеризуют, на какое количество процентов моделью регрессии объясняются варианты показателей результативной переменной по отношению к своему среднему уровню.
Формула
Показатель можно рассчитать при помощи теоремы разложения сумм квадратов. Формула следующая:

Коэффициент детерминации скорректированный
Суть данного понятия состоит в следующем: этот индекс показывает долю дисперсии (общей) результативной переменной, объясняющей вариантами факторных переменных, включаемых в модель регрессии: (с увеличением, уменьшением).
Скорректированный показатель детерминации учитывает при оценке модели соотношение кол-ва наблюдений и кол-ва оцениваемых параметров модели.
Данный показатель применим для решения задач двух видов:
Эмпирический коэффициент детерминации
Характеристика. Эмпирический коэффициент объясняет долю в дисперсии, приходящуюся на дисперсию, которая обусловлена влиянием вариаций условия, которое было положенного в основу группировки.