инфиксная и постфиксная формы записи
Инфиксные, префиксные и постфиксные выражения¶
Когда вы записываете арифметическое выражение вроде B * C, то его форма предоставляет вам достаточно информации для корректной интерпретации. В данном случае мы знаем, что переменная B умножается на переменную C, поскольку оператор умножения * находится в выражении между ними. Такой тип записи называется инфиксной, поскольку оператор расположен между (in between) двух операндов, с которыми он работает.
Рассмотрим другой инфиксный пример: A + B * C. Операторы + и * по-прежнему располагаются между операндами, но тут уже есть проблема. С какими именно операндами они будут работать? + работает с A и B или * принимает B и C? Выражение выглядит неоднозначно.
Фактически, вы можете читать и писать выражения такого типа долгое время, и они не будут вызывать у вас вопросов. Причина в том, что вы кое-что знаете о + и *. Каждый оператор имеет свой приоритет. Операторы с высоким приоритетом используются прежде операторов с низким. Единственной вещью, которая может изменить порядок приоритетов, являются скобки. Для арифметических операций умножение и деление стоят выше сложения и вычитания. Если появляются два оператора одинакового приоритета, то используются порядок слева направо, или их ассоциативность.
Давайте интерпретируем вызвавшее затруднение выражение A + B * C, используя приоритет операторов. B и C перемножаются первыми, затем к результату добавляется A. (A + B) * C заставит выполнить сложение A и B перед умножением. В выражении A + B + C по очерёдности (через ассоциативность) первым будет вычисляться самый левый +.
Хотя это очевидно для вас, помните: компьютер нуждается в точном знании того, как и в какой последовательности вычисляются операторы. Одним из способов записи выражения, гарантирующим, что не возникнет путаницы по отношению к порядку операций, является создание того, что называется выражением с полностью расставленными скобками. Такой тип выражения использует пару скобок для каждого оператора. Скобки диктуют порядок операций, так что здесь не возникает многозначности. Так же отпадает необходимость помнить правила расстановки приоритетов.
Выражение A + B * C + D может быть переписано как ((A + (B * C)) + D) с целью показать, что умножение происходит в первую очередь, а затем следует крайнее левое сложение. A + B + C + D перепишется в (((A + B) + C) + D), поскольку операции сложения ассоциируются слева направо.
Существует ещё два очень важных формата выражений, которые на первый взгляд могут показаться вам неочевидными. Рассмотрим инфиксную запись A + B. Что произойдёт, если мы поместим оператор перед двумя операндами? Результирующее выражение будет + A B. Также мы можем переместить оператор в конец, получив A B +. Всё это выглядит несколько странным.
A + B * C в префиксной нотации можно переписать как + A * B C. Оператор умножения ставится непосредственно перед операндами B и C, указывая на приоритет * над +. Затем следует оператор сложения перед A и результатом умножения.
В постфиксной записи выражение выглядит как A B C * +. Порядок операций вновь сохраняется, поскольку * находится непосредственно после B и C, обозначая, что он имеет приоритет выше следующего +. Хотя операторы перемещаются и теперь находятся до или после соответствующих операндов, порядок последних по отношению друг к другу остаётся в точности таким, как был.
| Инфиксная запись | Префиксная запись | Постфиксная запись |
|---|---|---|
| A + B | + A B | A B + |
| A + B * C | + A * B C | A B C * + |
А сейчас рассмотрим инфиксное выражение (A + B) * C. Напомним, что в этом случае запись требует наличия скобок для указания выполнить сложение перед умножением. Однако, когда A + B записывается в префиксной форме, то оператор сложения просто помещается перед операндами: + A B. Результат этой операции является первым операндом для умножения. Оператор умножения перемещается в начало всего выражения, давая нам * + A B C. Аналогично, в постфиксной записи A B + явно указывается, что первым происходит сложение. Умножение может быть выполнено для получившегося результата и оставшегося операнда C. Соответствующим постфиксным выражением будет A B + C *.
Рассмотрим эти три выражения ещё раз (см. таблицу 3). Происходит что-то очень важное. Куда ушли скобки? Почему они не нужны нам в префиксной и постфиксной записи? Ответ в том, что операторы больше не являются неоднозначными по отношению к своим операндам. Только инфиксная запись требует дополнительных символов. Порядок операций внутри префиксного и постфиксного выражений полностью определён позицией операторов и ничем иным. Во многом именно это делает инфиксную запись наименее желательной нотацией для использования.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| (A + B) * C | * + A B C | A B + C * |
Таблица 4 демонстрирует некоторые дополнительные примеры инфиксных выражений и эквивалентных им префиксных и постфиксных записей. Убедитесь, что вы понимаете, почему они эквивалентны с точки зрения порядка выполнения операций.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| A + B * C + D | + + A * B C D | A B C * + D + |
| (A + B) * (C + D) | * + A B + C D | A B + C D + * |
| A * B + C * D | + * A B * C D | A B * C D * + |
| A + B + C + D | + + + A B C D | A B + C + D + |
Преобразование инфиксного выражения в префиксное и постфиксное¶
До сих пор мы использовали специальные методы для преобразования между инфиксными выражениями и эквивалентными им префиксной и постфикской записями. Как вы можете ожидать, существуют алгоритмические способы выполнения таких преобразований, позволяющие корректно трансформировать любое выражение любой сложности.
Первой из рассматриваемых нами техник будет использование идеи полной расстановки скобок в выражении, рассмотренной нами ранее. Напомним, что A + B * C можно записать как (A + (B * C)), чтобы явно показать приоритет умножения перед сложением. Однако, при более близком рассмотрении вы увидите, что каждая пара скобок также отмечает начало и конец пары операндов с соответствующим оператором по середине.
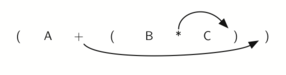
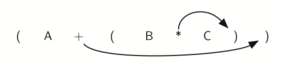
Взгляните на правую скобку в подвыражении (B * C) выше. Если мы передвинем символ умножения с его позиции и удалим соответствующую левую скобку, получив B C *, то произойдёт конвертирование подвыражение в постфиксную нотацию. Если оператор сложения тоже передвинуть к соответствующей правой скобке и удалить связанную с ним левую скобку, то результатом станет полностью постфиксное выражение (см. рисунок 6).
Рисунок 6: Перемещение операторов вправо для постфиксной записи
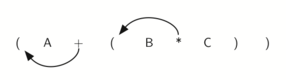
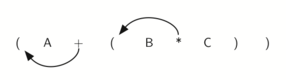
Если мы сделаем тоже самое, но вместо передвижения символа на позицию к правой скобке, сдвинем его к левой, то получим префиксную нотацию (см. рисунок 7). Позиция пары скобок на самом деле является ключом к окончательной позиции заключённого между ними оператора.
Рисунок 7: Перемещение операторов влево для префиксной записи.
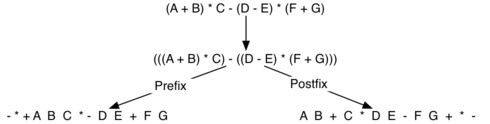
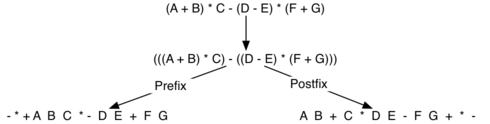
Рисунок 8: Преобразование сложного выражения к префиксной и постфиксной записи.
Обобщённое преобразование из инфиксного в постфиксный вид¶
Нам необходимо разработать алгоритм преобразования любого инфиксного выражения в постфиксное. Для этого посмотрим ближе на сам процесс конвертирования.
Рассмотрим ещё раз выражение A + B * C. Как было показано выше, его постфиксным эквивалентом является A B C * +. Мы уже отмечали, что операнды A, B и C остаются на своих местах, а местоположение меняют только операторы. Ещё раз взглянем на операторы в инфиксном выражении. Первым при проходе слева направо нам попадётся +. Однако, в постфиксном выражении + находится в конце, так как следующий оператор, *, имеет приоритет над сложением. Порядок операторов в первоначальном выражении обратен результирующему постфиксному выражению.
В процессе обработки выражения операторы должны где-то храниться, пока не найден их соответствующий правый операнд. Также порядок этих сохраняемых операторов может быть обратным (из-за их приоритета), как в данном примере со сложением и умножением. Поскольку оператор сложения, появляющийся перед оператором умножения, имеет более низкий приоритет, то он должен появиться после использования последнего. Из-за такого обратного порядка имеет смысл рассмотреть использование стека для хранения операторов до тех пор, пока они не понадобятся.
Что насчёт (A + B) * C? Напомним его постфиксный эквивалент: A B + C *. Повторимся, что обрабатывая это инфиксное выражение слева направо, первым мы встретим +. В этом случае, когда мы увидим *, + уже будет помещён в результирующее выражение, поскольку имеет преимущество над * в силу использования скобок. Теперь можно приступить к рассмотрению работы алгоритма преобразования. Когда мы видим левую скобку, то сохраняем её как знак, что должен будет появиться другой оператор с высоким приоритетом. Он будет ожидать, пока не появится соответствующая правая скобка, чтобы отметить его местоположение (вспомните технику полной расстановки скобок). После появления правой скобки оператор выталкивается из стека.
Поскольку мы сканируем инфиксное выражение слева направо, то для хранения операторов будем использовать стек. Это предоставит нам обратный порядок, который был отмечен в первом примере. На вершине стека всегда будет последний сохранённый оператор. Когда бы мы не прочитали новый оператор, мы должны сравнить его по приоритету с операторами в стеке (если таковые имеются).
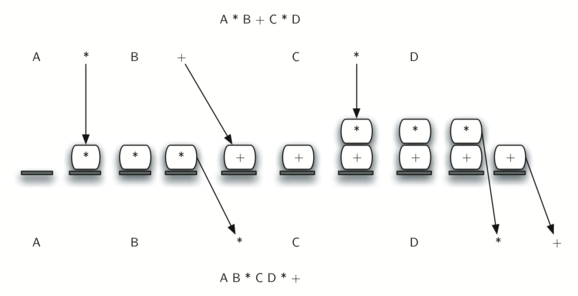
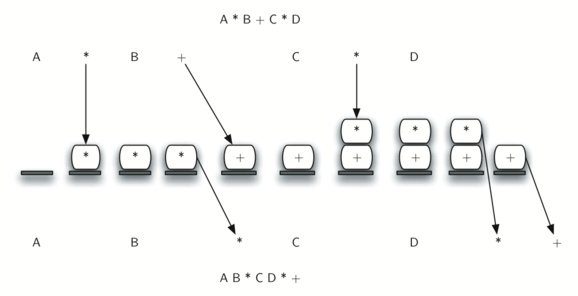
Рисунок 9 демонстрирует алгоритм преобразования, работающий над выражением A * B + C * D. Заметьте, что первый оператор * удаляется до того, как мы встречаем оператор +. Также + остаётся в стеке, когда появляется второй *, поскольку умножение имеет приоритет перед сложением. В конце инфиксного выражения из стека дважды происходит выталкивание, удаляя оба оператора и помещая + как последний элемент в результирующее постфиксное выражение.
Рисунок 9: Преобразование A * B + C * D в постфиксную запись
Чтобы закодировать алгоритм на Python, мы будем использовать словарь под именем prec для хранения значений приоритета операторов. Он связывает каждый оператор с целым числом, которые можно сравнивать с числами других операторов, как уровень приоритетности (для этого мы произвольно выбрали целые числа 3, 2 и 1). Левая скобка получит самое низкое значение. Таким образом, любой сравниваемый с ней оператор будет иметь приоритет выше и располагаться над ней. Строка 15 определяет, что операнды могут быть любыми символами в верхнем регистре или цифрами. Полная функция преобразования показана в ActiveCode 8.
Обратная польская запись
Два плюс два, умножить на два?
Не знаю как вы, но я в школе долго мучился, пытаясь разобраться с приоритетом операций и скобками. Потом, как и каждый начинающий программист, я мучился с приоритетом операций и скобками, когда писал собственный калькулятор. А оказалось, что все эти мучения были напрасны. Ведь существует прекрасный механизм, известный, как обратная польская запись. О том, что это такое и как с этим работать я и хочу вам рассказать.
В математике существует древняя традиция помещать оператор между операндами (x+y), а не после операндов (xy+). Форма с оператором между операндами называется инфиксной записью. Форма с оператором после операндов называется постфиксной, или обратной польской записью в честь польского логика Я. Лукасевича (1958), который изучал свойства этой записи.
Обратная польская запись имеет ряд преимуществ перед инфиксной записью при выражении алгебраических формул. Во-первых, любая формула может быть выражена без скобок. Во-вторых, она удобна для вычисления формул в машинах со стеками. В-третьих, инфиксные операторы имеют приоритеты, которые произвольны и нежелательны. Например, мы знаем, что ab+c значит (ab)+c, а не a(b+c), поскольку произвольно было определено, что умножение имеет приоритет над сложением. Но имеет ли приоритет сдвиг влево перед операцией И? Кто знает? Обратная польская запись позволяет устранить такие недоразумения.
Постановка задачи
На вход программы поступает выражение, состоящее из односимвольных идентификаторов и знаков арифметических действий. Требуется преобразовать это выражение в обратную польскую запись или же сообщить об ошибке.
Алгоритм перевода в обратную польскую запись
Существует несколько алгоритмов для превращения инфиксных формул в обратную польскую запись. Мы рассмотрим переработанный алгоритм, идее которого предложена Э. Дейкстра (E.W. Dijkstra). Предположим, что формула состоит из переменных, двухоперандных операторов +,-,*,/,^, а также левой и правой скобок. Чтобы отметить конец формулы, мы будем вставлять символ после её последнего символа и перед первым символом следующей формулы.
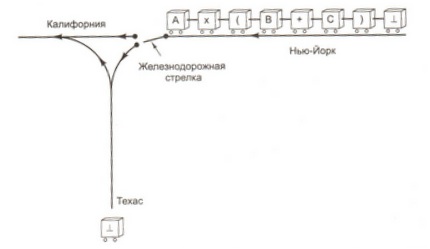
На рисунке схематично показана железная дорога из Нью-Йорка в Калифорнию с ответвлением, ведущим в Техас. Каждый символ формулы представлен одним вагоном. Поезд движется на запад (налево). Перед стрелкой каждый вагон должен останавливаться и узнавать, должен ли он двигаться прямо в Калифорнию, или ему нужно будет по пути заехать в Техас. Вагоны, содержащие переменные, всегда направляются в Калифорнию и никогда не едут в Техас. Вагоны, содержащие все прочие символы, должны перед прохождением стрелки узнавать о содержимом ближайшего вагона, отправившегося в Техас.
В таблице показана зависимость ситуации от того, какой вагон отправился в Техас последним и какой вагон находится у стрелки. Первый вагон (помеченный символом ⊥) всегда отправляется в Техас.
Числа соответствуют следующим ситуациям:
1. Вагон на стрелке отправляется в Техас
2. Последний вагон, направившийся в Техас, разворачивается и направляется в Калифорнию
3. Вагон, находящийся на стрелке, и последний вагон, отправившийся в Техас, угоняются и исчезают
4. Остановка. Символы, находящиеся на Калифорнийской ветке, представляют собой формулу в обратной польской записи, если читать слева направо
5. Остановка. Произошла ошибка. Изначальная формула была некорректно сбалансирована
После каждого действия производится новое сравнение вагона, находящегося у стрелки (это может быть тот же вагон, что и в предыдущем сравнении, а может быть следующий вагон), и вагона, который на данный момент последним ушёл на Техас. Этот процесс продолжается до тех пор, пока не будет достигнут шаг 4. Отметим, что линия на Техас используется как стек, где отправка вагона в Техас – это помещение элемента в стек, а разворот отправленного в Техас вагона в сторону Калифорнии – это выталкивание элемента из стека.
Порядок следования переменных в инфиксной и постфиксной записи одинаков. Однако порядок следования операторов не всегда один и тот же. В обратной польской записи операторы появляются в том порядке, в котором они будут выполняться.
Пример вычисления выражения в обратной польской записи
Обратная польская запись идеально подходит для вычисления формул на компьютере со стеком. Формула состоит из n символов, каждый из которых является либо операндом, либо оператором. Алгоритм для вычисления формулы в обратной польской записи с использованием стека прост. Нужно просто прочитать обратную польскую запись слева направо. Если встречается операнд, его нужно пометить в стек. Если встречается оператор, нужно выполнить заданную им операцию.
В качестве примера рассмотрим вычисление следующего выражения: (8+2*5)/(1+3*2-4). Соответствующая формула в обратной польской записи выглядит так: 825*+132*+4-/
Число на вершине стека – это правый операнд (а не левый). Это очень важно дл операций деления, вычитания и возведения в степень, поскольку порядок следования операндов в данном случае имеет значение (в отличие от операций сложения и умножения). Другими словами, операция деления действует следующим образом: сначала в стек помещается числитель, потом знаменатель, и тогда операция даёт правильный результат. Отметим, что преобразовать обратную польскую запись в машинный код очень легко: нужно просто двигаться по формуле в обратной польской записи, записывая по одной команде для каждого символа. Если символ является константой или переменной, нужно вписывать команду помещения этой константы или переменной в стек, если символ является оператором, нужно вписывать команду выполнения это операции. 
P.S. Исходные коды вы, как всегда, можете скачать на моём сайте, пока он не ляжет под хабраэффектом.
P.P.S. Теперь все могут написать свой калькулятор. С блэкджеком и скобками.
Инфиксные, префиксные и постфиксные выражения¶
Когда вы записываете арифметическое выражение вроде B * C, то его форма предоставляет вам достаточно информации для корректной интерпретации. В данном случае мы знаем, что переменная B умножается на переменную C, поскольку оператор умножения * находится в выражении между ними. Такой тип записи называется инфиксной, поскольку оператор расположен между (in between) двух операндов, с которыми он работает.
Рассмотрим другой инфиксный пример: A + B * C. Операторы + и * по-прежнему располагаются между операндами, но тут уже есть проблема. С какими операндами они будут работать? + работает с A и B или * принимает B и C? Выражение выглядит неоднозначно.
Фактически, вы можете читать и писать выражения такого типа долгое время, и они не будут вызывать у вас вопросов. Причина в том, что вы кое-что знаете о + и *. Каждый оператор имеет свой приоритет. Операторы с высоким приоритетом используются прежде операторов с низким. Единственной вещью, которая может изменить порядок приоритетов, являются скобки. Для арифметических операций умножение и деление стоят выше сложения и вычитания. Если появляются два оператора одинакового приоритета, то используются порядок слева направо или их ассоциативность.
Давайте интерпретируем вызвавшее затруднение выражение A + B * C, используя приоритет операторов. B и C перемножаются первыми, затем к результату добавляется A. (A + B) * C заставит выполнить сложение A и B перед умножением. В выражении A + B + C по очерёдности (через ассоциативность) первым будет вычисляться самый левый +.
Хотя это и может быть очевидным для вас, помните, что компьютер нуждается в точном знании того, как и в какой последовательности вычисляются операторы. Одним из способов записи выражения, гарантирующим, что не возникнет путаницы по отношению к порядку операций, является создание того, что называется выражением с полностью расставленными скобками. Такой тип выражения использует пару скобок для каждого оператора. Скобки диктуют порядок операций, так что здесь не возникает многозначности. Так же отпадает необходимость помнить правила расстановки приоритетов.
Выражение A + B * C может быть переписано как ((A + (B * C)) + D) с целью показать, что умножение происходит в первую очередь, а затем следует крайнее левое сложение. A + B + C + D перепишется в (((A + B) + C) + D), поскольку операции сложения ассоциируются слева направо.
Существует ещё два очень важных формата выражений, которые на первый взгляд могут показаться вам неочевидными. Рассмотрим инфиксную запись A + B. Что произойдёт, если мы поместим оператор перед двумя операндами? Результирующее выражение будет + A B. Также мы можем переместить оператор в конец, получив A B +. Всё это выглядит несколько странным.
A + B * C можно переписать как + A * B C в префиксной нотации. Оператор умножения ставится непосредственно перед операндами B и C, указывая на приоритет * над +. Затем следует оператор сложения перед A и результатом умножения.
В постфиксной записи выражение выглядит как A B C * +. Порядок операций вновь сохраняется, поскольку * находится непосредственно после B и C, обозначая, что он имеет приоритет выше следующего +. Хотя операторы перемещаются и теперь находятся до или после соответствующих операндов, порядок последних по отношению друг к другу остаётся в точности таким, как был.
| Инфиксная запись | Префиксная запись | Постфиксная запись |
|---|---|---|
| A + B | + A B | A B + |
| A + B * C | + A * B C | A B C * + |
А сейчас рассмотрим инфиксное выражение (A + B) * C. Напомним, что в этом случае запись требует наличия скобок для указания выполнить сложение перед умножением. Однако, когда A + B записывается в префиксной форме, то оператор сложения просто помещается перед операндами: + A B. Результат этой операции является первым операндом для умножения. Оператор умножения перемещается в начало всего выражения, давая нам * + A B C. Аналогично, в постфиксной записи A B + явно указывается, что первым происходит сложение. Умножение может быть выполнено для получившегося результата и оставшегося операнда C. Соответствующим постфиксным выражением будет A B + C *.
Рассмотрим эти три выражения ещё раз (см. Таблицу 3). Происходит что-то очень важное. Куда ушли скобки? Почему они не нужны нам в префиксной и постфиксной записи? Ответ в том, что операторы больше не являются неоднозначными по отношению к своим операндам. Только инфиксная запись требует дополнительных символов. Порядок операций внутри префиксного и постфиксного выражений полностью определён позицией операторов и ничем иным. Во многом именно это делает инфиксную запись наименее желательной нотацией для использования.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| (A + B) * C | * + A B C | A B + C * |
Таблица 4 демонстрирует некоторые дополнительные примеры инфиксных выражений и эквивалентных им префиксных и постфиксных записей. Убедитесь, что вы понимаете, почему они эквивалентны с точки зрения порядка выполнения операций.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| A + B * C + D | + + A * B C D | A B C * + D + |
| (A + B) * (C + D) | * + A B + C D | A B + C D + * |
| A * B + C * D | + * A B * C D | A B * C D * + |
| A + B + C + D | + + + A B C D | A B + C + D + |
Преобразование инфиксного выражения в префиксное и постфиксное¶
До сих пор мы использовали специальные методы для преобразования между инфиксными выражениями и эквивалентными им префиксной и постфикской записями. Как вы можете ожидать, существуют алгоритмические способы выполнения таких преобразований, позволяющие корректно трансформировать любое выражение любой сложности.
Первой из рассматриваемых нами техник будет использование идеи полной расстановки скобок в выражении, рассмотренной нами ранее. Напомним, что A + B * C можно записать как (A + (B * C)), чтобы явно показать приоритет умножения перед сложением. Однако, при более близком рассмотрении вы увидите, что каждая пара скобок также отмечает начало и конец пары операндов с соответствующим оператором по середине.
Взгляните на правую скобку в подвыражении (B * C) выше. Если мы передвинем символ умножения с его позиции и удалим соответствующую левую скобку, получив B C *, то полученный эффект конвертирует подвыражение в постфиксную нотацию. Если оператор сложения тоже передвинуть к соответствующей правой скобке и удалить связанную с ним левую скобку, то результатом станет полное постфиксное выражение (см. Изображение 6).
Рисунок 6: Перемещение операторов вправо для постфиксной записи
Если мы сделаем тоже самое, но вместо передвижения символа на позицию к правой скобке, сдвинем его к левой, то получим префиксную нотацию (см. Рисунок 7). Позиция пары скобок на самом деле является ключом к окончательной позиции заключённого между ними оператора.
Рисунок 7: Перемещение операторов влево для префиксной записи.
Рисунок 8: Преобразование сложного выражения к префиксной и постфиксной записи.
Обобщённое преобразование из инфиксного в постфиксный вид¶
Нам необходимо разработать алгоритм преобразования любого инфиксного выражения в постфиксное. Для этого посмотрим ближе на сам процесс конвертирования.
Рассмотрим ещё раз выражение A + B * C. Как было показано выше, его постфиксным эквивалентом является A B C * +. Мы уже отмечали, что операнды A, B и C остаются на своих местах, а местоположение меняют только операторы. Ещё раз взглянем на операторы в инфиксном выражении. Первым при проходе слева направо нам попадётся +. Однако, в постфиксном выражении + находится в конце, так как следующий оператор, *, имеет приоритет над сложением. Порядок операторов в первоначальном выражении обратен результирующему постфиксному выражению.
В процессе обработки выражения операторы должны где-то храниться, пока не найден их соответствующий правый операнд. Также порядок этих сохраняемых операторов может быть обратным (из-за их приоритета). Это случай со сложением и умножением в данном примере. Поскольку оператор сложения, появляющийся перед оператором умножения, имеет более низкий приоритет, то он должен появиться после использования оператора умножения. Из-за такого обратного порядка имеет смысл рассмотреть использование стека для хранения операторов до тех пор, пока они не понадобятся.
Что насчёт (A + B) * C? Напомним, что его постфиксный эквивалент A B + C *. Повторимся, что обрабатывая это инфиксное выражение слева направо, первым мы встретим +. В этом случае, когда мы увидим *, + уже будет помещён в результирующее выражение, поскольку имеет преимущество над * в силу использования скобок. Теперь можно начать рассматривать, как будет работать алгоритм преобразования. Когда мы видим левую скобку, мы сохраняем её как знак, что должен будет появиться другой оператор с высоким приоритетом. Он будет ожидать, пока не появится соответствующая правая скобка, чтобы отметить его местоположение (вспомните технику полной расстановки скобок). После появления правой скобки оператор выталкивается из стека.
Поскольку мы сканируем инфиксное выражение слева направо, то будем использовать стек для хранения операторов. Это предоставит нам обратный порядок, который мы отмечали в первом примере. На вершине стека всегда будет последний сохранённый оператор. Когда бы мы не прочитали новый оператор, мы должны сравнить его по приоритету с операторами в стеке (если таковые имеются).
Рисунок 9 демонстрирует алгоритм преобразования, работающий над выражением A * B + C * D. Заметьте, что первый оператор * удаляется до того, как мы встречаем оператор +. Также + остаётся в стеке, когда появляется второй *, поскольку умножение имеет приоритет перед сложением. В конце инфиксного выражения из стека дважды происходит выталкивание, удаляя оба оператора и помещая + как последний элемент в результирующее постфиксное выражение.
Рисунок 9: Преобразование A * B + C * D в постфиксную запись
Для того, чтобы закодировать алгоритм на Python, мы будем использовать словарь под именем prec для хранения значений приоритета операторов. Он связывает каждый оператор с целым числом, которые можно сравнивать с другими операторами как уровень приоритетности (мы произвольно выбрали для этого целые числа 3, 2 и 1). Левая скобка получит самое низкое значение. Таким образом, любой сравниваемый с ней оператор будет иметь приоритет выше и располагаться над ней. Строка 15 определяет, что операнды могут быть любыми символами в верхнем регистре или цифрами. Полная функция преобразования показана в ActiveCode 8.