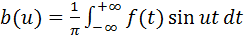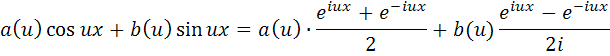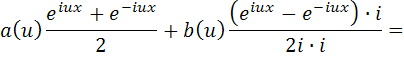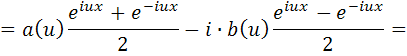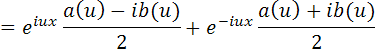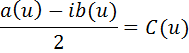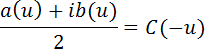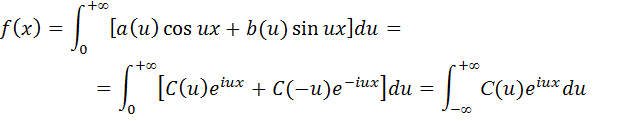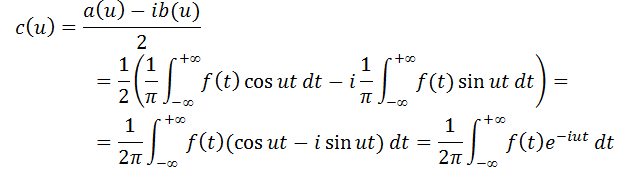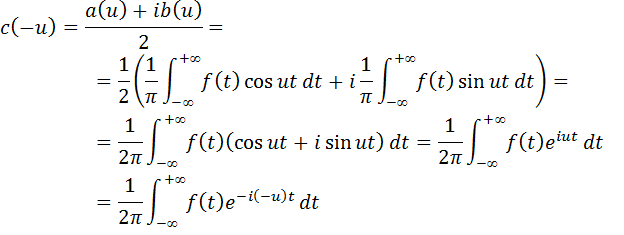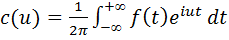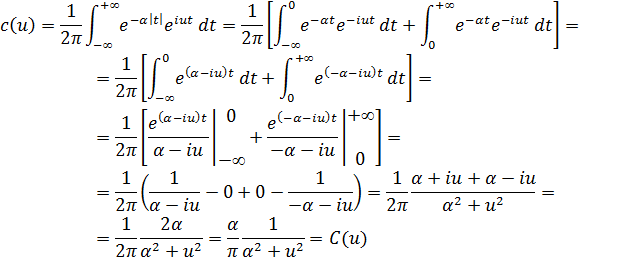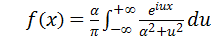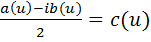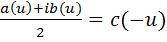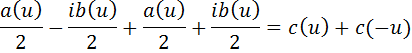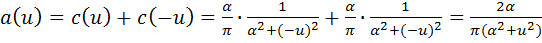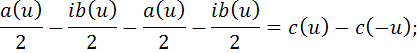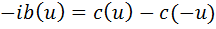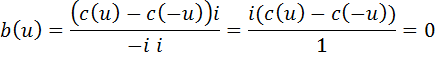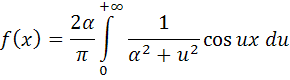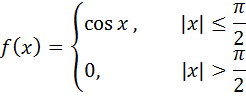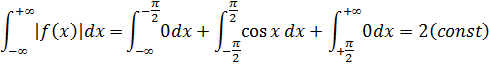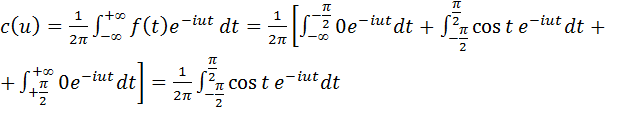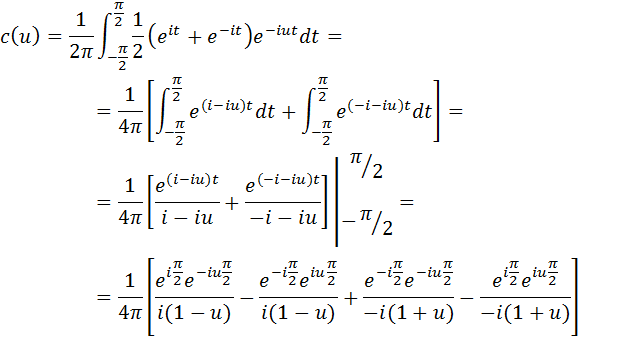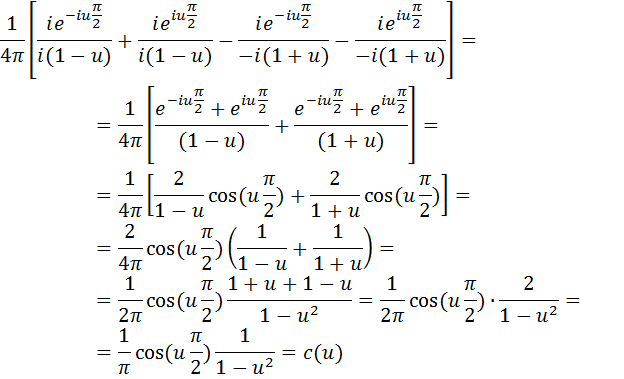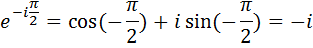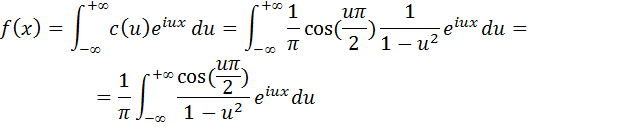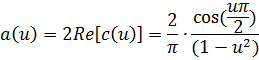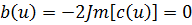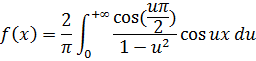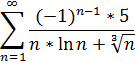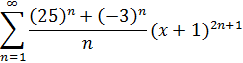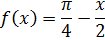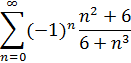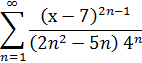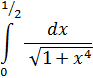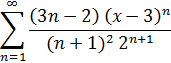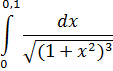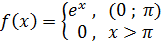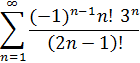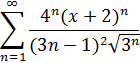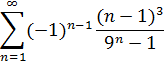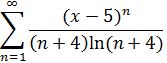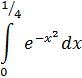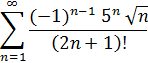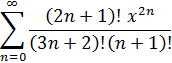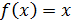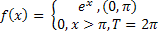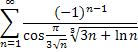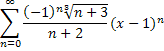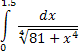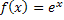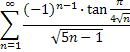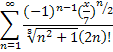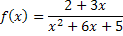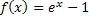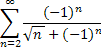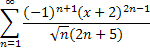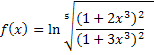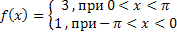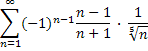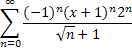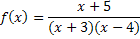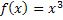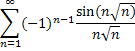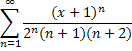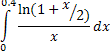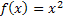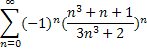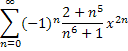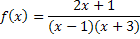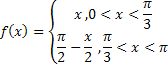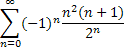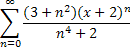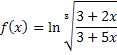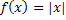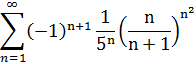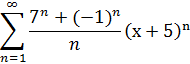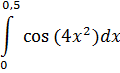интеграл фурье в комплексной форме

Комплексная форма интеграла Фурье

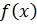
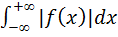
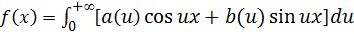
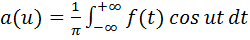
Пусть функция может быть представлена интегралом Фурье (функция отвечает условиям Дирихле и абсолютно интегрируема, то есть — сходится). Запишем для этой функции в действительной форме интеграл Фурье:
, где

;

Используя формулы Эйлера (4.14) и (4.15), преобразуем подынтегральное выражение (5.5):

Домножим числитель и знаменатель второй дроби на мнимую единицу i:

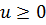
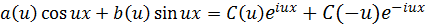
при . Тогда подынте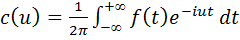гральная функция в выражении (5.5) запишется в виде:

и

Т.е. (5.9)

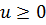
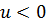
Равенство (5.9) получено при условии, что , но можно показать, что формула (5.9) справедлива и при .

То есть равенство (5.9) справедливо при всех действительных значениях u. Окончательно можно записать комплексную форму интеграла Фурье:

при

(5.10)

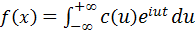
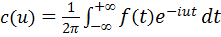
Пример: записать интеграл Фурье в комплексной форме для функции

( )

, где

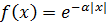
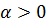
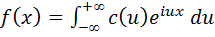
Вычислим для заданного примера коэффициент c(u):

Итак, интеграл Фурье в комплексной форме для заданной функции имеет следующий вид:

Перейдем от комплексной формы интеграла Фурье к действительной форме интеграла Фурье для этой же функции.

Сложим первое и второе равенства, тогда

Вычтем из первого равенства второе, тогда:

Тогда коэффициент b(u) соответственно равен:

Интеграл Фурье для данной функции в обычной, действительной форме примет вид:

Пример: представить интегралом Фурье в комплексной форме функцию

— кусочно-гладкая и кусочно-монотонная, абсолютно интегрируемая функция, так как

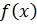
то есть данную функцию можно представить с помощью интеграла Фурье:

, где

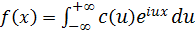
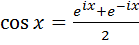
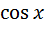
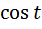
По формуле Эйлера , в нашем случае меняем на .

При вычислениях учитывали, что

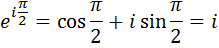
Тогда комплексная форма интеграла Фурье для данной функции примет вид:

Перейдем к действительной форме интеграла Фурье для той же функции:

Действительная форма интеграла Фурье для данной функции примет вид:

Приложение.

Варианты индивидуальных домашних заданий.

Вариант № 1

1. Исследовать ряд на сходимость.

2. Найти область сходимости степенного ряда.

3. Разложить в ряд Тейлора по степеням “ x “ функцию

, найти интервал сходимости ряда к .

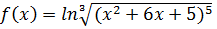
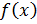
4. Разложить в ряд Фурье на интервале (0 ; π) по косинусам функцию:

Вариант № 2

1. Исследовать ряд на сходимость.

2. Найти область сходимости степенного ряда.

3. Вычислить приближенно

учитывая 2 члена разложения подынтегральной функции. Оценить погрешность приближения.

4. Разложить в ряд Фурье функцию по синусам:

0

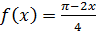
3. Вычислить с точностью до 0.001

4. Разложить в ряд Фурье функцию по синусам.

Вариант № 4

1. Исследовать ряд на сходимость.

2. Найти область сходимости степенного ряда.

3. Разложить в ряд Маклорена функцию

, найти интервал сходимости ряда к .

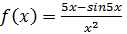
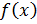
4. Разложить в ряд Фурье функцию:

по синусам.

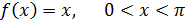
Вариант № 5

1. Исследовать ряд на сходимость.

2. Найти область сходимости степенного ряда.

3. Вычислить с точностью до 0,001

4. Разложить в ряд Фурье функцию:

по синусам.

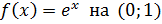
Вариант № 6

1. Исследовать ряд на сходимость.

2. Найти область сходимости степенного ряда.

3. Разложить в ряд Маклорена функцию

, найти интервал сходимости ряда к .

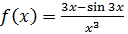
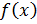
4. Разложить в ряд Фурье

4. Разложить функцию в ряд Фурье по косинусам

Вариант №10

1. Исследовать ряд на сходимость

2. Найти область сходимости степенного ряда

3. Вычислить с точностью до 0.001

4. Разложить в ряд Фурье функцию на отрезке (0; 1) по косинусам

Вариант № 11

1. Исследовать ряд на сходимость

2. Найти область сходимости степенного ряда

3. Разложить в ряд Тейлора по степеням (х-2) функцию

найти интервал сходимость к f(x)

4. Разложить в ряд Фурье функцию на интервале (0;2π)

Вариант № 12

1. Исследовать ряд на сходимость

2. Найти область сходимости степенного ряда

3. Разложить функцию в ряд Тейлора по степеням X, определить интервал сходимости

4. Разложить в ряд Фурье периодическую функцию с 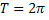, если:

Вариант №13

1. Исследовать ряд на сходимость

2. Найти область сходимости степенного ряда

3. Разложить в ряд Тейлора по степеням (х+1) функцию

найти интервал сходимость к f(x)

4. Представить функцию рядом Фурье на интервале (-π, π)

Вариант №14

1. Исследовать ряд на сходимость

2. Найти область сходимости степенного ряда

3. Вычислить с точностью до 0.001

4. Разложить функцию в ряд Фурье на интервале (0, π) по синусам

Вариант №15

1. Исследовать ряд на сходимость числовой ряд

2. Найти область сходимости степенного ряда

3. Разложить в ряд Тейлора по степеням X функцию

найти интервал сходимости ряда к f(x).

4. Представить рядом Фурье периодическую функцию с Т=π

Вариант №16

1. Исследовать числовой ряд на сходимость

2. Найти область сходимости степенного ряда

3. Разложить в ряд Тейлора по степеням X функцию

найти интервал сходимость к f(x).

4. Представить рядом Фурье функцию на интервале (-3, 3).

Вариант № 17

1. Исследовать числовой ряд на сходимость:

2. Найти область сходимости степенного ряда:

3. Вычислить с точностью до 0,001:

4. Представить рядом Фурье функцию: 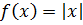на интервале (-1

Источник

Преобразование Фурье. Интеграл Фурье. Комплексная форма интеграла

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

исследования задач математической физики является метод интегральных преобразований. Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(x) называется функция где К(х, ш) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существуете собственном или несобственном смысле). §1.

Интеграл Фурье Всякая функция f(x), которая на отрезке [-f, I] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом Коэффициенты а*, и 6„ ряда (1) определяются по формулам Эйлера—Фурье: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения Ряд в правой части равенства (1) можно записать в иной форме.

С этой целью внесем в него из формул (2) значения коэффициентов а» и оп, подведем под знаки интегралов cos ^ х и sin х (что возможно, поскольку переменной интегрирования является т) О) и используем формулу для косинуса разности. Будем иметь Если функция/(ж) первоначально была определена на интервале числовой оси, большем, чем отрезок [-1,1] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-1,1] и продолжит се на всю числовую ось как периодическую функцию с периодом 21 (рис. 1).

Возможно вам будут полезны данные страницы:

Положим так, что Тогда сумма в правой части (3) примет вид В силу абсолютной сходимости интеграла эта сумма при больших I мало отличается от выражения которое напоминает интегральную сумму для функции переменного £ составленную для интервала (0, +оо) изменения Поэтому естественно ожидать, что при сумма (5) перейдет в интеграл Сдругой стороны, при фиксировано) из формулы (3) вытекает, что и мы получаем равенство Достаточное условие справедливости формулы (7) выражается следующей теоремой.

Теорема 1:

Если функция f(x) абсолютно интегрируема на всей числовой оси и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке [а, 6], то справедливо равенство При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции /(ж), значение интеграла в правой части (7) равно Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралом Фурье.

Это — интегральное преобразование функции /(г) на интервале (-оо,+оо) с ядром Используя интегральную формулу Фурье получаем Это так называемое обратное преобразование Фурье, дающее переход от F(£) к /(х). Иногда прямое преобразование Фурье задают так: Тогда обратное преобразование Фурье определится формулой Преобразование Фурье функции /(ж) определяют также следующим образом: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения.

Тогда, в свою очередь, При этом положение множителя ^ достаточно произвольно: он может входить либо в формулу (1″), либо в формулу (2″).

Полагая в (4) £ = 0, найдем С = F(0). В силу (3) имеем Известно, что В частности, для ) получаем, что Пример 2 (разред кокдемсетора через сопропиление). Рассмотрим функцию 4 Для спектрам ыюй функции F(£) получаем Отсюда (рис.2). Условие абсолютной интегри-руемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как ) = cos ж, f(x) = е1, для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.

Функция называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x) Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc(£). Иными словами, функции / и Fc являются взаимными косинус-преобразованиями. Определение. Функция называется синус-преобразованием Фурье функции f(x). Из (7) получаем, что для нечетной функции f(x) т.е. f и Fs являются взаимными синус-преобразованиями.

Пример 3 прамоугольный импульс:

Пусть f(t) — четная функция, определенная следующим образом: (рис. 3). Воспользуемся полученным результатом для вычисления интеграла В силу формулы (9) имеем Рис.3 0 0 В точке t = 0 функция f(t) непрерывна и равна единице. Поэтому из (12′) получим 2.2. Амплитудный и фазовый спектры интеграла Фурье Пусть периодическая с периодом 2т функция /(х) разлагается в ряд Фурье Это равенство можно записать в виде где — амплитуда колебания с частотой п, — фаза. На этом пути мы приходим к понятиям амплитудного и фазового спектров периодической функции.

Пример 4:

Найти амплитудный и фазовый спектры функции 4 Находим спектральную функцию Отсюда Графики этих функций изображены на рис. 4. §3. Свойства преобразования Фурье 1. Линейность. Если и G(0 — преобразования Фурье функций /(х) и д(х) соответственно, то при любых постоянных а и р преобразованием Фурье функции a f

Если функция f(x) имеет глад*«е абсолютно интефируемые производные до порядка m включительно и все они, как и сама функция f(x), стремятся к нулю при то, интегрируя по частям нужное число раз, получим Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину и тем самым упрощает задачуинтегрирования некоторых видов дифференциальных уравнений.

Нетрудно установить следующие свойства свертки: 1) линейность: 2) коммутативность: §4. Приложения преобразования Фурье 1. Пусть Р(^) — линейный дифференциальный оператор порядка m с постоянными коэффициентами, Используя формулу для преобразования Фурье производных функции у(х), находим ‘ Рассмотрим дифференциальное уравнение где Р — введенный выше дифференциальный оператор. Предположим, что искомое решение у(х) имеет преобразование Фурье у (О. а функция f(x) имеет преобразование /(£)•

Это ограничение можно обойти, если ввести в рассмотрение так называемые обобщенные функции. Однако в ряде случаев преобразование Фурье все же применимо в своей классической форме. Пример. Найти решение а = а(х, t) уравнения (а = const), при начальных условиях Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник