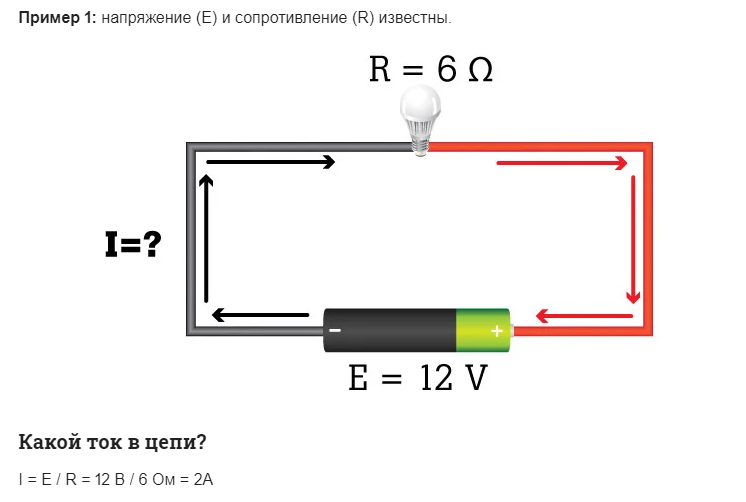
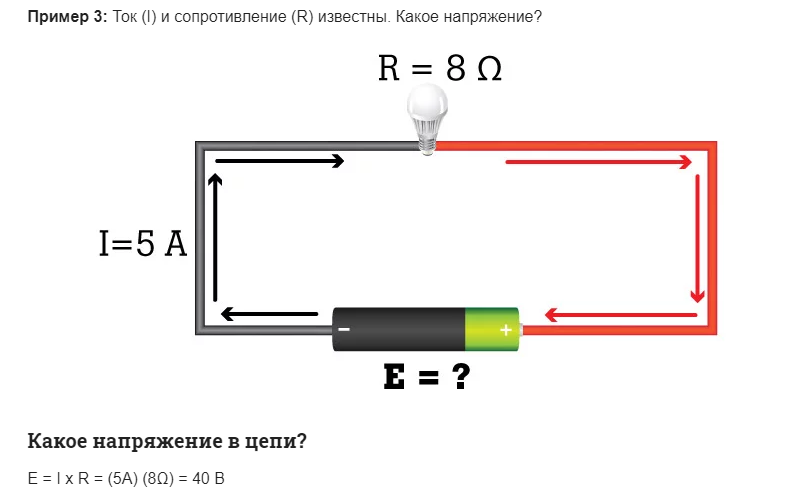
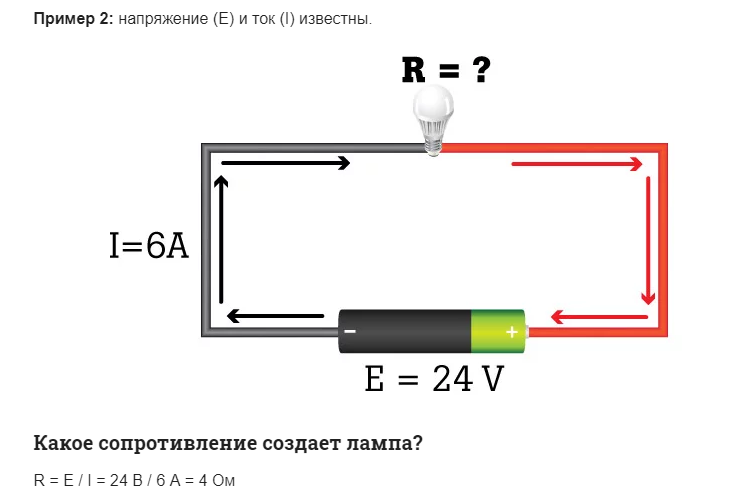
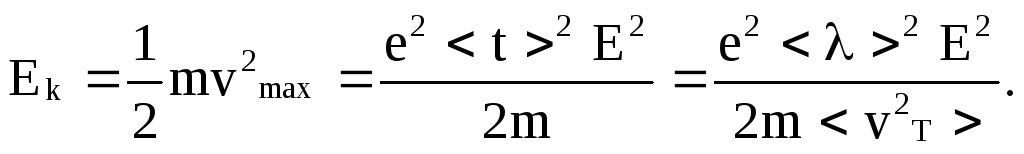интегральная и дифференциальная форма записи закона ома
Закон Ома в интегральной и дифференциальной форме
Понятие сопротивление доходчиво
Электрическое сопротивление — это величина, которая определяет способность проводника пропускать электрический ток. Полезно также освежить знания про электрический ток
Представить это проще всего, исходя из строения металлов.
По классической теории металл состоит из кристаллической решетки, а между структурными элементами этой решетки путешествуют свободные электроны.
Внешнее электрическое поле заставляет их перемещаться и образуется электрический ток, т.е. направленное упорядоченное движение частиц.
Решетка металла мешает им двигаться по своему объему. Электроны трутся об её узлы и не могут протиснуться. Вот это явление и образует сопротивление. Это «сила», которая мешает перемещению.
Ситуация аналогично ситечку на раковине. Вода проходит, но медленнее, чем проходила бы без ситечка.
Аналогичная ситуация присутствует во всех материалах, правда род и тип частичек может меняться. Тип строения тоже разный. Но условно можно принять, что всегда структура мешает им двигаться что в дереве, что в металле.
В некоторых телах вообще таких частичек не будет, там сопротивление бесконечное (некоторые виды резин, например).
Ну и из сказанного очевидно, что сопротивление будет зависеть от геометрических параметров проводника (т.е. площадь сечения S, длина l) и типа проводника (который тут описывается понятием удельное сопротивление и является табличной величиной). Ещё оно зависит от температуры (чем выше тем больше для большинства тел), но это мы совсем от самого закона уходим… Для задачек на закон Ома знаний уже вполне достаточно.
Формулировка закона Ома
В результате множества экспериментов Ом вывел зависимость, которая определяет связь между силой тока в проводнике, напряжением и тем самым сопротивлением, которое мы описали выше.
Звучит закон так: Cила тока на участке электрической цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна его сопротивлению
Напряжение — это «поток», который эти частицы несет. Вот вроде бы всё и увязали.
Если рассматривать цепь, то сопротивление по элементам распределяется согласно их техническим характеристикам и вычисляется согласно закону Ома. Т.е. мы не можем утверждать, что на каждом элементе есть одинаковое сопротивление.
Например, если в цепи с последовательным подключением две лампочки, т омы помним что сила тока во всей цепи при таком соединении одинаковая, а вот напряжение на элементах разное. Замеряем его на точках подключения лампочек, записываем и запихиваем в закон Ома. Вот всё и посчитали :)…
Закон Ома для участка цепи
Когда закон ома записан в такой форме, как мы привели выше, то он называется закон ома для участка цепи.
Почему для участка цепи? Для участка, потому что тут не учитывается сопротивление всей цепи. Можно измерить сопротивление на каждом участке исходя из приведенных характеристик.
Закон Ома для полной цепи
Полной цепью (в отличие от участка цепи, применительно к которому мы излагали всё выше) называется цепь с учетом источника тока.
Именно потому, что если мы представим себе электрическую цепь условно как систему труб для воды, то участок цепи это будет незамкнутый кусок трубы, а полная цепь — зацикленная система.
Из примера может показаться, что участок цепи есть незамкнутая в электрическом смысле цепь. Нет, пример приведен не для этого. И там, и там электрическая цепь замкнута.
Просто нам нужно обозначить, что без учета источника тока и его внутреннего сопротивления (r) цепь не полная, а расчёт не всегда способен учитывать все значимые характеристики.
Ну а внутреннее сопротивление, как вы наверное догадались — это то сопротивление, которым обладает источник тока. Да, току в цепи сложно проходить и через сам источник! Даже сам источник провоцирует энергетические потери. А вот считать его аналогично расчёту для участка цепи нельзя.
Получается, что в закон Ома добавится ещё и внутренне сопротивление. И всё! Ничего страшного.
Формулировка закона Ома для полной цепи немного изменится. Теперь у нас слово напряжение заменится словом ЭДС (электродвижущая сила), а слово сопротивление заменится суммой внешнего сопротивления цепи и внутреннего сопротивления источника тока. Ну и формула будет такая:
Добавилось понятие электродвижущая сила (ЭДС), обозначенная в формуле E прописное. Что это за зверь?
ЭДС — это, по сути дела, и есть напряжение.
Разница в том, что если мы опять сравним напряжение с напором воды в водопроводе, то напряжением будет являться разница напора между двумя произвольными точками в водопроводе, а ЭДС — это напор на насосе, который качает воду.
При использовании термина ЭДС мы вспоминаем, что у источника есть внутреннее сопротивление, как оно есть и у насоса, который препятствует движению воды через самого себя. Если же мы считали бы именно напряжение источника, то мы бы приняли, что система идеальная и источник движению тока сам не препятствует.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
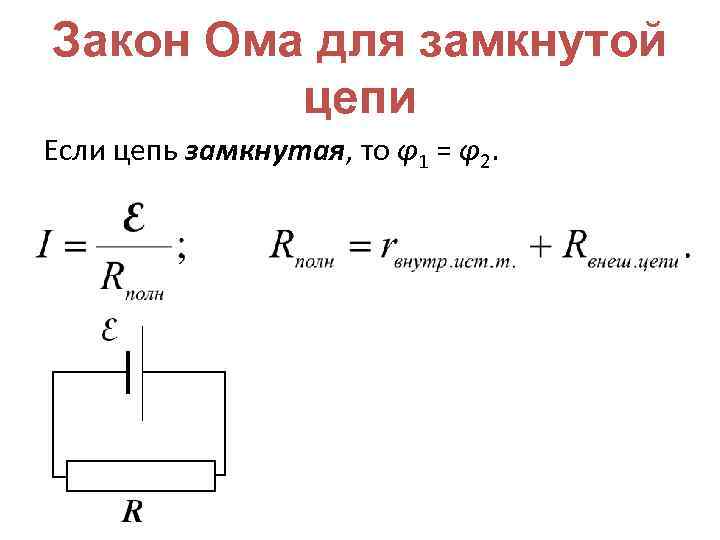
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Следствия закона Ома.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Закон Ома в интегральной форме для неоднородного участка цепи
Проинтегрируем получившееся соотношение на конкретном участке цепи постоянного тока между поперечными сечениями S1 и S2:
интегральный закон Ома для участка цепи
Мнемоническая диаграмма для закона Ома
Схема, иллюстрирующая три составляющие закона Ома
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления
U — электрическое напряжение;
I — сила тока;
P — электрическая мощность;
R — электрическое сопротивление
В соответствии с этой диаграммой формально может быть записано выражение:
которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.
В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:
Трактовка и пределы применимости закона Ома
Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.
В классическом приближении закон Ома можно вывести при помощи теории Друде:
Проводники и элементы, для которых соблюдается закон Ома, называются омическими.
Закон Ома может не соблюдаться:
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
Интересно почитать: инструкция как прозвонить транзистор.
Где и когда можно применять закон Ома?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Закон Ома в дифференциальной и интегральной форме
Закон Ома для участка цепи утверждает: сила тока I прямо пропорциональна напряжению U на участке цепи и обратно пропорциональна сопротивлению R
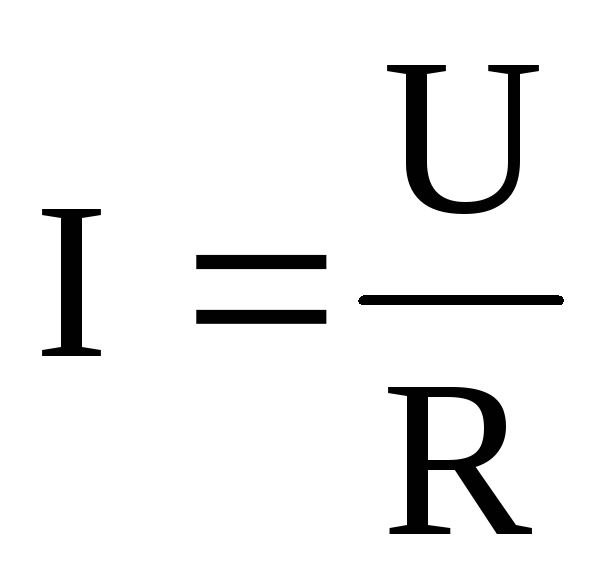
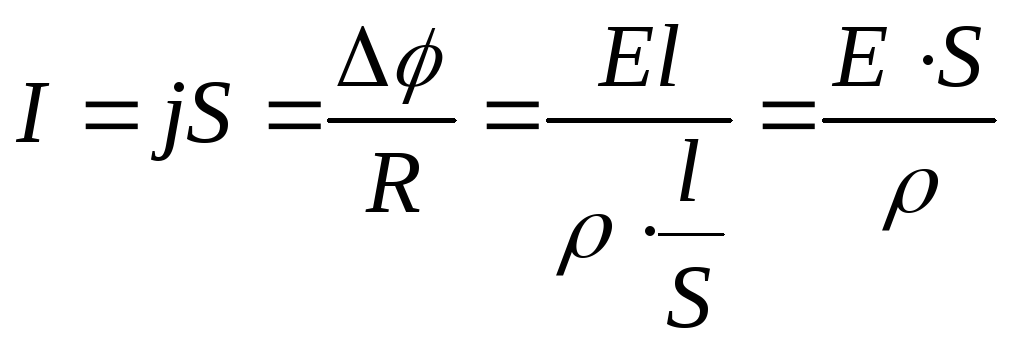
Отсюда 

Плотность тока в проводнике прямо пропорциональна напряженности электрического поля в нем.
Это есть выражение закона Ома в интегральной форме.
Закон Джоуля-Ленца в дифференциальной и интегральной форме
Опытом установлено, что если в проводнике течет ток, то работа сторонних сил расходуется на его нагревание. Предположим, что на концах участка проводника имеется разность потенциалов U = φ1 – φ2.
Тогда работа по переносу заряда q на этом участке равна
Если ток постоянный, то 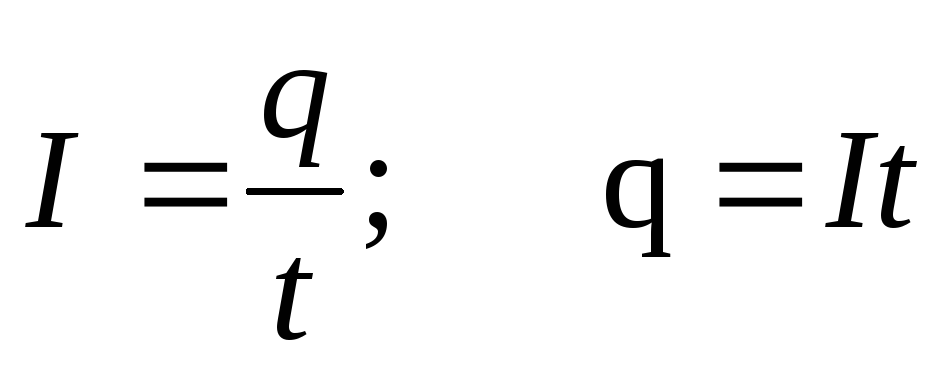
Эта работа равна количеству теплоты Q и формула Q = I U t выражает закон Джоуля-Ленца в интегральной форме.
Используя выражение закона Ома 
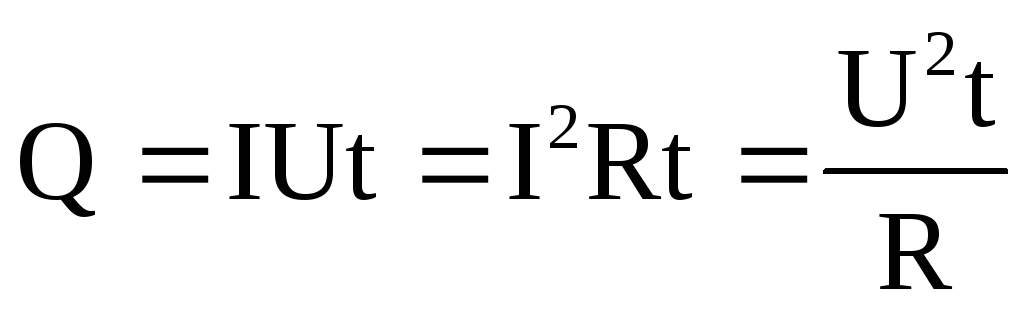
Преобразуем закон Джоуля–Ленца. Введем плотность тепловой мощности w – величину, равную энергии, выделяемой за время t прохождения тока в единице объема проводника:

Здесь 
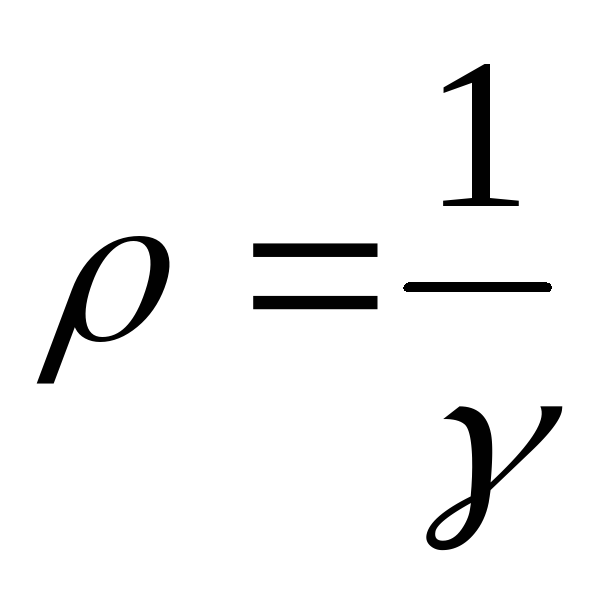
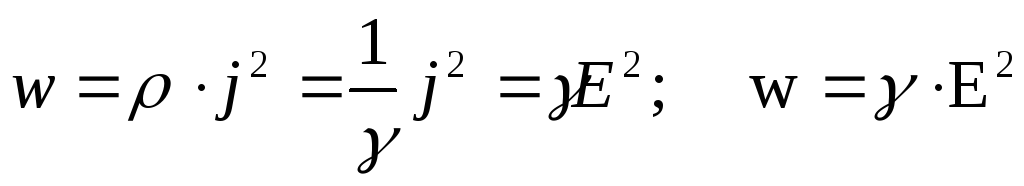
Это есть выражение закона Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности в проводнике, по которому течет ток, прямо пропорциональна квадрату напряженности поля в проводнике. Коэффициентом пропорциональности является удельная проводимость проводника.
Вывод законов Ома и Джоуля-Ленца из классических электронных представлений
Какова природа носителей тока в металлах? В 1901 г. Рикке проделал опыты: через 3 цилиндра, установленных друг на друга в течение 3-х лет пропускал постоянный ток. Был пропущен заряд, равный 3,5·10 6 Кл. Взвешивание показало неизменный вес цилиндров. Исследование торцов цилиндров не показало следов переноса вещества. Из этого был сделан вывод, что носители заряда не ионы, а открытые Томпсоном в 1897 г. электроны.
Чтобы отождествить носители заряда с электронами, нужно было определить знак и величину удельного заряда носителей.
Если в металле имеются легко перемещающиеся заряженные частицы, то при торможении металлического проводника эти частицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет перенесен некоторый заряд.
Мандельштам и Папалекси в 1913 г. проделали такой опыт – они приводили в быстрое крутильное колебание катушку с проводом вокруг ее оси. К концам катушки подключили телефон, в котором был слышен звук, обусловленный импульсами тока. Был получен качественный результат – зарегистрирован импульс тока.
Толмен и Стюарт в 1916 г. получили количественный результат. Катушка с проводом длиной 500 м приводилась во вращение со скоростью v=300 м/с. Катушка резко тормозилась и с помощью баллистического гальванометра измеряли заряд, протекавший в цепи во время торможения. Вычисленное значение отношения заряда к массе e/m получалось очень близким для электронов. Таким образом было доказано, что носителем тока являются электроны. Исходя из представлений о свободных электронах была создана классическая теория электропроводности металлов в предположении, что:
— электроны в металле ведут себя подобно молекулам идеального газа;
— движение электронов подчиняется законам классической механики;
— взаимодействие электронов сводится к соударениям с ионами кристалли-ческой решетки;
— силами взаимодействия между электронами можно пренебречь и они между собой не сталкиваются;
— электроны в отсутствие электрического поля движутся хаотически.
Вычислим плотность тока j в проводнике, возникающего под действием поля напряженностью Е.
На каждый электрон действует сила F = eE = ma, поэтому электрон приобретает ускорение 
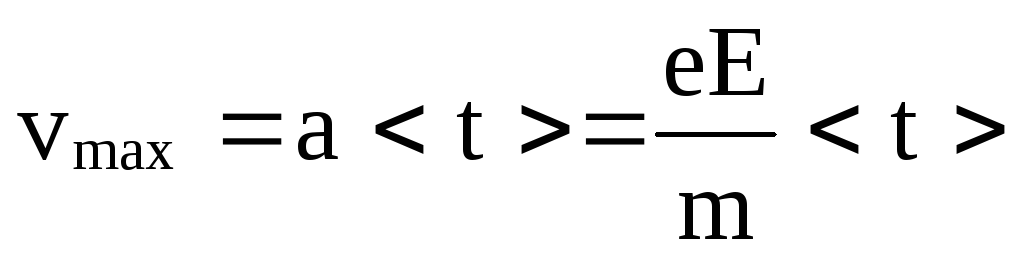

Подставляя в формулу для j, получим
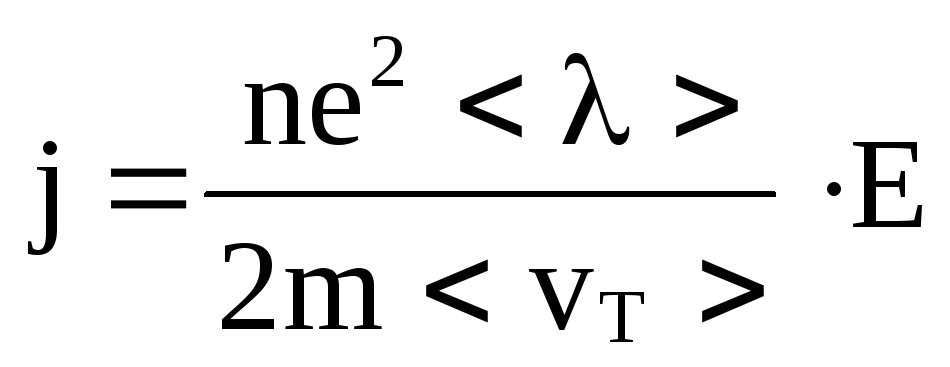
т.е. плотность тока прямо пропорциональна Е, а это и есть выражение закона Ома в дифференциальной форме. Если положить, что

Удельная проводимость γ
T, поэтому проводимость снижается с ростом температуры, а удельное сопротивление 
Предполагается, что вся энергия при соударении передается узлу кристаллической решетки и переходит в тепло. За 1 с электрон испытывает / cоударений, а значит выделяет во столько же раз больше тепла. Если в единице объема n электронов, то в единице объема за единицу времени выделится количество тепла
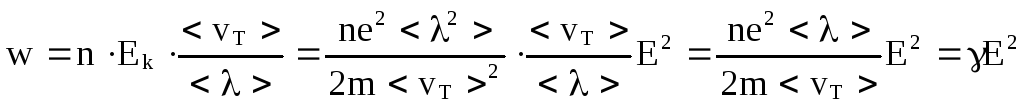
Таким образом, 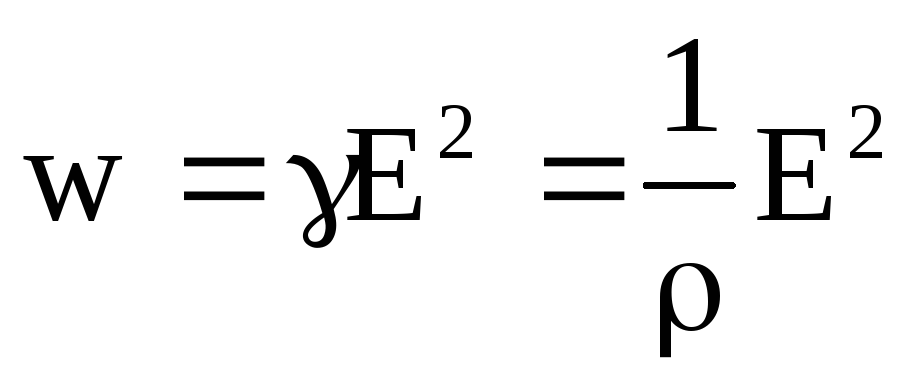
Закон Ома в дифференциальной и интегральной форме



Закон Ома для участка цепи утверждает: сила тока I прямо пропорциональна напряжению U на участке цепи и обратно пропорциональна сопротивлению R
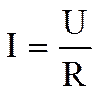
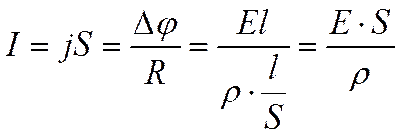
Отсюда 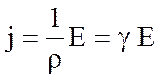
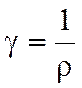
j = γ E.
Плотность тока в проводнике прямо пропорциональна напряженности электрического поля в нем.
Это есть выражение закона Ома в интегральной форме.
Про закон Ома в популярном изложении
Электрический ток и опасное напряжение невозможно услышать (за исключением гудящих высоковольтных линий и электроустановок). Токоведущие части, находящиеся под напряжением, ничем не отличаются по внешнему виду.
Невозможно узнать их и по запаху, и повышенной температурой в штатных режимах работы они не отличаются. Но включаем в безмолвную и тихую розетку пылесос, щелкаем выключателем – и энергия словно берется из ниоткуда, сама по себе, материализуясь в виде шума и компрессии внутри бытового прибора.
Опять же, если мы воткнем в разъемы розетки два гвоздя и возьмемся за них, то буквально всем своим телом ощутим реальность и объективность существования электрического тока. Делать это, конечно, настоятельно не рекомендуется.
Но примеры с пылесосом и гвоздями наглядно демонстрируют нам, что изучение и понимание основных законов электротехники способствует безопасности при обращении с бытовым электричеством, а также устранению суеверных предубеждений, связанных с электрическим током и напряжением.
Итак, рассмотрим один, самый ценный закон электротехники, который полезно знать. И попытаемся сделать это в как можно более популярной форме.
Содержание статьи
Открытие закона Ома
В 1827 г. немецкий физик Георг Симон Ом сформулировал закон, связывающий величины электрического тока, электродвижущей силы батареи и сопротивления простой электрической цепи, составленной из батареи и соединяющих ее полюса последовательно включенных разнородных проводников. Кроме того, он обнаружил, что различные вещества оказывают электрическому току различное сопротивление.
Ом экспериментально установил, что в последовательной цепи, составленной из нескольких участков с проводниками разного сопротивления, ток во всех участках одинаков, различна только разность потенциалов на проводниках, которую Ом назвал «падением напряжения».
В нормальном, несверхпроводящем металлическом проводнике имеет место закон Ома. Для участка проводника, не содержащего источника электродвижущей силы (гальванического элемента, аккумулятора, генератора, термопары, источника фотоэдс и т. д.), закон Ома заключается в том, что сила тока пропорциональна разности потенциалов на концах участка. Коэффициент пропорциональности называют сопротивлением.
Первая запись о законе Ома в лабораторной книге Георга Симона Ома сегодня хранится в архивах Немецкого музея в Мюнхене:
Открытие закона Ома было очень важным этапом исследований электрических и магнитных явлений, имевших большое практическое значение. Закон Ома и открытые в дальнейшем законы Кирхгофа впервые дали возможность производить расчеты электрических цепей и легли в основу зародившейся электротехники.
Виды законов Ома
1. Дифференциальная форма записи закона Ома
Самый главный закон электротехники – это, конечно, закон Ома. О его существовании знают даже люди, не имеющие отношения к электротехнике. Но между тем вопрос «А знаешь ли ты закон Ома?» в технических ВУЗах является ловушкой для зарвавшихся и самонадеянных школяров. Товарищ, разумеется, отвечает, что закон Ома знает отлично, и тогда к нему обращаются с просьбой привести этот закон в дифференциальной форме. Тут-то и выясняется, что школяру или первокурснику еще учиться и учиться.
Однако дифференциальная форма записи закона Ома на практике почти неприменима. Она отражает зависимость между плотностью тока и напряженностью поля:
где G – это проводимость цепи; Е – напряженность электрического тока.
Все это – попытки выразить электрический ток, принимая во внимание только физические свойства материала проводника, без учета его геометрических параметров (длина, диаметр и тому подобное). Дифференциальная форма записи закона Ома – это чистая теория, знание ее в быту совершенно не требуется.
2. Интегральная форма записи закона Ома для участка цепи
Иное дело – интегральная форма записи. Она тоже имеет несколько разновидностей. Самой популярной из них является закон Ома для участка цепи: I=U/R
Говоря по-другому, ток в участке цепи всегда тем выше, чем больше приложенное к этому участку напряжение и чем меньше сопротивление этого участка.
Вот этот «вид» закона Ома просто обязателен к запоминанию для всех, кому хоть иногда приходится иметь дело с электричеством. Благо, и зависимость-то совсем простая. Ведь напряжение в сети можно считать неизменным.
Для розетки оно равно 220 вольт. Поэтому получается, что ток в цепи зависит только от сопротивления цепи, подключаемой к розетке. Отсюда простая мораль: за этим сопротивлением надо следить.
Короткие замыкания, которые у всех на слуху, случаются именно по причине низкого сопротивления внешней цепи. Предположим, что из-за неправильного соединения проводов в ответвительной коробке фазный и нулевой провода оказались напрямую соединены между собой. Тогда сопротивление участка цепи резко снизится практически до нуля, а ток так же резко возрастет до очень большой величины.
Если электропроводка выполнена правильно, то сработает автоматический выключатель, а если его нет, или он неисправен или подобран неправильно, то провод не справится с возросшим током, нагреется, расплавится и, возможно, вызовет пожар.
Но бывает, что приборы, включенные в розетку и отработавшие уже далеко не один час, становятся причиной короткого замыкания. Типичный случай – вентилятор, обмотки двигателя которого подверглись перегреву из-за заклинивания лопастей.
Изоляция обмоток двигателя не рассчитана на серьезный нагрев, она быстро приходит в негодность. В результате появляются межвитковые короткие замыкания, которые снижают сопротивление и, в соответствии с законом Ома, также ведут к увеличению тока.
Повышенный ток, в свою очередь, приводит изоляцию обмоток в полную негодность, и наступает уже не межвитковое, а самое настоящее, полноценное короткое замыкание. Ток идет помимо обмоток, сразу из фазного в нулевой провод. Правда, все сказанное может случиться только с совсем простым и дешевым вентилятором, не оборудованным тепловой защитой.
Шпаргалка по закону Ома для участка цепи:
Закон Ома для переменного тока
Надо отметить, что приведенная запись закона Ома описывает участок цепи с постоянным напряжением. В сетях переменного напряжения существует дополнительное реактивное сопротивление, а полное сопротивление приобретает значение квадратного корня из суммы квадратов активного и реактивного сопротивления.
Закон Ома для участка цепи переменного тока принимает вид: I=U/Z,
где Z – полное сопротивление цепи.
Но большое реактивное сопротивление свойственно, прежде всего, мощным электрическим машинам и силовой преобразовательной технике. Внутреннее электрическое сопротивление бытовых приборов и светильников практически полностью является активным. Поэтому в быту для расчетов можно пользоваться самой простой формой записи закона Ома: I=U/R.
3. Интегральная форма записи для полной цепи
Раз есть форма записи закона для участка цепи, то существует и закон Ома для полной цепи: I=E/(r+R).
Здесь r – внутреннее сопротивление источника ЭДС сети, а R – полное сопротивление самой цепи.
За физической моделью для иллюстрации этого подвида закона Ома далеко ходить не надо – это бортовая электрическая сеть автомобиля, аккумулятор в которой является источником ЭДС.
Нельзя считать, что сопротивление аккумулятора равно абсолютному нулю, поэтому даже при прямом замыкании между его клеммами (отсутствии сопротивления R) ток вырастет не до бесконечности, а просто до высокого значения.
Однако этого высокого значения, конечно, хватит для того, чтобы вызвать расплавление проводов и возгорание обшивки авто. Поэтому электрические цепи автомобилей защищают от короткого замыкания при помощи предохранителей.
Такой защиты может оказаться недостаточно, если замыкание произойдет до блока предохранителей относительно аккумулятора, или если вовсе один из предохранителей заменен на кусок медной проволоки. Тогда спасение только в одном – необходимо как можно быстрее разорвать цепь полностью, откинув «массу», то есть минусовую клемму.
4. Интегральная форма записи закона Ома для участка цепи, содержащего источник ЭДС
Следует упомянуть и о том, что есть и еще одна разновидность закона Ома – для участка цепи, содержащего источник ЭДС:
Здесь U – это разность потенциалов в начале и в окончании рассматриваемого участка цепи. Знак перед величиной ЭДС зависит от направленности ее относительно напряжения.
Воспользоваться законом Ома для участка цепи нередко приходится при определении параметров цепи, когда часть схемы недоступна для детального изучения и не интересует нас.
Допустим, она скрыта неразъемными деталями корпуса. В оставшейся схеме имеется источник ЭДС и элементы с известным сопротивлением. Тогда, замерив напряжение на входе неизвестной части схемы, можно вычислить ток, а после этого – и сопротивление неизвестного элемента.
В каких случаях не выполняется закон Ома
Закон Ома не является универсальной связью между током и напряжением. Для металлов (в несверхпроводящем состоянии) закон Ома имеет место вплоть до весьма больших плотностей тока. Для полупроводников и газов пропорциональность между током и напряжением наблюдается лишь при малых напряжениях.
Выводы
Таким образом, мы можем увидеть, что «простой» закон Ома далеко не так прост, как кому-то, возможно, казалось. Зная все формы интегральной записи законов Ома, можно понять и легко запомнить многие требования электробезопасности, а также приобрести уверенность в обращении с электричеством.
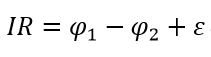


.png/250px-Zakon_Oma_(pererisovannyj).png)