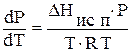интегральная форма уравнения клапейрона клаузиуса

Интегральная форма уравнения клапейрона клаузиуса

Энтальпии процессов плавления, испарения и возгонки при данной температуре и давлении связаны соотношением:
ΔH_возг = ΔH_пл + ΔH_исп

Энтальпию испарения жидкости также можно приближенно оценить по уравнению Трутона:
ΔS_исп = ΔH_исп/T_Т.Н.К. ≈88,66 Дж/моль*К
данное правило хорошо выполняется для неполярных жидкостей.

Задача 1.1.
Достаточно ли емкости тигля 1,4 л, чтобы расплавить в нем 10 кг олова. Температурный коэффициент давления составляет: dT/dP = 0,0033 град/атм. Все необходимые данные взять в справочнике. (1 Дж = 9,86 см 3 *атм)

Решение
В справочнике находим плотность твердого олова, температуру энтальпию плавления при стандартном давлении
(Р = 101325 Па).
ρ = 7,29 г/см 3
ΔH_пл = 7,2 кДж/моль = 7020 Дж/моль
Т_пл = 231,9 0 С = 505,05 0 К

По уравнению Клайперона –Клаузиуса для фазовых переходов:
dP/dT = ΔH_ф.п./(T_ф.п.*ΔV_ф.п.)
где dP/dT – изменение давления приизменении температуры, ΔH_ф.п – энтальпия фазового перехода, T_ф.п. – температура фазовогоперехода ΔV_ф.п. – разность объемов фаз.

Найдем изменение объема при плавлении 1 моль олова. Энтальпию плавления переводим в данные см 3 *атм/моль
1/0,0033 = 7020*9,86/505,05*ΔV
303,03*505,05*ΔV = 69217,2
ΔV = 0,452 см 3
Это изменение объема при плавлении 1 моль олова.

Найдем число моль олова в 10 кг.
n = m/M = 10000/119 = 84.03 моль.
Тогда общее изменение объема составит 0,452*84,03 = 37,98 см 3

Найдем объем твердого олова.
V_тв= m/ρ = 10000/7,29 = 1371,74 cм 3

Объемжидкого олова составит:
V_ж = 1371,74 + 37,98 = 1409,72 см 3 =1,41 л.

Таким образом, получаем, что объема тигля в 1,4 литра не хватит.

Решение.
Записываем полное уравнение Клапейрона –Клаузиуса для фазовых переходов:
dP/dT = ΔH_ф.п./(T_ф.п.*ΔV_ф.п.)

Задача 1.3.
Определить температуру, при которой давление СО₂ над СаСО₃ будет равно 10 5 Па, если при 1000 0 К давление составляет 11152 Па. Тепловой эффект реакции разложения карбоната при этой температуре равен 162,93 кДж/моль.

Задача 1.4.
Температура кипения чистого брома при ст. условиях составляет 59,2 0 С. Оцените давление паров брома при 15 0 С.
рассчитайте энтальпию плавления брома, если энтальпия возгонки равна 38,94 кДж/моль и сравните ее с табличным значением (ΔH_пл = 9,44 кДж/моль)

Энтальпию испарения брома можно рассчитать по правилу Трутона:
ΔH_исп/T_Т.Н.К. ≈88,66 Дж/моль*К
Получаем:
ΔH_исп = 88,66*(59,2 + 273,15) = 29466,15 Дж/моль = 29,47 кДж/моль

Источник

Уравнение Клапейрона—Клаузиуса

Как мы знаем из молекулярно-кинетической теории, атомы или молекулы в жидкостях и газах находятся в состоянии постоянного движения. Время от времени отдельные молекулы жидкости, движущиеся достаточно быстро, могут «срываться» с ее поверхности. Таким образом, над любой жидкостью какое-то количество молекул данного вещества будет находиться в виде пара. Давление этих молекул, если нет посторонних примесей, называется давлением пара этого вещества. Иногда можно почувствовать это присутствие пара над жидкостью — вспомните характерное ощущение влажности на берегу моря или океана.

ln p = H / RT + константа

где ln p — натуральный логарифм, взятый от величины давления пара, а R — постоянная Ридберга. Температура T измеряется в кельвинах.

Первым эту зависимость в 1834 году вывел инженер-конструктор паровых машин Бенуа Клапейрон. Естественно, в силу его специальности, Клапейрона интересовала прежде всего теплота парообразования, и он использовал свое уравнение преимущественно в инженерно-прикладных целях. Для науки же уравнение теплоты фазового перехода было повторно открыто почти два десятилетия спустя Рудольфом Клаузиусом, автором формулировки второго начала термодинамики.

Чаще всего уравнение Клапейрона—Клаузиуса используется для простого расчета или измерения теплоты испарения различных веществ. Измеряя давление пара при различных температурах и нанося его на график, по одной оси которого откладывается значение lnp, а по другой — величина 1/Т, ученые по полученной линейной зависимости (углу наклона прямой) определяют теплоту испарения вещества.

Французский физик и инженер. Родился Париже. Окончил Политехническую школу и Школу минного дела. В 1820-1830 гг. работал в Институте инженеров путей сообщения в Петербурге. По возвращении во Францию стал профессором Школы мостов и дорог в Париже. Прославился как проектировщик железных дорог, конструктор железнодорожных мостов и паровозов. Доказал «теорему о трех моментах», используемую для расчета несущих конструкций с тремя и более точками опоры. Однако самый большой вклад Клапейрона в науку внес благодаря изучению тепловых процессов, за что и был избран действительным членом Академии наук Франции.

Немецкий физик. Родился в Кёслине (ныне Кошалин, Польша) в семье пастора. Учился в частной школе, директором которой был его отец. В 1848 году окончил Берлинский университет. По окончании университета предпочел физику и математику истории, которую первоначально изучал, преподавал в Берлине и Цюрихе, занимал кафедру профессора физики университетов в Цюрихе, Вюрцбурге и Бонне. С 1884 года — ректор Боннского университета. Главные работы Клаузиуса посвящены основам термодинамики и кинетической теории газов. К сожалению, тяжелые ранения, полученные во время службы добровольцем в качестве санитара во время Франко-прусской войны, помешали Клаузиусу в полной мере реализовать свой научный потенциал. Тем не менее, уже после войны и ранений, именно он сформулировал второе начало термодинамики в его современном виде.

Источник

Однокомпонентные гетерогенные системы. Уравнение Клапейрона – Клаузиуса

Однокомпонентная гетерогенная система состоит из индивидуального вещества, которое может существовать в различных агрегатных состояниях или полиморфных модификациях.

Рассмотрим равновесный процесс перехода вещества из фазы 1 в фазу 2. В условиях равновесия молярная энергия Гиббса вещества в первой и второй фазах равны:

Изменение температуры и давления вызовет изменение энергии Гиббса в каждой фазе [см. (2.53)]:

где V₁, V₂ – молярные объёмы, а S_1, S₂ – молярные энтропии вещества в соответствующих фазах. При равновесии между фазами dG₁ = dG₂.

. (4.9)

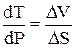
Изменение энтропии при температуре фазового перехода

, (4.10)

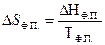
где ΔН_Ф.П. молярная теплота фазового перехода.

При подстановке (4.10) в уравнение (4.9) получим уравнение

(4.11)

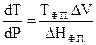
Уравнение Клапейрона – Клаузиуса характеризует зависимость температуры фазового перехода от внешнего давления в однокомпонентной системе. В данной форме уравнение применимо к любому двухфазному равновесному переходу.

Для процесса плавления dТ/dР – изменение температуры плавления при изменении давления на единицу. Поскольку плавление всегда сопровождается поглощением тепла, то знак производной dТ/dР зависит от знака ΔV= V_ж – V_тв, то есть изменения объёма при плавлении (следует помнить, что при определении изменения объёма всегда вычитают из конечного значения параметра – начальное). Чаще всего, V_ж > V_тв, поэтому с увеличением давления температура плавления вещества повышается. Реже наблюдается обратная закономерность: ΔV

(4.12)

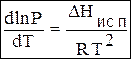
Уравнение (4.12) тоже называется уравнением Клапейрона-Клаузиуса.

Здесь следует снова обратить внимание на то, что под знаком логарифма оказывается величина, имеющая размерность. Не приводя здесь преобразований этой величины в безразмерную, отметим только, что для соблюдения правил применения математического аппарата к вычислениям физических параметров, будем считать, что под знаком логарифма и в этом случае, как и в предыдущем разделе курса, [например см. (2.77) и далее] мы подставим относительное давление, то есть давление, отнесённое к Р 0 – стандартному давлению. Если давление выражено в атмосферах, то Р 0 = 1 атм.

Для равновесия «кристаллы ↔ пар», зависимость давления насыщенного пара вещества, равновесного с кристаллами, от температуры выражается аналогичным уравнением. Тогда вместо DН_исп. следует записать DН_возг. –молярная теплота возгонки, Т – температура возгонки (или сублимации).

Проинтегрируем уравнение (4.12) в пределах от состояния 1 до состояния 2, считая DН_исп. величиной постоянной (не зависящей от температуры):

(4.13)

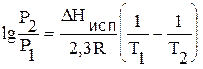
Или неопределенный интеграл:

(4.14)

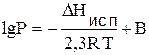
Уравнения Клапейрона-Клаузиуса широко используются при расчете фазовых равновесий.

Пример. На вершине горы атмосферное давление Р = 634 мм рт. ст. При какой температуре закипит вода в этих условиях? Известно, что теплота испарения воды DН_исп. = 40587 Дж/моль, и при Р₁= 760 мм рт. ст. температура кипения воды Т₁=373 К. Подставив эти данные в уравнение (4.13), рассчитаем Т₂. При заданных условиях вода закипит при Т=368 К, или при 95°С.

Источник

ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.

ТЕПЛОВЫЕ ЭФФЕКТЫ ФАЗОВЫХ ПЕРЕХОДОВ.

УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА.

Переход компонента из одной фазы в другую сопровождается выделением или поглощением теплоты, которую можно определить количественно на основе фундаментального уравнения термодинамики:

(*)

ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.

Для любого равновесного перехода вещества из одной фазы α в другую фазу β, применяя уравнение (*) к каждой из фаз, можно написать

Индексы α и β отражают принадлежность параметров к соответствующей фазе. В равновесных условиях между фазами α и β изменение энергии Гиббса отсутствует, т.е.

,

Приравнивая правые части уравнений 1 и 2, получим

Для равновесного обратимого процесса согласно уравнениям и запишем

,

а уравнение (3) примет вид

,

где ∆H_пер – теплота фазового перехода.

Тепловой эффект, сопровождающий фазовый переход, определяется следующим образом:

уравнение

где ∆V – изменение объема в результате фазового перехода; dP/dT – изменение давления в зависимости от температуры при сохранении равновесия между двумя фазами.

Уравнение Клапейрона–Клаузиуса связывает тепловой эффект процесса с изменением давления насыщенного пара, температурой и изменением объема в процессе фазового перехода.

Для процессов испарения ж→п и сублимации тв→п уравнение Клапейрона–Клаузиуса можно представить следующим образом:

В процессе испарения и сублимации наблюдается значительное изменение удельного объема ∆V и существенное изменение величины dP/dT. При плавлении, напротив, изменение ∆V невелико, и величина dP/dT незначительна.

Это значение показывает, что для понижения температуры таяния льда на один градус Кельвина необходимо увеличить давление на 1,34∙10 7 Па, т.е. примерно на 134 атмосферы, что нереально, поскольку такое давление лед не выдерживает – трескается.

Таяние льда происходит в основном в результате трения и превращения работы в теплоту при скольжении конька по льду, а не за счет повышения давления на лед.

Пар подчиняется законам идеального газа: PV=RT , тогда , преобразуем уравнение, переставляя давление Р в левую часть уравнения, а dT в правую часть. Получаем:

или

Проведем интегрирование уравнения (1) в пределах от Т₁ до Т₂ и соответственно от Р₁ до Р₂ при условии, что в области невысоких давлений пара ∆Н_исп ≈ const; в результате интегрирования получим:

∆Н_исп / R = const, выносим за знак интеграла

Зависимость lnP от 1/Т будет линейной, а тангенс угла наклона этой прямой равен , т.е. , а

Расчетные значения ∆Н_исп получаются с достаточной для практики точностью, не уступающей точности непосредственного измерения. Возможно использование уравнения (2) для обратного расчета, когда по значению ∆Н_исп определяют изменение давления при изменении температуры в процессе испарения.

Теплоту фазовых переходов можно определить и по величине стандартной энтальпии образования, в зависимости от фазового состояния продуктов реакции.

Пример. Лучше всего это показать на примере теплоты образования воды из газообразных кислорода и водорода, которая составляет

а теплота превращения воды в лед:

Как видно, тепловой эффект фазовых переходов значительно меньше теплоты образования веществ.

В результате фазовых переходов происходит изменение энтропии. Такие изменения в зависимости от температуры представим на рисунке.

Как известно, энтропия идеального кристалла при абсолютном нуле равна нулю. С ростом температуры атомы (ионы) флуктуировать относительно равновесного положения, число возможных способов их размещения растет, и энтропия увеличивается (ΔS>0). При достижении температуры плавления (точка А на рисунке) кристаллическая решетка разрушается скачкообразно (отрезок АБ), увеличивается термодинамическая вероятность системы W, а в соответствии с формулой S=k∙lnW (где k – постоянная Больцмана) энтропия при переходе от твердого в жидкое состояние растет. Более значительный скачок энтропии имеет место при переходе из жидкого состояния в газообразное (отрезок ВГ), когда ближний порядок расположения частиц друг относительно друга нарушается, и движение частиц становится хаотичным.

Пример. Оценим скачок энтропии на примере фазовых переходов воды:

,

когда известны стандартные абсолютные значения энтропии S_тв 0 =39,4; S_ж 0 =69,9; S_г 0 =188,7 Дж/(моль·К).

В соответствии с рисунком для воды

По известной энтальпии фазового перехода можно рассчитать изменение энтропии в соответствии с формулой

Пример.Вычислим изменение энтропии в процессе парообразования 1 моля этилхлорида при 12,3 0 С, когда теплота испарения ∆Н_исп =24,16 кДж/моль.

Молекулярная масса = 64,5 г/моль.

В заключение отмечу, что мы рассматривали лишь фазовые переходы I рода. При фазовых переходах I рода свойства веществ, выражаемые, например, через химический потенциал, первыми производными одной из характеристических функций, изменяются скачком при непрерывном изменении соответствующих параметров: температуры, давления, объема и энтропии. При этом выделяется или поглощается теплота перехода ∆Н_пер в соответствии с уравнением Клапейрона–Клаузиуса.

Кроме них, однако, существуют фазовые переходы II рода. Они не сопровождаются выделением или поглощением теплоты, для них уравнение Клапейрона–Клаузиуса теряет смысл. Эти переходы характеризуют изменения в системе, которые не определяются объемом и запасом энергии. В этом случае первые производные одной из характеристических функций непрерывны, а вторые производные (например, теплоемкость) изменяются скачком. К фазовым переходам II рода относятся переходы парамагнетика в ферромагнетик, диэлектрика в сегнетоэлектрик, а также процессы возникновения сверхтекучести, сверхпроводимости и др.

В настоящее время насчитывается около 400 твердых минералов, для которых наблюдаются фазовые переходы II рода: рутил, анатаз, алмаз и особенно кварц, который имеет семь модификаций, причем наряду с фазовыми переходами I рода наблюдаются фазовые переходы II рода. Так, при 573 0 С и переходе модификации кварца β α теплоемкость и коэффициент линейного расширения изменяются скачкообразно (I род), но при этом поглощается теплота 10,9 кДж/моль (II род).

Источник

Савельев И.В. Курс общей физики, том I

Загрузить всю книгу

Титульный лист

Главная редакция физико-математической литературы

Механика, колебания и волны,

КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I

Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.

Предисловие к четвертому изданию

При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.

Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.

Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.

Ноябрь 1969 г. И. Савельев

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Источник