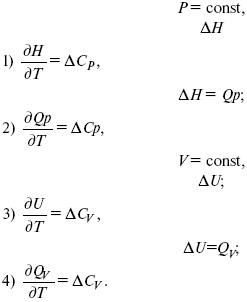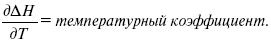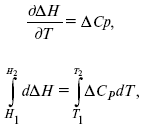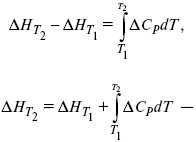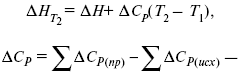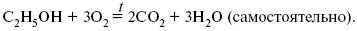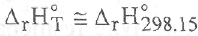интегральная форма уравнения кирхгофа для частного случая химической реакции
3. Закон Кирхгоффа. Интегральная форма уравнений Кирхгоффа
3. Закон Кирхгоффа. Интегральная форма уравнений Кирхгоффа
3акон Кирхгоффа
Это уравнения Кирхгоффа в дифференциальной форме.
Когда идет изменение функции по t – температурный коэффициент:
Закон Кирхгоффа: температурный коэффициент теплового эффекта равен изменению теплоемкости данного процесса.
Интегральная форма уравнений Кирхгоффа:
интегральная форма уравнений Кирхгоффа, Т 1 = 298 К.
Пример 3. Рассчитать тепловой эффект химической реакции при Т= 1000 К (реакция сгорания С 2Н 5ОН).
С 2Н 5ОН + 30 2 = 2С0 2 + ЗН 20 (самостоятельно).
Все реакции – как реакции образования:
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
VII. Какова форма Вселенной?
2. Закон Гесса
2. Закон Гесса При изобарных и изохорных условиях теплота является функцией состояния.В 1840 г. Г. Н. Гесс формулирует закон: «Тепловой эффект химической реакции не зависит от промежуточных стадий, а зависит только от начального и конечного состояния системы».?QP = dH,?QV = dUвн,QP =
6.4. Об инвариантности уравнений Максвелла
6.4. Об инвариантности уравнений Максвелла Требование инвариантности (неизменности) уравнений Максвелла при описании распространения электромагнитного излучения в системе, относительно которой источник движется с некоторой скоростью, является математической формой
Закон Ньютона
Закон Ньютона Закон всемирного тяготения после обсуждения в третьем чтении был отправлен на доработку… Фольклор Проверка закона Ньютона. Осмысление закона Ньютона до сих пор играет очень важную роль для осмысления представлений о гравитации вообще. Как можно
3. Построение уравнений Эйнштейна
3. Построение уравнений Эйнштейна Теперь мы в состоянии построить уравнения гравитации в ОТО. Как мы рассказали в главе 6, в начале XX века было постулировано, что гравитационное взаимодействие выражается в искривлении пространства-времени. При этом пространство-время
4. Решение уравнений Эйнштейна
4. Решение уравнений Эйнштейна Но если есть уравнения, значит их нужно решать. То есть при ограничениях и условиях каждой конкретной задачи или модели нужно найти метрические коэффициенты в каждой точке пространства-времени и тем самым определить его геометрические
Закон инерции
Закон инерции Не приходится спорить – инерциальная система отсчета удобна и обладает неоценимыми преимуществами.Но единственная ли это система или, может быть, существует много инерциальных систем? Древние греки, например, стояли на первой точке зрения. В их сочинениях
Закон Архимеда
Закон Архимеда Подвесим гири к безмену. Пружина растянется и покажет вес гири. Не снимая гири с безмена, опустим ее в воду. Изменится ли показание безмена? Да, вес тела как бы уменьшится. Если опыт проделать с килограммовой железной гирей, то «уменьшение» веса составит
Закон Авогадро
Закон Авогадро Пусть вещество представляет собой смесь различных молекул. Нет ли такой физической величины, характеризующей движение, которая была бы одинакова для всех этих молекул, например для водорода и кислорода, находящихся при одинаковой температуре?Механика
Обтекаемая форма
Обтекаемая форма Движение в воздухе, как мы говорили выше, почти всегда «быстрое», т.е. основную роль играет турбулентное, а не вязкое сопротивление. Турбулентное сопротивление испытывают самолеты, птицы, парашютисты. Если человек падает в воздухе без парашюта, то через
Глава 2 Форма времени
Глава 2 Форма времени О том, что теория относительности придает времени форму и как это можно примирить с квантовой теорией Что такое время? Тот ли оно вечно катящийся поток, что смывает все наши мечты, как говорится в старинном псалме?[3] Или это колея железной дороги?
Закон преломления
Закон преломления В работе Dioptrique Декарт излагает свою теорию света, основанную на вихрях, и обсуждает законы отражения и преломления, впервые выразив принцип, что отношение углов падения и преломления зависит от среды, через которую проходит свет.Уже греки знали, что
Пролог Форма и субстанция
Пролог Форма и субстанция Из чего сделан мир?Подобные простые вопросы терзали человеческий разум с тех самых пор, как человек стал способен рационально мыслить. Конечно, сегодня этот вопрос стал гораздо сложнее и подробнее, а ответы на него – гораздо запутаннее и
VII. Какова форма Вселенной?
2.14. Зависимость теплового эффекта от температуры. Уравнение Кирхгофа
Химические превращения далеко не всегда осуществляются при 298 К. Поэтому необходимо знать процедуру пересчета данных о тепловом эффекте процесса от базисной температуры к той, при которой реально происходит реакция.
Чтобы вывести соответствующее уравнение проведем дифференцирование по температуре выражения для энтальпии реакции:
и в результате получим:
Учитывая определительное уравнение для теплоемкости, можем записать:
Таким образом, температурный коэффициент теплового эффекта химической реакции, осуществляемой в условиях постоянства давления, равен разности сумм изобарных тетоёмкостей продуктов и исходных веществ с учетом стехиометрическш коэффициентов в уравнении химической реакции.
Это выражение называют уравнением Кирхгофа в дифференциальной форме. Применительно к процессам, протекающим при постоянном объеме, уравнение приобретает вид:
Из уравнения Кирхгофа следует, что масштаб и знак изменения энтальпии реакции с температурой определяется знаком и величиной изменения теплоемкости в ходе процесса.
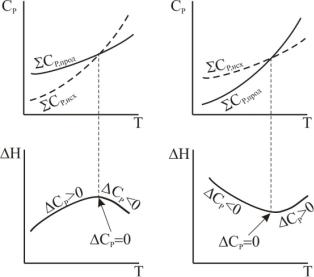
Здесь можно представить несколько ситуаций, показанных на рис.9.
Рис. 9. Схематическое представление зависимостей 2^Ср,1 и ^г^ от
Температуры:
а) ЛгСр > 0; б) ДгСр 0, то энтальпия реакции возрастает с повышением температуры и тем сильнее, чем больше ДгСр;
(Z v i C p,i)np v i C P,iW
• энтальпия реакции проходит через минимум в случае, если поведение веществ противоположно охарактеризованному в предыдущем пункте.
Изложенное выше характеризует влияние температуры на энтальпию химического процесса в качественной форме. Чтобы дать аналитическое описание зависимости энтальпии реакции от температуры, необходимо перейти к интегральной форме уравнения Кирхгофа с учётом температурной зависимости АГС°
2.15. Интегрирование уравнения Кирхгофа
Интегрирование уравнения Кирхгофа осуществляют от базисной до требуемой температуры. Поскольку основной массив справочных данных отнесен к 298,15 К, то обычно эту температуру и выбирают в качестве
Если в интервале температур 298 + Т фазовое состояние веществ, принимающих участие в реакции, остается неизменным, то процедура расчета теплового эффекта сводится к нахождению интеграла:
Интегрирование уравнения предполагает наличие данных о температурной зависимости теплоемкости. Учитывая, что в реакции могут
** В случае реакций с участием идеальных газов в качестве базисной температуры принимают абсолютный нуль. Это связано с тем, что термодинамические свойства веществ, находящихся в идеально-газовом состоянии, рассчитывают из данных о значениях молекулярных
одновременно принимать участие вещества органические и неорганические, подынтегральное выражение представляют в виде:

которое объединяет оба упоминавшихся ранее полиномиальных уравнения для температурной зависимости теплоемкости.
После интегрирования получают:
В этом выражении слагаемое, связанное с коэффициентами «а» и всеми остальными, находят из однотипных уравнений вида:
Объединяя все независящие от температуры члены, приходят к уравнению:
Константа А при этом не имеет смысла АГН298 • ^ на также не имеет смысла энтальпии процесса при абсолютном нуле температуры (ДГН0) по той причине,
что уравнения температурной зависимости теплоемкости, представленные в виде рядов по температуре, справедливы только при Т>298 К,
Для некоторых реакций в справочных руководствах можно найти информацию о температурной зависимости теплового эффекта в записанной выше форме с указанием значений всех констант. Однако в большинстве случаев расчет энтальпии процесса приходится выполнять самостоятельно с помощью процедуры интегрирования, основанного на данных о величинах Лга,АгЬ,Дгс, Дгс’.
Для реакций, происходящих с участием идеальных газов, это уравнение принимает вид:
Процедура интегрирования с учетом всех слагаемых подынтегрального выражения оказывается излишней при отсутствии сведений о температурной зависимости теплоемкости для одного или нескольких участников процесса. В этом случае принимают
Наконец, при полном отсутствии данных о теплоемкости полагают АГС° =0, и,следовательно,
Вычислительная процедура становится достаточно трудоемкой в случае, когда внутри рассматриваемого температурного интервала происходит один или несколько фазовых переходов. В этой ситуации для нахождения энтальпии реакции используют уравнение:
которое включает сумму трех слагаемых, второе из которых учитывает изменение энтальпии за счет теплоёмкостной составляющей, а третье связано с наличием фазовых переходов I рода. После каждого фазового превращения зависимость ArHx=f(T) претерпевает скачок, а зависимость ArC°=f(T)-
полное изменение в отношении характеризующего ее набора констант Дга, ДГЬ, Дгс’ и Дгс.
3.5. Уравнение Кирхгофа. Зависимость теплового эффекта реакции от температуры
Дифференцируя по температуре (при постоянном давлении) ра-
∂(ΔН)/∂T= (∂Н 2 /∂T) P – (∂Н 1 /∂T) P
Н – тепловой эффект химической реакции, а индексы 1 и 2
относятся, соответственно, к продуктам реакции и исходным веществам. Здесь полезным может быть напоминание определения такой характеристики вещества, как теплоемкость. Т.е., как было рассмотрено в разд. 3.2.1, теплоемкость – количество теплоты, которое надо подать системе, чтобы увеличить ее температуру на один градус. Так как производная (∂Н/∂T) P является теплоемкостью системы при постоянном давлении, то выражение (3.100) можно переписать
∂( Н)/∂T = С P2 – С P1 = С P
либо с учетом определенного подведенного количества тепла к системе выражение (3.101) можем переписать
Здесь С P – изменение изобарной теплоемкости системы в химическойреакцииприпостояннойтемпературе. Дляреакции, представленной в общем виде, aA + bВ = cC + dD величина С P будет равна
С P = (c·C P (C) + d·C P (D)) − (a·C P (A) + b C P (B)),
здесь a, b, c и d – стехиометрические коэффициенты в уравнении реакции с участием веществ A, B, C и D.
Для изохорного процесса можно получить таким же путем анало-
Из уравнений Кирхгофа следует, что температурный коэффициент теплового эффекта процесса равен изменению теплоемкости системы, происходящему в результате процесса.
Уравнение(3.101)строгосправедливолишьприусловии,чтодавление над каждым из компонентов при искомой температуре будет таким же, как и при данной температуре. Из (3.101) следует, что чув-
При ∆ С P > 0 тепловой эффект реакции растет с увеличением температуры, при ∆ С P ∆ С р = 0 не зависит от тем-
пературы. Следует обратить внимание на то, что знак ∆ С р связан и с выбором знака тепловых эффектов.
Характер изменения ∆ Н с изменением температуры обусловлен характером изменения ∆ С р с Т. Нарис.3.8 схематическиизображены всевозможныеслучаи, крометех, когда ∆ Н является линейнойфунк-
цией температуры. Экстремум на кривых ∆ Н = f(Т) наблюдается сравнительно редко, так как обычно интервалы температур не очень
велики. Однако сама возможность появления экстремума служит указанием на недопустимость значительной экстраполяции температурной зависимости теплового эффекта за пределы опытных данных или гарантированной точности формул.
Рис. 3.8 Схема зависимостей CP и ∆ H от температуры
Практически приходится чаще использовать уравнения Кирхгофа в интегральном виде. Для того, чтобы получить эти выражения, разделим переменные и проинтегрируем выражение (3.101) и (3.102). Тогда тепловые эффекты при температурах Т 1 и Т 2 будут связаны следующими выражениями
Прииспользованииуравнений(3.103)и(3.104) надо иметь в виду, что в температурном интервале от Т 1 до Т 2 не должно быть фазовых переходов веществ, участвующих в реакции.
При расчете ∆ H можно рассматривать несколько степеней приближения:
1. при ∆ С р = 0, ∆ H T 2 = ∆ H T 1 ;
2. при ∆ С р = const, ∆ H T 2 = ∆ H T 1 + ∆ C p ( T 2 − T 1 ) ;
3. если зависимость теплоемкости каждого вещества выража-
∆ a = ( ν 3 a 3 + ν 4 a 4 ) − ( ν 1 a 1 + ν 2 a 2 ) = ∑ ν i a i ;
∆ b = ( ν 3 b 3 + ν 4 b 4 ) − ( ν 1 b 1 + ν 2 b 2 ) = ∑ ν i b i ;
∆ c ′ = ( ν 3 c 3 ′ + ν 4 c 4 ′ ) − ( ν 1 c 1 ′ + ν 2 c 2 ′ ) = ∑ ν i c i ′ ;
∆ H T 2 = ∆ H T 1 + ∆ a ( T 2 − T 1 ) +
Аналогично рассчитывается изменение внутренней энергии ∆ U.
1. Приведите несколько формулировок первого закона термодинамики и покажите, что они не противоречат друг другу. Запишите
математические выражения 1-го закона термодинамики в дифференциальной и интегральной формах.
2. Изменение каких величин в математических выражениях первого закона термодинамики представляет собой бесконечно-малые величины или является полным дифференциалом?
3. Перечислите способы передачи энергии от одной системы к другой. Что такое теплота и работа? Это функции состояния или функции перехода?
4. Дайте определение внутренней энергии. Каково значение ее в выражениипервогозаконатермодинамики?Перечислитееесвойства
и какие виды энергии входят и не входят в это понятие?
5. Дайте определение энтальпии. Удовлетворяет ли энтальпия свойствам функции состояния системы?
6. Запишите общее математическое выражение для работы расширения идеального газа.
7. Запишите уравнения состояния идеального газа в разных процессах: изотермическом, изохорном, изобарном, адиабатном.
8. Что такое калорическое уравнение состояние и калорические коэффициенты?
9. Дайте определение идеального газа. Что собой представляет внутренняя энергия идеального газа?
10. Почему термодинамика рассматривает не абсолютное значение внутренней энергии, а только ее изменение?
11. Что такое энтальпия и какова ее связь с внутренней энергией? Почему для конденсированных систем разница между энтальпией и внутренней энергией мала, а для систем газообразных значительна?
12. Дайте определение теплоемкости. Как связаны между собой удельная и молярная теплоемкости? Какая связь существует между молярнымитеплоемкостямиприпостоянном давленииипостоянном объеме?
13. Классификация теплоемкости по разным признакам.
14. В каких единицах измеряется теплоемкость?
15. Покажите математически переходы между различными видами теплоемкостей.
16. Приведите графическое представление средней и истинной теплоемкостей.
17. Запишите выражения для теплоемкости при постоянном давлении для:
— одноатомных молекул идеального газа;
— двухатомных и линейных многоатомных молекул;
— для нелинейных трехатомных и многоатомных молекул.
18. Какова взаимосвязь молярной или атомной теплоемкости для идеальных газов при постоянном объеме и при постоянном давлении (вывод уравнения Майера)?
19. Как зависит теплоемкость от температуры? Приведите примеры степенных рядов теплоемкости.
20. Дайте понятие политропного процесса. Запишите уравнение политропы относительно pV переменных. Опишите в общем виде частные случаи политропного процесса (изопроцессы).
21. Запишите основные соотношения между термодинамическими параметрами в политропном процессе (расчет теплоты, внутренней энергии и работы).
22. Дайте определение политропному процессу, приведите примеры частных случаев политропного процесса (теплота и работа изопроцессов относительно уравнения Менделеева – Клапейрона).
23. Выведите основные соотношения между термодинамическими параметрами в политропном процессе (расчет теплоты, внутренней энергии и работы).
24. Выведите уравнение политропы в pV переменных.
25. Напишите уравнения, выражающие максимальную работу расширения идеального газа при изотермическом, изобарном, изохорном и адиабатическом процессах.
26. Дайте определение обратимым и необратимым термодинамическим процессам.Приведите примеры.Можно лиреальные природные процессы считать полностью обратимыми?
27. Что называется тепловым эффектом химической реакции?
28. СформулируйтезаконГессаиследствия,вытекающиеиз него. Каковозначениеданногозакона? ПочемуQVиQpнезависятотпути протекания процесса?
29. Какая разница между понятиями: теплота в выражении для первого закона термодинамики и тепловыми эффектами Qp и QV в законе Гесса?
30. Объясните, почему закон Гесса есть частный случай первого закона термодинамики?
31. Применяя математическое выражение первого закона термодинамики, покажите, что тепловой эффект при постоянном давлении есть изменение энтальпии, а тепловой эффект при постоянном объеме – изменение внутренней энергии химической реакции.
32. Напишите уравнение, выражающее связь между тепловым эффектом при постоянном давлении и тепловым эффектом при постоянном объеме.
33. В каких случаях теплота – это функция процесса, а в каких – функция состояния?
34. Что понимают под стандартными условиями и стандартным состоянием?
35. Какие следствия закона Гесса Вы знаете?
36. Дайте определение понятиям: «теплота образования», «теплота разложения», «теплота растворения», «теплота сгорания», «теплота нейтрализации».
37. Какие уравнения называются термохимическими? Каким свойством они обладают?
38. Какие основные термодинамические методы для расчета тепловых эффектов химических реакций Вы знаете?
39. Почему для конденсированных систем разница междуизменением энтальпии и изменением внутренней энергии мала, а для газообразных значительна?
40. Какзависит тепловойэффектхимическойреакцииоттемпературы? Каков вид аналитической зависимости теплового эффекта реакции от температуры (уравнение Кирхгофа)?
41. Какие виды приближений используются при интегрировании уравнения Кирхгофа? В каких случаях тепловой эффект химической реакции не зависит от температуры?
Закон Гесса. Уравнение Кирхгофа
2.2 Закон Гесса. Уравнение Кирхгофа
Закон Гесса утверждает:
Тепловой эффект химической реакции зависит только от вида и состояния исходных веществ и продуктов реакции и не зависит от её пути.
Из закона Гесса вытекает ряд следствий:
Если совершаются две реакции, приводящие из двух различных начальных состояний (Н1 и Н2) к одному и тому же конечному состоянию (К), то разность между тепловыми эффектами этих реакций равна тепловому эффекту превращения одного начального состояния в другое.
Если совершаются две реакции, приводящие из одного начального состояния (Н) к двум разным конечным состояниям (К1 и К2), то разность между тепловыми эффектами этих реакций равна тепловому эффекту превращения одного конечного состояния в другое.
Закон Гесса и его следствия позволяют рассчитывать тепловые эффекты некоторых реакций. Гораздо большее значение для расчётов тепловых эффектов любых реакций имеет правило, вытекающее из закона Гесса.
Стандартная энтальпия химической реакции равна разности энтальпий образования продуктов реакции и энтальпий образования исходных веществ с учётом коэффициентов перед веществами в уравнении реакции, т.е.
Это же правило можно использовать для расчёта стандартных изменений и других функций состояния, например, для расчёта изменения энтропии химической реакции:
В этом случае из таблицы термодинамических величин нужно взять стандартные энтропии веществ So298.
Описанный подход не применим для расчёта изменения функций состояния системы для нестандартных условий, так как отсутствуют необходимые для такого расчёта справочные данные. В этом случае необходимо воспользоваться уравнением Кирхгофа, которое устанавливает зависимость изменения энтальпии или энтропии реакции от температуры:
∆HT = ∆H298 + ∆a∙(T – 298) + ∆b/2∙(T2 – 2982) + ∆c/3∙(T3 – 2983) –∆c’∙(1/T – 1/298),
Здесь ∆a, ∆b, ∆c, ∆c’ – изменения соответствующих коэффициентов в химической реакции. Для расчёта этих величин необходимо в справочнике найти коэффициенты a, b, c, c’ и рассчитать изменения по общепринятой в термодинамике методике. Например,
Для расчёта изменения энергии Гиббса ∆G химической реакции следует воспользоваться формулой
где Т – любая (стандартная или нестандартная) температура. При расчётах по последней формуле необходимо использовать значения ∆H и ∆S, соответствующие этой температуре.
2.3 Расчёты изменения термодинамических функций химических реакций
Проведём расчёт изменений энтальпии, энтропии и энергии Гиббса химической реакции
4 СО(г) + 2 SO2(г) = S2(г) + 4 CO2(г)
для стандартной (298К) и нестандартной (500К) температур. Перед началом расчётов необходимо ещё раз убедиться в том, что реакция уравнена.
Расчёт показывает, что изучаемая экзотермическая реакция (знак энтальпии) при стандартных условиях может протекать самопроизвольно (знак энергии Гиббса).
Для расчёта нестандартных величин по уравнениям Кирхгофа требуется рассчитать ∆a, ∆b, ∆c, ∆c’. Для удобства и компактности расчётов составим таблицу 1.
| Номер строки | Вещество | Cp = f(T), Дж/моль∙К | |||
| a | b∙103 | c’∙10-5 | c∙106 | ||
| 1 | S2 | 36,11 | 1,09 | -3,51 | 0 |
| 2 | CO2 | 44,14 | 9,04 | -8,54 | 0 |
| 3 | 4 CO2 | 176,56 | 36,16 | -34,16 | 0 |
| 4 | ∑кон a,b,c,c’ | 212,67 | 37,25 | -37,67 | 0 |
| 5 | CO | 28,41 | 4,10 | -0,46 | 0 |
| 6 | 4 CO | 113,64 | 16,40 | -1,84 | 0 |
| 7 | SO2 | 46,19 | 7,87 | -7,70 | 0 |
| 8 | 2 SO2 | 92,38 | 15,74 | -15,40 | 0 |
| 9 | ∑исх a,b,c,c’ | 206,02 | 32,14 | -17,24 | 0 |
| 10 | ∆a,∆b,∆c,∆c’ | 6,65 | 5,11 | -20,43 | 0 |
Строки 1, 2, 5 и 7 содержат справочные значения всех коэффициентов. Данные строк 3, 6 и 8 являются результатом умножения чисел в строках 2, 5 и 7 на соответствующий множитель (коэффициент перед данным веществом в уравнении реакции). Цифры в 10-й строке – результат вычитания данных 9-й строки из данных 4-й строки. Коэффициент а для всех веществ имеет истинное значение. Остальные коэффициенты либо увеличены, либо уменьшены в 10n раз. Это сделано для компактности таблицы 1 (общепринятый способ представления табличных данных). Истинные значения коэффициентов b, c, c’ равны значащим цифрам из таблицы 1, умноженным на 10-n, т.е. знак показателя степени множителя следует изменить на противоположный. Коэффициент с для всех веществ изучаемой реакции равен нулю. Рассчитаем ∆H500.
Видно, что рассчитанное значение незначительно отличается от стандартного.
Найдём изменение энергии Гиббса ∆G500.
Изучаемая реакция может протекать самопроизвольно и при 500 К.