интерпретация результата учет реальных ограничений примеры
Интерпретация результата учет реальных ограничений примеры
Математика
2.1.12. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
В данной статье предложены примеры и решения содержательных задач с использованием математического аппарата.
В первую очередь рассмотрим несколько советов, которые помогают понять, с чего начинать решение любой задачи и как действовать поэтапно.
Сначала прочитайте задачу ознакомительно. Нужно попытаться получить информацию и представить ее в другом виде: рисунок, таблица или просто краткая запись условия задачи. При решении задач короткую запись задачи можно сделать с помощью рисунка или таблицы. Таблица является универсальным средством и позволяет решать большое количество идейно близких задач.
Второе прочтение имеет своей целью выбор неизвестных, при этом не обращаем внимание на числа и «мелочи». Главное, чтобы неизвестные соответствовали условию задачи, при составлении соответствующей “математической модели” (уравнение, неравенство, система уравнений или неравенств). При третьем прочтении задачи следует ее условие расчленить на логические части. Необходимо следить за тем, что соответствует каждой фразе текста задачи в полученной математической записи и чему в тексте задачи соответствует каждый “знак” полученной записи (сами неизвестные, действия над ними, полученные уравнения, неравенства или их системы).
Очень важно не только составить уравнение, неравенство, систему уравнений или неравенств, но и решить составленное. Если решение задачи не получается, то нужно ещё раз прочитать и проанализировать задачу (заданный текст и полученную запись). Иногда по условию задачи достаточно отыскать не сами неизвестные, а их комбинации.
Можно выделить вопросы, которые дают верное направление решению задач разных типов:
О каком процессе идёт речь? Какими величинами характеризуется этот процесс? (Количество величин соответствует числу столбцов таблицы).
Сколько процессов в задаче? (Количество процессов соответствует числу строк в таблице).
Какие величины известны? Что надо найти? (Таблица заполняется данными задачи; ставится знак вопроса).
Как связаны величины в задаче? (Вписать основные формулы, выяснить связи и соотношения величин в таблице).
Какую величину (величины) удобно выбрать в качестве неизвестной или неизвестных? (Клетки в таблице заполняются в соответствии с выбранными неизвестными).
Какие условия используются для составления “модели”? (Выписать полученную “модель”)
Легко ли решить полученное? (Если решить сложно, ввести новые переменные, использовать другие соотношения).
Рассмотрим примеры
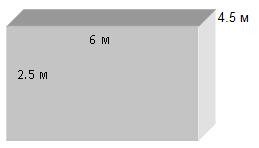
Пример 1
\(S = 2,5 \cdot 2 \cdot (6 + 4,5) = 52,2\)
\(Su
\(Su
Пример 2
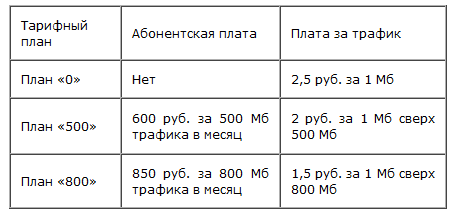
Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.
Пользователь планирует, что его трафик составит 600 Мб и, исходя из этого, выбирает наиболее дешевый тарифный план. Сколько рублей должен заплатить пользователь за месяц, если его трафик действительно будет равен 600 Мб?
Просчитаем затраты по каждому варианту тарифных планов:
Таким образом, самым выгодным оказывается второй тарифный план «500»
Истолкование (интерпретация) результата Решение математической задачи
Математическое моделирование и принятие решений
Хотя аналогия часто вводит в заблуждение, это
Наименьшее из того, что вводит нас в заблуждение.
С. Батлер
Если проблему удастся перенести на язык формул, то она сильно упрощается. Математический подход прост еще и потому, что он подчиняется вполне определенным жестким правилам, которые нельзя отменить указом или иным способом.
Сложность нашей жизни как раз и состоит в том, что все, что в ней случается, свободно от пут условностей.
Математика имеет дело с упрощенными моделями явлений. Природные корни некоторых математических наук скрыты от нас паутиной времени, в других, более молодых, они видны явно. По существу, формула (или совокупность формул) представляет собой определенный этап в построении математической модели.
Математические методы и моделирование в целенаправленной деятельности
Математической моделью, с формальной точки зрения, можно назвать любую совокупность элементов и связывающих их операций. С содержательной точки зрения интересны модели, являющиеся изоморфным отображением реальных или реализуемых объектов, процессов и явлений. С математическими моделями непосредственно связан математический метод познания отображаемых моделью объектов.
Соотношение между элементами а, Ь и с, выражаемое формулой а + Ь = с, это математическая модель. Она изоморфно отображает операцию объединения двух куч камней с их числами а и b в общую кучу камней, которых окажется с = а + Ь. В этом смысле операция сложения отвечает объединению двух куч в одну, а модель а + Ъ = с изоморфнаэтому слиянию. При этом, не объединяя кучи и не считая в ней камней, можно предсказать, что их будет с.
Этот элементарный пример поясняет общий математический метод познания. Он состоит в построении для изучаемого объекта, процесса или явления изоморфной математической модели (на основе элементов и операций операционной системы), в изучении этой математической модели (для чего требуется выполнимость используемых в ней операций) и переносе в силу изоморфизма результатов, полученных для модели, на исходный изучаемый объект.
В этом направлении математика не только создала свои разнообразные внутренние модели алгебры, геометрии, функции комплексного переменного, дифференциальных уравнений и т. д., но и помогла естествознанию в построении великих математических моделей механики, электродинамики, термодинамики, химической кинетики, микромира, пространства-времени и тяготения, вероятностей, передачи сообщений, управления, логического вывода и др. В создании своих моделей математика часто опережала потребности естествознания и техники.
Построение модели
Реальный объект Содержательная модель Математическая модель
Истолкование (интерпретация) результата Решение математической задачи
Реализация универсального математического метода познания и есть, по-видимому, основная цель и задача современной математики. Она включает, в первую очередь, построение новых неведомых математических моделей, в частности в биологии, для познания жизни и деятельности мозга, мироздания и микромира,новых фантастических техно-логий и техники, а также познание экономических и социальных явлений опять же с помощью математических моделей.
Не следует забывать и о дальнейшем расширении и обогащении операционной системы и ее реальных возможностей, гигантски усиливаемых вычислительными методами, вычислительными машинами и средствами программирования.
Одним из мощных программных средств обеспечения математического моделирования систем любого назначения является интегрированный пакет MathCad;есть и другие автоматизированные системы численных и аналитических расчетов, обладающие дружественным к пользователю интерфейсом и большими вычислительными возможностями.
Примерами таких математических пакетов являются Derive, MATLAB, Maple, Mathematica, SPSS, Statistica.
Кроме них имеется много узко специализированных или менее известных пакетов.
Математические методы: аналитические, численные, графические, прямые, итерационные.
В современном мире управление — дело отнюдь нелегкое, поскольку политическая, экономическая и социальная структура общества является сложной и постоянно усложняется еще больше. И то же время для эффективного управления необходимо учитывать характер взаимоотношений между различными элементами организации, а также все ее взаимодействия с окружающей ее средой.
Один из мощных инструментов анализа, которым располагают люди, ответственные за управление сложными системами, — моделирование.
Модель является представлением реального объекта, системы или понятия (идеи) в некоторой форме, отличной от формы их фактического реального существования. Обычно модель служит средством, помогающим в объяснении, понимании или совершенствовании системы. Модель какого-либо объекта может быть или точной копией этого объекта (хотя, возможно, и выполненной в другом масштабе или из другого материала),или отображать некоторые характерные свойства объекта в абстрактной форме, в частности в виде математической модели.
Анализ математических моделей дает в руки менеджеров, управляющих и других руководителей эффективный инструмент, который может использоваться для предсказания поведения систем и сравнения получаемых результатов. Таким образом, моделирование позволяет логическим путем прогнозировать последствия альтернативных действий и дос
таточно уверенно показывает, какому из них следует отдать предпочтение. Применение моделей дает руководителям и менеджерам метод, повышающий эффективность их суждений и интуиции.
Математическая модель может использоваться традиционным способом, т.е. для получения какого-то частного решения, но в сфере управления она наиболее успешно применяется для имитационного моделирования.
Имитация (от лат. lmitatio — подражание) — это воспроизведение на модели той или иной реальной ситуации, ее исследование и в конечном счете нахождение наиболее удачного решения. Имитационное моделирование основывается, главным образом, на теории сложных систем, теории вероятностей и математической статистике. Но в то же время имитационное моделирование и экспериментирование, как и само управление, во многом остаются творческими процессами.Собственно имитационное моделирование состоит из конструирования математической модели реальной системы и постановки на ней экспериментов, чтобы оценить (с точки зрения потребности в ресурсах, например) различные стратегии, обеспечивающие достижение цели данной системы.
Когда нужно принимать ответственное решение, т. е. при проектировании сложных технических систем, при управлении промышленным или сельскохозяйственным производством, руководстве военными действиями, большое значение имеет практический опыт, дающий возможность выделить наиболее существенные факторы, охватить ситуацию в целом и выбрать оптимальный путь для достижения поставленной цели.
Открытый урок по математике «Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений».
Открытый урок по теме:
«Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений».
преподавателя математики Козыревой Т.А.
Развивающие. Развитие интереса к предмету. Развитие математического кругозора учащихся.Повышение интереса учащихся к логике, специфике логического знания.
Воспитательные. Формирование коммуникативных качеств, умения слушать и работать в группе. Воспитание ответственности, умение принимать самостоятельные решения
Формы работы: фронтальная, групповая, индивидуальная, работа в парах не запрещается.
Методы урока: практические: решение в группах с элементами соревнования, активные методы оценки деятельности обучающихся: рейтинговый, комментирование ответа, иллюстративный, выборочный, выравнивающий контроль.
знать: математические методы решения задач из различных областей науки и практики ( вычисление площадей многоугольников; расстояний, расчет % от числа, вычисление стоимости покупки);
уметь: применять методы решения практических задач, работать с графиками, диаграммами,
Интерактивная доска , карточки с заданиями для групп, презентация. Таблица с общими баллами. 3 листа бумаги для конкурса шпаргалок (моделирование опорной схемы для каждого типа задач). Музыкальное сопровождение. Филворд «Великие математики», ребусы, составленные студентами.
Эпиграф: Особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, как располагать своими средствами для достижения по возможности большей выгоды. (П.Л. Чебышев)
Студенты, заходя в кабинет, выбирают себе фигурку (квадрат, треугольник или круг, на обратной стороне которой должны написать свою фамилию) и рассаживаются по группам.
1. Мотивация к учебной деятельности:
С ДОБРЫМ УТРОМ! НАЧАТ ДЕНЬ.
ПЕРВЫМ ДЕЛОМ ГОНИМ ЛЕНЬ.
НА УРОКАХ НЕ СКУЧАТЬ,
А РАБОТАТЬ И играТЬ!
ДОБРЫЙ ДЕНЬ, ДОБРЫЙ ЧАС!
КАК Я РАДА ВИДЕТЬ ВАС!
ДРУГ НА ДРУГА ПОСМОТРЕЛИ
И ТИХОНЕЧКО ВСЕ СЕЛИ.
Вступительное слово преподавателя математики:
2. Сначала повторим термины, которые будут встречаться у нас сегодня на уроке:(3мин.)
4.Составим «Корзину идей» (2мин.)
По итогам работы записать цели на доске:
Рассмотреть различные методы к решению практических задач, применяемых в различных областях науки, а также навыков математического моделирования реальных процессов.
Расширить свои представления о математике, ее применении, показать свою работу в группах.
6.Актуализация опорных знаний: (Эстафета (Ответы записать на листик и в тетрадь)- презентация)- 5 мин.
Собрать ответы, подвести итог работы. Студенты проверяют свои ответы, записанные в тетрадь.
6А.)Математический бой: Д/з Использование математических методов в медицине, спорте, химии, биологии, в практической деятельности (Мы должны будем выбрать лучшую защиту своего проекта) по 5мин.=15мин.
Каждой группе предлагаются задачи. В течение 10 минут обсуждение и решение в группе, затем по одному представителю от группы у доски рассказывают решение.
В ходе выполнения отметьте, какие задания вызывают у вас затруднения. Какие задания вы готовы решить прямо сейчас?
Примеры интерпретации результатов исследования
Анализ различий
Пример интерпретации анализа различий взят из статьи Сунцовой Я.С. «Социально-психологические факторы суицидального риска в юношеском возрасте (на примере исследования удмуртского этноса)» (Вестник Удмуртского университета. 2008. Вып. 2. С. 17-30.)
Анализ результатов исследования с помощью непараметрического критерия Манна-Уитни позволил выявить статистически значимые различия в уровне выраженности социально-психологических факторов суицидального риска у учащихся, несклонных/склонных к суицидальному поведению.
При сравнительном анализе данных, полученных с помощью методики социально-психологической адаптации, были обнаружены значимые межгрупповые различия по показателям социально-психологической адаптации (U = 1,500; р = 0,0001); самопринятия (U = 3,000; р = 0,0001); принятия других (U = 1,000; р = 0,0001); эмоциональной комфортности (U = 1,000; р = 0,0001); интернальности (U = 1,000; р = 0,0001); стремления к доминированию (U = 29,000; р = 0,029) и показателю ухода от проблем (U = 34,500; р = 0,054). При этом средние значения показателей социально-психологической адаптации: самопринятия, принятия других, эмоциональной комфортности, интернальности, стремления к доминированию выше у испытуемых, несклонных к суицидальному риску, а уход от проблем в большей степени выражен у испытуемых, склонных к суицидальному риску.
Также значимые различия были обнаружены между представителями двух групп по показателю самооценки (U = 14,000; р = 0,002), уровень которого выше у испытуемых, склонных к суицидальному риску.
Анализ результатов по шкалам методики Спилбергера-Ханина позволил выявить значимые различия по показателям ситуативной (U = 21,000; р = 0,008) и личностной тревожности (U = 21,000; р = 0,008), при этом как ситуативная, так и личностная тревожность в большей степени выражены у учащихся, склонных к суицидальному риску.
Также значимые различия были выявлены по показателю болезненного самолюбия (U = 30,000; р = 0,033), средний уровень выраженности которого выше у учащихся, несклонных к суицидальному риску.
Таким образом, при сравнительном анализе социально-психологических факторов суицидального риска было выявлено, что учащиеся первой группы (несклонные к суицидальному риску) характеризуются значимым преобладанием таких особенностей, как адаптация, самопринятие, принятие других, эмоциональная комфортность, интернальность, стремлением к доминированию и болезненное самолюбие. А учащиеся второй группы (склонные к суицидальному риску) отличаются значимым преобладанием ухода от проблем, ситуативной и личностной тревожностью, высокой самооценкой.
Корреляционный анализ
Пример интерпретации корреляционного анализа взят из статьи Сунцовой Я.С. «Социально-психологические факторы суицидального риска в юношеском возрасте (на примере исследования удмуртского этноса)» (Вестник Удмуртского университета. 2008. Вып. 2. С. 17-30.).
Корреляционный анализ с использованием коэффициента ранговой корреляции Спирмена позволил выявить взаимосвязи между показателями социально-психологических факторов суицидального риска в двух группах учащихся.
Структура социально-психологических факторов суицидального риска отличается в рассмотренных группах как по степени выраженности (тесноты) связи, их количеству, так и по их специфике. При этом наиболее целостная и выраженная по количеству связей структура наблюдается в группе учащихся, склонных к суицидальному риску, что может свидетельствовать о большой развитости их внутренней структуры и характеризует большие возможности для проявления суицидального риска.
Следует отметить, что в обеих группах учащихся отдельные группы социально-психологических факторов не изолированы, но отличаются количеством связей; в группе учащихся, несклонных к суицидальному риску, 10 связей, из них 9 отрицательных, в группе учащихся, склонных к суицидальному риску, 19 связей, из них 1 прямая.
Наибольшее количество связей (3) в группе учащихся, несклонных к суицидальному риску, имеют показатели «принятие других» и «эмоциональная комфортность», при этом по показателю «принятие других» выявлены отрицательные корреляционные связи с показателями «фрустрированность» (r = –0,421), «болезненное самолюбие» (r = –0,457), «импульсивность» (r = –0,360), которые также связаны между собой (рис. 1).
Рис. 1. Графическое отображение корреляционных связей показателей социально-психологических факторов суицидального риска
А показатель «эмоциональная комфортность» отрицательно связан с бескомпромиссностью (r = –0,468), ситуативной (r = –0,407) и личностной (r = – 0,486) тревожностью (рис. 2).
Рис. 2. Графическое отображение корреляционных связей показателей социально-психологических факторов суицидального риска
Аналогичные отрицательные связи были выявлены между показателями «адаптация» и «личностная тревожность» (r = –0,398), «самопринятие» и «настойчивость» (r = –0,460), «интернальность» и «эмоциональная неустойчивость» (r = –0,404).
Единственная положительная связь была зафиксирована между показателями «стремление к доминированию» и «фрустрированность» (r = 0,401).
Наличие подобных связей может свидетельствовать о том, что учащиеся, несклонные к суицидальному риску, обладают определенными комплексами социально-психологических факторов (принятие других и эмоциональная комфортность), обеспечивающих их большую устойчивость к проявлению суицидального риска в определенных жизненных ситуациях.
В группе учащихся, склонных к суицидальному риску, наибольшее количество корреляционных связей (5) выявлено по показателям «дезадаптация», «эмоциональный дискомфорт», «экстернальность». При этом показатель дезадаптации имеет значимые положительные корреляционные связи с болезненным самолюбием (r = 0,913), импульсивностью (r = 0,917), эмоциональной настойчивостью (r = 0,913), самооценкой (r = 0,913), фрустрированностью (r = 0,913).
Показатели «эмоциональный дискомфорт» и «экстернальность» имеют положительные корреляционные связи с аналогичными показателями. Также следует отметить, что дезадаптация, эмоциональный дискомфорт и экстернальность также связаны между собой, представляя при этом взаимосвязанный комплекс социально-психологических факторов суицидального риска.
Также в группе учащихся, склонных к суицидальному риску, значимые корреляционные связи были зафиксированы между показателями самопринятия и показателями личностной (r = 0,913) и ситуативной тревожности. При этом с показателем ситуативной тревожности имеется единственная отрицательная связь (r = – 0,892).
Обращает на себя внимание наличие положительных корреляционных связей показателей непринятия других (r = 0,913) и ведомости (r = 0,913) с показателем импульсивности, которые также положительно коррелируют между собой.
Таким образом, наличие подобных связей может свидетельствовать о том, что учащиеся, склонные к суицидальному риску, обладают определенными комплексами социально-психологических факторов (дезадаптация, эмоциональный дискомфорт и экстернальность), выступающих в качестве причин суицидального риска.
В качестве вывода по эмпирической части исследования следует отметить, что структура социально-психологических факторов учащихся, несклонных/склонных к суицидальному риску, отличается как по степени выраженности тесноты связи, их количеству, так и по их специфике.
В группе испытуемых, несклонных к суицидальному риску, было зафиксировано меньшее количество связей и меньшая степень выраженности (тесноты связи) между показателями социально-психологических факторов суицидального риска по сравнению с испытуемыми, склонными к суицидальному риску.
Факторный анализ
Пример интерпретации факторного анализа взят из статьи Лужецкой А.М. «Факторы личностной направленности педагогов разного возраста» (Вестник КГУ им. Н.А. Некрасова. № 1. 2010. – С. 258-261.)
«Факторизация результатов каждой группы, а также в общей выборке методом максимального правдоподобия с варимакс – вращением по критерию Г. Кайзера позволила выявить базовые факторы личностной направленности педагогов. В общей выборке испытуемых все параметры исследования объединились в факторы следующим образом:
Первый фактор – 5 переменных, которые отражают базовые показатели позитивного самоотношения личности (интегральное чувство «за» собственное «Я»; самоуважение, аутосимпатия, самоинтерес, самопринятие). Мы обозначили этот фактор как «позитивное самоотношение».
Второй фактор – 7 переменных, характеризующих сущность мотивационной структуры личности и определяющих сам характер направленности (мотивы комфорта, общения, общей и творческой активности, социальной полезности, рабочей и общежитейской направленности). Таким образом, этот фактор отражает «баланс мотивов труда и отдыха».
Третий фактор – 4 переменных самоактуализации, которые отражают сущность психического здоровья и цельности личности (автономность, спонтанность, аутосимпатия, гибкость в общении). Такое содержание позволяет определить этот фактор как «субъектность»личности.
Четвертый фактор – 6 переменных СЖО, которые, по словам Д.А. Леонтьева, являются составляющими смысла жизни (цели жизни, процесс жизни, результат жизни, локус личного и жизненного контроля и общий показатель осмысленности). В соответствии с концепцией автора этот фактор назван «смысложизненные ориентации».
Пятый фактор – 3 переменных, которые характеризуют достиженческую ориентацию личности (вызов, интеграция и предпринимательство). Условно назовем его «мотивы достижения».
Таким образом, такие факторы, как позитивное самоотношение, баланс мотивов труда и отдыха, субъектность личности, смысложизненные ориентации, а также мотивы достижения, составляют структуру направленности личности педагогов.
Сравнительный анализ факторизации результатов позволил выделить те переменные, которые наблюдаются и в факторах возрастных групп, и в общей выборке. Ими оказались: интегральный показатель самоотношения (у всех групп положительная модальность, кроме педагогов после 55 лет), аутосимпатия, самоуважение, самопринятие, рабочая направленность, осмысленность жизни (отрицательная модальность у педагогов после 55 лет и 34–43 лет), общая активность, гибкость в общении, результат жизни (отрицательная модальность в группе 34–43 лет), локус контроля «Я» (отрицательная модальность в той же группе) и социальная полезность.
Отличительными особенностями факторизации результатов педагогов разных возрастных групп являются следующие.
Педагоги до 25 лет: 1) каждый из пяти факторов сочетает параметры разных компонентов личностной направленности, а значит, отражает все ее свойства; 2) один из факторов включает отрицательное значение по параметру самообвинения; 3) в факторы включены такие переменные, как финансовые и интеллектуальные ценности, а также мотивы менеджмента и автономии.
Педагоги 26–32 лет: в состав факторов этой группы входят такие переменные, как контактность, спонтанность и взгляд на природу человека.
Педагоги 33–42 лет: 1) все факторы, как и в общей выборке, включают в состав параметры какого-либо одно компонента направленности; 2) в состав факторов входят такие параметры, как самообвинение и духовные ценности; 3) смысложизненные ориентации в составе факторов имеют отрицательный характер.
Педагоги 43–54 лет: в состав факторов этой группы включены параметры креативности и общественные ценности.
Педагоги старше 55 лет: 1) такие переменные, как самоуверенность, потребность в познании и осмысленность жизни в составе факторов имеют отрицательный характер; 2) финансовые ценности, ориентация во времени и спонтанность включены в состав факторов этой группы».
[1] Более подробно требования к оформлению будут рассмотрены ниже.
[2] Более подробно требования к библиографии будут описаны ниже в разделе «Оформление списка литературы».
[3] Оформление «подстрочной сноски» более подробно приводится выше в разделе «Сноски».