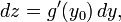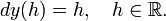инвариантность формы первого дифференциала функции нескольких переменных

Свойства первого дифференциала функции.

На мой взгляд, основным необходимым навыком для успешного вычисления неопределенных интегралов является умение вносить функцию под знак дифференциала или извлекать таковую из-под знака дифференциала, основанное на свойствах его инвариантности и линейности.

Свойство инвариантности первого дифференциала функции.

Точнее, свойство инвариантности его формы или формулы.

Такая формулировка вопроса часто встречается в экзаменационных билетах по математическому анализу в зимнюю сессию. Как правило, этот вопрос студенты относят к нежелательным: формализованным и непонятным. А зря. В самом деле, это свойство очень простое, полезное и весьма востребованное в процессе вычисления неопределённых интегралов. Оно является следствием правила дифференцирования сложной функции:

Таким образом, мы получили формулы одного и того же вида для дифференциала функции f (φ(x)) от независимой переменной x и для дифференциала функции f(u) от промежуточного аргумента u, представляющего собой дифференцируемую функцию от x.
Это и есть свойство инвариантности формы (формулы) первого дифференциала.

Пример,
пусть y(x) = sin (π − √x _ )

Свойство инвариантности, утверждающее, что это один и тот же дифференциал, позволяет записать следующиую цепочку равенств

Чтобы внести функцию под знак дифференциала, надо построить такую же цепочку в обратную сторону. Для этого уже потребуется определять не производные, а первообразные функций, стоящих перед знаком дифференциала. Например,

Функция косинус внесена под знак дифференциала. Для этого мы сначала убедились в идентичности переменных под знаками функции и дифференциала (здесь явной заменой переменных, что необязательно), а затем просто вспомнили, что первообразной косинуса является синус.

Дробь с квадратным корнем внесена под знак дифференциала. Здесь числитель и знаменатель дроби зависели от разных переменных, поэтому мы вынуждены были сначала выделить сомножитель, соответствующий производной корня второй степени, а затем записать его первообразную, т.е. сам корень, под знаком дифференциала.

Чем лучше вы ориентируетесь в производных и первообразных основных элементарных функций, тем легче будет увидеть следующий шаг. Полагаю, что и таблицу производных, и таблицу первообразных вы уже изучали, но теперь удобнее свести их в одну. Поэтому рекомендую повторить Единую таблицу производных и первообразных.

Свойства линейности первого дифференциала функции.

( f (x) ± C ) ‘ = f ‘ (x) ± 0 = f ‘ (x)
( C·f (x) ) ‘ = C·f ‘ (x)
.

О последней из них часто забывают и, пользуясь полной формулой дифференцирования дроби, делают совершенно необязательные ошибки из серии «на невнимательность». Поэтому напоминаю еще раз, постоянный множитель можно выносить за знак производной. Ориентируйтесь следующие примеры.

Поскольку дифференциал функции определяется через её производную, при вычислении дифференциала срабатывают те же свойства и правила.

Следствием этого свойства является возможность дописывать под знаком дифференциала любое постоянное слагаемое. Например,

Чтобы использовать это свойство при вычислении неопределенных интегралов, бывает удобно умножить и разделить на одно и то же число функцию, которую нужно внести под знак дифференциала. Например,

Дополнительные примеры и упражнения.

Пример 1.

Сначала расставили скобки, чтобы разобраться в сложных функциях, и выделили выражение с независимой переменной.

Первообразной синуса, является функция минус косинус того же аргумента. Вносим косинус логарифма под дифференциал. Получившееся выражение содержит только функцию cos ln x как под знаком дифференциала, так и вне его.

Здесь удалось внести под знак дифференциала всё выражение. К сожалению, это не всегда просто и даже не всегда возможно. Поэтому и интегрирование сложнее дифференцирования. Чаще всего мы можем внести под знак дифференциала только часть подынтегрального выражения, но и это существенно упрощает задачу.

Вынести функции из-под знака дифференциала

Внести функции под знак дифференциала

dx ______ √1 − x 2 _____ = d ( _______ )

√3x + 7 _____ dx = d ( 3 _______ 2 √3x + 7 _____ )

В первом выражении потеряны коэффициент и знак первообразной синуса.
Во втором, вероятно, была неправильно выделена производная арктангенса. В знаменателе этой функции должна стоять единица(!) плюс квадрат переменной.
В третьем случае вместо первообразной внесена под знак дифференциала производная, что является грубой ошибкой.
Ниже правильные решения подробно. Как уже упоминалось, замену переменных можно делать явно, как в первых двух случаях, или устно, как в последнем.

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.

Источник

14. Дифференциал функции нескольких переменных. Инвариантность формы первого дифференциала. Приближенные вычисления.

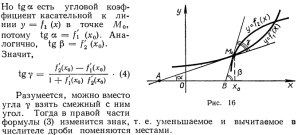
Пусть функция u = u(x) дифференцируема в точке x0, а функция y = f(u) дифференцируема в соответствующей точке u0 = u(x0), тогда сложная функция y = f(u(x)) дифференцируема в точке x0, причем

df(u(x)) = f ‘(u0)u ‘(x0)dx.Так как u ‘(x0)dx = du, то df(u(x)) = f ‘(u0)du

Последняя формула показывает, что дифференциал функции записывается формулой одного и того же вида как в случае функции от независимой переменной, так и в случае функции от функции.

Это свойство первого дифференциала называют инвариантностью (неизменностью)

Следует обратить внимание на то, что инвариантна (неизменна) именно лишь форма дифференциала, так как в содержании формулы дифференциала фкнкции есть существенное отличие от содержания формулы дифференциала от независимой переменной

Заметим, что дифференциалы высших порядков свойством инвариантности не обладают

Инвариантность формы первого дифференциала

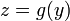
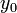
Дифференциал функции в точке имеет вид:

где 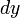— дифференциал тождественного отображения :

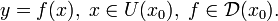
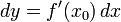
Пусть теперь Тогда , и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.

15. Геометрические приложения производной функции нескольких переменных.

16. Производные и дифференциалы сложных функций.

17. Производные высших порядков явно заданной функции

Производная у’=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.

Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у»

Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'» (или ƒ'»(х)). Итак, у'»=(y»)’

Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:

Производные порядка выше первого называются производными высших порядков.

Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уν или у(5)— производная пятого порядка).

18.Дифференциалы высших порядков

Рассмотрим дифференцируемую функцию независимой переменной y = f(x). Дифференциал этой функции dy = f'(x)dx зависит от х и dx = Dх. Приращение dx от х не зависит, так как приращения в данной точке х можно выбирать независимо от этой точки. Рассматривая dy = f'(x)dx только как функцию от х (то есть считая dx постоянным), можно найти дифференциал этой функции. Дифференциал от дифференциала данной функции y = f(x) называется ее вторым дифференциалом или дифференциалом второго порядка и обозначается символом d2у или d2 f(x). Таким образом, по определению d2у = d(dу). Вычислим второй дифференциал функции y = f(x).

Источник

Дифференцируемость функции многих переменных

Частные производные.

Пусть функция
$$
f(x) = f(x_<1>, \ldots, x_)\nonumber
$$
определена в окрестности точки \(x^ <0>= (x_<1>^<0>, \ldots, x_^<0>)\). Рассмотрим функцию одной переменной
$$
\varphi (x_<1>) = f(x_<1>,x_<2>^<0>, \ldots, x_^<0>)\nonumber
$$
Функция \(\varphi (x_<1>)\) может иметь производную в точке \(x_<1>^<0>\). По определению такая производная называется частной производной \(\frac<\partial f><\partial x_<1>>(x^<0>)\).

Аналогично определяются частные производные (первого порядка)
$$
\frac<\partial f><\partial x_>(x_<1>^<0>, \ldots, x_^<0>), i = \overline<2, n>.\nonumber
$$

Функция двух переменных может иметь в точке \(x^<0>, y^<0>\) две частные производные первого порядка
$$
\frac<\partial f><\partial x>(x^<0>, y^<0>),\quad \frac<\partial f><\partial y>(x^<0>, y^<0>).\nonumber
$$

Поскольку при вычислении частных производных все переменные, кроме одной, фиксируются, то техника вычисления частных производных такая же, как техника вычисления производных функции одной переменной.

Дифференцируемость функции многих переменных в точке.

Дадим определение дифференцируемости функции в точке.

Функция \(f(x) = f(x_<1>, \ldots, x_)\) называется дифференцируемой в точке \(x^ <0>= (x_<1>^<0>, \ldots, x_^<0>)\), если она определена в некоторой окрестности этой точки и существуют такие числа \(A_<1>, \ldots, A_\), что
$$
f(x) — f(x^<0>) = \sum_ <\substack>^<\substack>A_(x_ — x_^<0>) + o(\rho(x, x^<0>)),\quad при \ x \rightarrow x^<0>.\label
$$

Функция \(f(x)\) дифференцируема в точке \(x^<0>\) в том и только том случае, когда в некоторой окрестности точки \(x^<0>\) функция \(f(x)\) может быть представлена в следующем виде:
$$
f(x) = f(x^<0>) + \sum_^f_(x)(x_ — x_^<0>)\label
$$
где функции \(f_(x)\) непрерывны в точке \(x^<0>\).

\(\circ\) Пусть функция \(f(x)\) дифференцируема в точке \(x^<0>\). Тогда выполнено условие (1). Заметим, что равенство \(\psi(x) = o(\rho(x, x^<0>))\) при \(x \longrightarrow x^<0>\) означает, что \(\psi(x) = \varepsilon(x)\rho(x, x^<0>)\), где \(\displaystyle\lim_<\substack>>\varepsilon(x) = 0\).

Доопределим функции \(\varepsilon_(x)\) в точке \(x^<0>\) по непрерывности, полагая \(\displaystyle\lim_<\substack>>\varepsilon_(x) = \varepsilon_(x^<0>) = 0\).

Показать, что функция
$$
f(x, y) = \sqrt [3] + y^<4>>\nonumber
$$
дифференцируема в точке \((0,0)\).

\(\vartriangle\) Покажем, что существует число \(C > 0\) такое, что для любых \(x \in \boldsymbol \) и \(y \in \boldsymbol \) справедливо неравенство
$$
|\sqrt [3] + y^<4>> — x| \leq C |y|^<4/3>\label
$$

Если \(y = 0\), то неравенство \eqref справедливо при любом \(C\). Пусть \(y \neq 0\). Положим \(t = xy^<-4/3>\). Тогда неравенство \eqref эквивалентно неравенству \(\vert \psi(t) \vert Пример 2.

Показать, что функция
$$
f(x, y) = \sqrt [3] + y^<3>>\nonumber
$$
недифференцируема в точке (0,0).

\(\triangle\) Первый способ. Пусть функция дифференцируема в точке \((0,0)\), тогда, согласно определению, существуют числа \(A\) и \(B\) такие, что
$$
f(x, y) — f(0, 0) = Ax + By + o(\rho),\quad \rho = \sqrt + y^<2>>,\nonumber
$$
где \(f(x, y) = \sqrt [3] + y^<3>>, \ f(0, 0) = 0, \ A =\displaystyle \frac<\partial f(0, 0)> <\partial x>= 1, \ B = \frac<\partial f(0, 0)> <\partial y>= 1\).

Пусть \(x = y > 0\), тогда
$$
\sqrt [3] <2>x = 2x + o(x)\nonumber
$$
или \((\sqrt [3] <2>— 2) x = o(x)\) при \(x \rightarrow 0\), что противоречит определению символа \(o(x)\). Следовательно, функция \(\sqrt [3] + y^<3>>\), недифференцируема в точке \((0, 0)\).

Второй способ. Если функция \(f(x, y)\) дифференцируема в точке \((0,0)\), то ее можно в некоторой окрестности этой точки, согласно теореме 1, представить в следующем виде:
$$
\sqrt [3] + y^<3>> = x \varphi (x, y) + y \psi (x, y),\label
$$
где функции \(\varphi (x, y)\) и \(\psi (x, y)\) непрерывны в точке \((0,0)\).

Пусть \(k\) — произвольное число. Положим в \eqref \(y = kx\). Тогда
$$
\sqrt[3]<1 + k^<3>>=\varphi(x,kx)+k\psi(x,kx).\nonumber
$$
Переходя к пределу при \(x \rightarrow 0\) и пользуясь непрерывностью функций \(\varphi (x, y)\) и \(\psi (x, y)\) в точке \((0,0)\), получаем, что при любом \(k\) выполняется равенство
$$
\sqrt [3] <1 + k^<3>> = \varphi (0, 0) + k \psi (0, 0) = a + kb.\nonumber
$$
Это неверно, так как функция \(\sqrt [3] <1 + k^<3>>\) не есть линейная функция (ее вторая производная по \(k\) не обращается тождественно в нуль). \(\blacktriangle\)

Необходимое условие дифференцируемости функции в точке.

Если функция \(f(x)\) дифференцируема в точке \(x^ <0>\in R^\), то она имеет в точке \(x^<0>\) все частные производные \(\displaystyle\frac<\partial f><\partial x_>(x^<0>),\ i = \overline<1, n>\), и
$$
f(x) — f(x^<0>) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial x_>(x^<0>)(x_ — x_^<0>) + o(\rho(x, x^<0>))\quad при\ x \rightarrow x^<0>.\label
$$

\(\circ\) Пусть функция \(f(x)\) дифференцируема в точке \(x^<0>\). Тогда найдутся такие числа \(A_<1>, \ldots, A_\), что при \(x \rightarrow x^<0>\) будет выполнено равенство \eqref. Пусть в этом равенстве \(x_ <1>\neq x_<1>^<0>\), а \(x_ <2>= x_<2>^<0>, \ldots, x_ = x_^<0>\). Тогда равенство \eqref принимает следующий вид:
$$
f(x_<1>, x_<2>^<0>, \ldots, x_^<0>) — f(x_<1>^<0>, \ldots, x_^<0>) = A_ <1>(x_ <1>— x_<1>^<0>) + o (|\Delta x_<1>|)\nonumber
$$
при \(x_ <1>— x_<1>^ <0>= \Delta x_ <1>\longrightarrow 0\).

Аналогично доказывается, что у функции \(f(x)\) в точке \(x^<0>\) существуют и остальные частные производные и что
$$
A_ = \frac<\partial f><\partial x_>(x^<0>),\ i = \overline<2, n>.\nonumber
$$

Подставляя эти выражения в равенство \eqref, получаем \eqref. \(\bullet\)

Так как функция \(f(x, y) = \sqrt [3] + y^<3>>\) примера 2 недифференцируема в точке \((0,0)\), то этот пример показывает, что из существования частных производных в точке не следует дифференцируемость функции в этой точке. Существование частных производных функции в точке не гарантирует даже непрерывности функции в этой точке. Так, функция
$$
f(x, y) = \begin
\displaystyle\frac<2xy> + y^<2>> & \text <при \(x^<2>+ y^ <2>> 0\)>\\
0 & \text<при \(x = y = 0\)>
\end\nonumber
$$
не имеет предела при \(x, y) \rightarrow (0, 0)\), а поэтому и не является непрерывной в точке \((0,0)\). Тем не менее у этой функции в точке \((0,0)\) существуют обе частные производные:
$$
\frac<\partial f><\partial x>(0,0) = \lim_<\substack>\frac = 0,\quad \frac<\partial f><\partial y>(0,0) = 0.\nonumber
$$

Достаточные условия дифференцируемости функции в точке.

Если все частные производные \(\frac<\partial f><\partial x_>(x),\ i = \overline<1, n>\), определены в окрестности точки \(x^ <0>\in R^\) и непрерывны в точке \(x^<0>\), то функция \(f(x)\) дифференцируема в точке \(x^<0>\).

\(\circ\) Рассмотрим случай функции трех переменных. Общий случай рассматривается аналогично. Пусть функции \(\displaystyle \frac<\partial f><\partial x>(x, y, z),\ \frac<\partial f><\partial y>(x, y, z),\ \frac<\partial f><\partial z>(x, y, z)\), определены в некотором шаре \(S_<\varepsilon>(x^<0>, y^<0>, z^<0>)\) и непрерывны в центре шара \((x^<0>, y^<0>, z^<0>)\).

Запишем приращение функции в следующем виде:
$$
f(x, y, z) — f(x^<0>, y^<0>, z^<0>) = f(x, y, z) — f(x^<0>, y, z) +\\+ f(x^<0>, y, z) — f(x^<0>, y^<0>, z) + f(x^<0>, y^<0>, z) — f(x^<0>, y^<0>, z^<0>).\nonumber
$$

Пусть \(x^ <0>0\)>\\
0, & \text<при \(x = y = 0\)>
\end\nonumber
$$
дифференцируема в точке \((0,0)\), так как
$$
f(x, y) = 0 \cdot x + 0 \cdot y + o(\sqrt + y^<2>>)\nonumber
$$
при \((x, y) \rightarrow (0, 0)\).

Но при \(x^ <2>+ y^ <2>> 0\) частная производная
$$
\frac<\partial f><\partial x>(x, y) = 2x \sin \frac<1> <\sqrt+ y^<2>>> — \frac <\sqrt+ y^<2>>> \cos \frac<1> <\sqrt+ y^<2>>>\nonumber
$$
не имеет предела при \((x, y) \rightarrow (0, 0)\) и, следовательно, не является непрерывной функцией в точке \((0,0)\). Чтобы в этом убедиться, достаточно показать, что \(\displaystyle\frac<\partial f (x, 0)><\partial x>\) не имеет предела при \(x \rightarrow 0\).

Дифференцируемость сложной функции.

Пусть функции \(\varphi_ <1>(x), \ldots, \varphi_ (x)\) дифференцируемы в точке \(x^ <0>= (x_<1>^<0>, \ldots, x_^<0>) \in R^,\ y^ <0>= (\varphi_ <1>(x^<0>), \ldots, \varphi_ (x^<0>)) \in R^\) и функция \(f(y) = f(y_<1>, \ldots, y_)\) дифференцируема в точке \(y^<0>\).

\(\circ\) Так как функция \(f(y)\) дифференцируема в точке \(y^<0>\), то в силу теоремы 1 найдутся функции \(f_(y),\ y = \overline<1, m>\), непрерывные в точке \(y^ <0>= (y_<1>^<0>, \ldots, y_^<0>)\) и такие, что
$$
f(y) — f(y^<0>) = \sum_ <\substack>^<\substack>f_(y)(y_ — y_^<0>),\quad f_(y^<0>) = \frac<\partial f><\partial y_>(y^<0>).\label
$$

Воспользовавшись тем, что дифференцируемая в точке функция непрерывна в этой точке, а также теоремой о непрерывности сложной функции, получаем, что функции
$$
\psi_ (x) = f_(\varphi_ <1>(x), \ldots, \varphi_ (x)),\quad j = \overline<1, m>,\label
$$
непрерывны в точке \(x^<0>\), причем
$$
\psi_ (x^<0>) = f_(\varphi_ <1>(x^<0>), \ldots, \varphi_ (x^<0>)) = f_(y^<0>) = \frac<\partial f><\partial y_>(y^<0>).\label
$$

Подставив в \eqref \(y_ <1>= \varphi_ <1>(x), \ldots, y_ = \varphi_ (x)\) и воспользовавшись обозначениями \eqref, получаем
$$
\Phi (x) — \Phi (x^<0>) = \sum_ <\substack>^<\substack>\psi_(x)(\varphi_ (x^<0>) — \varphi_ (x^<0>)).\label
$$

Но функции \(\varphi_ (x^<0>),\ j = \overline<1, m>\), дифференцируемы в точке \(x^<0>\), поэтому найдутся такие непрерывные в точке \(x^<0>\) функции \(\varphi_(x)\), что
$$
\begin
\displaystyle \varphi_ (x) — \varphi_ (x^<0>) = \sum_ <\substack>^<\substack>\varphi_(x)(x_ — x_^<0>),\quad \varphi_(x^<0>)=\frac<\partial \varphi_><\partial x_>(x^<0>),\\ i = \overline<1, n>,\quad j = \overline<1, m>.
\end\label
$$

Так как функции \(\psi_(x)\) и \(\varphi_(x)\) непрерывны в точке \(x^<0>\), то и функции \(\Phi_(x)\) непрерывны в точке \(x^<0>\). А это означает, что сложная функция \(\Phi(x)\) дифференцируема в точке \(x^<0>\) (теорема 1).

Вторая из формул \eqref дает правило нахождения частных производных сложной функции, аналогичное соответствующему правилу для функций одной переменной.

Пусть функция \(f(x, y)\) дифференцируема во всех точках пространства \(R^<2>\). Перейти к полярным координатам и найти выражения для \(\displaystyle\frac<\partial f><\partial r>\) и \(\displaystyle\frac<\partial f><\partial \varphi>\).

Дифференциал. Инвариантность формы первого дифференциала. Правила дифференцирования.

Пусть функция \(f(x)\) дифференцируема в точке \(x^<0>\). Тогда при \(x \rightarrow x^<0>\) ее можно записать в виде \eqref:
$$
f(x) = f(x^<0>) + \sum_ <\substack>^<\substack>\frac<\partial f(x^<0>)><\partial x_>(x^<0>)(x_ — x_^<0>) + o(\rho(x, x^<0>)).\nonumber
$$

Положим по определению
$$
dx_ = \Delta x_ = x_ — x_^<0>.\nonumber
$$

Если функция \(f(x)\) дифференцируема в точке \(x^<0>\), то линейную форму относительно приращений независимых переменных
$$
df(x^<0>) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial x_>(x^<0>)dx_\label
$$
назовем дифференциалом функции \(f(x)\) в точке \(x^<0>\). Тогда
$$
f(x) = f(x^<0>) + d f(x^<0>) + o(\rho(x, x^<0>)) \ \mbox <при>\ x \rightarrow x^<0>.\nonumber
$$

Иногда выражение \eqref называют первым дифференциалом функции \(f(x)\) в точке \(x^<0>\).

Если бы \(y_<1>, \ldots, y_\) были независимыми переменными, то \(df(y^<0>)\) отличался бы от дифференциала сложной функции \eqref только тем, что в выражении \eqref \(dy_(x^<0>)\) — дифференциалы функций \(\varphi_\), а в
$$
df(y^<0>) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial y_>(y^<0>)dy_\nonumber
$$
\(dy_\) — дифференциалы независимых переменных. Формальная запись дифференциала в обоих случаях одинакова. Говорят, что форма первого дифференциала инвариантна относительно замены переменных.

Инвариантность формы первого дифференциала является весьма удобным его свойством. При записи \(df(y^<0>)\) в виде \eqref мы можем не задумываться о том, являются ли переменные \(y_<1>, \ldots, y_\) независимыми. Заметим, что во многих прикладных задачах часто бывает затруднительно выяснить вопрос о независимости переменных.

Пусть функция \(f(x)\) дифференцируема во всех точках некоторого открытого множества \(G \subset R^\). Тогда в каждой точке \(x \in G\) можно вычислить дифференциал
$$
df(x) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial x_>(y^<0>)dx_.\nonumber
$$

Он будет функцией \(2n\) переменных \(x_<1>, \ldots, x_\), \(dx_<1>, \ldots, dx_\), причем при фиксированных \(x_<1>, \ldots, x_\) дифференциал есть линейная функция \(dx_<1>, \ldots, dx_\). Правила дифференцирования такие же, как и для функций одной переменной:

Докажем, например, что \(d(uv) = u\ dv + v\ du\).

Найти дифференциал функции \(\displaystyle\operatorname\frac\).

Формула конечных приращений Лагранжа.

Пусть функция \(f(x)\) дифференцируема в выпуклой области \(G \subset R^\). Напомним, что выпуклая область есть открытое множество, любые две точки которого можно соединить отрезком, лежащим в области. Тогда для любых двух точек \(x = (x_<1>, \ldots, x_) \in G,\ y = (y_<1>, \ldots, y_) \in G\) найдется число \(\theta \in (0, 1)\) такое, что
$$
f(y) — f(x) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial y_>(x + \theta(y — x))(y_ — x_).\label
$$

Формула \eqref называется формулой конечных приращений Лагранжа. Докажем ее.

\(\circ\) Пусть точки \(x, y \in G\). Так как область \(G\) выпукла, то отрезок, соединяющий точки \(x\) и \(y\), лежит в области \(G\). Поэтому определена функция одной переменной
$$
\varphi (t) = f(x_ <1>+ t(y_ <1>— x_<1>), \ldots, x_ + t(y_ — x_)),\ 0 \leq t \leq 1.\label
$$

Очевидно, что \(\varphi (0) = f(x),\ \varphi (1) = f(y)\) и что функция \(\varphi (t)\) дифференцируема на отрезке [0,1]. По правилу нахождения производной сложной функции имеем
$$
\varphi'(t) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial x_>(x_ <1>+ t(y_ <1>— x_<1>), \ldots, x_ + t(y_ — x_))(y_ — x_).\label
$$

Применим к функции \(\varphi (t)\) формулу конечных приращений Лагранжа для функции одной переменной. Получаем, что найдется число \(\theta \in (0, 1)\) такое, что \(\varphi (1) — \varphi (0) = \varphi’ (\theta)\). Используя формулы \eqref и \eqref, теперь легко получаем формулу \eqref. \(\bullet\)

Касательная плоскость к графику функции двух переменных. Геометрический смысл дифференциала.

Пусть функция \(f(x, y)\) дифференцируема на открытом множестве \(G \subset R^<2>\). Рассмотрим ее график
$$
\operatorname f = \<(x, y, z):\ z = f(x, y),\ (x, y) \in G\>.\nonumber
$$

Пусть точка \(P(x_<0>, y_<0>, z_<0>)\) лежит на \(\operatorname f\), то есть \(z_ <0>= f(x_<0>, y_<0>)\), и пусть гладкая кривая
$$
\Gamma = \\nonumber
$$
лежит на графике и проходит через точку \((x_<0>, y_<0>, z_<0>)\). Это означает, что
$$
z(t) = f(x(t), y(t));\ (x(t_<0>),\ y(t_<0>),\ z(t_<0>) = (x_<0>, y_<0>, z_<0>),\ t_ <0>\in (\alpha, \beta).\label
$$

Дифференцируя тождество \eqref в точке \(t_<0>\) и пользуясь инвариантностью формы первого дифференциала, получаем
$$
dz = \frac<\partial f><\partial x>(x_<0>, y_<0>)dx + \frac<\partial f><\partial y>(x_<0>, y_<0>)dy.\label
$$

Вектор \(d \tau = (dx, dy, dz)\) есть касательный вектор к кривой \(\Gamma\) в точке \((x_<0>, y_<0>, z_<0>)\). Введем вектор
$$
\textbf = \left(- \frac<\partial f><\partial x>(x_<0>, y_<0>),\ — \frac<\partial f><\partial y>(x_<0>, y_<0>),\ 1\right).\label
$$

Условие \eqref означает, что вектор \(\textbf\) ортогонален к касательной к кривой \(\Gamma\) в точке \((x_<0>, y_<0>, z_<0>)\). Говорят, что вектор \(\textbf\) ортогонален к кривой \(\Gamma\) в точке \(P\). Но \(\Gamma\) — любая гладкая кривая, лежащая на \(\operatorname f\) и проходящая через точку \(P\). Поэтому вектор \(\textbf\) ортогонален к любой кривой, лежащей на \(\operatorname f\) и проходящей через точку \(P\). Он называется вектором нормали к \(\operatorname f\) в точке \(P\).

Плоскость, проходящая через точку \(P\) и ортогональная вектору нормали \(\textbf\), называется касательной плоскостью к \(\operatorname f\) в точке \(P\). Ее уравнение есть
$$
Z — f(x_<0>, y_<0>) = \frac<\partial f><\partial x>(x_<0>, y_<0>)(X — x_<0>) + \frac<\partial f><\partial y>(x_<0>, y_<0>)(Y — y_<0>).\label
$$

Прямая, проходящая через точку \(P\) и параллельная вектору \(N\), называется нормалью к \(\operatorname f\) в точке \(P\). Ее уравнение —
$$
\frac><- f_(x_<0>, y_<0>)> = \frac><- f_(x_<0>, y_<0>)> = Z — f(x_<0>, y_<0>).
$$

Найдем значение аппликаты касательной плоскости, построенной в точке \(P(x_<0>, y_<0>, z_<0>) \in \operatorname f\).

Таким образом, \(d\ f(x_<0>, y_<0>)\) есть приращение аппликаты касательной плоскости (рис. 26.1).

Рис. 26.1

Производная по направлению. Градиент.

Пусть функция \(f(x, y, z)\) определена в области \(G \subset R^<3>\), и пусть точка \(P(x_<0>, y_<0>, z_<0>) \in G\). Рассмотрим луч, проходящий через точку и параллельный направлению
$$
\textbf = (\cos \alpha, \cos \beta, \cos \gamma),\nonumber
$$
где
$$
\cos^ <2>\alpha + \cos^ <2>\beta + \cos^ <2>\gamma = 1.\nonumber
$$

Если функция \(f(x, y, z)\) дифференцируема в точке \(P(x_<0>, y_<0>, z_<0>) \in G\), то производную по направлению \(\textbf\) в этой точке можно вычислить при помощи следующей формулы:
$$
\frac<\partial f><\partial l>(x_<0>, y_<0>, z_<0>) = \left.\frac