инвариантность формы первого дифференциала это

Свойства первого дифференциала функции.

На мой взгляд, основным необходимым навыком для успешного вычисления неопределенных интегралов является умение вносить функцию под знак дифференциала или извлекать таковую из-под знака дифференциала, основанное на свойствах его инвариантности и линейности.

Свойство инвариантности первого дифференциала функции.

Точнее, свойство инвариантности его формы или формулы.

Такая формулировка вопроса часто встречается в экзаменационных билетах по математическому анализу в зимнюю сессию. Как правило, этот вопрос студенты относят к нежелательным: формализованным и непонятным. А зря. В самом деле, это свойство очень простое, полезное и весьма востребованное в процессе вычисления неопределённых интегралов. Оно является следствием правила дифференцирования сложной функции:

Таким образом, мы получили формулы одного и того же вида для дифференциала функции f (φ(x)) от независимой переменной x и для дифференциала функции f(u) от промежуточного аргумента u, представляющего собой дифференцируемую функцию от x.
Это и есть свойство инвариантности формы (формулы) первого дифференциала.

Пример,
пусть y(x) = sin (π − √x _ )

Свойство инвариантности, утверждающее, что это один и тот же дифференциал, позволяет записать следующиую цепочку равенств

Чтобы внести функцию под знак дифференциала, надо построить такую же цепочку в обратную сторону. Для этого уже потребуется определять не производные, а первообразные функций, стоящих перед знаком дифференциала. Например,

Функция косинус внесена под знак дифференциала. Для этого мы сначала убедились в идентичности переменных под знаками функции и дифференциала (здесь явной заменой переменных, что необязательно), а затем просто вспомнили, что первообразной косинуса является синус.

Дробь с квадратным корнем внесена под знак дифференциала. Здесь числитель и знаменатель дроби зависели от разных переменных, поэтому мы вынуждены были сначала выделить сомножитель, соответствующий производной корня второй степени, а затем записать его первообразную, т.е. сам корень, под знаком дифференциала.

Чем лучше вы ориентируетесь в производных и первообразных основных элементарных функций, тем легче будет увидеть следующий шаг. Полагаю, что и таблицу производных, и таблицу первообразных вы уже изучали, но теперь удобнее свести их в одну. Поэтому рекомендую повторить Единую таблицу производных и первообразных.

Свойства линейности первого дифференциала функции.

( f (x) ± C ) ‘ = f ‘ (x) ± 0 = f ‘ (x)
( C·f (x) ) ‘ = C·f ‘ (x)
.

О последней из них часто забывают и, пользуясь полной формулой дифференцирования дроби, делают совершенно необязательные ошибки из серии «на невнимательность». Поэтому напоминаю еще раз, постоянный множитель можно выносить за знак производной. Ориентируйтесь следующие примеры.

Поскольку дифференциал функции определяется через её производную, при вычислении дифференциала срабатывают те же свойства и правила.

Следствием этого свойства является возможность дописывать под знаком дифференциала любое постоянное слагаемое. Например,

Чтобы использовать это свойство при вычислении неопределенных интегралов, бывает удобно умножить и разделить на одно и то же число функцию, которую нужно внести под знак дифференциала. Например,

Дополнительные примеры и упражнения.

Пример 1.

Сначала расставили скобки, чтобы разобраться в сложных функциях, и выделили выражение с независимой переменной.

Первообразной синуса, является функция минус косинус того же аргумента. Вносим косинус логарифма под дифференциал. Получившееся выражение содержит только функцию cos ln x как под знаком дифференциала, так и вне его.

Здесь удалось внести под знак дифференциала всё выражение. К сожалению, это не всегда просто и даже не всегда возможно. Поэтому и интегрирование сложнее дифференцирования. Чаще всего мы можем внести под знак дифференциала только часть подынтегрального выражения, но и это существенно упрощает задачу.

Вынести функции из-под знака дифференциала

Внести функции под знак дифференциала

dx ______ √1 − x 2 _____ = d ( _______ )

√3x + 7 _____ dx = d ( 3 _______ 2 √3x + 7 _____ )

В первом выражении потеряны коэффициент и знак первообразной синуса.
Во втором, вероятно, была неправильно выделена производная арктангенса. В знаменателе этой функции должна стоять единица(!) плюс квадрат переменной.
В третьем случае вместо первообразной внесена под знак дифференциала производная, что является грубой ошибкой.
Ниже правильные решения подробно. Как уже упоминалось, замену переменных можно делать явно, как в первых двух случаях, или устно, как в последнем.

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.

Источник

Инвариантность формы дифференциала

Формула дифференциала функции имеет вид

,

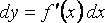
где — дифференциал независимой переменной.

Пусть теперь дана сложная (дифференцируемая) функция , где,.Тогда по формуле производной сложной функции находим

,

так как .

Итак, , т.е. формула дифференциала имеет один и тот же вид для независимой переменнойи для промежуточного аргумента, представляющего собой дифференцируемую функцию от.

Это свойство принято называть свойством инвариантности формулы или формы дифференциала. Заметим, что производная этим свойством не обладает.

Связь между непрерывностью и дифференцируемостью.

Теорема (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство. Пусть функция у=f(x) дифференцируема в точке х₀. Дадим в этой точке аргументу приращениех. Функция получит приращение у. Найдем .

.

Следствие. Если х₀ – точка разрыва функции, то в ней функция не дифференцируема.

Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.

Дифференциал. Геометрический смысл. Применение дифференциала к приближенным вычислениям.

Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается какили. Таким образом:

Дифференциал функции составляет основную часть ее приращения.

Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:

Формулу для дифференциала функции можно записать в виде:

Отсюда получаем, что

Геометрический смысл дифференциала

Дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента.

Основные правила дифференцирования. Производная постоянной, производная суммы.

Пусть функции 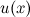иимеют производные в точке. Тогда

1. Константу можно выносить за знак производной.

5. Дифференциал константы равен нулю.

2. Производная суммы/разности.

Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.

Основные правила дифференцирования. Производная произведения.

3. Производная произведения.

Основные правила дифференцирования. Производная сложной и обратной функции.

5. Производная сложной функции.

Производная сложной функции равна производной этой функции по промежуточному аргументу , умноженной на производную от промежуточного аргументапо основному аргументу.

и имеют производные соответственно в точкахи. Тогда

(О производной обратной функции)

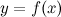
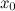
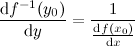
Если функция непрерывна и строго монотонна в некоторой окрестности точкии дифференцируема в этой точке, то обратная функцияимеет производную в точке, причем.

Формулы дифференцирования. Производная показательной функции.

Источник

Производная функции, заданной параметрически. Инвариантность формы первого дифференциала

Инвариантность формы первого дифференциала.

Из формулы (1) получаем, что f'(x) = 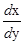, (2) то есть производная функции f(x) равна отношению дифференциалов функции и аргумента также и в том случае, когда аргумент является не независимой переменной, а дифференцируемой функцией какой-то независимой переменной.

В качестве следствия из формулы (2) выведем формулу производной функции, заданной параметрически.

Пусть x и y заданы как функции независимой переменной t, которую мы назовём параметром.

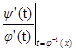
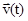
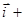
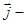
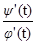
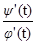
f'(x) = (4)

= j(t) y(t) вектор скорости. Докажем, что этот вектор направлен по касательной к траектории. В самом деле, tg a = . = f'(x) Þ tga = f'(x). А это и означает, что вектор скорости направлен по касательной.

Пример: x = cos t (cos t есть j(t)), y = sin t (sin t есть y(t)), 0

Источник

Инвариантность формы дифференциала

Формула дифференциала функции имеет вид

,

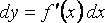
где — дифференциал независимой переменной.

Пусть теперь дана сложная (дифференцируемая) функция , где,.Тогда по формуле производной сложной функции находим

,

так как .

Итак, , т.е. формула дифференциала имеет один и тот же вид для независимой переменнойи для промежуточного аргумента, представляющего собой дифференцируемую функцию от.

Это свойство принято называть свойством инвариантности формулы или формы дифференциала. Заметим, что производная этим свойством не обладает.

Связь между непрерывностью и дифференцируемостью.

Теорема (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство. Пусть функция у=f(x) дифференцируема в точке х₀. Дадим в этой точке аргументу приращениех. Функция получит приращение у. Найдем .

.

Следствие. Если х₀ – точка разрыва функции, то в ней функция не дифференцируема.

Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.

Дифференциал. Геометрический смысл. Применение дифференциала к приближенным вычислениям.

Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается какили. Таким образом:

Дифференциал функции составляет основную часть ее приращения.

Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:

Формулу для дифференциала функции можно записать в виде:

Отсюда получаем, что

Геометрический смысл дифференциала

Дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента.

Основные правила дифференцирования. Производная постоянной, производная суммы.

Пусть функции 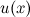иимеют производные в точке. Тогда

1. Константу можно выносить за знак производной.

5. Дифференциал константы равен нулю.

2. Производная суммы/разности.

Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.

Основные правила дифференцирования. Производная произведения.

3. Производная произведения.

Основные правила дифференцирования. Производная сложной и обратной функции.

5. Производная сложной функции.

Производная сложной функции равна производной этой функции по промежуточному аргументу , умноженной на производную от промежуточного аргументапо основному аргументу.

и имеют производные соответственно в точкахи. Тогда

(О производной обратной функции)

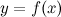
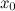
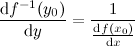
Если функция непрерывна и строго монотонна в некоторой окрестности точкии дифференцируема в этой точке, то обратная функцияимеет производную в точке, причем.

Формулы дифференцирования. Производная показательной функции.

Источник