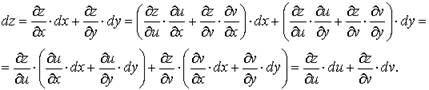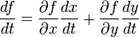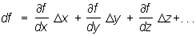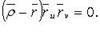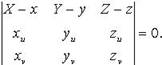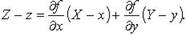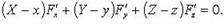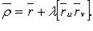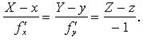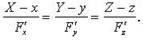инвариантность формы полного дифференциала
Инвариантность формы полного дифференциала
Выражение полного дифференциала функции нескольких переменных имеет тот же вид вне зависимости от того, являются ли u и v независимыми переменными или функциями других независимых переменных.
Доказательство опирается на формулу полного дифференциала
Что и требовалось доказать.
5.Полная производная функции— производная функции по времени вдоль траектории. Пусть функция имеет вид 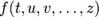
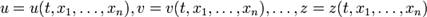
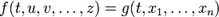

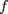
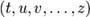
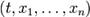
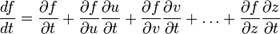
где 
Например, полная производная функции 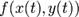
Здесь нет 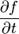

Полный дифференциал
функции f (x, у, z. ) нескольких независимых переменных — выражение
в случае, когда оно отличается от полного приращения
на величину, бесконечно малую по сравнению с
Касательная плоскость к поверхности
1.
2.
3.
4.
Нормаль к поверхности
1.
2.
3.
4.
Понятие дифференциала. Геометрический смысл дифференциала. Инвариантность формы первого дифференциала.
Рассмотрим функцию y = f(x), дифференцируемую в данной точке x. Приращение Dy ее представимо в виде
D y = f'(x)D x +a (D x) D x,
где первое слагаемое линейно относительно Dx, а второе является в точке Dx = 0 бесконечно малой функцией более высокого порядка, чем Dx. Если f'(x)№ 0, то первое слагаемое представляет собой главную часть приращения Dy. Эта главная часть приращения является линейной функцией аргумента Dx и называется дифференциалом функции y = f(x). Если f'(x) = 0, то дифференциал функции по определению считается равным нулю.
Определение 5 (дифференциал). Дифференциалом функции y = f(x) называется главная линейная относительно Dx часть приращения Dy, равная произведению производной на приращение независимой переменной
Заметим, что дифференциал независимой переменной равен приращению этой переменной dx = Dx. Поэтому формулу для дифференциала принято записывать в следующем виде: dy = f'(x)dx. (4)
Выясним каков геометрический смысл дифференциала. Возьмем на графике функции y = f(x) произвольную точку M(x,y) (рис21.). Проведем касательную к кривой y = f(x) в точке M, которая образует угол f с положительным направлением оси OX, то есть f'(x) = tgf. Из прямоугольного треугольника MKN
KN = MNtgf = D xtg f = f'(x)D x,
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение Dx.
Отметим основные свойства дифференциала, которые аналогичны свойствам производной.
3. d(u(x) ± v(x)) = d u(x) ± d v(x);
4. d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x);
Укажем еще на одно свойство, которым обладает дифференциал, но не обладает производная. Рассмотрим функцию y = f(u), где u = f (x), то есть рассмотрим сложную функцию y = f(f(x)). Если каждая из функций f и f являются дифференцируемыми, то производная сложной функции согласно теореме ( 3) равна y’ = f'(u)· u’. Тогда дифференциал функции
dy = f'(x)dx = f'(u)u’dx = f'(u)du,
так как u’dx = du. То есть dy = f'(u)du. (5)
Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.
Замечание. Отметим, что в формуле ( 4) dx = Dx, а в формуле ( 5) du яляется лишь линейной частью приращения функции u.
Интегральное исчисление — раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения. И. и. тесно связано с дифференциальным исчислением и составляет вместе с ним одну из основных частей
Дата добавления: 2018-05-12 ; просмотров: 990 ; Мы поможем в написании вашей работы!
Дифференцируемость функции многих переменных
Частные производные.
Пусть функция
$$
f(x) = f(x_<1>, \ldots, x_
$$
определена в окрестности точки \(x^ <0>= (x_<1>^<0>, \ldots, x_
$$
\varphi (x_<1>) = f(x_<1>,x_<2>^<0>, \ldots, x_
$$
Функция \(\varphi (x_<1>)\) может иметь производную в точке \(x_<1>^<0>\). По определению такая производная называется частной производной \(\frac<\partial f><\partial x_<1>>(x^<0>)\).
Аналогично определяются частные производные (первого порядка)
$$
\frac<\partial f><\partial x_>(x_<1>^<0>, \ldots, x_
$$
Функция двух переменных может иметь в точке \(x^<0>, y^<0>\) две частные производные первого порядка
$$
\frac<\partial f><\partial x>(x^<0>, y^<0>),\quad \frac<\partial f><\partial y>(x^<0>, y^<0>).\nonumber
$$
Поскольку при вычислении частных производных все переменные, кроме одной, фиксируются, то техника вычисления частных производных такая же, как техника вычисления производных функции одной переменной.
Дифференцируемость функции многих переменных в точке.
Дадим определение дифференцируемости функции в точке.
Функция \(f(x) = f(x_<1>, \ldots, x_
$$
f(x) — f(x^<0>) = \sum_ <\substack
$$
Функция \(f(x)\) дифференцируема в точке \(x^<0>\) в том и только том случае, когда в некоторой окрестности точки \(x^<0>\) функция \(f(x)\) может быть представлена в следующем виде:
$$
f(x) = f(x^<0>) + \sum_
$$
где функции \(f_(x)\) непрерывны в точке \(x^<0>\).
\(\circ\) Пусть функция \(f(x)\) дифференцируема в точке \(x^<0>\). Тогда выполнено условие (1). Заметим, что равенство \(\psi(x) = o(\rho(x, x^<0>))\) при \(x \longrightarrow x^<0>\) означает, что \(\psi(x) = \varepsilon(x)\rho(x, x^<0>)\), где \(\displaystyle\lim_<\substack
Доопределим функции \(\varepsilon_(x)\) в точке \(x^<0>\) по непрерывности, полагая \(\displaystyle\lim_<\substack
Показать, что функция
$$
f(x, y) = \sqrt [3]
$$
дифференцируема в точке \((0,0)\).
\(\vartriangle\) Покажем, что существует число \(C > 0\) такое, что для любых \(x \in \boldsymbol
$$
|\sqrt [3]
$$
Если \(y = 0\), то неравенство \eqref
Показать, что функция
$$
f(x, y) = \sqrt [3]
$$
недифференцируема в точке (0,0).
\(\triangle\) Первый способ. Пусть функция дифференцируема в точке \((0,0)\), тогда, согласно определению, существуют числа \(A\) и \(B\) такие, что
$$
f(x, y) — f(0, 0) = Ax + By + o(\rho),\quad \rho = \sqrt
$$
где \(f(x, y) = \sqrt [3]
Пусть \(x = y > 0\), тогда
$$
\sqrt [3] <2>x = 2x + o(x)\nonumber
$$
или \((\sqrt [3] <2>— 2) x = o(x)\) при \(x \rightarrow 0\), что противоречит определению символа \(o(x)\). Следовательно, функция \(\sqrt [3]
Второй способ. Если функция \(f(x, y)\) дифференцируема в точке \((0,0)\), то ее можно в некоторой окрестности этой точки, согласно теореме 1, представить в следующем виде:
$$
\sqrt [3]
$$
где функции \(\varphi (x, y)\) и \(\psi (x, y)\) непрерывны в точке \((0,0)\).
Пусть \(k\) — произвольное число. Положим в \eqref
$$
\sqrt[3]<1 + k^<3>>=\varphi(x,kx)+k\psi(x,kx).\nonumber
$$
Переходя к пределу при \(x \rightarrow 0\) и пользуясь непрерывностью функций \(\varphi (x, y)\) и \(\psi (x, y)\) в точке \((0,0)\), получаем, что при любом \(k\) выполняется равенство
$$
\sqrt [3] <1 + k^<3>> = \varphi (0, 0) + k \psi (0, 0) = a + kb.\nonumber
$$
Это неверно, так как функция \(\sqrt [3] <1 + k^<3>>\) не есть линейная функция (ее вторая производная по \(k\) не обращается тождественно в нуль). \(\blacktriangle\)
Необходимое условие дифференцируемости функции в точке.
Если функция \(f(x)\) дифференцируема в точке \(x^ <0>\in R^
$$
f(x) — f(x^<0>) = \sum_ <\substack
$$
\(\circ\) Пусть функция \(f(x)\) дифференцируема в точке \(x^<0>\). Тогда найдутся такие числа \(A_<1>, \ldots, A_
$$
f(x_<1>, x_<2>^<0>, \ldots, x_
$$
при \(x_ <1>— x_<1>^ <0>= \Delta x_ <1>\longrightarrow 0\).
Аналогично доказывается, что у функции \(f(x)\) в точке \(x^<0>\) существуют и остальные частные производные и что
$$
A_ = \frac<\partial f><\partial x_>(x^<0>),\ i = \overline<2, n>.\nonumber
$$
Подставляя эти выражения в равенство \eqref
Так как функция \(f(x, y) = \sqrt [3]
$$
f(x, y) = \begin
\displaystyle\frac<2xy>
0 & \text<при \(x = y = 0\)>
\end
$$
не имеет предела при \(x, y) \rightarrow (0, 0)\), а поэтому и не является непрерывной в точке \((0,0)\). Тем не менее у этой функции в точке \((0,0)\) существуют обе частные производные:
$$
\frac<\partial f><\partial x>(0,0) = \lim_<\substack
$$
Достаточные условия дифференцируемости функции в точке.
Если все частные производные \(\frac<\partial f><\partial x_>(x),\ i = \overline<1, n>\), определены в окрестности точки \(x^ <0>\in R^
\(\circ\) Рассмотрим случай функции трех переменных. Общий случай рассматривается аналогично. Пусть функции \(\displaystyle \frac<\partial f><\partial x>(x, y, z),\ \frac<\partial f><\partial y>(x, y, z),\ \frac<\partial f><\partial z>(x, y, z)\), определены в некотором шаре \(S_<\varepsilon>(x^<0>, y^<0>, z^<0>)\) и непрерывны в центре шара \((x^<0>, y^<0>, z^<0>)\).
Запишем приращение функции в следующем виде:
$$
f(x, y, z) — f(x^<0>, y^<0>, z^<0>) = f(x, y, z) — f(x^<0>, y, z) +\\+ f(x^<0>, y, z) — f(x^<0>, y^<0>, z) + f(x^<0>, y^<0>, z) — f(x^<0>, y^<0>, z^<0>).\nonumber
$$
Пусть \(x^ <0>0\)>\\
0, & \text<при \(x = y = 0\)>
\end
$$
дифференцируема в точке \((0,0)\), так как
$$
f(x, y) = 0 \cdot x + 0 \cdot y + o(\sqrt
$$
при \((x, y) \rightarrow (0, 0)\).
Но при \(x^ <2>+ y^ <2>> 0\) частная производная
$$
\frac<\partial f><\partial x>(x, y) = 2x \sin \frac<1> <\sqrt
$$
не имеет предела при \((x, y) \rightarrow (0, 0)\) и, следовательно, не является непрерывной функцией в точке \((0,0)\). Чтобы в этом убедиться, достаточно показать, что \(\displaystyle\frac<\partial f (x, 0)><\partial x>\) не имеет предела при \(x \rightarrow 0\).
Дифференцируемость сложной функции.
Пусть функции \(\varphi_ <1>(x), \ldots, \varphi_
\(\circ\) Так как функция \(f(y)\) дифференцируема в точке \(y^<0>\), то в силу теоремы 1 найдутся функции \(f_(y),\ y = \overline<1, m>\), непрерывные в точке \(y^ <0>= (y_<1>^<0>, \ldots, y_
$$
f(y) — f(y^<0>) = \sum_ <\substack
$$
Воспользовавшись тем, что дифференцируемая в точке функция непрерывна в этой точке, а также теоремой о непрерывности сложной функции, получаем, что функции
$$
\psi_ (x) = f_(\varphi_ <1>(x), \ldots, \varphi_
$$
непрерывны в точке \(x^<0>\), причем
$$
\psi_ (x^<0>) = f_(\varphi_ <1>(x^<0>), \ldots, \varphi_
$$
Подставив в \eqref
$$
\Phi (x) — \Phi (x^<0>) = \sum_ <\substack
$$
Но функции \(\varphi_ (x^<0>),\ j = \overline<1, m>\), дифференцируемы в точке \(x^<0>\), поэтому найдутся такие непрерывные в точке \(x^<0>\) функции \(\varphi_
$$
\begin
\displaystyle \varphi_
\end
$$
Так как функции \(\psi_
Вторая из формул \eqref
Пусть функция \(f(x, y)\) дифференцируема во всех точках пространства \(R^<2>\). Перейти к полярным координатам и найти выражения для \(\displaystyle\frac<\partial f><\partial r>\) и \(\displaystyle\frac<\partial f><\partial \varphi>\).
Дифференциал. Инвариантность формы первого дифференциала. Правила дифференцирования.
Пусть функция \(f(x)\) дифференцируема в точке \(x^<0>\). Тогда при \(x \rightarrow x^<0>\) ее можно записать в виде \eqref
$$
f(x) = f(x^<0>) + \sum_ <\substack
$$
Положим по определению
$$
dx_ = \Delta x_ = x_ — x_^<0>.\nonumber
$$
Если функция \(f(x)\) дифференцируема в точке \(x^<0>\), то линейную форму относительно приращений независимых переменных
$$
df(x^<0>) = \sum_ <\substack
$$
назовем дифференциалом функции \(f(x)\) в точке \(x^<0>\). Тогда
$$
f(x) = f(x^<0>) + d f(x^<0>) + o(\rho(x, x^<0>)) \ \mbox <при>\ x \rightarrow x^<0>.\nonumber
$$
Иногда выражение \eqref
Если бы \(y_<1>, \ldots, y_
$$
df(y^<0>) = \sum_ <\substack
$$
\(dy_
Инвариантность формы первого дифференциала является весьма удобным его свойством. При записи \(df(y^<0>)\) в виде \eqref
Пусть функция \(f(x)\) дифференцируема во всех точках некоторого открытого множества \(G \subset R^
$$
df(x) = \sum_ <\substack
$$
Он будет функцией \(2n\) переменных \(x_<1>, \ldots, x_
Докажем, например, что \(d(uv) = u\ dv + v\ du\).
Найти дифференциал функции \(\displaystyle\operatorname
Формула конечных приращений Лагранжа.
Пусть функция \(f(x)\) дифференцируема в выпуклой области \(G \subset R^
$$
f(y) — f(x) = \sum_ <\substack
$$
Формула \eqref
\(\circ\) Пусть точки \(x, y \in G\). Так как область \(G\) выпукла, то отрезок, соединяющий точки \(x\) и \(y\), лежит в области \(G\). Поэтому определена функция одной переменной
$$
\varphi (t) = f(x_ <1>+ t(y_ <1>— x_<1>), \ldots, x_
$$
Очевидно, что \(\varphi (0) = f(x),\ \varphi (1) = f(y)\) и что функция \(\varphi (t)\) дифференцируема на отрезке [0,1]. По правилу нахождения производной сложной функции имеем
$$
\varphi'(t) = \sum_ <\substack
$$
Применим к функции \(\varphi (t)\) формулу конечных приращений Лагранжа для функции одной переменной. Получаем, что найдется число \(\theta \in (0, 1)\) такое, что \(\varphi (1) — \varphi (0) = \varphi’ (\theta)\). Используя формулы \eqref
Касательная плоскость к графику функции двух переменных. Геометрический смысл дифференциала.
Пусть функция \(f(x, y)\) дифференцируема на открытом множестве \(G \subset R^<2>\). Рассмотрим ее график
$$
\operatorname
$$
Пусть точка \(P(x_<0>, y_<0>, z_<0>)\) лежит на \(\operatorname
$$
\Gamma = \
$$
лежит на графике и проходит через точку \((x_<0>, y_<0>, z_<0>)\). Это означает, что
$$
z(t) = f(x(t), y(t));\ (x(t_<0>),\ y(t_<0>),\ z(t_<0>) = (x_<0>, y_<0>, z_<0>),\ t_ <0>\in (\alpha, \beta).\label
$$
Дифференцируя тождество \eqref
$$
dz = \frac<\partial f><\partial x>(x_<0>, y_<0>)dx + \frac<\partial f><\partial y>(x_<0>, y_<0>)dy.\label
$$
Вектор \(d \tau = (dx, dy, dz)\) есть касательный вектор к кривой \(\Gamma\) в точке \((x_<0>, y_<0>, z_<0>)\). Введем вектор
$$
\textbf
$$
Условие \eqref
Плоскость, проходящая через точку \(P\) и ортогональная вектору нормали \(\textbf
$$
Z — f(x_<0>, y_<0>) = \frac<\partial f><\partial x>(x_<0>, y_<0>)(X — x_<0>) + \frac<\partial f><\partial y>(x_<0>, y_<0>)(Y — y_<0>).\label
$$
Прямая, проходящая через точку \(P\) и параллельная вектору \(N\), называется нормалью к \(\operatorname
$$
\frac
$$
Найдем значение аппликаты касательной плоскости, построенной в точке \(P(x_<0>, y_<0>, z_<0>) \in \operatorname
Таким образом, \(d\ f(x_<0>, y_<0>)\) есть приращение аппликаты касательной плоскости (рис. 26.1).
Рис. 26.1
Производная по направлению. Градиент.
Пусть функция \(f(x, y, z)\) определена в области \(G \subset R^<3>\), и пусть точка \(P(x_<0>, y_<0>, z_<0>) \in G\). Рассмотрим луч, проходящий через точку и параллельный направлению
$$
\textbf
$$
где
$$
\cos^ <2>\alpha + \cos^ <2>\beta + \cos^ <2>\gamma = 1.\nonumber
$$
Если функция \(f(x, y, z)\) дифференцируема в точке \(P(x_<0>, y_<0>, z_<0>) \in G\), то производную по направлению \(\textbf
$$
\frac<\partial f><\partial l>(x_<0>, y_<0>, z_<0>) = \left.\frac
$$
\(\circ\) Формула \eqref
Если ввести символический вектор (оператор Гамильтона)
$$
\nabla = \textbf\frac<\partial> <\partial x>+ \textbf
$$
и договориться, что векторы, стоящие слева от \(\nabla\), перемножаются с \(\nabla\) по правилам векторной алгебры, а на величины, стоящие справа, \(\nabla\) действует как дифференциальный оператор, то
$$
(\textbf
$$
Тогда формулу \eqref
$$
\frac<\partial f><\partial l>(x_<0>, y_<0>, z_<0>) = (\textbf
$$