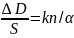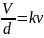инвариантные отношения в восприятии
Теория перцептивных уравнений. Экспериментальные доказательства инвариантных отношений в восприятии.
теория перцептивных уравнений (Иттельсон).
К = f (Я, К) = f (сетчаточное изображение эталонного стимула; субъективная информация об условиях восприятия).
Ядерная переменная – определённая характеристика сетчаточного образа объекта, константность которого измеряется, то есть эталон стимула (при измерении константности размера – размер сетчаточного изображения эталонного стимула, константности формы – сетчаточный образ формы эталонного изображения).
Контекстная переменная – субъективная информация об условиях восприятия эталонного стимула.
Всё зависит от того, как субъективно воспринимает наблюдатель расстояние до объекта. Если субъект оценивает расстояние правильно, то и размер оценивает правильно; если расстояние оценивается ближе, то размер стимула меньше, если расстояние больше, то размер оценивается как больший.
ВР (видимый размер) = 2 tg a / 2 ВУ (видимое удаление)
Данная теория претендует на большую точность в объяснении механизмов константности восприятия. Она способна объяснить, почему в той или иной конкретной ситуации (эксперимент Боринга) у испытуемых появляется сверхконстантность или не полная константность. Это связанно с тем, что испытуемые ошибались в ту или иную сторону в своём субъективном восприятии расстояния до эталонного стимула. Эти ошибки лежат в основе некоторых известных иллюзий:
1 иллюзия: возникает при рассматривании людей одинакового роста, поставленных в комнату Эймса – сторонники перцептивного подхода связывают это с ошибками восприятия удалённости (субъективного восприятия);
2 иллюзия: иллюзия луны, известна со 2 века до нашей эры и описана Платоном – когда мы смотрим на луну, находящуюся в зените, мы воспринимаем её меньше, чем если она находится на линии горизонта. Это объясняется тем, что когда наблюдатель смотрит на луну в зените, он воспринимает небосвод и расстояние до луны субъективно оценивается как меньшее.
Экспериментальные доказательства теории перцептивных уравнений.
ВР (видимый размер) = 2 tg a / 2 ВУ (видимое удаление)
1 эксперимент: проверка закона Эмерта – он устанавливает линейную зависимость между видимым размером последовательного образа и воспринимаемой удалённости. Чем больше видимая удалённость экранов, на которые спроецированы последовательные образы, тем больше его воспринимаемый размер. Если провести прямые измерения ВР и ВУ то окажется, что между ними существует линейная зависимость или существуют инвариантные отношения: ВР/ВУ = 2 tg a/2 – прямое подтверждение теории перцептивных уравнений.
2 эксперимент: эксперимент Этельсона с картами – 3 карты разных размеров по величине, следовательно, с разными угловыми размерами, которые соотносятся как 0,5 /1 / 2. Испытуемый видит их как расположенные на разных расстояниях: ближе всего 2, потом 1, и 0,5. Чем больше угловой размер этой карты, тем ближе она воспринимается.
Исследования восприятия пространства, движения и константности в рамках экологической теории Гибсона.
В экологической теории возникло новое представление о механизмах восприятия пространства и движения. В этом объяснении полностью отсутствует понятие признака. С точки зрения Гибсона вся информация об удалённости, глубине находится в инвариантных структурах светового потока. Его исследования направлены на выявление конкретных структур светового потока, которые содержат информацию о глубине и удалённости.
Исследования строятся в 2 этапа:
1)выявление и описание конкретных инвариантных структур, в которых может содержаться нужная информация;
2)эмпирическая проверка (выявленные структуры предъявляются испытуемым с целью вызвать определённые перцептивные эффекты).
Исследование восприятия глубины: эксперимент с оптическим тоннелем.
Тоннель – трубка, внутри раскрашенная чёрно-белыми кольцами, каждый последующий угол меньше предыдущего; в этом структурированном свете выделяется инвариантная характеристика – это градиент плотности структуры светового потока.
Оптический тоннель – пластинки с вырезанной окружностью, равной диаметру реального тоннеля. Эти пластинки устанавливаются друг за другом на равном расстоянии. При этом телесные углы абсолютно равны углам обычного тоннеля. После предъявления испытуемому у него происходит восприятие реального тоннеля, по которому можно прокатить бильярдный шар.
Для того чтобы показать, что именно в градиенте плотности светового потока задана информация о глубине, Гибсон проводит эксперимент, в котором меняет величину градиента. По идее должен меняться и перцептивный эффект. Если градиент плотности равен нулю (все телесные углы равны между собой), следовательно, этого легко добиться, расставив пластинки по-другому, а именно, каждую последующую пластинку ставить подальше от предыдущей.
Что увидит испытуемый? Он увидит некую плоскую мишень для стрельбы. Эти эксперименты доказывают, что для восприятия глубины никаких специальных признаков нет.
Гибсон критикует предшествующие две теории за то, что они были разработаны на материале исследований, проведённых в лаборатории, и они очень мало напоминают естественные условия (испытуемому предъявляются, например, объекты, висящие на экранах; при этом испытуемый не имеет возможности свободно двигаться и их осматривать. В жизни человек чаще сталкивается с объектами на опорах и к тому же может активно осматривать их, следовательно, исследователи собирают в своих лабораториях артефакты и теориями объясняют их. Это замечание Гибсон подтверждает эмпирически.
Эксперимент в открытом поле с вехами: он проводился на свежевспаханном поле, по которому недавно прошла борона. На этом поле располагались эталонные стимулы – вехи (колышки определённой длины, вбитые в землю). В этих условиях измерялась константность восприятия этих вех. В лабораторных условиях получалось, что при увеличении расстояния до объектов коэффициент константности значительно падает. В экспериментах Гибсона было показано, коэффициент константности оставался в пределах 100%, то есть в естественных условиях константность не нарушается, так как в естественных условиях структурированный свет, отражаемый от опорных поверхностей на которых располагаются объекты, содержит в себе инвариантные структуры, в которых объективна задана вся необходимая информация о константности воспринимаемых объектов. Гибсон указывает на 2 конкретные инвариантные структуры: описать эти структуры сложно, это возможно сделать через компоненты окружающего мира, через которые они задаются: объекты окружающего мира имеют 3 измерения: длина, ширина, высота (а,в,с). Это первая инвариантная структура, которая содержит информацию о длине и ширине объектов, она задаётся количеством текстурных элементов, которые пересекают или заслоняют объект, так как при удалении объекта это количество остаётся постоянным. Объект, независимо от того на каком расстоянии он находится от наблюдателя, заслоняет одно и тоже количество элементов. Вторая инвариантная структура, содержащая информацию о высоте объектов, может задаваться постоянством частей объектов, на которые его делит линия горизонта. С точки зрения Гибсона гипотезы о существовании ядерной или контекстной переменной являются излишними, так как вся информация о константности воспринимаемых объектов содержится в оптическом строе, так как K = f (инвариантных структур светового потока).
Общая психология. В 7 томах. Том 2. Ощущение и восприятие Алексей Гусев ( DJVU, стр. 262 )
Настоящее издание продолжает серию учебников по базовому курсу «Общая психология», подготовленных кафедрой общей психологии факультета психологии МГУ им. М.В.Ломоносова.
В учебнике рассмотрены классические и современные представления об ощущениях и восприятиях. Представлены описания и анализ важнейших сенсорных феноменов и лежащих в их основе психологических механизмов. Подробно обсуждается роль индивидуальных различий и культурно-исторических факторов развития и функционирования чувственной сферы человека.
Для студентов, обучающихся по психологическим специальностям. Книга может быть полезна аспирантам, преподавателям вузов, всем интересующимся проблемами психологии.
вал на то, «что пока не было предложено механизмов, посредством которых можно было бы обнаруживать и использовать эти инварианты, как нет доказательств того, что они вообще используются» [116, 316].
Подводя итог рассмотрению теорий константности восприятия, следует подчеркнуть, что вряд ли стоит искать один-единственный подход, объясняющий все виды константностей восприятия, поскольку в силу своего разнообразия они могут реализовываться совершенно разными физиологическими и психологическими механизмами.
7.3. Эмпирические исследования инвариантных отношений в восприятии
7.3.1. Эксперимент А. Холвея и З.Боринга
Описываемый ниже эксперимент является в определенной степени модельным, поскольку представляет собой хорошую иллюстрацию того, как происходит исследование феномена константности.
Основная идея классического зкспериментального исследования константности восприятия размера, проведенного американскими психологами А. Холвеем и Э.Борингом (1941) состояла в том, что константность восприятия размера объекта зависит от точности оценки наблюдателем удаленности до этого объекта. Испытуемый сидел на пересечении
9. Ядер-контекстная теория константности. Экспериментальные доказательства.
Ядер-контекстная теория константности восприятия – предложенное Э.Борингом объяснение константности восприятия величины; видимая величина объекта – определённый баланс между доминированием в восприятии ядерного стимула (сетчаточная проекция) и контекстных стимулов (стимулы, несущие информацию об удалённости).
Классическая теория константности предполагает, что в ходе индивидуального развития человек при взаимодействии с окружающей средой приобретает перцептивный опыт, усваивая объективные перцептивные законы. Усвоив реальное соотношение между рядом параметров проксимальной стимуляции и отношение между физическими характеристиками окружающей среды, человек выводит бессознательные умозаключения, или решает своего рода перцептивное уравнение. В ходе исследований установили строгую количественную зависимость между физическими параметрами стимуляции, размером проксимального стимула и величиной воспринимаемых характеристик образа.
10. Теория перцептивных уравнений. Экспериментальные доказательства инвариантных отношений в восприятии.
Ряд экспериментальных исследований обнаружил закономерные эффекты взаимодействия между феноменальными параметрами зрительного образа. Перцептивные уравнения – количественное выражение результата взаимодействия различного рода стимульных и феноменальных параметров, характеризующих разные виды константностей.
Отношение видимой величины и видимой удалённости может быть выражено следующей формулой:
Где альфа – зрительный угол (проксимальная величина объекта); S – видимая величина объекта;D- его видимая удалённость; k – коэффициент пропорциональности.
При альфа=const видимая величина тестового круга в эксперименте Холвея и Боринга пропорциональна его видимой удалённости. Из этого следует закон зрительного угла: при D=constвидимая величина меняется пропорционально зрительному углу.
Закон Эммерта: при неизменности площади сетчаточной проекции изменение видимого расстояния до экрана, на который проецируется послеобраз, влечет за собой пропорциональное увеличение его видимого размера.
У.Годжел показал, что при редукции всех зрительных признаков наблюдаются интересные феномены, названные им тенденцией к равноудалённости (все видимые объекты кажутся расположенными на одной плоскости) и специфической удалённости (при полной редукции зрительных признаков человек склонен воспринимать объекты расположенными на на одной и той же удалённости от себя, примерно 1,5 – 2,5м).
S=const, то есть если известна видимая величина объекта, то видимая удалённость будет пропорционально углу зрения. (эксперимент с игральными картами)
Феномен константности видимой величины: видимая величина объекта постоянна, если видимая удалённость изменяется обратно пропорционально величине зрительного угла.
В работах У.Годжела также исследовано отношение, связывающее видимую глубину и видимую удалённость:
Где дельта D – видимая удалённость, D – видимая абсолютная удалённость, n – диспарантность, k – коэфф. пропорциональности.
Инвариантное отношение, связывающее видимую величину, видимую глубину, диспаратность и зрительный угол (и видимая величина может определять восприятие глубины):
А.Д.Логвиненко описывает инвариантное отношение видимой скорости и абсолютной удалённости:
d – абсолютная удалённость; v – скорость перемещения объекта по сетчатке; V – видимая скорость.
Выведение формул чрезвычайно сложно, так как требует исключения влияния всех других факторов.
Теория перцептивных уравнений. Экспериментальные доказательства инвариантных отношений в восприятии.
теория перцептивных уравнений (Иттельсон).
К = f (Я, К) = f (сетчаточное изображение эталонного стимула; субъективная информация об условиях восприятия).
Ядерная переменная – определённая характеристика сетчаточного образа объекта, константность которого измеряется, то есть эталон стимула (при измерении константности размера – размер сетчаточного изображения эталонного стимула, константности формы – сетчаточный образ формы эталонного изображения).
Контекстная переменная – субъективная информация об условиях восприятия эталонного стимула.
Всё зависит от того, как субъективно воспринимает наблюдатель расстояние до объекта. Если субъект оценивает расстояние правильно, то и размер оценивает правильно; если расстояние оценивается ближе, то размер стимула меньше, если расстояние больше, то размер оценивается как больший.
ВР (видимый размер) = 2 tg a / 2 ВУ (видимое удаление)
Данная теория претендует на большую точность в объяснении механизмов константности восприятия. Она способна объяснить, почему в той или иной конкретной ситуации (эксперимент Боринга) у испытуемых появляется сверхконстантность или не полная константность. Это связанно с тем, что испытуемые ошибались в ту или иную сторону в своём субъективном восприятии расстояния до эталонного стимула. Эти ошибки лежат в основе некоторых известных иллюзий:
1 иллюзия: возникает при рассматривании людей одинакового роста, поставленных в комнату Эймса – сторонники перцептивного подхода связывают это с ошибками восприятия удалённости (субъективного восприятия);
2 иллюзия: иллюзия луны, известна со 2 века до нашей эры и описана Платоном – когда мы смотрим на луну, находящуюся в зените, мы воспринимаем её меньше, чем если она находится на линии горизонта. Это объясняется тем, что когда наблюдатель смотрит на луну в зените, он воспринимает небосвод и расстояние до луны субъективно оценивается как меньшее.
Экспериментальные доказательства теории перцептивных уравнений.
ВР (видимый размер) = 2 tg a / 2 ВУ (видимое удаление)
1 эксперимент: проверка закона Эмерта – он устанавливает линейную зависимость между видимым размером последовательного образа и воспринимаемой удалённости. Чем больше видимая удалённость экранов, на которые спроецированы последовательные образы, тем больше его воспринимаемый размер. Если провести прямые измерения ВР и ВУ то окажется, что между ними существует линейная зависимость или существуют инвариантные отношения: ВР/ВУ = 2 tg a/2 – прямое подтверждение теории перцептивных уравнений.
2 эксперимент: эксперимент Этельсона с картами – 3 карты разных размеров по величине, следовательно, с разными угловыми размерами, которые соотносятся как 0,5 /1 / 2. Испытуемый видит их как расположенные на разных расстояниях: ближе всего 2, потом 1, и 0,5. Чем больше угловой размер этой карты, тем ближе она воспринимается.
Исследования восприятия пространства, движения и константности в рамках экологической теории Гибсона.
В экологической теории возникло новое представление о механизмах восприятия пространства и движения. В этом объяснении полностью отсутствует понятие признака. С точки зрения Гибсона вся информация об удалённости, глубине находится в инвариантных структурах светового потока. Его исследования направлены на выявление конкретных структур светового потока, которые содержат информацию о глубине и удалённости.
Исследования строятся в 2 этапа:
1)выявление и описание конкретных инвариантных структур, в которых может содержаться нужная информация;
2)эмпирическая проверка (выявленные структуры предъявляются испытуемым с целью вызвать определённые перцептивные эффекты).
Исследование восприятия глубины: эксперимент с оптическим тоннелем.
Тоннель – трубка, внутри раскрашенная чёрно-белыми кольцами, каждый последующий угол меньше предыдущего; в этом структурированном свете выделяется инвариантная характеристика – это градиент плотности структуры светового потока.
Оптический тоннель – пластинки с вырезанной окружностью, равной диаметру реального тоннеля. Эти пластинки устанавливаются друг за другом на равном расстоянии. При этом телесные углы абсолютно равны углам обычного тоннеля. После предъявления испытуемому у него происходит восприятие реального тоннеля, по которому можно прокатить бильярдный шар.
Для того чтобы показать, что именно в градиенте плотности светового потока задана информация о глубине, Гибсон проводит эксперимент, в котором меняет величину градиента. По идее должен меняться и перцептивный эффект. Если градиент плотности равен нулю (все телесные углы равны между собой), следовательно, этого легко добиться, расставив пластинки по-другому, а именно, каждую последующую пластинку ставить подальше от предыдущей.
Что увидит испытуемый? Он увидит некую плоскую мишень для стрельбы. Эти эксперименты доказывают, что для восприятия глубины никаких специальных признаков нет.
Гибсон критикует предшествующие две теории за то, что они были разработаны на материале исследований, проведённых в лаборатории, и они очень мало напоминают естественные условия (испытуемому предъявляются, например, объекты, висящие на экранах; при этом испытуемый не имеет возможности свободно двигаться и их осматривать. В жизни человек чаще сталкивается с объектами на опорах и к тому же может активно осматривать их, следовательно, исследователи собирают в своих лабораториях артефакты и теориями объясняют их. Это замечание Гибсон подтверждает эмпирически.
Эксперимент в открытом поле с вехами: он проводился на свежевспаханном поле, по которому недавно прошла борона. На этом поле располагались эталонные стимулы – вехи (колышки определённой длины, вбитые в землю). В этих условиях измерялась константность восприятия этих вех. В лабораторных условиях получалось, что при увеличении расстояния до объектов коэффициент константности значительно падает. В экспериментах Гибсона было показано, коэффициент константности оставался в пределах 100%, то есть в естественных условиях константность не нарушается, так как в естественных условиях структурированный свет, отражаемый от опорных поверхностей на которых располагаются объекты, содержит в себе инвариантные структуры, в которых объективна задана вся необходимая информация о константности воспринимаемых объектов. Гибсон указывает на 2 конкретные инвариантные структуры: описать эти структуры сложно, это возможно сделать через компоненты окружающего мира, через которые они задаются: объекты окружающего мира имеют 3 измерения: длина, ширина, высота (а,в,с). Это первая инвариантная структура, которая содержит информацию о длине и ширине объектов, она задаётся количеством текстурных элементов, которые пересекают или заслоняют объект, так как при удалении объекта это количество остаётся постоянным. Объект, независимо от того на каком расстоянии он находится от наблюдателя, заслоняет одно и тоже количество элементов. Вторая инвариантная структура, содержащая информацию о высоте объектов, может задаваться постоянством частей объектов, на которые его делит линия горизонта. С точки зрения Гибсона гипотезы о существовании ядерной или контекстной переменной являются излишними, так как вся информация о константности воспринимаемых объектов содержится в оптическом строе, так как K = f (инвариантных структур светового потока).
Эксперименты Дж. Гибсона по константности восприятия размера
Дж. Гибсон описывал оригинальные эксперименты, показывающие, что константность размера оцениваемого объекта можно объяснить наличием инвариантной оптической информации — градиентом текстуры [34]. Его опыты проводились на большом поле, простиравшемся до горизонта. Оно было хорошо перепахано и выглядело как хорошо текстурированная комочками земли ровная поверхность. От испытуемых требовалось оценить высоту столбиков-вех, которые были расставлены по полю на расстоянии до 800 м от испытуемого. Результаты обнаружили, что обычные нетренированные испытуемые давали достаточно точные оценки высоты вех, и эти оценки не уменьшались даже тогда, когда они были удалены на 800 м. С увеличением расстояния увеличивался лишь разброс индивидуальных оценок. Таким образом, при изменении удаленности воспринимаемого объекта в больших пределах наблюдается константность восприятия его размера.
Рис. 114. Два объекта цилиндрической формы на фоне выраженного градиента текстуры. Основания обоих цилиндров покрывают одинаковое число элементов текстуры, это свидетельствует о равенстве их размеров
Дж. Гибсон сделал принципиальное заключение о природе константности зрительного восприятия величины объекта: «. наблюдатели неосознанно извлекают определенное инвариантное отношение, а размер сетчаточного изображения не играет никакой роли. Независимо от того, насколько далеко находится объект, он пересекает или заслоняет одно и то же число текстурных элементов земли. Это число является инвариантным» [34, 233]. Далее Гибсон указывает на еще один мощный оптический инвариант: «На каком бы расстоянии ни находилась веха, отношение, в котором ее делит горизонт, также является инвариантным» (там же). Важно, что это не признаки для дальнейшей ментальной переработки, а оптическая информация для прямого восприятия размера объекта (рис. 114).
7.3.5. Измерения инвариантных отношений в восприятии
Ряд экспериментальных исследований обнаружил закономерные эффекты взаимодействия между феноменальными параметрами зрительного образа. Рассмотрим несколько вариантов изученных перцептивных взаимодействий, которые получили свое выражение в виде так называемых перцептивных уравнений [73]. Это и есть количественное выражение результата взаимодействия различного рода стимульных и феноменальных параметров, характеризующих разные виды константностей.
Отношение видимой величины и видимой удаленности может быть выражено следующей формулой:
где а — зрительный угол (проксимальная величина объекта); 5 — видимая величина объекта; В — его видимая удаленность; к — коэффициент пропорциональности.
Наглядное следствие из этой формулы дают описанные выше результаты Холвея и Боринга: при а = соп81 видимая величина тестового круга пропорциональна его видимой удаленности^ Из нее следует хорошо известный закон зрительного угла: при В = соп$1 видимая величина изменяется пропорционально зрительному углу.
Еще одно классическое подтверждение «работы» этого инвариантного отношения представляет закон Эммерта: при неизменности площади сетчаточной проекции изменение видимого расстояния до экрана, на который проецируется послеобраз, влечет за собой пропорциональное увеличение его видимого размера.
В работах У. Годжела было показано, что при редукции всех зрительных признаков 1 наблюдаются интересные феномены, названные им тенденцией к равноудаленности и тенденцией к специфической удаленности [73]. Тенденция к специфической удаленности заключается в том, что при полной редукции зрительных признаков человек склонен воспринимать объекты расположенными на одной и той же удаленности от себя, примерно на 1,5 — 2,5 м. Аналогичная тенденция к равноудаленности состоит в том, что все видимые объекты кажутся расположенными в одной плоскости.
Третье следствие из данного инвариантного отношения имеет место при 5 = СОП81, тогда, естественно, В = к/а. Это означает, что если известна видимая величина объекта, то видимая удаленность будет пропорциональна углу зрения. Блестящая иллюстрация данного следствия — эксперимент с игральными картами, описанный в главе 5.
И наконец, последнее следствие из описываемого инвариантного отношения «видимая величина — видимая удаленность», собственно, и описывает феномен константности видимой величины: видимая величина объекта постоянна, если видимая удаленность изменяется обратно пропорционально величине зрительного угла.
В работах У. Годжела также исследовано и другое инвариантное отношение, связывающее видимую глубину и видимую удаленность 2 :
1 Хороший пример восприятия пространства при редукции зрительных при
знаков дают нам отчеты космонавтов, осуществлявших оценки абсолютной и
относительной удаленности объектов в так называемом безориентированном
космическом пространстве.
2 Это соотношение справедливо для удаленностей до двух метров, свыше этого
расстояния в знаменателе формулы параметр В включается без показателя степени.
где АО — видимая относительная удаленность; В — видимая абсолютная удаленность; ц — диспаратность; к — здесь и далее некоторый коэффициент пропорциональности.
Кроме того, было установлено инвариантное отношение, связывающее видимую величину, видимую глубину, диспаратность и зрительный угол:
• Его смысл в том, что не только видимая абсолютная удаленность, но и видимая величина могут определять восприятие глубины.
А.Д.Логвиненко описывает и другие инвариантные отношения: «видимая скорость—абсолютная удаленность»:
где й — абсолютная удаленность; V — скорость перемещения объекта по сетчатке; V — видимая скорость.
Необходимо отметить, что проведение исследований инвариантных отношений в восприятии чрезвычайно сложное дело, требующее от экспериментатора высокого мастерства, поскольку само изучение эффекта влияния одного феноменального параметра на другое требует создания такой стимул ьной ситуации, при которой были бы исключены влияния других феноменальных признаков.
Демонстрация А. Эймса
Блестящей демонстрации некоторых инвариантных отношений в восприятии пространства мы обязаны А.Эймсу, сконструировавшему специальную комнату; в которой «нарушаются» наши привычные представления о размере и удаленности находящегося там объекта [169].
Иллюзия «комнаты Эймса» заключается в том, что испытуемый смотрит в эту комнату одним глазом через искусственный зрачок и видит там в ее правом дальнем углу маленького мальчика большого роста, а в левом углу взрослого мужчину. маленького роста (рис. 115). Если туда поместить двух людей абсолютно одинакового роста, то результат будет тем же: в правом углу — большой человек, в левом — маленький.
Причина этого ошибочного восприятия состоит в конструкции самой комнаты. С помощью специально подобранных признаков удаленности (художник особым образом нарисовал окна, стены, пол) создается иллюзия, что комната имеет обычную прямоугольную форму, т.е. видимая удаленность этих двух человек одинакова, а на самом деле ее площадь представляет трапецию и левый дальний угол комнаты реально расположен от наблюдателя почти вдвое дальше, чем правый (рис. 116).
 |
Рис. 115. Что видит испытуемый в комнате Эймса. Мальчик в действительности маленького роста, а мужчина — это обычный и достаточно высокий взрослый человек
Особенно важно, что видимая величина не просто уменьшилась при увеличении реального расстояния, и, следовательно, при уменьшении размера сетчаточного изображения, а уменьшилась во столько раз, во сколько раз уменьшилось видимое расстояние. Из этой демонстрации следует, что зрительный угол определяет не видимую величину объекта, а отношение видимой величины к видимой удаленности. Что, собственно, и следует из приведенного выше перцептивного уравнения. Таким образом, если меняется один из феноменальных параметров (видимая удаленность), то