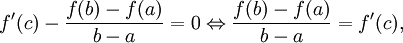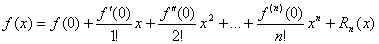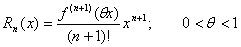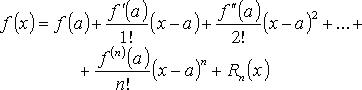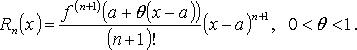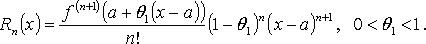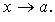инвариантность формы первого дифференциала первого порядка

Свойства первого дифференциала функции.

На мой взгляд, основным необходимым навыком для успешного вычисления неопределенных интегралов является умение вносить функцию под знак дифференциала или извлекать таковую из-под знака дифференциала, основанное на свойствах его инвариантности и линейности.

Свойство инвариантности первого дифференциала функции.

Точнее, свойство инвариантности его формы или формулы.

Такая формулировка вопроса часто встречается в экзаменационных билетах по математическому анализу в зимнюю сессию. Как правило, этот вопрос студенты относят к нежелательным: формализованным и непонятным. А зря. В самом деле, это свойство очень простое, полезное и весьма востребованное в процессе вычисления неопределённых интегралов. Оно является следствием правила дифференцирования сложной функции:

Таким образом, мы получили формулы одного и того же вида для дифференциала функции f (φ(x)) от независимой переменной x и для дифференциала функции f(u) от промежуточного аргумента u, представляющего собой дифференцируемую функцию от x.
Это и есть свойство инвариантности формы (формулы) первого дифференциала.

Пример,
пусть y(x) = sin (π − √x _ )

Свойство инвариантности, утверждающее, что это один и тот же дифференциал, позволяет записать следующиую цепочку равенств

Чтобы внести функцию под знак дифференциала, надо построить такую же цепочку в обратную сторону. Для этого уже потребуется определять не производные, а первообразные функций, стоящих перед знаком дифференциала. Например,

Функция косинус внесена под знак дифференциала. Для этого мы сначала убедились в идентичности переменных под знаками функции и дифференциала (здесь явной заменой переменных, что необязательно), а затем просто вспомнили, что первообразной косинуса является синус.

Дробь с квадратным корнем внесена под знак дифференциала. Здесь числитель и знаменатель дроби зависели от разных переменных, поэтому мы вынуждены были сначала выделить сомножитель, соответствующий производной корня второй степени, а затем записать его первообразную, т.е. сам корень, под знаком дифференциала.

Чем лучше вы ориентируетесь в производных и первообразных основных элементарных функций, тем легче будет увидеть следующий шаг. Полагаю, что и таблицу производных, и таблицу первообразных вы уже изучали, но теперь удобнее свести их в одну. Поэтому рекомендую повторить Единую таблицу производных и первообразных.

Свойства линейности первого дифференциала функции.

( f (x) ± C ) ‘ = f ‘ (x) ± 0 = f ‘ (x)
( C·f (x) ) ‘ = C·f ‘ (x)
.

О последней из них часто забывают и, пользуясь полной формулой дифференцирования дроби, делают совершенно необязательные ошибки из серии «на невнимательность». Поэтому напоминаю еще раз, постоянный множитель можно выносить за знак производной. Ориентируйтесь следующие примеры.

Поскольку дифференциал функции определяется через её производную, при вычислении дифференциала срабатывают те же свойства и правила.

Следствием этого свойства является возможность дописывать под знаком дифференциала любое постоянное слагаемое. Например,

Чтобы использовать это свойство при вычислении неопределенных интегралов, бывает удобно умножить и разделить на одно и то же число функцию, которую нужно внести под знак дифференциала. Например,

Дополнительные примеры и упражнения.

Пример 1.

Сначала расставили скобки, чтобы разобраться в сложных функциях, и выделили выражение с независимой переменной.

Первообразной синуса, является функция минус косинус того же аргумента. Вносим косинус логарифма под дифференциал. Получившееся выражение содержит только функцию cos ln x как под знаком дифференциала, так и вне его.

Здесь удалось внести под знак дифференциала всё выражение. К сожалению, это не всегда просто и даже не всегда возможно. Поэтому и интегрирование сложнее дифференцирования. Чаще всего мы можем внести под знак дифференциала только часть подынтегрального выражения, но и это существенно упрощает задачу.

Вынести функции из-под знака дифференциала

Внести функции под знак дифференциала

dx ______ √1 − x 2 _____ = d ( _______ )

√3x + 7 _____ dx = d ( 3 _______ 2 √3x + 7 _____ )

В первом выражении потеряны коэффициент и знак первообразной синуса.
Во втором, вероятно, была неправильно выделена производная арктангенса. В знаменателе этой функции должна стоять единица(!) плюс квадрат переменной.
В третьем случае вместо первообразной внесена под знак дифференциала производная, что является грубой ошибкой.
Ниже правильные решения подробно. Как уже упоминалось, замену переменных можно делать явно, как в первых двух случаях, или устно, как в последнем.

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.

Источник

4.2.5. Инвариантность формы дифференциала первого порядка

dy=(f(g(t)) dt=f(x)g(t)dt=f(x)dg=f(x)dx. Вид первого дифференциала такой же, как если бы x являлось независимой переменной. Это свойство называется свойством инвариантности дифференциала первого порядка.

Для дифференциалов высших порядков свойства инвариантности, вообще говоря, нет.

Замечание. (Важный частный случай, когда свойство инвариантности наблюдается и для старших дифференциалов). В случае, когда внутренняя функция суперпозиции линейна, свойство инвариантности сохраняется для дифференциалов произвольных порядков.

n-ый дифференциал d n f=f (n) dx n имеет такой же вид, как и в случае независимого переменного x.

4.2.6. Дифференцирование функций, заданных неявно

Рассмотрим функцию, заданную неявно уравнением

и пусть y=f(x) однозначная ветвь этой функции с областью определения X.

Для вычисления дифференциала dy(x₀) функции достаточно продифференцировать равенство . В результате такого дифференцирования получится соотношение вида

где A(x,y), B(x,y) будут представлять собой некоторые выражения, включающие в себя x и y . Из последнего соотношения можно найти выражение для dy в нужной точке.

2xdx+2ydy=0, dy= dx. Для нахождения второго дифференциала следует использовать равенство xdx+ydy=0, дифференцируя которое, получим

dxdx+xd 2 x+dydy+yd 2 y=0 или dx 2 +dy 2 + yd 2 y=0 , откуда получаем d 2 y= .

4.3 Теоремы о среднем для дифференцируемых функций

Теормы о среднем: Ферма, Ролля, Лагранжа, Коши.

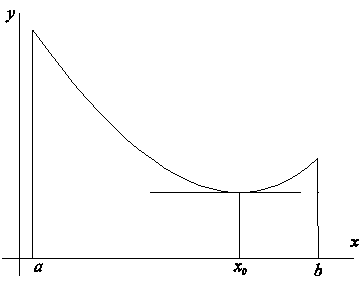
4.3.1. Теорема Ферма о нуле производной

Доказательство. Для случая наименьшего значения

Геометрическая интерпретация. Во внутренних точках, где функция принимает наибольшее или наименьшее значение, касательная к графику функции будет горизонтальна.

4.3.2. Теорема Ролля о нуле производной

Доказательство. Положим ,

. Хотя бы одна из точек x₁, x₂ будет внутренней ( ) и для этой точки утверждение следует из теоремы Ферма.

4.3.3. Теорема Лагранжа о конечных приращениях

Теорема. Если f непрерывна на [a,b], дифференцируема на (a,b), то

Доказательство. Рассмотрим функцию

. Для этой функции F(a)=F(b)=0, и к ней применима теорема Ролля

.

Существует точка, касательная в которой, параллельна хорде, соединяющей точки A и B графика функции.

Источник

25. Дифференциал функции. Геометрический смысл дифференциала. Инвариантность формы дифференциала первого порядка.

Понятие дифференциала функции

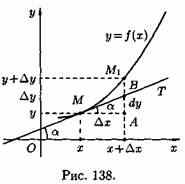
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.

Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать D у/D х=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.

Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых ƒ'(х)•∆х и а•∆х, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как 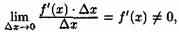а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:

Поэтому первое слагаемое ƒ'(х)· ∆х называют главной частью приращения функции ∆у.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х)•∆х.

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.

Так как у’=х’=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Поэтому формулу (24.1) можно записать так: dy=ƒ'(х)dх, иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Геометрический смысл дифференциала функции

Выясним геометрический смысл дифференциала.

Для этого проведем к графику функции у=ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке ½ АМ½ =∆х, |AM₁|=∆у. Из прямоугольного треугольника МАВ имеем:

Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.

Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

В этом и состоит геометрический смысл дифференциала.

Рассмотрим функцию y = f(u), где u = f (x), то есть рассмотрим сложную функцию y = f(f(x)). Если каждая из функций f и f являются дифференцируемыми, то производная сложной функции согласно теореме (3) равна y’ = f'(u)· u’. Тогда дифференциал функции dy = f'(x)dx = f'(u)u’dx = f'(u)du, du=f(u)du так как u’dx = du. То есть

Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.

26. Теорема о связи дифференцируемости функции и существовании производной (доказательство).

Критерий дифференцируемости: пусть функция f(x) определена в некотором интервале (а, b) и , тогда функция f(x) дифференцируема в точке тогда и только тогда, когда у неё в точке существует производная.

.

, то есть производная существует.

Пусть у функции f(x) в точке существует производная, то есть существует конечный предел .

.

.Теорема доказана.

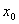
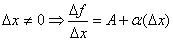
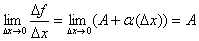
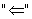
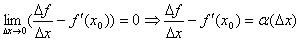
. Теорема Ферма (об обращении производной в нуль). Графическая интерпретация.

Теорема. Если f(x) – определена на (a,b) и дифференцируема в точке x₀ ϵ (a,b), принимает в точке x₀ наибольшее или наименьшее значение, то f¢(x₀)=0.

Доказательство. Для случая наименьшего значения

f¢(x₀+0)= ³ 0, f¢(x₀-0)= £ 0 Þ f¢(x₀)=0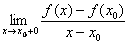

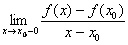
. Теорема Лагранжа (о конечных приращениях). Геометрическая интерпретация.

Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка , что

.

Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Введем функцию 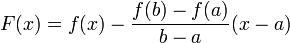. Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю:

что и требовалось доказать.

. Вывод формулы Маклорена для полинома.

Формулой Маклорена называется формула Тейлора при а = 0:

Мы получили так называемую формулу Маклорена с остаточным членом в форме Лагранжа.

. Формула Тейлора для гладкой функции. Представления остаточного члена.

Остаточный член формулы Тейлора

при

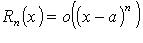
В интегральной форме:

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

4.5 Инвариантность формы первого дифференциала

В начале главы показано, что если функция f : X R → R дифференцируема в точке x 0 и x — независимая переменная ее, то

df x 0 (Δx) = f 0 (x 0 )dx, где dx = x.

(f ◦ ψ) 0 (t 0 ) = f 0 (ψ(t 0 ))ψ 0 (t 0 ) = f 0 (x 0 )ψ 0 (t 0 ).

Поскольку t — независимая переменная функции y = f ◦ ψ(t), то

d(f ◦ ψ) t 0 (Δt) = (f ◦ ψ) 0 (t 0 )dt = f 0 (x 0 )ψ 0 (t 0 )dt, где dt = t.

Кроме того, ψ 0 (t 0 )dt = dψ t 0 (Δt). Если обозначить dx = dψ t 0 (Δt), то получим

d(f ◦ ψ) t 0 (Δt) = f 0 (x 0 )dx.

Сопоставляя полученную формулу с (4.8), замечаем, что форма дифференциала функции y = f(x) не зависит от того, является ли x независимой переменной или дифференцируемой функцией другой переменной. Это свойство называют свойством инвариантности формы дифференциала. Следует заметить, что в формуле (4.8) dx = x, а в (4.9) dx = dψ t 0 (Δt).

4.6 Производные высших порядков

f (n) (x 0 ) = (f (k) ) (n−k) (x 0 ).

Покажем, что функция f дифференцируема любое число раз на (0, +∞).В силу примера 4 функция f дифференцируема на (0, +∞) и

Поскольку f 0 является произведением постоянной и степенной функций, то по теореме 4.4 она дифференцируема на интервале (0, +∞). Следовательно, функция f дважды дифференцируема на нем и

Заметим, что если α = 1, то f 0 (x) = 1 и f 00 (x) = 0, x (0, +∞). Предположим, что n N, n > 2, функция f (n − 1) раз дифферен-

является произведением числа α(α − 1). (α − n + 2)

В частности, если α = k 0 N, то

дифференцируема любое число раз при x > − a b и

Наконец, согласно теореме 4.4, многочлен

дифференцируем на R любое число раз и

Пример 4.12. Докажем, что функция f(x) = ln x дифференцируема любое число раз на (0, +∞).

Замечание. Функция y = ln(ax + b) дифференцируема любое число

раз в области её определения и

ренцируемы любое число раз на R и n N

(sin(ax + b)) (n) = a n sin

(cos(ax + b)) (n) = a n cos

(f ϕ) (n) = f (n) ϕ + nf (n−1) ϕ 0 +

Последняя формула носит имя Лейбница и очень напоминает бином Ньютона. Только её и докажем, используя метод математической индукции. При n = 1 по утверждению 2) теоремы 4.4 имеем: f · ϕ дифференцируема на множестве X и (f ϕ) 0 = f 0 ϕ + ϕ 0 f, поэтому доказываемое утверждение верно при n = 1. Предположим, что для некоторого номера m X

(f (k+1) ϕ (m−k) + f (k) ϕ (m−k+1) ) =

Пример 4.13. Используя формулу Лейбница, найдем n−ую производную функции f(x) = 2x 2 sin 2 x.

Так как f(x) = x 2 (1 − cos 2x) = x 2 − x 2 cos 2x и производные порядка выше, чем степень многочлена, тождественно равны нулю, то при n > 2

f (n) (x) = −x 2 (cos 2x) (n) − 2xn(cos 2x) (n−1) − n(n − 1) 2(cos 2x) (n−2) = 2

π 2 − nx2 n cos 2x + (n − 1) π 2 − −n(n − 1)2 n−2 cos 2x + (n − 2) π 2 =

4.7 Дифференциалы высших порядков

Пусть функция f, определенная на множестве X R, дифференцируема n раз (n ≥ 2) на X. Зафиксируем число x 6= 0 и рассмотрим функцию df(Δx), определенную на множестве X. Так как

то функция df(Δx) дифференцируема на X. Если x 0 X, то величину d(df(Δx)) x 0 (Δx) называют вторым дифференциалом функции f в точке

Для сокращения записи, используются обозначения

Следовательно, второй дифференциал функции f в точке x 0 вычисляется по формуле

По условию функция f дважды дифференцируема на множестве X, поэтому на X определена функция x → d 2 f x (Δx) ( x — фиксированное число), которую называют вторым дифференциалом функции f на множестве X, соответствующим приращению x независимой переменной. Ее обозначают d 2 f(Δx). В силу предыдущего

Индуктивно вводится понятие n-го дифференциала функции f в точке x 0 из X и на множестве X. По индукции легко доказывается, что

Лемма 4.3. Дифференциалы второго и высших порядков, вообще говоря, не обладают свойством инвариантности формы.

d 2 (f ◦ ϕ)(Δt) = d (d(f ◦ ϕ) (Δt)) (Δt) = d((f 0 ◦ ϕ) dϕ(Δt))(Δt) =

= d(f 0 ◦ ϕ)(Δt) dϕ(Δt) + (f 0 ◦ ϕ) d 2 ϕ(Δt) =

= (f 00 ◦ ϕ) (dϕ(Δt)) 2 + (f 0 ◦ ϕ) d 2 ϕ(Δt).

Источник

4.5 Инвариантность формы первого дифференциала

В начале главы показано, что если функция f : X R → R дифференцируема в точке x 0 и x — независимая переменная ее, то

df x 0 (Δx) = f 0 (x 0 )dx, где dx = x.

(f ◦ ψ) 0 (t 0 ) = f 0 (ψ(t 0 ))ψ 0 (t 0 ) = f 0 (x 0 )ψ 0 (t 0 ).

Поскольку t — независимая переменная функции y = f ◦ ψ(t), то

d(f ◦ ψ) t 0 (Δt) = (f ◦ ψ) 0 (t 0 )dt = f 0 (x 0 )ψ 0 (t 0 )dt, где dt = t.

Кроме того, ψ 0 (t 0 )dt = dψ t 0 (Δt). Если обозначить dx = dψ t 0 (Δt), то получим

d(f ◦ ψ) t 0 (Δt) = f 0 (x 0 )dx.

Сопоставляя полученную формулу с (4.8), замечаем, что форма дифференциала функции y = f(x) не зависит от того, является ли x независимой переменной или дифференцируемой функцией другой переменной. Это свойство называют свойством инвариантности формы дифференциала. Следует заметить, что в формуле (4.8) dx = x, а в (4.9) dx = dψ t 0 (Δt).

4.6 Производные высших порядков

f (n) (x 0 ) = (f (k) ) (n−k) (x 0 ).

Покажем, что функция f дифференцируема любое число раз на (0, +∞).В силу примера 4.3.1 функция f дифференцируема на (0, +∞) и

Поскольку f 0 является произведением постоянной и степенной функций, то по теореме 4.4 она дифференцируема на интервале (0, +∞). Следовательно, функция f дважды дифференцируема на нем и

Заметим, что если α = 1, то f 0 (x) = 1 и f 00 (x) = 0, x (0, +∞). Предположим, что n N, n > 2, функция f (n − 1) раз дифферен-

является произведением числа α(α − 1). (α − n + 2)

В частности, если α = k 0 N, то

дифференцируема любое число раз при x > − a b и

Наконец, согласно теореме 4.4, многочлен

дифференцируем на R любое число раз и

Пример 4.6.2. Докажем, что функция f(x) = ln x дифференцируема любое число раз на (0, +∞).

Замечание. Функция y = ln(ax + b) дифференцируема любое число

раз в области её определения и

ренцируемы любое число раз на R и n N

(sin(ax + b)) (n) = a n sin

(cos(ax + b)) (n) = a n cos

(f ϕ) (n) = f (n) ϕ + nf (n−1) ϕ 0 +

Последняя формула носит имя Лейбница и очень напоминает бином Ньютона. Только её и докажем, используя метод математической индукции. При n = 1 по утверждению 2) теоремы 4.4 имеем: f · ϕ дифференцируема на множестве X и (f ϕ) 0 = f 0 ϕ + ϕ 0 f, поэтому доказываемое утверждение верно при n = 1. Предположим, что для некоторого номера m X

(f (k+1) ϕ (m−k) + f (k) ϕ (m−k+1) ) =

Пример 4.6.3. Используя формулу Лейбница, найдем n−ую производную функции f(x) = 2x 2 sin 2 x.

Так как f(x) = x 2 (1 − cos 2x) = x 2 − x 2 cos 2x и производные порядка выше, чем степень многочлена, тождественно равны нулю, то при n > 2

f (n) (x) = −x 2 (cos 2x) (n) − 2xn(cos 2x) (n−1) − n(n − 1) 2(cos 2x) (n−2) = 2

π 2 − nx2 n cos 2x + (n − 1) π 2 − −n(n − 1)2 n−2 cos 2x + (n − 2) π 2 =

4.7 Дифференциалы высших порядков

Пусть функция f, определенная на множестве X R, дифференцируема n раз (n ≥ 2) на X. Зафиксируем число x 6= 0 и рассмотрим функцию df(Δx), определенную на множестве X. Так как

то функция df(Δx) дифференцируема на X. Если x 0 X, то величину d(df(Δx)) x 0 (Δx) называют вторым дифференциалом функции f в точке

Для сокращения записи, используются обозначения

Следовательно, второй дифференциал функции f в точке x 0 вычисляется по формуле

По условию функция f дважды дифференцируема на множестве X, поэтому на X определена функция x → d 2 f x (Δx) ( x — фиксированное число), которую называют вторым дифференциалом функции f на множестве X, соответствующим приращению x независимой переменной. Ее обозначают d 2 f(Δx). В силу предыдущего

Индуктивно вводится понятие n-го дифференциала функции f в точке x 0 из X и на множестве X. По индукции легко доказывается, что

Лемма 4.7.1. Дифференциалы второго и высших порядков, вообще говоря, не обладают свойством инвариантности формы.

d 2 (f ◦ ϕ)(Δt) = d (d(f ◦ ϕ) (Δt)) (Δt) = d((f 0 ◦ ϕ) dϕ(Δt))(Δt) =

= d(f 0 ◦ ϕ)(Δt) dϕ(Δt) + (f 0 ◦ ϕ) d 2 ϕ(Δt) =

= (f 00 ◦ ϕ) (dϕ(Δt)) 2 + (f 0 ◦ ϕ) d 2 ϕ(Δt).

Источник