измерение искажений формы сигналов

Современный метод измерения импульсной характеристики и нелинейных искажений

В 2000 году профессор Пармского университета Анджело Фарина предложил оригинальный метод одновременного измерения импульсной характеристики и нелинейных искажений с помощью гармонического сигнала экспоненциально изменяющейся частоты (далее ESS – exponential sine sweep).

Для получения этих характеристик необходимо записать воздействие ESS-сигнала на испытуемое устройство и найти взаимную корреляционную функцию записанного сигнала с исходным ESS-сигналом, но промодулированным по амплитуде (подробнее об этом можно узнать в публикациях А.Фарина).

В результате получается набор импульсных характеристик (ИХ), последняя из которых является линейной импульсной характеристикой устройства. Ей предшествует импульсная характеристика квадратичной нелинейности устройства, перед ней – импульсная характеристика кубической нелинейности и т.д. На практике удаётся зафиксировать нелинейности до 20 порядка.

Эта особенность (отделение продуктов нелинейности от линейной импульсной характеристики) является уникальным преимуществом ESS-метода по сравнению с другими методами. ESS-метод обладает и другими преимуществами:

Несмотря на очевидные преимущества, ESS-метод имеет и свои границы применения. Сам автор метода перечисляет следующие ограничения:

Другой энтузиаст, Katja Vetter в своём исследовании обнаружил другую проблему, связанную с тем, что каждая октава сигнала начинаются не в нулевой фазе. Это накладывает погрешность на измерение гармоник. В качестве решения автор предложил новый подход к формированию ESS-сигнала: каждая октава должна начинаться с нулевой фазы.

Источник

Опции темы

Переписка Теоретика с ИГВИНом по теме предложенного способа. Простое объяснение.

переписка

Teoretic:
Да. Букварев, Гапонов и К. Ребята нащупали универсальный метод измерения нелинейности именно на музыкальном сигнале. Мощность современных компьютеров позволяет это проделывать даже любителям.
Суть понять не трудно. Методика позволяет сравнить исходный сигнал с воспроизведенным и нечувствительна к линейным искажениям (это бич всех компенсационных/векторных методов). Примеры разностных файлов (чистые нелинейные искажения) можно послушать (выложены по ссылкам в теме http://forum.vegalab.ru/showthread.php?t=72049 )

ИГВИН:
По Букваревской методике надо мне разобраться в сути.
Что с чем сравниваем, как именно. Мельком я не понял.

Teoretic:
В двух словах. Берем музыкальный фрагмент. Пропускаем его через тракт (какой хотите, вплоть до динамиков), записываем результат. Преобразуем фрагмент. Снова пропускаем его через тракт и делаем обратное преобразование. Вычитаем из первого фрагмента второй. Результат (разностный сигнал) соответствует только нелинейным искажениям тракта.

ИГВИН:
Спасибо, суть понятна. Неясно, как это выполнить практически.

Teoretic:
Преобразование Гильберта сдвигает все спектральные составляющие исходного сигнала на 90 градусов.
Поэтому преобразованный сигнал «ортогональный». В принципе, это все.
Если в тракте есть нелинейные искажения, то прямой и ортогональный сигнал будут искажены по-разному.
Из ортогонального сигнала восстанавливаем обратно прямой. По разнице не преобразованного и восстановленного сигнала судим об искажениях. Эту разницу можно просто послушать.
Меру для величины таким образом полученных искажений еще не определили.

ИГВИН:
Сдвигает по фазе на 90 градусов? Относительно чего? Основная (первая) гармоника остаётся в своей фазе? или тоже отъезжает на 90?
Чем это отличается от задержки?

Teoretic:
Все гармоники сдвигаются на 90 градусов относительно гармоник исходного сигнала. Это совсем не задержка. При временной задержке сдвиг фазы пропорционален частоте, а у нас фаза постоянна. Это идеальный фазовращатель.

Мне самому стало интересно.
Я взял простой сигнал: меандр с ограниченным спектром (от первой до одиннадцатой гармоники):
h(x)=cos(x)-cos(3*x)/3+cos(5*x)/5-cos(7*x)/7+cos(9*x)/9-cos(11*x)/11
После сдвига всех гармоник на 90 градусов получим сигнал
g(x)=sin(x)-sin(3*x)/3+sin(5*x)/5-sin(7*x)/7+sin(9*x)/9-sin(11*x)/11
(все косинусы стали синусами).
И построил их графики. Вот они, «ортогональные» сигналы:
https://drive.google.com/open?id=0B8. GJwZTR6VFk4NTQ

ИГВИН:
Вижу. Здорово.
Интегралы по площади равны, форма сильно разная.

09.02.2018 КАК ПРОВЕСТИ ИЗМЕРЕНИЯ (ВРЕМЕННЫЙ СПОЙЛЕР)

Скрытый текст

По ссылке находятся десять тестовых файлов: https://drive.google.com/drive/folde. b_?usp=sharing

Эти файлы делятся на группы по названию:
тесты определения коэффициента гармоник и шумовой полки
-test-1KHz-48.wav
-test_multitone_48.wav

тесты на основе FFT фильтра
-test-nonstationar—NoMercy-FFT-48KHz.wav
-test-nonstationar—NoMercy-FFT-EN-48KHz.wav
-test-nonstationar—NoMercy-FFT-FRQ-48KHz.wav
-test-nonstationar—NoMercy-FFT-FRQ-EN-48KHz.wav

Вначале записать сигнал напрямую, чтобы привязаться к «сквозному каналу».

Потом включить в тракт усилитель под нагрузкой, и записать повторно. Записанные файлы назвать, как считаете нужным.

Между записями разных файлов ничего в системе не изменять.

Потом заменить усилитель (если есть желание и возможность измерить несколько аппаратов), и повторить запись.

По минимуму нужно записать первые шесть файлов из списка. Обязательно записывать ЦЕЛИКОМ. Можно даже оставить в начале и в конце паузы.

Источник

Опции темы

Переписка Теоретика с ИГВИНом по теме предложенного способа. Простое объяснение.

переписка

Teoretic:
Да. Букварев, Гапонов и К. Ребята нащупали универсальный метод измерения нелинейности именно на музыкальном сигнале. Мощность современных компьютеров позволяет это проделывать даже любителям.
Суть понять не трудно. Методика позволяет сравнить исходный сигнал с воспроизведенным и нечувствительна к линейным искажениям (это бич всех компенсационных/векторных методов). Примеры разностных файлов (чистые нелинейные искажения) можно послушать (выложены по ссылкам в теме http://forum.vegalab.ru/showthread.php?t=72049 )

ИГВИН:
По Букваревской методике надо мне разобраться в сути.
Что с чем сравниваем, как именно. Мельком я не понял.

Teoretic:
В двух словах. Берем музыкальный фрагмент. Пропускаем его через тракт (какой хотите, вплоть до динамиков), записываем результат. Преобразуем фрагмент. Снова пропускаем его через тракт и делаем обратное преобразование. Вычитаем из первого фрагмента второй. Результат (разностный сигнал) соответствует только нелинейным искажениям тракта.

ИГВИН:
Спасибо, суть понятна. Неясно, как это выполнить практически.

Teoretic:
Преобразование Гильберта сдвигает все спектральные составляющие исходного сигнала на 90 градусов.
Поэтому преобразованный сигнал «ортогональный». В принципе, это все.
Если в тракте есть нелинейные искажения, то прямой и ортогональный сигнал будут искажены по-разному.
Из ортогонального сигнала восстанавливаем обратно прямой. По разнице не преобразованного и восстановленного сигнала судим об искажениях. Эту разницу можно просто послушать.
Меру для величины таким образом полученных искажений еще не определили.

ИГВИН:
Сдвигает по фазе на 90 градусов? Относительно чего? Основная (первая) гармоника остаётся в своей фазе? или тоже отъезжает на 90?
Чем это отличается от задержки?

Teoretic:
Все гармоники сдвигаются на 90 градусов относительно гармоник исходного сигнала. Это совсем не задержка. При временной задержке сдвиг фазы пропорционален частоте, а у нас фаза постоянна. Это идеальный фазовращатель.

Мне самому стало интересно.
Я взял простой сигнал: меандр с ограниченным спектром (от первой до одиннадцатой гармоники):
h(x)=cos(x)-cos(3*x)/3+cos(5*x)/5-cos(7*x)/7+cos(9*x)/9-cos(11*x)/11
После сдвига всех гармоник на 90 градусов получим сигнал
g(x)=sin(x)-sin(3*x)/3+sin(5*x)/5-sin(7*x)/7+sin(9*x)/9-sin(11*x)/11
(все косинусы стали синусами).
И построил их графики. Вот они, «ортогональные» сигналы:
https://drive.google.com/open?id=0B8. GJwZTR6VFk4NTQ

ИГВИН:
Вижу. Здорово.
Интегралы по площади равны, форма сильно разная.

09.02.2018 КАК ПРОВЕСТИ ИЗМЕРЕНИЯ (ВРЕМЕННЫЙ СПОЙЛЕР)

Скрытый текст

По ссылке находятся десять тестовых файлов: https://drive.google.com/drive/folde. b_?usp=sharing

Эти файлы делятся на группы по названию:
тесты определения коэффициента гармоник и шумовой полки
-test-1KHz-48.wav
-test_multitone_48.wav

тесты на основе FFT фильтра
-test-nonstationar—NoMercy-FFT-48KHz.wav
-test-nonstationar—NoMercy-FFT-EN-48KHz.wav
-test-nonstationar—NoMercy-FFT-FRQ-48KHz.wav
-test-nonstationar—NoMercy-FFT-FRQ-EN-48KHz.wav

Вначале записать сигнал напрямую, чтобы привязаться к «сквозному каналу».

Потом включить в тракт усилитель под нагрузкой, и записать повторно. Записанные файлы назвать, как считаете нужным.

Между записями разных файлов ничего в системе не изменять.

Потом заменить усилитель (если есть желание и возможность измерить несколько аппаратов), и повторить запись.

По минимуму нужно записать первые шесть файлов из списка. Обязательно записывать ЦЕЛИКОМ. Можно даже оставить в начале и в конце паузы.

Источник

Измерение нелинейных искажений

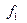
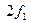
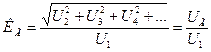
При прохождении гармонического сигнала через нелинейные элементы (у которых ток не пропорционален приложенному напряжению) форма сигнала изменяется. Искаженный гармонический сигнал содержит в своем спектре постоянную составляющую, первую гармонику с частотой и высшие гармоники. , … Количественная оценка отличия реального сигнала от синусоидальной формы производится с помощью коэффициента гармоник, который равен отношению среднеквадратического напряжения гармоник сигнала (кроме первой) к среднеквадратическому значению напряжения первой гармоники:

. (12.10)

Нелинейные искажения сигнала любой формы принято оценивать коэффициентом нелинейности:

. (12.11)

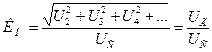
Коэффициенты гармоник и нелинейности связаны между собой соотношением:

. (12.12)

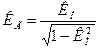
При малой нелинейности эти коэффициенты практически одинаковы.

Используют два метода измерения нелинейных искажений сигнала, аналитический (спектральный) и интегральный (квазигармонический).

Аналитический (гармонический) метод основан на применении селективных приборов (анализаторов спектра, селективных вольтметров и др.), с помощью которых измеряют абсолютные и относительные значения амплитуд первой и высших гармоник, а затем по формуле вычисляют значение коэффициента гармоник.

Интегральный метод позволяет оценить влияние всех высших гармоник на форму сигнала без определения их значений в отдельности. Для этого можно или подавлять первую гармонику, или выделять ее. Наибольшее распространение получил метод, основанный на подавлении первой гармоники.

Приборы, предназначенные для измерения коэффициента нелинейных искажений в соответствии с принятой системой классификации измерительных приборов, относятся к виду С6.

Схема измерителя нелинейных искажении, работающая по интегральному методу с подавлением первой гармоники, представлена на рисунке.

Рис. 12.10 Структурная схема измерителя нелинейных искажений.

Входное устройство обеспечивает согласование входного сопротивления прибора с выходным сопротивлением исследуемого объекта. Широкополосный усилитель служит для усиления всего сигнала до величины, удобной для отсчета. Перестраиваемый заграждающий фильтр служит для подавления напряжения основной частоты.

Процесс измерения нелинейных искажений сводится к выполнению двух операций. При переводе ключа рода работы в положение «Калибр.» электронный вольтметр прибора измеряет напряжения всего исследуемого сигнала. При этом добиваются показаний вольтметра на отметке 100% шкалы с помощью регуляторов во входном устройстве и усилителе. При переводе ключа в положение «Измерение» в схему подключается заграждающий фильтр, который препятствует прохождению первой гармоники сигнала и пропускает на вход вольтметра напряжение высших гармоник исследуемого сигнала. При соответствующей калибровке вольтметра результат измерения нелинейных искажений можно отсчитывать непосредственно по шкале прибора.

В измерителе нелинейных искажений обычно предусматривается дополнительный режим работы для измерения переменного напряжения синусоидальной и несинусоидальной форм.

Кроме рассмотренных параметров спектра сигналов, с использованием анализатора спектра можно измерять частоты и амплитуды линейчатых спектров, спектры шумов и смешанных сигналов, АЧХ трактов передачи сигналов, АЧХ четырехполюсников и другие параметры сигналов.

Источник

Измерение нелинейных искажений

Из курсов ТЭЦ и ТЭС мы знаем, что электрические цепи делятся на линейные, нелинейные и параметрические. Последние два типа цепей отличаются от линейных тем свойством, что могут создавать новые гармонические составляющие в спектре отклика по сравнению со спектром входного сигнала.

Нелинейное преобразование сигнала может быть желательным и полезным (например, при детектировании), а может быть вредным, сопутствующим (например, в усилителях). В этом случае, когда это явление не используется в устройстве, содержащем данную цепь, оно весьма нежелательно, так как часто создает вредные побочные эффекты. Поэтому форма сигнала на выходе этих устройств будет отличаться от формы сигнала на их входе. Изменение формы сигнала называется нелинейным искажением.

Причина нелинейных искажений заключается в том, что при подаче на вход гармонического сигнала частотой f на выходе появляется сигнал, содержащий постоянную составляющую, основную частоту и высшие гармоники с частотами 2f, 3f, 4f и т.д. Амплитуды высших гармоник с увеличением их номеров быстро убывают. Определяющими обычно бывают вторая и третья гармоники.

Источником нелинейных искажений являются элементы цепей, у которых ток не пропорционален приложенному напряжению, т.е. имеющие нелинейную вольтамперную характеристику. Это, как правило, электронные лампы, транзисторы, диоды, катушки c ферромагнитными сердечниками.

Необходимость измерения нелинейных искажений связана с исследованием параметров усилителей и генераторов синусоидальных колебаний.

Нелинейные искажения представляют собой сложной явление, зависящее от многих параметров: состава электрической цепи, ее амплитудно-частотной характеристики, формы сигнала, его амплитуды и т. п. С увеличением амплитуды нелинейные искажения увеличиваются. Обычно при увеличении частоты нелинейные искажения в усилителе также увеличиваются.

Коэффициент гармоник К _Г определяется как отношение среднеквадратического (действующего) значения напряжения суммы всех гармоник сигнала, кроме первой, к среднеквадратическому (действующему) значению напряжения первой гармоники по формуле (34):

Коэффициент К _Г характеризует отличие формы данного периоди­ческого сигнала от гармонической.

Нетрудно увидеть, что при отсутствии в выходном сигнале высших гармоник, К _Г = 0, т.е. синусоидальный сигнал со входа на выход передается без искажений.

Коэффициент нелинейных искажений Кн определяется, как отношение среднеквадратического (действующего) значения напряжения высших гармоник к среднеквадратическому (действующему) значению всего сигнала по формуле (35):

Самыми распространенными одночастотными методами измерения являются:

1. Метод подавления основной гармоники.

2. Метод анализа напряжений.

Измерение нелинейных искажений методом подавления основной гармоники

В соответствии с формулой для определения коэффициента нелинейных иска­жений необходимо измерить действующее значение исследуемого сигнала и дейст­вующее значение высших гармонических составляющих.

Существуют специальные приборы, измеряющие коэффициент нелинейных искажений, называемые измерителями нелинейных искажений.

Упрощенная структурная схема аналогового измерителя нелинейных искажений приведена на рисунке 1.

Рисунок 1 – Упрощенная структурная схема аналогового измерителя нелинейных искажений

Схема прибора сод ержит входное устройство, перестраиваемый режекторный фильтр и квадратичный вольтметр с аттенюатором.

Принцип действия прибора основан на раздельном измерении среднеквадратического значения напряжения исследуемого сигнала и среднеквадратического значения напряжения высших гармоник этого же сигнала.

Входное устройство обеспечивает необходимую величину входного сопротивления и служит для согласования измерительного прибора с источником исследуемого сигнала.

Режекторный фильтр в идеальном случае должен иметь бесконечно большое затухание на частоте первой (основной) гармоники и нулевое затухание на частотах высших гармоник. Обычно режекторный фильтр реализуется с помощью мостовой схемы Вина, состоящей из резисторов и конденсаторов (см. рисунок 2).

Измерение нелинейных искажений методом анализа напряжений

Измерение нелинейных искажений методом анализа напряжений (по отдельным гармоникам) осуществляется с помощью избирательного измерителя уровней (ИИУ).

Схема измерения коэффициента гармоник с помощью ИИУ приведена на рисунке 3, и состоит из генератора, ФНЧ, исследуемого четырехполюсника, ИИУ.

Рисунок 3 – Измерение коэффициента гармоник методом анализа напряжения

ИИУ подключается к выходу исследуемого объекта. При одночастотном синусоидальном сигнале для контроля напряжения любой частоты, оказавшейся в нем в результате нелинейных искажений. При этом ИИУ последовательно настраивается на первую, вторую, третью гармоники (а при необходимости и на более высокие), напряжение (уровень) которых нужно проконтролировать. Таким образом, отдельно измеряются уровни всех интересующих гармоник исследуемого сигнала, и находится затухание нелинейности для каждой из них, при этом берется разность уровня первой гармоники и каждой из контролировавшихся частот:

Источник