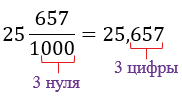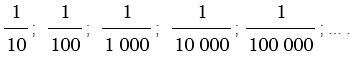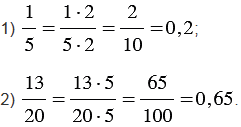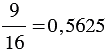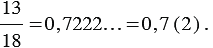к дробям с какими знаменателями применяют десятичную форму записи
383. Заполните пропуски.
1) Десятичную форму записи числа применяют к дробям, знаменатели которых равны 10,100,1000,10000 и т.д.
2) В записи десятичной дроби целую часть числа от дробной отделяет запятой.
3) Целая часть правильной дроби равно 0.
4) Запись дробной части десятичной дроби содержит столько цифр, сколько нулей в записи знаменателя соответствующей обыкновенной дроби.
5) В записи десятичной дроби после запятой идёт разряд десятых, далее разряд сотых, затем разряд тысячных и т.д.
384. Заполните таблицу.
385. Запишите числа, приведённые в таблице, в виде десятичной дроби.
386. Запишите данное число в виде десятичной дроби.
387. Выыделите целую и дробную часть числа и запишите данное число в виде десятичной дроби.
388. Запишите число в виде обыкновенной дроби или смешанного числа.
389. Запишите в виде десятичной дроби число, в котором:
1) четыре единицы, шесть десятых, две сотых
2) шесть десятков, одно единица, одна сотая, шесть тысячных
3) восемь десятых, семь сотых, пять десятитысячных.
390. Выразите в дециметрах и запишите в виде десятичной дроби.
391. Выразите в метрах и запишите в виде десятичной дроби.
392. Выразите в килограммах и запишите в виде десятичной дроби.
393. Найдите координаты точек, изображённых на рисунке.
394. Запишите в виде десятичной дроби частное.
Десятичная запись дробных чисел
Обратите внимание: после запятой стоит столько цифр, сколько нулей стоит в записи знаменателя соответствующей обыкновенной дроби.
Поэтому вместо 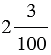
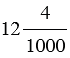
Разряды десятичных дробей
Разрядные единицы:
записываются так:
| При чтении десятичной дроби сначала называют ее часть, стоящую перед запятой, и добавляют слово «целых»; затем называют часть, стоящую после запятой, и добавляют название последнего разряда. |
Чтобы несократимую дробь 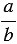
Примеры:
Несократимую дробь 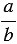
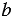
Примеры:
1) 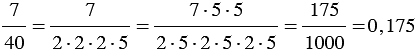
2) 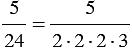
| Чтобы преобразовать обыкновенную дробь в десятичную, можно ее числитель разделить на знаменатель. |
Пример:
| — | 9 | 0 | 0 | 0 | 0 | 1 | 6 |
| 8 | 0 | 0 | 5 | 6 | 2 | 5 | |
| — | 1 | 0 | 0 | ||||
| 9 | 6 | ||||||
| — | 4 | 0 | |||||
| 3 | 2 | ||||||
| — | 8 | 0 | |||||
| 8 | 0 | ||||||
| 0 |
Не любую обыкновенную дробь можно записать в виде десятичной дроби. Например, дробь 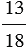
| — | 1 | 3 | 1 | 8 | |||||||
| 1 | 2 | 6 | 0 | , | 7 | 2 | 2 | 2 | . | . | . |
| — | 4 | 0 | |||||||||
| 3 | 6 | ||||||||||
| — | 4 | 0 | |||||||||
| 3 | 6 | ||||||||||
| — | 4 | 0 | |||||||||
| 3 | 6 | ||||||||||
| 4 |
При этом полученную периодическую дробь мы можем округлить до любого из разрядов, например, округлим дробь 0,72222. до десятых, получим:
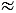
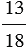
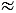
Чтобы найти десятичное приближение обыкновенной дроби до нужного разряда, надо:
1) выполнить деление до следующего разряда;
2) полученную конечную десятичную дробь или бесконечную периодическую десятичную дробь округлить до нужного разряда.
Поделись с друзьями в социальных сетях:
Десятичные дроби
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Мерзляк 5 класс — § 30. Представление о десятичных дробях
Вопросы к параграфу
1. К дробям с какими знаменателями применяют десятичную форму записи?
2. Что в записи десятичной дроби отделяет целую часть от дробной?
3. Чему равна целая часть правильной дроби?
Целая часть правильно дроби равна 0.
4. Сколько цифр содержит запись дробной части десятичной дроби?
Запись дробной части десятичной дроби содержит столько цифр, сколько нулей в записи знаменателя соответствующей обыкновенной дроби.
5. Назовите по порядку четыре разряда, идущих в записи десятичной дроби после запятой.
6. Как читают десятичную дробь?
При чтении сначала называют её целую часть, добавляя слово «целых», а затем называют дробную часть, называя название последнего разряда. Например:
Решаем устно
1. Какую часть:
1) метра составляет:
1 см = 0,01 м
3 дм = 0,3 м
4 мм = 0,004 м
2) тонны составляет:
1 кг = 0,001 т
5 ц = 0,1 т
346 кг = 2,346 т
3) квадратного метра составляет:
1 дм² = 0,01 м²
8 см² = 0,0008 м²
2. Во сколько раз:
1) 1 см меньше 1м
100 см : 1 см = 100
Ответ: в 100 раз
2) 10 г меньше 1 кг
1 000 г : 10 г = 100
Ответ: в 100 раз
3) 9 м больше 9 дм
90 дм : 9 дм = 10
Ответ: в 10 раз
4) 4 ц больше 20 кг
4 000 кг : 20 кг = 200
Ответ: в 200 раз
3. К сумме чисел 28 и 6 прибавьте сумму чисел 12 и 14.
(28 + 6) + (12 + 14) = 34 + 26 = 60
4. Из разности чисел 30 и 16 вычтите разность чисел 42 и 29.
(30 — 16) — (42 — 29) = 14 — 13 = 1
5. Произведение чисел 12 и 5 умножьте на произведение чисел 15 и 4.
(12 • 5) • (15 • 4) = 60 • 60 = 3 600
6. Частное чисел 90 и 15 разделите на частное чисел 84 и 14.
(90 : 15) : (84 : 14) = 6 : 6 = 1
Упражнения
797. Запишите в виде десятичной дроби:
1) = 0,8
2) = 0,34
3) = 0,683
4) = 14,5
5) = 6,27
6) = 42,174
7) = 9,03
8) = 17,024
9) = 5,001
10) = 63,00019
11) = 0,0032
12) = 0,004
13) = 0,000003
14) = 3,15
15) = 3,015
16) = 3,0015
798. Прочитайте десятичную дробь:
1) 1,6 — Одна целая шесть десятых
2) 12,8 — Двенадцать целых восемь десятых
3) 5,24 — Пять целых двадцать четыре сотых
4) 6,325 — Шесть целых триста двадцать пять тысячных
5) 17,4192 — Семнадцать целых четыре тысячи сто девяносто две десятитысячных
6) 0,5 — Ноль целых пять десятых
7) 0,05 — Ноль целых пять сотых
8) 0,005 — Ноль целых пять тысячных
9) 3,04 — Три целых четыре сотых
10) 0,0304 — Ноль целых триста четыре десятитысячных
11) 12,098 — Двенадцать целых девяносто восемь тысячных
12) 0,01012 — Ноль целых тысяча двенадцать стотысячных
799. Запишите в виде десятичной дроби:
1) = 0,7
2) = 0,27
3) = 0,574
4) = 21,8
5) = 9,83
6) = 56,144
7) = 1,05
8) = 18,045
9) = 2, 003
10) = 74,00013
11) = 0,006
12) = 0,0012
13) = 0,00005
14) = 1,1
15) = 1,01
16) = 1,001
800. Выделите целую и дробную части числа и запишите данное число в виде десятичной дроби:
1)
2)
3)
4)
5)
6)
801. Выделите целую и дробную части числа и запишите данное число в виде десятичной дроби:
1)
2)
3)
4)
5)
6)
802. Запишите число в виде обыкновенной дроби или смешанного числа:
1) 2,4 =
2) 3,18 =
3) 46,52 =
4) 1,06 =
5) 9,074 =
6) 0,9 =
7) 0,04 =
8) 0,30 =
9) 0,68 =
10) 0,001 =
11) 0,072 =
12) 0,234 =
803. Запишите число в виде обыкновенной дроби или смешанного числа:
1) 4,9 =
2) 8,95 =
3) 1,567 =
4) 0,2 =
5) 0,043 =
6) 0,008 =
7) 5,06 =
8) 12,018 =
804. Запишите в виде десятичной дроби число, в котором:
805. Запишите в виде десятичной дроби число, в котором:
806. Выразите в дециметрах и запишите в виде десятичной дроби:
807. Выразите в килограммах и запишите в виде десятичной дроби:
808. Выразите в метрах и запишите в виде десятичной дроби:
809. Запишите в виде десятичной дроби частное:
810. Запишите в виде десятичной дроби частное:
811. Какие числа на координатном луче соответствуют:
Ответ запишите в виде десятичных дробей.
1) точкам A, B, C, D, F, E (рис. 204)
A (0,4); B (0,8); C (1,1); D (1,7); F (1,9); E (2,2).
2) точкам M, N, K, P, R, S (рис. 205)
M (5,9); N (6,3); K (6,6); P (7,2);R (7,7); S (8,4).
812. Начертите координатный луч, взяв за единичный такой отрезок, длина которого в десять раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам 0,3; 0,7; 0,9; 1,1; 1,5; 2,1.
A (0,3); B (0,7); C (0,9); D (1,1); F (1,5); E (2,1).
813. Начертите координатный луч, взяв за единичный такой отрезок, длина которого в десять раз больше стороны клетки тетради. Отметьте на луче точки, которые соответствуют числам 0,1; 0,6; 0,8; 1,4; 1,9; 2,2.
A (0,1); B (0,6); C (0,8); D (1,4); F (1,9); E (2,2).
Упражнения для повторения
814. Мама поручила сыну купить продукты. На хлеб он потратил всех денег, на молоко —
, на овощи —
, а
всех денег — на фрукты. На какую покупку было потрачено наибольшее количество денег? Наименьшее количество денег? Остались ли деньги у мальчика после покупок?
Наибольшее количество денег было потрачено на покупку фруктов — всех денег.
Наименьшее количество денег было потрачено на хлеб — всех денег.
Всего было потрачено +
+
+
=
всех денег. Так как
Ответ: На фрукты, на хлеб, деньги остались.
815. Во сколько раз мин меньше, чем 4 мин 10 с?
1) 60 : 6 • 5 = 10 • 5 = 50 (с) — включают в себя минуты.
2) 4 • 60 + 10 = 240 + 10 = 250 (с) составляют 4 мин 10 с.
3) 250 : 50 = 5 (раз) — минуты меньше, чем 4 мин 10 с.
816. Во сколько раз 5 ч 50 мин больше, чем ч?
1) 60 : 12 • 7 = 5 • 7 = 35 (мин) — включают в себя часа.
2) 5 • 60 + 50 = 300 + 50 = 350 (мин) — составляют 5 ч 50 мин
3) 350 : 35 = 10 (раз) — 5 ч 50 мин больше, чем часа.
817. Какие цифры можно поставить вместо звёздочки, чтобы образовалось верное неравенство:
Ответ: Цифры 0, 1 и 2.
2) 4 *40 > 4 735
Ответ: Цифры 7, 8 и 9.
818. В числах стёрли несколько цифр и вместо них поставили звёздочки. Сравните эти числа:
1) 35 *** и 32 ***
3 5 *** > 3 2 ***, так как оба числа пятизначные, но у первого числа цифра в разряде тысяч больше, чем у второго числа (5 > 2).
2) 52* и * *98
Задача от мудрой совы
819. Как поделить поровну 7 яблок между 12 друзьями, если каждое яблоко можно разрезать не более чем на 4 части?
Для этого надо разрезать яблоки следующим образов:
В этом случае все получат поровну: и
части яблока.