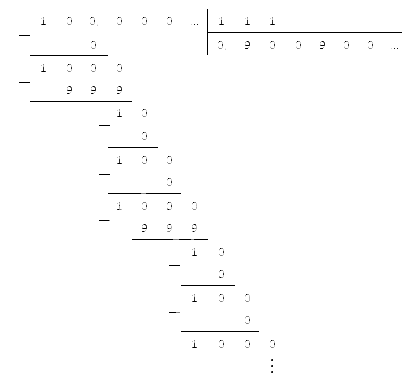
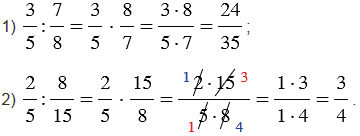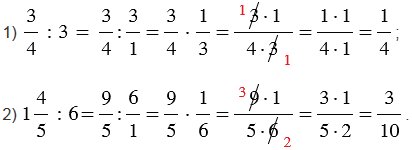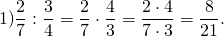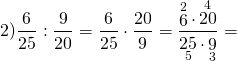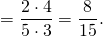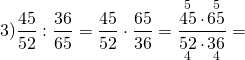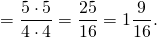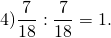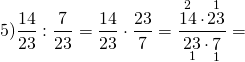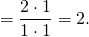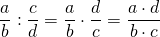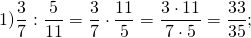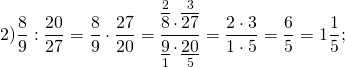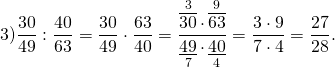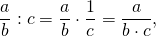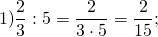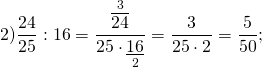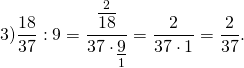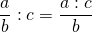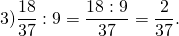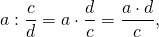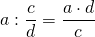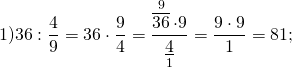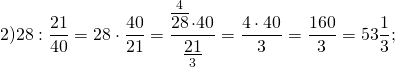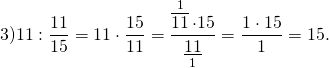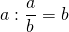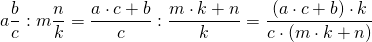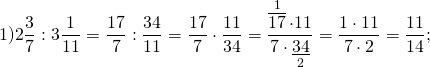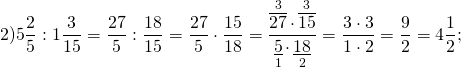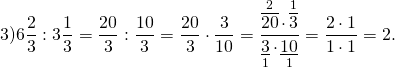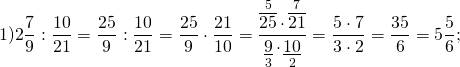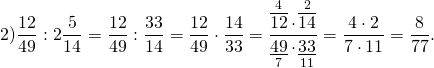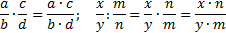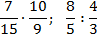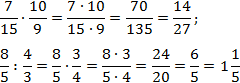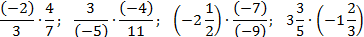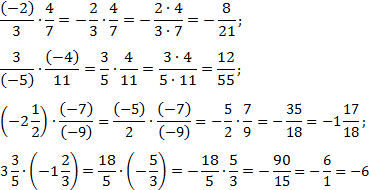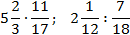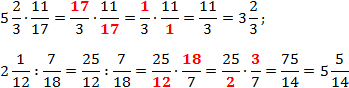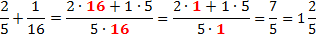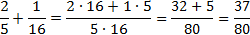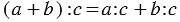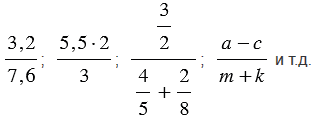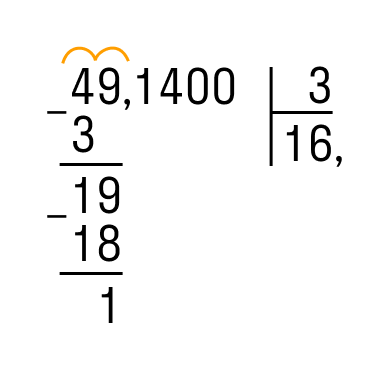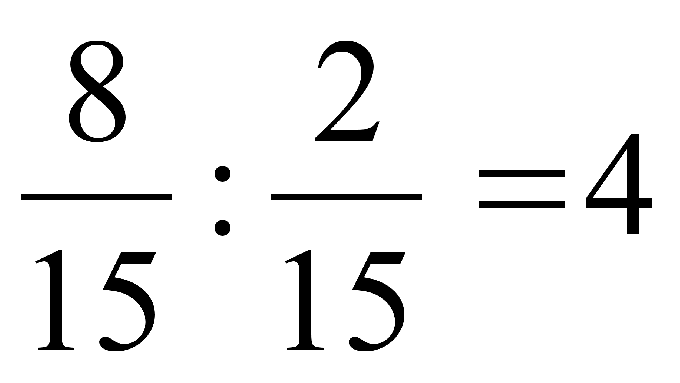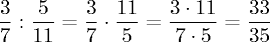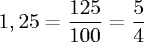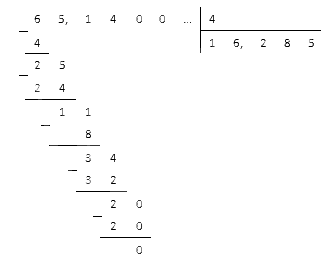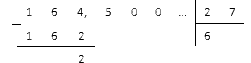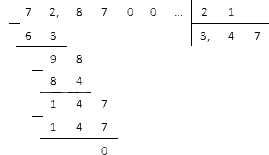Как делятся дроби
Как делятся дроби
Деление обыкновенных дробей
| Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное делителю. |
Примеры:
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Деление смешанных чисел
| Чтобы выполнить деление смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом деления дробей. |
Примеры:
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Деление на натуральное число
При делении дроби на натуральное число, учитываем то, что любое натуральное число можно представить в виде дроби со знаменателем 1, затем пользуемся правилом деления дробей.
Примеры:
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Нахождения числа по его дроби
| Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь |
Примеры:
1) Найдите число, если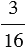 
данного числа равны 27:
2) Найдите число, если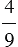 
данного числа равны 
:
Поделись с друзьями в социальных сетях:
Деление дробей: теория и практика
Понятие дроби
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b.
Существует два формата записи:
обыкновенный вид — 1/2 или a/b,
десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Основные свойства дроби
1. Дробь не имеет значения, при условии, если знаменатель равен нулю.
2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
3. Две дроби a/b и c/d называются равными, если a * d = b * c.
4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление дробных чисел
Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.
Свойства деления:
При делении на единицу получится такое же число: a : 1 = a.
На ноль делить нельзя.
При делении нуля на что-либо получится ноль: 0 : a = 0.
При делении числа на само себя получится единица: a : a = 1.
При деления суммы на какое-либо число, можно разделить на него каждое слагаемое и сложить полученные результаты: (a + b) : c = a : c + b : c.
При делении произведения двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель: (a * b) : c = (a : c) · b = a * (b : c).
Деление обыкновенных дробей
Как делить дробь на дробь? Выполняем следующую последовательность действий:
числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам не важно, одинаковые знаменатели или нет.
Деление дроби на натуральное число
Для деления дроби на натуральное число нужно:
представить данный делитель в виде неправильной дроби, где числитель равен этому числу, а знаменатель единица;
произвести деление по предыдущему правилу.
Деление натурального числа на дробь
Чтобы поделить натуральное число на обыкновенную дробь нужно:
делимое записать в виде дроби;
умножить полученную дробь на дробь, обратную делителю, воспользовавшись алгоритмом, который мы уже разобрали выше.
Деление на смешанное число
Для деления смешанных чисел необходимо:
представить числа в виде неправильных дробей
Деление дробей. Правила. Примеры.
Следующее действие, которое можно выполнять с дробями это деление. Выполнять деление дробей достаточно просто главное знать несколько правил деления. Разберем правила деления и рассмотрим решение примеров на данную тему.
Деление дроби на дробь.
Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.
Деление дроби на число.
Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.
Выполните деления дроби на натуральное число \(\frac<4> <7>\div 3\).
Как мы уже знаем, что любое число можно представить в виде дроби \(3 = \frac<3> <1>\).
Деление числа на дробь.
Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.
Выполните деление числа на дробь.
Деление смешанных дробей.
Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.
Выполните деление смешанных дробей.
Деление числа на число.
Чтобы поделить простые числа, нужно представить их в виде дроби и выполнить деление по правилам деления дроби на дробь.
Примечание к теме деление дробей:
На нуль делить нельзя.
Вопросы по теме:
Как делить дроби? Как разделить дробь на дробь?
Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.
Как делить дроби с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.
Пример №1:
Выполните деление и назовите делитель, дробь, обратную делителю: а) \(\frac<5> <9>\div \frac<8><13>\) б) \(2\frac<4> <5>\div 1\frac<7><8>\)
\( \frac<8><13>\) – делитель, \( \frac<13><8>\) – обратная дробь делителя.
\( \frac<15><8>\) – делитель, \( \frac<8><15>\) – обратная дробь делителя.
Пример №2:
Вычислите деление: а) \(5 \div 1\frac<1><4>\) б) \(9\frac<2> <3>\div 8\)
Деление дробей
Научившись умножать обыкновенные дроби, несложно научиться их делить. Как обычно, рассмотрим какие случаи могут нам встретиться при вычислении примеров на деление дробей.
Деление дроби на дробь
Чтобы разделить одну обыкновенную дробь на другую, отличную от нуля, нужно:
Другими словами, деление дробей сводится к умножению. Поэтому правила деления дробей можно записать следующим образом.
Чтобы разделить одну дробь на другую, надо делимое (первую дробь) умножить на обратную дробь делителю.
Как дробь разделить на число
Чтобы разделить дробь на натуральное число, можно использовать следующий способ.
Мы представляем натуральное число в виде неправильной дроби с числителем, равным самому числу, а знаменатель равным единице.
Затем призводим деление по правилу деления дроби на дробь.
Деление смешанных чисел
При делении смешанных чисел надо представить числа в виде неправильных дробей, а потом разделить их друг на друга по правилу деления дроби на дроби.
Деление обыкновенных дробей: правила, примеры, решения
С дробями можно выполнять все действия, в том числе и деление. Данная статья показывает деление обыкновенных дробей. Будут даны определения, рассмотрены примеры. Подробно остановимся на делении дробей на натуральные числа и наоборот. Будет рассмотрено деление обыкновенной дроби на смешанное число.
Деление обыкновенных дробей
Деления является обратным умножению. При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.
Отсюда получим и сформулируем правило деления обыкновенных дробей:
Запишем правило в виде выражения: a b : c d = a b · d c
Правила деления сводятся к умножению. Чтобы придерживаться его, нужно хорошо разбираться в выполнении умножения обыкновенных дробей.
Перейдем к рассмотрению деления обыкновенных дробей.
Ответ: 9 7 : 5 3 = 27 35 .
При сокращении дробей следует выделять целую часть, если числитель больше знаменателя.
Для решения нужно перейти от деления к умножению. Запишем это в такой форме: 8 15 : 24 65 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Необходимо произвести сокращение, а это выполняется следующим образом: 8 · 65 15 · 24 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Деление необыкновенной дроби на натуральное число
Рассмотрим данное деление дроби на число.
Решение
Ответ: 16 45 : 12 = 4 135 .
Деление натурального числа на обыкновенную дробь
Ответ: 25 : 15 28 = 46 2 3 .
Деление обыкновенной дроби на смешанное число
При делении обыкновенной дроби на смешанное число легко можно свети к делению обыкновенных дробей. Нужно совершить перевод смешанного числа в неправильную дробь.
Деление смешанного числа производится таким же образом, как и обыкновенных.
Дроби. Деление дробей.
Правила деления дробей.
1. Чтобы поделить 1-ну дробь на вторую, необходимо делимое умножить на число, которое обратно делителю.
2. Чтобы поделить дробь на натуральное число, необходимо делимое умножить на число, которое обратно делителю.
3. Иными словами, чтобы поделить дробь на натуральное число, необходимо знаменатель умножить на это число.
4. На ноль делить нельзя.
5. На смешанную дробь делить нельзя.
6. При определении результата пользуйтесь основным свойством дробей для сокращения дробей.
Для правильных и неправильных дробей правило деления следующее:
Чтобы поделить обыкновенную дробь, необходимо числитель делимого умножить на знаменатель делителя, а знаменатель делимого умножить на числитель делителя. Первое произведение берем числителем, а второе — знаменателем.
Деление дроби на дробь.
Чтобы разделить 1-ну обыкновенную дробь на вторую, не равную нулю, необходимо:
Иными словами, деление дробей переходит к умножению.
Чтоб поделить 1-ну дробь на вторую, необходимо делимое (1-ну дробь) умножить на обратную дробь делителю.
Деление дроби на число.
Схематически деление дроби на натуральное число выглядит так:
Чтобы поделить дробь на натуральное число, используют такой метод:
Выражаем натуральное число как неправильную дробь с числителем, который равен самому числу, а знаменатель равным 1-це.
Далее производим деление по правилу деления дроби на дробь.
Деление смешанных чисел.
При делении смешанных чисел необходимо представить числа как неправильные дроби, а далее делим их друг на друга по правилу деления дроби на дроби.
Деление дробей, формула
Деление правильных дробей
Определение
Чтобы разделить дробь на целое число, нужно преобразовать целое число в дробь (1), полученную дробь перевернуть (2) и умножить на первую дробь (3).
Иными словами: чтобы разделить дробь на целое число, нужно числитель оставить прежним, а знаменатель исходной дроби умножить на данное число.
Деление смешанных дробей
Определение
Чтобы разделить смешанные дроби, сначала нужно
преобразовать их в неправельные (1), а затем перевернуть
вторую дробь (2) и умножить на первую (3).
Пример
2 4 3 : 3 1 4 = 2 • 3 + 4 3 : 3 • 4 + 1 4 = 10 3 : 13 4 = 10 3 • 4 13 = 40 39 = 1 1 39 ;
Обратная дробь
Пример (взаимно обратные) 3 4 и 4 3 ;
Как делить дроби
Чтобы понять, как делить дроби, изучим правило и на примерах рассмотрим, как его применять.
Правило деления обыкновенных дробей
Чтобы разделить две дроби, надо первое число умножить на число, обратное ко второму (то есть первую дробь умножаем на перевернутую вторую).
Примеры деления обыкновенных дробей :
Чтобы разделить эти дроби, первую дробь переписываем и умножаем на дробь, обратную ко второй (делимое умножаем на число, обратное делителю). Сократить здесь ничего нельзя.
Чтобы разделить данные дроби, первое число переписываем без изменений и умножаем на число, обратное ко второму. Сокращаем 6 и 9 на 3, 20 и 25 — на 5. Полученная в результате дробь 8/15 — правильная и несократимая. Значит, это — окончательный ответ.
Первую дробь оставляем без изменений и умножаем на число, обратное ко второй дроби. Сокращаем 45 и 36 на 9, 65 и 52 — на 13. В результате получили неправильную дробь, из которой выделяем целую часть.
При деление двух равных чисел получаем единицу, поэтому сразу можем записать ответ.
Чтобы разделить дроби, первую умножаем на число, обратное ко второму. Сокращаем 23 и 23 на 23, 14 и 7 — на 7. Поскольку в знаменателе стоит единица, ответ — целое число.
В следующий раз рассмотрим, как разделить целое число на дробь.
6 Comments
Скажите пожалуйста, как разделить неправильную дробь на целую часть?
Надо делимое умножить на число, обратное делителю. Обратное к целому числу a — число 1/a. Наберите в поиске на сайте «Деление дробей», недавно всю информацию по делению обыкновенных дробей и смешанных чисел собрала в одном посте. Там и правила, и примеры на каждое правило.
Спасибо за объяснение! Очень понятно! Сайт просто класс! Недаром были Ваши труды- много счастливых пользователей! Удачи Вам и всех благ
Спасибо, Фатя, за такие тёплые слова! Успехов Вам в учёбе и всего хорошего!
Понял тему за 10 минут, чем учительница которая объясняет 40 минут
Может быть, в этот раз Вы были настроены на работу, а в предыдущий раз — нет. И вообще, самостоятельная работа приносит массу удовольствия.
Деление дробей
Деление дробей — тема, которая включает в себя действия с обыкновенными дробями, смешанными числами и десятичными дробями.
Запишем на одной странице все правила, касающиеся деления обыкновенных дробей, смешанных чисел и натуральных чисел.
Чтобы разделить дробь на дробь, надо делимое умножить на число, обратное делителю.
(то есть первую дробь нужно переписать без изменений и умножить её на «перевёрнутую» вторую дробь).
При умножении дробей проще сокращать множители, чем результат.
Если в результате получается неправильная дробь, нужно выделить из неё целую часть.
Примеры деления обыкновенных дробей :
Применив правило деления обыкновенных дробей
приходим к выводу:
Чтобы разделить дробь на натуральное число, надо знаменатель умножить на это число, а числитель оставить без изменения.
Примеры деления обыкновенной дроби на число :
Заметим, что если числитель дроби делится на число без остатка, при делении можно числитель разделить на число, а знаменатель оставить тем же:
Стоит ли запоминать ещё одно правило или использовать одно правило для всех случаев — решать вам.
Применив правило деления обыкновенных дробей
приходим к выводу:
чтобы разделить натуральное число на дробь, надо в числитель записать произведения этого числа и знаменателя, а в знаменатель записать числитель.
Можно запомнить это правило и применять его в дальнейшем. А можно делить число на дробь, применяя для всех случаев деления дробей одно правило. Выбирайте, что для вас удобнее.
Примеры деления натурального числа на дробь :
Здесь можно сделать ещё один вывод:
Чтобы разделить смешанные числа (смешанные дроби), надо превратить их в неправильные дроби и разделить по правилу деления обыкновенных дробей:
(эту формулу запоминать не надо. Достаточно знать, как переводить смешанные дроби в неправильные и делить обыкновенные дроби).
Примеры деления смешанных дробей :
Примеры деления смешанного числа и обыкновенной дроби :
В следующий раз рассмотрим все правила, касающиеся деления десятичных дробей.
Деление обыкновенных дробей: правила, примеры, решения.
Еще одним действием с обыкновенными дробями является деление. В этой статье мы поговорим про деление обыкновенных дробей. Сначала мы дадим правило деления обыкновенных дробей и рассмотрим примеры деления дробей. Дальше остановимся на делении обыкновенной дроби на натуральное число и числа на дробь. Наконец, рассмотрим, как проводится деление обыкновенной дроби на смешанное число.
Навигация по странице.
Деление обыкновенной дроби на обыкновенную дробь
Известно, что деление является действием, обратным умножению (смотрите связь деления с умножением). То есть, деление предполагает нахождение неизвестного множителя, когда известно произведение и другой множитель. Этот же смысл деления сохраняется и при делении обыкновенных дробей.
Обобщив всю приведенную информацию, получаем правило деления обыкновенных дробей: чтобы разделить обыкновенную дробь a/b на дробь c/d нужно делимое умножить на число, обратное делителю.
С помощью букв озвученное правило умножения обыкновенных дробей записывается так: 
.
Итак, правило деления обыкновенных дробей сводит деление к умножению. Таким образом, чтобы успешно выполнять деление дробей по этому правилу, надо уметь выполнять умножение обыкновенных дробей.
Рассмотрим примеры деления обыкновенных дробей.
.
Отметим, что не следует забывать про сокращение дробей и про выделение целой части из неправильной дроби.
Проведите деление дробей 
.
.
Деление обыкновенной дроби на натуральное число
Это правило деления напрямую следует из правила деления обыкновенных дробей. Действительно, представление натурального числа в виде дроби приводит к следующим равенствам 
.
Рассмотрим пример деления дроби на число.
.
Деление натурального числа на обыкновенную дробь
Согласно озвученному правилу, 
, а правило умножения натурального числа на обыкновенную дробь позволяет его переписать в виде 
.
Перейдем от деления к умножению, имеем 
. После сокращения и выделения целой части получаем 
.
.
Деление обыкновенной дроби на смешанное число
Деление обыкновенной дроби на смешанное число легко сводится к делению обыкновенных дробей. Для этого достаточно осуществить перевод смешанного числа в неправильную дробь.
Выполните деление дроби 35/16 на смешанное число 
.
.
Умножение и деление дробей
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
Задача. Найдите значение выражения:
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения. Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
Деление обыкновенных дробей: правила, примеры, решения
Время чтения: 7 минут
Из статьи вы узнаете, как поделить одну обыкновенную дробь на другую, обыкновенную дробь на натуральное число и натуральное число на обыкновенную дробь. Подробно расскажем о делении дробей и смешанных чисел.
Как проводить деление обыкновенных дробей
Правило деления обыкновенных дробей следующее:
Для деления обыкновенных дробей следует первую из них умножить на дробь обратную второй.
Деление дробей с разными знаменателями проводится аналогичным образом. Какие у них знаменатели, значения не имеет.
Поделить (3/5) на (7/8).
(3/5) : (7/8) = (3/5)*(8/7) = 24/35
Поделить (2/5) на (8/15).
(2/5) : (8/15) = (2/5) * (15/8) = (2*15)/(5*8).
Сокращаем на 5 и на 2.
В результате имеем (2/5) : (8/15) = ¾
Поделить (4/7) на (2/5).
(4/7) : (2/5) = (4/7) * (5/2) = 10/7
Полученная дробь неправильная, поэтому выделим из неё целое число. В результате получим 1(3/7).
Деление обыкновенных дробей на число
Как известно, любое натуральное число можно записать как дробь, у которой знаменатель равняется одному. Например, число 2 можно записать, как (2/1), а число 7 записать, как (7/1). При осуществлении деления обыкновенной дроби на натуральное число этим правилом очень активно пользуются.
Для деления дроби на натуральное число следует это самое число записать в виде дроби, а затем провести деление согласно правилам.
Пример: Поделить (5/9) на 2.
Деление смешанных чисел: правило, примеры
В этой статье мы рассмотрим правило, по которому выполняется деление смешанных чисел. Как делить смешанные числа? Как разделить целое число на смешанную дробь? Как делить целое число на смешанную дробь и как смешанную дробь разделить на целое число? Ответы на эти вопросы вы будете знать после прочтения материала.
Деление смешанного числа на смешанное число
Деление смешанного числа на смешанное число удобнее всего свести к делению обыкновенных дробей. Как выглядит правило деления смешанных чисел? Сформулируем его.
Правило деления смешанных чисел
Чтобы разделить смешанное число на смешанное число, нужно:
Перейдем к примеру и разберем ход его решения.
Пример 1. Деление смешанного числа на смешанное число
После перевода смешанных чисел в неправильные дроби, получаем:
1 1 35 = 1 · 35 + 1 35 = 36 35
3 6 7 = 3 · 7 + 6 7 = 27 7
Теперь делим обыкновенные дроби и сокращаем результат:
На этом деление смешанных чисел окончено.
Деление смешанного числа на натуральное число
Пример 2. Деление смешанного числа на натуральное число
Переходим от смешанного числа к обыкновенной неправильной дроби:
3 3 4 = 3 · 4 + 3 4 = 15 4
Осуществляем деление и сокращаем:
3 3 4 ÷ 75 = 15 4 ÷ 75 = 15 4 · 75 = 1 20
На этом деление смешанного числа на натуральное число окончено.
Деление натурального числа на смешанное число
Как и в предыдущем пункте, такое деление сводится к переводу смешанного числа в обыкновенную дробь.
Единственное отличие состоит в том, что раньше мы переводили в вид обыкновенной дроби делимое, а теперь будем обращать делитель.
Пример 3. Деление натурального числа на смешанное число
Переведем делимое в вид обыкновенной дроби:
8 3 10 = 8 · 10 + 3 10 = 83 10
Теперь выполняем деление:
Данная неправильная дробь несократима. Для удобства, можно перевести ее обратно в смешанное число
Это и есть результат деления.
Деление смешанного числа на обыкновенную дробь
Как и все предыдущие случаи, деление смешанного числа на обыкновенную дробь также сводится к делению обыкновенных дробей. В любой непонятной ситуации переводите смешанное число в обыкновенную дробь!
Пример 4. Деление натурального числа на смешанное число
Переводим делимое также в вид обыкновенной дроби:
Делим, сокращаем и получаем ответ:
98 45 ÷ 28 15 = 98 45 · 15 28 = 98 3 · 28 = 98 84 = 7 6 = 1 1 6
Как делятся дроби
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )
Эта операция гораздо приятнее сложения-вычитания! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:
Всё предельно просто. И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…
Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:
В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:
Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:
Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
В первом случае (выражение слева):
Во втором (выражение справа):
Чувствуете разницу? 4 и 1/9!
А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:
то делим-умножаем по порядочку, слева направо!
И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:
Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.
Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!
3. Все дроби сокращаем до упора.
4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы.
Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.
Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать. Вот они, ответы, через точку с запятой записаны.
0; 17/22; 3/4; 2/5; 1; 25.
Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но. Это решаемые проблемы.
В Особом разделе 555 «Дроби» разобраны все эти (и не только!) примеры. С подробными пояснениями что, зачем и как. Такой разбор здорово помогает при нехватке знаний и навыков!
Да и по второй проблеме там есть кое-что. ) Вполне практический совет, как стать внимательнее. Да-да! Совет, который может применить каждый.
Кроме знаний и внимательности для успеха нужен определенный автоматизм. Где его взять? Слышу тяжелый вздох… Да, только в практике, больше негде.
Если Вам нравится этот сайт.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
А вот здесь можно познакомиться с функциями и производными.
Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 
, т.е. 2 : 3 = .
Пример:
= 3 : 5; 
= 5 : 3.
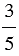
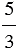
| В результате деления двух натуральных чисел может получится натуральное число или дробное число. |
Пример:
20 : 4 =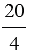 
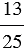
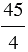
= 5; 13 : 25 = 
; 45 : 4 = 
.
| Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем. |
Пример:
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
| Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением. |
К дробным выражениям относятся:
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
, обычно запись упрощают, и пишут так: 
.
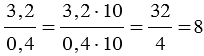
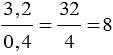
То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
.
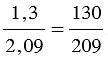
Поделись с друзьями в социальных сетях:
Деление десятичных дробей
5 класс, 6 класс
Как разделить десятичную дробь на натуральное число столбиком
Делить столбиком можно не только натуральные числа, но и дроби. Алгоритм мы подробно опишем здесь. Итак, как делить десятичные дроби на натуральные числа в столбик:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Выполнить деление по стандартной схеме. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться — получится периодическая дробь.
Пример: Разделить столбиком
Как решаем
1. Делим столбиком, предварительно дописав два нуля к десятичной дроби.
2. После того, как мы поделили целую часть дроби и получили 16, отделяем ответ запятой (16) и продолжаем деление уже для дробной части
В конце у нас нулевой остаток, значит деление завершено.
Ответ:
Как разделить столбиком одну десятичную дробь на другую
Для этого необходимо перенести запятую в делимом и делителе вправо на одинаковое количество знаков — так, чтобы делитель превратился в натуральное число. Далее выполняем описанную выше последовательность действий.
1. Переносим запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, дописываем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
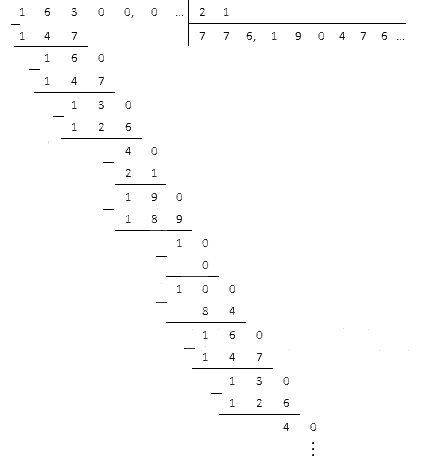
Пример: поделить столбиком 63,42 на 2,1
Как решаем
Переносим запятую на один знак вправо, чтобы делитель (2,1) стало натуральным числом. Запятую переносим в обоих числах — у нас получается 634,2÷21.
Затем производим деление:
Ответ:
Как разделить десятичные дроби на 1000, 100, 10 и другие
Как вы уже заметили, есть основное правило деления десятичных дробей: по нему деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и другие.
Чтобы выполнить действие, нужно просто перенести запятую влево на нужное количество цифр (равное нулям). Если значений в числе не хватит для переноса, нужно дописать справа нужное количество нулей:
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и другие
Правило из предыдущего пункта поможет нам без труда разделить дроби на указанные значения. Переводим эти числа в стандартные дроби и затем при делении действие будет аналогично умножению на 1000, 100, 10 (так как дробь, на которую делим переворачивается).
Чтобы найти ответ в подобных задачах, мы переносим запятую на одну, две, три цифры вправо (в зависимости от числа, на которое делим) и дописываем нули, если цифр в числе окажется недостаточно.
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Вот как поступим со смешанным числом: записываем его в виде неправильной дроби, десятичную — в виде обычной дроби и делим по уже стандартной схеме.
Урок 37 Бесплатно Деление и дроби
Сегодня на уроке речь пойдет о хорошо уже известной вам арифметической операции деления.
Вы уже имеете общее представление о делении натуральных чисел, знаете, как называются компоненты данной математической операции, и по каким правилам находится каждое из них.
До сих пор при решении различных задач на деление мы находили частое чисел, где делимое было большее делителя.
Давайте попробуем разобраться, возможно ли выполнять деление меньшего натурального числа на большее, выясним, что в таком случае будет получаться, и как данное действие правильно записывать.
Разберем решение уравнений, содержащих дроби.
Рассмотрим решение текстовых задач с использованием обыкновенных дробей.
Запись деления натуральных чисел в виде дробного числа
В жизни нам часто приходится что-то делить или чем-то делиться.
Например, в детском саду дети нередко делят игрушки; чтобы пицца или праздничный торт достались каждому гостю, мы делим его на кусочки; с друзьями мы всегда рады поделиться яблоком, мороженным, конфетами, шоколадкой и др.
Так, если нам придется поделить два яблока на двоих, то это для нас не составит большого труда.
Каждому, в таком случае, достанется по одному яблоку.
Математически данное действие запишем в виде равенства: 2 ÷ 2 = 1.
Рассмотрим ситуацию посложней.
Допустим у нас есть две груши и их нужно разделить между четырьмя друзьями.
Как же нам угостить каждого и не обидеть никого?
На первый взгляд это кажется невозможным (число 2 не делится нацело на 4).
Однако выход есть, разрежем первую и вторую грушу на четверти (т.е. каждую грушу разрежем на четыре равные части).
В итоге у нас получится 8 равных частей- 8 долей груши.
Каждая из этих частей- это \(\mathbf<\frac<1><4>>\) часть груши.
Всем четырем желающим попробовать фрукт достанется по \(\mathbf<\frac<1><4>>\) от каждой груши.
Таким образом каждый из друзей получит по две доли груши, т.е.\(\mathbf<\frac<1> <4>+ \frac<1><4>>\).
Сложим две дроби с одинаковым знаменателем, получим:
В итоге каждый друг получит\(\mathbf<\frac<2><4>>\) груши.
Дробь \(\mathbf<\frac<2><4>>\) образовалась при делении двух (яблок) на четыре (части).
В результате, никого не обидев, нам удалось разделить две груши на четверых желающих их попробовать.
Рассмотрим еще одну, казалось бы, неразрешимую ситуацию.
Разделим поровну две одинаковые плитки шоколада на троих друзей.
Как же это осуществить?
Шоколадных плиток две, а друзей трое (число 2 нацело не разделить на 3).
Давайте разломим каждую плитку шоколада на 3 равные части.
В результате у нас получится 6 равных частей- 6 долей шоколада.
Каждая такая доля шоколадной плитки представляет собой \(\mathbf<\frac<1><3>>\) плитки.
Угостим каждого друга \(\mathbf<\frac<1><3>>\) части от каждой шоколадной плитки.
В таком случае каждому из друзей достанется по две доли шоколадной плитки, т.е.\(\mathbf<\frac<1> <3>+ \frac<1><3>>\).
Сложим две дроби с одинаковым знаменателем, получим:
В итоге каждый друг получит\(\mathbf<\frac<2><3>>\) шоколадной плитки.
Дробь \(\mathbf<\frac<2><3>>\) образовалась при делении двух (шоколадных плиток) на три (части).
Так мы смогли, никого не обидев, разделить две шоколадные плитки на троих желающих попробовать шоколад.
Обобщая рассмотренные выше примеры, мы можем заметить, что обыкновенная дробь \(\mathbf<\frac
Мы получили прямую связь между обыкновенной дробью и арифметической операцией деления.
С помощью обыкновенной дроби можно записать частное двух любых натуральных чисел.
Дробную черту (горизонтальную или наклонную), которая отделяет числитель от знаменателя, применяют как знак деления.
Знак деления и дробная черта представляет одно и тоже арифметическое действие- деление, т.е. m ÷ n и \(\mathbf<\frac
Следовательно,m ÷ n и \(\mathbf<\frac
Результат деления двух натуральных чисел может быть натуральным числом или дробным числом.
Пример №1.
Пример №2.
Любое натуральное число можно представить в виде неправильной дроби, в которой числитель любое натуральное число, а знаменатель равен единице.
Пример №1.
Пример №2.
Четыре яблока разделили на восьмерых человек.
Сколько яблок достанется каждому?
Общее количество яблок (четыре) разделим на количество частей (восемь).
Деление m объектов на n частей можно представить в виде обыкновенной дроби \(\mathbf<\frac
В результате получаем: \(\mathbf
Нам известно, что одну и ту же обыкновенную дробь можно представить разными способами.
Разделить целое на восемь частей и взять четыре, будет тоже самое, что разделить это же целое на две части и взять одну.
Таким образом получаем \(\mathbf<\frac<4> <8>= \frac<1><2>>\).
Дробь \(\mathbf<\frac<1><2>>\) означает по своей сути половину чего-либо, следовательно, каждому достанется по одной половинке яблока.
Пройти тест и получить оценку можно после входа или регистрации
Примеры решения текстовых задач и решения уравнений, содержащих обыкновенные дроби
Рассмотрим несколько примеров решение уравнений и текстовых задач на нахождение неизвестного компонента арифметической операции деления.
Каждый компонент математической операции деления имеет свое название.
Взаимосвязь компонентов арифметической операции деления нам хорошо известна.
В общем виде деление мы можем записать следующим образом:
Делимое- это число, которое делят.
Делитель- это число, на которое делят делимое.
Частное- результат арифметической операции деления (число, которое получается в результате деления одного числа на другое).
Частное двух чисел можно записать в виде обыкновенной дроби, где числитель- это делимое, знаменатель- это делитель, а знак деления- это дробная черта.
Часто, решая задачи и уравнения, приходится находить неизвестный компонент операции деления.
Вспомним, по каким правилам можно найти каждый компонент деления.
Применим данные знания при решении текстовых задач и решении уравнений, содержащих обыкновенные дроби.
Правила нахождения неизвестных компонентов операции деления едино для любой формы записи частного двух чисел.
1. Нахождение неизвестного частного, если известны делимое и делитель.
Частное- это результат, полученный при выполнении деления, очевидно, что частное находят с помощью данной арифметической операции.
Зная делимое и делитель, можно найти частное, для этого необходимо делимое разделить на делитель.
Двенадцать пирожных стоят 300 рублей.
Сколько стоит одно пирожное?
300 руб.- стоимость двенадцати пирожных (делимое).
12 шт.- общее количество пирожных (делитель).
Чтобы найти частное, необходимо делимое разделить на делитель.
\(\mathbf<\frac<300> <12>= 25>\) (руб.) стоит одно пирожное.
Ответ: 25 (руб.)
2. Нахождение неизвестного делимого, если известны делитель и частное.
Правило: чтобы найти неизвестное делимое, необходимо частное умножить на делитель (или наоборот делитель умножить на частное).
Пример №1.
Решите уравнение \(\mathbf<\frac
Выражение, стоящее в левой части уравнения, является частным двух чисел.
Неизвестное х (числитель дроби)- делимое.
Найдем значение х, при котором уравнение обратится в верное равенство.
Так как числитель дроби- неизвестное делимое, следовательно, воспользуемся правилом нахождения неизвестного делимого.
Чтобы найти неизвестное делимое (х), необходимо частное (80) умножить на делитель (5).
х = 80 • 5
х = 400
Проверка: в исходное уравнение \(\mathbf<\frac
400 ÷ 5 = 80
80 = 80
Получили верное равенство, следовательно, корень уравнения найден верно.
Ответ: х = 400.
Решим текстовую задачу на нахождение неизвестного делимого алгебраическим способом.
Взаимосвязь компонентов математических операций применяют для решения текстовых задач.
Решить задачу алгебраическим способом- значит найти ответ на требование задачи, путем составления уравнения.
При составлении уравнения учитывают соотношения и взаимосвязи между величинами, которые могут быть даны в условии задачи или вытекать из смысла этой задачи.
Пример №2.
Сыну восемь лет. Он младше своего отца в четыре раза.
Определите возраст отца.
Пусть х (лет) возраст отца.
Тогда \(\mathbf<\frac
Зная, что сыну 8 лет, составим уравнение.
Решим полученное уравнение.
Выражение, стоящее в левой части уравнения- это частное двух чисел.
х— неизвестное делимое.
Найдем неизвестное делимое (х), для этого необходимо найти произведение частного (8) и делителя (4).
х = 8 • 4
х = 32 (года) возраст отца.
Ответ: х = 32 (года).
У меня есть дополнительная информация к этой части урока!
Любое натуральное число можно записать в виде обыкновенной дроби с любым натуральным знаменателем.
В таком случае числитель этой дроби будет равен произведению этого исходного натурального числа и знаменателя этой дроби.
Представим число 23 в виде дроби со знаменателем 7.
Искомая дробь должна быть со знаменателем равным 7, числитель этой дроби обозначим буквой х.
Найдем числитель дроби \(\mathbf<\frac
Числитель (х) этой дроби будет равен произведению заданного натурального числа (23) и знаменателя (7) этой дроби.
х = 23 • 7
х = 161
Подставим найденное значение числителя дроби в искомую дробь со знаменателем 7, получим следующий результат:
Натуральное число 23 можно представить в виде дроби \(\mathbf<\frac<161><7>>\).
3. Нахождение неизвестного делителя, если известны делимое и частное.
Правило: чтобы найти неизвестный делитель, необходимо делимое разделить на частное.
Пример №1.
Решите уравнение \(\mathbf<\frac<252>
Выражение, стоящее в левой части уравнения, является частным двух чисел.
Неизвестное х (знаменатель дроби)- это неизвестный делитель.
Найдем значение х, при котором уравнение обратится в верное равенство.
Так как знаменатель дроби- неизвестный делитель, то воспользуемся правилом нахождения неизвестного делителя.
Чтобы найти неизвестный делитель (х), необходимо делимое (252) разделить на частное (4).
х = 252 ÷ 4
х = 63
Проверка: в исходное уравнение \(\mathbf<\frac<252>
252 ÷ 63 = 4
4 = 4
Получили верное равенство, следовательно, корень уравнения найден верно.
Ответ: х = 63.
Решим текстовую задачу на нахождение неизвестного делителя.
Пример №2.
96 шоколадных конфет разложили в подарочные коробки.
В каждую коробку положили одинаковое количество конфет, получили 12 коробок.
Сколько конфет положили в каждую коробку?
Пусть х (конф.) в одной коробке.
Тогда \(\mathbf<\frac<96>
Зная, что всего получили 12 коробок конфет, составим уравнение.
Решим полученное уравнение.
Левая часть уравнения представляет собой частное двух чисел.
Неизвестная х, стоящая в знаменателе дроби- это неизвестный делитель.
Чтобы найти неизвестный делитель (х), необходимо делимое (96) разделить на частное (12).
х = 96 ÷ 12
х = 8 (конф.) в одной коробке.
Так как в каждую коробку положили одинаковое количество конфет, то в каждой подарочной коробке окажется 8 шоколадных конфет.
Ответ: х = 8 (конф.)
У меня есть дополнительная информация к этой части урока!
Решая уравнения и задачи алгебраическим способом, составленное уравнение часто приходится преобразовывать, применяя для этого различные методы упрощения, правила и свойства математических операций.
Рассмотрим некоторые свойства деления.
Нам известно правило: при сложении обыкновенных дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.
Данное правило в буквенном виде выглядит так:
Так как дробная черта- это знак деления, то получим еще одно верное равенство, которое уже знакомо нам.
a ÷ n + b ÷ n = (a + b) ÷ n (если суммируемые частные имеют общий делитель, то можно его вынести за скобку.
Верно и обратное равенство- это свойство деления суммы чисел на число:
(a + b) ÷ n = a ÷ n + b ÷ n
Чтобы разделить сумму чисел на число, можно разделить каждое слагаемое на это число, а потом полученные частные сложить.
Подобная ситуация складывается при делении разности на число.
Заменим знак деления на дробную черту, получим известное нам свойство вычитания дробей с одинаковым знаменателем записанное справа налево.
Пример №1.
Так как дробная черта- это знак деления, то \(\mathbf<\frac<30> <10>= 30 \div 10 = 3>\).
Пример №2.
Решите уравнение \(\mathbf<\frac
Первое и второе слагаемое имеют одинаковый знаменатель, следовательно, уравнение можно записать в виде:
Выражение, стоящее в левой части уравнения, является частным.
За неизвестное примем целое выражение х + 5.
х + 5— это неизвестное делимое.
Чтобы найти неизвестное делимое, необходимо найти произведение частного и делителя.
х + 5 = 3 • 5
х + 5 = 15
Получили простое уравнение с неизвестным слагаемым.
Чтобы найти неизвестное слагаемое (х), необходимо из суммы (15) вычесть известное слагаемое (5).
х = 10
Проверка: подставим в исходное уравнение \(\mathbf<\frac
3 = 3
Полученное равенство верно, следовательно, корень уравнения найден верно.
Ответ: х = 10.
Пример №3.
Решим задачу алгебраическим способом.
Купили 4 мороженных на палочке и 4 мороженных в стаканчике, причем за четыре мороженных на палочке заплатили в 2 раза больше, чем за четыре мороженных в стаканчике.
Общая стоимость одного мороженного в стаканчике и одного мороженного на палочке составляет 120 рублей.
Сколько стоит одно мороженное в стаканчике?
Сколько стоит одно мороженное на палочке?
Пусть х (руб.)- стоят 4 мороженных в стаканчике.
Тогда 2х (руб.)- стоят 4 мороженных на палочке.
\(\mathbf<\frac
\(\mathbf<\frac<2x><4>>\)- стоит одно мороженное на палочке.
Зная, что общая стоимость одного мороженного в стаканчике и одного мороженного на палочке составляет 120 рублей, составим уравнение.
Так как дроби имеют одинаковый знаменатель, уравнение запишем в виде:
Выражение, стоящее в левой части уравнения, является частным.
За неизвестное примем целое выражение х + 2х.
х + 2х (числитель дроби)- это неизвестное делимое.
Так как первое и второе слагаемое содержит одинаковую буквенную часть, то сложим их коэффициенты и умножим на буквенную часть.
х + 2х = (1 + 2) • х = 3х
Исходное уравнение примет вид:
В данном уравнении 3х— неизвестное делимое.
Чтобы найти неизвестное делимое (3х), необходимо частное (120) умножить на делитель (4).
3х = 120 • 4
3х = 480
Получили простое уравнение, в котором неизвестен множитель.
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
х = 480 ÷ 3
х = 160 (руб.) стоят четыре мороженных в стаканчике.
Известно, что одно мороженное в стаканчике стоит \(\mathbf<\frac
\(\mathbf<\frac
Известно, что \(\mathbf<\frac<2x><4>>\) (руб.) стоит одно мороженное на палочке, подставим вместо х найденное его значение (х = 160).
\(\mathbf<\frac<2x> <4>= (2 \cdot x) \div 4 = (2 \cdot 160) \div 4 = 320 \div 4 = 80>\) (руб.) стоит одно мороженное на палочке.
Ответ: 40 (руб.), 80 (руб.)
Пройти тест и получить оценку можно после входа или регистрации
Как разделить дробь на дробь
Для того, чтобы разделить обыкновенную дробь на обыкновенную дробь, нужно умножить первую дробь на «перевернутую» вторую дробь. Такая «перевернутая» обыкновенная дробь, где числитель и знаменатель поменяли местами называется обратной.
При делении дробей необходимо обратить внимание на то, чтобы вторая дробь не равнялась нулю. Иногда, если дробь имеет довольно-таки громоздкий вид, это сделать весьма затруднительно. Кроме того, вторая дробь может содержать некоторые переменные (неизвестные) величины, которые при определенных значениях обращают дробь в нуль. Также нужно уделить внимание тем случаям, когда знаменатель второй дроби обращается в нуль. При действиях с переменными все эти случаи необходимо указать в окончательном ответе.
Например: см. рис. 1
Чтобы разделить смешанную дробь на смешанную, смешанную дробь на обыкновенную или обыкновенную на смешанную, нужно привести смешанные дроби к обыкновенному виду. После чего произвести деление, как указано в шаге 1.
Для перевода смешанной дроби к обыкновенной необходимо целую часть смешанной дроби умножить на ее знаменатель и прибавить полученное произведение к числителю.
Пример: см. рис. 2
При делении десятичной дроби на обыкновенную (смешанную) или при делении обыкновенной (смешанной) дроби на десятичную, все дроби приводятся к обыкновенному виду. После этого деление производится согласно шагу 1. Для перевода десятичной дроби в обыкновенную, «выкидываем» из десятичной дроби запятую и записываем в числитель дроби, а в знаменатель пишем единицу и столько нулей, сколько цифр стояло справа от десятичной точки.
Пример: см. рис. 3
Для деления двух десятичных дробей нужно в делимом и делителе перенести десятичную точку на столько цифр вправо, чтобы из второй дроби получилось целое число и разделить полученные числа.
Если при этом в делимом для переноса десятичной запятой «не хватает» цифр, то недостающие знаки заменяются нулями.
Как делить дробь на дробь?
Как делить дробь на дробь?
Как делить обыкновенные дроби?
Как делить смешанные дроби?
Как делить десятичные дроби?
Про простые и смешанные дроби Людмила1979 все правильно объяснила.
Если открыть учебник, то мы там найдем правило деления простых дробей:
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй, а числитель второй умножить на знаменатель первой.
Ученик 4-5 класса, который это проходит, ничего не поймет и обязательно запутается.
А вот с десятичными мне объяснили так. Нужно передвинуть запятые в обоих дробях одновременно, чтобы получилось два целых числа, а потом делить.
0,5 : 0,23 = 50 : 23 (передвинули на 2 знака вправо).
0,0018 : 0,47 = 18 : 4700 (передвинули на 4 знака вправо).
38/47 : 0,19 = 38/47 : 19/100 = 38/47 * 100/19 = (38*100)/(47*19) = 200/47 (сократили на 19).
Деление и дроби. Запись числа в виде дроби
Содержание
На этом уроке поговорим о том, как при делении получаются дробные числа, а также о том, что любое натуральное число можно записать в виде дроби. Представить как дробь можно не только число, но и сумму чисел.
Как поделить то, что не делится?
Марина и Лена собирались пить чай, и тут к ним пришла их подруга Соня. Ей, конечно, тоже налили чая, девочки сели за стол и стали делить пирожные. Пирожных было только два, поэтому делили они их так: каждое пирожное разрезали на три части, а потом каждая взяла себе по одной части от каждого пирожного. У всех получилось поровну.
Получается, мы просто записываем пример в виде дроби. В нижней части у нас написано, на сколько кусочков мы делим то, что нам нужно поделить, а в верхней – сколько кусочков получается при делении.
Дробь – знак деления
Черту дроби можно понимать как знак деления.
Получается, иногда дробь можно «поделить до конца» и получить целое число. В таких случаях говорят, что деление выполняется нацело.
С помощью дробей можно записать результат деления двух любых натуральных чисел. Если деление выполняется нацело, то в частное – целое число. Если же разделить нацело нельзя, то частное будет дробным числом.
Выглядит это, как будто мы записали пример, а решать его поленились.
Как записать число в виде дроби
Любое число можно записать в виде дроби с каким-либо знаменателем. Числитель этой дроби будет равен произведению этого числа на знаменатель.
Это как если бы мы решали задачу, где нам известно, на сколько человек разделили конфеты, и сколько получил в итоге каждый человек, а неизвестно было бы, какое количество конфет было изначально.
Деление суммы на число
Мы знаем, что при сложении дробей с одинаковыми знаменателями нужно сложить числительные.
А если нам нужно не складывать дроби, а, наоборот, разделить сумму на число?
По-другому это можно записать так:
$$(a+b) : c = a : c + b : c$$
Получается, нам необязательно сначала складывать числа, а потом делить их – можно разделить каждое число и потом сложить результаты.
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
У нас получается вот такой пример:
$$(\textcolor
Деление суммы перекликается с нахождением среднего арифметического, о нём мы будем говорить на отдельном уроке.
Деление десятичных дробей: правила, примеры, решения
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
Точность результата будет зависеть от степени округления.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Решение
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Решение
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Решение
Делим сначала дробную часть и получаем:
Отделяем полученную цифру запятой и продолжаем делить:
Как разделить столбиком одну десятичную дробь на другую
Для деления одной конечной десятичной дроби на другую необходимо:
1. Перенести запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, допишем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
Разберем конкретную задачу.
Решение
Нам придется переносить запятую на три знака. В делителе для этого не хватит цифр, значит, нужно воспользоваться дополнительными нулями. Считаем, что получится в итоге:
Описанный нами метод позволяет делать и наоборот, то есть делить натуральное число на конечную десятичную дробь. Посмотрим, как это делается.
Решение
Как разделить десятичные дроби на 1000, 100, 10 и др.
В случае с бесконечными десятичными дробями мы поступаем таким же образом.
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и др.
Это правило действует и в случае с бесконечными десятичными дробями. Советуем только быть внимательными с периодом дроби, которая получается в ответе.
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Для этого надо заменить десятичные числа соответствующими обыкновенными дробями, а смешанное число записать в виде неправильной дроби.
Если мы делим непериодическую дробь на обыкновенную либо на смешанное число, нужно поступить наоборот, заменив обыкновенную дробь или смешанное число соответствующей им десятичной дробью.
ОБЫКНОВЕННАЯ ДРОБЬ
Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.
Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.
Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.
Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.
Основное свойство дроби
Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.
Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.
Сравнение дробей
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.
Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!
Общий случай сложения (вычитания) дробей.
Умножение дробей
Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.
При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.
Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.
Нахождение целого по его части (числа по его дроби)
Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.
Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.
Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:
Десятичные дроби
5 класс, 6 класс
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
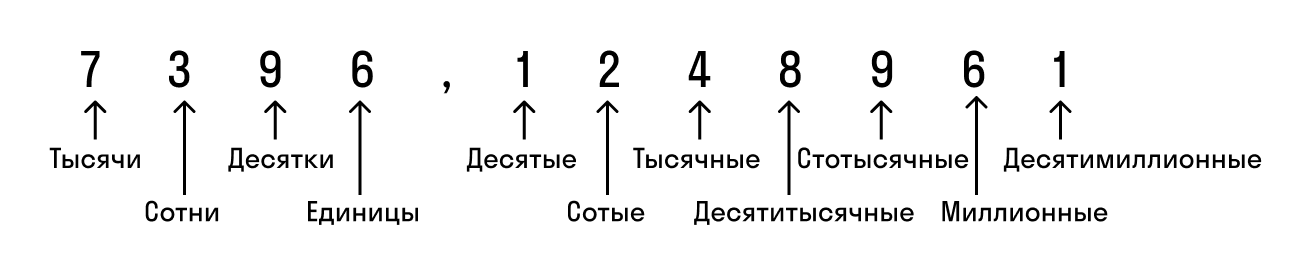
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Математика
План урока:
Умножение обыкновенных дробей
На уроке технологии девочки занимались выпечкой. Они готовили печенье. По рецепту на изготовление одного килограмма печенья уходит 3/8 килограмма сахара. Сколько сахара необходимо принести детям, чтобы приготовить 1/2 килограмма печенья?
числитель умножаем на числитель, а знаменатель на знаменатель. Первый результат пишем над чертой дроби, второй под чертой:
Получается, чтобы испечь нужное количество печенья школьницы должны подготовить 3/16 килограмма сахарного песка.
Нахождение дроби от числа
Разберем следующую ситуацию и узнаем, как найти дробь от числа.
Вениамин очень любит уроки изобразительного искусства. В его альбоме для рисования 48 листов. Мальчик удивленно заметил, что своими рисунками уже заполнил 7/8 альбома. Сколько всего рисунков получилось у школьника?
Задачу можно решить двумя способами. Подробно рассмотрим каждый из них.
Чтобы ответить на главный вопрос задачи нам нужно узнать, сколько листов соответствует записи 7/8. Для этого давайте вспомним, о чем нам говорят компоненты дробных выражений:
Теперь, можно сказать, что весь альбом разделили на 8 частей, а использовали только 7. Попробуем посчитать. Вначале, делим 48 на 8:
6 листов приходится на 1/8 часть альбома. Зная, что таких частей было взято 7, найдем произведение 6 и 7 :
Мы выяснили, что Вениамин нарисовал 42 рисунка.
Для решения задачи таким способом, нужно выполнить два действия, а это не всегда удобно. Так же, такой способ может вызывать трудности при вычислениях, если компоненты не делятся нацело.
В таких ситуациях, логичнее будет использование второго способа.
По условию нам известно число и часть этого числа, выраженная обыкновенной дробью. Нужно найти числовое значение соответствующее данной дроби. Задания такого вида имеют собственное название «Нахождение дроби от числа» и правило, используя, которое можно с легкостью вычислить любое числовое значение соответствующее дробному выражению:
Применим изученное правило на практике. Чтобы найти 7/8 от 48 нам нужно, просто умножить 7/8 на 48:
Мальчик нарисовал 42 рисунка.
Запомните оба способа, и применяйте их для решения различных заданий.
Деление обыкновенных дробей
Строительная бригада выполняла ремонт городской дороги.На ремонт определенного участка дороги, рабочие потратили 7/9 тонны асфальта. Определите, сколько километров дороги отремонтировали рабочие, если на ремонт одного километра уходит 3/7 тонны строительного материала.
По условию нам известно, что всего было использовано 7/9 тонны материала, при этом мы знаем, что на один километр требуется 3/7 тонны. Чтобы ответить на главный вопрос задачи нужно количество использованного асфальтаразделить на количество строительного материала, необходимое для починки одного километра. В результате мы получим число отремонтированных километров. В данном случае, в качестве делимого и делителя выступают обыкновенные дроби. И перед нами возникает проблема «Как же выполнить деление обыкновенных дробейс разными знаменателями?».
В арифметике на этот случай имеется определенное правило, которое расскажет, как выполнить деление обыкновенных дробей.
Выполним деление имеющихся чисел с применением рассмотренного правила
Выполним деление, имеющихся дробных чисел с применением рассмотренного правила. Разделим 7/9 на 3/7. Делимое 7/9 оставляем без изменений, а делитель 3/7 переворачиваем, и получаем 7/3. Находим произведение данных выражений:
Все очень просто. Главное помните, что при выполнении деления дробей с разными знаменателями делитель переворачиваем и находим произведение перевернутого делителя и делимого!
Нахождение числа по заданному значению его дроби
В школе проходила неделя экологии. Учащиеся шестого класса были приглашены лесничеством на высадку деревьев. До обеда, ребята высадили 6/11 всех саженцев. Сколько растений осталось высадить школьникам, если до обеда дети высадили 54 дерева?
Чтобы ответить на главный вопрос задачи, нужно определить число по заданному значению его дроби. В арифметике существует правило, используя, которое возможно с легкостью найти любое число по значению его дроби:
Теперь мы знаем, что для вычисления общего количества саженцев, нужно известное значение дроби разделить на саму дробь. Зная, что число – 54, а дробь – 6/11, имеем:
В результате получили неправильную дробь. Выделим из полученного произведения целую часть.Для этого разделим числитель на знаменатель:
Выходит, что за целый день школьникам нужно высадить 99 растений.
В математике часто встречаются задания, в которых требуется вычислить значение «многоэтажных» дробей. Как называются такие дробные выражения, каким способом их вычислять рассмотрим далее.
Дробные выражения
Когда ученик видит в учебнике задание в виде выражения:
то желание заниматься математикой сразу пропадает. Сегодня мы узнаем,как решать дробные выражения и докажем, что даже такие выражения совершенно не сложные, и выполнить вычисления сможет каждый желающий после изучения нашего урока!
Никого не пугает запись обыкновенной дроби – 3/7, 4/15, 8/14.
10/21 = 10 : 21 или 7/18 = 7 : 18.
Выходит, что частное чисел или выражений, в случае замены знака деления чертой дроби, называют дробным выражением.
Вот так, проведя два простых вычисления, мы выполнили задание, вызывающее недоумение у школьников. Математика интересная и простая наука. Если приложите немного внимания и терпения, то результат не заставит себя ждать!
Знаешь ли ты?
1) Ученые – селекционеры вывелиновый вид яблонь. Удивительным является то, что корни растения уходит в землю более чем на 49/50километра (около 980 метров), а общая длина корневища достигает 4000 метров.
2) За всю жизнь человек выпивает примерно 75 тонн воды. Подсолнечнику, например, достаточно 1/4 тонны(250 литров), чтобы вырасти и принести семена.
3) Италия в который раз удивила весь мир. Около вулкана Этна растет каштан, диаметр ствола которого, составляет,3/50 километра (около 60 метров),это чуть ли не половина футбольного стадиона.
4) Пальма Рафия Тедигера встречается только в Бразилии. Она интересна тем, что её листья имеют гигантские размеры. Черенок листка достигает1/200 километра (5 метров), длина листика – более1/50 километра (более 20 метров), ширина – более 5 метров (1/200 километра).
5) По сообщениям ихтиологов(ученых, занимающихся изучением рыб), самую большую длину в мире,имеют ремень-рыбы. Во взрослом возрасте они достигают длины более 1/100километра(более 10 метров), а длина молодых особей находится в пределах 0,003 километра или 3 метров.