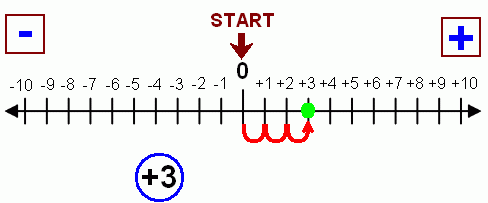
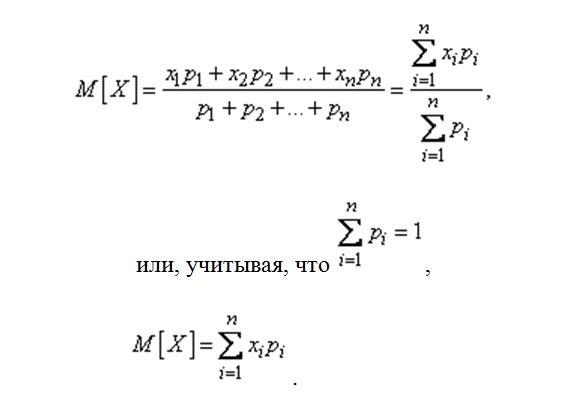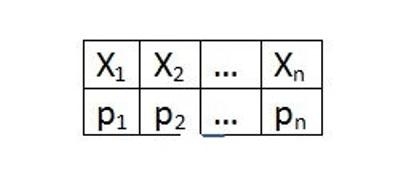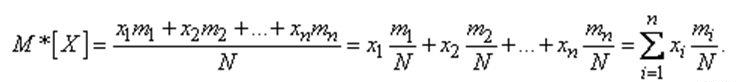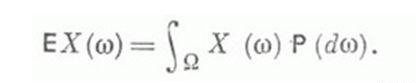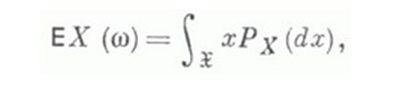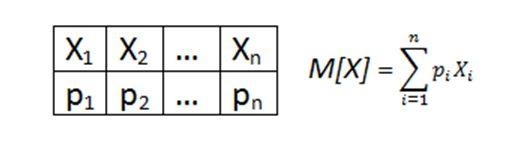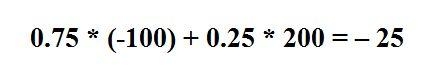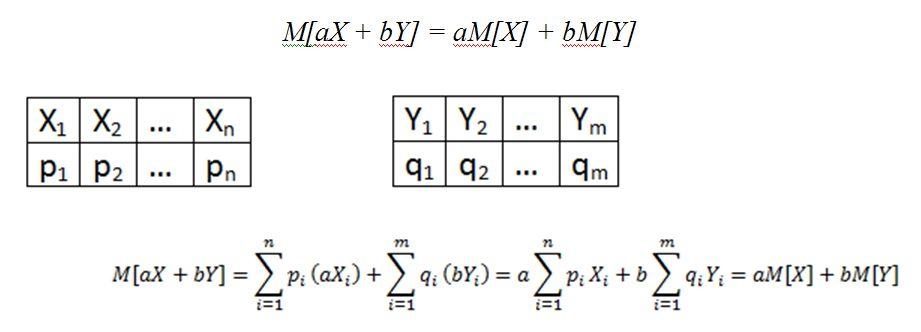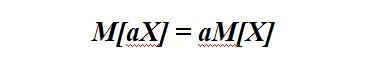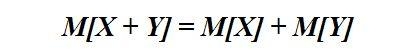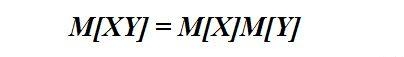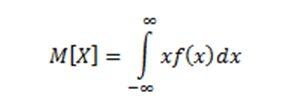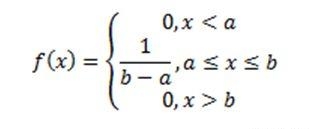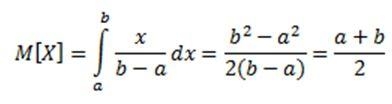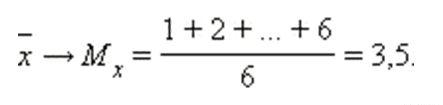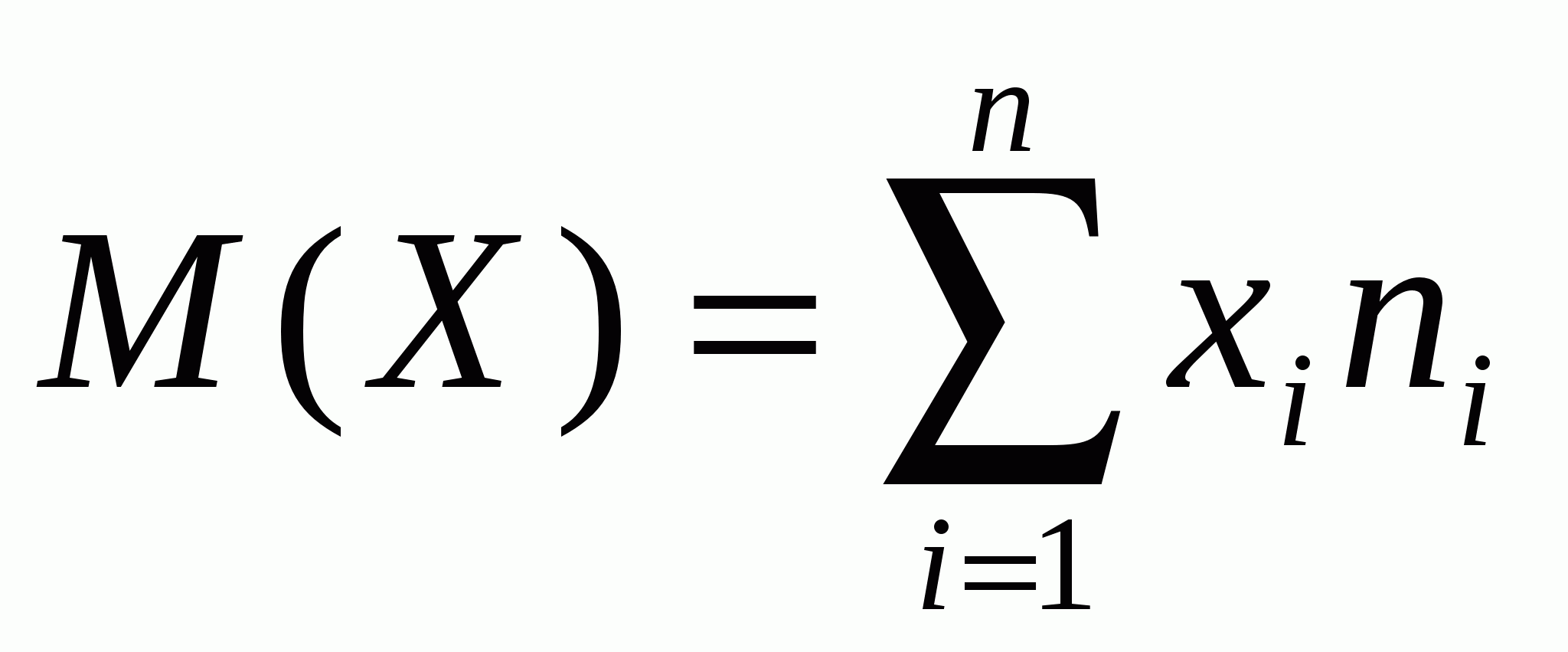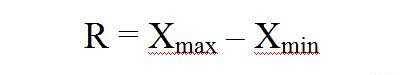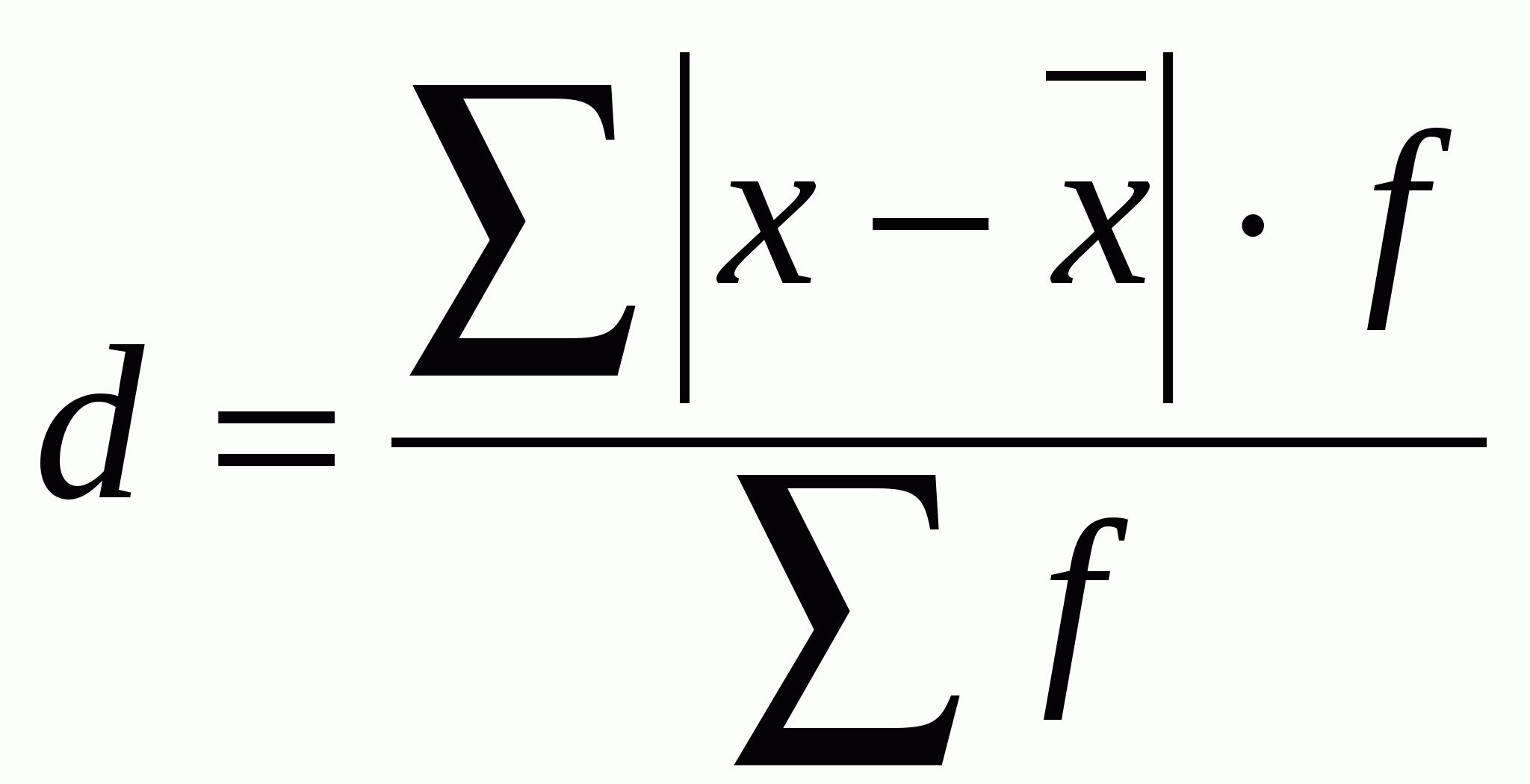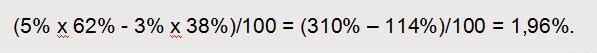Как найти математическое ожидание
Как найти математическое ожидание
Математика и информатика. Учебное пособие по всему курсу

Загрузить всю книгу
Титульный лист
Тольяттинский государственный университет
Кафедра «Компьютерные технологии и обработка материалов давлением»
МАТЕМАТИКА И ИНФОРМАТИКА
Учебное пособие по дисциплине «Математика и информатика» для студентов гуманитарных и педагогических специальностей очной формы обучения.
/сост. Егорова Э.В.– Тольятти: ТГУ, 2008.
В учебном пособии рассмотрены вопросы по математике: аксиоматический метод, теория множеств, основы теории вероятностей и математической статистики, а также вопросы по информатике: алгоримизация и программирование.
Изложено содержание теоретических вопросов по разделам математики и основам информатики в соответствии со стандартом. Рассмотрены примеры и даны вопросы для контроля по каждой теме.
Рекомендовано для студентов всех форм обучения гуманитарных направлений.
Научный редактор: к.т.н. Д.И. Панюков
Утверждено редакционно-издательской секцией методического совета института.
© Тольяттинский государственный университет, 2008
Случайные величины. Дискретная случайная величина.
Математическое ожидание
Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:
Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через 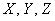
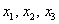
* Иногда используют 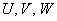
Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:
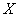
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина 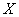
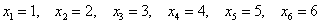
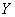
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:
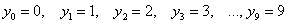
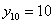
И, дабы соблюсти форму, немного физкультуры:
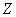
Её не в состоянии предугадать даже мастер спорта 🙂
Тем не менее, ваши гипотезы?
Коль скоро речь идёт о множестве действительных чисел, то случайная величина 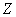
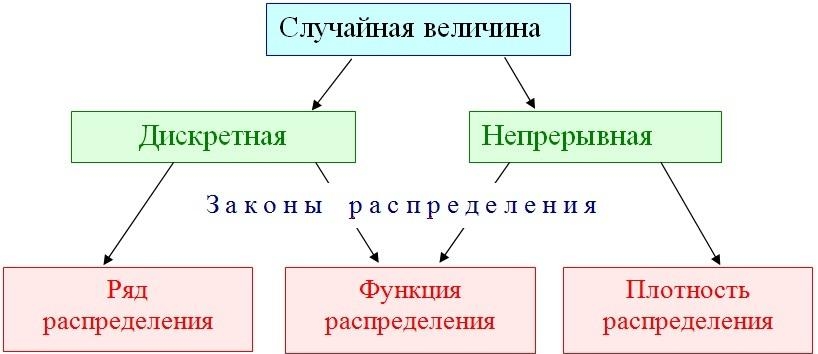
Таким образом, случайные величины целесообразно разделить на 2 большие группы:
1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.
…нарисовались непонятные термины? Срочно повторяем основы алгебры!
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ
Сначала разберём дискретную случайную величину, затем – непрерывную.
Закон распределения дискретной случайной величины
– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей: 
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».
А теперь очень важный момент: поскольку случайная величина 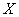
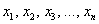
или, если записать свёрнуто:
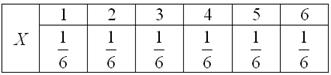
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:
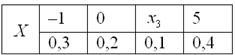
Некоторая игра имеет следующий закон распределения выигрыша:
Найти
…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.
Решение: так как случайная величина 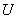
Разоблачаем «партизана»: 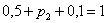
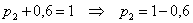
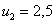
Контроль: 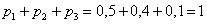
Ответ:
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины 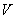
Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно 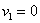
Всего таковых билетов 50 – 12 = 38, и по классическому определению:
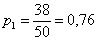
С остальными случаями всё просто. Вероятность выигрыша 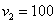
И для 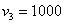
Проверка: 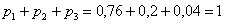
Ответ: искомый закон распределения выигрыша:
Следующее задание для самостоятельного решения:
Вероятность того, что стрелок поразит мишень, равна 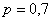
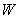
…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина 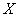
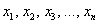
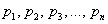
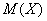
или в свёрнутом виде:
Вычислим, например, математическое ожидание случайной величины 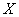
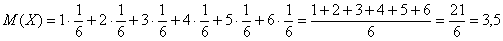
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
Теперь вспомним нашу гипотетическую игру:
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
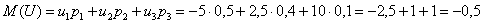
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины 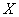
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
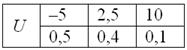
Случайная величина 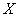
Найти 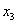
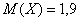
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
Решения и ответы:
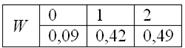
Пример 3. Решение: по условию 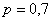
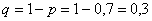
Составим 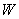
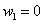
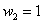
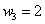
Проверка: 0,09 + 0,42 + 0,49 = 1
Ответ:
Примечание: можно было использовать обозначения 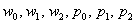
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: 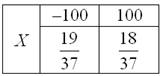
Вычислим математическое ожидание: 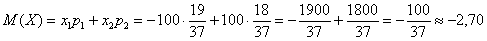
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания: 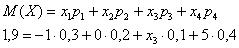
поменяем части местами и проведём упрощения: 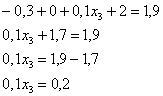
таким образом:
Выполним проверку: 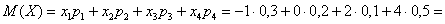
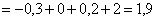
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Математическое ожидание
Математическое ожидание — это ожидаемый результат от какого-то действия.
Например, можно рассчитать ожидаемую стоимость инвестиции в определённый момент в будущем. Рассчитывая математическое ожидание перед тем, как инвестировать, можно выбрать наилучший сценарий который, по мнению инвестора, даст наилучший результат.
Случайная величина может быть двух типов:
Математическое ожидание дискретной случайной величины рассчитывается этой формулой:
Математическое ожидание дискретной случайной величины рассчитывается:
1. Сначала нужно умножить каждое из возможных результатов на свою вероятность (например: вероятность, что выпадет «1» — 1/6, «2» — 1/3, значит умножаем 1 на 1/6, 2 на 1/3, и т.д.),
2. Затем суммируем все эти значения (1 × 1/6 + 2 × 1/3 и т.д.).
Для непрерывной случайной величины используется эта формула:
В этом случае рассчитывается интеграл в заданном интервале.
Примеры вычисления математического ожидания
Пример 1
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | −1 | 1 | 2 | 3 | 4 |
| pi | 0,1 | 0,2 | 0,3 | 0,1 | 0,3 |
Используется формула для дискретной случайной величины:
M(X) = ∑ xi×pi = −1×0,1+ 1×0,2 + 2×0,3 + 3×0,1 + 4×0,3 = −0,1 + 0,2 + 0,6 + 0,3 + 1,2 = 2,2
Пример 2
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = 2x, при x∈(0,1) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:
Пример 3
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | 1 | 2 | 3 | 4 | 5 |
| pi | 0,3 | 0,3 | 0,1 | 0,1 | 0,2 |
Используется формула для дискретной случайной величины:
M(X) = ∑ xi×pi = 1×0,3 + 2×0,3 + 3×0,1 + 4×0,1 + 5×0,2 = 0,3 + 0,6 + 0,3 + 0,4 + 1 = 2,6
Пример 4
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = (1/10).(3x²+1), при x∈(0,2) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:
Математическое ожидание



Основные числовые характеристики дискретных и непрерывных случайных величин: математическое ожидание, дисперсия и среднее квадратическое отклонение. Их свойства и примеры.
Закон распределения (функция распределения и ряд распределения или плотность веро-ятности) полностью описывают поведение случайной величины. Но в ряде задач доста-точно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный во-прос. Рассмотрим основные числовые характеристики дискретных случайных величин.
Определение 7.1. Математическим ожиданием дискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности:
Если число возможных значений случайной величины бесконечно, то 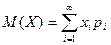
Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.
Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольше-го.
Замечание 3. Математическое ожидание дискретной случайной величины есть неслучай-ная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непре-рывных случайных величин.
Пример 1. Найдем математическое ожидание случайной величины Х – числа стандартных деталей среди трех, отобранных из партии в 10 деталей, среди которых 2 бракованных. Составим ряд распределения для Х. Из условия задачи следует, что Х может принимать значения 1, 2, 3. 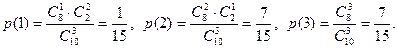
Пример 2. Определим математическое ожидание случайной величины Х – числа бросков монеты до первого появления герба. Эта величина может принимать бесконечное число значений (множество возможных значений есть множество натуральных чисел). Ряд ее распределения имеет вид:
| Х | … | п | … | ||
| р | 0,5 | (0,5) 2 | … | (0,5) п | … |
Тогда 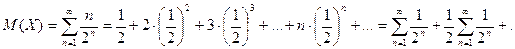
+ 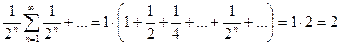
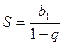
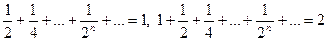
Свойства математического ожидания.
1) Математическое ожидание постоянной равно самой постоянной:
Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М(С) = С?1 = С.
2) Постоянный множитель можно выносит за знак математического ожидания:
Доказательство. Если случайная величина Х задана рядом распределения
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
то ряд распределения для СХ имеет вид:
| Сxi | Сx1 | Сx2 | … | Сxn |
| pi | p1 | p2 | … | pn |
Определение 7.2. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.
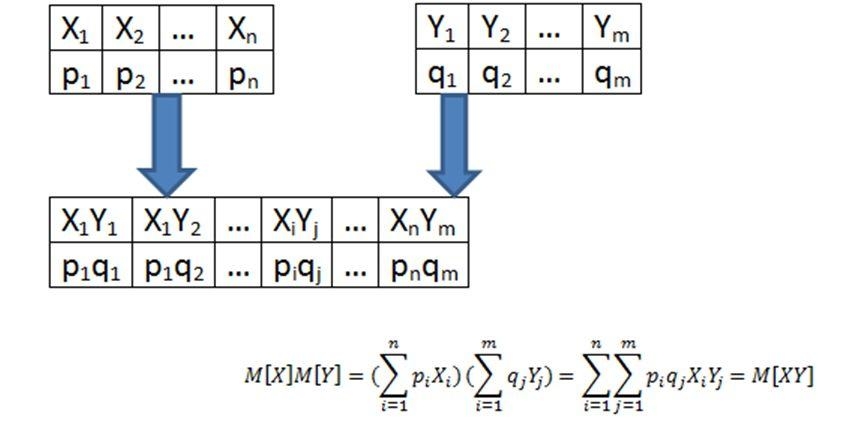
Определение 7.3. Назовем произведением независимых случайных величин Х и Y случайную величину XY, возможные значения которой равны произведениям всех возможных значений Х на все возможные значения Y, а соответствующие им вероят-ности равны произведениям вероятностей сомножителей.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
Доказательство. Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:
| xi | x1 | x2 |
| pi | p1 | p2 |
| уi | у1 | у2 |
| gi | g1 | g2 |
Тогда ряд распределения для XY выглядит так:
Замечание 1. Аналогично можно доказать это свойство для большего количества возможных значений сомножителей.
Замечание 2. Свойство 3 справедливо для произведения любого числа независимых случайных величин, что доказывается методом математической индукции.
Определение 7.4. Определим сумму случайных величин Х и Y как случайную величину Х + Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин – произведениям вероятности одного слагаемого на условную вероятность второго).
4) Математическое ожидание суммы двух случайных величин ( зависимых или незави-симых ) равно сумме математических ожиданий слагаемых:
Замечание. Из свойства 4 следует, что сумма любого числа случайных величин равна сумме математических ожиданий слагаемых.
Пример. Найти математическое ожидание суммы числа очков, выпавших при броске пяти игральных костей.
Найдем математическое ожидание числа очков, выпавших при броске одной кости:
М(Х1) = (1 + 2 + 3 + 4 + 5 + 6)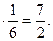
Дисперсия.
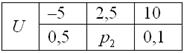
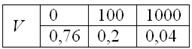
Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида
| Х | |||
| р | 0,1 | 0,8 | 0,1 |
| Y | ||
| p | 0,5 | 0,5 |
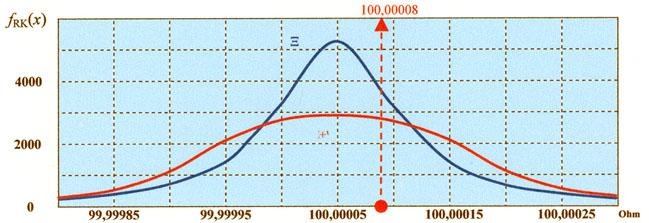
Найдем М(Х) = 49?0,1 + 50?0,8 + 51?0,1 = 50, М(Y) = 0?0,5 + 100?0,5 = 50. Как видно, мате-матические ожидания обеих величин равны, но если для Х М(Х) хорошо описывает пове-дение случайной величины, являясь ее наиболее вероятным возможным значением (при-чем остальные значения ненамного отличаются от 50), то значения Y существенно отсто-ят от М(Y). Следовательно, наряду с математическим ожиданием желательно знать, на-сколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.
Определение 7.5. Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
Найдем дисперсию случайной величины Х (числа стандартных деталей среди отобранных) в примере 1 данной лекции. Вычислим значения квадрата отклонения каждого возможно-го значения от математического ожидания:
(1 – 2,4) 2 = 1,96; (2 – 2,4) 2 = 0,16; (3 – 2,4) 2 = 0,36. Следовательно,
Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга.
Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.
Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме:
Используя то, что М(Х) – постоянная величина, и свойства математического ожидания, преобразуем формулу (7.6) к виду:
1) Дисперсия постоянной величины С равна нулю:
2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.
Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.
4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением.
Определение 7.6. Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:
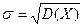
Пример. В предыдущем примере средние квадратические отклонения Х и Y равны соответственно
Математическое ожидание
Материал из MachineLearning.
Математическое ожидание — мера среднего значения случайной величины в теории вероятностей. В зарубежной литературе обозначается через (например, от англ. Expected value или нем. Erwartungswert), в русской (возможно, от англ. Mean value).
Содержание
Определение
Основные формулы для математического ожидания
Математическое ожидание дискретного распределения
то прямо из определения интеграла Лебега следует, что
Математическое ожидание целочисленной величины
то её математическое ожидание может быть выражено через производящую функцию последовательности
Теперь возьмём производящую функцию последовательности «хвостов» распределения
Математическое ожидание абсолютно непрерывного распределения
Математическое ожидание случайного вектора
Пусть — случайный вектор. Тогда по определению
то есть математическое ожидание вектора определяется покомпонентно.
Математическое ожидание преобразования случайной величины
Пусть — борелевская функция, такая что случайная величина имеет конечное математическое ожидание. Тогда для него справедлива формула:
если имеет дискретное распределение;
если имеет абсолютно непрерывное распределение.
Если распределение случайной величины общего вида, то
Простейшие свойства математического ожидания
Дополнительные свойства математического ожидания
Пусть — монотонная последовательность неотрицательных почти наверное интегрируемых случайных величин. Тогда
Примеры
равно среднему арифметическому всех принимаемых значений.
то есть математическое ожидание не определено.
Числовые характеристики распределения вероятностей. Математическое ожидание, дисперсия и стандартное отклонение
п.1. Закон распределения дискретной случайной величины
В табличном виде:
п.2. Математическое ожидание
Свойства математического ожидания
1) Размерность математического ожидания равна размерности случайной величины.
2) Математическое ожидание может быть любым действительным числом: положительным, равным 0, отрицательным.
3) Математическое ожидание постоянной величины равно этой постоянной:
4) Математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий:
5) Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий:
6) Постоянный множитель можно вынести за знак математического ожидания:
Например:
Пусть в результате экспериментов получено следующее распределение случайной величины X – числа появления белых шаров (см. пример 1, §40 данного справочника):
| Число белых шаров, xi | 0 | 1 | 2 | 3 | 4 | 5 |
| pi | \(\mathrm | \(\mathrm | \(\mathrm | \(\mathrm | \(\mathrm | \(\mathrm |
| 0,0074 | 0,0618 | 0,2060 | 0,3433 | 0,2861 | 0,0954 |
Найдём математическое ожидание для данного распределения:
п.3. Дисперсия
Свойства дисперсии
1) Размерность дисперсии равна квадрату размерности случайной величины.
2) Дисперсия может быть любым неотрицательным действительным числом.
3) Дисперсия постоянной величины равна нулю:
4) Дисперсия суммы независимых случайных величин равна сумме дисперсий:
5) Постоянный множитель можно вынести за знак дисперсии:
Например:
Продолжим исследование и найдём дисперсию для распределения случайной величины X – числа появления белых шаров. Составим расчётную таблицу:
Получаем: D(X) = 10,9375 – 3,125 2 ≈ 1,1719.
п.4. Среднее квадратичное отклонение
Свойства СКО
1) Размерность СКО равна размерности случайной величины.
2) СКО может быть любым неотрицательным действительным числом.
3) СКО постоянной величины равно нулю:
4) Постоянный множитель можно вынести за знак СКО:
п.5. Правило трёх сигм
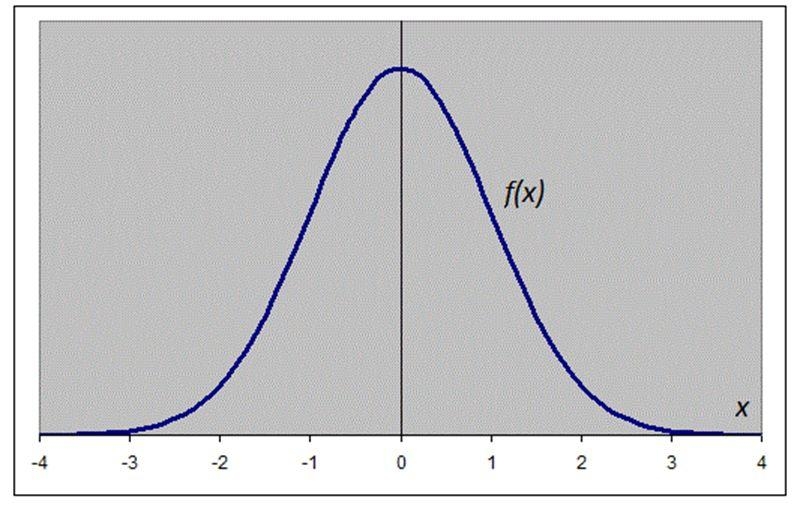
Большое количество случайных величин, измеряемых в экспериментах (например, в школьных лабораторных работах), имеет так называемое нормальное распределение.
В частности, при больших n, биномиальное распределение можно с хорошей точностью описывать как нормальное с M(X) = np и \(\mathrm<\sigma(X)=\sqrt
График плотности нормального распределения p(x) похож на колокол, с максимумом, соответствующим M(X) = Xcp – среднему значению измеряемой величины.
Величина СКО σ(X) характеризует степень отклонения X от среднего значения M(X).
п.6. Примеры
Пример 1. Найдите математическое ожидание, дисперсию и СКО при бросании кубика.
Закон распределения величины X – очки на верхней грани при бросании кубика и расчётная таблица:
Пример 2*. Найти математическое ожидание, дисперсию и СКО суммы очков при бросании двух кубиков.
Пример 3*. Докажите, что в опытах по схеме Бернулли математическое ожидание M(X)=np, а дисперсия D(X)=npq.
Проведем один опыт. В нём может быть только два исхода: «успех» и «неудача».
Составим расчётную таблицу:
Мат.ожидание первого опыта \(\mathrm
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. \(\mathrm
По свойству мат.ожидания суммы независимых событий: \begin
По свойству дисперсии суммы независимых событий: \begin
Пример 4. 100 канцелярских кнопок высыпали на стул. Вероятность, что кнопка упала острием вверх, равна 0,4. Найдите среднее количество, дисперсию и СКО для числа кнопок, упавших острием вверх. Найдите интервал оценки для количества этих кнопок по правилу «трёх сигм».
По условию n = 100, p = 0,4.
Для каждой кнопки может быть два исхода: упасть острием вверх или вниз.
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. \begin
Ответ: \(\mathrm
Пример 5*. В тесте 10 задач с 4 вариантами ответов. Ответы выбираются наугад. Постройте распределение величины X = «количество угаданных ответов», найдите числовые характеристики этого распределения.
Найдите интервал оценки для количества угаданных ответов по правилу «трёх сигм».
Какова вероятность угадать хотя бы 1 ответ? Хотя бы 5 ответов? Угадать все 10 ответов?
| \(\mathrm | \(\mathrm | \(\mathrm<3^k>\) | \(\mathrm | \(\mathrm | \(\mathrm | \(\mathrm |
| 0 | 1 | 1 | 0,0563135 | 0,0000000 | 0 | 0,0000000 |
| 1 | 10 | 3 | 0,1877117 | 0,1877117 | 1 | 0,1877117 |
| 2 | 45 | 9 | 0,2815676 | 0,5631351 | 4 | 1,1262703 |
| 3 | 120 | 27 | 0,2502823 | 0,7508469 | 9 | 2,2525406 |
| 4 | 210 | 81 | 0,1459980 | 0,5839920 | 16 | 2,3359680 |
| 5 | 252 | 243 | 0,0583992 | 0,2919960 | 25 | 1,4599800 |
| 6 | 210 | 729 | 0,0162220 | 0,0973320 | 36 | 0,5839920 |
| 7 | 120 | 2187 | 0,0030899 | 0,0216293 | 49 | 0,1514053 |
| 8 | 45 | 6561 | 0,0003862 | 0,0030899 | 64 | 0,0247192 |
| 9 | 10 | 19683 | 0,0000286 | 0,0002575 | 81 | 0,0023174 |
| 10 | 1 | 59049 | 0,0000010 | 0,0000095 | 100 | 0,0000954 |
| Σ | 1 | 2,5 | 8,125 |
Вероятность угадать хотя бы один ответ: \begin
Вероятность угадать хотя бы 5 ответов: \begin
Вероятность угадать все 10 ответов: p10≈ 0,000001. Шанс – один из миллиона.
Математическое ожидание случайной величины
Содержание
Математическое ожидание случайной величины [ править ]
| Определение: |
| Математическое ожидание (англ. mean value) [math] \left( E\xi \right) [/math] — мера среднего значения случайной величины, равная [math]E\xi = \sum \xi(\omega) \cdot p(\omega)[/math] |
Пример [ править ]
Пусть наше вероятностное пространство — «честная кость»
[math] \xi(i) = i [/math]
[math] E\xi = 1\cdot \dfrac<1><6>+2\cdot \dfrac<1> <6>\dots +6\cdot \dfrac<1> <6>= 3.5[/math]
Свойства математического ожидания [ править ]
| Утверждение (о матожидании случайной величины на событии вероятности нуль): |
| Утверждение (о матожидании двух независимых случайных величин): | |
Линейность математического ожидания [ править ]Использование линейности [ править ]Рассмотрим три задачи. Пример 1 [ править ]Найти математическое ожидание суммы цифр на случайной кости домино. Получаем ответ [math]E(\xi+\eta)=2E(\xi)=6[/math] Пример 2 [ править ]Итоговый результат: [math]E(\xi)=<\sum_ Пример 3 [ править ]Пусть [math] \xi [/math] — случайная величина, которая возвращает количество инверсий в перестановке. Очевидно, что вероятность любой перестановки равна [math] \dfrac<1> Докажем, что количество инверсий в этих двух перестановках равно [math] \dfrac Примеры распределений [ править ]Распределение Бернулли [ править ]Случайная величина [math]\xi[/math] имеет распределение Бернулли, если она принимает всего два значения: [math]1[/math] и [math]0[/math] с вероятностями [math]p[/math] и [math]q \equiv 1-p[/math] соответственно. Таким образом: [math]P(\xi = 1) = p[/math] [math]P(\xi = 0) = q[/math] Тогда несложно догадаться, чему будет равно математическое ожидание: [math]E(\xi) = 1 \cdot p + 0 \cdot q = p[/math] Гипергеометрическое распределение [ править ]Гипергеометрическое распределение в теории вероятностей моделирует количество удачных выборок без возвращения из конечной совокупности. Пусть имеется конечная совокупность, состоящая из [math]N[/math] элементов. Предположим, что [math]D[/math] из них обладают нужным нам свойством. Оставшиеся [math]N-D[/math] этим свойством не обладают. Случайным образом из общей совокупности выбирается группа из [math]n[/math] элементов. Пусть [math]a[/math] — случайная величина, равная количеству выбранных элементов, обладающих нужным свойством. Тогда функция вероятности [math]a[/math] имеет вид: где [math]C_n^k \equiv \dfrac Формула математического ожидания для гипергеометрического распределения имеет вид: Основы теории вероятностей. Математическое ожидание величины.Каждая, отдельно взятая величина полностью определяется своей функцией распределения. Также, для решения практических задач хватает знать несколько числовых характеристик, благодаря которым появляется возможность представить основные особенности случайной величины в краткой форме. К таким величинам относят в первую очередь математическое ожидание и дисперсия. Математическое ожидание — среднее значение случайной величины в теории вероятностей. Обозначается как Самым простым способом математическое ожидание случайной величины Х(w), находят как интеграл Лебега по отношению к вероятностной мере Р исходном вероятностном пространстве Еще найти математическое ожидание величины можно как интеграл Лебега от х по распределению вероятностей РХ величины X: где при этом интегрируемость X в смысле (*) соответствует конечности интеграла если X имеет абсолютно непрерывное распределение с плотностью вероятности р(х), то при этом существование математического ожидания равносильно абсолютной сходимости соответствующего ряда или интеграла. Свойства математического ожидания случайной величины.если сходится ряд: Алгоритм вычисления математического ожидания.Свойства дискретных случайных величин: все их значения можно перенумеровать натуральными числами; каждому значению приравнять отличную от нуля вероятность. 2. Складываем произведение каждой пары xipi. Функция распределения дискретной случайной величины ступенчатая, она возрастает скачком в тех точках, вероятности которых имеют положительный знак. Пример: Найти математическое ожидание по формуле: Найти математическое ожидание по формуле: |  |
Математическое ожидание M[X] равно:
Дисперсию найдем по формуле:
Математическое ожидание и дисперсия случайной величины
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Математическое ожидание дискретной случайной величины
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных её значений на вероятности этих значений:
Решение. Средний выигрыш мы найдём, если общую сумму выигрышей, которая равна 10*400 + 20*300 + 100*200 + 200*100 = 50000 руб, разделим на 1000 (общая сумма выигрышей). Тогда получим 50000/1000 = 50 руб. Но выражение для подсчёта среднего выигрыша можно представить и в следующем виде:
С другой стороны, в данных условиях размер выигрыша является случайной величиной, которая может принимать значения 10, 20, 100 и 200 руб. с вероятностями, равными соответственно 0,4; 0,3; 0,2; 0,1. Следовательно, ожидаемый средний выигрыш равен сумме произведений размеров выигрышей на вероятности их получения.
| Число проданных экземпляров | Вероятность | Затраты |
| 500 | 0,20 | 225000 |
| 1000 | 0,40 | 250000 |
| 2000 | 0,25 | 300000 |
| 3000 | 0,10 | 350000 |
| 4000 | 0,05 | 400000 |
Найти ожидаемую прибыль издателя.
| Число | Прибыль x i | Вероятность p i | x i p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Всего: | 1,00 | 25000 |
Таким образом, получаем математическое ожидание прибыли издателя:


Найти математическое ожидание случайной величины самостоятельно, а затем посмотреть решение
Подсказка: вероятность значений случайной величины найти по формуле Бернулли.
Свойства математического ожидания
Рассмотрим свойства математического ожидания.
Свойство 1. Математическое ожидание постоянной величины равно этой постоянной:
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
Свойство 3. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий:
Свойство 4. Математическое ожидание произведения случайных величин равно произведению их математических ожиданий:
Свойство 5. Если все значения случайной величины X уменьшить (увеличить) на одно и то же число С, то её математическое ожидание уменьшится (увеличится) на то же число:
Когда нельзя ограничиваться только математическим ожиданием
В большинстве случаев только математическое ожидание не может в достаточной степени характеризовать случайную величину.
Пусть случайные величины X и Y заданы следующими законами распределения:
| Значение X | Вероятность |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Значение Y | Вероятность |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Однако характер распределения их различный. Случайная величина X может принимать только значения, мало отличающиеся от математического ожидания, а случайная величина Y может принимать значения, значительно отклоняющиеся от математического ожидания. Аналогичный пример: средняя заработная плата не даёт возможности судить об удельном весе высоко- и низкооплачиваемых рабочих. Иными словами, по математическому ожиданию нельзя судить о том, какие отклонения от него, хотя бы в среднем, возможны. Для этого нужно найти дисперсию случайной величины.
Дисперсия дискретной случайной величины
Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения её от математического ожидания:
Средним квадратическим отклонением 

Пример 5. Вычислить дисперсии и средние квадратические отклонения случайных величин X и Y, законы распределения которых приведены в таблицах выше.
Решение. Математические ожидания случайных величин X и Y, как было найдено выше, равны нулю. Согласно формуле дисперсии при Е(х)=Е(y)=0 получаем:
Тогда средние квадратические отклонения случайных величин X и Y составляют


Пример 6. У инвестора есть 4 альтернативных проекта инвестиций. В таблице обобщены данные об ожидаемой прибыли в этих проектах с соответствующей вероятностью.
| Проект 1 | Проект 2 | Проект 3 | Проект 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Найти для каждой альтернативы математическое ожидание, дисперсию и среднее квадратическое отклонение.
Решение. Покажем, как вычисляются эти величины для 3-й альтернативы:


В таблице обобщены найденные величины для всех альтернатив.
| Проект 1 | Проект 2 | Проект 3 | Проект 4 | |
| μ | 500 | 500 | 500 | 500 |
| σ² | 0 | 2500 | 1250 | 500000 |
| σ | 0 | 500 | 354 | 7071 |
Свойства дисперсии
Приведём свойства дисперсии.
Свойство 1. Дисперсия постоянной величины равна нулю:

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат:

Свойство 3. Дисперсия случайной величины равна математическому ожиданию квадрата этой величины, из которого вычтен квадрат математического ожидания самой величины:

где 
Свойство 4. Дисперсия суммы (разности) случайных величин равна сумме (разности) их дисперсий:
Закон распределения случайной величины:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
Дисперсию данной случайной величины вычислим по формуле из свойства 3 дисперсии:
Найти математическое ожидание случайной величины самостоятельно, а затем посмотреть решение
Решение. Случайная величина X может принимать значения 0, 1, 2, 3. Соответствующие им вероятности можно вычислить по правилу умножения вероятностей. Закон распределения случайной величины:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Отсюда математическое ожидание данной случайной величины:
Дисперсия данной случайной величины:
Математическое ожидание и дисперсия непрерывной случайной величины
Для непрерывной случайной величины механическая интерпретация математического ожидания сохранит тот же смысл: центр массы для единичной массы, распределённой непрерывно на оси абсцисс с плотностью f(x). В отличие от дискретной случайной величиной, у которой аргумент функции x i изменяется скачкообразно, у непрерывной случайной величины аргумент меняется непрерывно. Но математическое ожидание непрерывной случайной величины также связано с её средним значением.
Чтобы находить математическое ожидание и дисперсию непрерывной случайной величины, нужно находить определённые интегралы. Если дана функция плотности непрерывной случайной величины, то она непосредственно входит в подынтегральное выражение. Если дана функция распределения вероятностей, то, дифференцируя её, нужно найти функцию плотности.
Арифметическое среднее всех возможных значений непрерывной случайной величины называется её математическим ожиданием, обозначаемым 

Математическое ожидание 

если он сходится абсолютно.
Дисперсией непрерывной случайной величины называется величина интеграла

если он сходится.
Среднее квадратичное отклонение непрерывной случайной величины определяется как арифметическое значение квадратного корня из дисперсии.
Найти математическое ожидание и дисперсию непрерывной случайной величины самостоятельно, а затем посмотреть решение
Это наиболее простой пример, так как функция распределения вероятностей дифференцируется и интегралы находятся в нём весьма просто. Поэтому пример предлагается для самостоятельного решения.
Пример 10. Дана функция распределения вероятностей непрерывной случайной величины:
Найти математическое ожидание и дисперсию непрерывной случайной величины.
Пример 11. Дана функция распределения вероятностей непрерывной случайной величины:
Найти математическое ожидание и дисперсию непрерывной случайной величины.
Таким образом, функция плотности:
Математическим ожиданием данной непрерывной случайной величины будет следующий интеграл:

Этот интеграл найдём, интегрируя по частям. Для этого ведём следующие обозначения:
Таким образом, находим математическое ожидание:
Дисперсией непрерывной случайной величины будет следующий интеграл:

Его также найдём по частям. Введём обозначения:

Вновь интегрируем по частям. Вводим обозначения:
И находим дисперсию данной непрерывной случайной величины:
Пример 12. Дана непрерывная случайная величина. Её плотность вероятности 


Решение. Сначала определим параметр с. Разбивая отрезок интегрирования на части, получаем
так как остальные два интеграла равны нулю вследствие равенства нулю плотности вероятности на этих интервалах. Следовательно,

откуда 
При 
(пределы интегрирования 0 и 10 установлены по тем же соображениям, что и при нахождении параметра с). Дисперсию вычисляем при a=5 и f(x)=0,1:
Математическое ожидание
Математическое ожидание – это распределение вероятностей случайной величины
Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет, свойства, задачи, оценка матожидания, дисперсия, функция распределения, формулы, примеры расчета
Содержание
Мат ожидание – это одно из важнейших понятий в математической статистике и теории вероятностей, характеризующее распределение значений или вероятностей случайной величины. Обычно выражается как средневзвешенное значение всех возможных параметров случайной величины. Широко применяется при проведении технического анализа, исследовании числовых рядов, изучении непрерывных и продолжительных процессов. Имеет важное значение при оценке рисков, прогнозировании ценовых показателей при торговле на финансовых рынках, используется при разработке стратегий и методов игровой тактики в теории азартных игр.
Мат ожидание – это мера среднего значения случайной величины в теории вероятности. Мат ожидание случайной величины x обозначается M(x).
Мат ожидание – это число, вокруг которого сосредоточены значения случайной величины.
Мат ожидание – это в теории вероятности средневзвешенная величина всех возможных значений, которые может принимать эта случайная величина.
Мат ожидание – это сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Мат ожидание – это средняя выгода от того или иного решения при условии, что подобное решение может быть рассмотрено в рамках теории больших чисел и длительной дистанции.
Мат ожидание – это в теории азартных игр сумма выигрыша, которую может заработать или проиграть спекулянт, в среднем, по каждой ставке. На языке азартных спекулянтов это иногда называется «преимуществом спекулянта» (если оно положительно для спекулянта) или «преимуществом казино» (если оно отрицательно для спекулянта).
Мат ожидание – это процент профита на выигрыш, умноженный на среднюю прибыль, минус вероятность убытка, умноженная на средний убыток.
Математическое ожидание случайной величины в математической теории
Одной из важных числовых характеристик случайной величины является мат ожидание. Введем понятие системы случайных величин. Рассмотрим совокупность случайных величин, которые являются результатами одного и того же случайного эксперимента. Если — одно из возможных значений системы, то событию соответствует определенная вероятность удовлетворяющая аксиомам Колмогорова. Функция, определенная при любых возможных значениях случайных величин, называется совместным законом распределения. Эта функция позволяет вычислять вероятности любых событий из. В частности, совместный закон распределения случайных величин и, которые принимают значения из множества и, задается вероятностями.
Термин «мат. ожидание» введён Пьером Симоном маркизом де Лапласом (1795) и произошёл от понятия «ожидаемого значения выигрыша», впервые появившегося в 17 веке в теории азартных игр в трудах Блеза Паскаля и Христиана Гюйгенса. Однако первое полное теоретическое осмысление и оценка этого понятия даны Пафнутием Львовичем Чебышёвым (середина 19 века).
Закон распределения случайных числовых величин (функция распределения и ряд распределения или плотность вероятности) полностью описывают поведение случайной величины. Но в ряде задач достаточно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный вопрос. Основными числовыми характеристиками случайных величин являются мат ожидание, дисперсия, мода и медиана.
Мат ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности. Иногда мат. ожидание называют взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов. Из определения мат ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего. Мат ожидание случайной величины есть неслучайная (постоянная) величина.
Мат ожидание имеет простой физический смысл: если на прямой разместить единичную массу, поместив в некоторые точки некоторую массу (для дискретного распределения), или «размазав» её с определенной плотностью (для абсолютно непрерывного распределения), то точка, соответствующая мат ожиданию, будет координатой «центра тяжести» прямой.
Среднее значение случайной величины есть некоторое число, являющееся как бы её «представителем» и заменяющее её при грубо ориентировочных расчетах. Когда мы говорим: «среднее время работы лампы равно 100 часам» или «средняя точка попадания смещена относительно цели на 2 м вправо», мы этим указываем определенную числовую характеристику случайной величины, описывающую её местоположение на числовой оси, т.е. «характеристику положения».
Из характеристик положения в теории вероятностей важнейшую роль играет мат ожидание случайной величины, которое иногда называют просто средним значением случайной величины.
Рассмотрим случайную величину Х, имеющую возможные значения х1, х2, …, хn с вероятностями p1, p2, …, pn. Нам требуется охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Для этой цели естественно воспользоваться так называемым «средним взвешенным» из значений xi, причем каждое значение xi при осреднении должно учитываться с «весом», пропорциональным вероятности этого значения. Таким образом, мы вычислим среднее случайной величины X, которое мы обозначим M |X|:
Это среднее взвешенное значение и называется мат ожиданием случайной величины. Таким образом, мы ввели в рассмотрении одно из важнейших понятий теории вероятностей – понятие мат. ожидания. Мат. ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Мат. ожидание случайной величины Х связано своеобразной зависимостью со средним арифметическим наблюденных значений случайной величины при большом числе опытов. Эта зависимость того же типа, как зависимость между частотой и вероятностью, а именно: при большом числе опытов среднее арифметическое наблюденных значений случайной величины приближается (сходится по вероятности) к ее мат. ожиданию. Из наличия связи между частотой и вероятностью можно вывести как следствие наличие подобной же связи между средним арифметическим и математическим ожидание. Действительно, рассмотрим случайную величину Х, характеризуемую рядом распределения:
Пусть производится N независимых опытов, в каждом из которых величина X принимает определенное значение. Предположим, что значение x1 появилось m1 раз, значение x2 появилось m2 раз, вообще значение xi появилось mi раз. Вычислим среднее арифметическое наблюденных значений величины Х, которое, в отличие от мат ожидания М|X| мы обозначим M*|X|:
При увеличении числа опытов N частоты pi будут приближаться (сходиться по вероятности) к соответствующим вероятностям. Следовательно, и среднее арифметическое наблюденных значений случайной величины M|X| при увеличении числа опытов будет приближаться (сходится по вероятности) к её мат ожиданию. Сформулированная выше связь между средним арифметическим и мат. ожиданием составляет содержание одной из форм закона больших чисел.
Мы уже знаем, что все формы закона больших чисел констатируют факт устойчивости некоторых средних при большом числе опытов. Здесь речь идет об устойчивости среднего арифметического из ряда наблюдений одной и той же величины. При небольшом числе опытов среднее арифметическое их результатов случайно; при достаточном увеличении числа опытов оно становится «почти не случайным» и, стабилизируясь, приближается к постоянной величине – мат. ожиданию.
Свойство устойчивости средних при большом числе опытов легко проверить экспериментально. Например, взвешивая какое-либо тело в лаборатории на точных весах, мы в результате взвешивания получаем каждый раз новое значение; чтобы уменьшить ошибку наблюдения, мы взвешиваем тело несколько раз и пользуемся средним арифметическим полученных значений. Легко убедиться, что при дальнейшем увеличении числа опытов (взвешиваний) среднее арифметическое реагирует на это увеличение все меньше и меньше и при достаточно большом числе опытов практически перестает меняться.
Следует заметить, что важнейшая характеристика положения случайной величины – мат. ожидание – существует не для всех случайных величин. Можно составить примеры таких случайных величин, для которых мат. ожидания не существует, так как соответствующая сумма или интеграл расходятся. Однако для практики такие случаи существенного интереса не представляют. Обычно случайные величины, с которыми мы имеем дело, имеют ограниченную область возможных значений и, безусловно, обладают мат ожиданием.
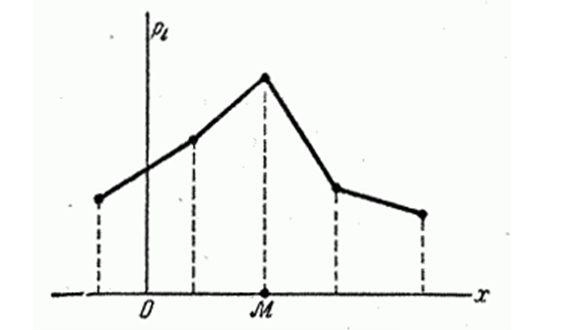
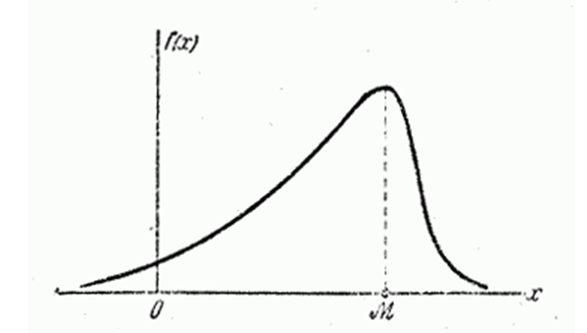
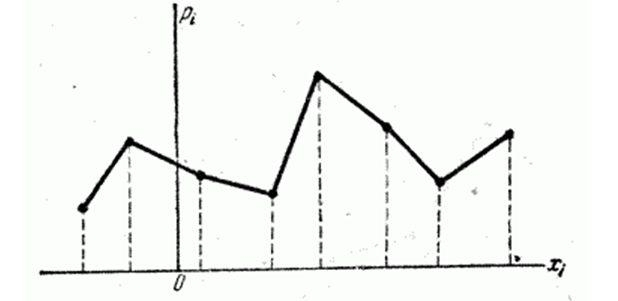
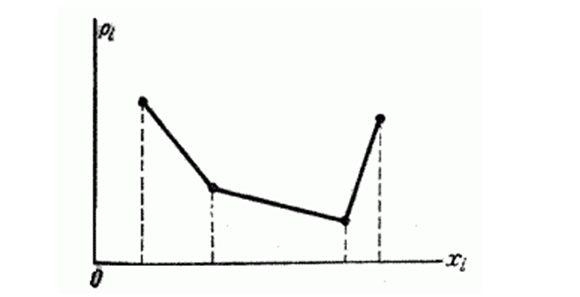
Модой случайной величины называется её наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. На рисунках показана мода соответственно для прерывной и непрерывной случайных величин.
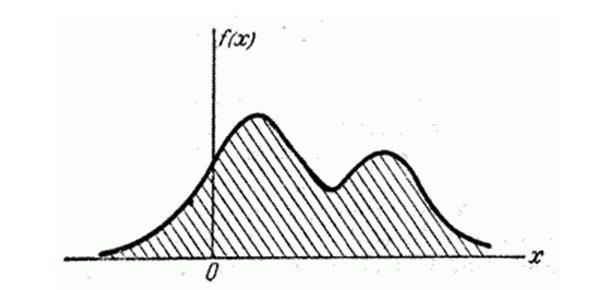
Если многоугольник распределения (кривая распределения) имеет более одного максимума, распределение называется «полимодальным».
Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом. Такие распределения называют «антимодальными».
В общем случае мода и мат ожидание случайной величины не совпадают. В частном случае, когда распределение является симметричным и модальным (т.е. имеет моду) и существует мат. ожидание, то оно совпадает с модой и центром симметрии распределения.
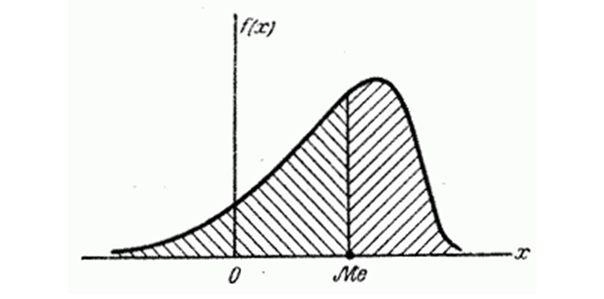
Часто применяется еще одна характеристика положения – так называемая медиана случайной величины. Этой характеристикой пользуются обычно только для непрерывных случайных величин, хотя формально можно её определить и для прерывной величины. Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.
В случае симметричного модального распределения медиана совпадает с мат. ожиданием и модой.
Мат. ожидание может быть вычислено и как интеграл Лебега от х по распределению вероятностей рх величины X:
Естественным образом можно определить понятие случайной величины с бесконечным мат ожиданием. Типичным примером служат времена репатриации в некоторых случайных блужданиях.
С помощью мат. ожидания определяются многие числовые и функциональные характеристики распределения (как мат. ожидание соответствующих функций от случайной величины), например, производящая функция, характеристическая функция, моменты любого порядка, в частности дисперсия, ковариация.
Математическое ожидание дискретной случайной величины
Пусть есть некоторая случайная величина, которая может принять одно из нескольких числовых значений (допустим, количество очков при броске кости может быть 1, 2, 3, 4, 5 или 6). Часто на практике для такой величины возникает вопрос: а какое значение она принимает «в среднем» при большом количестве тестов? Каков будет наш средний доход (или убыток) от каждой из рискованных операций?
Теперь обобщим наши примеры:
Обратимся к только что приведённой картинке. Слева табличка распределения случайной величины. Величина X может принимать одно из n возможных значений (приведены в верхней строке). Никаких других значений не может быть. Под каждым возможным значением снизу подписана его вероятность. Справа приведена формула, где M(X) и называется мат. ожиданием. Смысл этой величины в том, что при большом количестве испытаний (при большой выборке) среднее значение будет стремиться к этому самому мат ожиданию.
Посчитаем мат. ожидание для выше описанной лотереи. Табличка будет выглядеть вот так:
Тогда мат ожидание составит, как мы установили выше.:
Другое дело, что так же «на пальцах», без формулы, было бы трудновато, если бы имелось больше вариантов. Ну скажем, имелось бы 75% проигрышных билетов, 20% выигрышных билетов и 5% особо выигрышных.
Теперь некоторые свойства мат ожидания.
Мат. ожидание является линейным. Доказать это просто:
Постоянный множитель допускается выносить за знак мат. ожидания, то есть:
Это является частным случаем свойства линейности мат ожидания.
Другое следствие линейности мат. ожидания:
то есть мат. ожидание суммы случайных величин равно сумме математических ожиданий случайных величин.
Это тоже несложно доказать) Произведение XY само представляет собой случайную величину, при этом если исходные величины могли принимать n и m значений соответственно, то XY может принимать nm значений. Вероятность каждого из значений вычисляется исходя из того, что вероятности независимых событий перемножаются. В итоге получаем вот что:
Математическое ожидание непрерывной случайной величины
Если известна плотность распределения, то мат ожидание ищется так:
Пусть, например, есть равномерное распределение:
Найдём мат. ожидание:
Это вполне соответствует интуитивному пониманию. Скажем, если мы получаем при равномерном распределении много случайных действительных чисел, каждое из отрезка |0; 1|, то среднее арифметическое должно быть около 0,5.
Взаимосвязь математического ожидания с другими статистическими показателями
В статистическом анализе наряду с мат ожиданием существует система взаимозависимых показателей, отражающих однородность явлений и устойчивость процессов. Часто показатели вариации не имеют самостоятельного смысла и используются для дальнейшего анализа данных. Исключением является коэффициент вариации, который характеризует однородность данных, что является ценной статистической характеристикой.
Степень изменчивости или устойчивости процессов в статистической науке может измеряться с помощью нескольких показателей.
Наиболее важным показателем, характеризующим изменчивость случайной величины, является Дисперсия, которая самым тесным и непосредственным образом связана с мат. ожиданием. Этот параметр активно используется в других видах статистического анализа (проверка гипотез, анализ причинно-следственных связей и др.). Как и среднее линейное отклонение, дисперсия также отражает меру разброса данных вокруг средней величины.
Формула для расчета дисперсии выглядит так:
Однако в чистом виде, как, например, средняя арифметическая, или индекс, дисперсия не используется. Это скорее вспомогательный и промежуточный показатель, который используется для других видов статистического анализа. У нее даже единицы измерения нормальной нет. Судя по формуле, это квадрат единицы измерения исходных данных.
Пусть мы измеряем случайную величину N раз, например, десять раз измеряем скорость ветра и хотим найти среднее значение. Как связано среднее значение с функцией распределения?
Или будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Среднее арифметическое выпавших очков, подсчитанных за все броски кубика, тоже является случайной величиной, однако при больших N оно стремится ко вполне конкретному числу – мат. ожиданию Mx. В данном случае Mx = 3,5.
Каким образом получилась эта величина? Пусть в N испытаниях n1 раз выпало 1 очко, n2 раз – 2 очка и так далее. Тогда количество исходов, в которых выпало одно очко:
Аналогично для исходов, когда выпало 2, 3, 4, 5 и 6 очков.
Предположим теперь, что мы знаем закон распределения случайной величины x, то есть знаем, что случайная величина x может принимать значения x1, x2. xk с вероятностями p1, p2. pk.
Мат ожидание Mx случайной величины x равно:
Мат ожидание не всегда является разумной оценкой какой-нибудь случайной величины. Так, для оценки средней заработной платы разумнее использовать понятие медианы, то есть такой величины, что количество людей, получающих меньшую, чем медиана, зарплату и большую, совпадают.
Вероятность р1 того, что случайная величина х окажется меньшей х1/2, и вероятность р2 того, что случайная величина x окажется большей х1/2, одинаковы и равны 1/2. Медиана определяется однозначно не для всех распределений.
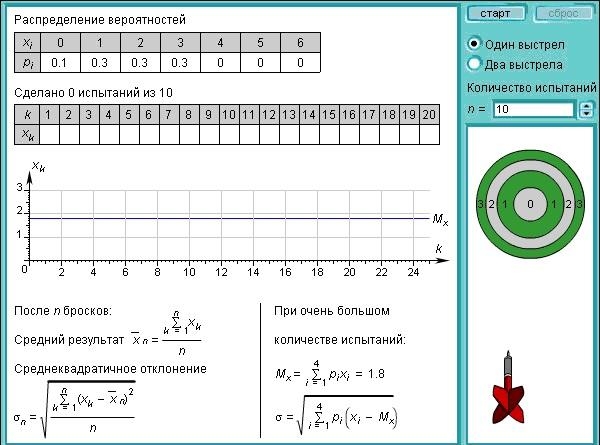
Пример. В условиях испытаний при стрельбе по мишени вычислить дисперсию и среднеквадратическое отклонение случайной величины:
Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности. Этот показатель дает самое общее представление о колеблемости изучаемого признака, так как показывает разницу только между предельными значениями вариантов. Зависимость от крайних значений признака придает размаху вариации неустойчивый, случайный характер.
Среднее линейное отклонение представляет собой среднее арифметическое из абсолютных (по модулю) отклонений всех значений анализируемой совокупности от их средней величины:
Математическое ожидание в теории азартных игр
Мат ожидание – это среднее количество денег, которое спекулянт в азартные игры может выиграть или проиграть на данной ставке. Это очень существенное понятие для спекулянта, потому что оно является основополагающим для оценки большинства игровых ситуаций. Мат ожидание – это также оптимальный инструмент для анализа основных карточных раскладов и игровых ситуаций.
Ваш часовой выигрыш равен нулю. Часовой выигрыш – это то количество денег, которое вы ожидаете выиграть за час. Вы можете кидать монету 500 раз в течение часа, но вы не выиграете и не проиграете, т.к. ваши шансы ни положительны, ни отрицательны. Если смотреть, с точки зрения серьезного спекулянта такая система ставок неплоха. Но это попросту потеря времени.
Каждый раз, делая ставку с лучшим исходом (ставка, которая может оказаться выгодной на длинной дистанции), когда шансы в вашу пользу, вы обязательно что-то выигрываете на ней, и не важно теряете ли вы ее или нет в данной раздаче. И напротив, если вы сделали ставку с худшим исходом (ставка, которая невыгодна на длинной дистанции), когда шансы не в вашу пользу, вы что-то теряете независимо от того, выиграли вы или проиграли в данной раздаче.
Вы делаете ставку с лучшим исходом, если матожидание у вас положительно, а оно является положительным, если шансы на вашей стороне. Делая ставку с худшим исходом, у вас отрицательное матожидание, которое бывает, когда шансы против вас. Серьезные спекулянты делают ставки только с лучшим исходом, при худшем – они пасуют. Что означает шансы в вашу пользу? Вы можете в итоге выиграть больше, чем приносят реальные шансы. Реальные шансы на то, что выпадет решка 1 к 1, но у вас выходит 2 к 1 за счет соотношения ставок. В данном случае шансы в вашу пользу. Вы точно получаете лучший исход с положительным ожиданием в 50 центов за одну ставку.
Спекулянт, который собирается выиграть больше, чем ставит, как в примере выше, – ловит шансы. И напротив, он губит шансы, когда предполагает выиграть меньше, чем ставит. Спекулянт, делающий ставку может иметь либо положительное, либо отрицательное матожидание, которое зависит от того, ловит он или губит шансы.
Математическое ожидание при игре в Покер
Игра в Покер является наиболее показательным и наглядным примером с точки зрения использования теории и свойств мат ожидания.
Мат. ожидание (англ. Expected Value) в Покере – средняя выгода от того или иного решения при условии, что подобное решение может быть рассмотрено в рамках теории больших чисел и длительной дистанции. Успешная игра в покер заключается в том, чтобы всегда принимать ходы только с положительным математическим ожиданием.
Математический смысл мат. ожидания при игре в покер заключается в том, что мы часто сталкиваемся со случайными величинами при принятии решения (мы не знаем, какие именно карты на руках у оппонента, какие карты придут на последующих кругах торговли). Мы должны рассматривать каждое из решений с точки зрения теории больших чисел, которая гласит, что при достаточно большой выборке среднее значение случайной величины будет стремиться к её мат ожиданию.
Среди частных формул для вычисления мат ожидания, в покере наиболее применима следующая:
Ожидание говорит вам о том, что вы можете ожидать (прибыль или убыток) на каждый рискуемый вами доллар. Казино зарабатывают деньги, поскольку мат ожидание от всех игры, которые практикуются в них, в пользу казино. При достаточно длинной серии игры можно ожидать, что клиент потеряет свои деньги, поскольку «вероятность» в пользу казино. Однако профессиональные спекулянты в казино ограничивают свои игры короткими промежутками времени, тем самым увеличивая вероятность в свою пользу. То же самое касается и инвестирования. Если ваше ожидание является положительным, вы можете заработать больше денег, совершая много сделок в короткий период времени. Ожидание это ваш процент профита на выигрыш, умноженный на среднюю прибыль, минус ваша вероятность убытка, умноженная на средний убыток.
Покер также можно рассмотреть с точки зрения мат ожидания. Вы можете предположить, что определенный ход выгоден, но в некоторых случаях он может оказаться далеко не лучшим, потому что выгоднее другой ход. Допустим, вы собрали фулл-хаус в пятикарточном покере с обменом. Ваш соперник делает ставку. Вы знаете, что если повысите ставку, он ответит. Поэтому повышение выглядит лучшей тактикой. Но если вы все же поднимите ставку, оставшиеся двое спекулянтов, точно сбросят карты. Но если вы уравняете ставку, то будете полностью уверены, что двое других спекулянтов после вас поступят также. При повышении ставки вы получаете одну единицу, а просто уравнивая – две. Таким образом, уравнивание дает вам более высокое положительное математическое ожидание, и будет являться наилучшей тактикой.
Другой важной причиной для понимания сути мат. ожидания является то, что оно дает вам чувство спокойствия независимо от того, выиграли вы ставку или нет: если вы сделали хорошую ставку или вовремя спасовали, вы будете знать, что вы заработали или сберегли определенное количество денег, которое спекулянт слабее не смог уберечь. Гораздо сложнее сбросить карты, если вы расстроены тем, что соперник на обмене собрал более сильную комбинацию. При всем при этом, деньги, которые вы сберегли, не играя, вместо того, чтобы ставить, прибавляются к вашему выигрышу за ночь или за месяц.
Просто помните, что если поменять ваши руки, ваш соперник ответил бы вам, и как вы увидите в статье «фундаментальная теорема покера» это лишь одно из ваших преимуществ. Вы должны радоваться, когда это случится. Вам даже можно научиться получать удовольствие от проигранной раздачи, потому что вы знаете, что другие спекулянты на вашем месте проиграли бы гораздо больше.
За большой промежуток времени суммарный выигрыш спекулянта составляет сумму его математических ожиданий в отдельных раздачах. Чем больше вы играете с положительным ожиданием, тем больше выигрываете, и наоборот, чем больше раздач с отрицательным ожиданием вы сыграете, тем больше вы проиграете. Вследствие этого, следует отдавать предпочтение игре, которая сможет максимально увеличить ваше положительное ожидание или сведет на нет отрицательное, чтобы вы смогли поднять до максимума ваш часовой выигрыш.
Положительное математическое ожидание в игровой стратегии
Если вы знаете, как считать карты, у вас может быть преимущество перед казино, если они не заметят этого и не выкинут вас вон. Казино обожают пьяных спекулянтов и не переносят считающих карты. Преимущество позволит вам со временем выиграть большее число раз, чем проиграть. Хорошее управление капиталом при использовании расчетов мат ожидания может помочь извлечь больше профита из вашего преимущества и сократить потери. Без преимущества вам лучше отдать деньги на благотворительность. В игре на бирже преимущество дает система игры, создающая большую прибыль, чем потери, разница цен и комиссионные. Никакое управление капиталом не спасет плохую игровую систему.
Положительное ожидание определяется значением, превышающим ноль. Чем больше это число, тем сильнее статистическое ожидание. Если значение меньше нуля, то мат. ожидание также будет отрицательным. Чем больше модуль отрицательного значения, тем хуже ситуация. Если результат равен нулю, то ожидание является безубыточным. Вы можете выиграть только тогда, когда у вас положительное математическое ожидание, разумная система игры. Игра по интуиции приводит к катастрофе.
Математическое ожидание и биржевая торговля
Мат ожидание – достаточно широко востребованный и популярный статистический показатель при осуществлении биржевых торгов на финансовых рынках. В первую очередь данный параметр используют для анализа успешности торговли. Не сложно догадаться, что чем больше данное значение, тем больше оснований считать изучаемую торговлю успешной. Конечно, анализ работы трейдера не может производиться только лишь с помощью данного параметра. Тем не менее, вычисляемое значение в совокупности с другими способами оценки качества работы, может существенно повысить точность анализа.
Мат ожидание часто вычисляется в сервисах мониторингов торговых счетов, что позволяет быстро оценивать работу, совершаемую на депозите. В качестве исключений можно привести стратегии, в которых используется “пересиживание” убыточных сделок. Трейдеру может некоторое время сопутствовать удача, а потому, в его работе может не оказаться убытков вообще. В таком случае, ориентироваться только по матожиданию не получится, ведь не будут учтены риски, используемые в работе.
В торговле на рынке мат ожидание чаще всего применяют при прогнозировании доходности какой-либо торговой стратегии или при прогнозировании доходов трейдера на основе статистических данных его предыдущих торгов.
В отношении управления капиталом очень важно понимать, что при совершении сделок с отрицательным ожиданием нет схемы управления деньгами, которая может однозначно принести высокую прибыль. Если вы продолжаете играть на бирже в этих условиях, то независимо от способа управления деньгами вы потеряете весь ваш счет, каким бы большим он ни был в начале.
Эта аксиома верна не только для игры или сделок с отрицательным ожиданием, она истинна также для игры с равными шансами. Поэтому единственный случай, когда у вас есть шанс получить выгоду в долгосрочной перспективе, — это заключение сделок с положительным математическим ожиданием.
Различие между отрицательным ожиданием и положительным ожиданием — это различие между жизнью и смертью. Не имеет значения, насколько положительное или насколько отрицательное ожидание; важно только то, положительное оно или отрицательное. Поэтому до рассмотрения вопросов управления капиталом вы должны найти игру с положительным ожиданием.
Если у вас такой игры нет, тогда никакое управление деньгами в мире не спасет вас. С другой стороны, если у вас есть положительное ожидание, то можно, посредством правильного управления деньгами, превратить его в функцию экспоненциального роста. Не имеет значения, насколько мало это положительное ожидание! Другими словами, не имеет значения, насколько прибыльна торговая система на основе одного контракта. Если у вас есть система, которая выигрывает 10 долларов на контракт в одной сделке (после вычета комиссионных и проскальзывания), можно использовать методы управления капиталом таким образом, чтобы сделать ее более прибыльной, чем систему, которая показывает среднюю прибыль 1000 долларов за сделку (после вычета комиссионных и проскальзывания).
Имеет значение не то, насколько прибыльна система была, а то, насколько определенно можно сказать, что система покажет, по крайней мере, минимальную прибыль в будущем. Поэтому наиболее важное приготовление, которое может сделать трейдер, — это убедиться в том, что система покажет положительное математическое ожидание в будущем.
Для того чтобы иметь положительное математическое ожидание в будущем, очень важно не ограничивать степени свободы вашей системы. Это достигается не только упразднением или уменьшением количества параметров, подлежащих оптимизации, но также и путем сокращения как можно большего количества правил системы. Каждый параметр, который вы добавляете, каждое правило, которое вы вносите, каждое мельчайшее изменение, которое вы делаете в системе, сокращает число степеней свободы. В идеале, вам нужно построить достаточно примитивную и простую систему, которая постоянно будет приносить небольшую прибыль почти на любом рынке. И снова важно, чтобы вы поняли, — не имеет значения, насколько прибыльна система, пока она прибыльна. Деньги, которые вы заработаете в торговле, будут заработаны посредством эффективного управления деньгами.
Торговая система — это просто средство, которое дает вам положительное математическое ожидание, чтобы можно было использовать управление деньгами. Системы, которые работают (показывают, по крайней мере, минимальную прибыль) только на одном или нескольких рынках или имеют различные правила или параметры для различных рынков, вероятнее всего, не будут работать в режиме реального времени достаточно долго. Проблема большинства технически ориентированных трейдеров состоит в том, что они тратят слишком много времени и усилий на оптимизацию различных правил и значений параметров торговой системы. Это дает совершенно противоположные результаты. Вместо того, чтобы тратить силы и компьютерное время на увеличение профитов торговой системы, направьте энергию на увеличение уровня надежности получения минимальной профита.
Любому трейдеру для успеха в своей работе необходимо решить три самые важные задачи:. Добиться, чтобы число удачных сделок превышало неизбежные ошибки и просчеты; Настроить свою систему торговли так, чтобы возможность заработка была как можно чаще; Достичь стабильности положительного результата своих операций.
И здесь нам, работающим трейдерам, неплохую помощь может оказать мат. ожидание. Данный термин в теории вероятности является одним из ключевых. С его помощью можно дать усредненную оценку некоторому случайному значению. Мат ожидание случайной величины подобно центру тяжести, если представить себе все возможные вероятности точками с различной массой.
Что означает данное число? Оно говорит о том, что, следуя правилам данной системы, в среднем мы будет получать 1,708 доллара от каждой закрытой сделки. Поскольку полученная оценка эффективности больше нуля, то такую систему вполне можно использовать для реальной работы. Если же в результате расчета мат ожидание получится отрицательным, то это уже говорит о среднем убытке и такая торговля приведет к разорению.
Размер профита на одну сделку может быть выражен также и относительной величиной в виде %. Например:
В этом случае мат. ожидание составит:
То есть, средняя сделка принесет 1,96%.
Можно разработать систему, которая несмотря на преобладание убыточных сделок будет давать положительный результат, поскольку ее МО>0.
Впрочем, одного ожидания мало. Сложно заработать, если система дает очень мало торговых сигналов. В этом случае ее доходность будет сопоставима с банковским процентом. Пусть каждая операция дает в среднем всего лишь 0,5 доллара, но что если система предполагает 1000 операций в год? Это будет очень серьезная сумма за сравнительно малое время. Из этого логически вытекает, что еще одним отличительным признаком хорошей торговой системы можно считать короткий срок удержания позиций.

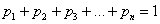
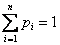
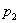
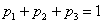
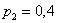
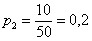
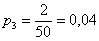
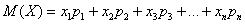
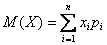
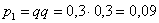
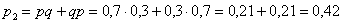
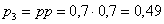
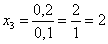
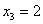







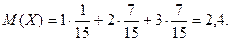
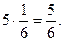
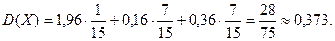
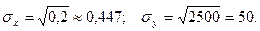


 .
.

 — множество всех возможных значений X.
— множество всех возможных значений X.