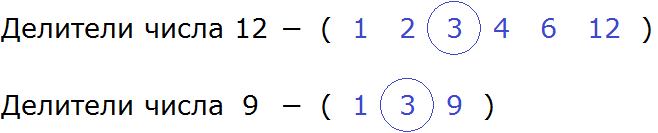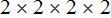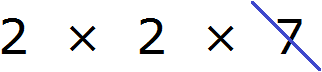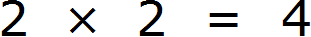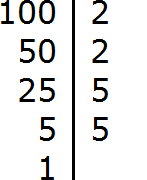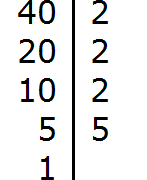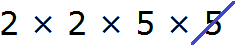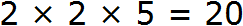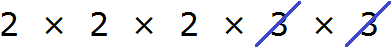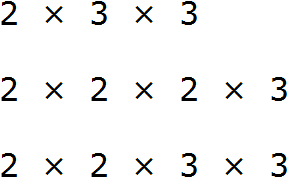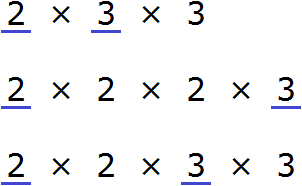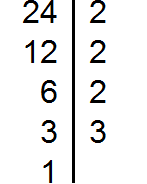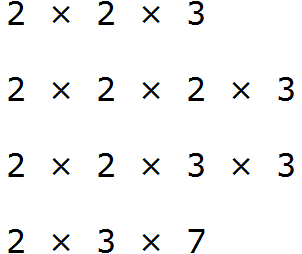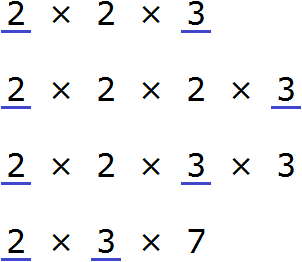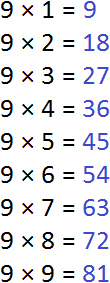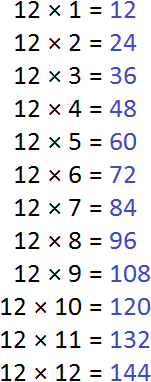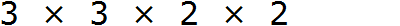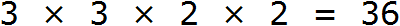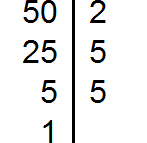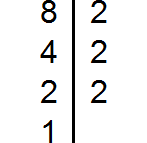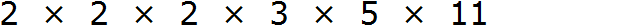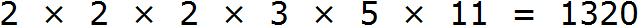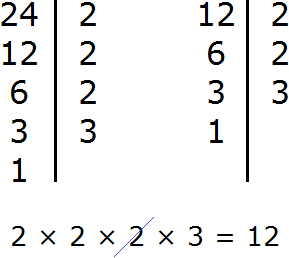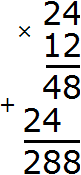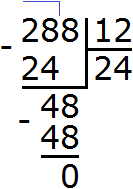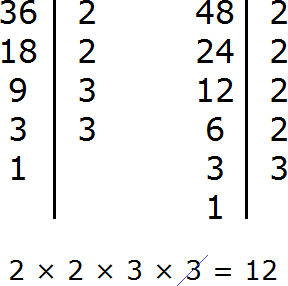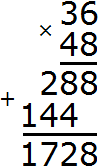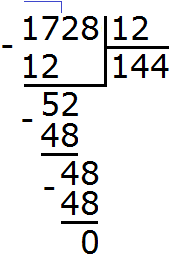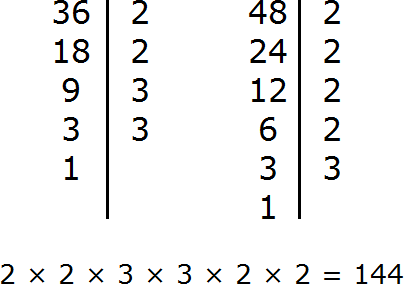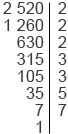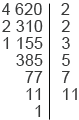Как найти наименьшее общее кратное
Как найти наименьшее общее кратное
Наименьшее общее кратное
Для того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).
Кратное числу « a » — это число, которое само делится на число « a » без остатка.
Числа кратные 8 (то есть, эти числа разделятся на 8 без остатка): это числа 16, 24, 32 …
Кратные 9: 18, 27, 36, 45 …
Чисел, кратных данному числу a бесконечно много, в отличии от делителей этого же числа. Делителей — конечное количество.
Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.
Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
Количество одинаковых множителей в разложениях чисел может быть разное.
24 = 2 · 2 · 2 · 3
НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48
Ответ: НОК (12, 16, 24) = 48
Особые случаи нахождения НОК
На нашем сайте вы также можете с помощью специального калькулятора найти наименьшее общее кратное онлайн, чтобы проверить свои вычисления.
Наименьшее общее кратное
Общее кратное
Число может быть кратно не одному, а сразу нескольким числам, такое число называется общим кратным данных чисел.
Числу 3 кратны числа: 6, 9, 12, 15 и т. д.
Числу 4 кратны числа: 8, 12, 16, 20 и т. д.
Можно заметить, что одно и тоже число (12) делится нацело сразу на оба числа 3 и 4. Следовательно, число 12 есть общее кратное чисел 3 и 4.
Общее кратное чисел — это любое число, которое делится без остатка на каждое из данных чисел.
Найти общее кратное нескольких натуральных чисел достаточно легко, можно просто перемножить данные числа, полученное произведение и будет их общим кратным.
Пример. Найти общее кратное для чисел 2, 3, 4, 6.
2 · 3 · 4 · 6 = 144.
Число 144 — общее кратное чисел 2, 3, 4 и 6.
Для любого количества натуральных чисел существует бесконечно много кратных.
Пример. Для чисел 12 и 20 кратными будут числа: 60, 120, 180, 240 и т. д. Все они являются общими кратными для чисел 12 и 20.
Наименьшее общее кратное
Наименьшее общее кратное (НОК) нескольких чисел — это самое маленькое натуральное число, которое делится без остатка на каждое из этих чисел.
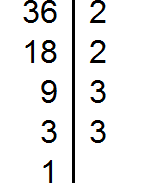
Пример. Наименьшим общим кратным чисел 3, 4 и 9 является число 36, никакое другое число меньше 36 не делится одновременно на 3, 4 и 9 без остатка.
Наименьшее общее кратное записывается так:
Числа в круглых скобках могут быть указаны в любом порядке.
Пример. Запишем наименьшее общее кратное чисел 3, 4 и 9:
Как найти НОК
Рассмотрим два способа нахождения наименьшего общего кратного: с помощью разложения чисел на простые множители и нахождение НОК через НОД.
С помощью разложения на простые множители
Чтобы найти НОК нескольких натуральных чисел, надо разложить эти числа на простые множители, затем взять из этих разложений каждый простой множитель с наибольшим показателем степени и перемножить эти множители между собой.
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Решение: разложим каждое из этих чисел на простые множители:
Наименьшее общее кратное должно делиться на 99, значит, в его состав должны входить все множители числа 99. Далее НОК должно делиться и на 54, т. е. в его состав должны входить множители и этого числа.
Выпишем из этих разложений каждый простой множитель с наибольшим показателем степени и перемножим эти множители между собой. Получим следующее произведение:
2 · 3 3 · 11 = 594.
Это и есть наименьшее общее кратное данных чисел. Никакое другое число меньше 594 не делится нацело на 99 и 54.
Ответ: НОК (99, 54) = 594.
Так как взаимно простые числа не имеют одинаковых простых множителей, то их наименьшее общее кратное равно произведению этих чисел.
Пример. Найдите наименьшее общее кратное двух чисел 12 и 49.
Решение: разложим каждое из этих чисел на простые множители:
12 = 2 · 2 · 3 = 2 2 · 3,
Применяя к этому случаю правило, мы придём к заключению, что взаимно простые числа надо просто перемножить:
2 2 · 3 · 7 2 = 12 · 49 = 588.
Ответ: НОК (12, 49) = 588.
Таким же образом надо поступать, когда нужно найти наименьшее общее кратное простых чисел.
Пример. Найдите наименьшее общее кратное чисел 5, 7 и 13.
Решение: так как данные числа являются простыми, то просто перемножим их:
Ответ: НОК (5, 7, 13) = 455.
Если большее из данных чисел делится на все остальные числа, то это число и будет наименьшим общим кратным данных чисел.
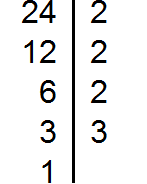
Пример. Найдите наименьшее общее кратное чисел 24, 12 и 4.
Решение: разложим каждое из этих чисел на простые множители:
24 = 2 · 2 · 2 · 3 = 2 3 · 3,
12 = 2 · 2 · 3 = 2 2 · 3,
Можно заметить, что разложение большего числа содержит все множители остальных чисел, значит большее из этих чисел делится на все остальные числа (в том числе и само на себя) и является наименьшим общим кратным:
Ответ: НОК (24, 12, 4) = 24.
Нахождение НОК через НОД
НОК двух натуральных чисел равно произведению этих чисел, поделённого на их НОД.
Правило в общем виде:
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Теперь мы можем вычислить НОК этих чисел по формуле:
НОК (99, 54) = 99 · 54 : НОД (99, 54) = 5346 : 9 = 594.
Ответ: НОК (99, 54) = 594.
Чтобы найти НОК трёх или более чисел используется следующий порядок действий:
Пример. Найдите наименьшее общее кратное чисел 8, 12 и 9.
Решение: сначала находим наибольший общий делитель любых двух из этих чисел, например, 12 и 8:
Вычисляем их НОК по формуле:
НОК (12, 8) = 12 · 8 : НОД (12, 8) = 96 : 4 = 24.
Теперь найдём НОК числа 24 и оставшегося числа 9. Их НОД:
Вычисляем НОК по формуле:
НОК (24, 9) = 24 · 9 : НОД (24, 9) = 216 : 3 = 72.
Ответ: НОК (8, 12, 9) = 72.
Калькулятор НОК
Наименьшее общее кратное (НОК): определение, примеры и свойства
Приступим к изучению наименьшего общего кратного двух и более чисел. В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач.
Общие кратные – определение, примеры
В данной теме нас будет интересовать только общие кратные целых чисел, отличных от нуля.
Общее кратное целых чисел – это такое целое число, которое кратно всем данным числам. Фактически, это любое целое число, которое можно разделить на любое из данных чисел.
Определение общих кратных чисел относится к двум, трем и большему количеству целых чисел.
0 является общим кратным для любого множества целых чисел, отличных от нуля.
Для всех ли чисел можно найти НОК?
Общее кратное можно найти для любых целых чисел.
Сколько всего общих кратных могут иметь данные целые числа?
Группа целых чисел может иметь большое количество общих кратных. Фактически, их число бесконечно.
Наименьшее общее кратное (НОК) – определение, обозначение и примеры
Вспомним понятие наименьшего числа из данного множества чисел, которое мы рассматривали в разделе «Сравнение целых чисел». С учетом этого понятия сформулируем определение наименьшего общего кратного, которое имеет среди всех общих кратных наибольшее практическое значение.
Наименьшее общее кратное данных целых чисел – это наименьшее положительное общее кратное этих чисел.
Не для всех групп данных чисел наименьшее общее кратное очевидно. Часто его приходится вычислять.
Связь между НОК и НОД
Наименьшее общее кратное и наибольший общий делитель связаны между собой. Взаимосвязь между понятиями устанавливает теорема.
Установление связи между НОК и НОД позволяет находить наименьшее общее кратное через наибольший общий делитель двух и более данных чисел.
Теорема имеет два важных следствия:
Наименьшее общее кратное трех и большего количества чисел
Для того, чтобы найти наименьшее общее кратное нескольких чисел, необходимо последовательно найти НОК двух чисел.
Доказать верность второй теоремы нам поможет первое следствие из первой теоремы, рассмотренной в данной теме. Рассуждения строятся по следующему алгоритму:
Наименьшее общее кратное: как найти
Наименьшее общее кратное — что это такое
Число, которое можно без остатка разделить на выбранные числа, является их общим кратным. Наименьшее из таких чисел — наименьшее общее кратное или сокращенно «нок».
Действия с дробями, имеющими различный знаменатель, можно значительно облегчить, если найти наименьшее общее кратное (НОК). Это такое число, например, кратное числу а, которое можно разделить на это а целиком, без остатка.
К числам, кратным 8, относятся 16, 24, 32, 40 и т.п. Кратными 9-ти являются 9, 18, 27, 36 и т.п.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Существует бесчисленное множество чисел, делящихся на а без остатка, т.е. кратных ему. В то же время, этого нельзя сказать о числе делителей. Так, делителями для 9-ти являются 9, 3, 1.
Если для двух или более натуральных чисел существует число, делящееся на оба без остатка, то оно является наименьшим общим кратным. А то из, них, которое самое маленькое, является нок.
Вычисление НОК, правила в математике
Для нахождения нок в математике существует несколько правил или алгоритмов. Самый простой вариант — вычисление НОК для двух чисел-участников. Способ легкий, но приемлем для маленьких натуральных чисел.
Нужно составить ряды чисел, кратных каждому из выбранных значений.
К (4) — 4, 8, 12, 16, 20, 24;
К (6) — 6, 12, 18, 24, 30.
Из рядов видно, что в обоих рядах встречаются числа 12 и 24. Это общие кратные. Однако 12 из них — меньшее число.
Поэтому НОК (4, 6) — 12.
Как найти НОК через НОД
Определение НОК можно провести с использованием НОД (наибольшего общего делителя).
В этом блоке изложения материала следует уточнить некоторые понятия.
Простым называется такое натуральное число, которое целиком можно разделить только само на себя либо на единицу.
Наименьшим простым числом является двойка. Она же — единственное четное натуральное простое число. Все остальные — нечетные.
Множество чисел делятся не только на 1 и на себя, но и на другие целые натуральные числа:
8 делится на 1, 2, 4, 8;
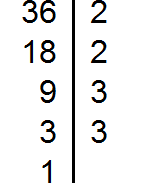
36 — на 1, 2, 3, 4, 6, 8 и т.д.
Эти числа — делители восьми и тридцати шести (делимых). Именно они могут разделить 8 и 36 без остатка. В обоих приведенных примерах делимые (8, 36) являются составными числами, поскольку имеют более двух делителей.
В приведенных рядах существуют одинаковые делители. Это 1, 2, 4, 8.
Самое большое число — 8. Оно и является наибольшим общим делителем.
Наибольший общий делитель (НОД) — число, на которое без остатка делится выбранная пара (либо больше) чисел.
Бывают пары чисел, которые из общих делителей имеют только единицу. Тогда они называются взаимно простыми: НОД (9, 8)=1, НОД (12, 10)=1.
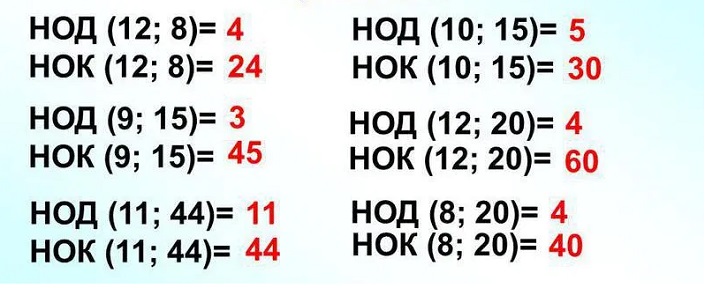
На следующем примере показаны пары чисел со значениями их НОД и НОК.
Решение задачи по нахождению НОК через НОД сводится к следующей формуле:
НОК чисел a,b равняется частному произведения a и b на наибольший общий делитель чисел a и b (по-другому НОД (a, b).
Исходя из этого заключения получается, что НОК и НОД взаимосвязаны друг с другом. Наименьшее общее кратное можно легко найти через наибольший общий делитель для двух или более натуральных чисел.
Как найти НОК через разложение чисел
Кроме составления рядов значений, кратных каждому из двух выбранных натуральных чисел, для правильного определения НОК пользуются методом разложения на множители.
Найденные простые множители первого разложения сравниваются с аналогичными из второго разложения, после чего они перемножаются.
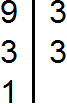
После разложения числа 9 на простые множители получается ряд:
После разложения 12-ти получается ряд:
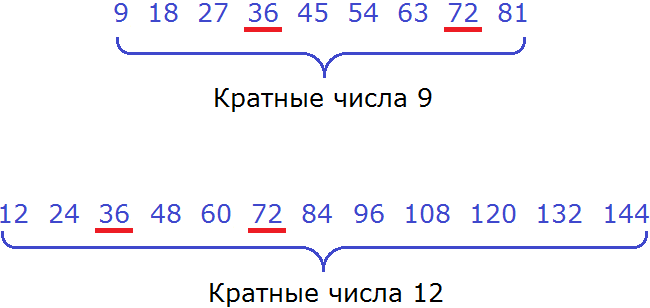
После разложения на множители числа 9 получаем: 3*3. После разложения на множители 12-ти получаем: 2*2*3. Объединяя множители обеих вариантов, получаем произведение: 3*3*2*2=36.
Наименьшее общее кратное чисел 9 и 12 — 36.
В качестве проверки произведем действия:
На практике записывают: НОК (9, 12)=36.
Такими действиями можно найти НОК более сложных чисел.
Найти НОК чисел 50 и 180.
Число 50 делится на 1, 2, 5, 10, 25, 50.
Число 180 на: 1, 5, 15, 30, 45, 90, 180.
Разложив на множители 50, получаем: 2, 5, 5.
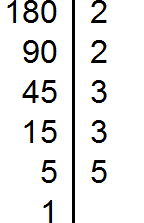
Разложив 180, получаем: 2, 2, 3, 3, 5.
Из первого разложения выписываем: 2*5*5. Сравнивая со вторым разложением, описываем одну двойку и две тройки. После перемножения полученного ряда получается произведение: 2*5*5*2*3*3=900. Это и есть наименьшее общее кратное чисел 50 и 180.
Следовательно, НОК (50, 180)=900.
Существует еще один быстрый способ находить НОК. Он приемлем для вариантов, когда одно число нацело делится на другое. Например: НОК (15, 30)=30, НОК (20, 80)=80, НОК (16, 48)=48.
Для случаев, когда у двух чисел не имеется общих делителей, их можно просто перемножить и получить НОК. Например, НОК (7, 8)=56, НОК (4, 9)=36, НОК (7, 9)=63.
Нахождение НОК трех и большего количества чисел
Если предстоит найти НОК для большего, чем 2, количества чисел, их нужно разложить на простые множители. Например,
Сравнивая множители в каждом случае разложения натуральных чисел и выстраивая их в один ряд для умножения, получаем, что НОК (32, 40, 80) = 2*2*2*2*2*5 = 160.
В математике принято для нахождения НОК трех и более чисел применять следующую теорему:
Дано задание вычислить НОК для чисел 140 (a1), 9 (a2), 54 (а3), 250 (а4).
Для нахождения НОК (140, 9) производим действия. 140=15*9+5; 9=5*1+4.
Последующее разложение: 5=4*1+1, 4=4*1.
Следовательно, НОД (140, 9)=1. НОК (140, 9)=140*9/НОД (140, 9)=140*9/1=1260.
По аналогии вычисляем m3 (=3780) и m4 (=94500). Это и есть ответ решения задачи по нахождению НОК чисел 140, 9, 54, 250.
НОД и НОК
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:
Получили два разложения: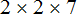 
и 
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
НОД (100 и 40) = 20.
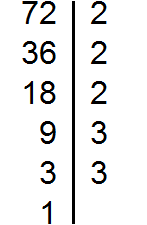
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Перемножим оставшиеся числа:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
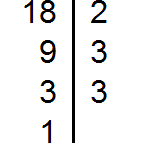
Разложим на множители число 18
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12
Разложим на множители число 24
Разложим на множители число 36
Разложим на множители число 42
Получили четыре разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
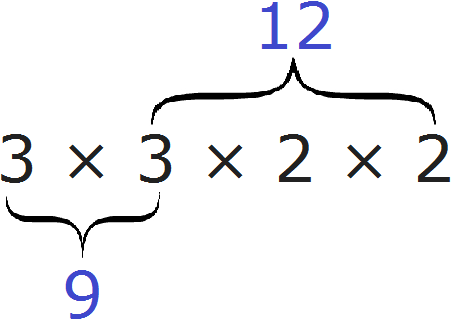
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
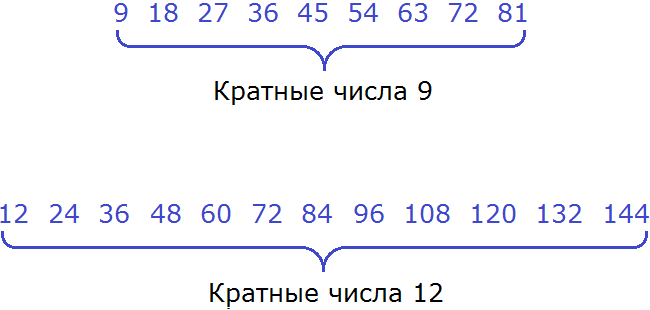
Теперь выпишем кратные обоих чисел:
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
Разложим на множители число 9
Разложим на множители число 12
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
Разложим на множители число 180
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
НОК (50 и 180) = 900
Пример 3. Найти НОК чисел 8, 15 и 33
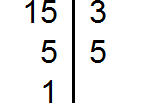
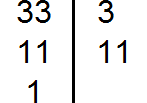
Разложим на множители число 8
Разложим на множители число 15
Разложим на множители число 33
Выпишем первое разложение:
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Теперь перемножаем эти множители:
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
Разделим полученное число 288 на НОД чисел 24 и 12
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
Найдем НОД чисел 36 и 48
Перемножим числа 36 и 48
Разделим 1728 на НОД чисел 36 и 48
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Наименьшее общее кратное
Содержание
Необходимо разобрать ещё одно математическое понятие, тесно связанное с наименьшим общим знаменателем. Это наименьшее общее кратное чисел, сокращённо НОК. Есть целых три способа его нахождения.
Повторение понятия кратности
При нахождении общего знаменателя мы также находим общее кратное число, то есть число, которое делится и на один, и на второй знаменатель.
Так, мы можем умножить два числа друг на друга, и произведение будет кратно и одному, и второму числу. Но при действиях с обыкновенными дробями вычисления будут тем проще, чем меньше будут числа, которыми мы будем оперировать.
Сравните два примера:
Очевидно, что проще и удобнее считать второй вариант. Поэтому мы стремимся найти не просто кратное, а наименьшее общее кратное (НОК).
Наименьшее общее кратное для двух заданных чисел – это наименьшее число, которое делится без остатка на оба заданных числа.
Первый способ вычисления НОК
Один из способов нахождения НОК – нахождение кратных заданных чисел. Те числа, которые будут общими для обоих заданных чисел, будут общими кратными, и среди них нужно будет определить самое малое.
Как найти наименьшее общее кратное, НОК для двух и более чисел
Школьникам задают немало заданий по математике. Среди них очень часто встречаются задачи с такой формулировкой: имеются два значения. Как найти наименьшее общее кратное для заданных чисел? Необходимо уметь выполнять такие задания, поскольку полученные навыки применяют для работы с дробями при разных знаменателях. В статье разберем, как найти НОК и основные понятия.
Основные понятия
Прежде чем найти ответ на вопрос как находить НОК, нужно определиться с термином кратное. Чаще всего формулировка этого понятия звучит следующим образом: кратным некоторому значению А называют такое натуральное число, которое без остатка будет делиться на А. Так, для 4 кратными будут 8, 12, 16, 20 и так далее, до необходимого предела.
При этом количество делителей для конкретного значения может быть ограниченным, а кратных бесконечно много. Также есть такая же величина для натуральных значений. Это такой показатель, которое делится на них без остатка. Разобравшись с понятием самого меньшего значения для определенных показателей, перейдем к тому, как его находить.
Находим НОК
Наименьшее кратное двух или больше показателей является наименьшим натуральным числом, которое целиком делится на все указанные числа.
Существует несколько способов найти такое значение, рассмотрим следующие способы:
Теперь мы знаем, какова общая методика нахождения самого небольшого значения для двух, трех и более значений. Однако есть и частные методы, помогающие искать НОК, если предыдущие не помогают.
Как находить НОД и НОК.
Частные способы нахождения
Как и для любого математического раздела, имеются частные случаи нахождения НОК, которые помогают в специфических ситуациях:
Частные случаи встречаются реже, нежели стандартные примеры. Но благодаря им можно научиться работать с дробями различной степени сложности. Особенно это актуально для дробей, где имеются неодинаковые знаменатели.
Немного примеров
Разберем несколько примеров, благодаря которым можно понять принцип нахождения наименьшего кратного:
Благодаря примерам можно понять, как находится НОК, какие есть нюансы и в чем заключается смысл таких манипуляций.
Находит НОК гораздо проще, чем может показаться изначально. Для этого применяется как простое разложение, так и умножение простых значений друг на друга. Умение работать с данным разделом математики помогает при дальнейшем изучении математических тем, в особенности дробей разной степени сложности.
Не забывайте периодически решать примеры различными методами, это развивает логический аппарат и позволяет запомнить многочисленные термины. Изучайте методы нахождения такого показателя и вы сможете хорошо работать с остальными математическими разделами. Удачного изучения математики!
Видео
Это видео поможет вам понять и запомнить, как находить наименьшее общее кратное.
Как найти наименьшее общее кратное
Вы будете перенаправлены на Автор24
Поиск наименьшего общего кратного — задача, с которой все мы сталкиваемся при необходимости найти общий знаменатель для дроби. Ниже для удобства обозначения мы будем использовать не только термин «наименьшее общее кратное», но и его сокращение — НОК.
Давайте рассмотрим подробнее, что значит НОК.
Нахождение НОК
Существует несколько различных приёмов для определения НОК:
Как искать НОК через наибольший общий делитель
Для начала вспомним, что такое наибольший общий делитель.
Наибольшим общим делителем называют наибольшее число, в результате деления на которое двух или более чисел не остаётся остатка.
$НОД(a, b) \cdot НОК(a, b)=a \cdot b$.
Способы нахождения НОД для определения НОК:
Алгоритм Евклида для поиска НОК рассмотрен подробнее в другой статье на нашем сайте.
Также НОД можно вычислить через каноническое разложение чисел на простые множители. Для этого числа, для которых ищется НОД, сначала раскладывают на простые множители.
После этого отдельной строкой выписывают все простые множители, входящие в каждое разложение хотя бы один раз.
После к простым множителям подписывают их наименьшую степень и перемножают. Полученное произведение будет являться наибольшим общим делителем данных чисел.
Готовые работы на аналогичную тему
Если же НОД уже известен, то для определения НОК через этот метод можно воспользоваться следующей формулой:
Как найти НОК через разложение чисел
Представление числа через произведение простых чисел, возведённых в разные степени, называется разложением числа на простые множители.
Из этого определения можно сделать следующий вывод: любое натуральное число кроме единицы либо является простым, либо его можно разложить до простых множителей, причём единственным способом. Числа, которые можно разложить на простые множители, называются составными.
Для осуществления разложения числа на множители используют признаки делимости чисел.
Существуют пары чисел, наибольший общий делитель которых равен единице. Такие числа называются взаимно простыми.
При поиске НОК для взаимно простых чисел их разложения не содержат одних и тех же простых множителей.
Существует ещё одна закономерность для взаимно простых чисел: если число делится на каждое из взаимно простых чисел, то оно делится и на их произведение.
Наиболее частым является каноническое разложение, при его использовании числа раскладываются на множители в порядке возрастания.
Теперь, узнав основные используемые понятия, можно перейти к алгоритму определения НОК данным методом.
Алгоритм определения НОК
Как найти НОК трех чисел и более
Для того чтобы найти НОК более чем для двух чисел, сначала необходимо выбрать 2 любых числа из необходимых и найти НОК для них, после этого нужно взять следующее число и найти НОК для него и уже посчитанного ранее наименьшего общего кратного.
Эту процедуру необходимо выполнять до тех пор, пока не закончатся числа, для которых необходимо найти наименьшее общее кратное.
Другим способом найти НОК сразу для нескольких чисел является выписывание в строку всех простых множителей, содержащихся в разложениях, с их наибольшей степенью и затем их последующее перемножение.
Приведите дроби к общему знаменателю:
Решение:
$104=1 \cdot 2^3 \cdot 13$;
$520=1 \cdot 2^3 \cdot 5 \cdot 13$.
Теперь вычислим наименьшее общее кратное. Чтобы это сделать, выпишем каждый простой множитель, встречающийся в разложениях обоих чисел хотя бы раз с его наибольшей степенью, имеем:
$НОК= \cdot 2^3 \cdot 5 \cdot 13=520$.
$132=1 \cdot 2^2 \cdot 3^1 \cdot 11^1$;
$154= 1 \cdot 2 \cdot 7^1 \cdot 11^1$.
$НОК=2^2 \cdot 3 \cdot 7 \cdot 11 = 924$.
Сначала разложим на простые множители знаменатели дробей
$60=1 \cdot 2^2 \cdot 3 \cdot 5$;
$75= 1 \cdot 3 \cdot 5^2$;
Выпишем все множители при старших степенях для вычисления НОК:
$НОК=2^2 \cdot 3 \cdot 5^2=300$.
В результате приведения к общему знаменателю получим:
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 20.03.2022
Наименьшее общее кратное НОК.
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
— число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;
— число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.
Общим кратным нескольких чисел называется число, которое делится на каждое из этих чисел. Например, числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 – тоже их общие кратные. Среди всех jбщих кратных всегда есть наименьшее, в данном случае это 90. Это число называется наименьшим общим кратным (НОК).
НОК всегда натуральное число, которое должно быть больше самого большого из чисел, для которых оно определяется.
Наименьшее общее кратное (НОК). Свойства.
— Коммутативность: 
— Ассоциативность: 
— Связь с наибольшим общим делителем gcd(a,b):
— В частности, если 
и 
— взаимно-простые числа, то: 
— 
при 
— Наименьшее общее кратное двух целых чисел m и n является делителем всех других общих кратных m и n. Более того, множество общих кратных m, n совпадает с множеством кратных для НОК(m, n).
— Асимптотики для 
могут быть выражены через некоторые теоретико-числовые функции.
Так, функция Чебышёва 
. А также:
— 
.
Это следует из определения и свойств функции Ландау g(n).
— 
, что следует из закона распределения простых чисел.
Нахождение наименьшего общего кратного (НОК).
НОК(a, b) можно вычислить несколькими способами:
1. Если известен наибольший общий делитель, можно использовать его связь с НОК:
2. Пусть известно каноническое разложение обоих чисел на простые множители:
где p1. pk — различные простые числа, а d1. dk и e1. ek — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении).
Тогда НОК (a,b) вычисляется по формуле:
Другими словами, разложение НОК содержит все простые множители, входящие хотя бы в одно из разложений чисел a, b, причём из двух показателей степени этого множителя берётся наибольший.
Вычисление наименьшего общего кратного нескольких чисел может быть сведено к нескольким последовательным вычислениям НОК от двух чисел:
Правило. Чтобы найти НОК ряда чисел, нужно:
— разложить числа на простые множители;
— перенести во множители искомого произведения самое большое разложение (произведение множителей самого большого числа из заданных), а потом добавить множители из разложения других чисел, которые не встречаются в первом числе или стоят в нем меньшее число раз;
— полученное произведение простых множителей будет НОК заданных чисел.
Любые два и более натуральных чисел имеют свое НОК. Если числа не кратны друг другу или не имеют одинаковых множителей в разложении, то их НОК равно произведению этих чисел.
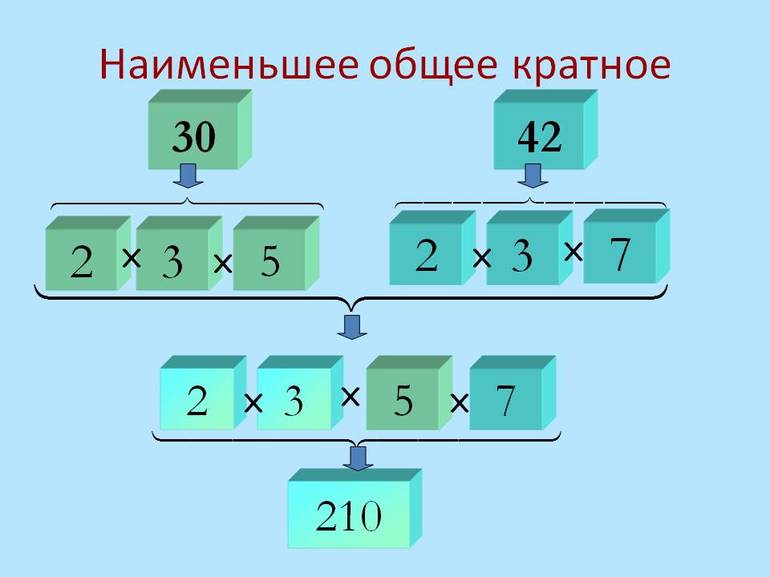
Простые множители наибольшего числа 30 дополнили множителем 5 числа 25, полученное произведение 150 больше самого большого числа 30 и делится на все заданные числа без остатка. Это наименьшее произведение из возможных (150, 250, 300. ), которому кратны все заданные числа.
Числа 2,3,11,37 — простые, поэтому их НОК равно произведению заданных чисел.
Правило. Чтобы вычислить НОК простых чисел, нужно все эти числа перемножить между собой.
Еще один вариант:
Чтобы найти наименьшее общее кратное (НОК) нескольких чисел нужно:
1) представить каждое число как произведение его простых множителей, например:
2) записать степени всех простых множителей:
3) выписать все простые делители (множители) каждого из этих чисел;
4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;
5) перемножить эти степени.
Выписываем наибольшие степени всех простых делителей и перемножаем их:
Нахождение наименьшего общего кратного
Наименьшее общее кратное используется, например, для приведения обыкновенных дробей к общему знаменателю, что позволит сложить, вычесть или сравнить их.
В данной статье мы разберемся, каким образом выполняется эта операция, а также разберем практические примеры для закрепления изложенного материала.
Определение наименьшего общего кратного
Кратных чисел может быть бесконечное множество.
Общее кратное двух натуральных чисел – такое число, которое нацело делится на оба этих числа.
Наименьшее общее кратное двух натуральных чисел – наименьшее число из общих кратных этих чисел. Обозначается как НОК.
Например, НОК (5, 9) – это наименьшее общее кратное чисел 5 и 9.
Нахождение НОК
Чтобы найти наименьшее общее кратное, можно воспользоваться одним из двух способов ниже:
Для двух/небольших чисел
Когда мы имеем дело с двумя числами (или небольшими), процесс нахождения НОК состоит из следующих действий:
Пример
Найдем наименьшее общее кратное чисел 6 и 14.
Таким образом, НОК (6, 14) = 42.
Для нескольких/больших чисел
Данный способ подойдет, если мы имеем дело с большим числами, или когда требуется найти НОК для трех и более чисел.
Пример
Давайте найдем НОК (12, 28, 32).
Решение
Разложим данные числа на простые множители.
Среди множителей меньшего числа (12) в состав бОльшего (32) не входит цифра 3, среди множителей среднего числа (28) – цифра 7.
Следовательно, НОК (12, 28, 32) = 32 ⋅ 3 ⋅ 7 = 672.
Иные случаи
1. Если одно из чисел, для которых требуется найти наименьшее общее кратное, нацело делится на другие числа, то это число и есть НОК.
Например: НОК (20, 40, 80) = 80.
2. НОК взаимно простых чисел является произведение данных чисел, т.к. они не имеют общих простых множителей.
Например: НОК (3, 5) = 3 ⋅ 5 = 15.
Базовые понятия
Для вычисления НОК (наименьшее общее кратное) необходимо разобраться с терминами и определениями. Если любое натуральное число делится на Х без остатка, это число считается кратным Х. Например, 14, 49, 63 кратны 7.
Любое число в математике может иметь бесконечное множество кратных. А вот количество делителей для него самого ограничено. У простых чисел их всего 2 — это единица и само простое число.
НОК может быть общим сразу для нескольких величин. Если какая-то из них делится без остатка сразу на 2 числа, она называется общим кратным этой пары. Например, 10 кратно одновременно 2 и 5, то есть его можно разделить нацело на 2 и на 5. Однако для 2 и 5 кратным может быть не только 10, но и другие величины — 20, 50, 100 и так далее. С математической точки зрения, важно определить меньшую из этих величин.
Наименьшее общее кратное или НОК для величин А и В — это самое маленькое число, которое одновременно делится на А и на В. То есть оно кратно сразу А и В.
Вместо переменных можно подставлять любые числа и искать для них этот показатель.
Методы нахождения
Чтобы найти НОК 2 чисел, в математике используются три способа. Каждый из них может быть применен для проведения вычислений. Если все операции совершены правильно, в результате получится один и тот же ответ при всех методах.
Первый способ
При этом способе применяется метод простого подбора. Для многих учеников он самый простой. Порядок вычисления будет такой:
Пример: необходимо найти НОК для 6 и 8. Сначала составляется ряд кратных 6. Он будет выглядеть так: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 и так далее. Для числа 8 ряд кратных будет иметь вид: 8, 16, 24, 32, 40. 48, 56, 64, 72, 80 и так далее. Если изучить оба ряда, можно обнаружить 2 одинаковых числа — 24 и 48. Меньшим из них является 24. Это и есть НОК для 6 и 8. Для проверки делят 24 на эти величины. В обоих случаях получаются целые величины без остатка.
Второй вариант
Для вычисления вторым способом нужно разложить на простые множители обе величины. Простым множителем в математике принято называть число, которое делится без остатка только на 1 и на себя.
Следующий шаг — выписываются все множители из первого ряда. Затем добавляются те цифры, которых не было в первом ряду, но были во втором. Получится цепочка из нескольких простых чисел. Их необходимо перемножить между собой, в результате чего получится НОК.
Пример: требуется найти НОК для 8 и 12. Для начала нужно разложить на простые множители 8. Получится 2, 2 и 2. Дальше раскладывается аналогичным образом число 12. Получается 2, 2 и 3. Выписываются множители из первого разложенного ряда 2х2х2. Далее добавляются цифры из второго ряда, которых нет в первом — 2х2х2х3.
После перемножения этих величин получается 24. Это и будет НОК для 12 и 8, поскольку оно делится нацело на оба числа. Фактически все действие сводится к разложению на простые множители двух величин одновременно.
Третий алгоритм
Существует еще один метод нахождения НОК. Решать примеры с его помощью можно только для двух чисел. Необходимо заранее знать наибольший общий делитель — НОД. Так принято называть самое большое число, на которое 2 какие-либо переменные делятся без остатка. Вместо переменных можно ввести конкретные данные. НОД возможно вычислить не только для 2, но и для большего количества величин. В математике это понятие принято записывать кратко НОД (х, у).
Пример: требуется рассчитать НОД для 90 и 117. При разложении на простые множители 90 получается ряд 2,3,3,5. Ту же операцию проводят с числом 117 — получается 3,3,13. Для вычисления НОД умножают общие для двух рядов множители — 3х3=9. Значит, НОД (90,117) = 9.
Часто получается, что наибольший общий делитель равняется одному из чисел. Так бывает, если на него можно разделить все остальные. Например, для 10, 20 и 30 наибольшим делителем будет 10.
Если в задаче необходимо найти одновременно НОД и НОК, применяют третий способ вычисления. Алгоритм работы следующий:
Пример: требуется найти НОД и НОК для чисел 115 и 175. Вначале вычисляется НОД. В этом случае он будет равняться 5. Затем 25 и 40 перемножают, получается 20125.
Полученный результат делят на 5, в итоге НОК 15 и 40 равно 4025.
Чтобы проверить достоверность результата, можно вычислить НОК первым или вторым методами.
Например, нужно найти НОК (25, 40).
Наибольшим делителем для них будет 5. Тогда (25х40):5 = 200.
Проверка вторым способом:
Такой же результат будет получен и при решении вторым методом.
Особые случаи
Не во всех случаях вычисление проводится стандартными способами. Существуют пары чисел с особыми свойствами, для которых найти НОК можно без громоздких вычислений.
К таким случаям относятся следующие:
Большинство учащихся быстро усваивают, как найти НОК двух чисел.
Однако некоторых вводят в растерянность ситуации, когда требуется вычислить НОК или НОД для трех или более исходных. В этом случае необходимо последовательно находить кратное для каждой пары из имеющегося ряда.
Для этих случаев в математике есть особая теорема. Если имеется числовой ряд с формулой А1, А2, А3… Ах, то НОК для всех показателей вычисляется последовательно. Вначале НОК (А1, А2), затем для А2, А3 и так далее.
Однако такой путь может оказаться довольно трудоемким.
Чтобы сэкономить время, можно воспользоваться другим методом поиска:
Применение онлайн-калькулятора
Современные технологии позволяют не рассчитывать нужные данные на бумаге. Любой пользователь может найти в интернете НОД и НОК калькулятор, работающий в онлайн-режиме. Такой онлайн-сервис особенно удобен, если нужно найти делитель и кратное для 3 и более чисел.
Чтобы получить нужные расчеты, достаточно ввести в окошки калькулятора исходные данные и выбрать НОД или НОК. Поскольку между этими понятиями существует тесная связь, обычно они вычисляются вместе. Внизу находится кнопка «найти», которую нужно нажать. Через 2−3 секунды внизу появится ответ. Кроме того, некоторые сервисы выдают не только конечные результаты, но и пошаговый порядок расчетов. Здесь же можно найти онлайн-тесты на заданную тему.
Таким образом, учащийся может понять алгоритм действий и усвоить правило при вычислении НОК онлайн. Это всегда проще сделать на практическом примере.
Как найти НОД и НОК
Как найти НОК двух чисел
Наименьшее общее кратное (НОК) двух или нескольких чисел – это самое маленькое число, которое можно разделить на каждое из этих чисел без остатка.
Для того чтобы найти наименьшее общее кратное (НОК) двух чисел можно воспользоваться следующим алгоритмом (5 класс):
Пример
Для примера определим НОК чисел 8 и 22.
1) Раскладываем на простые множители:
2) Выделим все множители 8-ми, которых нет у 22-х:
3) Добавим выделенные множители 8-ми к множителям 22-х:
НОК (8; 22) = 2 · 11 · 2 · 2
4) Вычисляем НОК:
НОК (8; 22) = 2 · 11 · 2 · 2 = 88
Как найти НОД двух чисел
Наибольший общий делитель (НОД) двух или нескольких чисел – это наибольшее натуральное целое число, на которое эти числа можно разделить без остатка.
Чтобы найти наибольший общий делитель (НОД) двух чисел, для начала необходимо разложить их на простые множители. Затем нужно выделить общие множители, которые имеются и у первого числа и у второго. Перемножаем их – это и будет НОД. Чтобы лучше понять алгоритм рассмотрим пример:
Пример
Для примера определим НОД чисел 20 и 30.
Наименьшее общее кратное
Наименьшее общее кратное чисел – это наименьшее число, которое делится на все заданные числа.
Алгоритм поиска НОК
Вычисление НОК похоже на поиск НОД. Чтобы найти наименьшее общее кратное, нужно использовать следующий алгоритм:
Если среди множителей чисел не были найдены одинаковые, НОК числа находится перемножением этих чисел.
Примеры поиска наименьшего общего кратного
Рассмотрим, как найти НОК с помощью алгоритма на нескольких примерах.
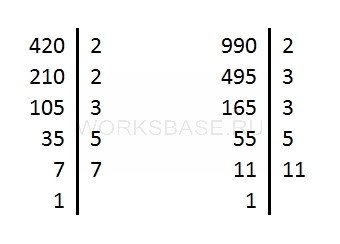
Найдите наименьшее общее кратное чисел 420 и 990.
Разложим оба числа на простые множители:
420 = 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7
990 = 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 11
Выпишем все совпадающие множители:
Выпишем все несовпадающие множители:
2, 7 – из первого числа
3, 11 – из второго числа
Перемножим полученные множители:
2 ⋅ 3 ⋅ 5 ⋅ 2 ⋅ 7 ⋅ 3 ⋅ 11 = 13860
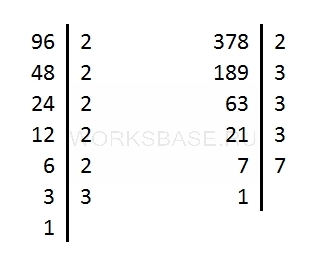
Найдите наименьшее общее кратное чисел 96 и 378.
Разложим оба числа на простые множители:
96 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3
378 = 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 7
Выпишем все совпадающие множители:
Выпишем все несовпадающие множители:
2, 2, 2, 2 – из первого числа
3, 3, 7 – из второго числа
Перемножим полученные множители:
НОК = 2 ⋅ 3 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 7 = 6048
Найдите наименьшее общее кратное чисел 330 и 343.
Разложим оба числа на простые множители:
330 = 2 ⋅ 3 ⋅ 5 ⋅ 11
Совпадающих множителей у этих 2 чисел нет, поэтому для получения НОК будет достаточно перемножить исходные числа:
НОК = 330 ⋅ 343 = 113190
Поделитесь статьей с одноклассниками «НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ, алгоритм как найти НОК».
Наименьшее общее кратное
Задача:
Петя строит железную дорогу из частей, длина которых 4 см, а Сережа, из частей длина которых 6 см. Какую наименьшую протяженность дорожного полотна построят мальчики равной длины?
Длина дороги, построенной мальчиками, должна делиться нацело на 4 и 6, так как части, из которых строят дорогу Петя и Сережа равны 4 см и 6 см соответственно, то есть длина построенной железной дороги должна быть кратной и 4, и 6.
Числа кратные 4:
Числа кратные 6:
То есть общими кратными чисел 4 и 6 являются числа (выделено синим):
Но наименьшим из них является 12. Это число называется наименьшим общим кратным.
То есть наименьшая протяженность дорожного полотна равной длины у Пети и Сережи 12 см.
| Наименьшее натуральное число, которое делится нацело на каждое из двух данных натуральных чисел, то есть кратно каждому из них, называют наименьшим общим кратным этих чисел. |
Наименьшее общее кратное чисел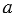 
и 
обозначают так: НОК(; ), то есть мы можем записать НОК(4; 6) = 12.
Нахождение наименьшего общего кратного:
Найдем НОК(12; 15).
Выбираем наибольшее из двух чисел, в нашем случае это число 15, и записываем числа кратные ему, до тех пор, пока не получим число, которое будет кратно второму числу, в нашем случае числу 12.
Число 60 является наименьшим общим кратным чисел 12 и 15, то есть НОК(12; 15) = 60.
Разложим данные числа на простые множители:
12 = 2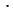
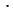
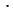
23 15 = 35.
Далее для выписываем простые множители, которые входят в разложение первого числа, и добавляем множители из разложения второго числа, которых нет в разложении первого, то есть в нашем случае, это множитель 5.
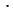
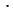
Итак, мы получим 4 множителя 2235, произведение данных множителей равно числу 60, которое является наименьшим общим кратным чисел 12 и 15, то есть мы снова получили НОК(12; 15) = 60.
Таким же образом можно найти НОК трех и более чисел.
Чтобы найти НОК нескольких натуральных чисел, надо:
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел.
Найдем НОК(2520; 4620). Для это разложим данные числа на простые множители и запишем разложение в виде произведения степеней:
Далее используем правило:
Поделись с друзьями в социальных сетях:
Математика. 5 класс
Наименьшее общее кратное (НОК)
Порядок нахождения НОК
Необходимо запомнить
Признак делимости на 3: если сумма цифр делится на 3, то и само число делится на 3.
Признак делимости на 2: если число оканчивается одной из цифр 0, 2, 4, 6, 8, то оно делится на 2.
Признак делимости на 5: если число оканчивается одной из цифр 0 или 5, то оно делится на 5.
Разложение на простые множители:
Число, которое раскладываем на простые множители
Делитель (простое число)
Делитель (простое число)
Первое правило нахождения НОК:
Второе правило нахождения НОК:
НОК любых двух простых чисел или двух соседних натуральных чисел будет равен произведению этих чисел.
Если одно из двух чисел нацело делится на другое, то НОК этих чисел равен большему из них.
Решение задачи при помощи НОК
Некоторые задачи можно решить при помощи НОК проще, чем каким-либо другим способом. Например, рассмотрим такую задачу. Девочка решила купить несколько плиток шоколада по 38 руб., но у неё только пятирублёвые монеты, а в магазине нет сдачи. Какое наименьшее количество плиток шоколада она сможет купить?
Решение. Чтобы решить эту задачу, нужно найти НОК (5; 38).
Математика. 5 класс
Конспект урока
Наименьшее общее кратное (НОК)
Перечень рассматриваемых вопросов:
– разложение на простые множители;
Кратное число – это число, делящееся на данное целое число без остатка.
Простое число – это такое натуральное число, которое больше 1 и делится только на 1 и само на себя.
Составные числа – это непростые натуральные числа, большие 1.
Взаимно простые числа – это числа, которые не имеют общих простых делителей
Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, которое делится на m и n без остатка.
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Ранее мы узнали, что такое кратное, ввели понятие делителя, научились находить наибольший общий делитель, а можно ли каким-либо способом найти общее кратное нескольких чисел? Оказывается, можно, этим сегодня мы и будем заниматься. Но находить не просто общее кратное нескольких чисел, а их наименьшее общее кратное – НОК.
Итак, для начала вспомним, что называется кратным. Это число, делящееся на данное натуральное число без остатка.
Теперь найдём, например, общие кратные чисел 12 и 15. Для этого выпишем все кратные чисел 12 и 15.
12 – его кратные 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …
15 – его кратные 15, 30, 45, 60, 75, 90, 105, 120, 135, …
Из представленных чисел общие кратные – это числа 60 и 120. Меньшее из них – 60. Это и есть наименьшее общее кратное чисел.
Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, которое делится на m и n без остатка.
Для нахождения наименьшего общего кратного двух чисел можно использовать несколько способов. Один из них мы рассмотрели на примере нахождения НОК 12 и 15. Этот способ заключается в том, что выписываются все кратные двух чисел и затем находится наименьший общий из них.
Узнаем ещё одно правило нахождения НОК.
Во-первых, разложим числа на простые множители. Далее подчеркнём одинаковые множители этих чисел. Затем перемножим общие множители одного из чисел и добавим произведение всех остальных множителей от каждого числа. Это и будет НОК заданных чисел.
Найдём НОК (15; 16). Разложим числа на простые множители:
Видно, что из всех множителей общий лишь единица, значит, это взаимно простые числа.
НОК взаимно простых чисел – это произведение всех их множителей или произведение этих чисел.
В данном случае НОК равен 240.
Т. е. НОК любых двух простых чисел или двух соседних натуральных чисел будет равен произведению этих чисел.
Найдём НОК (10; 100). Разложим числа на простые множители:
Выделим общие делители у этих чисел, это 2 и 5.
Умножим их, а результат умножим ещё на оставшиеся простые множители от чисел 100 и 10.
НОК (10; 100) = 2 · 5 · 2 · 5 = 100
Обратите внимание на то, что 100 делится нацело на 10, и НОК тоже равен 100. Поэтому можно сделать вывод: если одно из двух чисел делится нацело на другое, то НОК этих чисел равен большему из них.
Некоторые задачи можно решить при помощи НОК проще, чем каким-либо другим способом. Например, рассмотрим такую задачу.
Решение: чтобы решить эту задачу, нужно найти НОК (5;38).
Разложим числа на множители:
Мы видим, что НОК (5; 38) = 5 · 38 = 190 – это будет сумма покупки за шоколад.
Теперь найдём, сколько девочка купит плиток.
Для этого сумму покупки разделим на стоимость одной плитки шоколада.
190 : 38 руб. = 5 – наименьшее количество плиток шоколада, которые сможет купить девочка.
№ 1. Какую цифру нужно подставить в число НОК (7; 2_) вместо пропуска, чтобы получить НОК = 21?
Варианты ответов: 1; 2; 3.
Решение: для решения этой задачи, надо разложить на множители оба числа, при этом вместо пропуска нужно подставить по порядку все цифры. А далее найти подходящий НОК этих чисел, равный 21.
Из всех разложений на множители под НОК (7; 2_) = 21 подходит только число 21.
Ответ: искомая цифра – 1.
№ 2. Какой наименьшей длины должен быть рулон ткани, чтобы от него без остатка можно было отрезать куски по 3 м и 7 м?
Решение: чтобы решить эту задачу, нужно найти НОК заданных чисел, он и будет являться искомым ответом, т. е. наименьшей длиной рулона ткани.
Как найти наименьшее общее кратное?
Наименьшее общее кратное (сокр. НОК) в математике определяется для нескольких чисел. Это наименьшее натуральное число, делящееся на каждое их данных чисел без остатка.
Для того, чтобы найти наименьшее общее кратное нужно:
1) Разложить каждое число на простые множители.
2) Домножить одно из чисел на те множители, которые не входят в его разложение, но входят в разложение других чисел.
Пример
Требуется найти наименьшее общее кратное для трёх чисел: 6, 10 и 15.
1) Разложим числа на простые множители.
Следовательно, НОК (6, 10, 15) = 30.
Другой способ
Если требуется найти наименьшее общее кратное двух чисел, то можно поступить таким образом:
1) Умножить одно число на другое.
2) Разделить полученное произведение на НОД (наибольший общий делитель).
Найдём наименьшее общее кратное чисел 8 и 6.
НОК (8, 6) = 48 / 2 = 24.
Складывать, умножать, делить, приводить к общему знаменателю и другие арифметические действия очень увлекательное занятие, особенно восхищают примеры, занимающие целый лист.
Итак найти общее кратное для двух чисел, которое будет являться самым маленьким числом на которое делятся два числа. Хочу заметить, что не обязательно в дальнейшем прибегать к формулам, чтобы найти искомое, если можешь считать в уме (а это можно натренировать), то цифры сами всплывают в голове и потом дроби щелкаются как орешки.
Для начала усвоим, что можно умножить два числа друг на друга, а потом эту цифру уменьшать и делить поочередно на данные два числа, так мы найдем наименьшее кратное.
Например, два числа 15 и 6. Умножаем и получаем 90. Это явно больше число. Причем 15 делится на 3 и 6 делится на 3, значит 90 тоже делим на 3. Получаем 30. Пробуем 30 разделить 15 равно 2. И 30 делим 6 равно 5. Так как 2 это предел, то получается, что наименьшее кратное для чисел 15 и 6 будет 30.
С цифрами побольше будет немного трудней. но если знать, какие цифры дают нулевой остаток при делении или умножении, то трудностей, в принципе, больших нет.
Нахождение наименьшего общего кратного, способы, примеры нахождения НОК.
Навигация по странице.
Вычисление наименьшего общего кратного (НОК) через НОД
Нахождение НОК с помощью разложения чисел на простые множители
Другой способ нахождения наименьшего общего кратного базируется на разложении чисел на простые множители. Если составить произведение из всех простых множителей данных чисел, после чего из этого произведения исключить все общие простые множители, присутствующие в разложениях данных чисел, то полученное произведение будет равно наименьшему общему кратному данных чисел.
Разложив числа 441 и 700 на простые множители, найдите наименьшее общее кратное этих чисел.
Нахождение НОК трех и большего количества чисел
Наименьшее общее кратное трех и большего количества чисел может быть найдено через последовательное нахождение НОК двух чисел. Напомним соответствующую теорему, дающую способ нахождения НОК трех и большего количества чисел.
Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.
Во многих случаях наименьшее общее кратное трех и большего количества чисел удобно находить с использованием разложений данных чисел на простые множители. При этом следует придерживаться следующего правила. Наименьшее общее кратное нескольких чисел равно произведению, которое составляется так: ко всем множителям из разложения первого числа добавляются недостающие множители из разложения второго числа, к полученным множителям добавляются недостающие множители из разложения третьего числа и так далее.
Рассмотрим пример нахождения наименьшего общего кратного с использованием разложения чисел на простые множители.
Нахождение наименьшего общего кратного отрицательных чисел
Урок 7 Бесплатно Наименьшее общее кратное
Мы узнаем, что такое кратные числа, познакомимся с историей этого понятия и научимся находить одно и то же кратное различных чисел.
Наименьшее общее кратное
Если первое натуральное число делится на второе нацело, то второе называют делителем первого числа.
Пример
1) найти 10 кратных чисел для 3 и 5
2) из них найти общие кратные
3) наименьшее общее кратное чисел 3 и 5
Решение:
1. Кратные 3: 3, 6, 9, 12, 15, 18, 21, 24, 27,30.
Кратные 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
2. Общие кратные 3 и 5: 15, 30. На самом деле общих кратных будет больше, но в нашем примере было ограничение в 10 кратных чисел.
3. Из 15 и 30 меньшим будет первое. Значит, оно и будет тем, что нам требуется.
Наименьшее натуральное число, кратное каждому из взятых в отдельности, будет наименьшим общим кратным всех взятых чисел вместе.
Наименьшее общее кратное чисел x и y обозначают НОК (x, y)
Как же можно найти этот НОК?
I способ: начинаем перебирать кратные у самого большого из взятых чисел.
НОК (12, 18)=36
II способ: расписываем числа в виде разложения на простые множители.
В этих разложениях встречаются числа 3, 5, 2, 2
Пример 1
Запишите НОК чисел a и b в виде разложения на множители, если:
Решение:
Пример 2
Найдите наименьшее общее кратное чисел:
А) 15 и 25
Б) 10 и 6
В) 100 и 84
Г) 36 и 69
Д) 74 и 12
Е) 96 и 50
Решение:
У меня есть дополнительная информация к этой части урока!
«Крат» в древней Руси XI века значило дословно «раз».
Получается, что «многократно» расшифровывается как «много раз».
Самим понятием кратности часто пользуются в обиходе. Например, бывают разные виды годов, которые получились при использовании нашего математического понятия. На каждые обычные три года из 365 дней приходится один, в котором 366 дней. Это связано с тем, что в таком году в феврале 29 дней, а не 28. Этот год называется високосным.
Пройти тест и получить оценку можно после входа или регистрации
Свойства НОК
Алгоритм нахождения НОК согласно этому свойству:
Проверить, не будет ли самое большое из данных чисел делиться на другие из них.
Если делится, тогда это число будет НОК всех данных чисел.
Если не делится, то проверить, не будет ли делиться на остальные числа удвоенное большее число, утроенное и т.д.
Так проверять до тех пор, пока не найдется самое маленькое число, которое будет делиться на каждое из остальных чисел.
Например, НОК (18, 54) = 54; НОК (27, 81) = 81
Пример 1
Выясните, будут ли числа 35 и 88 взаимно простыми?
Найдите НОК чисел 35 и 88. Равно ли оно произведению 35 и 88?
Найдите НОК получившегося произведения.
Решение:
Одинаковых множителей, кроме 1, в разложениях чисел 35 и 88 не нашлось. Можно сделать вывод, что они взаимно простые.
Наименьшее общее кратное чисел 35 и 88 находится как произведение этих чисел.
Пример 2
Найдите наименьшее общее кратное чисел:
а) 45 и 135; б) 34 и 170
Равно ли оно одному из данных чисел?
Решение:
Пример 3
Вдоль дороги от пункта А поставлены столбы через каждые 75 м. Эти столбы решили заменить другими, поставив их на расстоянии 30 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который будет стоять на месте старого, кроме столба в точке А.
Решение:
Надо найти НОК (75; 30).
Ответ: расстояние от пункта А до ближайшего столба, который будет стоять на месте старого, равно 150 м.
У меня есть дополнительная информация к этой части урока!
По разобранным примерам видно, что в НОК не входит наибольший общий делитель чисел.
Получаем такое свойство: произведение любой пары натуральных чисел равно произведению их наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК)
Пример использования формулы:
Используем алгоритм Евклида:
Итак, можно выделить еще один, уже третий по счёту алгоритм вычисления НОК:
его можно применять для пары чисел, для которых уже найден их НОД.
Рациональнее его применять в задачах на нахождение НОД и НОК, так как тогда он даёт выигрыш во времени решения таких задач. Во всех других случаях вы потратите почти в два раз больше времени, если выберете этот алгоритм, а не предыдущие два.
Нужно найти НОД и НОК чисел 24 и 12.
Первым шагом вычислим НОД этих чисел:
Теперь для нахождения НОК чисел 24 и 12, нужно найти их произведение и полученный результат разделить на их НОД, который мы посчитали в первом шаге.
Произведение чисел 24 и 12, равно 288
288 : 12 = 24
В частном получили 24. Значит НОК чисел 24 и 12 равно 24
НОК (12; 24) = 24
Пройти тест и получить оценку можно после входа или регистрации
Нахождение НОК и НОД двух натуральных чисел
Что такое НОК и НОД двух натуральных чисел
Натуральными числами называют числа, которые используются при счете – 1, 2, 3, 16, 25, 101, 2560 и далее до бесконечности. Ноль, отрицательные и дробные или нецелые числа не относятся к натуральным.
Наименьшее общее кратное (НОК) двух натуральных чисел a и b – это наименьшее число, которое делится без остатка на каждое из рассматриваемых чисел.
Наибольший общий делитель (НОД) двух натуральных чисел a и b – это наибольшее число, на которое делится без остатка каждое рассматриваемое число.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свойства НОК и НОД для натуральных чисел a и b
Особенности вычисления, алгоритм Евклида
Рассмотрим два способа определения НОД и НОК с помощью алгоритма Евклида:
Чтобы вычислить НОД, первоначально нужно выбрать наибольшее из двух чисел и поделить его на меньшее. Пока остаток не станет равным нулю, повторяется цикл деления делителя на остаток от деления в соответствии с формулой.
Вычислим НОД для чисел 12 и 20. Делим 20 на 12 и получаем 1 и 8 в остатке. Запишем иначе:
НОД (12;20) = 4
НОК получаем согласно свойству \(НОК (a, b) = НОК\;(a,b)=\frac
НОК (12; 20) = \(12\times20\div4=60\)
НОК (12;20) = 60
Здесь повторяется цикл вычитания из наибольшего числа меньшего числа до момента, пока разность не станет равна нулю. НОД равен предшествующей нулю разности.
Вычислим НОД для тех же чисел, 12 и 20.
20 – 12 = 8 (разность не равна нулю, продолжаем)
НОД (12;20) = 4
НОК находим также, как и при методе деления.
Правило нахождения наибольшего общего делителя (НОД)
Для нахождения наибольшего общего делителя воспользуемся пошаговым алгоритмом:
Возьмем натуральные числа 24 и 36.
Правильно записать следующим образом:
В случае, когда одно или оба числа относятся к простым, т.е. делятся только на единицу и на само себя, то их НОД равняется 1.
Правило нахождения наименьшего общего кратного (НОК)
Для нахождения наименьшего общего кратного воспользуемся подробным алгоритмом:
Возьмем натуральные числа 9 и 12.
\(9=3\times3\) (видим, что у числа 12 отсутствует одна тройка)
Как найти наименьшее общее кратное
Для двух натуральных чисел \(a\) и \(b\) зависимость между вышеописанными величинами имеет следующее выражение:
где \(НОК\) – наименьшее общее кратное, \(НОД\) – наибольший общий делитель.
Методы вычисления наименьшего общего кратного
Разберем приемы нахождения наименьшего общего кратного, их несколько:
Разберем детальнее эти приемы
1. Для определения наименьшего общего кратного с применением наибольшего общего делителя применяют несколько методов:
2. Для расчета наименьшего общего кратного с применением разложения чисел разберемся сперва, что это обозначает.
Разложение числа на простые множители являет собой преобразование числа в форму произведения простых чисел, возводимых в различные степени.
Значит, все натуральные числа, за исключением единицы, есть простые или могут разлаживаться на простые множители. Последние имеют название – составные.
Не нашли что искали?
Просто напиши и мы поможем
В процессе раскладывания чисел на простые множители, следует помнить и соблюдать базовые принципы делимости.
Существуют взаимно простые числа, это такие пары чисел, для которых наибольший общий делитель равняется единице. Во время расчета наименьшего общего кратного для подобных чисел, в процессе их расклада не существует общих простых множителей.
Еще одно правило, касающееся взаимно простых чисел, гласит о том, что если некоторое число можно без остатка разделить на два взаимно простых числа, то данное число также разделится на их произведение.
Зачастую применяют принцип канонического разложения, в процессе него числа раскладывают по возрастанию.
Порядок расчета наименьшего общего кратного разложением числа на простые множители выглядит так:
Методы расчета наименьшего общего кратного для трех и более чисел
При расчете наименьшего общего кратного более, чем двух чисел, прибегают к тем же методам, что и для расчета наименьшего общего кратного двух чисел, которые мы рассмотрели выше, а именно методу разложения числа и методу расчета наибольшего общего делителя.
При расчете способом вычисления наибольшего общего делителя. Вначале берут два любых числа из заданного множества чисел, считают для них наименьшее общее кратное, потом берут еще одно число, и считают наименьшее общее кратное для него и посчитанного наименьшего общего кратного двух предыдущих чисел. Так повторяют, пока не задействуют все числа множества.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Разберем некоторые решения подобных задач
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Нахождение (вычисление) НОД и НОК
Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей.
Пример: для чисел 6 и 9 наибольший общий делитель равен 3.
Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел m или n не равно нулю.
В школьной программе обозначается так: НОД(m, n)
Наименьшее общее кратное (НОК) двух целых чисел m и n это наименьшее натуральное число, которое делится на m и n без остатка. В школьной программе обозначается так: НОК(m, n)
Пример: НОК(16, 20) = 80
Одно из наиболее частых применений НОК — приведение дробей к общему знаменателю.
С помощью данной математической программы вы можете найти (вычислить) НОД и НОК двух целых чисел.
Программа нахождения НОД и НОК не только выводит ответ задачи, но и отображает процесс вычисления НОД и НОК двух чисел.
Вводить можно только целые положительные числа.
Найти НОД и НОК
Немного теории.
Наибольший общий делитель (НОД). Взаимно простые числа
Определение. Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем (НОД) этих чисел.
Найдём наибольший общий делитель чисел 24 и 35.
Делителями 24 будут числа 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут числа 1, 5, 7, 35.
Видим, что числа 24 и 35 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми.
Определение. Натуральные числа называют взаимно простыми, если их наибольший общий делитель (НОД) равен 1.
Наибольший общий делитель (НОД) можно найти, не выписывая всех делителей данных чисел.
Разложим на множители числа 48 и 36, получим:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа (т. е. две двойки).
Остаются множители 2 * 2 * 3. Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36. Так же находят наибольший общий делитель трёх и более чисел.
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3) найти произ ведение оставшихся множителей.
Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Например, наибольшим общим делителем чисел 15, 45, 75 и 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.
Наименьшее общее кратное (НОК)
Определение. Наименьшим общим кратным (НОК) натуральных чисел а и b называют наименьшее натуральное число, которое кратно и a и b. Наименьшее общее кратное (НОК) чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5.
Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения второго числа (т.е. объединяем множители).
Получаем пять множителей 2 * 2 * 3 * 5 * 5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.
Так же находят наименьшее общее кратное для трёх и более чисел.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение получившихся множителей.
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел.
Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа.
Пифагор (VI в. до н. э.) и его ученики изучали вопрос о делимости чисел. Число, равное сумме всех его делителей (без самого числа), они называли совершенным числом. Например, числа 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные числа — 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенных числа. Четвёртое — 8128 — стало известно в I в. н. э. Пятое — 33 550 336 — было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор учёные не знают, есть ли нечётные совершенные числа, есть ли самое большое совершенное число.
Интерес древних математиков к простым числам связан с тем, что любое число либо простое, либо может быть представлено в виде произведения простых чисел, т. е. простые числа — это как бы кирпичики, из которых строятся остальные натуральные числа.
Вы, наверное, обратили внимание, что простые числа в ряду натуральных чисел встречаются неравномерно — в одних частях ряда их больше, в других — меньше. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: существует ли последнее (самое большое) простое число? Древнегреческий математик Евклид (III в. до н. э.) в своей книге «начала», бывшей на протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т. е. за каждым простым числом есть ещё большее простое число.
Для отыскания простых чисел другой греческий математик того же времени Эратосфен придумал такой способ. Он записывал все числа от 1 до какого-то числа, а потом вычёркивал единицу, которая не является ни простым, ни составным числом, затем вычёркивал через одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее вычёркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). в конце концов оставались невычеркнутыми только простые числа.