Как найти нок двух чисел
Как найти нок двух чисел
Наименьшее общее кратное двух, трех и более чисел
Данный калькулятор предназначен для нахождения наименьшего общего кратного двух, трех и более чисел онлайн.
Кратное числа n – это число, которое делится на данное число n без остатка. Число может иметь бесконечное число кратных.
Несколько чисел могут иметь одинаковые кратные, которые будут называться общими кратными чисел.
Среди общих кратных выделяют наименьшее из них. Наименьшее общее кратное (сокращенно НОК) двух, трех и более чисел – наименьшее число, которое делится без остатка на каждое из этих чисел. Нахождение наименьшего общего кратного полезно, например, при сложении и вычитании дробей, когда необходимо найти общий знаменатель дробей.
Для тех пользователей, кого интересует вопрос, как находить наименьшее общее кратное двух, трех и более чисел самостоятельно, представим последовательность решения данной задачи двумя способами. Первый способ хорошо применим для небольших чисел. Он заключается в выписывании кратных для всех чисел до тех пор, пока не найдется одинаковое, наименьшее из них. Второй способ сложнее и состоит из нескольких этапов, но при этом он применим для больших чисел. Во-первых, необходимо разложить числа на простые множители. Во-вторых, составляется произведение из всех найденных простых множителей. В-третьих, необходимо исключить общие множители, которые присутствуют в разложении чисел. В-четвертых, перемножив оставшиеся простые множители, получаем наименьшее общее кратное.
Чтобы найти наименьшее общее кратное нескольких чисел, проще всего использовать данный калькулятор, так как самостоятельные расчеты займут слишком много времени и усилий, особенно это касается большого количества больших чисел. Просто введите числа в соответствующие ячейки калькулятора и нажмите кнопку «Вычислить».
Наименьшее общее кратное (НОК) – определение, примеры и свойства.
В этой статье всесторонне рассмотрено наименьшее общее кратное (НОК) данных чисел. Сначала дано определение общих кратных, на основании которого дано определение наименьшего общего кратного. После этого введены обозначения НОК, и приведены примеры. Дальше рассмотрена теорема, устанавливающая связь НОК и НОД данных чисел. В заключение показано, как нахождение наименьшего общего кратного трех и большего количества чисел сводится к последовательному вычислению НОК двух чисел.
Навигация по странице.
Общие кратные – определение, примеры
Если знать, что такое кратные числа, то определение общих кратных воспримется очень естественно. Мы будем говорить лишь об общих кратных таких целых чисел, которые отличны от нуля.
Общие кратные данных целых чисел – это такие целые числа, кратные всех данных чисел. Другими словами, общим кратным данных целых чисел называется любое целое число, которое делится на каждое из данных чисел.
Определение общих кратных относится как к двум целым числам, так и к трем, и к большему количеству целых чисел. То есть, мы можем говорить об общих кратных двух, трех, четырех и так далее целых чисел.
Приведем примеры общих кратных.
Отдельно отметим, что число нуль является общим кратным любого множества ненулевых целых чисел.
Нужно еще обговорить два нюанса, которые мы сформулируем в виде вопросов и дадим на них ответы.
В заключение этого пункта скажем, что можно ограничиться рассмотрением общих кратных лишь целых положительных (то есть, натуральных) чисел. Это не ограничит общности, и связано с тем, что множество кратных данного числа и множество кратных числа, противоположного данному, совпадают (что следует из свойств делимости).
Наименьшее общее кратное (НОК) – определение, обозначение и примеры
Среди всех кратных данных чисел особый интерес и особую практическую значимость представляет наименьшее общее кратное (понятие наименьшего числа из данного множества чисел мы ввели, когда изучали сравнение целых чисел). Дадим определение наименьшего общего кратного.
Наименьшее общее кратное данных целых чисел – это наименьшее положительное общее кратное этих чисел.
Следует отметить, что в предыдущих примерах далеко не очевидно, что указанные числа являются наименьшими общими кратными соответствующих чисел. Этим мы хотим сказать, что в общем случае не удается сразу сказать, чему равен НОК данных чисел, и приходится провести вычисление наименьшего общего кратного.
Связь между НОК и НОД
Наименьшее общее кратное двух чисел непосредственно связано с наибольшим общим делителем этих чисел. Эта связь между НОД и НОК определяется следующей теоремой.
Доказанная связь между наименьшим общим кратным и наибольшим общим делителем двух данных чисел позволяет найти НОК через НОД.
Также нужно записать два важных следствия из рассмотренной теоремы.
Общие кратные двух чисел совпадают с кратными их наименьшего общего кратного.
Наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.
Наименьшее общее кратное трех и большего количества чисел
Нахождение наименьшего общего кратного трех и большего количества чисел можно свести к последовательному нахождению НОК двух чисел. Как это делается, указано в следующей теореме.
Онлайн калькулятор. Вычисление НОД и НОК двух чисел
Этот онлайн калькулятор поможет вам понять, как найти НОД и НОК двух чисел. Калькулятор вычисления НОД и НОК двух чисел очень просто и быстро вычислит наибольшее общее кратное и наименьший общий делитель двух чисел.
Найти НОД и НОК двух чисел
Наименьшее общее кратное (НОК)
Наибольший общий делитель (НОД)
Ввод данных в калькулятор вычисление НОД и НОК двух чисел
В онлайн калькулятор можно вводить только целые числа.
Дополнительные возможности вычисление НОД и НОК двух чисел
Теория о наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение НОД и НОК чисел
Онлайн-калькулятор «Нахождение НОД и НОК чисел«. Наш калькулятор поможет вам найти наибольший общий делить (НОД) и наименьшее общее кратное (НОК) чисел. Особенностью данного калькулятора является то, что он может находить НОК и НОД не только двух чисел, но и трех или четырех чисел. Введите натуральные числа и нажмите кнопку «Вычислить» и наш калькулятор не просто выдаст ответ, но и представит подробное решение, где последовательно будет изложен порядок нахождения НОД и НОК чисел.
| Первое число | Второе число |
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое эти числа делятся без остатка. Наибольший общий делитель обозначается следующим образом: НОД (18; 48) = 6
Наименьшее общее кратно нескольких чисел – это самое меньшее число, которое делится на каждое из этих чисел без остатка. Например: НОК (18; 48) = 144
Это следует знать! Как определить, что число делится на 3 без остатка? Очень просто – на 3 делятся только те числа, сумма цифр которых делится на 3. Например: число 795 делится на 3, так как сумма его цифр 7 + 9 + 5 = 21 делится на 3.
21 : 3 = 7
Как найти наименьшее общее кратное чисел
Содержание статьи
Нахождение наименьшего общего кратного: основные понятия
Чтобы понять, как вычислять НОК, следует определиться в первую очередь со значением термина «кратное».
Кратным числу А называют такое натуральное число, которое без остатка делится на А. Так, числами кратными 5 можно считать 15, 20, 25 и так далее.
Делителей конкретного числа может быть ограниченное количество, а вот кратных бесконечное множество.
Как найти наименьшее общее кратное чисел
Чтобы найти НОК, можно использовать несколько способов.
Для небольших чисел удобно выписать в строчку все кратные этих чисел до тех пор, пока среди них не найдется общее. Кратные обозначают в записи заглавной буквой К.
Например, кратные числа 4 можно записать так:
Так, можно увидеть, что наименьшим общим кратным чисел 4 и 6 является число 24. Эту запись выполняют следующим образом:
Если числа большие, или нужно найти наименьшее общее кратное трех и более чисел, то лучше использовать другой способ вычисления НОК.
Для выполнения задания необходимо разложить предложенные числа на простые множители.
В разложении каждого числа может присутствовать различное количество множителей.
Например, разложим на простые множители числа 50 и 20.
В разложении меньшего числа следует подчеркнуть множители, которые отсутствуют в разложении первого самого большого числа, а затем их добавить к нему. В представленном примере не хватает двойки.
Теперь можно вычислить наименьшее общее кратное 20 и 50.
НОК (20, 50) = 2 * 5 * 5 * 2 = 100
Так, произведение простых множителей большего числа и множителей второго числа, которые не вошли в разложение большего, будет наименьшим общим кратным.
Чтобы найти НОК трех чисел и более, следует их все разложить на простые множители, как и в предыдущем случае.
В качестве примера можно найти наименьшее общее кратное чисел 16, 24, 36.
Так, в разложение большего числа на множители не вошли только две двойки из разложения шестнадцати (одна есть в разложении двадцати четырех).
Таким образом, их нужно добавить к разложению большего числа.
НОК (12, 16, 36) = 2 * 2 * 3 * 3 * 2 * 2 = 9
Существуют частные случаи определения наименьшего общего кратного. Так, если одно из чисел можно поделить без остатка на другое, то большее из этих чисел и будет наименьшим общим кратным.
Например, НОК двенадцати и двадцати четырех будет двадцать четыре.
Если необходимо найти наименьшее общее кратное взаимно простых чисел, не имеющих одинаковых делителей, то их НОК будет равняться их произведению.
Наименьшее общее кратное (НОК). Как найти НОК двух и более чисел + калькулятор ⏳
К примеру, узнаем наименьшее общее кратное чисел 6 и 9.
Как найти наименьшее общее кратное (НОК:
Пример 1. Найдем НОК(6;9).
6 = 2 · 3
9 = 3 · 3
НОК(6;9) = 2 · 3 · 3 = 18
Пример 2. Найдите НОК(а;b), если а = 3 · 5 · 11, b = 3 · 5 · 2
Наши числа уже разложены на простые множители, осталось лишь выписать те, которые участвуют в нахождении НОК.
а = 3 · 5 · 11
b = 3 · 5 · 2
НОК(а;b) = 3 · 5 · 11 · 2 = 330
Пример 3. Найдите НОК(3;13).
НОК(3;13) = 3 · 13 = 39
Пример 4. Найдите НОК(44;25).
44 = 2·2·11
25 = 5·5
НОК(44, 25) = 2·2·11 · 5·5 = 44 · 25 = 1100
Из примера 3 и 4 следует, что НОК простых и взаимно простых чисел можно найти, перемножив эти числа.
Пример 5. Найдите НОК(108;144).
144 = 2·2·2·2·3·3
108 = 2·2·3·3· 3
НОК(108;144) = 2·2·2·2·3·3 · 3 = 432
Нахождение НОК трех, четырех и более чисел
Алгоритм точно такой же, как и при нахождении НОК двух чисел.
Найдите НОК(240; 144; 480)
480 = 2·2·2·2·2·3·5
240 = 2·2·2·2·3·5
144 = 2·2·2·2·3· 3
НОК(240; 144; 480) = 2·2·2·2·2·3·5 · 3 = 1440
Найдите наименьшее общее кратное пяти чисел 84, 6, 48, 7, 143.
Сначала разложим данные числа на простые множители:
84 = 2 · 2 · 3 · 7
6 = 2 · 3
48 = 2 · 2 · 2 · 2 · 3
7 (7 – простое число, оно совпадает со своим разложением на простые множители)
143 = 11 · 13
НОК(84, 6, 48, 7, 143) = 2·2·2·2·3·7·11·13 = 48 048.
Задачи на нахождение НОК
Мальчик хочет купить несколько пачек мороженного по 8 рублей, но у него только 5 рублевые монеты, а у продавца нет сдачи. Какое наименьшее число пачек мороженного он сможет купить?
1 способ. Нахождение НОК подбором:
Эта сумма должна делиться и на 8 рублей, и на 5 рублей без остатка.
1) Выпишем числа кратные 8: 8, 16, 24, 32, 40
2) Выпишем числа кратные 5: 5, 10, 15, 20, 25, 30, 35, 40
Выбираем наименьшее общее кратное.
Нашли, эта сумма = 40 рублей.
Теперь надо узнать сколько пачек можно купить на эту сумму:
40:8=5
Ответ: мальчик может купить 5 пачек мороженного.
2 способ (общепринятый). Нахождение НОК в общем случае:
Эта сумма должна делиться и на 8 рублей, и на 5 рублей без остатка.
1) Выполним разложение 8 и 5 на простые множители.
8 | 2 5 | 5
4 | 2 1 |
2 | 2
1
НОК(8,5) = 8 * 5 = 40
2) Поскольку у нас нет одинаковых множителей, то для нахождения наименьшего общего кратного мы перемножаем эти числа между собой. Нашли НОК, т.е. эта сумма = 40 рублей. Теперь узнаем количество пачек мороженного
Не забываем размерность и пишем ответ
Ответ: мальчик может купить 5 пачек мороженного.
Вдоль дороги от города (пункт А) до деревни (пункт В) были поставлены столбы через каждые 50 м. Их заменили другими, поставив на расстоянии 60 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который стоит на месте старого.
60 = 2·2·3·5
50 = 2·5·5
НОК(50;60) = 2·2·3·5·5 = 300 (м)
Ответ: 300 м от пункта А до ближайшего столба, который стоит на месте старого.
12 = 2·2·3
18 = 2·3· 3
21 = 3· 7
НОК(12;18;21) = 2·2·3 · 3 · 7 = 252 (сут.)
Ответ: через 252 суток они снова вместе уйдут в плавание.
В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй – 20 и третий – 12 суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трём маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание? Какое количество рейсов сделает каждый теплоход?
1) НОК (15,20 и 12) = 60 (суток) – время встречи.
2) 60 : 15 = 4 (рейса) – 1 теплоход.
3) 60 : 20 = 3 (рейса) – 2 теплоход.
4) 60 : 12 = 5 (рейсов) – 3 теплоход.
Ответ: 60 суток, 4 рейса, 3 рейса, 5 рейсов.
Маша для Медведя купила в магазине яйца. По дороге в лес она сообразила, что число яиц делится на 2,3,5,10 и 15. Сколько яиц купила Маша?
НОК (2;3;5;10;15) = 30 (яиц)
Ответ: Маша купила 30 яиц.
Требуется изготовить ящик с квадратным дном для укладки коробок размером 16 ͯ 20 см. Какова должна быть наименьшая длина стороны квадратного дна, чтобы уместить коробки в ящик вплотную?
Вдоль дороги от пункта К стоят столбы электролинии через каждые 45 м. Эти столбы решили заменить другими, поставив их на расстоянии 60 м друг от друга. Сколько столбов было и сколько будут стоять?
1) НОК (45 и 60) = 180.
2) 180 : 45 = 4 – было столбов.
3) 180: 60 = 3 – стало столбов.
Ответ: 4 столба, 3 столба.
Сколько солдат маршируют на плацу, если они будут маршировать строем по 12 человек в шеренге и перестраиваться в колонну по 18 человек в шеренге?
1) НОК (12 и 18) = 36 (человек) – маршируют.
Ответ: 36 человек.
Бегун Коля знает, что через каждые 400 м от старта стоит наблюдатель, а через каждые 700 м от старта можно попить воды. На каком минимальном расстоянии от старта можно попить воды и задать вопрос наблюдателю?
НОК(400;700) = 2800 (м)
Ответ: 2800 м.
Длина шага Бори 50 см, а его отца – 70 см. Боря утверждает, что первый раз, сделав целое количество шагов, они с папой окажутся на одинаковом расстоянии от начала пути через 3 метра, а папа не соглашается. Кто прав в этом споре?
НОК(50;70)= 350 см, а не 3 метра
Ответ: прав папа.
Заведующая хозяйством Раиса Максимовна дала поручение учителю труда Ильдару Олеговичу закупить доски, которые можно распилить на равные части и по 30 см, и по 40 см. Какой длины и сколько потребуется досок, если нужно 16 кусочков по 30 см и 12 кусочков по 40 см.
1) НОК(30; 40) = 120 (см)
2) 16:(120:30) = 4 (д.)
3) 12:(120:40) = 4 (д.)
Ответ: всего 8 досок по 120 см.
Родители Артема – люди очень интересных профессий. Мама – стюардесса, а папа – машинист скорого поезда. Мама бывает дома один раз в четыре дня, а папа – один раз в семь дней. Так получилось, что оба они 1 января 2015 года уходят в рейс. Когда Артем увидит своих родителей дома вместе?
НОК(4;7) = 28
Ответ: семья будет дома вместе 28 января.
Калькулятор определения НОД и НОК
Если что-либо осталось для вас непонятным, задавайте вопросы в комментариях.
Как найти число зная нок. Нахождение нок и нод правило
Приступим к изучению наименьшего общего кратного двух и более чисел. В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач.
Общие кратные – определение, примеры
В данной теме нас будет интересовать только общие кратные целых чисел, отличных от нуля.
Общее кратное целых чисел – это такое целое число, которое кратно всем данным числам. Фактически, это любое целое число, которое можно разделить на любое из данных чисел.
Определение общих кратных чисел относится к двум, трем и большему количеству целых чисел.
0 является общим кратным для любого множества целых чисел, отличных от нуля.
Для всех ли чисел можно найти НОК?
Общее кратное можно найти для любых целых чисел.
Сколько всего общих кратных могут иметь данные целые числа?
Группа целых чисел может иметь большое количество общих кратных. Фактически, их число бесконечно.
Наименьшее общее кратное (НОК) – определение, обозначение и примеры
Вспомним понятие наименьшего числа из данного множества чисел, которое мы рассматривали в разделе «Сравнение целых чисел». С учетом этого понятия сформулируем определение наименьшего общего кратного, которое имеет среди всех общих кратных наибольшее практическое значение.
Наименьшее общее кратное данных целых чисел – это наименьшее положительное общее кратное этих чисел.
Не для всех групп данных чисел наименьшее общее кратное очевидно. Часто его приходится вычислять.
Связь между НОК и НОД
Наименьшее общее кратное и наибольший общий делитель связаны между собой. Взаимосвязь между понятиями устанавливает теорема.
Установление связи между НОК и НОД позволяет находить наименьшее общее кратное через наибольший общий делитель двух и более данных чисел.
Теорема имеет два важных следствия:
Наименьшее общее кратное трех и большего количества чисел
Для того, чтобы найти наименьшее общее кратное нескольких чисел, необходимо последовательно найти НОК двух чисел.
Доказать верность второй теоремы нам поможет первое следствие из первой теоремы, рассмотренной в данной теме. Рассуждения строятся по следующему алгоритму:
Так мы доказали теорему.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Определение. Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем (НОД) этих чисел.
Наибольший общий делитель (НОД) можно найти, не выписывая всех делителей данных чисел.
Разложим на множители числа 48 и 36, получим:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа (т. е. две двойки).
Остаются множители 2 * 2 * 3. Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36. Так же находят наибольший общий делитель трёх и более чисел.
Чтобы найти наибольший общий делитель
2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3) найти произ ведение оставшихся множителей.
Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Например, наибольшим общим делителем чисел 15, 45, 75 и 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.
Наименьшее общее кратное (НОК)
Определение. Наименьшим общим кратным (НОК) натуральных чисел а и Ь называют наименьшее натуральное число, которое кратно и a, и b. Наименьшее общее кратное (НОК) чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5.
Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения второго числа (т.е. объединяем множители).
Получаем пять множителей 2 * 2 * 3 * 5 * 5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.
Так же находят наименьшее общее кратное для трёх и более чисел.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение получившихся множителей.
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел.
Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа.
Чтобы понять, как вычислять НОК, следует определиться в первую очередь со значением термина «кратное».
Кратным числу А называют такое натуральное число, которое без остатка делится на А. Так, числами кратными 5 можно считать 15, 20, 25 и так далее.
Делителей конкретного числа может быть ограниченное количество, а вот кратных бесконечное множество.
Как найти наименьшее общее кратное чисел
Чтобы найти НОК, можно использовать несколько способов.
Для небольших чисел удобно выписать в строчку все кратные этих чисел до тех пор, пока среди них не найдется общее. Кратные обозначают в записи заглавной буквой К.
Например, кратные числа 4 можно записать так:
Так, можно увидеть, что наименьшим общим кратным чисел 4 и 6 является число 24. Эту запись выполняют следующим образом:
Если числа большие, найти общее кратное трех и более чисел, то лучше использовать другой способ вычисления НОК.
Для выполнения задания необходимо разложить предложенные числа на простые множители.
В разложении каждого числа может присутствовать различное количество множителей.
Например, разложим на простые множители числа 50 и 20.
В разложении меньшего числа следует подчеркнуть множители, которые отсутствуют в разложении первого самого большого числа, а затем их добавить к нему. В представленном примере не хватает двойки.
Теперь можно вычислить наименьшее общее кратное 20 и 50.
НОК (20, 50) = 2 * 5 * 5 * 2 = 100
Так, произведение простых множителей большего числа и множителей второго числа, которые не вошли в разложение большего, будет наименьшим общим кратным.
Чтобы найти НОК трех чисел и более, следует их все разложить на простые множители, как и в предыдущем случае.
В качестве примера можно найти наименьшее общее кратное чисел 16, 24, 36.
Так, в разложение большего числа на множители не вошли только две двойки из разложения шестнадцати (одна есть в разложении двадцати четырех).
Таким образом, их нужно добавить к разложению большего числа.
НОК (12, 16, 36) = 2 * 2 * 3 * 3 * 2 * 2 = 9
Существуют частные случаи определения наименьшего общего кратного. Так, если одно из чисел можно поделить без остатка на другое, то большее из этих чисел и будет наименьшим общим кратным.
Например, НОК двенадцати и двадцати четырех будет двадцать четыре.
Если необходимо найти наименьшее общее кратное взаимно простых чисел, не имеющих одинаковых делителей, то их НОК будет равняться их произведению.
Например, НОК (10, 11) = 110.
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел. Обозначают НОД(a, b).
Рассмотрим нахождения НОД на примере двух натуральных чисел 18 и 60:
Разложим числа на простые множители:
324 = 2 × 2 × 3 × 3 × 3 × 3
432 = 2 × 2 × 2 × 2 × 3 × 3 × 3
Вычеркнуть из первого числа, множители которых нету во втором и третьем числе, получим:
2 × 2 × 2 × 2 × 3 × 3 × 3 = 3
Нахождение НОД с помощью алгоритма Евклида
Алгоритм Евклида
Пример Найти наибольший общий делитель чисел 7920 и 594
Наименьшее общее кратное
Для того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).
Числа кратные 8 (то есть, эти числа разделятся на 8 без остатка): это числа 16, 24, 32 …
Кратные 9: 18, 27, 36, 45 …
Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
Количество одинаковых множителей в разложениях чисел может быть разное.

НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48
Ответ: НОК (12, 16, 24) = 48
Особые случаи нахождения НОК
Например, НОК (60, 15) = 60
Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее кратное равно произведению этих чисел.
На нашем сайте вы также можете с помощью специального калькулятора найти наименьшее общее кратное онлайн, чтобы проверить свои вычисления.
Если натуральное число делится только на 1 и на само себя, то оно называется простым.
Любое натуральное число всегда делится на 1 и на само себя.
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа.
Натуральное число, которое имеет более двух делителей называется составным.
Кратко наибольший общий делитель чисел « a » и « b » записывают так :
Делители чисел в записи решения обозначают большой буквой «Д».
Как найти наибольший общий делитель
Чтобы найти НОД двух или более натуральных чисел нужно:
- Подчёркиваем одинаковые простые множители в обоих числах.
28 = 2 · 2 · 7
64 = 2 · 2 · 2 · 2 · 2 · 2
Находим произведение одинаковых простых множителей и записать ответ;
НОД (28; 64) = 2 · 2 = 4
Ответ: НОД (28; 64) = 4
Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».
Первый способ записи НОД

Второй способ записи НОД
На нашем информационном сайте вы также можете с помощью программы помощника найти наибольший общий делитель онлайн, чтобы проверить свои вычисления.
Нахождение наименьшего общего кратного, способы, примеры нахождения НОК.
Навигация по странице.
Вычисление наименьшего общего кратного (НОК) через НОД
Нахождение НОК с помощью разложения чисел на простые множители
Разложив числа 441 и 700 на простые множители, найдите наименьшее общее кратное этих чисел.
Нахождение НОК трех и большего количества чисел
Наименьшее общее кратное трех и большего количества чисел может быть найдено через последовательное нахождение НОК двух чисел. Напомним соответствующую теорему, дающую способ нахождения НОК трех и большего количества чисел.
Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.
Рассмотрим пример нахождения наименьшего общего кратного с использованием разложения чисел на простые множители.
Нахождение наименьшего общего кратного отрицательных чисел
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа, например, вместо переменной a подставим число 12, а вместо переменной b число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9, причем этот делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12: 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12: 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12: 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12: 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12: 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12: 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12: 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12: 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12: 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12: 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12: 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12: 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
9: 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9: 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9: 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9: 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9: 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9: 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9: 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9: 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9: 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить, какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Например, найдём НОД для чисел 28 и 16 этим способом. В первую очередь, раскладываем эти числа на простые множители:
Получили два разложения: и
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семерка. Её и вычеркнем из первого разложения:
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения:
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
2 × 2 × 2 × 2 × 2 × 2 × 2
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
Теперь выделим и подчеркнём общие множители в этих числах. Общие множители должны входить во все три числа:
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих множителей этих чисел.
Разложим на множители число 12
Разложим на множители число 42
Получили четыре разложения:
Теперь выделим и подчеркнём общие множители в этих числах. Общие множители должны входить во все четыре числа:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, при этом оно должно быть максимально маленьким.
Из определения понятно, что НОК это наименьшее число, которое делится без остатка на 9 и на 12. Этот НОК требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться двумя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9. Итак, начнём. Кратные будем выделять красным цветом:
Теперь находим кратные для числа 12. Для этого, поочерёдно умножаем 12 на все числа 1 до 12.
Как найти НОК (наименьшее общее кратное)
Данный способ удобен, когда оба числа небольшие и их несложно умножать на последовательность целых чисел. Однако, бывают случаи, когда нужно найти НОК для двузначных или трехзначных чисел, а также, когда исходных чисел три или даже больше.
Шаг 2. В простых множителях числа 12 осталось только число 3. Но оно присутствует в простых множителях числа 24. Вычеркиваем число 3 из обоих рядов, при этом для числа 16 никаких действий не предполагается.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Как видим, при разложении числа 12 мы «вычеркнули» все числа. Значит нахождение НОК завершено. Осталось только вычислить его значение.
Для числа 12 берем оставшиеся множители у числа 16 (ближайшего по возрастанию)
12 * 2 * 2 = 48
Это и есть НОК
Как видим, в данном случае, нахождение НОК было несколько сложнее, но когда нужно его найти для трех и более чисел, данный способ позволяет сделать это быстрее. Впрочем, оба способа нахождения НОК являются правильными.
Нахождение НОД и НОК чисел
Онлайн-калькулятор «Нахождение НОД и НОК чисел«. Наш калькулятор поможет вам найти наибольший общий делить (НОД) и наименьшее общее кратное (НОК) чисел. Особенностью данного калькулятора является то, что он может находить НОК и НОД не только двух чисел, но и трех или четырех чисел. Введите натуральные числа и нажмите кнопку «Вычислить» и наш калькулятор не просто выдаст ответ, но и представит подробное решение, где последовательно будет изложен порядок нахождения НОД и НОК чисел.
| Первое число | Второе число |
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое эти числа делятся без остатка. Наибольший общий делитель обозначается следующим образом: НОД (18; 48) = 6
Наименьшее общее кратно нескольких чисел – это самое меньшее число, которое делится на каждое из этих чисел без остатка. Например: НОК (18; 48) = 144
Это следует знать! Как определить, что число делится на 3 без остатка? Очень просто – на 3 делятся только те числа, сумма цифр которых делится на 3. Например: число 795 делится на 3, так как сумма его цифр 7 + 9 + 5 = 21 делится на 3.
21 : 3 = 7
Наименьшее общее кратное (НОК) — алгоритмы и примеры определения
trong>В школьную программу по математике входит понятие наименьшее общее кратное.Каждый ученик должен понимать и уметь находить эту величину. Это поможет проводить действия с дробями, знаменатели у которых отличаются. Вычислить этот показатель можно несколькими способами на бумаге или с помощью онлайн-калькуляторов.
Базовые понятия
Для вычисления НОК (наименьшее общее кратное) необходимо разобраться с терминами и определениями. Если любое натуральное число делится на Х без остатка, это число считается кратным Х. Например, 14, 49, 63 кратны 7.
Любое число в математике может иметь бесконечное множество кратных. А вот количество делителей для него самого ограничено. У простых чисел их всего 2 — это единица и само простое число.
НОК может быть общим сразу для нескольких величин. Если какая-то из них делится без остатка сразу на 2 числа, она называется общим кратным этой пары. Например, 10 кратно одновременно 2 и 5, то есть его можно разделить нацело на 2 и на 5. Однако для 2 и 5 кратным может быть не только 10, но и другие величины — 20, 50, 100 и так далее. С математической точки зрения, важно определить меньшую из этих величин.
Наименьшее общее кратное или НОК для величин А и В — это самое маленькое число, которое одновременно делится на А и на В. То есть оно кратно сразу А и В.
Вместо переменных можно подставлять любые числа и искать для них этот показатель.
Методы нахождения
Чтобы найти НОК 2 чисел, в математике используются три способа. Каждый из них может быть применен для проведения вычислений. Если все операции совершены правильно, в результате получится один и тот же ответ при всех методах.
Первый способ
При этом способе применяется метод простого подбора. Для многих учеников он самый простой. Порядок вычисления будет такой:
Пример: необходимо найти НОК для 6 и 8. Сначала составляется ряд кратных 6. Он будет выглядеть так: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 и так далее. Для числа 8 ряд кратных будет иметь вид: 8, 16, 24, 32, 40. 48, 56, 64, 72, 80 и так далее. Если изучить оба ряда, можно обнаружить 2 одинаковых числа — 24 и 48. Меньшим из них является 24. Это и есть НОК для 6 и 8. Для проверки делят 24 на эти величины. В обоих случаях получаются целые величины без остатка.
Второй вариант
Для вычисления вторым способом нужно разложить на простые множители обе величины. Простым множителем в математике принято называть число, которое делится без остатка только на 1 и на себя.
Следующий шаг — выписываются все множители из первого ряда. Затем добавляются те цифры, которых не было в первом ряду, но были во втором. Получится цепочка из нескольких простых чисел. Их необходимо перемножить между собой, в результате чего получится НОК.
Пример: требуется найти НОК для 8 и 12. Для начала нужно разложить на простые множители 8. Получится 2, 2 и 2. Дальше раскладывается аналогичным образом число 12. Получается 2, 2 и 3. Выписываются множители из первого разложенного ряда 2х2х2. Далее добавляются цифры из второго ряда, которых нет в первом — 2х2х2х3.
После перемножения этих величин получается 24. Это и будет НОК для 12 и 8, поскольку оно делится нацело на оба числа. Фактически все действие сводится к разложению на простые множители двух величин одновременно.
Третий алгоритм
Существует еще один метод нахождения НОК. Решать примеры с его помощью можно только для двух чисел. Необходимо заранее знать наибольший общий делитель — НОД. Так принято называть самое большое число, на которое 2 какие-либо переменные делятся без остатка. Вместо переменных можно ввести конкретные данные. НОД возможно вычислить не только для 2, но и для большего количества величин. В математике это понятие принято записывать кратко НОД (х, у).
Пример: требуется рассчитать НОД для 90 и 117. При разложении на простые множители 90 получается ряд 2,3,3,5. Ту же операцию проводят с числом 117 — получается 3,3,13. Для вычисления НОД умножают общие для двух рядов множители — 3х3=9. Значит, НОД (90,117) = 9.
Часто получается, что наибольший общий делитель равняется одному из чисел. Так бывает, если на него можно разделить все остальные. Например, для 10, 20 и 30 наибольшим делителем будет 10.
Если в задаче необходимо найти одновременно НОД и НОК, применяют третий способ вычисления. Алгоритм работы следующий:
Пример: требуется найти НОД и НОК для чисел 115 и 175. Вначале вычисляется НОД. В этом случае он будет равняться 5. Затем 25 и 40 перемножают, получается 20125.
Полученный результат делят на 5, в итоге НОК 15 и 40 равно 4025.
Чтобы проверить достоверность результата, можно вычислить НОК первым или вторым методами.
Например, нужно найти НОК (25, 40).
Наибольшим делителем для них будет 5. Тогда (25х40):5 = 200.
Проверка вторым способом:
Такой же результат будет получен и при решении вторым методом.
Особые случаи
Не во всех случаях вычисление проводится стандартными способами. Существуют пары чисел с особыми свойствами, для которых найти НОК можно без громоздких вычислений.
К таким случаям относятся следующие:
Большинство учащихся быстро усваивают, как найти НОК двух чисел.
Однако некоторых вводят в растерянность ситуации, когда требуется вычислить НОК или НОД для трех или более исходных. В этом случае необходимо последовательно находить кратное для каждой пары из имеющегося ряда.
Для этих случаев в математике есть особая теорема. Если имеется числовой ряд с формулой А1, А2, А3… Ах, то НОК для всех показателей вычисляется последовательно. Вначале НОК (А1, А2), затем для А2, А3 и так далее.
Однако такой путь может оказаться довольно трудоемким.
Чтобы сэкономить время, можно воспользоваться другим методом поиска:
Применение онлайн-калькулятора
Современные технологии позволяют не рассчитывать нужные данные на бумаге. Любой пользователь может найти в интернете НОД и НОК калькулятор, работающий в онлайн-режиме. Такой онлайн-сервис особенно удобен, если нужно найти делитель и кратное для 3 и более чисел.
Чтобы получить нужные расчеты, достаточно ввести в окошки калькулятора исходные данные и выбрать НОД или НОК. Поскольку между этими понятиями существует тесная связь, обычно они вычисляются вместе. Внизу находится кнопка «найти», которую нужно нажать. Через 2−3 секунды внизу появится ответ. Кроме того, некоторые сервисы выдают не только конечные результаты, но и пошаговый порядок расчетов. Здесь же можно найти онлайн-тесты на заданную тему.
Таким образом, учащийся может понять алгоритм действий и усвоить правило при вычислении НОК онлайн. Это всегда проще сделать на практическом примере.
Наименьшее общее кратное (НОК), калькулятор
Общие кратные
Онлайн калькулятор НОК
Данный калькулятор позволяет найти, рассчитать наименьшие общие кратные чисел до ста.
В первое поле с исходным значением XX введите число, НОК которого требуется вычислить, затем введите значение во второе поле XX далее нажмите на кнопку Вычислить для того что бы калькулятор произвел расчет.
Пример
| a = 72, b = 60 |
Общие кратные чисел 72 и 60 : 360, 720.
Схема нахождения НОК (a, b)
1. Разложить a и b на простые множители.
2. Подчеркнуть общие множители двух разложений.
Пример
| a = 18 = 2 • 3 • 3; |
b = 78 = 2 • 3 • 13;
НОК (18, 78) = 18 • 13 = 234.
2. Выписать все простые множители, встречающиеся в этих разложениях.
4. Перемножить полученные в п.3 множители.
Пример
| a = 6 = 2 • 3; |
Все простые множители: 2, 3, 5
НОК (6, 12, 25, 27) = 2 2 • 3 3 • 5 2 = 2700
Наглядная таблица кратных 3, 7, 3 и 7
Два и более чисел могут иметь общие кратные. Например, наименьшее общее кратное (НОК) 3 и 7 равно 21, т. е. произведению этих двух чисел, НОК 5 и 6 равно 30.
Наглядно кратные 3,7, а так же и 3 и 7 представлены в виде таблице ниже, также при необходимости можно сохранить ее себе на компьютер в виде картинки, чтобы иметь к ней доступ без подключения к интернету.
Математика. 5 класс
Наименьшее общее кратное (НОК)
Порядок нахождения НОК
Необходимо запомнить
Признак делимости на 3: если сумма цифр делится на 3, то и само число делится на 3.
Признак делимости на 2: если число оканчивается одной из цифр 0, 2, 4, 6, 8, то оно делится на 2.
Признак делимости на 5: если число оканчивается одной из цифр 0 или 5, то оно делится на 5.
Разложение на простые множители:
Число, которое раскладываем на простые множители
Делитель (простое число)
Делитель (простое число)
Первое правило нахождения НОК:
Второе правило нахождения НОК:
НОК любых двух простых чисел или двух соседних натуральных чисел будет равен произведению этих чисел.
Если одно из двух чисел нацело делится на другое, то НОК этих чисел равен большему из них.
Решение задачи при помощи НОК
Некоторые задачи можно решить при помощи НОК проще, чем каким-либо другим способом. Например, рассмотрим такую задачу. Девочка решила купить несколько плиток шоколада по 38 руб., но у неё только пятирублёвые монеты, а в магазине нет сдачи. Какое наименьшее количество плиток шоколада она сможет купить?
Решение. Чтобы решить эту задачу, нужно найти НОК (5; 38).
Наименьшее общее кратное (НОК)
Рассмотрим решение следующей задачи. Шаг мальчика составляет 75 см, а шаг девочки 60 см. Необходимо найти наименьшее расстояние, на котором они оба сделают по целому числу шагов.
Решение. Весь путь который пройдут ребята, должен делиться без остатка на 60 и на 70, так как они должны сделать каждый целое число шагов. Другими словами, в ответе должно быть число, кратное как 75 так и 60.
Сначала будем выписывать все кратные числа, для числа 75. Получаем:
Теперь выпишем числа, которые будут кратны 60. Получаем:
Теперь находим числа которые есть в обоих рядах.
Самое наименьшее из них, это число 300. Оно в данном случае будет называться наименьшим общим кратным чисел 75 и 60.
Возвращаясь к условию задачи, наименьшее расстояние, на котором ребята сделают целое число шагов будет 300 см. Мальчик пройдет этот путь за 4 шага, а девочке потребуется сделать 5 шагов.
Определение наименьшего общего кратного
Для того, чтобы найти наименьшее общее кратное двух чисел, не обязательно выписывть подряд все кратные для этих чисел.
Можно воспользоваться следующим методом.
Как найти наименьшее общее кратное
Сначала необходимо разложить данные числа на простые множители.
Теперь выпишем все множители которые есть в разложении первого числа (2,2,3,5) и добавим к нему все недостающие множители из разложения второго числа (5).
Получим в итоге ряд простых чисел: 2,2,3,5,5. Произведение этих чисел и будет наименьшим общим сомножителем для данных чисел. 2*2*3*5*5 = 300.
Общая схема нахождения наименьшего общего кратного
Данный способ универсален. С его помощью можно найти наименьшее общее кратное любого количества натуральных чисел.
Нахождение наиМЕНЬШЕГО общего кратного (НОК) и наиБОЛЬШЕГО общего делителя (НОД) натуральных чисел. Примерно 6-класс (11-12 лет)
Определение НОК: Наименьшим общим кратным (НОК) натуральных чисел а и в называют наименьшее натуральное число c, которное кратно и a, и b. Т.е. c это наименьшее натуральное число, для которого и а, и б являются делителями.
Нахождение наиМЕНЬШЕГО общего кратного (НОК) и наиБОЛЬШЕГО общего делителя НОД натуральных чисел. 6-класс (11-12 лет)
Памятка: Существуют два подхода к определению натуральных чисел
Отрицательные и нецелые (рациональные, вещественные, …) числа натуральными не являются. Ноль некоторые авторы включают в множество натуральных чисел, другие — нет. Множество всех натуральных чисел принято обозначать символом N
Определение как найти НОК в общем случае: Чтобы найти НОК (Наименьшее общее кратное) нескольких натуральных чисел надо:
1) Разложить их на простые множители. (Для этого Вам может очень пригодиться Таблица простых чисел.)
2) Выписать множители, входящие в разложение одного из них.
3) Добавить к ним недостающие множители из разложений других чисел.
4) Перемножить множители, получившиеся в п.3).
Задача 1 (на НОК): Коля Пузатов раньше съедал булочек на 60 рублей в день. Когда у него совсем не оставалось денег, он шел к любимой мамуле и получал определенную сумму авансом на булочки. Потом Коля Пузатов подрос и стал съедать булочек на 75 рублей в день. Получив ту же сумму от мамы он обнаружил, что сдачи у него опять совсем не остается. Какую наименьшую сумму давала ему мама на булочки авансом?
Пример 1.1. решения задачи на нахождение НОК. Нахождение НОК подбором.
Решение: Эта сумма дожна делиться и на 60 рублей, и на 75 рублей без остатка.
1) Выпишем числа кратные 60: 60, 120, 180, 240, 300, 360, 420, 480
2) Выпишем числа кратные 75: 75, 150, 225, 300 Выбираем наименьшее общее кратное. Опа-на! Нашли, эта сумма = 300. Не забываем размерность и пишем ответ:
Ответ: Мама дает по 300 рублей.
Пример 1.2. решения задачи на нахождение НОК. Нахождение НОК в общем случае.
Решение: Эта сумма дожна делиться и на 60 рублей, и на 75 рублей без остатка.
1)Выполним разложение 75 и 60 на простые множители. (Для этого Вам может очень пригодиться Таблица простых чисел.)




















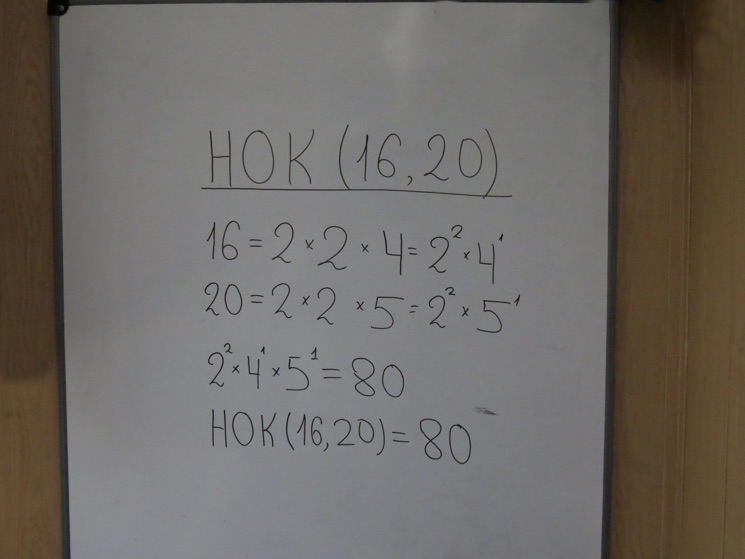
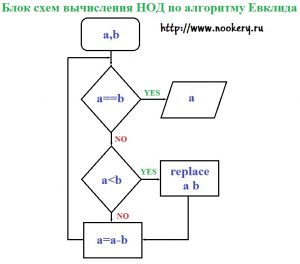
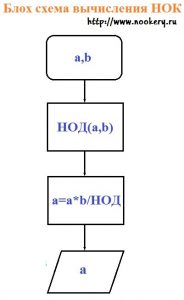 рис 3.
рис 3.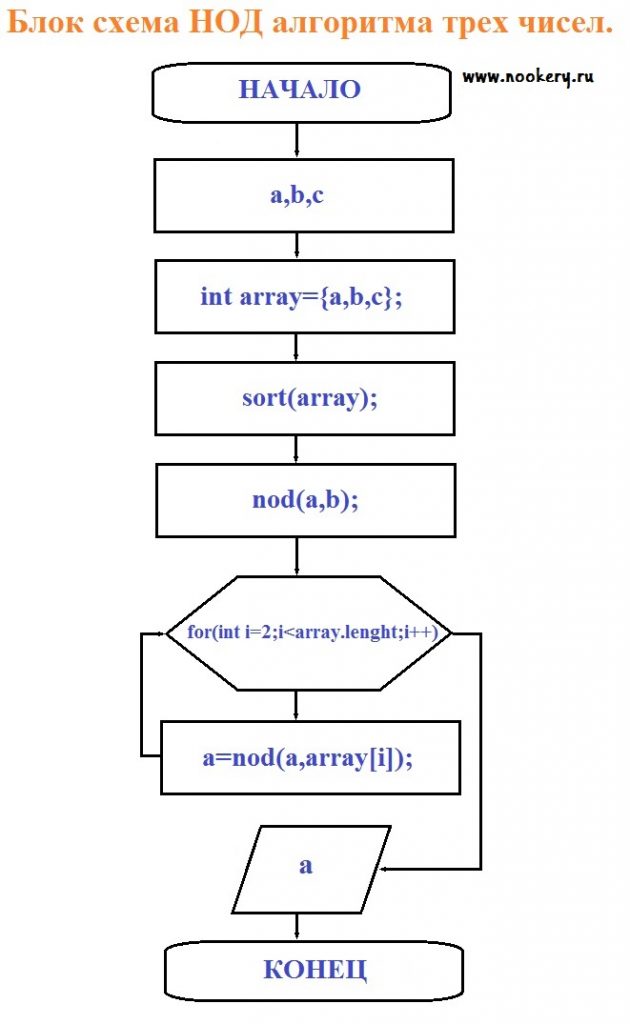












 и
и  — взаимно-простые числа, то:
— взаимно-простые числа, то: 
 при
при 
 могут быть выражены через некоторые теоретико-числовые функции.
могут быть выражены через некоторые теоретико-числовые функции. . А также:
. А также: .
. , что следует из закона распределения простых чисел.
, что следует из закона распределения простых чисел.


















 — различные простые числа, а
— различные простые числа, а  и
и  — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОК(a,b) вычисляется по формуле:
— неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОК(a,b) вычисляется по формуле:



























