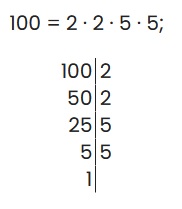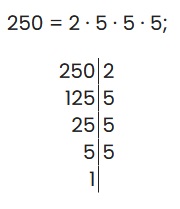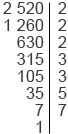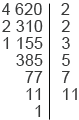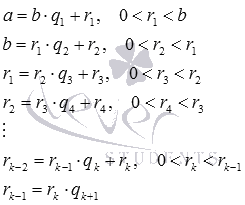Как найти нод двух чисел
Как найти нод двух чисел
Как найти НОД
Рассмотрим два способа нахождения наибольшего общего делителя.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наибольшего общего делителя путём разложения данных чисел на простые множители.
Чтобы найти НОД нескольких чисел, достаточно, разложить их на простые множители и перемножить между собой те из них, которые являются общими для всех данных чисел.
Пример 1. Найти НОД (84, 90).
Решение: Раскладываем числа 84 и 90 на простые множители:
Итак, мы подчеркнули все общие простые множители, осталось перемножить их между собой:
Таким образом, НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
Решение: Раскладываем 15 и 28 на простые множители:
Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.
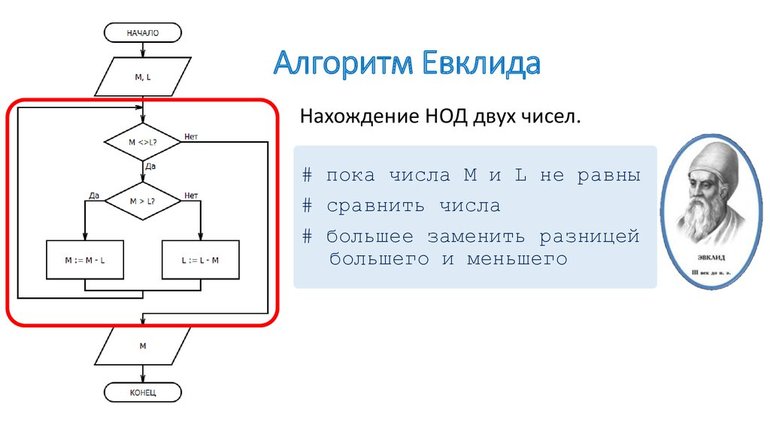
Алгоритм Евклида
Второй способ (иначе его называют способом Евклида) заключается в нахождении НОД путём последовательного деления.
Сначала мы рассмотрим этот способ в применении только к двум данным числам, а затем разберёмся в том, как его применять к трём и более числам.
Если большее из двух данных чисел делится на меньшее, то число, которое меньше и будет их наибольшим общим делителем.
Пример 1. Возьмём два числа 27 и 9. Так как 27 делится на 9 и 9 делится на 9, значит, 9 является общим делителем чисел 27 и 9. Этот делитель является в тоже время и наибольшим, потому что 9 не может делиться ни на какое число, большее 9. Следовательно:
В остальных случаях, чтобы найти наибольший общий делитель двух чисел используется следующий порядок действий:
Пример 2. Найдём наибольший общий делитель чисел 140 и 96:
1) 140 : 96 = 1 (остаток 44)
2) 96 : 44 = 2 (остаток 8)
3) 44 : 8 = 5 (остаток 4)
Последний делитель равен 4 — это значит:
Последовательное деление так же можно записывать столбиком:
Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:
Пример 3. Найдём наибольший общий делитель чисел 140, 96 и 48. НОД чисел 140 и 96 мы уже нашли в предыдущем примере (это число 4). Осталось найти наибольший общий делитель числа 4 и третьего данного числа — 48:
48 делится на 4 без остатка. Таким образом:
Наибольший общий делитель
Если натуральное число делится только на 1 и на само себя, то оно называется простым.
Любое натуральное число всегда делится на 1 и на само себя.
Число 2 — наименьшее простое число. Это единственное чётное простое число, остальные простые числа — нечётные.
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12 ) называются делителями числа.
Делитель натурального числа a — это такое натуральное число, которое делит данное число « a » без остатка.
Натуральное число, которое имеет более двух делителей называется составным.
Общий делитель двух данных чисел « a » и « b » — это число, на которое делятся без остатка оба данных числа « a » и « b ».
Наибольший общий делитель (НОД) двух данных чисел « a » и « b » — это наибольшее число, на которое оба числа « a » и « b » делятся без остатка.
Кратко наибольший общий делитель чисел « a » и « b » записывают так:
Делители чисел в записи решения обозначают большой буквой «Д».
Как найти наибольший общий делитель
Чтобы найти НОД двух или более натуральных чисел нужно:
Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа — делитель. Далее в левом столбце записываем значения частных.
Ответ: НОД (28; 64) = 4
Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».
Первый способ записи НОД

Второй способ записи НОД
На нашем информационном сайте вы также можете с помощью программы помощника найти наибольший общий делитель онлайн, чтобы проверить свои вычисления.
Математика. 5 класс
Конспект урока
Наибольший общий делитель (НОД)
Перечень рассматриваемых вопросов:
– разложение на простые множители;
Простое число – это натуральное число, которое больше 1 и делится только на 1 и само на себя.
Составные числа – это непростые натуральные числа больше 1.
Взаимно простые числа – это числа, которые не имеют общих простых делителей.
Теоретический материал для самостоятельного изучения
Начнём наше занятие словами известной поговорки: «Учить – ум точить». Сегодня мы будем оттачивать умение находить общие делители сразу нескольких чисел.
Итак, рассмотрим два числа: 12 и 15. Выпишем все делители этих чисел. 12 – делители 1, 2, 3, 4, 6, 12.
15 – делители 1, 3, 5, 15.
Найдём общие делители этих чисел – это числа 1 и 3. Введём новое понятие – «наибольший общий делитель», который кратко обозначают НОД.
У этих чисел наибольший общий делитель равен 3.
Записывается – НОД (12; 15) = 3. НОД чисел двенадцать и пятнадцать равен трём.
Правило нахождения НОД:
Найдём НОД чисел 15 и 16.
Разложим числа на простые множители.
Видно, что из всех множителей – общий лишь 1.
Такие числа, которые не имеют общих простых делителей, называются взаимно простыми числами. Любые два простых числа или два соседних натуральных числа будут взаимно простыми.
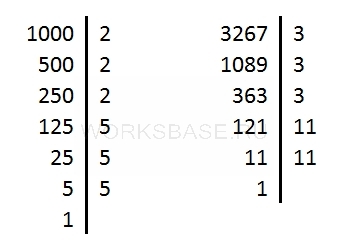
Найдём НОД (10; 100).
Разложим числа на простые множители.
Выделим общие делители у этих чисел, это 2 и 5.
Умножим их и получим наибольший общий делитель: НОД (10; 100) = 2 · 5 = 10.
Обратите внимание на то, что 100 делится нацело на 10 и НОД тоже равен 10. Поэтому можно сделать вывод: если одно из двух чисел делится нацело на другое, то НОД этих чисел равен меньшему из них.
Найдём наибольший общий делитель трёх чисел.
Разложим числа на простые множители:
Выделим общие делители у этих чисел, это 2 и 7.
Умножим их и получим наибольший общий делитель: НОД (42; 70; 98) = 2 · 7 = 14
Некоторые задачи можно решить при помощи НОД проще, чем каким-либо другим способом.
Например, решим такую задачу.
Для участия в соревнованиях нужно разделить 35 детей в возрасте 14 лет и 21 ребёнка в возрасте 12 лет на команды так, чтобы они состояли только из одновозрастных спортсменов. Какое наибольшее число участников одного возраста может быть в команде?
Решение: чтобы решить эту задачу нужно найти НОД (21; 35).
Разложим числа на простые множители:
Следовательно, НОД (21; 35) = 7 – это и будет наибольшим числом участников в команде.
Ответ: 7 человек.
№ 1. Какую цифру нужно подставить в число НОД (7; 2_) вместо пропуска, чтобы получить НОД = 7?
Варианты ответов: 1, 2, 3.
Решение: разложим на множители оба числа, при этом вместо пропуска подставим по порядку все цифры. А далее найдём подходящий НОД этих чисел, равный 7. Получим следующее разложение:
Из всех разложений на множители под НОД (7; 2) = 7 подходит только число 21.
Ответ: искомая цифра – 1.
№ 2. В продуктовых наборах должно быть одинаковое количество груш и апельсинов. Всего приготовили 120 груш и 126 апельсинов. В какое наибольшее количество наборов можно разложить их поровну?
Решение: чтобы решить эту задачу, нужно найти НОД заданных чисел, он и будет являться искомым ответом, т. е. наибольшим количеством наборов при равном разложении фруктов.
Нахождение НОД по алгоритму Евклида и с помощью разложения на простые множители
Рассмотрим два основных метода нахождения НОД двумя основными способами: с использованием алгоритма Евклида и путем разложения на простые множители. Применим оба метода для двух, трех и большего количества чисел.
Алгоритм Евклида для нахождения НОД
Алгоритм Евклида позволяет с легкостью вычислить наибольший общий делитель для двух положительных чисел. Формулировки и доказательство алгоритма Евклида мы привели в разделе «Наибольший общий делитель: определитель, примеры».
Суть алгоритма заключается в том, чтобы последовательно проводить деление с остатком, в ходе которого получается ряд равенств вида:
Решение
Решение
Решение
Нахождение НОД с помощью разложения чисел на простые множители
Для того, чтобы найти наибольший общий делитель двух чисел методом разложения на множители, необходимо перемножить все простые множители, которые получаются при разложении этих двух чисел и являются для них общими.
Решение
Найдем все простые множители чисел 72 и 96 :
72 36 18 9 3 1 2 2 2 3 3
96 48 24 12 6 3 1 2 2 2 2 2 3
Нахождение НОД трех и большего количества чисел
Решение
А теперь давайте рассмотрим еще один способ вычисления НОД для тех и большего количества чисел. Мы можем найти НОД, перемножив все общие простые множители чисел.
Решение
Нахождение НОД отрицательных чисел
Если нам приходится иметь дело с отрицательными числами, то для нахождения наибольшего общего делителя мы можем воспользоваться модулями этих чисел. Мы можем так поступить, зная свойство чисел с противоположными знаками: числа n и — n имеют одинаковые делители.
Решение
Решение
Как находить наибольший общий делитель (НОД) двух чисел
Одной из задач, вызывающих проблему у современных школьников, привыкших к месту и не к месту использовать калькуляторы, встроенные в гаджеты, является нахождение наибольшего общего делителя (НОД) двух и более чисел.
Невозможно решить никакую математическую задачу, если неизвестно, о чём собственно спрашивают. Для этого нужно знать, что означает то или иное выражение, используемое в математике.
Общие понятия и определения
Необходимо знать:
В математике приняты следующие записи:
Различные способы найти НОД
Проще всего ответить на вопрос как найти НОД в том случае, когда меньшее число является делителем большего. Оно и будет в подобном случае наибольшим общим делителем.
Например, НОД (15;45) = 15, НОД (48;24) = 24.
Но такие случаи в математике являются весьма редкими, поэтому для того, чтобы находить НОД используются более сложные приёмы, хотя проверять этот вариант перед началом работы все же весьма рекомендуется.
Способ разложения на простые сомножители
Если необходимо найти НОД двух или более различных чисел, достаточно разложить каждое из них на простые сомножители, а затем произвести процесс умножения тех из них, которые имеются в каждом из чисел.
Пример 1
Рассмотрим, как находить НОД 36 и 90:
НОД (36;90) = 1*2*3*3 = 18.
Теперь посмотрим как находить то же самое в случае трёх чисел, возьмём для примера 54; 162; 42.
Как разложить 36 мы уже знаем, разберёмся с остальными:
Таким образом, НОД (36;162;42) = 1*2*3 = 6.
Следует заметить, что единицу в разложении писать совершенно необязательно.
Рассмотрим способ, как просто раскладывать на простые множители, для этого слева запишем необходимую нам цифру, а справа станем писать простые делители.
Разделять колонки можно, как знаком деления, так и простой вертикальной чертой.
Искомое 36 = 2*2*3*3.
Евклидов способ
Этот вариант известен человечеству ещё со времён древнегреческой цивилизации, он во многом проще, и приписывается великому математику Евклиду, хотя весьма похожие алгоритмы применялись и ранее. Этот способ заключается в использовании следующего алгоритма, мы делим большее число с остатком на меньшее. Затем наш делитель делим на остаток и продолжаем так действовать по кругу пока не произойдёт деление нацело. Последнее значение и окажется искомым наибольшим общим делителем.
Приведём пример использования данного алгоритма:
попробуем выяснить какой НОД у 816 и 252:
Итак, по завершении нашего процесса мы получили НОД (816;252) = 12.
Действия при необходимости определения НОД если задано более двух значений
Мы уже разобрались, что делать в случае, когда имеется два различных числа, теперь научимся действовать, если их имеется 3 и более.
При всей кажущейся сложности, данная задача проблем у нас уже не вызовет. Сейчас мы выбираем два любые числа и определяем искомое для них значение. Следующим шагом отыскиваем НОД у полученного результата и третьего из заданных значений. Затем снова действуем по уже известному нам принципу для четвёртого пятого и так далее.
Заключение
Итак, при кажущейся большой сложности поставленной перед нами изначально задачи, на самом деле все просто, главное уметь выполнять безошибочно процесс делений и придерживаться любого из двух описанных выше алгоритмов.
Видео
С помощью видео вы сможете узнать, как найти наибольший общий делитель.
Наибольший общий делитель (НОД), свойства и формулы
5 класс, 6 класс
Понятие наибольшего общего делителя
Для начала разберемся, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.
Делитель натурального числа — это такое целое натуральное число, на которое делится данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.
Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общими делителями будут 4 и 1. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4.
Любое число можно разделить на 1 и на само себя. Значит, у любого набора целых чисел будет как минимум два общих делителя.
Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).
Например, для 4 и 16 НОД будет 4. Как мы к этому пришли:
Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.
Найдем наибольший общий делитель нескольких целых чисел: 10, 6, 44, 18. Он будет равен трем. Ответ можно записать так: НОД (12, 6, 42, 18) = 3. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.
Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.
Еще один пример. Рассчитаем НОД для 28 и 64.
Д (64) = 2 * 2 * 2 * 2 * 2 * 2
НОД (28; 64) = 2 * 2 = 4
Ответ: НОД (28; 64) = 4
Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.
Способы нахождения наибольшего общего делителя
Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.
1. Разложение на множители
Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.
Пример 1. Найти НОД (84, 90).
Ответ: НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
Ответ: НОД (15, 28) = 1.
Пример 3. Найти НОД для 24 и 18.
НОД (24, 18) =2 * 3 = 6
Ответ: НОД (24, 18) = 6
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
2. Алгоритм Евклида
Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.
Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.
Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.
Пример 1. Найти НОД для 24 и 8.
Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.
В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:
Пример 2. Найти наибольший общий делитель чисел 140 и 96:
Последний делитель равен 4 — это значит: НОД (140, 96) = 4.
Ответ: НОД (140, 96) = 4
Пошаговое деление можно записать столбиком:
Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:
Свойства наибольшего общего делителя
У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.
Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.
Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.
Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.
Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.
Доказательство
Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.
Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.
В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.
Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.
Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.
Доказательство
Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.
Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.
Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).
Доказательство
Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.
Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.
Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.
Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.
Нахождение НОД и НОК чисел
Онлайн-калькулятор «Нахождение НОД и НОК чисел«. Наш калькулятор поможет вам найти наибольший общий делить (НОД) и наименьшее общее кратное (НОК) чисел. Особенностью данного калькулятора является то, что он может находить НОК и НОД не только двух чисел, но и трех или четырех чисел. Введите натуральные числа и нажмите кнопку «Вычислить» и наш калькулятор не просто выдаст ответ, но и представит подробное решение, где последовательно будет изложен порядок нахождения НОД и НОК чисел.
| Первое число | Второе число |
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое эти числа делятся без остатка. Наибольший общий делитель обозначается следующим образом: НОД (18; 48) = 6
Наименьшее общее кратно нескольких чисел – это самое меньшее число, которое делится на каждое из этих чисел без остатка. Например: НОК (18; 48) = 144
Это следует знать! Как определить, что число делится на 3 без остатка? Очень просто – на 3 делятся только те числа, сумма цифр которых делится на 3. Например: число 795 делится на 3, так как сумма его цифр 7 + 9 + 5 = 21 делится на 3.
21 : 3 = 7
Наибольший общий делитель (НОД): определение, примеры и свойства
Что такое общие делители
Чтобы понять, что из себя представляет наибольший общий делитель, сначала сформулируем, что вообще такое общий делитель для целых чисел.
В статье о кратных и делителях мы говорили, что у целого числа всегда есть несколько делителей. Здесь же нас интересуют делители сразу некоторого количества целых чисел, особенно общие (одинаковые) для всех. Запишем основное определение.
Общим делителем нескольких целых чисел будет такое число, которое может быть делителем каждого числа из указанного множества.
Зная свойства делимости, мы можем утверждать, что любое целое число можно разделить на единицу и минус единицу, значит, у любого набора целых чисел уже будет как минимум два общих делителя.
Что такое наибольший общий делитель (НОД)
Переходим к формулировке основного определения.
Наибольшим общим делителем нескольких чисел является самое большое целое число, которое делит все эти числа.
Для трех и более чисел определение наибольшего общего делителя будет почти таким же.
Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.
Проверить правильность данного утверждения можно с помощью записи всех делителей этих чисел и последующего выбора наибольшего из них.
На практике часто встречаются случаи, когда наибольший общий делитель равен одному из чисел. Это происходит тогда, когда на данное число можно разделить все остальные числа (в первом пункте статьи мы привели доказательство этого утверждения).
Основные свойства НОД и алгоритм Евклида
У наибольшего общего делителя есть некоторые характерные свойства. Сформулируем их в виде теорем и докажем каждое из них.
Отметим, что данные свойства сформулированы для целых чисел больше нуля, а делители мы рассмотрим только положительные.
Данное свойство следует из самого определения НОД и не нуждается в доказательствах.
Докажем это утверждение.
Следующее свойство получило название алгоритма Евклида. С его помощью можно вычислить наибольший общий делитель двух чисел, а также доказать другие свойства НОД.
Рассмотрев данное свойство, заключаем, что множество общих делителей a и b аналогично множеству делителей НОД этих чисел. Это утверждение, которое является следствием из алгоритма Евклида, позволит нам вычислить все общие делители двух заданных чисел.
Перейдем к другим свойствам.
Докажем данное свойство. Запишем последовательность равенств по алгоритму Евклида:
Это все, что мы хотели бы рассказать о свойствах наибольшего общего делителя.
Целые числа (натуральные и отрицательные числа, НОК и НОД)
Чтобы намного упростить себе жизнь когда надо что-то вычислить, чтобы выиграть драгоценное время на ОГЭ или ЕГЭ, чтобы сделать меньше глупых ошибок, – читай эту статью!
Вот чему ты научишься:
Целые числа — коротко о главном
Множество целых чисел состоит из 3 частей:
Множество целых чисел обозначается буквой Z.
Натуральные числа
Натуральные числа – это числа, которые мы употребляем для счета предметов.
Множество натуральных чисел обозначается буквой N.
В операциях с целыми числами понадобится умение находить НОД и НОК.
Наибольший общий делитель (НОД)
Чтобы найти НОД, необходимо:
Наименьшее общее кратное (НОК)
Чтобы найти НОК, необходимо:
Отрицательные числа
Числа, противоположные натуральным, то есть:
Ноль
Натуральные числа
Множество целых чисел состоит из 3 частей:
Множество целых чисел обозначается буквой Z.
«Бог создал натуральные числа, всё остальное – дело рук человеческих» (c) Немецкий математик Кронекер.
Натуральные числа – это числа, которые мы употребляем для счета предметов, и именно на этом основывается их история возникновения – необходимости считать стрелы, шкуры и т.д.
1, 2, 3, 4… n
Множество натуральных чисел обозначается буквой N.
Кроме этого, не входят и все дробные числа (мы также не можем сказать « у меня есть 1,5 ноутбука», или «я продал 2,5 машины»)
Любое натуральное число можно записать с помощью 10 цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Таким образом, 14 – это не цифра. Это число. Из каких цифр оно состоит? Правильно, из цифр 1 и 4.
Натуральные числа можно складывать, вычитать, умножать и делить.
Сложение. Группировка при сложении чисел
Что интересного ты можешь сказать про эту процедуру?
Конечно, ты сейчас ответишь «от перестановки слагаемых значение суммы не меняется».
Казалось бы, примитивное, знакомое с первого класса правило, однако, при решении больших примеров оно моментально забывается!
Не забывай про него — используй группировку, чтобы облегчить себе процесс подсчета и снизить вероятность ошибок, ведь на ЕГЭ калькулятора у тебя не будет.
Смотри сам, какое выражение легче сложить?
Конечно же второе! Хотя результат один и тот же. Но! считая вторым способом у тебя меньше шансов ошибиться и ты все сделаешь быстрее!
Итак, ты в уме считаешь вот так:
4 + 5 + 3 + 6 = 4 + 6 + 5 + 3 = 10 + 5 + 3 = 18
Вычитание. Группировка при вычитании чисел
При вычитании мы также можем группировать вычитаемые числа, например:
32 — 5 — 2 — 6 = (32 — 2) — 5 — 6 = 30 — 5 — 6 = 19
А что, если вычитание чередуется в примере со сложением? Так же можно группировать, ответишь ты, и это правильно. Только прошу, не забывай о знаках перед числами, например: 32 — 5 — 2 — 6 = (32 — 2) — (6 + 5) = 30 — 11 = 19
Помни: неправильно проставленные знаки приведут к ошибочному результату.
Очевидно, что от перемены мест множителей значение произведения также не изменится:
Я не буду говорить тебе «используй это при решении примеров» (ты и сам понял намек, правда?), а лучше расскажу, как быстро умножать некоторые числа в уме.
Умножение. Как быстро умножать в уме
Итак, внимательно смотри таблицу:
И еще немного об умножении. Конечно, ты помнишь два особых случая…
Догадываешься, о чем я?
Ну что здесь можно сказать интересного?
Число может делиться на другое нацело (то есть, без остатка) и с остатком, который всегда меньше делителя, что вполне логично.
Особые случаи, если при делении у нас есть 0.
Чему будет равен пример, если 0 является делителем и чему равен пример, если он делимое?
Ах да, еще рассмотрим признаки делимости.
Всего существует 7 правил по признакам делимости, из которых первые 3 ты точно уже знаешь!
А вот остальные совсем не сложно запомнить.
Признаки делимости чисел
Первые три правила ты, конечно же, знаешь.
Четвертое и пятое легко запомнить – при делении на 3 и 9 мы смотрим, делится ли на это сумма цифр, составляющих число.
При делении на 4 мы обращаем внимание на две последние цифры числа — делится ли число, которое они составляют на 4?
При делении на 6 число должно одновременно делиться на 2 и на 3. Вот и вся премудрость.
Ты сейчас думаешь: «зачем мне все это»?
Во-первых, ЕГЭ проходит без калькулятора и данные правила помогут тебе сориентироваться в примерах.
А во-вторых, ты же слышал задачи про НОД и НОК? Знакомая аббревиатура? Начнем вспоминать и разбираться.
Наибольший общий делитель (НОД)
Наибольший общий делитель (НОД) — нужен для сокращения дробей и быстрых вычислений.
Допустим, у тебя есть два числа: 12 и 8.
На какое наибольшее число делятся оба этих числа? Ты, не задумываясь, ответишь 4, потому что знаешь, что:
12 = 4 * 3 = 2 * 2 * 3
8 = 4 * 2 = 2 * 2 * 2
Какие цифры в разложении общие?
Правильно, 2 * 2 = 4. Вот и твой ответ был 4.
Держа в голове этот простой пример, ты не забудешь алгоритм, как находить НОД.
Попробуй «выстроить» его у себя в голове. Получилось?
Чтобы найти НОД необходимо:
Понимаешь, зачем нам нужны были признаки делимости? Чтобы ты посмотрел на число и мог начать делить без остатка.
Найдем НОД числа 290
Глядя на него, ты сразу можешь сказать, что оно делится на 10, запишем:
29 больше разделить ни на что нельзя, а вот 10 можно – 5 и 2, получаем:
Найдем НОД числа 485.
По признакам делимости оно должно без остатка делиться на 5, так как на 5 заканчивается. Делим:
Проанализируем изначальное число.
На 2 оно делиться не может (последняя цифра – нечетная),
85 – не делится на 4, значит число тоже не делится на 4,
На 3 и на 9 также не делится (сумма цифр, входящих в число, не делится на 3 и на 9)
На 6 тоже не делится, так как не делится на 2 и 3,
На 8 тоже не делится, так как не делится на 2 и 4.
97 нельзя разделить на 7 нацело,
Значит, число 485 можно разложить только на 5 и 97.
А теперь найдем НОД этих чисел (290 и 485).
Какое это число?
Совет: глядя на числа можно иногда сразу найти хотя бы один общий делитель. Раздели сначала на него, а потом уже раскладывай дальше. При этом, необязательно общий делитель раскладывать на его составляющие – все равно потом ты будешь их снова перемножать.
Задача №1. Найти НОД чисел 6240 и 6800
1) Делю сразу на 10, так как оба числа 100% делятся на 10:
2) Разделю на 4 оставшиеся большие числа (624 и 680), так как 24 и 80 без остатка делятся на 4 (при этом, 10раскладывать не буду – он и так общий делитель):
3) Оставлю 4 и 10 в покое и начну рассматривать числа 156 и 170. Оба числа точно делятся на 2 (заканчиваются на четные цифры (0 в таком случае представляем как 10, а 10 можно разделить на 2)):
4) Работаем с числами 78 и 85. Есть ли у них общие делители? Так легко, как в предыдущих действиях, и не скажешь, поэтому дальше просто разложим их на простые множители:
5) Как мы видим, мы были правы: у 78 и 85 общих делителей нет, и теперь нам нужно перемножить 10⋅4⋅2=80.
НОД (6240; 6800)=80
Задача №2. Найти НОД чисел 345 и 324
Здесь не могу быстро найти хоть один общий делитель, так что просто раскладываю на простые множители (как можно меньше):
Точно, НОД (345; 324)=3, а я изначально не проверила признак делимости на 3, и, возможно, не пришлось бы делать столько действий.
Но ты-то проверил, верно?
Как видишь, это совсем несложно.
Наименьшее общее кратное (НОК) — экономит время, помогает решить задачи нестандартно
Допустим, у тебя есть два числа – 8 и 16. Какое существует самое маленькое число, которое делится 8 и 16 без остатка(то есть нацело)? Сложно представить? Вот тебе визуальная подсказка:
В данном случае НОК(8;16)=16.
Из этого простого примера вытекает несколько правил.
Наименьшее общее кратное (НОК)
Правила быстрого нахождения НОК.
Правило 1
Если одно из двух натуральных чисел делится на другое число, то большее из этих двух чисел является их наименьшим общим кратным.
Найди НОК у следующих чисел:
Конечно, ты без труда справился с этой задачей и у тебя получились ответы – 21,12, 15 и 33.
Заметь, в правиле мы говорим о ДВУХ числах, если чисел будет больше, то правило не работает.
Например, НОК (7;14;21) не равно 21, так как 21не делится без остатка на 14.
Правило 2
Если два (или более двух) числа являются взаимно простыми, то наименьшее общее кратное равно их произведению.
Найди НОК у следующих чисел:
Посчитал? Вот ответы – 21, 231, 42; 30.
Как ты понимаешь, не всегда можно так легко взять и подобрать этот самый х, поэтому для чуть более сложных чисел существует следующий алгоритм:
Найдем наименьшее общее кратное – НОК (345; 234)
Раскладываем каждое число:
Почему я сразу написал 3⋅2?
Вспомни признаки делимости на 6: делится на 2 (последняя цифра – четная) и сумма цифр делится на 3 (2+3+4=9).
Соответственно, можем сразу разделить 234 на 6, записав ее как 3⋅2.
Теперь выписываем в строчку наиболее длинное разложение – второе:
Добавим к нему числа из первого разложения, которых нет в том, что мы выписали:
Заметь: мы выписали все кроме 3, так как она у нас уже есть.
Теперь нам необходимо все эти числа перемножить!
НОК(345;234)=26910
Найди наименьшее общее кратное (НОК) (6240;6800) и (345;324)
Какие ответы у тебя получились?
Вот, что вышло у меня:
Сколько времени ты потратил на нахождение НОК? Мое время – 2 минуты, правда я знаю одну хитрость, которую предлагаю тебе открыть прямо сейчас!
Если ты очень внимателен, то ты наверное заметил, что по заданным числам мы уже искали НОД и разложение на множители этих чисел ты мог взять из того примера, тем самым упростив себе задачу, но это далеко не все.
Посмотри на картинку, возможно, к тебе придут еще какие-нибудь мысли:
Ну что? Сделаю подсказку: попробуй перемножить НОК и НОД между собой и запиши все множители, которые будут при перемножении. Справился? У тебя должна получиться вот такая цепочка:
Присмотрись к ней повнимательней: сравни множители с тем, как раскладываются 6240 и 6800.
Какой вывод ты можешь сделать из этого? Правильно! Если мы перемножим значения НОК и НОД между собой, то мы получим произведение этих чисел.
Соответственно, имея числа и значение НОД (или НОК), мы можем найти НОК (или НОД) по такой схеме:
1. Находим произведение чисел:
2. Делим получившееся произведение на наш НОД (6240; 6800) = 80:
Запишем правило в общем виде:
Попробуй найти НОД, если известно, что:
Справился? НОД(345; 234)=3.
Отрицательные числа – «лжечисла» и их признание человечеством
Как ты уже понял, это числа, противоположные натуральным, то есть:
Отрицательные числа можно складывать, вычитать, умножать и делить – все как в натуральных.
Казалось бы, что в них такого особенного?
А дело в том, что отрицательные числа «отвоевывали» себе законное место в математике аж до XIX века (до этого момента было огромное количество споров, существуют они или нет).
Само отрицательное число возникло из-за такой операции с натуральными числами, как «вычитание».
Действительно, из 3 вычесть 11 – вот и получается отрицательное число. Именно поэтому, множество отрицательных чисел часто называют «расширением множества натуральных чисел».
Отрицательные числа долго не признавались людьми.
Так, Древний Египет, Вавилон и Древняя Греция – светочи своего времени, не признавали отрицательных чисел, а в случае получения отрицательных корней в уравнении (например, как у нас 3−11), корни отвергались как невозможные.
Впервые отрицательные числа получили свое право на существование в Китае, а затем в VII веке в Индии.
Как ты думаешь, с чем связано это признание?
Правильно, отрицательными числами стали обозначать долги (иначе — недостачу).
Считалось, что отрицательные числа – это временное значение, которое в результате изменится на положительное (то есть, деньги кредитору все же вернут). Однако, индийский математик Брахмагупта уже тогда рассматривал отрицательные числа наравне с положительными.
В Европе к полезности отрицательных чисел, а также к тому, что они могут обозначать долги, пришли значительно позже, эдак, на тысячелетие.
Первое упоминание замечено в 1202 году в «Книге абака» Леонарда Пизанского (сразу говорю — к Пизанской башне автор книги отношения никакого не имеет, а вот числа Фибоначчи – это его рук дело (прозвище Леонардо Пизанского — Фибоначчи)).
Далее европейцы пришли к тому, что отрицательные числа могут обозначать не только долги, но и нехватку чего бы то ни было, правда, признавали это не все.
Так, в XVII веке Паскаль считал что 0−4=0.
Как думаешь, чем он это обосновывал?
Верно, «ничто не может быть меньше НИЧЕГО».
Отголоском тех времен остается тот факт, что отрицательное число и операция вычитания обозначается одним и тем же символом – минусом «-». И правда: 6−8. Число «8» положительное, которое вычитается из 6, или отрицательное, которое суммируется к 6?… Что-то из серии «что первое: курица или яйцо?» Вот такая вот, своеобразная эта математическая философия.
Отрицательные числа закрепили свое право на существование с появлением аналитической геометрии, иначе говоря, когда математики ввели такое понятие как числовая ось.
Именно с этого момента наступило равноправие. Однако все равно вопросов было больше чем ответов, например:
пропорция \( \displaystyle \frac<1><-1>=\frac<-1><1>\)
Данная пропорция носит название «парадокс Арно». Подумай, что в ней сомнительного?
В итоге, математики договорились до того, что Карл Гаусс (да, да, это тот самый, который считал сумму \( \displaystyle 40\) (или \( \displaystyle 100\)) чисел) в 1831 году поставил точку.
Он сказал, что отрицательные числа имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, так как дроби так же не применимы ко многим вещам (не бывает так, что яму роют \( \displaystyle 1,5\) землекопа, нельзя купить \( \displaystyle 4,5\) билета в кино и т.д.).
Успокоились математики только в XIX веке, когда Уильямом Гамильтоном и Германом Грассманом была создана теория отрицательных чисел.
Вот такие они спорные, эти отрицательные числа.
Возникновение «пустоты» или биография нуля
В математике \( \displaystyle 0\) – особенное число.
С первого взгляда, это ничто: прибавить \( \displaystyle 0\), отнять \( \displaystyle 0\) – ничего не изменится, но стоит только приписать его справа к «\( \displaystyle 1\)», и полученное число \( \displaystyle 10\) будет в \( \displaystyle 10\) раз больше изначального.
Умножением на ноль мы все превращаем в ничто, а разделить на «ничто», то есть \( \displaystyle 0\), мы не можем. Одним словом, волшебное число)
История нуля длинная и запутанная.
След нуля найден в сочинениях китайцев во 2 тыс. н.э. и ещё раньше у майя. Первое использование символа нуля, каковым он является в наши дни, было замечено у греческих астрономов.
Существует множество версий, почему было выбрано именно такое обозначение «ничего».
Некоторые историки склоняются к тому, что это омикрон, т.е. первая буква греческого слова ничто – ouden. Согласно другой версии, жизнь символу ноля дало слово «обол» (монета, почти не имеющая ценности).
Ноль (или нуль) как математический символ впервые появляется у индийцев (заметь, там же стали «развиваться» отрицательные числа).
Первые достоверные свидетельства о записи нуля относятся к 876 г., и в них «\( \displaystyle 0\)» – составляющая числа \( \displaystyle 270\).
В Европу ноль также пришел с запозданием — лишь в 1600г., и также как и отрицательные числа, сталкивался с сопротивлением (что поделаешь, такие они, европейцы).
«Нуль часто ненавидели, издавна боялись, а то и запрещали» — пишет американский математик Чарльз Сейф.
Так, турецкий султан Абдул-Хамид II в конце XIXв. приказал своим цензорам вычеркнуть из всех учебников химии формулу воды H2O, принимая букву «О» за нуль и не желая, чтобы его инициалы порочились соседством с презренным нулём».
На просторах интернета можно встретить фразу: «Ноль — самая могущественная сила во Вселенной, он может всё! Ноль создаёт порядок в математике, и он же вносит в неё хаос». Абсолютно верно подмечено:)
Нахождение НОД по алгоритму Евклида и с помощью разложения на простые множители.
Эта статья про нахождение наибольшего общего делителя (НОД) двух и большего количества чисел. Сначала рассмотрим алгоритм Евклида, он позволяет находить НОД двух чисел. После этого остановимся на методе, позволяющем вычислять НОД чисел как произведение их общих простых множителей. Дальше разберемся с нахождением наибольшего общего делителя трех и большего количества чисел, а также приведем примеры вычисления НОД отрицательных чисел.
Навигация по странице.
Алгоритм Евклида для нахождения НОД
В статье наибольший общий делитель (НОД), определение, примеры, свойства НОД мы сформулировали и доказали алгоритм Евклида. Алгоритм Евклида является универсальным способом, позволяющим вычислять наибольший общий делитель двух положительных целых чисел.
Рассмотрим примеры нахождения НОД по алгоритму Евклида.
Покажем решение еще одного примера, но теперь обойдемся без подробных пояснений шагов алгоритма Евклида.
Найдите НОД(661, 113) по алгоритму Евклида.
Нахождение НОД с помощью разложения чисел на простые множители
Рассмотрим еще один способ нахождения НОД. Наибольший общий делитель может быть найден по разложениям чисел на простые множители. Сформулируем правило: НОД двух целых положительных чисел a и b равен произведению всех общих простых множителей, находящихся в разложениях чисел a и b на простые множители.
Рассмотрим пример нахождения НОД по озвученному правилу.
Разложим на простые множители числа 72 и 96 :
Нахождение НОД трех и большего количества чисел
Давайте разберемся, как выглядит процесс нахождения НОД нескольких чисел, рассмотрев решение примера.
Разложение чисел на простые множители также позволяет вычислять НОД трех и большего количества чисел. В этом случае наибольший общий делитель находится как произведение всех общих простых множителей данных чисел.
Вычислите НОД чисел из предыдущего примера, используя их разложения на простые множители.
Нахождение НОД отрицательных чисел
Если одно, несколько или все числа, наибольший делитель которых нужно найти, являются отрицательными числами, то их НОД равен наибольшему общему делителю модулей этих чисел. Это связано с тем, что противоположные числа a и −a имеют одинаковые делители, о чем мы говорили при изучении свойств делимости.
Как найти нод двух чисел
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел. Обозначают НОД(a, b).
Рассмотрим нахождения НОД на примере двух натуральных чисел 18 и 60:
Пример Найти наибольший общий делитель чисел 324, 111 и 432
Разложим числа на простые множители:
324 = 2 × 2 × 3 × 3 × 3 × 3
111 = 3 × 37
432 = 2 × 2 × 2 × 2 × 3 × 3 × 3
Вычеркнуть из первого числа, множители которых нету во втором и третьем числе, получим:
2 × 2 × 2 × 2 × 3 × 3 × 3 = 3
В результате НОД(324, 111, 432)=3
Нахождение НОД с помощью алгоритма Евклида
Второй способ нахождения наибольшего общего делителя с помощью алгоритма Евклида. Алгоритм Евклида является наиболее эффективным способом нахождения НОД, используя его нужно постоянно находить остаток от деления чисел и применять рекуррентную формулу.
Алгоритм Евклида
Пример Найти наибольший общий делитель чисел 7920 и 594
Найдем НОД(7920, 594) с помощью алгоритма Евклида, вычислять остаток от деления будем с помощью калькулятора.
В результате получаем НОД(7920, 594) = 198
Наибольший общий делитель
Наибольшим общим делителем двух чисел, называют наибольшее число, на которые оба числа делятся без остатка.
Как найти наибольший общий делитель?
Существует несколько алгоритмов нахождения НОД. Рассмотрим их.
Алгоритм нахождения НОД через разложение на простые множители
Чтобы найти наибольший общий делитель нескольких натуральных чисел, необходимо:
Пример: найти НОД(100;250)
Подробнее о разложении чисел на простые множители, смотрите тут
Алгоритм Евклида для нахождения НОД
Для нахождения НОД по алгоритму Евклида необходимо:
Пример: реализуем предыдущий пример НОД(100;250), разобранным алгоритмом:
Согласно алгоритму 250 меняем на остаток 50, получаем 100 и 50. Возвращаемся к 1 пункту и продолжаем вычисления, пока остаток не будет равен 0.
Ответ: НОД(100;250) = 50
Пример: найти НОД(150;280)
Как найти НОД двух чисел по алгоритму Евклида
Что такое алгоритм Евклида
Алгоритм Евклида — один из наиболее ранних численных алгоритмов в истории. Название было дано в честь греческого математика Евклида, который впервые дал ему описание в книгах «Начала». Изначально назывался «взаимным вычитанием», так как его принцип заключался в последовательном вычитании из большего числа меньшего, пока в результате не получится ноль. Сегодня чаще используется взятие остатка от деления вместо вычитания, но суть метода сохранилась.
Алгоритм Евклида — это алгоритм, основная функция которого заключается в поиске наибольшего общего делителя (НОД) для двух целых чисел.
Простейшим случаем применения данного алгоритма является поиск наибольшего общего делителя для пары положительных целых чисел. Евклид, автор этого метода, предполагал его использование только для натуральных чисел и геометрических величин. Но позже алгоритм был обобщен и для других групп математических объектов, что привело к появлению такого понятия, как евклидово кольцо.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Понятие НОД
Аббревиатура НОД расшифровывается как «наибольший общий делитель».
Наибольший общий делитель — делитель, который делит без остатка два числа, при этом сам делится без остатка на любой другой делитель исходных двух чисел. То есть это самое большое число, на которое без остатка можно разделить пару чисел, для которых подбирается НОД.
Основная суть алгоритма Евклида
Суть алгоритма заключается в построении ряда следующего вида (при условии, что a больше b):
В нем каждое последующее число — это остаток от деления двух предыдущих, ряд заканчивается, когда остаток от деления становится равным 0 — при условии использования деления.
В нем каждое последующее число является результатом вычитания двух предыдущих, ряд заканчивается, когда частное становится равным 0 — при условии использования вычитания.
Последовательность нахождения НОД при помощи деления:
60 / 36 = 1 (остаток 24)
36 / 24 = 1 (остаток 12)
24 / 12 = 2 (остаток 0)
НОД для 60 и 36 равен 12 (делитель).
Последовательность нахождения НОД при помощи вычитания:
НОД для 60 и 36 равен 12 (уменьшаемое, вычитаемое)
Примеры решения задач с алгоритмом Евклида
Найти наибольший общий делитель для чисел 128 и 96.
128 / 96 = 1 (остаток 32)
Найти наибольший общий делитель для чисел 37 и 17.
37 / 17 = 2 (остаток 3)
17 / 3 = 5 (остаток 2)
3 / 2 = 1 (остаток 1)
2 / 1 = 2 (остаток 0)
Числа 37 и 17 являются простыми, соответственно, их НОД — единица. Совет: перед вычислениями проверяйте таблицу простых чисел.
Вычисление НОД — ошибка, которой не замечают
Что такое НОД, все знают еще со школы. Для тех, кто подзабыл, напомню: НОД — наибольший общий делитель, делящий два целых числа без остатка. Например, НОД чисел 100 и 45 равен 5, а НОД чисел 17 и 7 равен 1. Существует несколько различных алгоритмов поиска этого числа. Однако, несмотря на то, что это достаточно простые алгоритмы, часто совершают одну маленькую, но очень существенную ошибку.
Алгоритмы вычисления НОД
Естественно, чаще всего пишут первый вариант — он легко запоминается, быстро пишется и достаточно быстро работает.
Претесты
Реализации корректно работают на таких тестах:
Естественно, они будут работать и на подобных тестах, где в качестве аргументов выступают целые неотрицательные числа. Но что, если…
Первые тесты с подвохом
… если заменить одно из чисел нулем? Например так:
Классический алгоритм Евклида (№3) уже попадает в бесконечный цикл.
Копаем глубже
Согласно определению, НОД может быть определен для любых двух целых чисел. Так почему бы не попробовать тесты, где одно из чисел — отрицательное:
Все становится еще интереснее. Первые две реализации выдают в качестве ответа -5. Третий алгоритм снова попадает в бесконечный цикл. Вместе с ним в бесконечном цикле оказывается пятый алгоритм. Четвертый падает по StackOverFlow — скорее всего тоже попадает в бесконечный цикл.
Но ведь ответ -5 — неправильный. По определению НОД — наибольший общий делитель. А таковым является число 5. Ведь и первое, и второе число делятся без остатка на 5. Значит и первые две реализации не дают верный ответ.
Почему решения №№3-5 попадают в бесконечный цикл?
Алгоритм Евклида попадает в цикл из-за бесконечного увеличения аргументов, если один из них отрицательный. Действительно, если посмотреть на эти строки, то можно заметить, что при отрицательном a (или b) операция вычитания заменяется сложением.
Аналогичное происходит в четвертом и пятом алгоритме:
В ситуации, когда a или b равны 0, то происходит бесконечное вычитание нуля, которое никаким образом не меняет значения аргументов.
Так что же не так?
Все эти алгоритмы корректны для входных данных, когда оба числа a и b — целые неотрицательные числа. Но вспомним еще раз — НОД существует для любых двух целых чисел.
Что же делать?
В качестве аргументов в функцию можно передавать абсолютное значение чисел, тогда ответ будет корректен:
Второй способ решения задачи — возвращать абсолютное значение ответа:
Второй вариант гораздо предпочтительнее: будет производиться меньше лишних вычислений, чем в первом варианте.
Итоги
Мы рассмотрели пять различных вариантов вычисления наибольшего общего делителя. Для каждого из них мы указали входные данные, на которых ответ существует, но решение «падает», а также способ решения проблемы.
Такие небольшие ошибки чаще всего допускаются по причине того, что не замечают «скользкие» места решения какой-то задачи. Часть из них отлавливается в процессе тестирования, а часть остается незамеченной.
В ситуации с вычислением НОД почти все реализации приведены с ошибкой. В Сети я нашел лишь парочку корректно работающих решений, остальные идентичны тем, что приведены в начале поста.
Онлайн калькулятор позволяет быстро находить наибольший общий делитель и наименьшее общее кратное как для двух, так и для любого другого количества чисел.
Калькулятор для нахождения НОД и НОК
Найдено НОД и НОК:
Как пользоваться калькулятором
Как вводить числа
Что такое НОД и НОК?
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. Наибольший общий делитель сокращённо записывается как НОД.
Наименьшее общее кратное нескольких чисел – это наименьшее число, которое делится на каждое из исходных чисел без остатка. Наименьшее общее кратное сокращённо записывается как НОК.
Как проверить, что число делится на другое число без остатка?
Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.
Некоторые признаки делимости чисел
2. Признак делимости числа на 3
Число делится на 3 тогда, когда сумма его цифр делится на три. Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Пример: определить, делится ли число 34938 на 3.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.
4. Признак делимости числа на 9
Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.
Пример: определить, делится ли число 34938 на 9.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.
Как найти НОД и НОК двух чисел
Как найти НОД двух чисел
Наиболее простым способом вычисления наибольшего общего делителя двух чисел является поиск всех возможных делителей этих чисел и выбор наибольшего из них.
Рассмотрим этот способ на примере нахождения НОД(28, 36) :
Как найти НОК двух чисел
Наиболее распространены два способа нахождения наименьшего кратного двух чисел. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди них такое число, которое будет общим для обоих чисел и при этом наименьшем. А второй заключается в нахождении НОД этих чисел. Рассмотрим только его.
Для вычисления НОК нужно вычислить произведение исходных чисел и затем разделить его на предварительно найденный НОД. Найдём НОК для тех же чисел 28 и 36:
Нахождение НОД и НОК для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел. Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c).
Аналогичное соотношение действует и для наименьшего общего кратного чисел: НОК(a, b, c) = НОК(НОК(a, b), c)
Пример: найти НОД и НОК для чисел 12, 32 и 36.
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.
НОД и НОК двух чисел, алгоритм Евклида
Вы будете перенаправлены на Автор24
Наибольший общий делитель
$НОД \ (a;b) \ или \ D \ (a;b)$
Чтобы найти наибольший общий делитель двух, чисел необходимо:
Будем находить согласно представленному алгоритму. Для этого
разложить числа на простые множители
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Выбрать числа, которые входят в разложение этих чисел
$242=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Будем находить согласно представленному алгоритму. Для этого:
Разложим числа на простые множители
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Выбираем числа, которые входят в разложение этих чисел
$63=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Готовые работы на аналогичную тему
Найти НОД двух чисел можно и по-другому, используя множество делителей чисел.
Решение:
Определение НОК
Наименьшее из общих кратных будет называться наименьшим общим кратным и обозначается НОК$(a;b)$ или K$(a;b).$
Чтобы найти НОК двух чисел, необходимо:
Будем находить согласно представленному алгоритму. Для этого
Разложить числа на простые множители
$99=3\cdot 3\cdot 11$
Выписать множители, входящие в состав первого
добавить к ним множители, которые входят в состав второго и не ходят в состав первого
$НОК=3\cdot 3\cdot 11\cdot 7=693$
Составление списков делителей чисел часто очень трудоемкое занятие. Существует способ нахождение НОД, называемый алгоритмом Евклида.
Утверждения, на которых основан алгоритм Евклида:
Свойства НОД и НОК
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 29.06.2022
Понятие НОД
Определение, что такое НОД в математике, звучит следующим образом: наибольший делитель, общий для чисел a и b, есть такое наибольшее число, на которое описанные значения смогут разделиться без остатка.
Для наилучшего понимания того, как найти НОД двух чисел, вместо указанных переменных достаточно подставлять простые числа, например, 12 и 9. То есть самым наименьшим делимым числом для 12 и 9 является то, которое позволяет найти решение без остатка.
Задача по нахождению НОД может решаться тремя способами. Каждый из них применяется в зависимости от того, насколько быстро требуется найти необходимый показатель:
Лучше всего рассматривать применение указанных методов через определенный класс задач, которые помогают при дальнейшем изучении теорем, касающихся дробей. Формулы для указанной темы очень доступны для понимания ученикам и учителям.
Метод разложения
Суть второй методики заключается в разложении на простые множители и перемножении общих из них. В качестве примера можно рассмотреть представление НОД для показателей 18 и 24:
Способ является достаточно простым. Однако из-за некоторого объема операций можно оказаться в сложной ситуации с поиском общих делителей, поэтому следует рассмотреть еще один способ.
Вычеркивание показателей
Для третьей методики характерно вычеркивание из разложения тех показателей, которые не проходят во второе число. Есть такие виды НОД, которые могут сильно отличаться, но все равно позволяют найти нужный показатель. Например, нужно найти наибольший делитель для значений 28 и 16:
Аналогично можно отыскать для других значений, например, 100 и 40. После разложения из первого перечеркивается лишняя пятерка. Перемножение дает 20, который после поверки оказывается наибольшим делителем.
Несколько значений
Несмотря на кажущуюся сложность, доказать, что возможно найти НОД для нескольких чисел без помощи онлайн-калькуляторов, вполне реально. Значения, подлежащие поиску, необходимо разложить на множители. После чего ищется произведение общих простейших множителей.
Есть такие числа как 18, 24 и 36. Разложение 18 дает такие коэффициенты как 1, 2, 3, 6, 9 и 18. Затем 24 и 36 необходимо править по аналогичному методу. Если составить таблицу, то можно найти следующие общие показатели в виде 2 и 3. Они считаются общими для всех трех чисел.
Перемножив между собой, получается делимое число 6. Оно также подходит под разложение 18, 24 и 36, а также считается наибольшим общим делителем для всех трех параметров. Аналогичный принцип срабатывает и для четырех и более чисел, когда потребуется найти делитель на любом уровне сложности вплоть до максимального.
Наименьшее общее кратное
Помимо НОД, существует еще и наименьшее общее кратное, или НОК. Если сказать по-другому, то таковым свойством можно считать число, которое без остатка будет разделяться на число a и число b.
Как и для НОД, поиск НОК может осуществляться тремя похожими с предшествующими способами. Каждым из них можно воспользоваться в зависимости от ситуации и удобства решения задания:
На последнем методе стоит остановиться несколько подробнее. Он является не только сравнительно менее громоздким, но и обладает определенным преимуществом в виде уже найденного НОД и более простого алгоритма решения.
Совмещение делителей
Такая методика характерна для тех примеров, в которых требуется единовременное нахождение НОД и НОК двух чисел. Например, необходимо отыскать для чисел 24 и 12 НОК и НОК. Действовать нужно в следующем порядке:
Сходный механизм действует и при поиске НОК и НОД исходя из другой пары чисел. В каждом примере необходимо сначала отыскать наибольший делитель, перемножить два числа и получить наименьшее кратное.
Что касается решения с помощью интернет-ресурсов, то на сегодняшний день имеется много онлайн-калькуляторов и программ, которые дают возможность сравнительно быстро найти НОД и НОК и подсказать грамотные пути решения.
Нахождение наибольшего делителя и НОК является не только распространенной, но и сравнительно трудной задачей для учеников средней школы. Ведь если не рассмотреть подробно такую тему, то дальнейшее изучение дробей, которые включают в себя числитель и знаменатель, окажется практически невозможным.
Важно грамотно использовать ресурсы на специальных математических сайтах, где могут подробно и понятно объяснить разложение дробей и нахождение общих делителей. Бояться ошибиться в такой теме не стоит, поскольку при правильном подходе она пройдет достаточно быстро, а вычисление различных по уровню сложности примеров не составит особых сложностей.
НОД, НОД
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Определения:
Способы нахождения НОД двух чисел:
1 способ (следует из определения): Метод полного перебора для нахождения наибольшего общего делителя (НОД) натуральных чисел.
2 способ : Метод перебора делителей меньшего числа для нахождения наибольшего общего делителя (НОД) натуральных чисел.
3 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители.
4 способ: Алгоритм Евклида нахождения наибольшего общего делителя (НОД) двух натуральных чисел вычитанием.
Способы нахождения НОК двух чисел:
1 способ: Метод перебора
1. Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
2 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители
Свойства наименьшего общего кратного:
8 способов нахождения наибольшего общего делителя
Эта статья появилась на свет совершенно неожиданно. Мне на глаза случайно попался код вычисления НОД на C#.
С первого взгляда мне даже всё понравилось: простенько, лаконичненько и без лишнего выпендрёжа. Однако чем дольше я рассматривал этот код, тем больше возникало сомнений в его эффективности. Я решил сделать маленькое исследование.
В адаптации на C++ код выглядел примерно так:
Подготовка
Для такой несложной задачи я не стал связываться с профилировщиком, а использовал примитивный тайминг (подробности можно посмотреть в статье «Оптимизация кода через ручной тайминг»).
Окончательный вариант «испытательного стенда» приведён в конце статьи. А в процессе исследований я пользовался его упрощённым вариантом, обеспечивавшим запуск одной из испытуемых функций и таймирование.
В коде я не пользоваться библиотечными функциями, что бы максимальный объём кода был контролируемым. Использование библиотечных функций типа min или swap — отдельная тема для экспериментов. Оставляю её для особо дотошных читателей.
01 перебор от произвольного числа
Этот алгоритм – стартовая точка исследования. Идея алгоритма очень проста: гоним переменную цикла от первого числа до 1. Если оба числа делятся на переменную цикла без остатка, значит переменная цикла и равна НОД; цикл можно завершить досрочно. Если цикл прошёл до конца, значит для этих чисел НОД равен 1.
Очевидный недостаток – несимметричность относительно аргументов. Очевидно, что НОД меньше или равен меньшему из двух чисел. Поэтому гнать цикл от большего числа не имеет смысла.
02 перебор от минимального числа
Просто добавляем простейшую функцию для вычисления минимального числа для пары чисел и инициализируем переменную цикла меньшим из двух чисел. В половине случаев такая оптимизация работать не будет (когда первый аргумент и так меньше второго); зато в другой половине случаев выигрыш по времени может быть весьма значительным.
03 алгоритм с разложением на делители
Но второй вариант так и остался алгоритмом с последовательным перебором. Что можно попробовать ещё?
Из школьного курса математики известно, что НОД можно найти из разложения чисел на простые множители.
НОД будет равен произведению простых множителей, общих для обоих чисел. Например:
Реализуем эту идею:
Первый if отлавливает ситуацию, когда оба числа делятся нацело на переменную цикла и, следовательно, переменная цикла является общим простым (!) множителем для обоих чисел и учитывается для вычисления НОД. Остальные два if отлавливают случаи, когда только одно из чисел делится на переменную цикла; эти множители в НОД не входят.
Третий вариант по производительности не плох. Но пока это самопал. А что придумали умные люди за многовековую историю математики? «O’key, Гуг. то есть, Википедия, что такое НОД?» Вот, кстати, описано нахождение НОД через каноническое разложение на простые множители, которое мы уже реализовали. А вот что-то новенькое.
04 алгоритм Евклида (рекурсивный)
В самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары.
Реализуем рекурсивную версию:
Считается, что рекурсивные алгоритмы менее эффективны, чем итерационные, за счёт накладных расходов на вызов функции. Для проверки делаем и итерационный вариант.
05 алгоритм Евклида (итерационный)
Кстати, в Викиучебнике есть и другие реализации алгоритма Евклида.
06 бинарный алгоритм (рекурсивный)
Тестирование
Программа компилировалась под MS Visual Studio 2013 и TDM-GCC 4.8.1 в режиме 64-bit Release.
Как и ожидалось, первый алгоритм катастрофически неэффективен. Алгоритм №2 – минимальный костыль для №1 – работает почти в 2 раз быстрее.
Третий алгоритм неожиданно показал очень достойный результат: в 50 раз быстрее алгоритма №2.
Четвёртый и пятый варианты – алгоритм Евклида: рекурсивная версия, как ни странно, обогнала итерационную. По сравнению с третьим вариантом время улучшилось почти на порядок.
Бинарный алгоритм Евклида показал наилучшие результаты. Из трёх вариантов реализации рекурсивная версия – самая неторопливая. Наилучший результат у оптимизированной версии с использованием битовых операций.
Итого, самая производительная версия работает более чем в 2500 раз быстрее, чем изначальный вариант.
Примечание. Время, указанное в таблице – это время выполнения REPEAT_TIMES вызовов функции.
Выводы
Выводы достаточно банальны, но всё же:
Наибольший общий делитель (НОД). Как найти НОД двух и более чисел + калькулятор ⏳
Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка.
Общий делитель двух данных чисел — это число, на которое делятся без остатка оба данных числа.
Наибольший общий делитель нескольких чисел (НОД) – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка.
И как вы заметили, если одно число делится без остатка на другое, то меньшее число и будет наибольшим общим делителем.
Если НОД чисел равен 1, такие числа называют взаимно простыми.
Взаимно простые числа — это натуральные числа, которые имеют только один общий делитель — число 1.
Как найти наибольший общий делитель
Пример 1. Найдем НОД чисел 28 и 10. Разложим их на простые множители.
28| 2 10| 2
14|2 5|5
7|7 1|
1|
28 = 2 · 2 · 7
10 = 2 · 5
Пример 2. Найдем НОД чисел 28 и 36.
28| 2 36| 2
14| 2 18| 2
7|7 9|3
1| 3|3
1|
28 = 2 · 2 · 7
36 = 2 · 2 · 3 · 3
Общих множителей два: это 2 · 2. Чтобы найти НОД, нужно их перемножить.
НОД(28;36) = 2 · 2 = 4
То же самое при нахождении НОД трех и более чисел. Общий множитель находим во всех числах, а не только в паре.
Пример 3. Найдем НОД чисел 28, 36 и 48.
28| 2 36| 2 48| 2
14| 2 18| 2 24| 2
7|7 9|3 12|2
1| 3|3 6|2
1| 3|3
1|
28 = 2 · 2 · 7
36 = 2 · 2 · 3 · 3
48 = 2 · 2 · 2 · 2 · 3
НОД(28;36;48) = 2 · 2 = 4
Чтобы не путаться, можно подчеркивать общие множители только в одной строке (у одного числа), их и будем перемножать.
Таким образом у вас в голове должен сложиться алгоритм нахождения НОД:
Потренируемся нахождению НОД на примерах
1. Найдите НОД(а;b), если а = 2 · 3 · 7 · 13; b = 3 · 3 · 3 · 13
У нас уже имеется разложение на простые множители, осталось лишь подчеркнуть общие и найти НОД.
а = 2 · 3 · 7 · 13
b = 3 · 3 · 3 · 13
НОД(а;b) = 3 · 13 = 39
2. Найдите НОД(96;72)
1) Разложим числа на простые множители:
96 = 2 · 2 · 2 ·2·2· 3
72 = 2·2·2·3·3
2) Найдём общие множители введённых чисел: 2, 2, 2, 3
Наибольший общий делитель равен произведению найденных множителей:
НОД(96;72) = 2·2·2·3 = 24
3. Найдите НОД(840;1008;256)
1) Разложим числа на простые множители:
840 = 2 · 2 · 2 ·3·5·7
1008 = 2·2·2·2·3·3·7
256 = 2·2·2·2·2·2·2·2
2) Найдём общие множители введённых чисел: 2, 2, 2
Наибольший общий делитель равен произведению найденных множителей:
НОД(28;36;48) = 2·2·2 = 8
4. Найдите НОД(104;121). Являются ли эти числа взаимно простыми?
1) Разложим числа на простые множители:
104 = 2·2·2·13
121 = 11·11
2) Найдём общие множители введённых чисел: 1
НОД(104;121) = 1, значит это взаимно простые числа.
5. Докажите, что числа 102 и 119 не взаимно простые.
1) Разложим числа на простые множители:
102 = 2·3·17
119 = 7·17
2) Найдём общие множители введённых чисел: 17
6. Чему будет равен НОД чисел а и b, если а кратно b?
а кратно b, значит а делится на b без остатка. Это означает, что число b и есть наибольший общий делитель.
7. Пример нахождения НОД чисел 50, 75 и 325.
1) Разложим числа 50, 75 и 325 на простые множители.
50= 2 ∙ 5 ∙ 5
75= 3 ∙ 5 ∙ 5
325= 5 ∙ 5 ∙ 13
2) Из множителей входящих в разложение одного из этих чисел, вычеркнем те, которые не входят в разложение других.
50= 2 ∙ 5 ∙ 5
75= 3 ∙ 5 ∙ 5
325= 5 ∙ 5 ∙13
3) Найдём произведение оставшихся множителей
Ответ: НОД (50, 75 и 325) = 25
Задачи на нахождение НОД
Нахождение НОД используют при решении некоторых задач. Рассмотрим примеры задач.
Для учащихся 1 класса приготовили одинаковые подарки. Во всех подарках было 120 апельсинов, 280 шоколадок и 320 конфет. Сколько учащихся в 1 классе, если известно, что их больше 30?
Так как для учащихся приготовили одинаковые подарки, то в них должно быть поровну апельсинов, шоколадок и конфет. Следовательно, количество учащихся равно общему делителю количества апельсинов, шоколадок и конфет.
Разложим числа 120, 280 и 320 на множители и найдем их наибольший общий делитель.
120 = 2 * 2 * 2 * 3 * 5;
280 = 2 * 2 * 2 * 5 * 7;
320 = 2 * 2 * 2 * 2 * 2 * 2 * 5.
НОД(120;280;320) = 2 * 2 * 2 * 5 = 40.
Поскольку все делители чисел 120, 280 и 320 кроме 40, меньше 30 (а по условию задачи в классе больше 30 учащихся), то число учащихся 40.
Ответ: в первом классе 40 учащихся.
Между учащимися 6 класс поровну разделили 84 мандарина и 56 апельсинов. Сколько учащихся в классе, если известно, что их более 25?
Разложим числа на простые множители:
84 = 2 · 2 ·3· 7
56 = 2·2·2·7
НОД(84;56) = 2 · 2 · 7 = 28 (уч.)
Ответ: 28 учащихся в классе.
В гостиницу завезли 108 кроватей и 72 шкафа, которые поровну распределили по номерам. Сколько номеров в гостинице, если известно, что их больше 30?
108 = 2 · 2 · 3 · 3 ·3
72 = 2·2·2·3·3
НОД = 2·2·3·3 = 36 (н.)
Ответ: 36 номеров в гостинице.
Лист картона имеет форму прямоугольника, длина которого 48 см., а ширина 40 см. Этот лист надо разрезать без отходов на равные квадраты. Какие наибольшие квадраты можно получить из этого листа и сколько?
1) S = a ∙ b – площадь прямоугольника.
S= 48 ∙ 40 = 1960 см² – площадь картона.
2) a – сторона квадрата
48 : a – число квадратов, которое можно уложить по длине картона.
40 : а – число квадратов, которое можно уложить по ширине картона.
3) НОД (40 и 48) = 8 (см) – сторона квадрата.
4) S = a² – площадь одного квадрата.
S = 8² = 64 (см²) – площадь одного квадрата.
5) 1960 : 64 = 30 (к.)
Ответ: 30 квадратов со стороной 8 см каждый.
Камин в комнате необходимо выложить отделочной плиткой в форме квадрата. Сколько плиток понадобится для камина размером 195 ͯ 156 см и каковы наибольшие размеры плитки?
1) S = 196 ͯ 156 = 30420 (см ²) – S поверхности камина.
2) НОД (195 и 156) = 39 (см) – сторона плитки.
3) S = a² = 39² = 1521 (см ²) – площадь 1 плитки.
4) 30420 : = 20 (штук).
Ответ: 20 плиток размером 39 ͯ 39 (см).
Садовый участок размером 54 ͯ 48 м по периметру необходимо оградить забором, для этого через равные промежутки надо поставить бетонные столбы. Сколько столбов необходимо привезти для участка, и на каком максимальном расстоянии друг от друга будут стоять столбы?
1) P = 2( a + b) – периметр участка.
P = 2(54 + 48) = 204 м.
2) НОД (54 и 48) = 6 (м) – расстояние между столбами.
3) 204 : 6 = 34 (с.)
Ответ: 34 столба, на расстоянии 6 м.
Из 210 бордовых, 126 белых, 294 красных роз собрали букеты, причём в каждом букете количество роз одного цвета поровну. Какое наибольшее количество букетов сделали из этих роз и сколько роз каждого цвета в одном букете?
Таня и Маша купили одинаковое число почтовых наборов. Таня заплатила 90 руб., а Маша на 5 руб. больше. Сколько стоит один набор? Сколько наборов купила каждая?
Заместитель директора Вера Александровна организует проведение дня здоровья. 424 человека повезут на стадион “Спартак” для проведения эстафет, а 477 человек – в плавательный бассейн с морской водой. Для перевозки нужно заказать автобусы. Перевозчик имеет автобусы с одинаковым количеством мест, все места должны быть заняты. Сколько автобусов надо заказать и сколько пассажиров будет в каждом автобусе?
На празднике “Последнего звонка” выступающим первоклассникам принято дарить подарки. Ученики 11 “а” класса купили 58 конфет, ученики 11 “б” класс – 116 “чупа-чупсов”, а ученики 11 “в” класса – по одной мягкой игрушке. Сколько куплено мягких игрушек?
НОД (58;116) = 29
Ответ: куплено 29 мягких игрушек.
Друзья Алексей Николаевич и Борис Петрович решили заняться гостиничным бизнесом. Для своей гостиницы Алексей Николаевич завез 108 кроватей и 72 шкафа, а Борис Петрович – 128 кроватей и 64 шкафа. Кровати и шкафы распределяются по комнатам поровну. Сколько комнат в гостиницах каждого из друзей? У кого из них остановиться третьему другу Александру Ивановичу, если он отдыхает с семьей, состоящей вместе с ним из 8 человек?
Калькулятор определения НОД и НОК
Если что-либо осталось для вас непонятным, задавайте вопросы в комментариях.
Наибольший общий делитель

Средняя оценка: 4.3
Всего получено оценок: 173.
Средняя оценка: 4.3
Всего получено оценок: 173.
Наибольший общий делитель – это еще один показатель, позволяющий упростить работу с дробями. Очень часто в результате вычислений получаются дроби с очень большими значениями числителя и знаменателя. Сокращать поэтапно такие числа можно, но это крайне долго, поэтому проще сразу найти НОД и сократить на него. Разберемся в теме подробнее.
Что такое НОД?
Наибольший общий делитель (НОД) ряда чисел – это наибольшее число, на которое можно без остатка разделить каждое из чисел ряда.
Это значение чаще всего используется для ряда из двух чисел. Просто потому, что сокращаются обычно два числа: числитель и знаменатель дроби. Нахождение НОД для большего количества значений не всегда оправдано, но вырабатывает навык.
Как найти НОД?
Для того, чтобы найти НОД необходимо каждое из чисел разложить на простые множители и выделить общую часть.
Специальной формулы для этого не придумали, зато есть алгоритм вычисления.
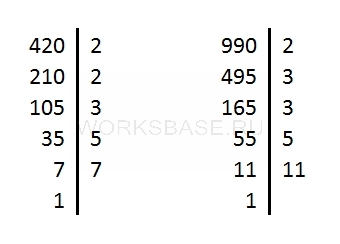
Приведем пример нахождения наибольшего общего делителя двух натуральных чисел: 540 и 252. Разложим 640 на простые множители. Последовательность действий такова:
Теперь проведем ту же процедуру на практике.
Запишем результат в виде равенства 540=2*2*3*3*3*5. Для того, чтобы записать результат, нужно последнее получившееся число умножить на все делители.
Аналогично поступим с числом 252:
Запишем результат: 252=2*2*3*3*7.
В каждом разложении есть одинаковые числа. Найдем их, это два числа 2 и два числа 3. Отличаются только 7 и 3*5.
Как можно это использовать?
НОД для двух этих чисел мы уже находили, теперь просто воспользуемся уже посчитанным значением.
Сократим числитель и знаменатель дроби на 36 и получим ответ.
$$ <252\over540>=<7\over15>$$ – чтобы быстро сократить, достаточно посмотреть на разложение чисел.
Если 540=2*2*3*3*3*5, а НОД=36=2*2*3*3, то 540 = 36*3*5. И если мы поделим 540 на 36, то получим 3*5=15.
Без НОД нам пришлось бы в одну длинную строку писать сокращения. К тому же, бывают случаи, когда непонятно, можно ли сократить дробь вообще. Для таких ситуаций в математике и придумали разложение чисел на простые множители и НОД.
Что мы узнали?
Мы узнали, что такое наибольший общий делитель пары чисел, разобрались, как можно использовать показатель на практике, решили задачу на нахождение НОД и применение НОД для сокращения дробей. Поняли, что с использованием НОД можно проще и быстрее сократить громоздкие дроби, найдя НОД для числителя и знаменателя.
Нахождение наибольшего общего делителя
В данной статье мы рассмотрим определение наибольшего общего делителя, научимся его находить для двух или нескольких чисел, а также разберем практические примеры для закрепления изложенного материала.
Определение наибольшего общего делителя
Если у числа больше двух делителей, его называют составным.
В отличие от кратных, количество делителей числа ограничено.
Общий делитель двух натуральных чисел – это такое число, на которое оба этих числа делятся без остатка.
Наибольший общий делитель двух натуральных чисел – наибольшее число из общих делителей данных чисел. Обозначается как НОД.
Например, НОД (12, 24) – это наибольший общий делитель чисел 12 и 24.
Нахождение НОД
Чтобы найти наибольший общий делитель, можно применить один из способов ниже.
Для двух (или небольших) чисел
Пример
Найдем наибольший делитель чисел 18 и 30.
Таким образом, НОД (18, 30) = 6.
Для нескольких (или больших) чисел
Этот метод обычно применяется, если приходится иметь дело с большим числами, или нужно найти НОД для нескольких чисел.
Пример
Найдем НОД (16, 24, 40).
Решение
Разложим эти числа на простые множители.
Для всех трех чисел одинаковыми являются три множителя – это три двойки.
Следовательно, НОД (16, 24, 40) = 2 ⋅ 2 ⋅ 2 = 8.
Наибольший общий делитель
Наибольший общий делитель чисел – это наибольшее число, на которое делятся все заданные числа.
Алгоритм поиска НОД
Вычисление НОД похоже на поиск НОК. Чтобы найти наибольший общий делитель, нужно использовать следующий алгоритм:
Если среди множителей чисел не были найдены одинаковые, числа являются взаимно простыми.
Примеры поиска наибольшего общего делителя
Рассмотрим, как найти НОД с помощью алгоритма на нескольких примерах.
Найдите наибольший общий делитель чисел 420 и 990.
Разложим оба числа на простые множители:
420 = 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7
990 = 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 11
Выпишем все совпадающие множители для обоих чисел и перемножим их:
НОД = 2 ⋅ 3 ⋅ 5 = 30
Найдите наибольший общий делитель чисел 588 и 1820.
Разложим оба числа на простые множители:
588 = 2 ⋅ 2 ⋅ 3 ⋅ 7 ⋅ 7
1820 = 2 ⋅ 2 ⋅ 5 ⋅ 7 ⋅ 13
Выпишем все совпадающие множители для обоих чисел и перемножим их:
НОД = 2 ⋅ 2 ⋅ 7 = 28
Найдите наибольший общий делитель чисел 1000 и 3267.
Разложим оба числа на простые множители:
1000 = 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 5
3267 = 3 ⋅ 3 ⋅ 3 ⋅ 11 ⋅ 11
Совпадающих множителей у этих 2 чисел нет, поэтому они являются взаимно простыми, то есть
Поделитесь статьей с одноклассниками «НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ, алгоритм как найти НОД».
Наибольший общий делитель
| Наибольшее натуральное число, на которое делятся нацело каждое из двух данных натуральных чисел, называют наибольшим общим делителем этих чисел. |
Наибольший общий делитель чисел 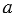

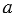

Предварительно разложив числа на простые множители, мы упростим нахождение наибольшего общего делителя многозначных чисел.
Найдем НОД(240; 165).
240 = 2






Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 3

Найдем НОД(2520; 4620).
2 520 = 2 










Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4





Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).
Таким же образом можно найти НОД трех и более чисел.
Чтобы найти НОД нескольких натуральных чисел, надо:
Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.
| Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1. |
Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:
2 520 = 2 3 


Тогда НОД мы можем найти по следующему правилу:
Найдем НОД(2520; 4620):
Поделись с друзьями в социальных сетях:
Наибольший общий делитель (НОД) – определение, примеры и свойства.
В этой статье мы изучим наибольший общий делитель (НОД). Сначала мы введем понятие общего делителя нескольких целых чисел и приведем примеры. Это позволит нам дать определение наибольшего общего делителя двух, а также трех и большего количества, дальше мы введем принятые обозначения, приведем примеры наибольших общих делителей. Наконец, перечислим основные свойства наибольшего общего делителя и представим их доказательства.
Навигация по странице.
Общие делители – определение, примеры
Чтобы подобраться к определению наибольшего общего делителя (кратко НОД), сначала узнаем, что такое общий делитель данных целых чисел.
В статье делители и кратные мы говорили о делителях одного данного целого числа. Сейчас мы будем одновременно рассматривать делители двух, трех и большего количества целых чисел, особо нас будут интересовать одинаковые, то есть, общие делители нескольких чисел.
Дадим определение общего делителя нескольких целых чисел.
Общий делитель нескольких целых чисел – это такое целое число, которое является делителем каждого из данных чисел.
Свойства делимости позволяют утверждать, что числа 1 и −1 являются делителями любого целого числа, следовательно, 1 и −1 всегда являются общими делителями любого набора целых чисел. Следовательно, любой набор целых чисел всегда имеет по крайней мере два общих делителя ( 1 и −1 ).
Можно ограничиться лишь положительными делителями (в этом случае все общие делители тоже будут положительными). Такой подход имеет право на существование, но при этом не следует забывать, что каждое целое число, противоположное положительному делителю, также является делителем данного числа.
Наибольший общий делитель (НОД) – определение, обозначение и примеры
Сейчас и в дальнейшем мы будем подразумевать, что хотя бы одно из данных чисел отлично от нуля. Если все данные числа равны нулю, то их общим делителем является любое целое число, а так как целых чисел бесконечно много, то мы не можем говорить о наибольшем из них. Следовательно, нельзя говорить о наибольшем общем делителе чисел, каждое из которых равно нулю.
Теперь мы можем дать определение наибольшего общего делителя двух чисел.
Наибольший общий делитель двух целых чисел – это наибольшее целое число, делящее два данных целых числа.
Определение наибольшего общего делителя трех и большего количества целых чисел аналогично определению НОД двух чисел.
Наибольший общий делитель трех и большего количества целых чисел – это наибольшее целое число, делящее одновременно все данные числа.
Свойства наибольшего общего делителя, алгоритм Евклида
Наибольший общий делитель обладает рядом характерных результатов, иными словами, рядом свойств. Сейчас мы перечислим основные свойства наибольшего общего делителя (НОД), формулировать их мы будем в виде теорем и сразу приводить доказательства.
Все свойства наибольшего общего делителя мы будем формулировать для положительных целых чисел, при этом будем рассматривать лишь положительные делители этих чисел.
Это свойство НОД напрямую следует из определения наибольшего общего делителя.
Обоснуем это свойство НОД.
Сейчас мы сформулируем и докажем теорему, которая представляет собой алгоритм Евклида. Алгоритм Евклида позволяет находить НОД двух чисел (смотрите нахождение НОД по алгоритму Евклида). Более того алгоритм Евклида позволит нам доказать приведенные ниже свойства наибольшего общего делителя.
Из рассмотренного свойства наибольшего общего делителя следует, что множество общих делителей чисел a и b совпадает с множеством делителей наибольшего общего делителя этих чисел. Это следствие из алгоритма Евклида позволяет найти все общие делители двух чисел как делители НОД этих чисел.
По алгоритму Евклида мы можем записать следующие равенства
Только что доказанное свойство наибольшего общего делителя лежит в основе приведения обыкновенных дробей к несократимому виду.
Сейчас озвучим свойство НОД, которое сводит задачу нахождения наибольшего общего делителя трех и большего количества чисел к последовательному отысканию НОД двух чисел.
На этом закончим обзор основных свойств наибольшего общего делителя.