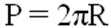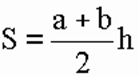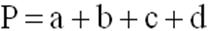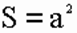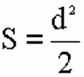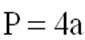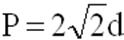Как найти периметр круга
Как найти периметр круга
Способы расчета периметра круга и длины окружности
Периметр круга — что это, определение
Круг — это геометрическое множество точек на плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит заданного неотрицательного числа.
Окружность — замкнутая кривая на плоскости, все точки которой равноудалены от центра окружности.
Эти определения плотно связаны друг с другом. Круг — это часть плоскости, ограниченная окружностью. Окружность — это граница круга.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
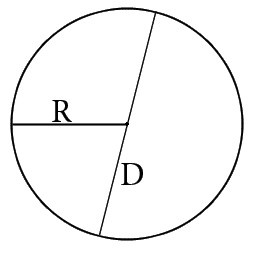
Радиус — расстояние от центра окружности до любой ее точки. Это отрезок, который соединяет центр круга с его границей.
Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Он равен двум радиусам.
Периметр — это длина окружности, ограничивающей круг.
Понятия «периметр круга» и «длина окружности» считаются синонимичными.
Как рассчитать периметр круга или длину окружности
Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно \(\pi=3,14159. \)
Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:
Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.
Через радиус
Длину окружности L можно найти по формуле через радиус:
где \(\pi \) — число Пи, R — радиус.
Через диаметр
Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:
Примеры решения задач
Задача
Каков периметр круга, если его радиус равен 0,5 см?
Решение
Задача
Какова длина окружности, если ее диаметр равен 2 см?
Онлайн калькулятор периметра круга. Как узнать длину круга, окружности.
Что такое длина окружности или периметр круга и как ее вычислить? Для того что бы это понять нам необходимо разобраться с тем чему равна длина окружности.
Длина окружности всегда равна числу π (Пи)
Давайте с вами разберемся что же такое число пи. Π – это постоянная величина равная 3,14159265…
Но обычно Пи приравнивают к 3,14 и это число используют для математических расчетов в которых не требуется оооооооооочень точное вычисление.
Откуда же взялось это число и почему оно всегда равно одному и тому же? Для того что бы нам понять что такое число пи нам необходимо разобрать простой пример. Допустим у нас имеется окружность с диаметром равному единицы, так вот длина окружности — это число «пи».
Иными словами Пи ≈ 3,14 диаметрам круга или окружности.
Теперь зная и понимая что такое π мы можем с легкостью высчитать периметр или длину окружности которая равна
P = D * π
или
P = 2 πR
где R –это радиус, а D – это диаметр
Периметр круга — онлайн калькулятор
Круг – двухмерная геометрическая фигура, границей которого по определению является окружность. Центром фигуры становится зафиксированная на плоскости точка, равноудаленная от любого места на замкнутой кривой. Прямая линия, соединяющая центр с каждой точкой окружности называется радиусом — R. Рассчитать длину окружности можно по одной из известных величин – радиусу или диаметру.
Достоверная формула для определения периметра и длины круга была выведена древнегреческим математиком Архимедом Сиракузским в III веке до нашей эры. Ученый первый обнаружил закономерность в соотношении общей длины тела к его диаметру, и предложил обозначить константой ∏. Абстрактное число было равно 3,14159265359 … и до бесконечности. Голландский математик Лудольф ван Цейлен рассчитал и ограничил ∏ до 32 знаков после запятой. Константа стала основой для современной формулы вычисления периметра и длины окружности через радиус.
В калькуляторе периметра круга используется классический принцип расчета:
Для вычисления параметров круга, достаточно вставить в строку известное значение радиуса и получить результат.
Примеры вычисления
С помощью удобного инструмента можно быстро и просто найти длину любого круглого тела. Например, чтобы узнать периметр экватора Земли, необходимо подставить значения в поля калькулятора. Согласно географическим данным, экваториальный радиус составляет 6 378.1 километра:
Значение полностью соответствует официально установленной протяженности экватора.
Расчет может применяться не только для определения абстрактных величин. В повседневной жизни формула является одной из самых востребованных. Например, чтобы сделать удачную покупку ювелирного кольца в интернет-магазине, не обязательно примерять десятки изделий для уточнения размера в традиционном бутике. Достаточно сантиметром измерить диаметр старого украшения, и разделить значение на 2. Например, если радиус кольца 9 мм, то длина равна:
Круг – одно из самых распространенных геометрических тел в повседневной жизни. Целая фигура и её отдельные части используются во всех сферах промышленности и народного хозяйства, от крупномасштабного строительства до производства посуды. Необходимость быстро вычислить параметры окружности возникает часто. Онлайн калькулятор периметра круга можно использовать для решения элементарных математических и бытовых задач.
Формула периметра круга
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE
= 2 \cdot \pi \cdot r \]
\[ \LARGE
= \pi \cdot d \]
\( P \) – периметр (длина окружности).
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки.
По формуле расстояния между двумя точками в заданной нами системе координат, получим:
Таким образом, мы и получаем, что уравнение (1) является уравнением окружности в декартовой системе координат.
Длина окружности (периметр круга)
Тогда, будем получать, что
Получаем, что отношение \( \frac<ρ><ρ'>=\frac<2τ> <2τ'>\) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \( n→∞ \) ), будем получать равенство:
Из последних двух равенств получим, что
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
Периметры фигур. Периметр круга. Длина окружности.
центром круга, не превосходит данного неотрицательного числа, именуемого радиусом круга.
Если радиус соответствует нулю, то круг становится точкой.
Границей круга, сообразно определению, есть окружность.
(центра), лежащей в той же плоскости, что и кривая. Еще круг можно найти как часть плоскости,
Отношение длины окружности к её диаметру идентично для всех окружностей. Это отношение и есть
трансцендентное число, означаемое буквой греческого алфавита пи:
π = 3.14159.
У периметра та же размерность величин, что и длина.
Связанные с кругом обозначения:
соединяет две точки границы круга и содержащий его центр.
ограничена дугой и двумя радиусами, соединяющими концы дуги с центром круга.
круг) можно найти по формуле:
где R – радиус круга.
при заданном периметре. Либо обладающей наименьшим периметром при данной площади.
Периметр круга или длина окружности
Отношение длины окружности к её диаметру одинаково для всех окружностей. Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: π = 3.14159.
Формула для вычисления длины окружности
Остались вопросы?
Здесь вы найдете ответы.
Периметр круга, также называемый длиной окружности, представляет собой число, получаемое в результате умножения его радиуса на два Пи, либо путем перемножения между собой его диаметра и числа Пи. Формула, используемая для расчета периметра круга, представлена в следующем виде:
d — диаметр круга,
π — это величина, которая является константой, выражающей отношение длины окружности к ее диаметру. Ее значение постоянно равно 3,14.
Под определением «расчет периметра круга» подразумевается процедура, направленная на установление длины окружности, ограничивающей его. В случае, когда длина радиуса круга является известной величиной, длина окружности может быть вычислена с применением приведенной ниже формулы:
в ней радиус круга обозначен как r.
Под радиусом окружности подразумевается отрезок, который соединяет центр окружности с любой из множества точек, находящихся на ней.
Значение длины окружности также может быть вычислено, если диаметр круга известен. С этой целью нужно произвести умножение ее диаметра (d) на число Пи (π). В этом случае следует пользоваться формулой:
Если раскрывать такое понятие, как «диаметр окружности», то стоит отметить, что им является отрезок, проходящий через ее центр и соединяющий две любые точки этой окружности.
Число Пи (π) является математической постоянной, рассчитываемой как отношение длины окружности к величине ее диаметра. Оно равно 3,14.
Периметр круга представлен величиной, равной длине окружности, которая ограничивает его. Это значит, что данная величина может быть рассчитана по формуле:
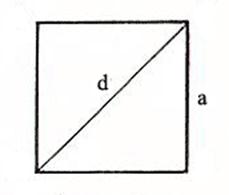
В описанном в задании случае сторона квадрата, в который вписан круг, выступает в роли его диаметра. Это дает основания для расчета периметра круга следующим образом:
P = 20 * 3,14 = 62,8 см.
Ответ: Периметр круга, который вписан в квадрат, имеющий сторону 20 см, равен 62,8 см.
Длина окружности представляет собой произведение, полученное в результате умножения ее диаметра (D) на число Пи (π): L = π*D = 30*π. В данном случае длина окружности – это ее периметр. Из этого следует, что диаметр окружности D равен 30.
Решение поставленной задачи следует начинать с расчета длины первого круга. Для этого число Пи, равное 3,14, нужно умножить на два, а затем полученное значение также умножить на длину радиуса круга. Формула, используемая при этом, выглядит так:
Принимая во внимание тот факт, что диаметр второго круга в три раза превышает диаметр первого из них, то можно с уверенностью говорить о том, что его радиус также будет троекратно превышать радиус первого круга. Это означает, что формула, применяемая для расчета длины второго круга, будет выглядеть так:
Подставив в формулу величины, приведенные в задании, можно получить следующий результат:
Ответ: Длина второго круга равна 10,8 дм.
В задании указано, что площадь круга составляет 25 дм.кв. Это значит, что произведение числа Пи и радиуса круга, возведенного в квадрат, равно 25 дм.кв. Из этого следует, что радиус данного круга равен величине, полученной в результате деления 5 на квадратный корень из числа Пи (r = 5/√π). На основании этого можно сделать вывод о том, что длина круга может быть высчитана по следующей формуле:
В результате получается число, приблизительно равное 17,72 дм.
Ответ: Длина круга равна примерно 17,72 дм.
Формула, которая предназначена для расчета длины круга выглядит так:
По сути, это произведение числа Пи и диаметра круга.
В случае, который описан в задании, длина круга равна 40 Пи см, а это значит следующее:
Число Пи сокращается в обеих частях получившегося уравнения, и в итоге получается, что диаметр круга равен 40 см:
Располагая информацией о длине круга, можно вычислить его радиус. Это можно сделать на основании приведенной ниже формулы:
r = L/(2*π) = 19,1:(2*3,14)=3 м.
Таким образом удалось установить, что радиус круга равен 3 м.
Теперь, зная длину радиуса круга, можно произвести расчет его площади по формуле:
π*r2 = 3,14*3*3 = 28,26 м².
Ответ: Площадь круга равна 28,26 м. кв.
При расчете таких показателей, как площадь и диаметр круга, следует использовать его длину. Она обозначается как с и равна 26 см. Согласно формуле вычисления длины круга, она равна произведению 2 Пи и радиуса круга, либо Пи и его диаметра (с=2πr или c=πd). Исходя из этого, диаметр круга можно найти путем деления длины круга на число Пи:
В данном случае d=26/3,14=8,28 см.
Теперь, когда все необходимые для вычисления площади круга параметры известны, можно перейти непосредственно к ее расчету:
В целях выполнения вычисления длины окружности по радиусу (r) следует произвести умножение величины, выражающей его значение, на два Пи. При этом используется следующая формула:
При расчете длины окружности используется формула, которая имеет следующий вид:
Согласно данной формуле, для того чтобы вычислить, чему равна длина окружности, необходимо произвести умножение ее диаметра на число Пи, равное 3,14.
Подставляя в приведенную выше формулу числа, указанные в задании, можно произвести расчет длины окружности, которая будет равна:
Ответ: Длина окружности диаметром в 4 м равна 12,56 м.
Площадь круга высчитывается при помощи формулы:
В данном конкретном случае указано, что площадь равна Пи м. кв. (S=π).
Исходя из вышеизложенного, можно произвести расчет величины радиуса, которая будет равна отношению корня квадратного из числа Пи и числа Пи:
Теперь можно приступить к вычислению непосредственно длины окружности, используя следующую формулу:
C = 2πR = 2π⋅1 = 2π.
Ответ: Длина окружности круга площадью Пи кв. м равна 2 Пи.
При расчете длины круга следует брать за основу формулу, которая предполагает умножения числа Пи, равного 3,14, на диаметр окружности круга. Если говорить о конкретном случае, упомянутом в задании, то расчет длины окружности будет выглядеть следующим образом:
L=16 см*3,14=50,24 см.
Ответ: Длина круга, диаметр которого равен 16 см, составляет 50,24 см.
Длина окружности рассчитывается с применением формулы, составными элементами которой являются диаметр (d) и число ПИ, равное 3,14. Для вычисления длины окружности упомянутые величины следует перемножить:
Ответ: Круг диаметром 5,8 дм имеет длину окружности, равную 18,212 дм.
Если диаметр круга является известной величиной, то ее вполне достаточно, для того чтобы произвести расчет длины данного круга. С этой целью следует использовать формулу, приведенную ниже:
Если подставить в данную формулу величины, заданные в вопросе, то можно получить следующий результат:
l = 3,14*18 = 56,52 м.
Ответ: Длина круга, диаметр которого равен 18 м, составляет 56,52 м.
Как найти периметр круга
Начнем с формулы периметра круга.
Формула периметра круга.
Формула круга может выражаться через радиус.
Формула периметра круга через радиус.
Формула периметра круга через диаметр.
Также можно выразить периметр круга через диаметр. Поскольку мы занем, что диаметр = 2 радиуса, то в верхней формуле заменяем 2R на D.
Формула периметра круга через диаметр.
Задача : найдите периметр круга если известен радиус.
Найдите периметр круга, если радиус круга равен 5см.
Вместо буквы R ставим наш радиус, и далее нам все нужно перемножить, на калькуляторе
Найденный периметр круга равен 31.4 см.
Задача : найдите диаметр круга, если известен периметр круга
Найдите диаметр круга, если известен периметр круга, который равен 94.2см.
Для того, чтобы найти периметр круга, нам нужно из формулы выразить диаметр через периметр, что будет выглядеть так :
Далее нам остается заменить букву P на значение из условия задачи 94.2см.
Если периметр круга равен 94.2см, то искомый диаметр равен 30см.
Периметр круга онлайн
Для того, чтобы найти периметр круга онлайн, нужно заполнить соответствующее поле :
В поле нужно напечатать значение радиуса круга.
Периметры фигур. Периметр круга. Длина окружности.
центром круга, не превосходит данного неотрицательного числа, именуемого радиусом круга.
Если радиус соответствует нулю, то круг становится точкой.
Границей круга, сообразно определению, есть окружность.
(центра), лежащей в той же плоскости, что и кривая. Еще круг можно найти как часть плоскости,
Отношение длины окружности к её диаметру идентично для всех окружностей. Это отношение и есть
трансцендентное число, означаемое буквой греческого алфавита пи:
π = 3.14159.
У периметра та же размерность величин, что и длина.
Связанные с кругом обозначения:
соединяет две точки границы круга и содержащий его центр.
ограничена дугой и двумя радиусами, соединяющими концы дуги с центром круга.
круг) можно найти по формуле:
где R – радиус круга.
при заданном периметре. Либо обладающей наименьшим периметром при данной площади.
Как найти периметр круга
Вы будете перенаправлены на Автор24
Очевидно, что границей любого круга является окружность. Поэтому понятие периметра круга совпадает с таким понятием, как длина окружности. Поэтому вначале вспомним, что является окружностью, и какие понятия с ней связаны.
Понятие окружности
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки (Рис. 1).
По формуле расстояния между двумя точками в заданной нами системе координат, получим:
Готовые работы на аналогичную тему
Таким образом, мы и получаем, что уравнение (1) является уравнением окружности в декартовой системе координат.
Длина окружности (периметр круга)
Тогда, будем получать, что
Из последних двух равенств получим, что
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
Пример задач
По формуле периметра круга, получим, что
По теореме Пифагора, гипотенуза равняется
Периметр круга, по формуле, равняется
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 21.07.2022
Онлайн калькулятор. Длина окружности. Периметр круга
Используя этот онлайн калькулятор, вы сможете найти длину окружности.
Воспользовавшись онлайн калькулятором для вычисления длины окружности (периметра круга), вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти длину окружности
Выберите известную величину
Ввод данных в калькулятор для вычисления периметрa окружности
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины.
Теория. Длина окружности
Формулы для вычисления длины окружности.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение длины окружности: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать длину/периметр окружности (круга) и разберем примеры решения задач.
Формула вычисления длины/периметра
1. Через радиус
Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π :
C = 2 * π * r
Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.
2. Через диаметр
Периметр/длина окружности считается как произведение ее диаметра на число π :
C = π * d
Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.
Примечание: в расчетах значение числа π округляется до 3,14.
Примеры задач
Задание 1
Найдите длину окружности, если ее радиус равен 12 см.
Решение:
Воспользуемся первой формулой, в которой участвует значение радиуса: C = 2 * 3,14 * 12 см = 75,36 см.
Задание 2
Найдите периметр круга, если ее диаметр составляет 15 см.
Решение:
Применим формулу, в которой используется диаметр: C = 3,14 * 15 см = 47,1 см.
Онлайн калькулятор. Длина окружности. Периметр круга.
Используя этот онлайн калькулятор, вы сможете найти длину окружности.
Воспользовавшись онлайн калькулятором для вычисления длины окружности (периметра круга), вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Калькулятор для вычисления периметрa окружности
Выберите известную величину
Ввод данных в калькулятор для вычисления периметрa окружности
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины.
Теория. Длина окружности
Формулы для вычисления длины окружности.
Периметры фигур. Периметр круга. Длина окружности.
центром круга, не превосходит данного неотрицательного числа, именуемого радиусом круга.
Если радиус соответствует нулю, то круг становится точкой.
Границей круга, сообразно определению, есть окружность.
(центра), лежащей в той же плоскости, что и кривая. Еще круг можно найти как часть плоскости,
Отношение длины окружности к её диаметру идентично для всех окружностей. Это отношение и есть
трансцендентное число, означаемое буквой греческого алфавита пи:
π = 3.14159.
У периметра та же размерность величин, что и длина.
Связанные с кругом обозначения:
соединяет две точки границы круга и содержащий его центр.
ограничена дугой и двумя радиусами, соединяющими концы дуги с центром круга.
круг) можно найти по формуле:
где R – радиус круга.
при заданном периметре. Либо обладающей наименьшим периметром при данной площади.
Вычислить длину окружности по диаметру, онлайн калькулятор
Нормальное ускорение при движении по окружности, онлайн расчет
Через диагональ
Формула для нахождения длины окружности через диагональ:
Как рассчитать диаметр по длине,площади или радиусу окружности формула
Найти какой диаметр окружности можно в нашем онлайн калькуляторе даже не зная формул, просто введите цифры и получите результат
Условные обозначения в формулах
Формула расчёта по диаметру
Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
Вычисление диаметра окружности с использованием радиуса, длины окружности или площади круга
Вычисление диаметра окружности из чертежа окружности
Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
Периметры фигур
Формула вычисления длины/периметра
1. Через радиус
Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π :
C = 2 * π * r
Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.
2. Через диаметр
Периметр/длина окружности считается как произведение ее диаметра на число π :
C = π * d
Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.
Примечание: в расчетах значение числа π округляется до 3,14.
Вычисление площади круга и длины окружности, когда радиус или диаметр выражены переменными
Уравнение окружности
r 2 = ( x – a ) 2 + ( y – b ) 2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:
| < | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Основные свойства касательных к окружности
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
Через длину стороны
Формула для нахождения длины окружности через радиус:
Центростремительное ускорение при движении по окружности, онлайн расчет
Найти длину окружности
Вводить можно числа или дроби (-2.4, 5/7, …).
Длина окружности
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см).
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м).
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:
следовательно, радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м). |
| 2 · 3,14 | 6,28 |
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2 ).
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Решение: Сначала найдём радиус круга, разделив его диаметр на 2:
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2 ).
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 · | 7 2 | = 3,14 · | 49 | = |
| 4 | 4 | 4 |
| = | 153,86 | = 38,465 (см 2 ). |
| 4 |
Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
Формула периметра круга (длины окружности)
1) Периметр круга равен произведению радиуса на два пи (3.1415).
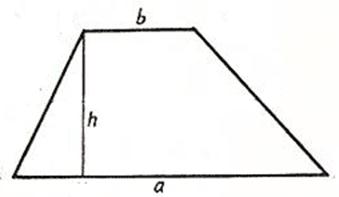
Формула площади трапеции:
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
См. также: Программа для расчета площади трапеции.
Формула периметра трапеции:
1) Периметр трапеции равен сумме 4-х её сторон (a, b, c, d).
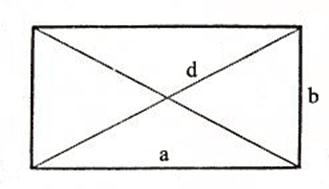
Квадрат — правильный четырёхугольник, у которого все стороны и углы равны между собой. Может быть определён как прямоугольник, у которого две смежные стороны равны между собой, или как ромб, у которого все углы прямые. У квадрата есть две диагонали, соединяющие несмежные вершины.
Формулы площади квадрата:
1) Площадь квадрата равна квадрату длины его стороны (a).
2) Площадь квадрата равна половине квадрата длины его диагонали (d).
См. также: Программа для расчета площади квадрата.
Формулы периметра квадрата:
1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).
2) Периметр квадрата равен произведению длины его диагонали на два корня из двух.
Онлайн калькулятор. Длина окружности. Периметр круга
Онлайн калькулятор
Для того чтобы рассчитать периметр круга (длину граничной окружности) вам необходимо знать его радиус или диаметр, либо его площадь.
Ликбез: Круг — часть плоскости, лежащая внутри окружности.
Как посчитать периметр круга зная радиус
Пример
Если радиус круга равен 0.5 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная диаметр
Каков периметр круга (L) если его диаметр d?
Пример
Если диаметр круга d = 1 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Пример задач
Получи деньги за свои студенческие работы Курсовые, рефераты или другие работы
Видео
Как рассчитать периметр круга или длину окружности
Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно \(\pi=3,14159…\)
Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:
Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.
Через радиус
Длину окружности L можно найти по формуле через радиус:
где \(\pi \) — число Пи, R — радиус.
Через диаметр
Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:
Примеры задач
Задание 1 Найдите длину окружности, если ее радиус равен 12 см.
Решение: Воспользуемся первой формулой, в которой участвует значение радиуса: C = 2 * 3,14 * 12 см = 75,36 см.
Задание 2 Найдите периметр круга, если ее диаметр составляет 15 см.
Решение: Применим формулу, в которой используется диаметр: C = 3,14 * 15 см = 47,1 см.
Как найти периметр окружности зная диаметр. Как найти и чему будет равна длина окружности. Основные формулы для вычислений
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE
= 2 \cdot \pi \cdot r \]
\[ \LARGE
= \pi \cdot d \]
\(P \) – периметр (длина окружности).
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки.
По формуле расстояния между двумя точками в заданной нами системе координат, получим:
Таким образом, мы и получаем, что уравнение (1) является уравнением окружности в декартовой системе координат.
Длина окружности (периметр круга)
Тогда, будем получать, что
Получаем, что отношение \(\frac<ρ><ρ">=\frac<2τ> <2τ">\) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \) ), будем получать равенство:
Из последних двух равенств получим, что
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Рассчитать площадь шара
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Основные понятия и определения
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Нахождение длины окружности и её площади
Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. В школьной математике она считается заранее известной табличной величиной, равной 3,14!
Теперь перепишем предыдущую формулу, чтобы найти длину окружности через её диаметр, помня, в чём состоит его разница по отношению к радиусу. Получится: l = 2*П*r = 2*r*П = П*d.
Из курса математики известно, что формула, описывающая площадь окружности, имеет вид: s = П*r^2.
Теперь перепишем предыдущую формулу, чтобы найти площадь окружности через её диаметр. Получим,
Определение длины радиуса и диаметра
Важно! Прежде всего узнаем, как измерить диаметр. Это очень просто — проводим любой радиус, продлеваем его в противоположную сторону до пересечения с дугой. Циркулем отмеряем полученное расстояние и с помощью любого метрического инструмента узнаем искомое!
Ответим на вопрос, как узнать диаметр окружности, зная её длину. Для этого выразим его из формулы l = П*d. Получим d = l/П.
Мы уже знаем как из длины окружности можно найти её диаметр, точно также найдём и радиус.
l = 2*П*r, отсюда r = l/2*П. Вообще, чтобы узнать радиус, его нужно выражать через диаметр и наоборот.
Решение типовых заданий
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски.
какой то “куцый” обзор… как будто спешили куда то
Ответ здесь
Вопросы и ответы обо всём на свете
Вопросы Доставка цветов. 7 причин заказать доставку цветов
Вопросы Достоинства обучения онлайн
Вопросы Дезинсекция помещений
Вопросы Что такое VIP-бонус в азартной игре?
Вопросы 7 причин ежедневно пить красное вино
Вопросы Может ли человек летать?
Вопросы Преимущества отдыха в Сочи
Вопросы Диваны-реклайнеры — преимущества, особенности
Как найти периметр круга?
Как найти периметр круга?
Поделиться «Как найти периметр круга?»
d — диаметр круга
Чтобы найти периметр круга, необходимо знать его диаметр.
Прежде всего, давайте уясним себе, что такое круг. Круг это часть плоскости, которая ограничена окружностью. Следовательно периметром круга будет являться длина этой окружности.
Чтобы найти длину окружности, необходимо знать ее диаметр.
Еще древнегреческие математики обратили внимание на тот факт, что отношение длины окружности к ее диаметру, есть величина постоянная и не зависит от диаметра окружности. Они назвали величину этого отношения «Число ПИ». Число это уникальное. современные математики при помощи мощных компьютеров вычислили число Пи с точностью до нескольких сот миллиардов знаков после запятой, но не смогли найти повторяемости порядка цифр или какой либо цикличности.
Начало числа Пи выглядит таким образом:
Таким образом, чтобы вычислить длину окружности, необходимо величину ее диаметра умножить на число Пи.
Давайте для примера найдем периметр круга, если известно, что его диаметр равен пяти сантиметрам.
Аналогичным образом можно вычислить периметр круга любого диаметра.
Если произвести обратное действие, то можно по периметру круга вычислить его диаметр, если периметр круга известен.
Как найти периметр трубы
Как найти периметр круга!? Формула периметра круга. Как на калькуляторе можно найти периметр круга!?
Наиболее часто встречающиеся словосочетания с периметром круга — радиус, диаметр, онлайн, калькулятор — разберем все темы!
О периметре круга
Начнем с формулы периметра круга.
Формула круга может выражаться через радиус.
Формула периметра круга через радиус
Где P — периметр круга,
R — радиус круга.
Формула периметра круга через диаметр
Также можно выразить периметр круга через диаметр. Поскольку мы занем, что диаметр = 2 радиуса, то в верхней формуле заменяем 2R на D.
Где P — периметр круга,
D — диаметр круга.
Задача : найдите периметр круга если известен радиус
Найдите периметр круга, если радиус круга равен 5см.
Такого рода задачки — это даже не задачки, это всего лишь одно действие с подстановкой данных.
Вместо буквы R ставим наш радиус, и далее нам все нужно перемножить, на калькуляторе
P = 2πR = 2π5 = 2 * 3.14 * 5 = 31.4 Ответ:
Найденный периметр круга равен 31.4 см.
Задача : найдите диаметр круга, если известен периметр круга
Найдите диаметр круга, если известен периметр круга, который равен 94.2см.
Для того, чтобы найти периметр круга, нам нужно из формулы выразить диаметр через периметр, что будет выглядеть так :
Далее нам остается заменить букву P на значение из условия задачи 94.2см.
Если периметр круга равен 94.2см, то искомый диаметр равен 30см.
Периметр круга онлайн
Для того, чтобы найти периметр круга онлайн, нужно заполнить соответствующее поле :
В поле нужно напечатать значение радиуса круга.
Нажмите найти периметр круга.
Периметр трубы по диаметру
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Онлайн калькулятор расчёта длины окружности (периметр круга)
Решение
Теория
Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка.
Органза с вышивкой турция
Диаметр окружности — это прямой отрезок соединяющий две точки на границе окружности и проходящий через её центр.
Радиус окружности — это прямой отрезок проведённый от центра до границы окружности.
Формула длины окружности
Чтобы посчитать периметр круга (длину окружности), необходимо знать размер диаметра или радиуса.
Онлайн калькулятор
Для того чтобы рассчитать периметр круга (длину граничной окружности) вам необходимо знать его радиус или диаметр, либо его площадь.
Ликбез: Круг — часть плоскости, лежащая внутри окружности.
Как посчитать периметр круга зная радиус
Чему равен периметр круга если
Формула
Пример
Если радиус круга равен 0.5 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная диаметр
Чему равен периметр круга если
Каков периметр круга (L) если его диаметр d?
Формула
Пример
Если диаметр круга d = 1 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная его площадь
Чему равен периметр круга если
Каков периметр круга (L) если его площадь S?
Формула
Пример
Сегмент круга
Сегмент круга
Формулы вычисления параметров сегмента
Длина хорды:
Высота сегмента: Точность вычисления
Знаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Знаков после запятой: 2
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Как рассчитать длину окружности, если не указан диаметр и радиус круга
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда.
С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты, устройства и механизмы, посуда и мебель имеют круглую форму.
Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга. …
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
Это интересно: как переводить градусы в радианы?
В пределах окружности имеются точки Х такие, что не изменяется и не равняется единице отношение АХ/ВХ.
В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга.
На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда. Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками, проходящее через центр фигуры.
Это интересно: какой четырёхугольник называется квадратом?
Как определить полезный объём трубы
Срок службы системы отопления зависит от того, правильно ли рассчитан полезный объём трубы. Мельчайшие погрешности в вычислениях создают в сети избыточное давление, которое приводит к преждевременному износу коммуникаций, а при неоправданно низком давлении отопление не будет нормально функционировать.
Отправной точкой для расчёта полезного объёма трубы становится определение её внутреннего диаметра. Вычтите из значения наружного диаметра отрезка удвоенную толщину стенок – и вы узнаете, каков внутренний диаметр трубопровода. Учтите, что большинство производителей по умолчанию указывают в технической документации и накладных значение наружного диаметра труб.
Зная внутренний диаметр проката, найти радиус проще простого – разделите величину наружного диаметра на два, а затем рассчитайте площадь сечения трубы по формуле, знакомой со школьных лет: S = π*r2, где S – площадь сечения трубы; π = 3,14; r – радиус изделия.
Все расчётные параметры сводят к общим метрическим единицам измерений; в нашем случае сантиметры и дюймы необходимо перевести в метры.
Полезный объём трубы рассчитывается по другой формуле: V = S*L, где V – полезный объём трубы; S – площадь сечения; L – протяжённость сети на участках трубопровода с одинаковым диаметром.
Расчёт параметров теплообменника «труба в трубе»
Теплообменный аппарат «труба в трубе» сконструирован из нескольких звеньев, которые располагают друг над другом и соединяют специальными креплениями. Каждое звено состоит из двух труб, вставленных одна в другую. Корпус внешней трубы последовательно соединяется с соседними элементами, а внутренние трубы соединяются друг с другом съёмными калачами.
Теплообмен осуществляется в результате прямого или опосредованного контакта двух сред. Нагреваемая среда циркулирует во внутренней трубе, а греющий пар – по каналу, который образуют стенки внутренней и внешней труб. Небольшое сечение внутренней трубы поддерживает высокую скорость теплоносителя. Конструкция «труба в трубе» обладает тремя важными преимуществами:
Для расчёта параметров теплообменника составляют уравнение теплового баланса, в которое закладывают множество переменных:
В ходе монтажа решающее значение приобретают такие показатели, как площадь и геометрические характеристики теплообменника и основных узлов, экономическая эффективность системы, потери напора и параметры теплоизоляции.
Если вам трудно разобраться во всех тонкостях вычислений, поручите эту задачу профессионалам: многие инженерные компании оказывают услуги проектирования теплообменников и отопительных систем с последующим техническим сопровождением проектов. В идеале проектирование, монтажные работы и сервисное обслуживание сетей отопления должна выполнять одна и та же организация, хорошо знакомая со спецификой проекта.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Это интересно: что такое горизонтально, что означает слово горизонталь?
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус.
Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Производство металлопластиковых труб
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Это интересно: формулировка и доказательство признаков параллелограмма.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
Длина окружности
), или умножив на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно,C
, — диаметр окружности, — радиус окружности.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода.
Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг, большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах.
Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Перед нами стоит вопрос: «Как рассчитать длину окружности?»
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Что такое полимерное покрытие трубы стальной
Еще в Древнем Вавилоне, почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали числом «Пи», именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Диаметр окружности представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге прямоугольный треугольник, где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их – получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Способ 3: как рассчитать длину окружности подручными средствами
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами.
Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки.
Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
Перед нами задача: как рассчитать длину окружности, если не даны никакие цифровые значения, кроме самого круга. Запоминаем алгоритм:
( 2 оценки, среднее 4.5 из 5 )
Калькулятор вычисления периметра и площади геометрических фигур
Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.
Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.
Окружность — это множество точек на плоскости, которые равноудалены от центра на некоторое расстояние, называемое радиусом. Многие считают круг и окружность синонимами, однако это не так.
Круг — это часть плоскости, ограниченная окружностью. Вы можете отыскать периметр и площадь круга, но у окружности найти можно только длину, так как она представляет собой кривую, не имеющую площади.
Длина окружности или периметр круга находятся по простой формуле:
Круги часто встречаются в реальной жизни. В основном это основания цилиндрических и конических деталей, а также просто круглые поверхности, например, круглые столики, диски, грампластинки или катушки. Вид окружности имеют колеса, обручи или кольца.
В трехмерной реальности окружность превращается в сферу, а круг — в шар. Форму этих геометрических тел имеют многие реальные и природные объекты. Благодаря своей эффективности круг охватывает максимальную площадь при минимальном периметре.
Именно поэтому форму шара имеют капли, снежные комья, метеориты или планеты.
Треугольник
Треугольник — первая гармоничная фигура на плоскости, ограниченная тремя отрезками. Свойства треугольника известны людям с античных времен: изучение фигуры стартовало в Древнем Египте и не завершено до сих пор.
Огромный вклад в изучение свойств фигуры внесли Евклид, Эйлер и Лобачевский, но даже сегодня продолжается работа над поиском замечательных точек треугольника, которых на данный момент найдено более 6 тысяч.
Для определения периметра фигуры достаточно сложить длины всех сторон треугольника по формуле:
Треугольники не слишком распространены в реальной повседневности. В природе они практически не встречаются, за исключением кристаллических решеток некоторых молекул или формы ушей у рыси. А вот в технике, геометрии и прикладных науках треугольник — царь и бог. Наибольшее применение находит следующий тип фигуры.
Прямоугольный треугольник
Прямоугольный треугольник — особая вариация фигуры, у которой две стороны обязательно образуют прямой угол. Эти стороны называются катетами, а противолежащая им сторона — гипотенузой.
Соотношение катетов и гипотенузы лежит в основе евклидовой геометрии — эти соотношения определяются теоремой Пифагора.
Изучение свойств прямоугольного треугольника положило начало одному из важных разделов математики — тригонометрии, которая используется в самых разных прикладных сферах от компьютерных игр до океанографии.
Формулы для вычисления периметра и площади прямоугольного треугольника ничем не отличаются от формул для обычных вариаций данной фигуры или вытекают из них.
Трапеция
Трапеция, как и слово трапеза, по-гречески означают «стол». Это плоская фигура, ограниченная четырьмя прямыми, две из которых параллельны, а две — нет. По сути, это выпуклый четырехугольник, поэтому параллелограмм и прямоугольник считаются частными случаями трапеции. В общем случае все стороны трапеции имеют разную длину, и для вычисления периметра используется формула:
Трапеция очень часто встречается в рукотворном мире. Грани многих предметов имеют вид этого четырехугольника, а буквально трапецеидальную форму имеют такие объекты как автомобильные окна, паруса, скаты крыш или юбки.
Параллелограмм
Параллелограмм — это элегантный четырехугольник, пары сторон которого параллельны друг другу.
Любой четырехугольник становится параллелограммом, если его противолежащие стороны параллельны, диагонали в точке пересечения разделяются пополам, а противоположные углы равны.
Для вычисления периметра параллелограмма используется простая формула, которая иллюстрирует сумму попарно равных сторон:
Параллелограммы часто встречаются в реальной жизни: это грани многих призматических объектов, очертания полей, спортивных площадок или клумб.
Форму параллелограммов имеют практически все отделочные материалы: плитка, кафель, гипсокартон, паркет.
Такое разнообразие обусловлено тем, что частными случаями параллелограмма являются прямоугольник, ромб и квадрат, формулы для определения периметров и площадей которых аналогичны или выводятся из теоремы Пифагора.
Частные случаи
Ромб — четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.
Прямоугольник — это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.
Квадрат — это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.
Многоугольник
Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:
И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:
Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.
Примеры из реальной жизни
Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.
Покраска забора
Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр.
Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов.
Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Отделка бахромой
Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:
Таким образом, нам понадобится 4 м бахромы для отделки платка.
Заключение
Плоские фигуры составляют реальный мир вокруг.
Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни.
И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
Формула периметра круга
Определение круга часто звучит, как часть плоскости, которая ограничена окружностью.
Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы.
Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415.
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(
Длина окружности (периметр круга)
Как мы знаем, сторона вписанного в окружность правильного ( n ) – угольника равняется
Формулы периметраМатематика Тригонометрия Формулы Геометрия ТеорияБольше интересного в телеграм @calcsbox
Найти периметр окружности радиуса ( r = 10 )см.
Периметр окружности равен ( P = 20 pi) см или (P approx 62,8 ) см.
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Калькулятор периметра треугольника онлайн
Предлагаем опробовать самый универсальный
лучший калькулятор периметра треугольника онлайн
на просторах Интернета. Наш
калькулятор периметра треугольника онлайн
не только поможет Вам найти
несколькими способами
в зависимости от известных данных, но и покажет
подробное решение
калькулятор периметра треугольника онлайн
удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений., представленный на нашем сайте, является подразделом
онлайн калькулятора периметра геометрических фигур
. Именно поэтому Вы можете не только
задать точность расчетов
удобной навигации
онлайн калькулятора
, без сверхусилий перейти к расчету любой из нижеперечисленных геометрических фигур: прямоугольника, квадрата, параллелограмма, ромба, трапеции, круга, эллипса, сектора круга, правильного многоугольника.
Также Вы можете буквально в два клика перейти в
онлайн калькулятор площади геометрических фигур
также несколькими способами
подробным решением
– это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. При этом точки называются
вершинами треугольника
, а отрезки — его сторонами.
Стороны треугольника
вершинах треугольника
три угла, поэтому
треугольник
можно также определить как
многоугольник
, у которого имеется ровно три угла.
Треугольник
является одной из важнейших
геометрических фигур
, повсеместно используемых в науке и технике, поэтому глубокое исследование его свойств проводилось начиная с глубокой древности. Во всяком
треугольнике
против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы. Каждый
внешний
равен разности между 180° и соответствующим внутренним углом. Для внешнего угла также имеет место теорема, согласно с которой внешний угол равен сумме двух других внутренних углов, с ним не смежных.
С помощью данного
калькулятора периметра треугольника онлайн
Вы сможете сделать следующими способами:
калькулятора периметра треугольника онлайн
Удобная навигация нашего
калькулятора периметра треугольника онлайн
позволит Вам также быстро перейти к расчету
периметра
калькулятор периметра треугольника онлайн
или нет, всё равно оставляйте комментарии и пожелания. Мы готовы проанализировать каждое замечание по поводу работы
калькулятора периметра треугольника онлайн
и сделать его лучше. Будем рады каждому положительному комментарию и благодарности, поскольку это не что иное, как подтверждение того, что наш труд и наши усилия оправданы, а
Как найти периметр два способа
Периметр
Периметр — это сумма длин всех сторон многоугольника.
Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».
Периметр измеряется в единицах длины: мм, см, м, км и т.д.
При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.
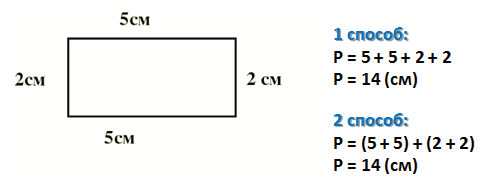
Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».
Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.
AB = 3 см, BC = 7 см
PABCD = (AB + BC) · 2
PABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)
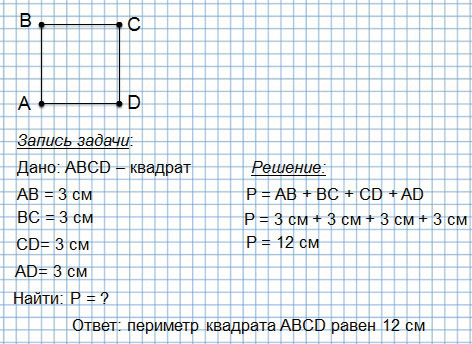
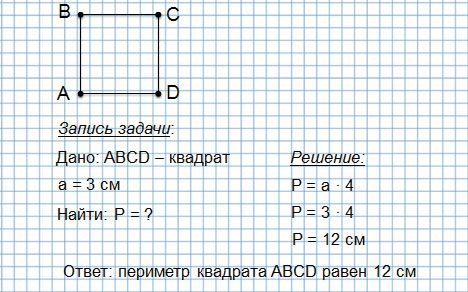
Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».
KE = 7 см
PEKFM = 4 · KE
PEKFM = 4 · 7 = 28 (см)
Как найти периметр многоугольника
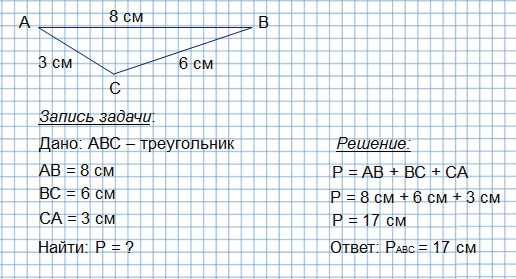
Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.
PABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)
Как найти периметр фигуры
О чем эта статья:
Определение периметра
Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Формула нахождения периметра
Рассмотрим пять фигур.
Треугольник
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.
P = 3 * a, где a — длина стороны.
Квадрат и ромб
Периметр квадрата — это произведение длины стороны на четыре. Формула ромба выглядит идентично.
P = 4 * a, где a — длина стороны.
Прямоугольник и параллелограмм
Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно.
P = 2 * (a + b), где a — ширина, b — высота.
Записывайтесь на онлайн уроки по математике к лучшим преподавателям! Уроки для учеников с 1 по 11 классы!
Равнобедренная трапеция
Формула для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.
P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
Ответ: две другие стороны равны 17см.
Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга.
Периметр многоугольника
Любой многоугольник — это замкнутая ломаная линия.
Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.
Значит, периметр многоугольника — это сумма длин всех его сторон.
В математике периметр обозначают буквой P (пэ).
Периметр прямоугольника
Например, найдём периметр данного прямоугольника.
Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.
Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.
Формула для подсчета периметра прямоугольника:
(a + b) • 2
a – длина прямоугольника
b – ширина прямоугольника.
Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:
Периметр треугольника
Периметр квадрата
Первый способ (когда мы еще не знаем действие умножения):
Второй способ (когда мы изучили действие умножения):
Поделись с друзьями в социальных сетях:
Как найти периметр прямоугольника
О чем эта статья:
Основные определения
Прямоугольником принято называть четырехугольник, у которого равны все углы. Они также являются прямыми и составляют 90°.
Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Формула нахождения периметра прямоугольника
Способ вычисления нужно выбрать, отталкиваясь от исходных данных. Далее рассмотрим четыре классические формулы.
Когда известны все или две соседние стороны
P = a + b + c + d, где a, b, c, d — стороны.
Когда известна любая сторона и площадь
P = 2 * (a + S : a), где a — сторона, S — площадь.
Площадь — это плоскость внутри замкнутой геометрической фигуры.
Когда известна любая сторона и диагональ
P = 2 * (a + √(d 2 — а 2 )), где a — сторона, d — диагональ.
Диагональ — это отрезок, который соединяет противоположные стороны фигуры.
Когда известна одна любая сторона и радиус описанной окружности
P = 2 * (a + √(4 * R 2 — a 2 )), где a — сторона, R — радиус окружности.
Радиус — отрезок, соединяющий центр и любую точку окружности.
Решение задач
А теперь практиковаться!
1. Одна сторона прямоугольника 9 см, а другая на 11 см длиннее. Как узнать периметр?
2. Площадь прямоугольника составляет 60 м², ширина равна 15 м. Чему равен периметр фигуры?
А еще можно вот так:
Ответ — такой же, 38 м.
3. Как найти периметр прямоугольника, если его диагональ в два раза больше длины равной 8 см?
Периметр прямоугольника — формулы или способы расчетов
Началом пропедевтики изучения геометрии являются знания, которые учащиеся получают, переходя во 2 класс. Применяя правила умножения, здесь впервые вычисляют периметр прямоугольника.
Переходя в следующий, 3 класс, школьники на основе этой формулы начинают знакомиться с правилами раскрытия скобок.
Как вычислить периметр прямоугольника
Учитывая, что периметр любой фигуры есть сумма длин её сторон, выводят две формы записи для нахождения этой величины.
В прямоугольнике противоположные стороны равны, поэтому, обозначив смежные стороны a и b, получают по определению:
откуда после приведения подобных слагаемых, вытекает формула
или, вынося двойку за скобки,
Рассматривая квадрат, как прямоугольник с равными сторонами, получают формулу его периметра:
Стандартный метод
В зависимости от сложности вычислений, применяют одну из формул, чтобы высчитать периметр. Учащиеся начальной школы знакомятся с понятием, сталкиваясь с практическими задачами.
Задача
Найти длину забора участка прямоугольной формы, который надо построить Сидору Карловичу, если общая граница с участком Ивана Петровича составляет 3 метра, а с плантацией Марии Ивановны – 5 метров.
Решение
Чтобы решить задачу и помочь незадачливому Сидору Карловичу, ученику приходится использовать формулу периметра прямоугольника. Учитывая, что a = 3, b = 5, дети легко находят, что длина забора равна
P = 2 (a + b) = 2 * (3 + 5) = 2 * 8 = 16 (метров)
Важные требования, предъявляемые к ученикам на данном этапе изучения материала, заключаются в правильном соизмерении длины и ширины, а также в умении начертить фигуру.
Работа выполняется только при одинаковых единицах измерения, все чертежи делаются строго с использованием инструментов!
Часто длина заданного отрезка измеряется непосредственно.
Нахождение периметра через площадь и одну сторону
При более близком знакомстве с прямоугольником, способы нахождения его периметра начинают варьироваться в зависимости от исходных данных в задаче.
Если известны одна из сторон и площадь, то, чтобы узнать, чему равен периметр, выражается неизвестная сторона, а затем она подставляется в формулу.
то есть, соотношение площади и периметра при известной стороне есть
Как найти периметр прямоугольной фигуры
В начальной школе для запоминания принципа детям часто предлагается понятие «неправильного четырёхугольника» (не прямоугольника).
Для нахождения его периметра предлагается рассчитать сумму длин сторон непосредственно, предварительно измерив каждую из них.
Для любой более сложной фигуры производят разбиение, если возможно, на небольшие прямоугольники, с которыми и работают.
Заключение
Современный онлайн калькулятор позволяет ввести значения сторон и задать необходимую точность вычислений, мгновенно производя расчёт и выдавая необходимый результат.
Урок математики по теме «Периметр. Длина окружности». 4-й класс
Класс: 4
Тип урока: урок открытия новых знаний.
Оборудование: индивидуальные листы с заданиями для учащихся; набор геометрических фигур для практической деятельности, нитки, стакан (любой), мультимедийная установка, экран, компьютер
I. Оргначало
– Хотела сказать: «Здравствуйте, дети!»
– Но, думаю: «А ведь нам предстоит решать такие проблемы, какие и не каждому взрослому под силу!»
– Предлагаю серьёзно и плодотворно поработать.
II. Актуализация опорных знаний. Постановка проблемы
Я предлагаю вам игру:
Пред вами ряд фигур
Внимательно на них взгляните
И на группы разделите
Предложения учащихся по способу разбиения:
– Назовите отличительные особенности каждой группы
– Выделим границы каждой фигуры.
– Как по-другому можно назвать границу многоугольника? (Периметр)
– Нужно ли нам знать понятие периметра и способ его нахождения? Обоснуйте своё мнение, приведите примеры. (Плинтус, оконные рамы, рамки картин и портретов, ограды участков, зданий и т.д.)
III. Постановка цели урока
– Решим практическую задачу:
«В парке решили разбить цветочные клумбы в виде различных геометрических фигур и выложить декоративной кирпичной кладкой бордюр. Сколько таких кирпичей понадобится для каждого бордюра, если на 1 м их необходимо 10 штук».
? – Как найти периметр бордюра каждой клумбы?
Закрепление способов нахождения периметра многоугольников с учётом их свойств, соответствующих формул, которые учащиеся записывают на доске:
Pкв. = a * 4 Pпр. = (a + b) * 2 Ррб.тр. = a * 2 + b
Ррв.тр. = a * 3
– Какая возникла проблема?
?! (Длину бордюра прямоугольника, квадрата и треугольников мы нашли, а вот длину бордюра клумбы круглой формы не умеем)
– Что является границей круга? (Окружность).
– Что нам сегодня предстоит выяснить? Какую цель для себя поставим? (Научиться находить длину окружности)
ТЕМА Периметр. Длина окружности.
ЦЕЛЬ Научиться находить длину окружности.
IV. Открытие нового
– Какие есть гипотезы?
– У меня в руках стакан и нитка. Какую форму имеет граница стакана? (Окружность)
– Как же можно использовать нитку, чтобы измерить длину данной границы? (Предложение учащихся: выложить нитку по границе поверхности стакана, отмерить, измерить по линейке)
?! – А как измерить длину окружности на плоскости?
– Давайте проведём исследование.
– Возьмите из набора фигур круг.
– Длину его окружности можно измерить, «прокатив» его по линейке. Но для начала нам необходимо знать, чему равна длина диаметра.
Диаметр – отрезок, соединяющий две точки окружности и проходящий через её центр.
– Как провести диаметр? Ваши предложения? (Перегнуть круг пополам, полученная линия сгиба и есть диаметр)
– Чему равен диаметр данной окружности? (9 см)
Учитель демонстрирует, как можно «прокатить» окружность вдоль линейки. Ребята проводят исследование.
– Что получилось? (Разные результаты. Приблизительно 28 см)
– Какой можно сделать вывод о практическом использовании данного способа? (Он неудобный, неточный)
– Продолжим исследование.
– Какие ещё геометрические фигуры есть у вас в наборе?
– Чем они интересны? (Эти многоугольники – треугольник, квадрат, восьмиугольник, шестнадцатиугольник – равносторонние)
– Подумайте, как можно использовать данные фигуры, чтобы найти длину окружности. (Предложения учащихся)
Если возникнут трудности, учитель подводит ребят наводящими вопросами:
– Какие фигуры можно назвать вписанными в окружность? (Фигуры, вершины которых принадлежат данной окружности)
– Попробуйте, используя модели фигур, «вписать» каждую в окружность. Что заметили? (Вписанные многоугольники тоже могут помочь определить длину окружности, причём, чем больше углов, тем фигура более приближена к границам окружности)
– Как вычисляли? (Сторона многоугольника, который мы выбрали – 2 см. Умножаем на количество сторон)
– Чему же равна длина окружности в этом случае? (32 см)
– Всё ли нас с вами устраивает? (Длина окружности установлена нами не точно, а, значит, расчёт необходимого материала может быть неправильным)
– Давайте рассуждать. Нам необходим более рациональный способ.
– Как вычисляли длину границы прямоугольника, квадрата, треугольника? (По формулам).
– Как думаете, есть ли формула, с помощью которой можно вычислить длину окружности?
(Предположения учащихся)
– Проведём ещё одно исследование.
– Внесём полученные в ходе нашего исследования данные в таблицу, где:
l – длина окружности
d – диаметр данной окружности и установим их соотношение, т.е. Вов сколько раз длина больше диаметра
– Вы видите, что результат во всех трёх случаях приблизительно равен 3.
– Вот так и было открыто волшебное число π ≈ 3,14, с которым более подробно вы познакомитесь в старших классах.
– Мы же с вами будем считать, что:
π ≈ 3
l : d = π,
– Значит, чтобы найти l, что нужно сделать?
– Радиус – половина диаметра: d = 2r.
– Как эту же формулу можно записать по-другому?
– Мы сейчас с вами совершили открытие. Сделали это практически так же, как это было сделано ещё тысячи лет назад.
СЛАЙД 1
В древности самым известным государством был Вавилон.
СЛАЙД 2
Около 6 тысяч лет назад в Вавилоне было сделано замечательное открытие: люди изобрели колесо.
СЛАЙД 3
Вавилонские воины на боевых колесницах, запряжённых лошадьми, легко побеждали пеших врагов.
СЛАЙД 4
Вавилонские горшечники стали делать на горшечном круге красивую круглую посуду с тонкими стенками, которую охотно покупал не только в Вавилоне, но и в других странах.
(иллюстрация)
СЛАЙД 5
Водоподъёмное колесо подавало воду в водопровод, откачивало воду из рудников, орошало поля.
СЛАЙД 6
Не удивительно, что вавилонские учёные старательно изучали свойства окружности – колёсного обода. Вот как они измеряли длину окружности.
(фигуры в каждом рисунке «выплывают» последовательно)
СЛАЙД 7
Окружность – это своего рода «колесо геометрии». Одно из свойств колеса – его ось – остаётся всё время на неизменном расстоянии от поверхности, по которой оно катается.
Радиус – отрезок, который соединяет центр с любой точкой на окружности. В переводе с латинского радиус – «спица колеса».
СЛАЙД 8
Для вычисления длины окружности достаточно знать, во сколько раз окружность длиннее диаметра. Отношение этих длин обозначается буквой ? (пи). Вавилонские учёные принимали ? равным 3,14159…
– Мы прикоснулись с вами лишь на миг к великой мировой истории, её замечательным достижениям и открытиям.
V. Закрепление пройденного
– Чтобы ещё раз убедиться в необходимости полученных на уроке знаниях для решения практических задач предлагаю подумать вот над чем:
«На спортивной площадке выделили территорию круглой формы для метания мяча. Её необходимо обнести специальным ограждением. Чему будет равна длина данного ограждения?»
– Перед вами план площадки (работа в паре)
– Есть решение?
– Мы знаем формулу, по которой можно найти длину окружности. Что необходимо знать для решения задачи? (Диаметр)
– Каким образом находили его в прошлый раз? (Перегибанием)
– В данном случае подобный способ возможен? Как же быть?
(Учащиеся должны обратить внимание на то, что даны стороны прямоугольной площадки. Ширина площадки равна диаметру окружности, что видно по плану)
VI. Домашнее задание (дифференцированное)
– У вас на листах есть задания для индивидуальной работы дома. Я предлагаю вам выбрать любое из них, в зависимости от того, какое вам покажется наиболее интересным. Попробуйте свои силы.
1. Найти длину окружности, используя рисунок:
2. Найти, чему равна длина беговой дорожки стадиона
VII. Итог
– Мы с вами – творцы! По-своему, первооткрыватели!
– Почему нас можно так назвать? (Мы нашли целых 3 способа вычислить длину окружности, вывели формулу)
– Я благодарю всех вас за прекрасную работу на уроке. Особенно хочу отметить смелость решений, творчество, инициативность.
– Но вы и сами можете оценить свою работу на уроке.
– Перед вами табличка:
Умения
Узнавать и называть фигуры
Вычислять периметр фигур с помощью изученных формул
Использовать формулу длины окружности
Решать задачи практического характера
– Изобразите в каждом столбце смайлик, в зависимости от того, насколько хорошо вы владеете данным умением.
– Закончить наш с вами урок я хотела бы так:
– Представьте себе, что мы все взялись за руки и образовали большой дружный круг.
– Чему будет равна длина окружности, которая у нас получилась?
Вытянутые руки – сажень, старинная русская мера длины, равная 2м 13 см (размах обеих рук взрослого человека)
– Значит, берём приблизительно 2 м.
– Что получилось?
– Ещё раз спасибо. Желаю вам удачи и новых открытий!