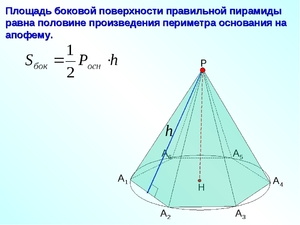
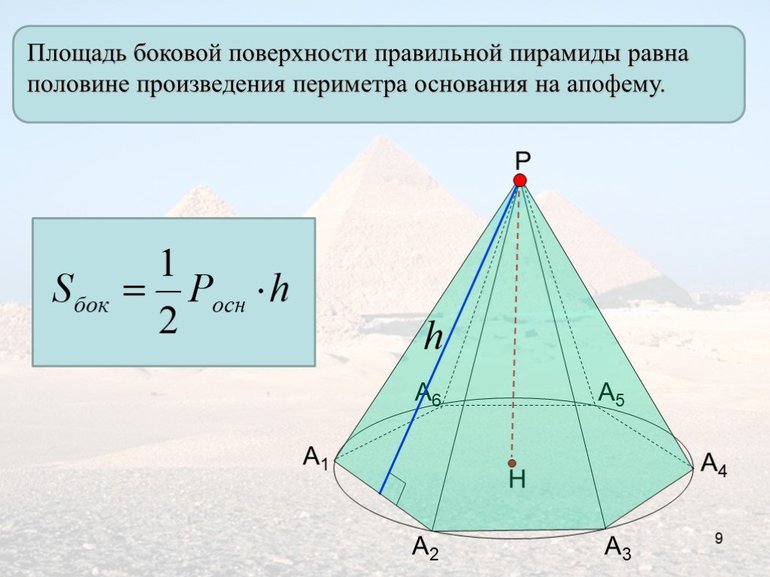
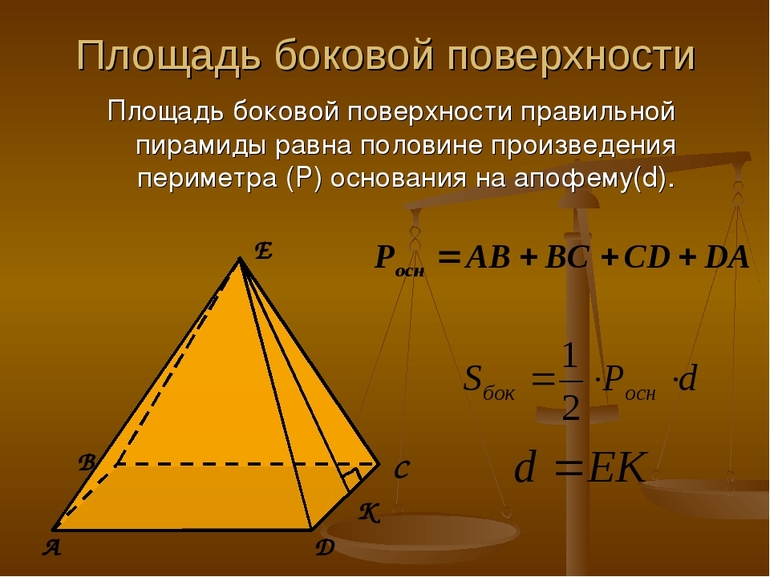
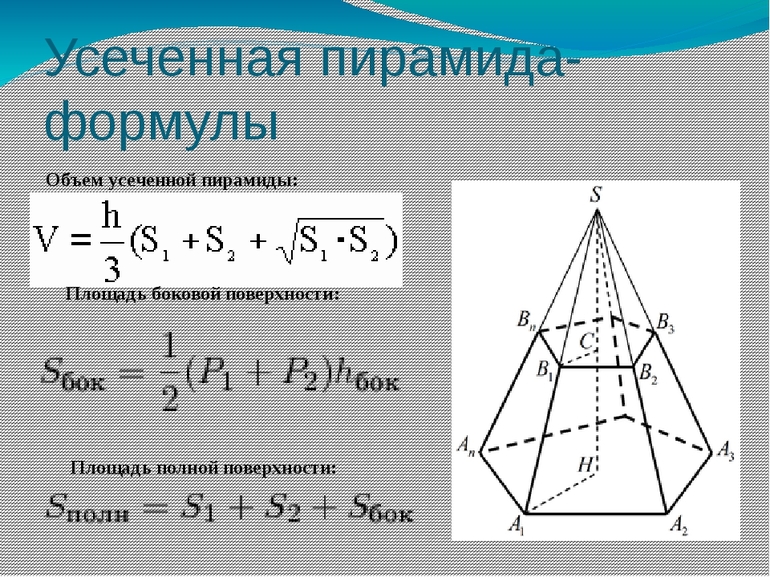
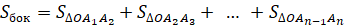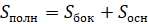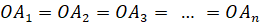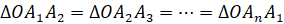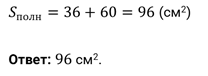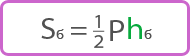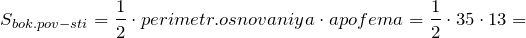Как найти площадь боковой поверхности пирамиды

Нахождение площади правильной пирамиды: формулы

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.

Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.

Формула площади правильной пирамиды

1. Общая формула

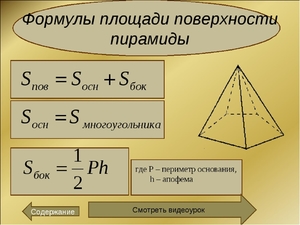
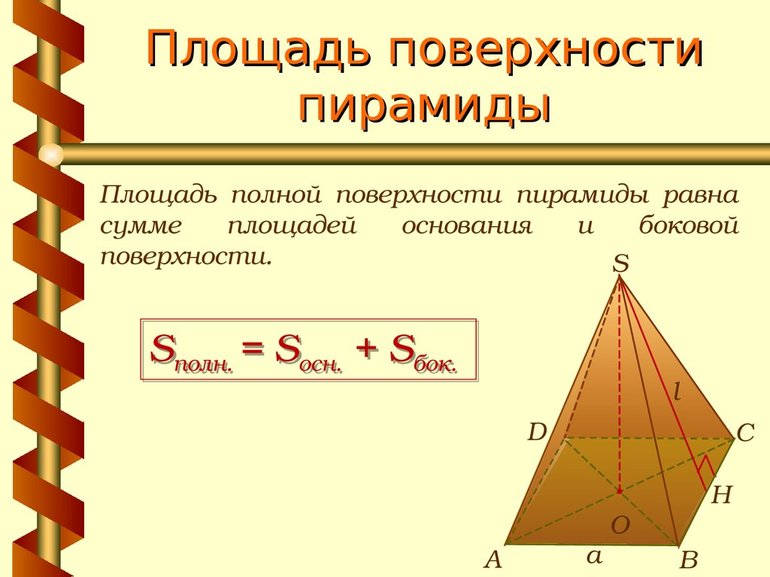
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.

Боковой гранью правильной пирамиды является равнобедренный треугольник.

Площадь треугольника вычисляется по формулам:

1. Через длину основания (a) и высоту (h):

2. Через основание (a) и боковую сторону (b):

Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.

2. Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.

Источник

Площадь боковой поверхности разных пирамид

Перед изучением вопросов о данной геометрической фигуре и её свойствах, следует разобраться в некоторых терминах. Когда человек слышит о пирамиде, ему представляются большущие постройки в Египте. Так выглядят самые простые из них. Но они бывают разных видов и форм, а значит и формула вычисления для геометрических фигур будет разной.

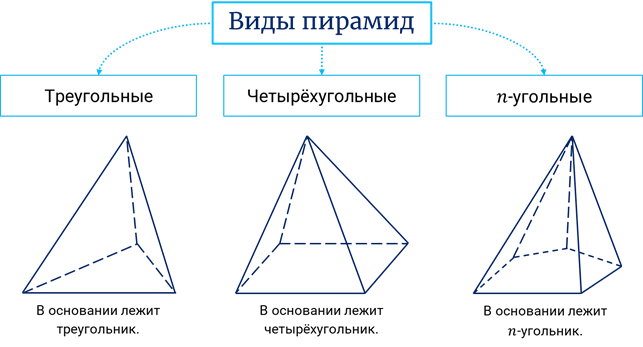
Виды фигуры

Пирамида – геометрическая фигура, обозначающая и представляющая собой несколько граней. По сути – это тот же многогранник, в основании которого лежит многоугольник, а по бокам расположены треугольники, соединяющиеся в одной точке – вершине. Фигура бывает двух основных видов:

В первом случае, в основании лежит правильный многоугольник. Тут все боковые поверхности равны между собой и сама фигура порадует глаз перфекциониста.

Термины и обозначения

Формулы площади

Находить площадь боковой поверхности пирамиды любого типа можно несколькими способами. Если фигура не симметричная и представляет собой многоугольник с разными сторонами, то в данном случае легче вычислить общую площадь поверхности через совокупность всех поверхностей. Иными словами – надо посчитать площадь каждой грани и сложить их вместе.

В зависимости от того, какие параметры известны, могут потребоваться формулы вычисления квадрата, трапеции, произвольного четырёхугольника и т.д. Сами формулы в разных случаях тоже будут иметь отличия.

В случае с правильной фигурой находить площадь намного проще. Достаточно знать всего несколько ключевых параметров. В большинстве случаев требуются вычисления именно для таких фигур. Поэтому далее будут приведены соответствующие формулы. В противном случае пришлось бы расписать всё на несколько страниц, что только запутает и собьёт с толку.

Основная формула для вычисления площади боковой поверхности правильной пирамиды будет иметь следующий вид:

S=½ Pa ( P – периметр основания, а – апофема)

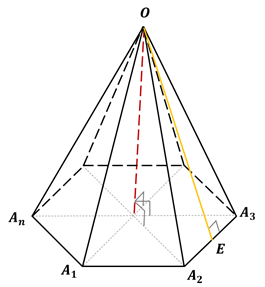
Рассмотрим один из примеров. Многогранник имеет основание с отрезками A1, А2, А3, А4, А5, и все они равны 10 см. Апофема пусть будет равна 5 см. Для начала надо найти периметр. Так как все пять граней основания одинаковые, можно находить так: Р=5*10=50 см. Далее применяем основную формулу: S =½*50*5=125 см в квадрате.

Площадь боковой поверхности правильной треугольной пирамиды вычислить легче всего. Формула имеет следующий вид:

S =½* ab *3, где а – апофема, b – грань основания. Множитель тройки здесь означает количество граней основания, а первая часть – площадь боковой поверхности. Рассмотрим пример. Дана фигура с апофемой 5 см и гранью основания 8 см. Вычисляем: S =1/2*5*8*3=60 см в квадрате.

Тут для начала следует найти периметры оснований: р_01 =3*4=12 см; р_02=6*4=24 см. Осталось подставить значения в основную формулу и получим: S =1/2*(12+24)*4=0,5*36*4=72 см в квадрате.

Таким образом, можно найти площадь боковой поверхности правильной пирамиды любой сложности. Следует быть внимательным и не путать эти вычисления с полной площадью всего многогранника. А если это всё же понадобится сделать – достаточно вычислить площадь самого большого основания многогранника и прибавить её к площади боковой поверхности многогранника.

Видео

Закрепить информацию о том, как найти площадь боковой поверхности разных пирамид, вам поможет это видео.

Источник

Площадь пирамиды

Вы будете перенаправлены на Автор24

На этой странице вы сможете познакомиться с формулами для вычисления площади полной и боковой поверхности пирамиды. Также на страницу добавлены онлайн-калькуляторы и примеры вычисления площадей пирамид.

Пирамида представляет собой объёмную фигуру, в основании которой лежит многоугольник, а боковые грани являются треугольниками. У правильной пирамиды в основании лежит правильный многоугольник, а боковые грани равны.

Рассмотрим, как вычислять площадь полной поверхности правильной пирамиды.

Полная площадь поверхности пирамиды через высоту и сторону основания

Суммарная площадь всех сторон и основания правильной пирамиды определяется по формуле:

$a$ — длина стороны основания;

$n$ — число сторон основания;

$H$ — высота пирамиды.

Для вычисления полной поверхности правильного тетраэдра можно применять более простую формулу.

Полная площадь тетраэдра

Для правильного тетраэдра полная площадь поверхности определяется по формуле:

$S =\sqrt3 \cdot a^2$, где

$a$ — длина стороны тетраэдра.

Рассмотрим пример использования формулы для правильного тетраэдра.

Задача

Решение:

Вспомним, чему равна площадь правильного треугольника:

$S_∆ = \sqrt3 \cdot \frac <4>= \sqrt3 \cdot \frac<7^2> <4>≈ 21.21$ кв. см.

Мы нашли площадь одной грани правильного тетраэдра. Всего у тетраэдра 4 грани, а это значит что вся площадь поверхности равна произведению площади одной грани на количество граней, равное четырём:

$S = 21.21 \cdot 4 = 84,87$ кв. см.

Полученный ответ проверим онлайн-калькулятором. Результаты совпадают, а значит ответ — верный.

Боковую поверхность правильной пирамиды чаще всего вычисляют по двум формулам — через периметр и апофему или через сторону основания и высоту.

Апофемой пирамиды называется высота боковой грани.

Источник

Как найти площадь боковой поверхности пирамиды

Прежде всего, стоит понять, что боковая поверхность пирамиды представлена несколькими треугольниками, площади которых можно найти с помощью самых различных формул, в зависимости от известных данных:

На самом деле, это лишь самые основные из известных формул для нахождения площади треугольника.

Рассчитав при помощи указанных выше формул площади всех треугольников, являющихся гранями пирамиды, можно приступить к исчислению площади боковой поверхности данной пирамиды. Делается это предельно просто: необходимо сложить площади всех треугольников, образующих боковую поверхность пирамиды. Формулой это можно выразить так:

Для большей ясности можно рассмотреть небольшой пример: дана правильная пирамида, боковые грани которой образованы равносторонними треугольникам, а в основании ее лежит квадрат. Длина ребра данной пирамиды составляет 17 см. Требуется найти площадь боковой поверхности данной пирамиды.

S = (17²*√3)/4 = (289*1.732)/4 = 125.137 см²

Известно, что в основании пирамиды лежит квадрат. Таким образом, понятно, что данных равносторонних треугольников четыре. Тогда площадь боковой поверхности пирамиды рассчитывается так:

125.137 см² * 4 = 500.548 см²

Ответ: площадь боковой поверхности пирамиды составляет 500.548 см²

Источник

Как найти площадь поверхности пирамиды

Соавтор(ы): Grace Imson, MA. Грейс Имсон — преподаватель математики с более чем 40 годами опыта. В настоящее время преподает математику в Городском колледже Сан-Франциско, ранее работала на кафедре математики в Сент-Луисском университете. Преподавала математику на уровне начальной, средней и старшей школы, а также колледжа. Имеет магистерскую степень по педагогике со специализацией на руководстве и контроле, полученную в Сент-Луисском университете.

Количество просмотров этой статьи: 107 489.

Площадь поверхности любой пирамиды равна сумме площади основания и площадей боковых граней. Если дана правильная пирамида, площадь ее поверхности вычисляется с помощью формулы, но нужно знать, как найти площадь основания пирамиды. Так как в основании пирамиды может лежать любой многоугольник, нужно уметь находить площади многоугольников, включая пяти- и шестиугольники. Площадь поверхности правильной квадратной пирамиды очень легко найти, если известны сторона квадрата (который лежит в основании) и апофема пирамиды.

Источник

Как найти площадь боковой поверхности пирамиды: формулы, пример задачи

В школьном курсе стереометрии изучают свойства разных пространственных фигур. Одной из них является пирамида. Данная статья посвящена вопросу о том, как найти у пирамиды площадь боковой поверхности. Также раскрывается вопрос определения этой площади для усеченной пирамиды.

Что такое пирамида?

Многие, услышав слово «пирамида», сразу представляют грандиозные сооружения Древнего Египта. Действительно, гробницы Хеопса и Хефрена являются правильными четырехугольными пирамидами. Тем не менее пирамидой также является тетраэдр, фигуры с пяти-, шести-, n-угольным основанием.

Вам будет интересно: Passive Voice: упражнения с ответами, таблица

Точка, с которой соединены все вершины углов основания, не лежит в его плоскости. Она называется вершиной пирамиды. Если из нее провести к основанию перпендикуляр, то мы получим высоту. Фигура, в которой высота пересекает основание в геометрическом центре, получила название прямой. Иногда прямая пирамида имеет правильное основание, например квадрат, равносторонний треугольник и так далее. В этом случае она называется правильной.

При вычислении у пирамиды площади боковой поверхности удобно работать с правильными фигурами.

Площадь поверхности боковой фигуры

Как найти у пирамиды площадь боковой поверхности? Можно понять это, если ввести соответствующее определение и рассмотреть развертку на плоскости для этой фигуры.

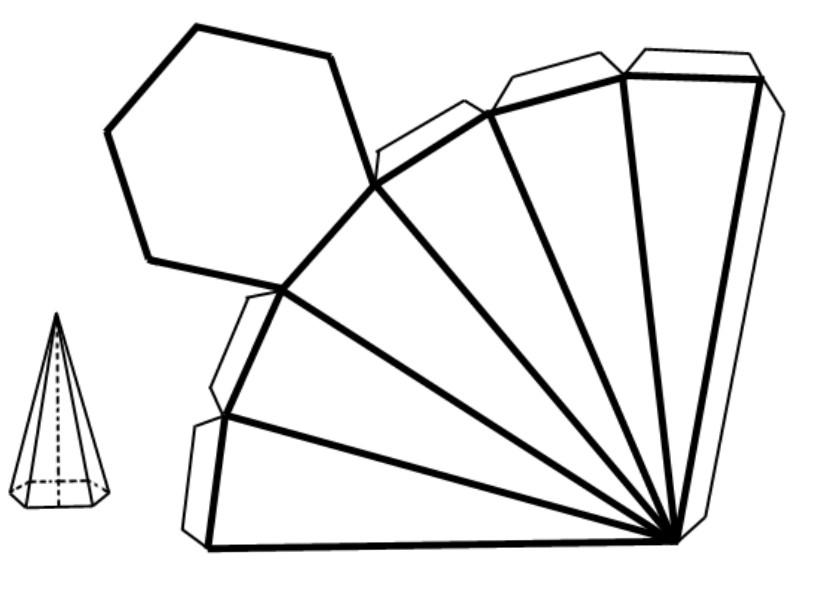
Если вдоль бокового ребра разрезать поверхность и развернуть ее на плоскости, то получится развертка пирамиды. Для примера ниже показана развертка шестиугольной пирамиды.

Видно, что боковая поверхность образована шестью одинаковыми треугольниками.

Теперь не трудно догадаться, как у пирамиды найти площадь боковой поверхности. Для этого следует сложить площади всех треугольников. В случае n-угольной правильной пирамиды, сторона основания которой равна a, для рассматриваемой поверхности можно записать формулу:

Усеченная пирамида и ее поверхность

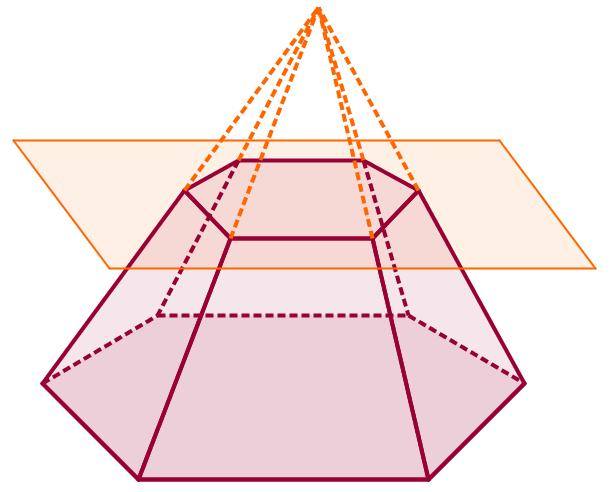
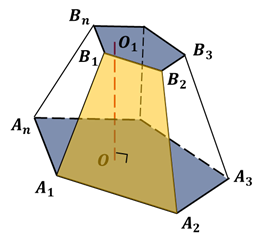
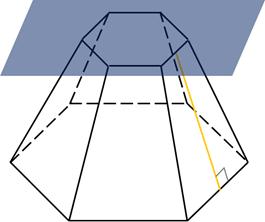
Как можно догадаться из названия, усеченную пирамиду можно получить из обычной фигуры. Для этого нужно отсечь плоскостью, параллельной основанию, вершину. Ниже рисунок демонстрирует этот процесс для шестиугольной фигуры.

Ее боковая поверхность представляет собой сумму площадей одинаковых равнобедренных трапеций. Формула для площади боковой поверхности усеченной пирамиды (правильной) имеет вид:

Расчет боковой поверхности для треугольной пирамиды

Покажем, как найти площадь боковой поверхности пирамиды. Допустим, у нас правильная треугольная, разберемся на примере конкретной задачи. Известно, что сторона основания, представляющего собой равносторонний треугольник, равна 10 см. Высота фигуры равна 15 см.

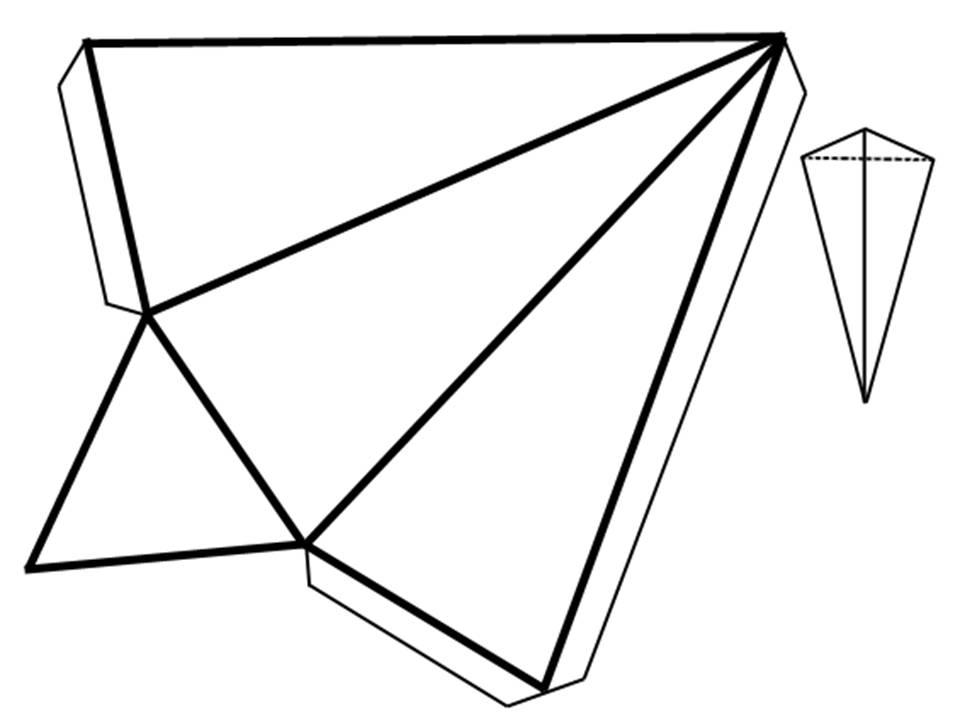
Развертка этой пирамиды показана на рисунке. Чтобы воспользоваться формулой для Sb, необходимо сначала найти апофему hb. Рассматривая прямоугольный треугольник внутри пирамиды, построенный на сторонах hb и h, равенство можно записать следующее:

Подставляем данные и получаем, что hb≈15,275 см.

Теперь можно воспользоваться формулой для Sb:

Sb = n*a*hb/2 = 3*10*15,275/2 = 229,125 см2

Заметим, что основание треугольной пирамиды, как и ее боковая грань, образовано треугольником. Тем не менее этот треугольник при вычислении площади Sb не учитывается.

Источник

Пирамида. Площади поверхностей. Объём

Урок 36. Подготовка к ЕГЭ по математике

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока «Пирамида. Площади поверхностей. Объём»

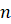
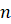
Напомним, что пирамида – это многогранник, в основании которого лежит –угольник, а остальные граней – треугольники с общей вершиной.

Многоугольник называется основанием пирамиды.

Треугольники , , …, называются боковыми гранями пирамиды.

Точка – вершиной пирамиды, а отрезки , , …, – её боковыми рёбрами.

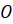
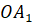
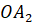
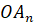
Отрезок, соединяющий вершину пирамиды с плоскостью её основания и перпендикулярный к этой плоскости, называется высотой пирамиды.

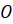
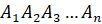
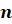
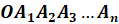
Пирамиду с вершиной и основанием называют -угольной пирамидой и обозначают так: .

Диагональное сечение – это сечение пирамиды плоскостью, которая проходит через два боковых ребра, не принадлежащих одной грани.

Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды.

Тогда площадью боковой поверхности пирамиды называется сумма площадей её боковых граней.

А площадью полной поверхности пирамиды называется сумма площадей всех её граней.

Объём пирамиды равен:

.

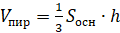
Пирамида, в зависимости от того, какой многоугольник лежит в основании, имеет своё название.

Пирамида называется правильной, если её основанием является правильный многоугольник, а все боковые рёбра равны.

Отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.

Высота боковой грани правильной пирамиды, проведённая из её вершины к ребру основания, называется апофемой.

Выше изображена правильная пирамида. 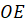– одна из её апофем. Все апофемы правильной пирамиды равны друг другу.

Отметим некоторые свойства правильной 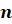-угольной пирамиды.

1. В правильной 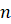-угольной пирамиде все боковые рёбра равны между собой.

2. Боковые рёбра равно наклонены к основанию.

3. Из равенства боковых рёбер пирамиды следует и равенство её боковых граней.

4. Боковые грани равно наклонены к основанию.

5. Вершина проектируется в центр основания (основание высоты совпадает с центром основания).

6. Площадь боковой поверхности правильной пирамиды равна:

.

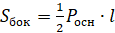
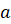
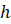
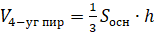
7. Объём правильной четырёхугольной пирамиды со стороной основания и высотой равен:

.

Параллельное сечение пирамиды – сечение пирамиды плоскостью, параллельной основанию.

Параллельное сечение пирамиды обладает следующими свойствами:

1. сечение, параллельное основанию пирамиды, отсекает на высоте пирамиды и боковых рёбрах пропорциональные отрезки;

2. в сечении получается многоугольник, подобный основанию;

3. площади сечения и основания относятся как квадраты их расстояний до вершины.

Усечённая пирамида – это часть пирамиды, заключённая между основанием и параллельным сечением пирамиды.

Основания усечённой пирамиды – подобные многоугольники, лежащие в параллельных плоскостях.

Боковые грани усечённой пирамиды – трапеции.

Высота усечённой пирамиды – это перпендикуляр, опущенный из любой точки верхнего основания на плоскость нижнего.

Площадь полной поверхности усечённой пирамиды равна сумме площади боковой поверхности и площадей двух оснований.

Объём усечённой пирамиды равен разности объёмов полной и отсечённой пирамиды, или его ещё можно вычислить по следующей формуле:

.

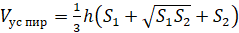
Правильная усечённая пирамида получается из правильной пирамиды.

Апофема – высота боковой грани правильной усечённой пирамиды.

Площадь боковой поверхности правильной усечённой пирамиды равна:

.

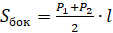
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

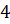
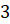
Задача первая. Дана треугольная пирамида, боковые рёбра которой взаимно перпендикулярны и равны см, см и см. Найдите площадь боковой поверхности пирамиды.

Задача вторая. Дана правильная четырёхугольная пирамида со стороной основания см и высотой см. Найдите площадь полной поверхности пирамиды.

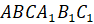
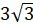
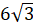
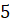
Задача третья. Найдите высоту правильной усечённой треугольной пирамиды , если стороны её оснований равны см и см, а боковое ребро равно см.

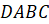
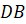
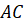
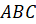
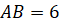
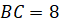
Задача четвёртая. В пирамиде боковое ребро перпендикулярно основанию и равно ребру . Треугольник – прямоугольный с катетами см и см. Найдите объём пирамиды.

Задача пятая. Найдите объём правильной треугольной пирамиды с ребром основания, равным 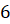см, и боковым ребром, равным см.

Источник

Как найти площадь боковой поверхности пирамиды

14.1. Определение пирамиды и её элементов

Определение. Пирамидой называется многогранник, у которого одна грань — многоугольник, а остальные грани — треугольники с общей вершиной (рис. 95, 96).

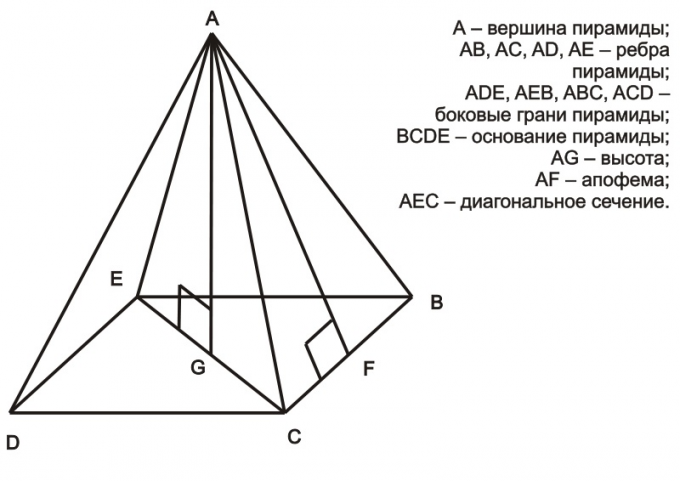
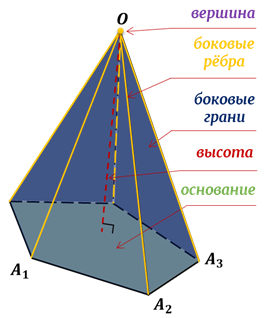
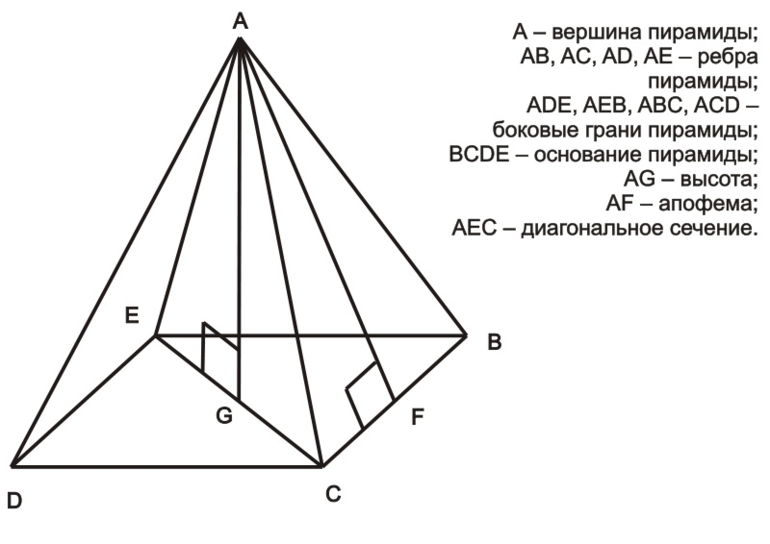
На рисунке 96 изображена четырёхугольная пирамида PABCD, у которой: четырёхугольник ABCD — основание пирамиды; точка Р — вершина пирамиды; отрезки РA, РВ, PC, PD — боковые рёбра пирамиды; отрезки АВ, ВС, CD, DA — стороны (рёбра) основания пирамиды; отрезок РО — высота пирамиды; треугольники РАВ, РВС, PCD, PDA — боковые грани пирамиды.

У n- угольной пирамиды имеется ( n + 1) вершин, 2 n рёбер и ( n + 1) граней. Диагоналей пирамида не имеет. В пирамиде различают плоские углы при её вершине и двугранные углы при её рёбрах. Двугранным углом при ребре пирамиды называют содержащий пирамиду двугранный угол, образованный плоскостями граней, проходящими через данное ребро.

Любую пирамиду можно разбить на некоторое число тетраэдров, а любой выпуклый многогранник — на некоторое число пирамид. Для этого достаточно, например, взять любую точку внутри данного многогранника и соединить её отрезками со всеми его вершинами. Такое разбиение часто используется при нахождении объёмов многогранников.

14.2. Некоторые виды пирамид

Если все боковые рёбра пирамиды составляют с плоскостью основания равные углы, то : а ) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды ; б ) все боковые рёбра пирамиды равны между собой.

б) Из ОА = OВ = ОС = OD = ОЕ = OF следует, что боковые рёбра РА, РВ, PC, PD, РЕ, PF пирамиды равны, как наклонные, имеющие равные проекции, т. е. РА = РВ = PC = PD = РЕ = PF. Что и требовалось доказать. ▼

Вы самостоятельно можете доказать обратные утверждения.

1. Если основание высоты пирамиды совпадает с центром окружности, описанной около её основания, то: а) все боковые рёбра пирамиды образуют с плоскостью основания равные углы; б) все боковые рёбра пирамиды равны между собой.

2. Если все боковые рёбра пирамиды равны, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые рёбра пирамиды составляют с плоскостью её основания равные между собой углы.

Также имеет место следующее утверждение.

Если высота пирамиды пересекает её основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в её основание.

Доказательств о. Пусть РО — высота пирамиды PABCDE, боковые грани которой образуют с плоскостью основания пирамиды двугранные углы, равные ϕ (рис. 99).

Самостоятельно докажите обратное утверждение.

Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.

Перечислим ещё несколько часто встречающихся в задачах видов пирамид.

• Пирамида, ровно одна боковая грань которой перпендикулярна плоскости основания. Высота такой пирамиды лежит в этой, перпендикулярной основанию, грани (рис. 100).

• Пирамида, две соседние боковые грани которой перпендикулярны плоскости основания. Высотой такой пирамиды служит боковое ребро, общее для этих граней (рис. 101).

• Пирамида, две не соседние боковые грани которой перпендикулярны плоскости основания. Высота такой пирамиды лежит на прямой пересечения плоскостей этих граней (рис. 102).

14.3. Правильная пирамида

Определение. Пирамида называется правильной, если её основание — правильный многоугольник и вершина пирамиды проектируется в центр этого основания.

Из определения следует алгоритм построения изображения правильных пирамид, что, в свою очередь, доказывает существование таких пирамид.

Для построения изображения правильной пирамиды достаточно построить изображение соответствующего правильного многоугольника (основания пирамиды) и его центра. Затем из построенного центра провести перпендикуляр к плоскости многоугольника и выбрать на этом перпендикуляре (в качестве вершины пирамиды) любую точку, отличную от центра многоугольника. Соединив отрезками прямых эту точку со всеми вершинами многоугольника, получим изображение правильной пирамиды.

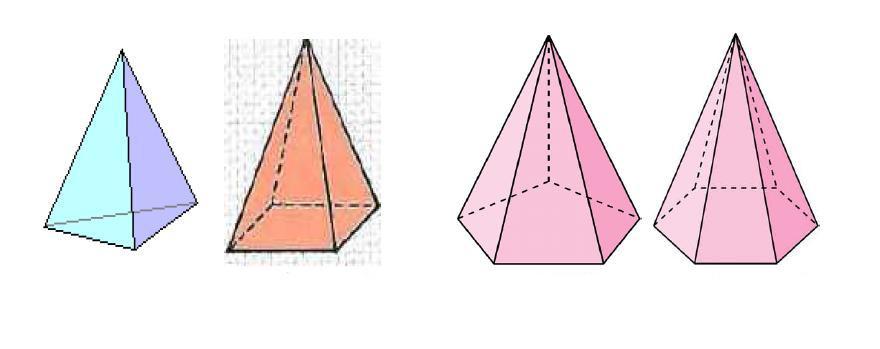
На рисунке 103, а, б, в построены изображения правильных пирамид: а) треугольной; б) четырёхугольной; в) шестиугольной.

Правильные пирамиды обладают замечательным свойством.

В правильной пирамиде все боковые рёбра равны, а все боковые грани — равные равнобедренные треугольники.

Таким образом, имеем:

Это свойство правильной пирамиды можно доказать при помощи поворота пирамиды вокруг оси, содержащей её высоту.

Следствием доказанного выше является утверждение.

Все боковые рёбра правильной пирамиды образуют с плоскостью основания равные углы, а все боковые грани — равные двугранные углы.

Докажите это предложение самостоятельно.

Высота боковой грани правильной пирамиды, проведённая к ребру её основания, называется апофемой пирамиды. На рисунке 104 отрезок РН — одна из апофем пирамиды.

Все апофемы правильной пирамиды равны вследствие равенства всех её боковых граней.

Имеют место признаки правильной пирамиды:

Пирамида, в основании которой лежит правильный многоугольник, является правильной, если: а) все её боковые рёбра равны; б) все её боковые рёбра образуют с плоскостью основания равные углы; в) все её боковые грани — равные равнобедренные треугольники.

Докажите это самостоятельно.

S сеч = • FL.

Найдём AD, МK и FL.

В △ OPF ( ∠ POF = 90 ° ):

OF = OP • tg α = h • tg α ; PF = = = PE.

EF = 2 FO = 2 h • tg α = ВС.

В плоскости PEF получаем:

Тогда в △ ЕFL : FL = ЕF • cos α = 2 h • tg α • cos α = 2 h sin α ;

PL = PF • sin (90 ° – 2 α ) = PF • cos 2 α = .

Так как MK | | BC, то △ МKР ∾ △ ВСР, откуда

∠ F 1 FL = ∠ OFP – ∠ OFL = (90 ° – α ) – α = 90 ° – 2 α ;

= ⇒
⇒ LF 1 = = .

= • L 1 F = • FL 1 = .

1 4.4. Площади боковой и полной поверхностей пирамиды

Поверхность пирамиды состоит из основания и боковых граней. В этой связи различают боковую и полную поверхности пирамиды, а также их площади.

Площадью полной поверхности пирамиды (обозначают S полн ) называется сумма площадей всех её граней, т. е. сумма площади основания пирамиды и площади её боковой поверхности.

О площади боковой поверхности правильной пирамиды имеет место следующая теорема.

Теорема 18. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды.

где Р — периметр основания пирамиды. Теорема доказана. ▼

Теорема 19. Если все боковые грани пирамиды наклонены к плоскости основания под углом ϕ и высота пересекает основание, то S бок = .

S бок = .

Если плоскость α параллельна основанию пирамиды и пересекает её, то в сечении пирамиды получается некоторый многоугольник (рис. 109).

Теорема 20. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые рёбра и высота делятся этой плоскостью на пропорциональные части; 2) в сечении получается многоугольник, подобный основанию; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

= = = = = k, (*)

Следствие. Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает пирамиду, подобную данной.

14.6. Усечённая пирамида

Таким образом, усечённой пирамидой называется часть полной пирамиды, заключённая между её основанием и параллельным ему сечением.

У n- угольной усечённой пирамиды 2 n вершин, 3 n рёбер, ( n + 2) грани и n ( n – 3) диагоналей.

Высотой усечённой пирамиды называется перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённой пирамиды. На рисунке 110 отрезки О 1 О, B 1 K — высоты усечённой пирамиды.

Усечённая пирамида называется правильной, если она получена из правильной пирамиды (рис. 111).

Из теоремы 20 следует, что основания правильной усечённой пирамиды — подобные правильные многоугольники, а боковые грани — равные равнобедренные трапеции.

Площадью боковой поверхности усечённой пирамиды называется сумма площадей всех её боковых граней.

Для правильной усечённой пирамиды имеет место

Проведите доказательство теоремы самостоятельно.

Полная поверхность усечённой пирамиды — это объединение её оснований и боковой поверхности, поэтому для усечённой пирамиды

где S 1 и S 2 — площади большего и меньшего оснований этой пирамиды.

Расположим пирамиды РАВС и P 1 A 1 B 1 C 1 так, чтобы их основания лежали в одной плоскости, а сами пирамиды были расположены по одну сторону от этой плоскости (рис. 112). Тогда любая плоскость, параллельная плоскости оснований и пересекающая первую пирамиду, пересекает и вторую, причём по теореме о параллельных сечениях пирамиды площади этих сечений равны. Следовательно, на основании принципа Кавальери равны и объёмы этих пирамид. Лемма доказана. ▼

Теорема 22. Объём любой треугольной пирамиды равен одной трети произведения площади основания на высоту.

Доказательств о. Пусть А 1 AВC — данная треугольная пирамида с вершиной A 1 и основанием ABC (рис. 113). Дополним эту пирамиду до треугольной призмы ABCA 1 B 1 C 1 с тем же основанием, одним из боковых рёбер которой является боковое ребро АA 1 данной пирамиды. Это означает, что высота призмы равна высоте данной пирамиды.

где Н — длина высоты данной пирамиды. Теорема доказана. ▼

Таким образом, объём любой пирамиды вычисляется по формуле

где S осн — площадь основания, Н — длина высоты пирамиды.

Итак, доказана теорема.

Теорема 23. Объём любой пирамиды равен одной трети произведения площади основания на высоту. ▼

14.8. Об объёме тетраэдра

У тетраэдра за основание можно принять любую его грань, на каждую из которых можно провести высоту тетраэдра из вершины, противоположной этой грани. Поэтому для объёма V одного и того же тетраэдра имеют место соотношения

где S k и h k ( k = 1, 2, 3, 4) — площадь грани и длина опущенной на неё высоты. Эти соотношения часто используют при решении задач.

Заметим, что не в любом тетраэдре все четыре высоты пересекаются в одной точке (для сравнения — все три высоты любого треугольника пересекаются в одной точке). Тетраэдр, все высоты которого пересекаются в одной точке, называется ортоцентрическим.

Интересен также тетраэдр (рис. 116, а ), все грани которого равны. Такой тетраэдр называется равногранным. Его развёрткой является остроугольный треугольник (рис. 116, б ).

Докажите самостоятельно, что в равногранном тетраэдре:

— скрещивающиеся рёбра попарно равны;

— все высоты равны;

— сумма плоских углов трёхгранного угла при каждой вершине тетраэдра равна 180 ° ;

— двугранные углы при скрещивающихся рёбрах тетраэдра равны.

Мы получили: объём тетраэдра равен одной шестой произведения длин любых двух его скрещивающихся рёбер, расстояния между ними и синуса угла между скрещивающимися прямыми, содержащими эти рёбра.

Отметим ещё несколько очевидных и менее очевидных свойств тетраэдров, связанных с их объёмами.

1. Объёмы тетраэдров с равными основаниями относятся как их высоты, опущенные на эти основания.

2. Объёмы тетраэдров с равными высотами относятся как площади их оснований.

3. Объёмы тетраэдров, имеющих равные трёхгранные углы, относятся, как произведения длин рёбер, образующих эти углы.

Используя рисунок 118, вы сможете легко доказать третье утверждение.

14.9. Объём усечённой пирамиды

S 1 : S 2 = ( H + x ) 2 : x 2 ⇒ : = ( H + x ) : x ⇒
⇒ x = .

Поэтому для объёма V усечённой пирамиды находим

Источник

Площадь пирамиды

Площадь пирамиды вычисляется через суммирование площади являющегося правильным многоугольником основания и площадей имеющих треугольную форму боковых граней.

Если в пирамиду добавить множество граней, в конечном варианте она превратится в являющийся частным случаем пирамиды конус. Данное утверждение позволяет с одинаковым подходом решать задачи вычисления площадей пирамиды и конуса.

Онлайн калькулятор позволяет без личных значительных усилий вычисления сложной математической формулы через высоту определять S всей поверхности данной объемной правильной фигуры. В соответствующие поля нужно занести значения высоты h, стороны a и числа сторон n основания. На выходе после нажатия на кнопку вычисления моментально будет выдан требуемый результат.

Вычисление площади пирамид для строительства чего-то вроде индейских или древнеегипетских гигантских строений сегодня не требуется. Но пирамиды в виде пирамидальных элементов металлических и бетонных конструкций в строительстве применяются довольно часто. При проектировании зданий, мостов, иных сооружений важно рассчитывать как прочностные, так и геометрические параметры данных фигур, в том числе и площадь пирамид.

Источник

Вычисление площади правильной треугольной пирамиды

Вычисление площади правильной треугольной пирамиды

Правильная треугольная пирамида (тетраэдр) — это многогранник, в основании которого лежит правильный треугольник со сторонами a и боковыми гранями в виде равнобедренных треугольников с основанием a и сторонами b.

Площадь поверхности такой фигуры складывается из площадей основания многогранника и трех боковых граней. В записи на математический язык это выглядит так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Нахождение площади основания пирамиды

Поскольку правильный тетраэдр основан на треугольнике, для определения площади основания рассматриваемого многогранника воспользуемся формулой нахождения площади треугольника:

Значение переменных: a — длина стороны равностороннего треугольника, h — его высота.

Далее произведем подстановку формулы вычисления высоты правильного треугольника и получим искомое выражение:

Вычисление площади боковых граней и полной поверхности

Боковые грани правильной треугольной пирамиды представлены тремя равнобедренными треугольниками. Выведем формулу расчета площади каждого из них из классического способа вычисления площади треугольника:

Здесь переменная a обозначает основание треугольника, h — его высоту.

Теперь выполним подстановку выражения, с помощью которого находится высота треугольника с одинаковыми бедрами, и получим уравнение определения площади равнобедренного треугольника:

В этом случае b — это боковые ребра треугольника, равные между собой.

Подставим в выражение (1) формулы (2) и (3) и получим уравнение, с помощью которого рассчитывается площадь полной поверхности правильного тетраэдра:

Примеры задач с решением

Задача

Дано

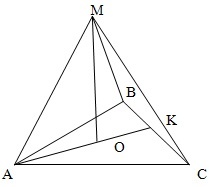
Правильный тетраэдр MABC с вершиной М. Высота основания AK=3 см.

∠MAB=∠MAC=∠MBA=∠MBC=∠MAB=∠MCA=∠MCB=45°. Необходимо вычислить площадь пирамиды MABC.

Решение

В основании правильного тетраэдра лежит равносторонний треугольник с известной длиной высоты. Применим свойство правильного треугольника, состоящее в следующем:

Преобразуем данное выражение так, чтобы вывести формулу стороны a:

Теперь найдем a:

Подставим полученное выражение в формулу нахождения площади основания правильного многогранника с тремя боковыми гранями:

Далее необходимо найти площадь боковых граней тетраэдра. Для этого произведем вычисление высоты MK. Так как угол между гранью и основанием пирамиды равен 45°, то ∠OKM=45°, следовательно:

По свойству правильного треугольника, отрезок OK равен радиусу вписанной в ΔABC окружности.

Найдем ее по соответствующей формуле:

Подставим найденную величину в отношение ОК к МК:

Из данной пропорции выведем выражение, по которому можно определить длину высоты MK:

Теперь, когда известны основание и высота равнобедренного треугольника, составляющего боковую грань пирамиды MABC, подставим значения в классическую формулу нахождения площади треугольника:

Суммируем площадь основания и боковых граней пирамиды:

Ответ, выраженный в квадратных сантиметрах: \(3\sqrt3+18\sqrt6\;(см^2)\)

Источник

Описание фигуры

С древнегреческого языка пирамида переводится, как многогранник с несколькими гранями — боковыми и основанием. Первые имеют вид треугольников с одной вершиной. С учётом количества углов фигура делится на треугольную (тетраэдр), четырёхугольную, пятиугольную, шестиугольную, n-угольную. Элементы многогранника:

Развертка — плоская фигура, образованная путём совмещения поверхности тела с плоскостью. Грани и другие элементы не накладываются друг на друга. Развёртка поверхности похожа на гибкую плёнку. По факту, это пятиугольная пирамида с равными сторонами и углами. В плоскости она напоминает звезду.

Свойства и теоремы

Для фигуры характерны некоторые свойства. БР одинаковы, если нижняя сторона вписывается в сферу либо окружность так, что вершина приходится на центр. Другие особенности фигуры:

При решении задач на сайтах онлайн либо из учебников по геометрии используются теоремы, которые связывают пирамиду с иными телами.

Для расчета нужной величины применяется калькулятор, подходящая формула, свойства многогранников. Учёные доказали, что вокруг пирамиды можно описать сферу, если в основании находится многоугольник с окружностью.

Центр сферы — точка, в которой пересекаются плоскости, проходящие через центральную часть ребер. Из теоремы вытекает, что около прямоугольной, квадратной и правильной пирамиды возможно описать сферу. В фигуру вписывается сфера, если биссекторные плоскости двугранных внутренних углов пересекаются в единой точке. Согласно другой теореме, конус вписан в пирамиду, если их вершины совпадают. Основание фигур и апофемы совпадают. Конус описывается вокруг пирамиды, если БР последней фигуры одинаковые.

Цилиндр находится внутри многоугольника, если любое его основание совмещено с окружностью. Цилиндр описан около пирамиды, если вершина последней фигуры находится на одном из его оснований. Другая его нижняя часть описана внизу пирамиды. Подобное действие возможно, если в основании пирамиды вписан многоугольник.

Для правильной пирамиды (нижняя сторона представлена в виде правильного многоугольника с вершиной в центре) характерны некоторые свойства: равенство БР, гранями являются равнобедренные конгруэнтные (равные) треугольники, внутрь и вокруг легко описывается и вписывается сфера. В последнем случае, когда центры сфер совпадают, сумма плоских углов равняется числу пи, а каждый — π/n, где n — количество сторон фигуры в основании.

Пирамида считается прямоугольной, если одно БР перпендикулярно нижней стороне. В таком случае ребро является высотой. В тетраэдре либо треугольной пирамиде любая грань принимается в качестве основания.

Практические задания

На ЕГЭ выпускники решают задачи с объёмом и площадью куба, правильного многоугольника. Фигуры размещены на плоскости либо в системе координат. Основные формулы, которые применяются для вычисления показателей:

Задача 1. Дан четырёхугольный многогранник с равными сторонами в 72 и боковыми ребрами — по 164. Нужно найти площадь четырехугольной пирамиды.

Решение: Так как S=Sбок+Sосн, подставив данные в формулу, получается 4S+a ². Так как Sбок состоит из 4-х одинаковых по площади треугольников, а основание представлено в виде квадрата, поэтому для нахождения площади Sбок используется формула Герона: S=√p (p-a)(p-b)(p-c).

Для вычисления полупериметра потребуется (a+b+c)/2. В формулу поставляются данные. Выходит, что P=(72+164+164)/2=200. Тогда S=√200 (200−72)(200−164)(200−164)=√200х128х36х36=√100х256х36х36=10х16х6х6х=5760. Подставив данные в формулу, находится площадь: S=4х5760+72х72=28224.

Задача 2. Стороны нижней части в шестиугольном многоугольнике равняются 22, а ребра — 61. Нужно найти Sбок. пов.

Решение: Основание фигуры представлено в форме шестиугольника с одинаковыми сторонами. Его площадь соответствует площади шести треугольников. Их стороны равны 61, 61 и 22. Величина вычисляется по формуле S=6S. Чтобы найти S, применяется формула Герона: S=√p (p-a)(p-b)(p-c). Полупериметр равен (a+b+c)/2.

Р=(61+61+22)/2=72. S=√72 (72−61)(72−61)(72−22)=√72х9х9х50=√36х2х9х9х2х25=540.

Данные, подставив в Sбок. пов., приведут к результату 3240. В задаче 1 и 2 можно вычислить площадь через апофему.

Задача 3. Необходимо определить S пов. прав. четырёхугольной пирамиды, когда стороны основания равняются 6, а высота — 4.

Решение: Для определения S вычисляются площади БП и основания. Используется формула Sбок +S осн=4S+ a ². S осн равняется 36, так как оно представлено в виде квадрата со сторонами в 6. БП состоит из 4-х граней либо равных треугольников. Для нахождения площади вычисляется основание и высота фигуры:

Площадь фигуры соответствует половине произведения апофемы и основания. Первый элемент проведён ко второму. Так как известно, что основание равно 6, поэтому находится высота. Если начертить и рассмотреть треугольник, можно заметить, что катет равен 4. Он же является высотой пирамиды. Значение второго катета — 3 (он соответствует ½ ребра основания).

Для вычисления гипотенузы используется теорема Пифагора:

Площадь БП вычисляется следующим образом:

При решении задач рекомендуется ориентироваться на чертеж, использовать общепринятые теоремы и свойства фигур. Для наглядности фигура размещается в плоскости в нескольких проекциях. В старших классах, чтобы найти объём либо площадь, многогранники отображаются с помощью координат, функций косинуса и синуса.

Последние переменные используются, чтобы найти значение углов, как острых, так и тупых. Через полученное число и дополнительные формулы, аксиомы вычисляется площадь разных составных элементов фигуры.

Источник

Формула площади боковой поверхности пирамиды произвольного типа и правильной: пример задачи

Каждый человек слышал о великих египетских каменных сооружениях, главным из которых является пирамида Хеопса. В курсе стереометрии рассматривают характеристики различных пирамид. Одним из важных параметров фигуры является площадь боковой поверхности. По какой формуле боковой поверхности площадь пирамиды следует рассчитывать, расскажет данная статья.

Что собой представляет пирамида в геометрии?

Прежде чем говорить о пирамиде и формуле площади боковой поверхности, дадим определение самой фигуры. Под ней полагают объемный многогранник, состоящий из одного n-угольного основания и n треугольников. Все треугольники имеют одну общую с основанием сторону, а также пересекаются в точке, которая называется вершиной. Ниже показана произвольная четырехугольная пирамида:

Вам будет интересно: Генералы чеченской войны: пофамильный список, краткая биография и фото

Любая пирамида состоит из:

Причем все названные элементы бывают двух типов: те, которые относятся к основанию, и те, которые принадлежат боковой поверхности.

Параметры боковой поверхности для фигуры произвольного типа

Как находить площадь (формула представлена ниже) поверхности боковой грани рассматриваемой фигуры? Ответить на этот вопрос несложно, если знать, что боковая поверхность образована n треугольниками. Это означает, что достаточно для каждого из них вычислить площадь, а затем сложить полученные значения и результатом будет искомый показатель. Тем не менее, сделать это не всегда просто для пирамиды произвольного типа. Приведем пример. Ниже рисунок демонстрирует три пирамиды, которые называются четырехугольными наклонными.

С первого взгляда видно, что все боковые треугольники являются разными. Это означает, что для определения их площадей необходимо знать все стороны основания и высоту каждого треугольника. Она называется «апофемой». Если апофему i-го треугольника обозначить символом hi, а длину соответствующей стороны основания назвать ai, тогда получим для общего типа пирамиды формулу боковой поверхности площади:

Таким образом, для вычисления величины S фигуры произвольного типа необходимо знать 2*n ее параметров.

Правильные пирамиды и их боковая поверхность

Приведенная в предыдущем пункте формула площади поверхности пирамиды общего типа принимает конкретный вид для правильных фигур. Правильной называется та пирамида, которая содержит в основании равностороннюю и равноугольную фигуру, а ее высота попадает точно в центр основания. На рисунке ниже показан набор правильных пирамид, изготовленных из бумаги:

Важно не путать величину h1 в формуле с высотой h пирамиды. Апофема h1 и высота h связаны единым равенством через длину основания для любой правильной пирамиды.

Задача на вычисление боковой поверхности треугольной пирамиды

Известно, что треугольная правильная пирамида имеет высоту 43 см и длину основания 12 см. Чему равна площадь ее боковой поверхности?

Рассмотрев прямоугольный треугольник внутри этой пирамиды, который образован сторонами h1, h и 1/3 высоты основания, получаем:

h1 = √(h2 + a2/12) = √(432+122/12) = 43,14 см.

Теперь осталось применить записанную выше формулу для S, учитывая при этом, что n=3. Получаем:

S = 1/2*n*a*h1 = 1/2*3*12*43,14 = 776,52 см2.

Записанная формула определения апофемы через высоту справедлива только для треугольной правильной пирамиды.

Источник

Площадь боковой поверхности пирамиды – формула, пример расчета

Фигура пирамида

Прежде чем приводить определение апофемы пирамиды, познакомимся с самой фигурой. Пирамида представляет собой многогранник, который образован одним n-угольным основанием и n треугольниками, составляющими боковую поверхность фигуры.

Всякая пирамида имеет вершину – точку соединения всех треугольников. Перпендикуляр, проведенный из этой вершины к основанию, называется высотой. Если высота пересекает в геометрическом центре основание, то фигура называется прямой. Пирамида прямая, имеющая равностороннее основание, называется правильной. На рисунке показана пирамида с шестиугольным основанием, на которую смотрят со стороны грани и ребра.

Элементы правильной пирамиды

Если в основании правильной пирамиды лежит треугольник, четырехугольник и т.д. то она называется правильной треугольной , четырехугольной и т.д.

Шестиугольная пирамида

В целом это одна из последних и самых сложных тем в стереометрии. Изучается где-то в 10-11 классах и рассматривается только вариант, когда в основании находится правильная фигура. Одно из труднейших заданий по ЕГЭ зачастую бывает связано с этим параграфом.

И-так, в основании правильной шестиугольной пирамиды лежит правильный шестиугольник. Что это значит? У фигуры в основании все стороны равны. Боковые же части состоят из равнобедренных треугольников. Вершины их соприкасаются в одной точке. Данная фигура представлена на фото ниже.

Какая пирамида будет изучаться

Правильная шестиугольная пирамида представляет собой фигуру в пространстве, которая ограничена одним равносторонним и равноугольным шестиугольником, и шестью одинаковыми треугольниками равнобедренными. Эти треугольники могут быть также равносторонними при определенных условиях. Эта пирамида ниже показана.

Здесь изображена одна и та же фигура, только в одном случае она повернута боковой гранью к читателю, а в другом – боковым ребром.

Правильная шестиугольная пирамида имеет 7 граней, которые были названы выше. Также ей принадлежат 7 вершин и 12 ребер. В отличие от призм, у всех пирамид имеется одна особая вершина, которая образована пересечением боковых треугольников. Для правильной пирамиды она играет важную роль, поскольку опущенный с нее на основание фигуры перпендикуляр является высотой. Далее высоту будем обозначать буквой h.

Показанная пирамида называется правильной по двум причинам:

Связь пирамиды с конусом

Формулы для правильной пирамиды

Формулы для нахождения объема и площади боковой поверхности:

Обозначения:
V – объем пирамиды
S – площадь основания
h – высота пирамиды
Sb – площадь боковой поверхности
a – апофема (не путать с α)
P – периметр основания
n – число сторон основания
b – длина бокового ребра
α – плоский угол при вершине пирамиды

Данная формула нахождения объема может применяться только для правильной пирамиды:

, где

V – объем правильной пирамиды
h – высота правильной пирамиды
n – число сторон правильного многоугольника, который является основанием для правильной пирамиды
a – длина стороны правильного многоугольника

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

Верно и обратное.

Найти площадь поверхности через:

периметр, площадь и апофему стороны и высотуПериметр основания (P):Площадь основания (Sосн):Апофема (L):Сторона основания (a):Число сторон основания (n):Высота пирамиды (h):

Пирамида – многогранник, основание которого — многоугольник, а остальные грани – треугольники, имеющие общую вершину.

Площадь поверхности правильной пирамиды формула:
, где P – периметр основания, Sосн – площадь основания, L – апофема (перпендикуляр, из вершины на ребро основания)

Площадь поверхности правильной пирамиды формула:
, где a – сторона основания, n – число сторон основания, h – высота пирамиды

Виды пирамид

Существуют 3 вида пирамид:

Объем пирамиды

Так же, как и площадь, объем шестиугольной правильной пирамиды является важным ее свойством. Этот объем рассчитывается по общей формуле для всех пирамид и конусов. Запишем ее:

Здесь символом S_o названа площадь шестиугольного основания, то есть S_o = S₆.

Подставляя в формулу для V записанное выше выражение для S₆, приходим к конечному равенству для определения объема пирамиды шестиугольной правильной:

Тетраэдры. Правильные тетраэдры

Определение 5. Произвольную треугольную пирамиду называют тетраэдром.

где буквой D обозначена середина ребра AC (рис. 6).

,

.

По теореме Пифагора из треугольника BSO находим

Ответ.

Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.

L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.

Правильная усеченная пирамида

Если провести сечение, параллельное основанию пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Это сечение для усеченной пирамиды является одним из её оснований.

Высота боковой грани (которая является равнобокой трапецией ), называется — апофема правильной усеченной пирамиды.

Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная.

Как быть при нахождении площади основания пирамиды?

Оно может быть совершенно любой фигурой: от произвольного треугольника до n-угольника. И это основание, кроме различия в количестве углов, может являться правильной фигурой или неправильной. В интересующих школьников заданиях по ЕГЭ встречаются только задания с правильными фигурами в основании. Поэтому речь будет идти только о них.

То есть равносторонний. Тот, у которого все стороны равны и обозначены буквой «а». В этом случае площадь основания пирамиды вычисляется по формуле:

Формула для вычисления его площади самая простая, здесь «а» – снова сторона:

Произвольный правильный n-угольник

У стороны многоугольника то же обозначение. Для количества углов используется латинская буква n.

Источник

Площадь поверхности пирамиды

Пирамида – это объемное тело, ограниченное пирамидальной поверхностью. Пирамидальная поверхность состоит из боковых граней, представляющих собой треугольники, и основания пирамиды.

O – вершина пирамиды

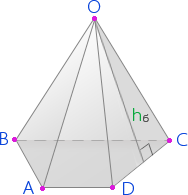
h _б– высота боковой грани пирамиды

Площадь поверхности пирамиды – это площадь ограничивающей его пирамидальной поверхности.

Площадь поверхности пирамиды состоит из площади боковой поверхности пирамиды и площади основания пирамиды.

Площадь боковой поверхности пирамиды (S_б) равна произведению полупериметра основания пирамиды (1/2∙P) на высоту боковой грани пирамиды ( h _б):

Полная площадь поверхности пирамиды определяется по формуле:

Источник

Площадь поверхности пирамиды

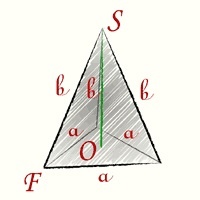
Площадь поверхности пирамиды. В этой статье мы рассмотрим с вами задачи с правильными пирамидами. Напомню, что правильная пирамида – это пирамида, основанием которой является правильный многоугольник, вершина пирамиды проецируется в центр этого многоугольника.

Боковая грань такой пирамиды это равнобедренный треугольник. Высота этого треугольника, проведенная из вершины правильной пирамиды, называется апофемой, SF – апофема:

В типовых заданиях, как правило, рассматриваются правильные треугольные, четырёхугольные и шестиугольные пирамиды. Задач с правильными пятиугольными и семиугольными пирамидами пока не встречал.

Кстати, на проекте youclever неплохой визуальный гид по пирамиде: с красивыми картинками, основными формулами и свойствами. Подходит тем, кто лучше воспринимает информацию визуально. Там весь учебник по геометрии такой — мало задач, но много понятных рисунков.

Формула площади всей поверхности проста — требуется найти сумму площади основания пирамиды и площади её боковой поверхности:

Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.

Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:

*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.

Площадь боковой стороны пирамиды можем вычислить воспользовавшись формулой Герона :

Таким образом, площадь поверхности пирамиды равна:

Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.

Основанием правильной шестиугольной пирамиды является правильный шестиугольник.

Площадь боковой поверхности данной пирамиды состоит из шести площадей равных треугольников с сторонами 61,61 и 22:

Найдём площадь треугольника, воспользуемся формулой Герона:

Таким образом, площадь боковой поверхности равна:

*В представленных выше задачах площадь боковой грани можно было найти используя другую формулу треугольника, но для этого нужно вычислить апофему.

27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

Для того, чтобы найти площадь поверхности пирамиды нам необходимо знать площадь основания и площадь боковой поверхности:

Площадь основания равна 36, так как это квадрат со стороной 6.

Боковая поверхность состоит из четырёх граней, которые являются равными треугольниками. Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):

*Площадь треугольника равна половине произведения основания и высоты проведённой к этому основанию.

Основание известно, оно равно шести. Найдём высоту. Рассмотрим прямоугольный треугольник (он выделен жёлтым):

Один катет равен 4, так как это высота пирамиды, другой равен 3, так как он равен половине ребра основания. Можем найти гипотенузу, по теореме Пифагора:

Значит площадь боковой поверхности пирамиды равна:

Таким образом, площадь поверхности всей пирамиды равна:

27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.

27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

Существуют ещё формулы площади боковой поверхности правильной пирамиды. В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:

где φ — двугранный угол при основании

Отсюда площадь полной поверхности правильной пирамиды может быть найдена по формуле:

Еще одна формула боковой поверхности правильной пирамиды:

P — периметр основания, l — апофема пирамиды

*Эта формула основывается на формуле площади треугольника.

Если хотите узнать подробнее как эти формулы выводятся, не пропустите, следите за публикацией статей. На этом всё. Успеха Вам!

Источник

Как найти площадь боковой поверхности пирамиды

Здравствуйте!
Помогите разобраться как найти площадь боковой поверхности пирамиды.
Спасибо!

Как найти площадь боковой поверхности пирамиды
Поскольку пирамида — это многогранник, у которого основанием является многоугольник, а боковые грани — треугольники, имеющие общую вершину, то для вычисления площади боковой поверхности нужно найти площади всех боковых граней и вычислить их сумму.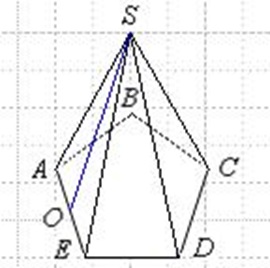

Если пирамида является правильной, то все боковые грани, как и их площади, будут равными между собой.
Для правильной пирамиды площадь боковой поверхности вычисляется по формуле:

Апофемой является высота боковой грани, проведенная из ее вершины. На рисунке апофема обозначена OS.
Разберем вычисление площади боковой поверхности пирамиды на примере.

Пример.
Вычислить площадь боковой поверхности пирамиды, если известно, что ее основанием является правильный пятиугольник со стороной 7 см, а апофема равна 13 см.

Решение.
Используем формулу, рассмотренную выше:

Вычислим периметр основания. Из условия известно, что в основании пирамиды лежит правильный пятиугольник со стороной 7 см. Его периметр равен сумме всех сторон или произведению количества сторон на длину одной стороны:
(см).
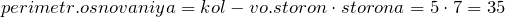
Подставим полученное значение в формулу площади:

(кв. см).

Источник

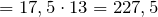
Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок № 15. Пирамида

Перечень вопросов, рассматриваемых в теме:

Глоссарий по теме

Пирамида – многогранник, составленный из n-угольника и n треугольников

Основание пирамиды – грань пирамиды, являющаяся n-угольником

Вершина пирамиды – общая точка всех треугольников, лежащих в боковых гранях.

Боковая грань – грань пирамиды, являющаяся треугольником

Боковые ребра – общие отрезки боковых граней

Высота – перпендикуляр, опущенный из вершины пирамиды на ее основание

Апофема – высота боковой грани правильной пирамиды

Правильная пирамида – пирамида, в основании которой лежит правильный многоугольник, а отрезок, соединяющий вершину и центр основания пирамиды, является высотой

Усеченная пирамида – многогранник, образованный двумя n-угольниками, расположенными в параллельных плоскостях (нижнее и верхнее основание) и n-четырехугольников (боковые грани).

Площадь полной поверхности пирамиды – сумма площадей всех граней пирамиды

Площадь боковой поверхности пирамиды – сумма площадей боковых граней пирамиды

Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. и профильным изучением математики общеобразоват. Учреждений.. – М.: Дрофа, 2009. – 368 с.: ил. (117 с. – 121 с.)

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255 с. (65 с. – 68 с.)

Открытые электронные ресурсы:

Многогранники.ru – сайт о создании моделей многогранников из бумаги https://www.mnogogranniki.ru/

Теоретический материал для самостоятельного изучения

Рассмотрим многоугольник A₁A₂. A_n и точку Р, не лежащую в плоскости этого многоугольника (рис.1). Соединив точку Р с вершинами многоугольника, получим n треугольников: PA₁A₂, PA₂A₃,…, PA_nA₁.

Многогранник, составленный из n-угольника A₁A₂. A_n и n треугольников, называется пирамидой. Многоугольник A₁A₂. A_n называется основанием, а треугольники PA₁A₂, PA₂A₃,…, PA_nA₁ – боковые грани пирамиды, отрезки PA₁, PA₂,…, PA_n – боковые ребра пирамиды, точка Р – вершина пирамиды. Пирамиду с основанием A₁A₂. A_n и вершиной Р называют n-угольной пирамидой и обозначают PA₁A₂. A_n.

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 PH является высотой. Обратите внимание, что высота может лежать и вне пирамиды (рис. 3) или быть одним из боковых ребер (рис. 4).

Рисунок 3 – высота вне пирамиды

Будем называть пирамиду правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Напомним, что центром правильного многоугольника называется центр вписанной в него (или описанной около него) окружности (рис.5).

Рисунок 5 – Правильная пирамида

Правильная пирамида обладает несколькими хорошими свойствами. Давайте выясним, какими.

Рассмотрим правильную пирамиду PA₁A₂. A_n (рис. 5).

Пусть О – центр описанной около основания окружности, тогда РО – высота пирамиды, значит РО перпендикулярен любой прямой, лежащей в плоскости основания. Таким образом, высота РО перпендикулярна радиусам А₁О, А₂О. А_nО.

Боковые ребра пирамиды равны, значит боковые грани – равнобедренные треугольники. Основания этих треугольников равны друг другу, так как в основании лежит правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников.

Таким образом, верны следующие утверждения:

Введем еще одно определение. Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины. На рисунке 5 PE – одна из апофем.

Все апофемы правильной пирамиды равны друг другу как высоты в равных треугольниках.

Возьмем произвольную пирамиду PA₁A₂. A_n и проведем секущую плоскость β, параллельную плоскости основания пирамиды α и пересекающую боковые ребра в точках В₁,В₂. В_n (рис. 6). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники A₁A₂. A_n и В₁В₂. В_n (нижнее и верхнее основания соответственно), расположенные в параллельных плоскостях и n четырехугольников A₁A₂B₂B₁, A₂A₃B₃B₂, … A₁A_nB_nB₁ (боковые грани), называется усеченной пирамидой.

Рисунок 6 – Усеченная пирамида

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой усеченной пирамиды. На рисунке 7 отрезки HH₁ и В1O –высоты усеченной пирамиды.

Рисунок 7 – Высота усеченной пирамиды

Площадь поверхности пирамиды

Площадью полной поверхности пирамиды называются сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.

Для пирамиды, верно равенство S_полн= S_бок+S_осн.

Докажем теорему для площади боковой поверхности правильной пирамиды.

Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Для площади боковой поверхности усеченной пирамиды верна следующая теорема

Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

Примеры и разбор решения заданий тренировочного модуля

Задание 1. В пятиугольной пирамиде все боковые грани равны между собой. Площадь основания равна 42, а площадь боковой грани на 15 меньше. Чему равна площадь полной поверхности пирамиды?

Поскольку в пирамиде все боковые грани равны, то и площади их будут равны. Знаем, что площадь боковой грани на 15 меньше площади основания, значит она равна 27. В пятиугольной пирамиде боковых граней 5. Таким образом площадь полной поверхности равна 27*5+42 = 177.

Задание 2. В правильной пирамиде высота боковой грани равна 10, а в основании лежит квадрат со стороной 4. Чему равна площадь боковой поверхности?

Боковая грань пирамиды – это треугольник. Все боковые грани этой пирамиды равны между собой, так как пирамида правильная. Вычислим площадь треугольника: ½*4*10=20. В основании пирамиды лежит квадрат, значит боковых граней будет 4. Таким образом, площадь боковой поверхности равна 4* 20=80.

Источник

Математика. «Площадь поверхности пирамиды»

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Площадь боковой поверхности пирамиды

Пирамида – это многогранная фигура, в основании которой лежит многоугольник, а остальные грани представлены треугольниками с общей вершиной.

Если в основании лежит квадрат, то пирамиду называется четырехугольной, если треугольник – то треугольной. Высота пирамиды проводится из ее вершины перпендикулярно основанию. Также для расчета площади используется апофема – высота боковой грани, опущенная из ее вершины.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей ее боковых граней, которые равны между собой. Однако этот способ расчета применяется очень редко. В основном площадь пирамиды рассчитывается через периметр основания и апофему:

Рассмотрим пример расчета площади боковой поверхности пирамиды.

Площадь правильной треугольной пирамиды

Правильная треугольная пирамида состоит из основания, в котором лежит правильный треугольник и трех боковых граней, которые равны по площади.
Формула площади боковой поверхности правильной треугольной пирамиды может быть рассчитана разными способами. Можно применить обычную формулу расчета через периметр и апофему, а можно найти площадь одной грани и умножить ее на три. Так как грань пирамиды – это треугольник, то применим формулу площади треугольника. Для нее потребуется апофема и длина основания. Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.

Дана пирамида с апофемой a = 4 см и гранью основания b = 2 см. Найдите площадь боковой поверхности пирамиды.
Для начала находим площадь одной из боковых граней. В данном случае она будет:
Подставляем значения в формулу:
Так как в правильной пирамиде все боковые стороны одинаковы, то площадь боковой поверхности пирамиды будет равна сумме площадей трех граней. Соответственно:

Площадь усеченной пирамиды

Усеченной пирамидой называется многогранник, который образовывается пирамидой и ее сечением, параллельным основанию.
Формула площади боковой поверхности усеченной пирамиды очень проста. Площадь равняется произведению половины суммы периметров оснований на апофему:

Рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.

Дана правильная четырехугольная пирамида. Длины основания равны b = 5 см, c = 3 см. Апофема a = 4 см. Найдите площадь боковой поверхности фигуры.
Для начала найдем периметр оснований. В большем основании он будет равен:
В меньшем основании:
Посчитаем площадь:

Таким образом, применив несложные формулы, мы нашли площадь усеченной пирамиды.

Источник

Площадь боковой поверхности усеченной пирамиды

Усеченная пирамида – это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:

Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:

Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции. Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.

Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:

Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:

Таким же образом находим периметр меньшего основания:

Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:

Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.

Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований.

Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.

Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата. Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:


Теперь используем найденные значения для расчета площади боковой поверхности.

Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.

Источник