Как найти площадь круга зная диаметр
Как найти площадь круга зная диаметр
Формулы площади круга и расчет онлайн
Здесь вы можете рассчитать площадь круга по известным параметрам. Для вычисления достаточно знать радиус, диаметр круга или длину его окружности.
Окружность и круг — в чём отличие?
Часто понятия круг и окружность путают, хотя это разные вещи. Окружность — это замкнутая линия, а круг — это плоская фигура, ограниченная окружностью. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от одной заданной точки — центра окружности.
Круг — бесконечное множество точек на плоскости, которые удалены от заданной точки, называемой центром круга, на значение, не превышающее заданного неотрицательного числа, называемого радиусом этого круга.

Площадь круга
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
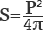
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Онлайн калькулятор. Площадь круга
Используя этот онлайн калькулятор, вы сможете найти площадь круга зная его радиус, диаметр или длину окружности.
Воспользовавшись онлайн калькулятором для вычисления площади круга, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти площадь круга
Ввод данных в калькулятор для вычисления площади круга
В онлайн калькулятор вводить можно числа или дроби 3, 0.4, 5/7. Более подробно читайте в правилах ввода чисел.
Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Теория. Площадь круга
Формулы для вычисления площади круга:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Площадь круга: как найти, формулы
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Как вычислить площадь круга
Соавтор(ы): Grace Imson, MA. Грейс Имсон — преподаватель математики с более чем 40 годами опыта. В настоящее время преподает математику в Городском колледже Сан-Франциско, ранее работала на кафедре математики в Сент-Луисском университете. Преподавала математику на уровне начальной, средней и старшей школы, а также колледжа. Имеет магистерскую степень по педагогике со специализацией на руководстве и контроле, полученную в Сент-Луисском университете.
Количество просмотров этой статьи: 240 352.
Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала нужно запомнить формулу, по которой вычисляется площадь круга: S = π r 2 <\displaystyle S=\pi r^<2>> 
Площадь круга
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность. 
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности: 
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: 

После того, как найдем диагональ – мы сможем рассчитать радиус: 
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Площадь круга
Существует несколько формул для нахождения площади круга. На нашем сайте мы предлагаем вам расчет по трем формулам. В зависимости от исходных данных, площадь круга можно найти через:
Круг — множество точек плоскости, удаленных от заданной точки этой плоскости (эту точку называют центр круга) на расстояние, не превышающее заданное (это расстояние — радиус круга).
Площадь круга онлайн калькулятор
Площадь круга через радиус
Чтобы найти площадь круга, зная его радиус, необходимо воспользоваться формулой:
S= \pi r^2
В этой формуле r — радиус круга, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга через диаметр
Диаметр — отрезок, проходящий через центр окружности и соединяющий две точки на окружности. Диаметр равен двум радиусам.
Если известен диаметр круга, то его площадь можно найти по формуле:
S= \dfrac<\pi><4>d^2
Здесь d — диаметр круга, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга через длину окружности
Длина окружности — это длина замкнутой плоской кривой, ограничивающей круг.
В случае, когда известна длина окружности, площадь круга можно рассчитать по следующей формуле:
S= \dfrac
Здесь l — длина окружности, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга: формулы, как найти
Нужно найти площадь круга – как можно решить задачу и какие методы для этого использовать? Подробно рассмотрим эту тему и научимся без труда решать типовые задания по математике.
Определения и основные понятия
Перед тем, как приступить к разбору формул и решению задач, нужно запомнить основные определения:
Площадь круга через диаметр
Для нахождения площади круга можно использовать несколько методов в зависимости от того, о чем говорится в задании. Если мы знаем величину диаметра, то площадь можно найти по формуле S = d²:4*π. То есть диаметр нам нужно возвести в квадрат, а затем разделить получившееся значение на четыре и умножить на 3,14.
Также этим методом можно воспользоваться, если известен радиус. Для этого требуется умножить его на два, в результате чего удастся узнать диаметр. После этого площадь можно будет найти по указанной ранее формуле.
Площадь круга через радиус и длину окружности
Найти площадь такой фигуры, как круг, можно и через радиус, если воспользоваться формулой S = π*r², то есть квадрат радиуса нужно умножить на число Пи. В этом случае диаметр искать не придется, а значит задачу можно будет решить более простым путем.
Еще один способ доступен, если известна длина окружности. Ее требуется возвести в квадрат и разделить на произведение четырех и числа Пи: S = L²:(4*π).
Задачи для тренировки
Теперь, когда основные формулы уже рассмотрены, стоит закрепить свои знания на примере задач из школьной программы. Допустим, нам нужно найти S круга, если известно, что:
Тема, которую мы рассмотрели, не является сложной, особенно если тщательно ее разобрать. Это же касается и других тем по математике – важно своевременно закреплять свои знания, и тогда удастся преуспеть в изучении этого предмета.
Уделять внимание математике нужно с первых лет обучения в школе, ведь именно в начальных классах ребенку прививаются важнейшие базовые знания и навыки. Развитие математических способностей в младшем возрасте создаст надежную основу для дальнейшего обучения.
Как рассчитать площадь круга — все формулы
Площадь круга часто требуется рассчитать в различных задачах и это не только задачи по геометрии, иногда знать как рассчитывается площадь круга важно знать и в некоторых текстовых задачах алгебры. Итак, давайте разбираться.
Что такое площадь круга
Визуально, площадь круга это величина закрашенной области на рисунке:
Как можно найти площадь круга
Если дан радиус круга
Здесь все зависит от того, какие вам величины даны в самом начале. Если вам дан радиус круга, то площадь круга определяется по формуле:
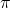
π = длина окружности круга/диаметр этого круга.
Таким образом, приблизительное значение 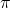
Это приблизительное значение, потому что число π — это то, что мы называем иррациональным числом. Оно не может быть записано как отношение двух целых чисел. Сегодня мы знаем более 12 000 миллиардов знаков после запятой. Однако до сих пор нет определенной модели, которая давала бы все эти значения.
Найти площадь круга можно и с помощью нашего онлайн калькулятора.
Площадь круга
Прежде чем определится, как рассчитать площадь круга, необходимо хорошо усвоить и понять в чём разница между окружностью и кругом. Что называется окружностью, а что подразумевают под словом круг.
Замкнутая кривая ( линия ), чьи точки лежат на одинаковом расстоянии от одной точки её центра, называется окружностью.
Окружность разбивает плоскость на две области: внутреннюю и внешнюю.
Та часть плоскости, которая лежит внутри окружности (вместе с самой окружностью) называется кругом.
Другими словами, для простоты понимания, следует запомнить:
Как найти площадь круга
Для расчета площади круга используется формула:
Как решать задачи на площадь круга
Теперь, зная, по какой формуле считается площадь круга, решим задачи на площадь круга.
Зубарева 6 класс. Номер 675(г)
Найдите площадь круга, радиус которого равен 1,2 см.
Воспользуемся формулой площади круга:
S = π R 2 = 3,14 · 1,2 2 = 3,14 · 1,44 = 4,5216 см 2
Обратите внимание, что площадь измеряется в квадратных единицах. Всегда проверяйте свои ответы, правильно ли вы указали единицы измерения.
Зубарева 6 класс. Номер 677(б)
Выразим из формулы радиус:
S = π R 2
R = √ S / π = √ 1,1304 / 3,14 = √ 0,36 = 0,6 см
Площадь круга
Площадь круга — это размер области внутри окружности, определенный в квадратных единицах измерения. Определять площадь круга можно по формулам, которые давно известны и использовались еще в Древнем мире для определения необходимого количества строительных материалов при построения зданий, амфитеатра и других архитектурных сооружений. В современном мире, с его быстрыми изменениями в архитектуре и в строительстве — определять площадь круга не менее важно. И в задачах алгебры и геометрии это умение пригодится.
Формулы площади круга
Площадь круга через радиус
В геометрии используются следующая формула для определения площади круга через радиус круга:
Здесь 

В формуле фигурирует 


Площадь круга через диаметр
Давайте получим формулу площади круга через диаметр.
Так как диаметр — это два радиуса, то, следовательно, радиус — это половина диаметра:

Подставим это выражение для радиуса в формулу площади круга, получим:
Таким образом, нами получена формула площади круга через диаметр круга:
Площадь круга через длину окружности
Окружность — это граница круга. Зная длину этой границы мы можем рассчитать площадь круга. Итак, формула длины окружности: 

И формула площади круга через длину окружности:
Примеры решения задач
Задача 1
Найдите площадь круга, если известен его радиус 
Решение: Для определения площади круга используем формулу (1):
Задача 2
Найдите площадь земельного участка, если известно, что форма участка — круг, а диаметр участка составляет 50 м.
Решение: Чтобы найти площадь земельного участка, мы должны рассчитать площадь круга с диаметром 50 м. Используем формулу (2):
Задача 3
Длина границы земельного участка круглой формы равна 64 м. Найдите площадь участка.
Решение: граница участка круглой формы — это окружность. Тогда длина этой границы — это длина окружности. Площадь участка — площадь круга, которую мы определим по формуле (3) через длину окружности:
Для того, чтобы определять площадь круга в задачах по геометрии вам нужно определить с тем, какие данные вам известны и использовать те формулы для определения площади круга, которые больше всего подходят.
Задача: определить площадь круга, если известен диаметр окружности
Диаметр окружности 2 см. Найти площадь круга, ограниченного этой окружностью.
Дано:
Диаметр окружности, D = 2 см
Найти площадь круга: S
Используем формулу площади круга через диаметр.
Подставим значения и вычислим результат.
Калькулятор для расчета площади круга через радиус
Нахождение площади круга: формула и примеры
Круг – это геометрическая фигура; множество точек на плоскости, которые лежат внутри окружности.
Формула вычисления площади
По радиусу
Площадь круга (S) равняется произведению числа π и квадрата его радиуса.
Радиус круга (r) – это отрезок, соединяющий его центр и любую точку на окружности.
Примечание: для расчетов значение числа π округляется до 3,14.
По диаметру
Площадь круга равняется одной четвертой произведения числа π и квадрата его диаметра:
Примеры задач
Задание 1
Найдите площадь круга, радиус которого равен 9 см.
Задание 2
Найдите площадь круга, диаметр которого равняется 8 см.
Калькулятор площади круга
Как нам известно из школьной программы, кругом принято называть плоскую геометрическую фигуру, которая состоит из множества точек, равноудалённых от центра фигуры. Так как все они находятся на одинаковом расстоянии, они формируют окружность.
Удобная навигация по статье:
Калькулятор расчета площади круга
Отрезок, соединяющий центр круга и точки его окружности называют радиусом. При этом, в каждой окружности все радиусы между собой равны. Диаметром круга называется прямая, которая соединяет две точки на окружности и проходит сквозь её центр. Всё это нам понадобится для правильного расчёта площади круга. Кроме того, данная величина рассчитывается при помощи числа Пи.
Как рассчитать площадь круга
Итак, Вы можете рассчитать площадь круга через константу Пи, а также радиус окружности. Для этого необходимо воспользоваться следующей формулой: S=
К примеру, у нас имеется круг с радиусом четыре сантиметра. Давайте рассчитаем его площадь: S=<3,14>*4^2=<3,14>*16=50,24. Таким образом, площадь окружности составляет 50,24 квадратных сантиметра.
Также, существует специальная формула для расчёта площади круга через диаметр: S=
Давайте рассмотрим пример такого расчёта круга через его диаметр, зная радиус фигуры. Например, мы имеем круг с радиусом равным четырём сантиметрам. Сначала необходимо найти диаметр, который в два раза больше самого радиуса: d=2R, d=2*4=8.
Теперь следует использовать полученные данные для расчёта площади круга по вышеописанной формуле: S=<<3,14>/4 >*8^2=0,785*64=50,24.
Как видите, в итоге мы получаем тот же ответ, что и в первом случае.
Знание описанных выше стандартных формул для правильного расчёта площади круга помогут Вам с лёгкостью находить недостающие величины и определять площадь секторов.
Итак, нам известно, что формула для расчёта площади окружности рассчитывается при помощи умножения неизменной величины Пи на квадрат радиуса самой окружности. Сам же радиус можно выразить через фактическую длину окружности, подставив в формулу выражение через длину окружности. То есть: R=l/2pi.
Теперь необходимо подставить в формулу расчёта площади круга данное равенство и в итоге мы получаем формулу нахождения площади этой геометрической фигуры через длину окружности: S=pi<(l/2pi)>^2=l^2/<4pi>.
К примеру, нам дан круг, длина окружности которого составляет восемь сантиметров. Подставляем значение в рассмотренную формулу: S=<8^2>/<4*3,14>=64/<12,56>=5. И получаем площадь круга равную пяти квадратным сантиметрам.
Площадь круга через диаметр: онлайн-калькулятор
Автоматическое вычисление на нашем сайте поможет быстро освоить незнакомый материал или не отвлекаться на уже знакомые подсчеты. Для этого понадобится только ввести данные в соответствующее окно и получить готовое решение и ответ. Мы не тратим ваше время на регистрацию, не ограничиваем количество расчетов.
Услугами сервиса пользуются школьники и студенты при подготовке к занятиям и во время контрольных, самостоятельных работ. Алгоритмы, заложенные в вычисления, позволяют быстро получить точную цифру без погрешностей.
Материалы, которые помогут вам лучше разобраться в теме:
Калькулятор площади круга по формуле через диаметр
В нашем сервисе используется формула:
где d – диаметр круга,
Почему площадь круга через диаметр в онлайн-калькуляторе и другие задачи лучше находить на нашем сайте
Если вам понадобилось найти решение с использованием других данных или произвести расчет задания на иную тему, найдите подходящий раздел из предложенных на сайте. При затруднении в освоении темы или повышенной сложности заданий напишите консультанту. Он подберет преподавателя под ваш запрос, который поможет быстро и по невысокой цене освоить проблемный материал.
Площадь круга – формулы, примеры расчетов
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Окружность и круг — в чём отличие?
Часто понятия круг и окружность путают, хотя это разные вещи. Окружность — это замкнутая линия, а круг — это плоская фигура, ограниченная окружностью. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от одной заданной точки — центра окружности.
Круг — бесконечное множество точек на плоскости, которые удалены от заданной точки, называемой центром круга, на значение, не превышающее заданного неотрицательного числа, называемого радиусом этого круга.
Площади фигур
Уравнение окружности
r 2 = ( x – a ) 2 + ( y – b ) 2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:
| < | x = a + r cos t |
| y = b + r sin t |
Найти площадь кругаОнлайн калькулятор
 |  |
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Формула площади круга через диаметр
Формула площади круга через радиус
Таблица с формулами площади круга
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула | |
| 1 | радиус |  | |
| 2 | диаметр |  | |
| 3 | длина окружности |  | |
| 4 | сторона квадрата вписанного в круг |  | |
| 5 | сторона квадрата, в который вписан круг |  | |
| 6 | стороны треугольника |  | |
| 7 | сторона равностороннего треугольника |  | |
| 8 | высота равностороннего треугольника |  | |
| 9 | боковая сторона и основание равнобедренного треугольника |  | |
| 10 | стороны при прямом угле треугольника |  | |
| 11 | боковая сторона и основание равнобедренного треугольника |  | |
| 12 | боковые стороны равнобедренного треугольника и угол между ними |  | |
| 13 | стороны прямоугольного треугольника |  | |
| 14 | сторона и угол при основании треугольника |  | |
| 15 | сторона равностороннего треугольника |  | |
| 16 | сторона и угол при основании трапеции |  | |
| 17 | боковые стороны и диагональ трапеции |  | |
| 18 | стороны прямоугольника |  | |
| 19 | сторона и количество сторон многоугольника |  | |
| 20 | сторона шестиугольника |  |
Длина окружности круга
Для примера решим простую задачу, где нужно найти длину окружности, у которой известен радиус r =2 см.
Подставляем известные данные в формулу длины окружности и получаем, что длина окружности примерно равна 12,56 см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: 

После того, как найдем диагональ – мы сможем рассчитать радиус: 
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Центральный угол, вписанный угол и их свойства
Основные свойства касательных к окружности
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Онлайн калькулятор для расчета площади круга
Площадь круга можно найти, если известны:
Расчет площади круга — это не только учебная задача для школьников шестого класса. Круглых предметов довольно много и в реальной жизни, а необходимость посчитать их площадь хотя и не так часто, но возникает. Например, это может потребоваться для определения количества краски для ремонта круглой столешницы или для расчета площади остекления дома, спроектированного и построенного в готическом стиле.
Сложность вычисления площади круга связана с тем, что практически во всех формулах встречается иррациональное число пи, которое в обычных расчетах принимается равным 3,14. Даже если вы с детства неплохо владеете устным счетом, вычислить в уме площадь круга, радиус которого выражается дробным числом, будет довольно затруднительно. Но теперь это и не нужно, поскольку мы разработали для вас удобный сервис, который сделает все расчеты за несколько мгновений. Причем необязательно пересчитывать известные вам размеры конструкции так, чтобы получить значение радиуса в явном виде. Наш калькулятор умеет считать площадь круга практически по всем параметрам, которые могут быть известны на практике.
Расчет площади круга по его радиусу
Формула площади круга через диаметр
Если вам известен диаметр круга, можно разделить его пополам и подставить в предыдущую формулу. Но можно поступить еще проще. Перейдите на вторую вкладку и введите диаметр D в качестве исходных данных. Калькулятор использует формулу S = π · D2 / 4 и рассчитывает площадь круга прямо в процессе вашего ввода. Если после вывода результата вы измените значение диаметра, результат пересчитается автоматически.
Площадь круга через длину окружности
Для начала на всякий случай определимся с терминологией: окружность — это линия, каждая точка которой удалена на одинаковое расстояние от центра, а круг — это все, что находится внутри нее. Таким образом, окружность представляет собой внешнюю границу круга. Ее длина равна 2 · π · R (за R по-прежнему обозначаем радиус круга и окружности). Теоретически отсюда можно вычислить радиус и посчитать площадь круга по классической формуле. Но, опять же, есть более простой способ: воспользоваться нашим онлайн-калькулятором и ввести известную длину окружности, не выполняя ненужных промежуточных действий. Результат, как и всегда, будет выведен мгновенно.
Расчет площади круга по стороне вписанного квадрата
Как найти площадь круга, если известна сторона описанного вокруг него квадрата
Предположим, вы хотите купить бассейн, под который у вас выделен квадратный участок известных размеров. Вполне закономерно желание поставить резервуар максимальной емкости, которая определяется его высотой и площадью. То есть нужно найти площадь круга максимального радиуса, вписанного в квадрат, что и приводит к необходимости ее расчета через сторону этого квадрата. Нетрудно заметить, что задача сводится к вычислению площади круга по известному диаметру, так как сторона описанного вокруг него квадрата как раз и есть его диаметр. Но мы сделали для этого варианта отдельную вкладку, чтобы не заставлять вас запоминать ненужную информацию. Просто вводите длину стороны квадрата и получайте результат точно так же, как и во всех предыдущих случаях.
Вычисление площади круга через диагональ описанного квадрата
Расчет площади круга по площади описанного вокруг него квадрата
Условия использования онлайн-калькулятора расчета площади круга
Вы можете пользоваться данным сервисом совершено бесплатно. Количество расчетов не ограничено, калькулятор запускается из любого браузера, ничего устанавливать на ваш компьютер не нужно. Если наш сайт оказался полезным для вас, напишите об этом в комментариях и не забудьте сохранить его в закладках, чтобы иметь возможность выполнять любые математические вычисления, не отходя от компьютера.
Способы вычисления площади круга
Основные способы вычисления площади круга, формулы
Перед тем, как рассмотреть методы нахождения площади круга, введем основные понятия.
Круг — это участок плоскости, который расположен внутри окружности.
Окружность — это замкнутая плоская кривая, включающая множество точек, находящихся на одинаковом расстоянии от центра.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Радиус представляет собой отрезок, ограниченный с одной стороны центром круга, с другой — любой точкой, находящейся на внешней окружности данной фигуры.
Диаметром называется такой отрезок, который проходит через центр окружности и соединяет две точки рассматриваемой кривой.
Теперь разберем основные способы нахождения площади круглой фигуры.
Через радиус
Данный метод предполагает, что нам известен радиус круга, площадь которого нужно найти. Вычисления выполняются по формуле, согласно которой площадь круга равна квадрату радиуса, умноженному на число Пи. В записи указанная формула имеет вид:
Через диаметр
Если мы располагаем информацией о диаметре, то для расчета площади круга можно применить выражение, по которому искомая величина будет равна квадрату диаметра, умноженного на частное числа Пи и 4. То есть формула выглядит так:
Через длину окружности
Для того, чтобы воспользоваться этим способом, необходимо знание длины окружности (L). В этом случае площадь круга представлена как частное, в котором делитель равен квадрату длины окружности, а делитель — это произведение числа Пи и 4. На математическом языке данная формула записывается так:
Площадь круга описанного вокруг квадрата
Бывают ситуации, когда внутри круга расположен квадрат, а все его четыре вершины принадлежат окружности заданного круга. Чтобы найти площадь круга, достаточно знать сторону правильного четырехугольника, который он описывает. Тогда площадь поверхности заданной фигуры равняется произведению числа Пи и половины квадрата этой стороны, то есть:
Нахождение через площадь сектора круга
Сектор круга представляет собой участок круговой плоскости, которая ограничена с двух сторон радиусами, а с третьей стороны — дугой.
Существует два метода расчета площади кругового сектора:
Примеры задач с решением
Найдите площадь круга, если известно, что длина окружности составляет 85 миллиметров.
Произведем расчеты на основании известной формулы:
Детская песочница имеет квадратную форму со стороной, равной 1,5 метрам. По технологии песочницу устанавливают на прорезиненном участке круглой формы, равном кругу, в который можно вписать такую песочницу. Найдите площадь территории, на которую нужно уложить резиновую крошку.
Воспользуемся формулой: \(S=0,5a^2\mathrm\pi=0,5\cdot1,5^2\cdot13,14=14,7825 \)
Как узнать площадь круга, зная длину его окружности?
Например, нужно вычислить площадь круглой колонны. Диаметр не измеришь. Какие формулы использовать, чтобы высчитать её площадь.
S = П*r²
Формула длины окружности (периметра):
P = 2*П*r
Из окружности находим радиус:
r = P/2П
И подставляем это в формулу площади:
S = П*(P/2П)² = П*P²/4П²
Если я правильно раскрыл скобки со степенями, то:
S = P²/4П
Для того, чтобы найти площадь круга через длину окружности, нужно сначала вспомнить формулы, по которым вычисляется:
1) Длина окружности.
2) Площадь круга.
Итак, формула для длины окружности:
l =2πR.
Что касается площади круга, то она вычисляется по формуле:
C = πR².
Если известна длина окружности, то легко выразить её радиус. После этого остаётся лишь подставить полученное значение в формулу для площади круга.
C = π * (l / 2π)² = l² / 4π.
Пример
Дана длина окружности l = 20 см. Нужно найти площадь круга.
C = l² / 4π = (20 * 20) / (4 * 3,14) = 400 / 12,56 = 31,85 см.
Таким образом, если длина окружности равна 20 см., то площадь круга будет составлять 31,85 см.
Площадь круга можно легко рассчитать по известной формуле, в которую входит радиус круга (или окружности, что одно и то же):
S = πR²;
В свою очередь, длина окружности тоже рассчитывается через его радиус:
С = 2πR;
S = π(C/ 2π)².
После возведения в квадрат и необходимых сокращений, получим окончательную искомую формулу:
S = C²/4π
Эта именно та формула, в которой площадь (S) круга выражена через его длину окружности (С).
Площадь круга: формула и примеры. Как найти площадь круга?
В данном материале разберёмся, как найти площадь круга, и зачем это может пригодиться в реальной жизни.
Начнём с формулы, а затем рассмотрим из чего она состоит.
Примеры
Рассмотрим несколько простых примеров расчёта площади круга.
Радиус круга равен 5 сантиметрам. Необходимо найти площадь круга.
Далее перейдём к практическим примерам. Дело в том, что недавно я убедился в том, что некоторые люди не очень хорошо понимают зависимость площади круга от его диаметра. Речь о выборе диаметра пиццы. Многие полагают, что между пиццей диаметром 30 и 40 см очень небольшая разница – четверть, а разница в цене более ощутимая. Но дело в том, что площадь пиццы отличается куда серьёзнее. Давайте посчитаем!
Сразу учтём, что радиус, используемый в формуле, это половина диаметра, рассчитывать отдельно не будем.
Разница намного существеннее 25%, правда? Она составляет 1 — (1256 : 706) = 0,779 или 77,9%. Так что пицца 40 см примерно на три четверти больше пиццы 30 см, а не на одну. Давайте теперь сравним пиццу 20 см и пиццу 30 см.
Пицца 30 см в 2,248 раза (или на 124,8%) больше пиццы 20 см.
Разумеется, геометрии можно найти и куда более полезное применение. Но, надеюсь, теперь всё стало предельно понятно. А для расчёта просто запомните формулу — S=πR².
Площадь круга через диаметр или радиус, калькулятор онлайн
Калькулятор площади круга
Варианты расчёта площади круга через радиус или диаметр
Выбираем вариант расчёта площади
Визуально выглядит так:

Вводим диаметр или радиус:
Площадь круга равна :
Площадь круга с радиусом r равна πr2. Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1⁄2 × 2πr × r).
Как рассчитать площадь круга по диаметру или радиусу, формулы
Найти площадь круга по диаметру или радиусу можно в нашем онлайн калькуляторе. Расчёты можно производить в любых единицах, в метрах(м), дециметрах(дцм), сантиметрах(см), миллиметрах(мм). Просто вводим цифры и получаем результат.
Условные обозначения в формулах
Формула расчёта через радиус
Формула расчёта через диаметр
Что такое площадь круга, как с ней работать.
Круг от руки нарисовать не получиться, рисуют круг с помощью циркуля, но циркуль был не всегда. В самом начале ещё до того как появился циркуль, обычно использовали какую-то верёвку. Как делают, круг начинается с какой-то точки, это называется центр круга. Круг всегда начинается с этой точки по центру.
Окружность она равноудалена от центра поэтому мы берём расстояние, замеряем, и берём верёвку равную этой длине. Обычно верёвку прибивали прямо на землю или ещё куда-то, очень четко фиксировали и чертили круг.
Чтобы так не мучиться, придумали циркуль, с помощью циркуля это делается легко и просто. Расстояние от центра до линии круга оно везде одинаковое, это расстояние называется радиус.
Ещё есть число Пи, многие его знают как 3,14. Что это за число и откуда оно взялось мы говорить не будем в этой статье. Площадь считается как число Пи умножить на радиус в квадрате. Чтобы посчитать площадь круга, нам всего-навсего нужно знать радиус, потому что число Пи всегда известно.
Давайте какой-нибудь пример разберём. Например у нас есть радиус длиной 3 м, и вот у нас получился круг у которого радиус 3 метра, как мы тогда будем считать площадь. Площадь равна Пи умножить на радиус в квадрате, радиус равен трём.
Нам нужно найти площадь, тогда мы берём нашу формулу
где S- площадь; Пи= 3,14; r- радиус.
Подставляем пи 3,14 и R-радиус равен трём и в квадрат. Что значит в квадрате, это значит 3 умножается сама на себя, 3х3=9
Как посчитать, 3 на 3 будет 9 и потом только умножаем на 3,14. В результате получаем 28,26- это и есть площадь круга.
Задача: определить площадь круга, если известна длина окружности
Условие задачи:
Длина окружности 5 м. Найти площадь круга, ограниченного этой окружностью.
Дано:
Длина окружности, L = 5 м
Найти площадь круга: S
Используем формулу площади круга через радиус. Но нам пока не известен радиус, его надо найти.
Определить радиус, нам поможет формула длины окружности.
После преобразования, выразим радиус через длину окружности и подставим значения.
Получили значение радиуса окружности.
В формулу площади круга, подставляем найденное значение радиуса.
Ответ:
Если в формулу площади круга подставить выраженный радиус через длину окружности, то получим следующую формулу, в которой площадь круга сразу выражена через длину окружности. Проверим, подставив наше значение
Площадь круга через длину окружности: онлайн-калькулятор
Сервис с расчетами по алгебре, геометрии и другим предметам создан компанией Zaochnik для студентов и школьников. Благодаря возможности бесплатно производить вычисления, учащиеся смогут закреплять пройденный учебный материал самостоятельно.
Вы увидите не только ответ, но и пошаговое решение. Так можно быстро сориентироваться на самостоятельной или контрольной, найти ошибку в собственных подсчетах, тренироваться отрабатывать понятные и не до конца усвоенные темы. Мы не ограничиваем количество проверок и не тратим ваше время на регистрацию.
Материалы, которые помогут вам лучше разобраться в теме:
Вычисление площади круга через длину окружности по формуле
В основу расчетов заложена формула:
Использование онлайн-калькулятора на нашем сайте помогает:
Возможно, условие вашего задания и условия для ввода в программу не совпадают. В разделе площадей фигур есть алгоритмы с использованием других данных. Найдите нужный и получайте подробное решение.
Если вам нужна помощь в решении задач или сопровождение на контрольной, напишите об этом консультанту. Исполнитель подключится к вам во время проверки знаний и подскажет ответы или выполнит работу к нужной дате.
Онлайн-калькулятор площади круга: формулы через радиус, диаметр и длину окружности
С помощью нашего онлайн калькулятора можно найти площадь круга зная его радиус, диаметр, длину окружности.
3 основных формулы площади круга:
Через радиус
Через диаметр
Через длину окружности
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Чтобы окончательно разобраться в теме “Круг и его площадь”, смотрите видео урок на котором учитель математики понятно рассказывает все, что вам нужно знать.
Средняя оценка / 5. Количество голосов:
Или поделись статьей
Видим, что вы не нашли ответ на свой вопрос.
Площадь круга
Существует множество сложных задач о площади круга и его частей: секторов, сегментов, пересечений.
После прочтения этой статьи они станут для тебя простыми!
А еще посмотри задачи на окружности (ЕГЭ 16) из нашего курса подготовки.
Площадь круга — коротко о главном
Основные формулы:
Правило нахождения нестандартной части круга:
Непонятную фигуру нужно разделить на несколько стандартных (сектор, сегмент, треугольник и т.д.), потом посчитать площадь каждой стандартной фигуры и сложить все площади.
Площадь круга — подробнее
\( \displaystyle R\) — радиус,
\( \displaystyle \pi \) – число \( \displaystyle \approx 3,1415\)
Производит впечатление? Представляешь, сколько времени математики думали, пока не додумались, что…
…площадь круга радиуса \( \displaystyle R\) ровно (!) в \( \displaystyle \pi \) раз больше площади квадрата со стороной \( \displaystyle R\).
Ну вот, а теперь – площадь части круга.
Площадь сектора круга
Смотри на картинку, это такая «хорошая» часть круга.
где \( \displaystyle a \) – величина угла сектора в радианах (т.е. в числах \( \displaystyle \frac<\pi ><6>\), \( \displaystyle \frac<\pi ><4>\), \( \displaystyle \frac<\pi ><27>\) и т.д.)
Подробнее о радианах смотри в теме «Окружность. Вписанный угол».
Площадь сегмента круга
А это «плохая» часть круга – опять смотри на картинку:
Площадь других частей круга
Иногда бывает, что нужно посчитать площадь какой-нибудь странной части круга. Эта часть может не быть ни сектором, ни сегментом.
Давай рассмотрим два примера.
Пример 1
Окружности радиусов \( \displaystyle 2\) и \( \displaystyle 4\) пересекаются по хорде, равной \( \displaystyle 2\).
Найти площадь общей части кругов.
Решение:
Обрати внимание, что общая часть кругов состоит из двух сегментов: красного и голубого.
Найдем площадь голубого сегмента.
Для этого нужно посмотреть на окружность с центром \( \displaystyle <
\( \displaystyle \Delta A<
Если не помнишь, как считается площадь правильного треугольника, загляни в тему «Равносторонний треугольник».
А вот найти \( \displaystyle \angle A<
Придется применять теорему косинусов!
Пример 2
На стороне \( \displaystyle AB\) треугольника \( \displaystyle ABC\) как на диаметре построена окружность.
Найти площадь общей части треугольника и круга, если \( \displaystyle AB=4\), \( \displaystyle \angle A=30<>^\circ \), \( \displaystyle \angle B=140<>^\circ \).
Решение:
Проведем \( \displaystyle OD\).
Опять наша непонятная фигура разделилась на две стандартные:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Перед вами вебинары, связанные с окружностями и 16 заданием ЕГЭ.
ЕГЭ 16 математика. Метод вспомогательной окружности. Из реального ЕГЭ 2016 года
Метод вспомогательной окружности — это очень классный метод, но, к сожалению, он не всегда очевиден.
Иногда в задаче нет даже намёка ни на какие окружности, но тем не менее, если догадаться её на рисунке достроить, решение становится в разы проще!
Как минимум, сразу же становятся равными друг другу очень неочевидные углы — те, которые опираются на одну дугу, но без окружности увидеть это было бы нереально сложно. Либо произведения отрезков хорд равны друг другу.
Это очень крутой и удобный метод — но нужно понимать, в каких ситуациях он применяется, ведь далеко не всегда нужно на и без того сложный рисунок лепить ещё и окружность.
ЕГЭ 16 Планиметрия Статград март 2021
Задача №16 из мартовского статграда на планиметрию ничем не удивляет: снова окружность и пропорциональные отрезки в ней, прямоугольные треугольники, вот это всё.
Скучно… Раз-два, и ответ готов!
Но погодите-ка, а почему у нас с вами ответ получился разный? И вроде бы оба делаем всё правильно…
На уроках нашего курса я рассказывал о таких задачах, но их уже давненько не попадалось на ЕГЭ, и все уж думали, что ушла эпоха. Конечно, никакого парадокса в этой задаче нет, нужно всего лишь (ха-ха) быть очень внимательными:)
Смотрите видео, и узнаете, в чём же особенность этой задачи, как её правильно решать и оформлять, а также – как ничего не упустить на экзамене и не потерять баллы!
ЕГЭ 16. Планиметрия. Окружности. Задача из олимпиады Физтеха 2020
Планиметрия и окружности! Куда же деться от них в 16 задаче на ЕГЭ?
Те, кто ходил на наш курс подготовки, посвященный 16 задаче, знают, что окружности в задачах на планиметрию попадаются чаще всего.
Никуда не деться от окружностей — остается только научится их решать и получать удовольствие от красивых задач!
В этом видео мы разберём, что бы вы думали? Задачу 16 из ЕГЭ?
Нет! Пойдём дальше — разберём задачу из олимпиады Физтеха прошлого года.
Стойте, не разбегайтесь! Олимпиады далеко не всегда бывают сложными (особенно, если вы прошли наш курс по 16-й задаче).
Эта задача вполне себе ЕГЭ-шного уровня. Про окружности и прямоугольные треугольники. Готовьтесь и “разминайте” свои теоремы Пифагора, теорему синусов и прочих косинусов.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий курсов
Добавить комментарий Отменить ответ
Один комментарий
Некоторые комментарии прошлых лет к этой статье:
Сережа
07 апреля 2019
Как рассчитать площадь треугольника с криволинейной (выпуклой дугой) гипотенузой? Размеры катетов и дуги известны.
Алексей Шевчук
04 сентября 2019
Сережа, проведи прямую гипотенузу, таким образом ты разобьёшь фигуру на 2 части. Вычисли площадь каждой из них, потом сложи.
Роберт
23 ноября 2019
Как найти площадь усеченной полу окружности?
Алексей Шевчук
24 ноября 2019
Роберт, разрежьте её на два сектора и треугольник, посчитайте площадь каждой части, потом сложите.
Владислав
26 января 2020
Как найти площадь наложенных друг на друга секторов, с центрами внутри одной окружности?
Алексей Шевчук
27 января 2020
Владислав, не совсем понятно, это секторы одной окружности, то есть с общим центром? Или центры не совпадают?
Нодир Юлдашев
09 июня 2020
Алексей, как можно посчитать, сколько процентов площади первого круга затмил второй круг исходя из того, сколько части диаметра первого круга затмил второй круг? Сейчас почитал про предстоящее кольцеобразное солнечное затмение 21 июня 2020 года и мне стало интересно. Диаметры кругов могут немножко отличаться из-за периодического изменения расстояния до Солнца и до Луны (в максимуме этого затмения видимый диаметр Солнца будет 31′ 28,4″ (0,524(5)°), а Луны — 30′ 48″ (0,51(3)°)). https://heavens-above.com/SolarEclipse.aspx?jdmax=2459021.77865012 (вкладка «Местные условия»)
Алексей Шевчук
09 июня 2020
Нодир, можно. Углы, которые здесь написаны, пропорциональны диаметрам (а значит, и радиусам) кругов. Отношение площадей равно квадрату отношения радиусов или диаметров (если поделить две формулы площади круга друг на друга, пи сокращается). Делим угловой диаметр Луны на Солнца, возводим в квадрат. Числа должны быть переведены в единицы измерения одного типа, например, в граусы: (0,513 / 0,525)^2 = 0.977^2 = 0.955 = 95.5%
Нодир Юлдашев
09 июня 2020
Алексей, спасибо за ответ, это тоже запомню, я хотел спросить о частичном затмении, которое у нас можно будет наблюдать. Луна подойдёт к Солнцу справа (с запада) и начинает его закрывать. В максимальной фазе Луна закроет 0,652 части диаметра Солнца (это величина (магнитуда) затмения) и 56,4% его площади (это максимальная фаза, %) (нижнюю часть Солнца). Центр Луны через центр Солнца у нас не пройдёт. Потом будет двигаться дальше налево (на восток) и выйдет из солнечного диска. Хотел поинтересоваться, а можно ли составить формулу для вычисления процента площади затмения исходя из величины (магнитуды) затмения. Я сам не школьник, я бухгалтер, и мне просто стало интересно. 🙂
Площадь круга
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
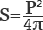
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Результат работы калькулятора так же округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
Калькулятор площади круга
Данный онлайн-калькулятор поможет рассчитать площадь круга по диаметру, через радиус или длину окружности, даже если известно только что-то одно. Формула даёт расчет в квадратных метрах (м 2 ), сантиметрах (см 2 ) и миллиметрах (мм 2 ).
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчет будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 2 2 = 3,14 × 4 = 12,56 м 2 (квадратных метров).
Через диаметр
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 35 2 = ¼ × 3,14 × 1225 = 962 см 2 (квадратных сантиметра).
Зная длину окружности
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 120 2 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм 2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 35 2 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Есть что добавить?
Поделитесь комментарием или этой страницей в соцсетях.
Площадь круга
Длина окружности и площадь круга
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
где C – длина окружности, π – константа, D – диаметр окружности, R – радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
следовательно радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м) |
| 2 · 3,14 | 6,28 |
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
где S – площадь круга, а r – радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | )2 = π | D2 | = π | D2 |
| 2 | 22 | 4 |
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 22 = 3,14 · 4 = 12,56 (см2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
теперь вычислим площадь круга по формуле:
S = πr2 ≈ 3,14 · 3,52 = 3,14 · 12,25 = 38,465 (см2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D2 | ≈ 3,14 | 72 | = 3,14 | 49 | = | 153,86 | = 38,465 (см2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м2.
Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
следовательно радиус будет равен:
r ≈ √12,56 : 3,14 = √4 = 2 (м)
Число π
Длину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно.
Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге.
В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
| Ведро | Таз | Бочка | Тарелка | Стакан | |
| Окружность | 91 см | 157 см | 220 см | 78,5 см | 23,9 см |
| Диаметр | 29 см | 50 см | 70 см | 25 см | 7,6 см |
| Отношение (с точн. до 0,01) | 3,14 | 3,14 | 3,14 | 3,14 | 3,14 |
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π.
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π. В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Площадь круга
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром.
Формула площади круга рассчитывается с помощью математической константы – числа π..
: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров.
Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.
Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Сектор кругового кольца – это плоская фигура, которая представляет собой часть плоскости между дугами двух окружностей с общим центром и разным радиусами, ограниченных двумя радиальными линиями, которые проведены к концам дуги с большим радиусом.
Формула площади сектора кольца, выраженная через внешний и внутренний радиусы
Пусть дана окружность радиуса R и окружности радиуса r. Причем R>r. Совместим центры этих окружностей. Возьмем на окружности с большим радиусом две произвольные точки. Проведем к ним радиусы, которые образуют угол α. Эти радиусы отсекут от окружностей некоторые дуги.
Площадь сектора круга с радиусом r выражается формулой:
где l–длина дуги равная Подставим выражение длины дуги в формулу площади сектора. Получим:
Площадь круга с радиусом R выражается формулой:
где L–длина дуги равная Подставим выражение длины дуги в формулу площади сектора.
Тогда площадь кольца будет равна: Таким образом, площадь сектора кольца равна произведению площади единичного сектора кольца, то есть сектору, соответствующему центральному углу с мерой равной единице на меру центрального угла, соответствующего данному сектору.
Формула имеет вид:
Подставив значения из условия задачи, имеем:
Page 3
Чтобы найти объем конуса необходимо произвести дополнительные построения.
Построим вписанную в конус правильную n-угольную пирамиду и опишем вокруг данного конуса правильную n-угольную пирамиду.Вписанная пирамида содержится в конусе. Из этого следует, что ее объем не больше объема конуса.
Описанная пирамида содержит конус, а это значит, что ее объем не меньше объема конуса.
Впишем в основание вписанной пирамиды окружность.
Если радиус вписанного правильного n-угольника равен R, то радиус вписанной в него окружности будет равен:
Объем вписанной пирамиды вычисляется по формуле:
где S – основание пирамиды.
Площадь данного круга вычисляется по формуле: Площадь основания вписанной пирамиды не меньше площади круга, содержащегося в ней
Поэтому утверждение, что объем вписанной в конус пирамиды не меньше верно.
А следовательно, мы может утверждать, что объем конуса, содержащий эту пирамиду будет больше или равен
V≥
Теперь опишем окружность вокруг основания описанной вокруг конуса пирамиды.
Радиус этой окружности будет равен:
Площадь данного круга вычисляется по формуле:
Основание описанной пирамиды содержится в круге описанном вокруг него. Поэтому площадь основания пирамиды не больше
Поэтому утверждение,что объем описанной пирамиды не больше верно.
А следовательно, мы может утверждать, что объем конуса, содержащий в эту пирамиду будет меньше или равен
Два полученных неравенства равны при любом n.
Если то
Тогда из первого неравенства следует, что V≥
Из второго неравенства
Отсюда следует, что
Объем конуса равен одной трети произведения радиуса на высоту.
Пример расчета объема конусаНайти объем конуса, если его радиус основания равен 3 см, а образующая 5 см.
Объем конуса вычисляется по формуле:
Для того, чтобы воспользоваться данной формулой необходимо найти высоту конуса. Образующая конуса, его высота и радиус основания образуют прямоугольный треугольник.
Воспользовавшись теоремой Пифагора имеем:
Подставим значение радиуса и высоты в формулу объема конуса.Имеем:
Page 4
При нахождении объема усеченного конуса целесообразней рассматривать разность объема полного конуса и объема отсеченного конуса.
Высота усеченного конуса будет равна разности объема полного конуса с радиусом R1и высотой x и объема полного конуса с радиусом R2. и высотой x-h.
Из подобия этих конусов получаем:
Выразим x:
Тогда объем усеченного конуса можно выразить:
Применив формулу разницы кубов, имеем:
Таким образом, формула объема усеченной пирамиды имеет вид:
Объем усеченного конуса вычисляется по формуле:
Для того, чтобы воспользоваться данной формулой необходимо найти высоту конуса. Образующая конуса, его высота и разница радиусов оснований образуют прямоугольный треугольник.
Воспользовавшись теоремой Пифагора получаем: Так как образующая относится к высоте как 17:15, то L=17x, H=15x.
Тогда высота усеченного конуса будет равна:
Подставим значения в формулу объема усеченного конуса. Получим:
Page 5
При нахождении объема усеченного конуса целесообразней рассматривать разность объема полного конуса и объема отсеченного конуса. Читать далее
Чтобы найти объем конуса необходимо произвести дополнительные построения. Читать далее
Усеченный конус – это часть конуса, ограниченная между двумя параллельными основаниями перпендикулярными его оси симметрии. Читать далее
Пусть α– плоскость, точка S– точка, не лежащая в этой плоскости. Возьмем на плоскости произвольный круг с радиусом R. Читать далее
Сектор кругового кольца – это плоская фигура, которая представляет собой часть плоскости между дугами двух окружностей с общим центром и разным радиусами, ограниченных двумя радиальными линиями, которые проведены к концам дуги с большим радиусом. Читать далее
Кольцо – это плоская геометрическая фигура, которая представляет собой часть плоскости между двумя окружностями с общим центром, но имеющими разный радиус. Читать далее
Очень часто на практике приходится сталкиваться с задачей нахождения длины дуги. Читать далее
Шестиугольной пирамидой называется многогранник, в основании которого лежит правильный шестиугольник, а боковые грани образуются одинаковыми равнобедренными треугольниками. Читать далее
Многогранник, в основании которого лежит правильный треугольник, а остальные грани представлены равнобедренными треугольниками называется треугольной пирамидой. Читать далее
Четырехугольной пирамидой называется многогранник, в основании которого лежит квадрат, а все боковые грани являются одинаковыми равнобедренными треугольниками. Читать далее
Page 6
У большинства детей младшего школьного возраста хорошо развита механическая память, которая задействуется при выучивании правил.
Но для отдельных детей, а особенно творческих личностей, зубрежка является невыносимой.
Родители, думающие, что их чадо не способно освоить изучение таблицы умножения и поэтому в дальнейшем будет отставать в математике, заблуждаются. На самом деле к нему нужен совершенно другой, особый подход.
Ниже представлена таблица степеней от 2 до 10 натуральных чисел от 1 до 20.
Читать далее
Таблица кубов натуральных чисел от 1 до 100
Читать далее
Таблица факториалов от 1 до 40
Читать далее
Page 7
При нахождении объема усеченного конуса целесообразней рассматривать разность объема полного конуса и объема отсеченного конуса. Читать далее
Чтобы найти объем конуса необходимо произвести дополнительные построения. Читать далее
Усеченный конус – это часть конуса, ограниченная между двумя параллельными основаниями перпендикулярными его оси симметрии. Читать далее
Пусть α– плоскость, точка S– точка, не лежащая в этой плоскости. Возьмем на плоскости произвольный круг с радиусом R. Читать далее
Сектор кругового кольца – это плоская фигура, которая представляет собой часть плоскости между дугами двух окружностей с общим центром и разным радиусами, ограниченных двумя радиальными линиями, которые проведены к концам дуги с большим радиусом. Читать далее
Кольцо – это плоская геометрическая фигура, которая представляет собой часть плоскости между двумя окружностями с общим центром, но имеющими разный радиус. Читать далее
Очень часто на практике приходится сталкиваться с задачей нахождения длины дуги. Читать далее
Шестиугольной пирамидой называется многогранник, в основании которого лежит правильный шестиугольник, а боковые грани образуются одинаковыми равнобедренными треугольниками. Читать далее
Многогранник, в основании которого лежит правильный треугольник, а остальные грани представлены равнобедренными треугольниками называется треугольной пирамидой. Читать далее
Четырехугольной пирамидой называется многогранник, в основании которого лежит квадрат, а все боковые грани являются одинаковыми равнобедренными треугольниками. Читать далее
Площадь круга и его частей. Длина окружности и ее дуг
| Справочник по математике | Геометрия (Планиметрия) | Окружность и круг |








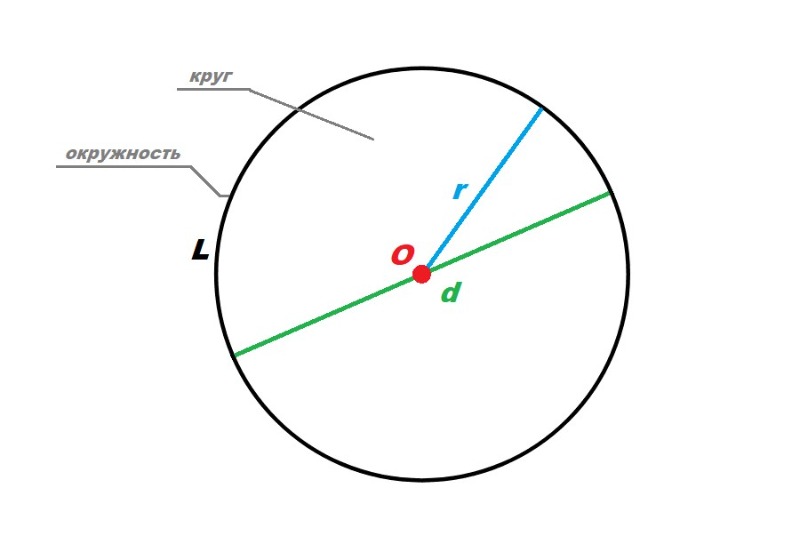












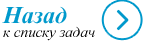
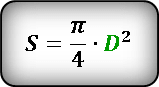
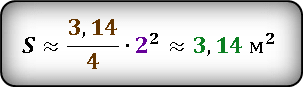
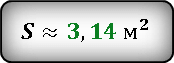















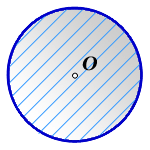
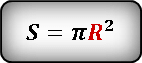
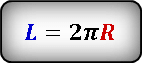
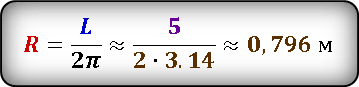

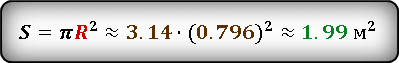













 , где
, где  — радиус круга.
— радиус круга.


 после замены радиуса на диаметр
после замены радиуса на диаметр  (радиус круга — это половина его диаметра). Получаем
(радиус круга — это половина его диаметра). Получаем  .
. , то определяя радиус
, то определяя радиус  и подставляя в начальную формулу площади круга
и подставляя в начальную формулу площади круга  .
. 

 берется равным 3,14.
берется равным 3,14.