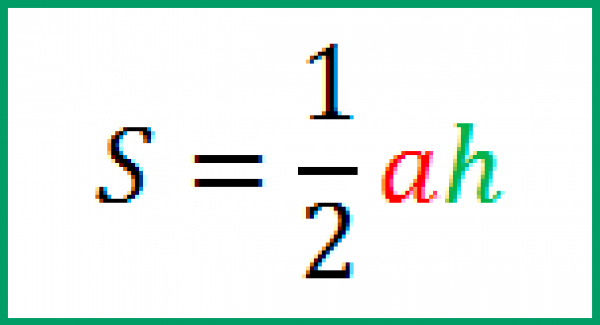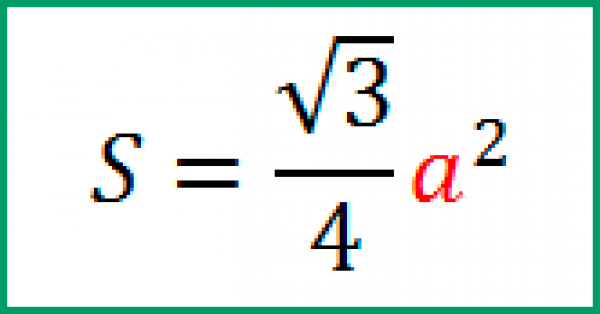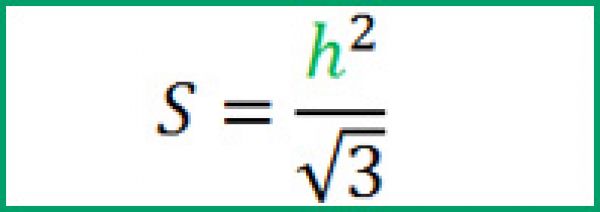Как найти площадь равностороннего треугольника формула
Как найти площадь равностороннего треугольника формула
Как найти площадь равностороннего треугольника
Онлайн калькулятор
Чтобы вычислить площадь равностороннего треугольника вам нужно знать следующие параметры (либо-либо):
Введите их в соответствующие поля и узнаете площадь равностороннего треугольника (S).
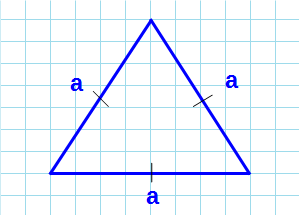
Как посчитать площадь равностороннего треугольника зная длину равных сторон
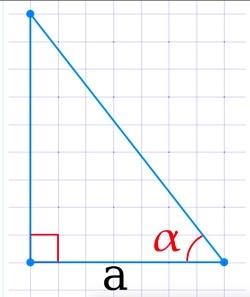
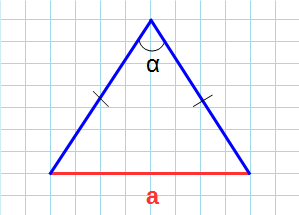
Какова площадь равностороннего треугольника (S) если известна длина сторон (a)?
Формула
Пример
Если сторона a = 2 см, то:
S = √3 /4 ⋅ 2² = 1.732 /4 ⋅ 4 ≈ 1.732 см 2
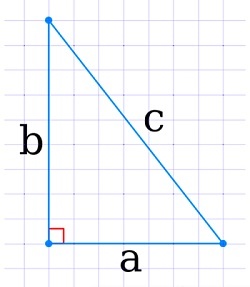
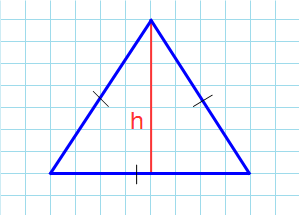
Как посчитать площадь равностороннего треугольника зная его высоту
Какова площадь равностороннего треугольника (S) если известна его высота (h)?
Формула
Пример
Если высота h = 3 см, то:
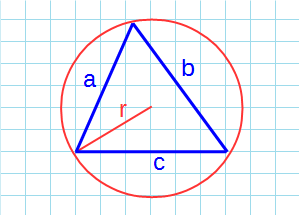
Как посчитать площадь равностороннего треугольника зная радиус описанной окружности
Какова площадь равностороннего треугольника (S) если известен радиус описанной окружности (R)?
Формула
Пример
Если радиус описанной окружности R = 4 см, то:
S = 3 ⋅ √3 /4 ⋅ 4² = 3 ⋅ 1.732 /4 ⋅ 16 = 1.299 ⋅ 16 ≈ 20.784 см 2
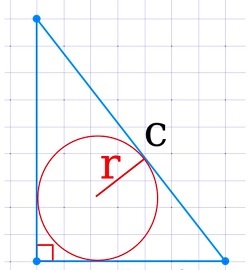
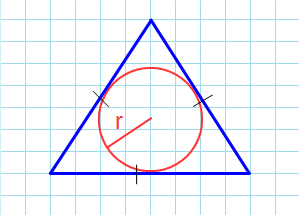
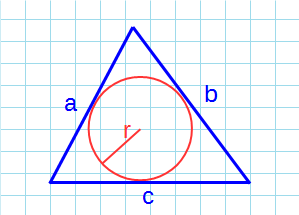
Как посчитать площадь равностороннего треугольника зная радиус вписанной окружности
Какова площадь равностороннего треугольника (S) если известен радиус вписанной окружности (r)?
Формула
Пример
Если радиус вписанной окружности r = 1 см, то:
S = 3⋅ √ 3 ⋅ 1² = 3 ⋅ 1.732 ⋅ 1 ≈ 5.196 см 2
Как посчитать площадь равностороннего треугольника зная его периметр
Какова площадь равностороннего треугольника (S) если известен его периметр (P)?
Формула
Пример
Если периметр P = 8 см, то:
S = √3 /36 ⋅ 8² = 1.732 /36 ⋅ 64 ≈ 3 см 2
Площадь равностороннего треугольника
Как найти площадь равностороннего треугольника?
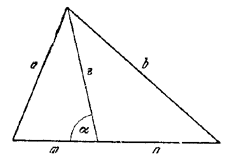
Площадь равностороннего треугольника можно найти и через сторону и проведенную к ней высоту, и через три стороны (по формуле Герона).
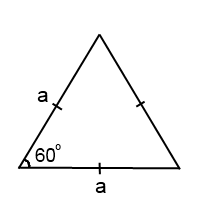
Но удобнее всего использовать формулу для вычисления площади треугольника по двум сторонам:
Все стороны равностороннего треугольника равны между собой: b=a.
Все углы равностороннего треугольника равны по 60 градусов.
Подставляем b=a и α=60º:
формула для нахождения площади равностороннего треугольника:
Как найти площадь равностороннего треугольника
Формула
Эту формулу легко получить из общей формулы для площади треугольника
Напомним, что треугольник называется равносторонним, если все его стороны равны.
Примеры вычисления площади равностороннего треугольника
Решение. Подставив заданное значение в формулу, будем иметь:
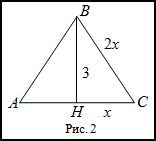
Решение. Сделаем чертеж (рис. 2).
$4 x^<2>-x^<2>=9 \Rightarrow 3 x^<2>=9 \Rightarrow x^<2>=3 \Rightarrow H C=x=\sqrt<3>$ (м)
Отсюда получаем, что
А тогда искомая площадь
Остались вопросы?
Здесь вы найдете ответы.
Согласно формуле, по которой вычисляется площадь S треугольника с равными сторонами, она равна:
S = √3/4*а, в которой а – это длина стороны фигуры.
Площадь можно также найти следующим образом:
S = a*h/2, где h – это высота.
Высоту можно вычислить, используя теорему Пифагора:
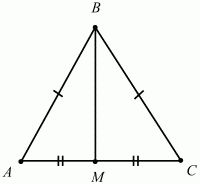
Обозначим имеющийся треугольник с равными сторонами как АВС. Обозначим длину стороны как а, и получим, что АВ=ВС=АС=а. Среднюю линию обозначим как МК. Тогда Sмвк = 6 см. кв.
В случае с равносторонним треугольником:
Зная свойство средней линии треугольника, можно записать следующее равенство:
В этом случае площадь отсекаемого треугольника равна:
Sмвк = (а/2)²*√3/4 = а²√3/16 см.кв.
В условии дано, что Sмвк = 6 см.кв., тогда:
Площадь равностороннего треугольника:
S = а²√3/4 = (96√3)/(4√3) = 96/4 =24 см.кв.
Найдем сторону равносторонней треугольной фигуры, разделив его периметр на 3:
Тогда площадь этой фигуры равна:
S =1/2a²sin 60° = 1/2*64*√3/2 = 16√3 см.кв.
Принимая во внимание то, что все стороны данной треугольной фигуры равны, то его высоту можно выразить через сторону и вычислить, используя теорему Пифагора:
h² = а²-(а/2)² = h² = а²- а²/4 = 3а²/4
Тогда площадь данной фигуры равна:
S = ½ a* h = ½ a*(а√3)/2 = (a²√3)/4
Для расчета площади треугольника, длины всех сторон которого равны, используется формула:
Перенесем 4 в правую часть равенства:
Если известно, что сторона равносторонней треугольной фигуры равна а, то его площадь рассчитывается так:
Треугольник имеет два катета – АВ и ВС. Его гипотенуза – ВС. Так как фигура является равносторонней, то АВ = АС.
Требуется доказать, что площадь треугольной фигуры, стороны которой одинаковы, равна произведению длин его катетов, разделенному на два.
Превратим имеющийся треугольник в квадрат, проведя перпендикуляр из его углов, и получим что:
Площадь квадрата равна:
Диагональ квадрата ВС является гипотенузой треугольника, которая делит квадрат на 2 равные части. Из этого следует, что площадь треугольника равна половине площади квадрата. Что и требовалось доказать.
Имеется треугольник АВС с равным сторонами.
Площадь данной фигуры находится по формуле:
в которой АС – основание треугольной фигуре, по длине равное любой из сторон (равносторонний Δ), ВН – высота.
Предположим, что АС = 2а см. Тогда:
АН = АС/2 = ½*2а = а см.
Согласно теореме Пифагора:
В данном случае:
Переносим а² в правую часть уравнения:
Теперь можно найти площадь:
Известна формула расчета площади треугольника:
Проведем высоту h, которая в равностороннем треугольнике представляет собой также биссектрису и медиану.
Воспользуемся теоремой Пифагора для вычисления высоты:
S = h*3 = 3√27 см.кв.
Доказать, что приведенное в задании утверждение является верным, можно, если превратить имеющуюся треугольную фигуру в параллелограмм/, площадь которого равна произведению длины стороны и высоты.
Параллелограмм состоит из двух треугольников, которые равны. Это значит, что площадь одной из треугольных фигур находится так:
Высоту можно выразить через определение синуса.
Все углы в равносторонней треугольной фигуре равны и составляют 60 градусов (180/3).
Из определения синуса следует:
Известно, что площадь любого треугольника можно найти по формуле:
Доказано, что каждый угол равносторонней треугольной фигуры составляют 60 градусов (sin60 =sqrt(3)/2), а его стороны имеют одинаковые длины. Если подставить эти значения в формулу, то получим:
Площадь треугольника с равными сторонами вычисляется по формуле:
В данном случае:
S= √3/4*12²= √3*144 /4*1 = 36√3 ≈ 62,35 см.кв.
Согласно формуле Герона:
Для данного треугольника:
Р = р/2 = 36/2 = 18 см.
S = √ (18× (18-12)³) = √(18*6³) = √(18×216)=√3888 ≈ 62,35 см. кв.
Площадь треугольника с одинаковыми сторонами считается как:
Радиус r окружности, которая вписана в данный Δ, равен a√3/6. Значит:
Считаем площадь треугольника:
Радиус R окружности, которая описана около правильной треугольной фигуры, равен a/√3. Следовательно, а = R√3.
Площадь треугольника равна:
В данном случае:
Если d = 10 см., то r = 10/2 = 5 см.
r = а√3/6, где а – это длина стороны правильного Δ.
SΔ = a²√3/4 =(10√3)³ *√3/4 = 75√3 см. кв.
S = 1/2 * a * a sin 60 = 1/2 * 4 * 4 * √3/2 = 4√3 дм.кв.
Площадь также можно найти так:
S = a²√3/4 = 16√3/4 = 4√3 дм.кв.
Длина окружности через радиус находится так:
Имеем правильный треугольник, значит длина его стороны:
S = √3/4a² = √3/43*3 = 3√3 у.е.кв.
В правильном треугольнике длины всех сторон одинаковы. Это значит, что каждую из них можно обозначить как х. Тогда:
Р (периметр) = х + х + х = 3х см.
Площадь будет равна:
S = 1/2 h * x = 14/2*x = 7х см.кв.
Площадь треугольной фигуры с равными сторонами считается как:
Радиус окружности, вписанной в этот Δ, составляет a√3/6. Тогда а = 2√3r.
Находим площадь треугольника:
Радиус R окружности, которая описана около правильного Δ, составляет a/√3. Это означает, что а = R√3.
Теперь можем высчитать площадь треугольника:
Центр правильно треугольной фигуры также является центральной точкой описанной около нее окружности. Ее радиус представляет собой расстояние от центра до вершины фигуры:
Все углы в правильном треугольнике являются одинаковыми и равны по 60 градусов (180/3).
Площадь треугольной фигуры рассчитывается как:
Предположим, что BD = 10 см., а АС = 12 см.
Диагонали ромба перпендикулярны и делятся на две равные части, пересекаясь в определенной точке.
ΔАВО: ∠АОВ = 90°, АО = АС/2 = 6, ВО = BD/2 = 5.
Согласно теореме Пифагора:
АВ = √(АО² + ВО²) = √(36 + 25) = √41.
Треугольник имеет равные стороны, длина каждой из которых аналогична длине стороны ромба:
SΔ = a²√3/4 = 41√3/4 см.кв.
Если длина стороны правильного треугольника указана, то его площадь вычисляется следующим образом:
Согласно определению правильного треугольника, длины всех его сторон одинаковые. Исходя из этого можно найти его сторону, разделив периметр на три:
Ищем площадь, подставив в равенство значение а:
S = 2²√3/4 = S 4√3/4 = √3 см.кв.
Площадь треугольника, имеющего стороны одинаковой длины, может быть рассчитана через длину его стороны без применения формулы радиуса окружности, которая вписана в него. Для данной фигуры верно утверждение о том, что высота, биссектриса и медиана делятся в точке пересечения в отношении 2:1. При схематичном изображении можно увидеть, что треугольная фигура АВС включает 6 треугольников с прямыми углами, которые имеют одинаковый катет (R) и гипотенузу (АО=ВО=СО). Следовательно, площадь треугольника АВС будет представлять собой сумму площадей всех 6 треугольников, формирующих его.
Если сказано, что сторона равносторонней треугольной фигуры равна а, то его площадь можно найти:
Если S=√3/4 а², то в данном случае S=9√3, что означает: 9√3=√3/4 а².
а² = 9√3:√3/4 = 9√3 x 4√3 = 36
Так как длина стороны не может быть отрицательным числом, то a = 6 см.
Доказано, что равносторонний треугольник имеет равные углы по 60 градусов. Также известна формула вычисления площади данной фигуры путем умножения длин двух его сторон и синуса угла, который они образуют:
S = 1/2*a*a*sin 60 = a²√3/4 см.кв.
Если указано, что длина стороны равностороннего треугольника составляет а, то его площадь равна:
Медиана, проведенная в треугольнике с равными сторонами, также представляет собой его биссектрису и высоту. Из этого следует, что:
Ответ: Площадь треугольника = a²√3/4 см.кв., его медиана = a√3/2 см.
В случае с треугольником с равными сторонами, высота представляет собой также медиану, делящую на две равные части сторону, на которую она опущена. Если применить в данном случае теорему Пифагора, то высота равна:
Теперь есть возможность найти площадь:
S = (1/2)*8√2*4√6 = 32√3 см. кв.
Площадь также можно найти по формуле для треугольника с равными сторонами:
S =(√3/4)*a² или S =(√3/4)*128 = 32√3 см. кв.
Для расчета площади треугольника с равными сторонами есть формула:
Найдем площадь меньшего из треугольников, подставив значение а:
S₁ = 12 √3/4 = √3/4 см.кв.
Известно, что площадь второго треугольника больше площади первой фигуры в три раза. Тогда:
Очевидно, что сторона большего треугольника составляет √3 см.
Формула площади для треугольника с равными сторонами:
Правильный треугольник. Площадь правильного треугольника
Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
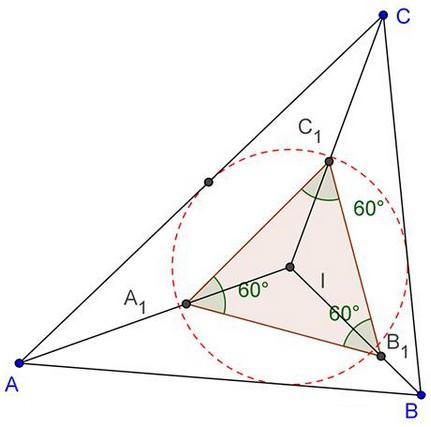
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.
Площадь равностороннего треугольника: онлайн калькулятор
Равносторонним называют треугольник, стороны которого имеют одинаковую длину. Площадь фигуры находится по формуле
Чтобы быстро и без ошибок вычислить площадь равностороннего треугольника онлайн-калькулятором:
Как найти площадь равностороннего треугольника с помощью онлайн-калькулятора
Для того, чтобы найти площадь равностороннего треугольника, нужно знать лишь сторону этого треугольника. Рассмотрим пример.
Пусть есть треугольник со стороной 4,5 см. Найдем его площадь с помощью онлайн-калькулятора:
Материалы, которые помогут вам лучше разобраться в теме:
Вычисление площади равностороннего треугольника онлайн
Существует несколько формул, которые можно использовать для решения задачи в зависимости от данных. Расчет площади равностороннего треугольника онлайн производится по его стороне. На сайте доступны калькуляторы, в основе которых заложены другие исходные данные. Поэтому с помощью нашего сервиса вы справитесь с решением любых задач.
К расчету площади равностороннего треугольника онлайн-калькулятором прибегают:
Созданный нашей компанией сервис облегчает учебный процесс. Полученное решение дает наглядный пример и путь вычислений. Данный алгоритм можно применять в дальнейшем самостоятельно.
На сайте Zaochnik можно не только рассчитать площадь равностороннего треугольника онлайн-калькулятором, но и заказать услуги по выполнению контрольных работ со скидкой.
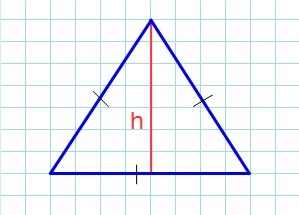
Треугольник с равными сторонами
Каждый школьник, в каком бы классе он ни учился, знает, что собой представляет треугольник. Он является самой простой замкнутой фигурой на плоскости и в пространстве, поскольку образован тремя отрезками (четырьмя ограничены следующие по сложности за ним фигуры: прямоугольник, квадрат, параллелограмм и т. д. ).
Состоит он из трех сторон, которые определяют 3 его угла (отсюда и название геометрического объекта). Для определения значений углов в градусах следует при решении задач использовать теорему о равенстве их суммы — 180. При этом неважно, к какому типу относится сама фигура (равнобедренный, прямоугольный и т. д. ), теорема остается справедливой всегда.
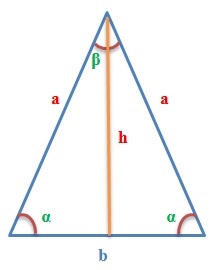
Исходя из названия, равносторонний треугольник — плоская фигура, все 3 стороны которой равны между собой. Для нее являются справедливыми следующие свойства:
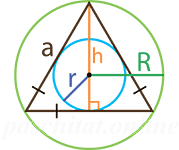
Длина высоты и ее частей
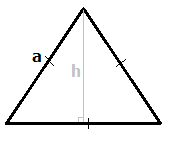
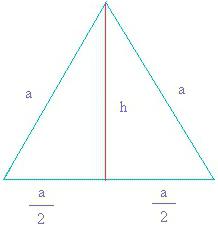
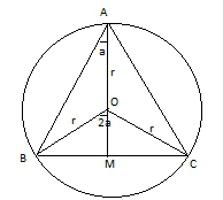
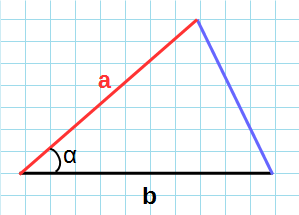
Прежде чем приводить формулы площади равностороннего треугольника, следует выяснить, какую длину имеют его биссектрисы, высоты или медианы. Пусть эта величина будет обозначаться латинской буквой h, а сторона фигуры обозначается a. Поскольку проведенная высота из любого угла делит его на 2 прямоугольных треугольника, этот факт можно использовать для вычисления величины h. Проще всего применить определение какой-либо тригонометрической функции, например, синуса:
Согласно определению, синусом угла называется отношения противолежащего катета (h) к гипотенузе (a). Поскольку значения функции sin (60) является табличной величиной, получается следующее выражение для h:
Из формулы следует, что высота h составляет приблизительно 87% от длины стороны a.
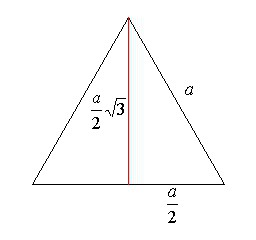
Для получения полной информации о свойствах биссектрис, медиан и высот треугольника, нужно определить, на какие части делит их точка пересечения. Следует ввести некоторые обозначения:
Треугольник PQB является прямоугольным. Прямым углом будет QPB. Поскольку угол QBP разделен биссектрисой на 2 одинаковые части, он составляет 30 градусов. Катет QP лежит против этого угла, поэтому будет иметь длину в 2 раза меньшую, чем гипотенуза BQ. Нетрудно увидеть, что сумма длин BQ и QP равна высоте h. Эти рассуждения позволяют получить следующие формулы:
Здесь введены новые буквы r и R для обозначения длин QP и BQ, соответственно.
Формулы площади
Чему равна площадь равностороннего треугольника можно определить с использованием нескольких формул. Для этого привлекаются в том числе понятия вписанной и описанной окружности.
Через величины a или h
Площадь абсолютно любого треугольника может быть определена как произведение его высоты на длину основания, которое следует поделить пополам. Если записать это выражение для равноугольного треугольника, можно получить следующие формулы:
Для получения этих выражений была использована формула связи между длинами высоты h и основания a. Уравнения справедливы для любого треугольника с равными сторонами. Для прямоугольного или равнобедренного эти выражения уже не подходят.
Формулы через длины h и a для площади S говорят, что для однозначного определения геометрической характеристики достаточно знать лишь один параметр треугольника, имеющий размерность длины.
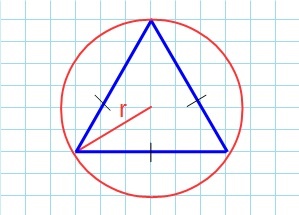
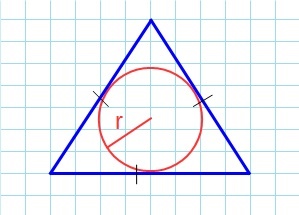
Через радиусы r или R
Чтобы определить площадь, достаточно узнать любой линейный параметр. Это необязательно может быть сторона или высота, но также радиусы вписанной и описанной окружностей.
Вписанной называется окружность, которая лежит внутри фигуры и касается всех ее сторон. В случае равностороннего треугольника ее центр находится в точке пересечения медиан (высот, биссектрис), то есть в точке Q. Ее радиус r равен отрезку QP и составляет:
Выразив из этого равенства сторону a и подставив ее в формулу для площади S через a, можно получить следующее выражение:
Центр вписанной окружности является для равностороннего треугольника центром описанной вокруг него. Ею принято называть в геометрии фигуру, которая проходит через все вершины многоугольника. Поскольку ее центр лежит в точке Q, радиус R будет равен длине отрезка QB. Формула для него уже известна:
Аналогичным образом, выражая из этого равенства величину a, и подставляя ее в формулу для S, можно получить следующее выражение:
Это равенство можно было также получить, если вспомнить, что радиус описанной окружности R в 2 раза больше радиуса r.
Примеры решения задач
Выведенные формулы можно с легкостью применять для решения разнообразных задач по геометрии. Для понимания, как их следует использовать, следует рассмотреть несколько примеров.
Описанная и вписанная окружности
Дан некоторый равноугольный треугольник. Известно, что разница между радиусами описанной и вписанной окружностей составляет 3 см. Следует найти площадь фигуры.
На первый взгляд может показаться, что нахождение решения этой задачи требует проведения некоторых промежуточных вычислений, но это не так. Если вспомнить, что радиус описанной окружности R ровно в 2 раза больше величины r, то их разница является не чем иным, как самим радиусом вписанной окружности r. Для получения ответа на задачу следует всего-навсего воспользоваться известной формулой и вычислить S:
Тетраэдр и его поверхность
Чтобы посчитать необходимую площадь, следует найти эту величину всего лишь для одного равностороннего треугольника, а затем полученное число умножить на 4. Из курса стереометрии известно, что объем тетраэдра рассчитывается по следующей формуле:
Отсюда можно получить длину стороны a:
Подставляя значение объема тетраэдра из условия задачи, можно рассчитать a = 9,467 см. Это значение округлено до третьего знака после запятой.
Теперь можно применить формулу для расчета площади S через a:
Получилась площадь одной грани тетраэдра. Поскольку объемная фигура состоит из четырех одинаковых треугольников, то площадь его поверхности St составит:
Таким образом, высокая симметрия равностороннего треугольника позволяет рассчитывать его площадь, зная всего один линейный параметр фигуры. Чаще всего таковым является высота, сторона основания или радиусы вписанной и описанной окружностей.
Площадь равностороннего треугольника
Свойства
Зная площадь равностороннего треугольника, можно вывести формулу его стороны, умножив площадь на четыре, разделив на корень из трех, и затем извлечь из всего этого выражения квадратный корень. a=√(4S/√3)=2√(S/√3)
Подставив полученное выражение вместо стороны, можно вычислить периметр равностороннего треугольника через площадь. P=3a=6√(S/√3)
В равностороннем треугольнике медиана, биссектриса и высота становятся одним и тем же построением, и имеют одну и ту же длину вне зависимости от того, на какую сторону они опущены. Вычислить высоту через площадь можно, подставив в формулу вместо стороны выведенное выше выражение. (рис. 97.2) h=m=l=(√3 a)/2=√3/2 2√(S/√3)=√(√3 S)
Средняя линия у равностороннего треугольника всего одна и она равна стороне, деленной на два. Если подставить вместо стороны удвоенное выражение через площадь, то коэффициенты сократятся, и останется только радикал. (рис.97.3) M=a/2=√(S/√3)
Радиус окружности, вписанной в равносторонний треугольник равен стороне, деленной на два корня из трех. Радиус вписанной окружности через площадь выглядит уже как квадратный корень из площади, деленной на три. (рис.97.4) r=a/(2√3)=2√(S/√3)*1/(2√3)=√S/3
Так как радиус окружности, описанной вокруг равностороннего треугольника, равен по определению стороне, деленной на корень из трех, следовательно, он равен удвоенному радиусу вписанной окружности, исходя из формул. Поэтому его можно представить через площадь, используя сразу радиус вписанной окружности. (рис.97.5) R=2r=(2√S)/3
Узнать ещё
Знание — сила. Познавательная информация
Площадь равностороннего треугольника
Площадь равностороннего треугольника может быть выведена с помощью одной из формул для вычисления площади треугольника. А с помощью этой ассоциации полученную формулу легко запомнить.
Сначала выведем формулу площади равностороннего треугольника.
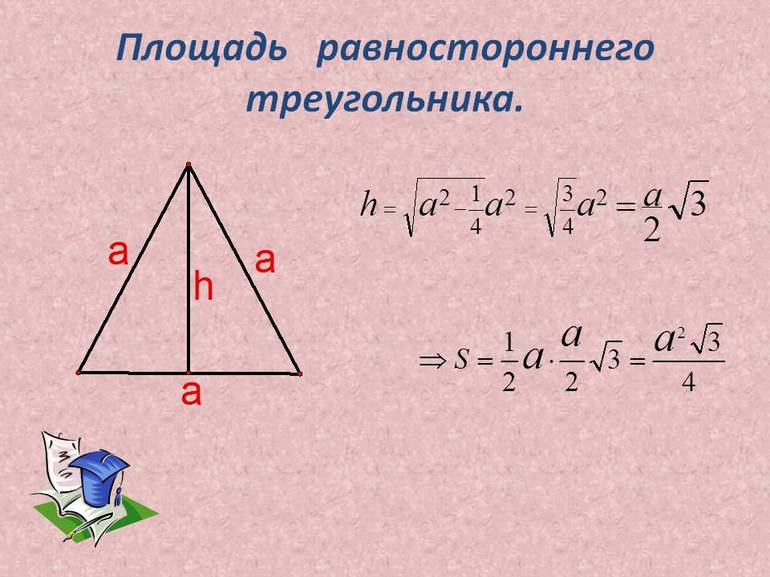
Таким образом, площадь равностороннего треугольника вычисляется по формуле:
Теперь взгляните на числа, входящие в эту формулу: 2,3,4.
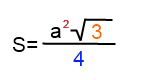
Можно еще отметить, что в площадь должна получаться в квадратных единицах. Поскольку из длин отрезков в формуле есть только а, то а — в квадрате, чтобы прийти к квадратным единицам.
Как узнать площадь равностороннего треугольника: основные формулы
Найти площадь равностороннего треугольника можно по любой формуле для произвольной фигуры данного типа или воспользоваться теми, в которых уже учтена особенность именно этой фигуры и математические выражения существенно упрощены.
Первый случай только требует замены всех сторон одинаковым значением и учета того, что все углы у треугольника равны 60º. Потом останется провести несложные преобразования, которые и приведут к формулам, данным в готовом виде немного ниже.
Формула 1: известна сторона
В этой и последующих формулах приняты стандартные обозначения величин треугольника. Подробнее их можно посмотреть в предложенной таблице.
| Величина | Ее обозначение |
| сторона | а |
| площадь | S |
| высота | н |
| радиусы окружностей вписанной и описанной | r и R, соответственно |
Расчет площади треугольника в этом случае будет осуществляться по формуле:
Она легко получается из той, которая известна для произвольной фигуры с тремя сторонами. Просто в формуле нужно учесть то, что все стороны у треугольника равны.
Так как скобок три, то у этого выражения появится третья степень. А значит, оно преобразится в а 3 /8.
Его еще нужно умножить на полупериметр, который определяется как сумма сторон, разделенная на 2. Получится выражение: 3а 4 /16. После извлечения квадратного корня как раз и останется то выражение, что дано в первой формуле для площади равностороннего треугольника.
Поэтому нет необходимости запоминать много формул. Можно просто запомнить одну — Герона. Из нее путем простых математических преобразований получаются все остальные, например, для равностороннего треугольника.
Формула 2: дан радиус вписанной окружности
Это выражение очень напоминает предыдущую запись. Но все же есть существенные отличия: используется другая буква, иррациональность ушла в знаменатель, появился множитель 3 и исчезла цифра 4. В общем, ее легко запомнить.
Эту формулу тоже легко получить из той, которая дана для произвольного треугольника. В ней радиус умножается на сумму сторон и делится на 4. Поскольку стороны имеют одинаковое значение, что сумма заменится на 3а. Теперь нужно убрать «а», чтобы осталось только значение радиуса. Для этого потребуется выражение, в котором сторона делится на произведение 2 и синуса противолежащего стороне угла. Так как угол равен 60º, то значение синуса будет √3/2. Тогда сторона выразится через радиус так: а = √3R. После несложного преобразования можно прийти к тому выражению для площади, которое дано вначале.
Формула 3: дана описанная окружность и ее радиус
Она очень похожа на первую. Только в ее числителе появляется цифра 3 и поменялась буква на R.
Поскольку радиус в два раза больше того, который рассматривался в предыдущем пункте, то понятно, как она получается. В ней просто вместо r ставится R/2. И проводятся необходимые преобразования.
Поэтому формулу можно не запоминать. Только держать в памяти соотношение радиусов вписанной и описанной около равностороннего треугольника окружностей.
Формула 4: известна высота
В этом случае площадь равностороннего треугольника равна:
S = н 2 / √3.
Чтобы понять, как получается такая формула, потребуется опять воспользоваться общей для всех треугольников. Она выглядит как произведение стороны на высоту и на ½. Теперь, чтобы узнать площадь равностороннего треугольника, придется вспомнить или вывести математическое выражение для высоты.
Пример №1
Условие. Вычислить площадь равностороннего треугольника, если известно, что его сторона имеет значение 4 см.
Решение. Поскольку известно значение сторон фигуры, то необходимо пользоваться первой формулой.
Сначала потребуется возвести в квадрат число 4. От этого действия получится число 16. Теперь оно сокращается с четверкой, стоящей в знаменателе. И в итоге в числителе остается 4 и √3, а знаменатель становится равным единице, значит, его можно просто не записывать. Это результат, который и требовалось найти в задаче.
Пример №2
Условие. Все стороны равностороннего треугольника равны 2√2 дм. Вычислить его площадь.
Решение. Рассуждения такие же, как в первой задаче. Только значение квадрата стороны будет другим. В нем нужно отдельно возвести во вторую степень 2 и иррациональность. И результат будет таким: 4*2 = 8. После сокращения со знаменателем остается 2 и √3 в числителе дроби, а знаменатель исчезает.
Пример №3
Условие. В равносторонний треугольник вписана окружность, ее радиус 2,5 см. Необходимо вычислить площадь треугольника.
Решение. Для расчета искомой величины потребуется воспользоваться второй формулой.
Сначала значение радиуса нужно возвести в квадрат. Получится 6,25. Потом это значение требуется умножить на 3. Результатом этого действия станет число 18,75. Но это еще не конечное значение: в нем будет множитель √3, который присутствует в используемой формуле.
Пример №4
Условие. Требуется определить, чему равна площадь равностороннего треугольника, если известна его высота — 3 дм.
Решение. Естественно, что выбрать нужно четвертую формулу. С ее помощью проще всего найти ответ этой задачи.
Достаточно только возвести в квадрат число 3, то есть высоту, что даст значение 9. А потом разделить его на √3, стоящий в формуле.
Поскольку в математике не принято оставлять иррациональность в знаменателе ответа, то от нее нужно избавиться. Для этого дробь 9/√3 потребуется умножить на дробь с одинаковыми числителем и знаменателем, а именно √3/√3. От этого действия в числителе появится значение 9√3, а в знаменателе появится число 3.
Эту дробь можно и нужно сократить на 3. Это конечный результат.
Пример №5
Решение. Поскольку речь идет о стороне, то подойдет первая формула. Из нее можно сразу вывести математическое выражение, которое позволит определить сторону треугольника.
Для этого площадь нужно умножить на 4 и разделить на квадратный корень из трех. Так получится значение для стороны в квадрате. Чтобы получить просто сторону, нужно извлечь корень. Выражение для стороны будет выглядеть так: а = 2 * √(S/√3).
Так как площадь известна, то можно сразу приступать к вычислениям. Подкоренное выражение выглядит как частное 27 и √3. Нужно избавиться от иррациональности в знаменателе. Получится 27√3, разделенное на 3. После сокращения в знаменателе остается 1, которую можно не писать, а в числителе остается 9√3.
√3 = 1,73; теперь из него еще раз извлекаем корень и получаем 1,32.
Осталось только умножить его на 2 и получить искомый результат.
Площадь равностороннего треугольника

Средняя оценка: 4.2
Всего получено оценок: 254.
Средняя оценка: 4.2
Всего получено оценок: 254.
Многоугольник, который имеет три вершины и три стороны, называется треугольником. Треугольник называется равносторонним или правильным, если все его три стороны одинаковые, а все три угла равны 60°. О методах вычисления площади равностороннего треугольника поговорим в этой статье.
Определение
Правильным треугольником называют часть плоскости, ограниченную тремя одинаковыми отрезками. Их соединяют точки, которые не принадлежат одной прямой. Здесь все три угла одинаковые и равняются по 60 градусов. Поэтому для определения площади правильного треугольника можно будет пользоваться упрощенными формулами.
Равносторонний треугольник является частным случаем равнобедренного треугольника.
Значение площади правильного треугольника вычисляется путем подстановки параметров фигуры в классическую формулу.
Нахождение площади правильного треугольника
В результате треугольник делиться на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для правильного треугольника.
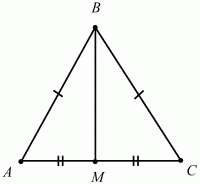
В прямоугольном треугольнике АВМ катет АМ можно выразить через синус угла АВМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет АМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.
Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.
Тогда формула будет выглядеть следующим образом:
Теперь вспомним классическую формулу площади треугольника:
$S= <1\over2>h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. Формула площади равностороннего треугольника будет выглядеть следующим образом:
ВС заменили на а, так как все стороны равны между собой, а значение высоты мы находили ранее. Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.
Только в правильном треугольнике возможно нахождение площади через сторону.
По той же причине нельзя использовать эту формулу для равнобедренного или произвольного треугольника. Прежде чем использовать эту формулу необходимо доказать, что треугольник правильный или убедиться, что это условие прописано в исходных данных задачи.
Что мы узнали?
Площадь правильного треугольника можно вычислить через сторону, поскольку речь идет о фигуре с одинаковыми параметрами, или через высоту по классической формуле. Здесь углы также будут одинаковыми. При решении некоторых задач по геометрии стоит помнить о том, что высоты данной плоской фигуры, ограниченной тремя сторонами, равны между собой.
Два способа найти площадь треугольника
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
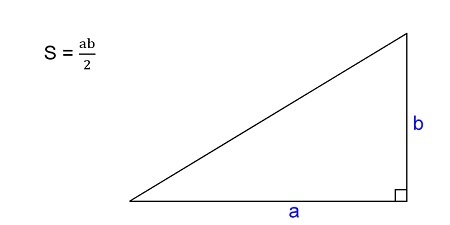
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
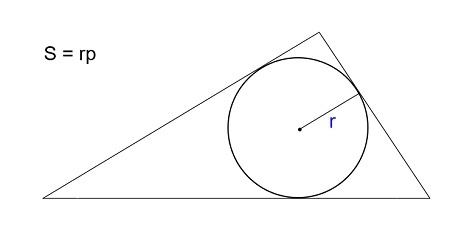
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
Если известна сторона и высота
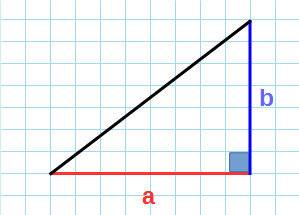
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
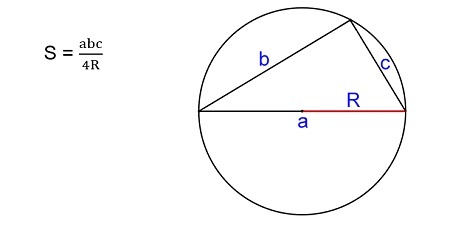
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Как найти площадь треугольника
О чем эта статья:
Основные понятия
Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Общая формула
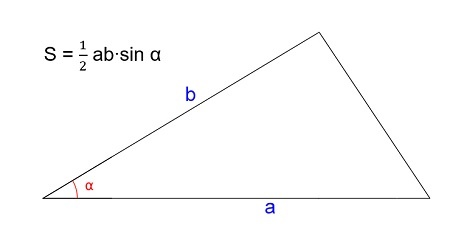
1. Площадь треугольника через две стороны и угол между ними.
2. Площадь треугольника через основание и высоту.
S = 0,5 * a * h, где a — основание, h — высота.
3. Площадь треугольника через описанную окружность и стороны.
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны.
S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.
Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:
S = r * p, где p — полупериметр.
5. Площадь треугольника по стороне и двум прилежащим углам.
S = a 2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.
6. Формула Герона для вычисления площади треугольника.
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
S = √ p * (p − a) * (p − b) * (p − c), где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам.
S = 0,5 * a * b, где a, b — стороны.
Площадь треугольника по гипотенузе и острому углу.
S = 0,25 * c 2 * sin(2α), где c — гипотенуза, α — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу.
S = 0,5 * a 2 * tg(α), где a — катет, α — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и по радиусу вписанной окружности.
S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.
Площадь треугольника вписанного в окружность.
Площадь прямого треугольника по формуле Герона.
S = (p − a) * (p − b), где a, b — катеты, p — полупериметр, который рассчитывается по формуле p = (a + b + c) : 2.
Для равнобедренного треугольника
Поиск площади через основание и сторону.
Вычисление площади через основание и угол.
S = 0,5 * a * b * sin(α), где a — боковая сторона, b — основание, α — угол между основанием и стороной.
Вычисление площади через основание и высоту.
S = 0,5 * b * h, где b — основание, h — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними.
S = 0,5 * a 2 * sin(α), где a — боковая сторона, α — угол между боковыми сторонами.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами.
S = b 2 : (4 * tgα/2), где b — основание, α — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности.
S = (3 * √ 3 * R 2 ) : 4, где R — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности.
Площадь равностороннего треугольника через сторону.
S = (√ 3 * a 2 ) : 4, где a — сторона.
Площадь равностороннего треугольника через высоту.
S = h 2 : √ 3, где h — высота.
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Площадь треугольника
Теперь вам не нужно тратить время на долгие вычисления, прежде чем вы сможете узнать площадь треугольника. Зная методы расчета, используемые для расчета площади треугольника, вы легко сможете это сделать самостоятельно. Действительно, всегда лучше знать формулы площади треугольника. Треугольники могут быть разными и вы это знаете, но как найти площадь треугольника если вам практически ничего неизвестно о треугольнике? И что нужно знать из размеров треугольника, чтобы найти его площадь. Давайте разбираться. При этом тема не так проста как кажется на первый взгляд, наверное, поэтому задачи нахождения площади треугольника есть и в ОГЭ и в ЕГЭ по математике.
Что такое треугольник
Треугольник — это геометрическая фигура. По определению, это многоугольник, имеющий три стороны. Следовательно, треугольник также должен иметь три угла.
Сумма трех углов треугольника должна быть равна 180°.
Чтобы иметь возможность вычислить площадь треугольника, мы должны сначала знать меру его основания, а также высоту. Основание треугольника представляет одну из его сторон. Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).
Прежде всего, помните, что треугольник состоит из трех сторон и трех углов. Это значит, что у него должно быть три вершины. Треугольник, вершинами которого являются A, B и C, может быть представлен как: ΔABC. Существуют разные виды треугольников. Они могут быть классифицированы двумя различными способами: либо по свойству его сторон, либо по свойству его углов.
Различные типы треугольников в зависимости от длины их сторон
Разносторонний треугольник
Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.
Равнобедренный треугольник
Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.
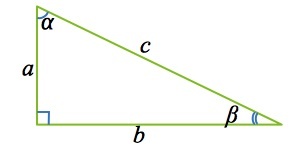
Прямоугольный треугольник
Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.
Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.
Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.
Равносторонний треугольник
Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.
Площадь треугольника
Площадь разностороннего треугольника
Вычисляем площадь треугольника без особенностей — все его стороны разные и все углы разные.
Если известны две стороны треугольника и угол между ними, то площадь разностороннего треугольника вычисляется по формуле «площадь треугольника через две стороны и угол между ними»:
Если известны высота в треугольнике и основание, то используется формула площади треугольника через основание и высоту:
Формула Герона определения площади треугольника
Если известны стороны любого треугольника, то его площадь можно определить по формуле Герона.
, где
Площадь равнобедренного треугольника
Площадь треугольника через основание и сторону можно найти, если известны сторона и основания равнобедренного треугольника.
К равнобедренному треугольнику также применима формула площади треугольника через основание, сторону и угол между ними:
Найти площадь равнобедренного треугольника можно также через боковые стороны и угол между ними.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами:
Площадь прямоугольного треугольника
Приведем формулы площади прямоугольного треугольника. Формула площади прямоугольного треугольника через катет и прилежащий угол:
Площадь прямоугольного треугольника по радиусу вписанной окружности и гипотенузе
Площадь прямоугольного треугольника, если в него вписана окружность:
Площадь равностороннего треугольника
Площадь равностороннего треугольника можно найти через радиус описанной окружности.
Если дан радиус вписанной окружности, то площадь равностороннего треугольника можно найти по формуле:
Площадь равностороннего треугольника, если известна высота треугольника:
Разные способы © 2022
Внимание! Информация, опубликованная на сайте, носит исключительно ознакомительный характер и не является рекомендацией к применению.
Площадь равностороннего треугольника
Площадь равностороннего треугольника — это число, характеризующее равносторонний треугольник в единицах измерения площади.
Равносторонний треугольник — это правильный треугольник, у которого все стороны и углы равны.
Содержание
[править] Обозначения
a — длина стороны;
r — радиус вписанной окружности;
R — радиус описанной окружности;
α — половинный центральный угол, α=π/3;
P3 — периметр правильного треугольника;
SΔ — площадь равнобедренного треугольника с основанием, равным стороне, и боковыми сторонами, равными радиусу описанной окружности;
S3 — площадь правильного треугольника.
[править] Формулы
[math]S_3=\frac<\sqrt<3>><4>a^2 \Leftrightarrow[/math] [math]\Leftrightarrow S_3=3S_<\triangle>, \ S_<\triangle>=\frac<\sqrt<3>><12>a^2 \Leftrightarrow[/math] [math]\Leftrightarrow S_3=\frac<1><2>P_3r, \ P_3=3a, \ r=\frac<\sqrt<3>><6>a \Leftrightarrow[/math] [math]\Leftrightarrow S_3=\frac<3\sqrt<3>><4>R^2, \ R=\frac<\sqrt<3>><3>a \Leftrightarrow[/math] [math]\Leftrightarrow S_3=3\sqrt<3>r^2, \ r=\frac<1><2>R[/math]
[править] См. также
[править] Другие многоугольники
Персональные инструменты
Пространства имён
Варианты
Просмотры
Действия
Поиск
Навигация
Инструменты
Текст страницы доступен по условиям лицензии GNU Free Documentation License. Материалы могут быть скопированы при условии указания активной ссылки на источник копирования в теле статьи (на той же странице). В отдельных случаях могут действовать условия лицензии Creative Commons Attribution-ShareAlike (CC BY-SA 3.0), информацию об этом можно просмотреть на странице обсуждения или в истории правок. В частности, условия лицензии CC BY-SA 3.0 действуют в отношении статей, перенесенных из Википедии (указание на факт переноса всегда есть в истории правок статьи или на ее странице обсуждения).
В текстах могут упоминаться организации, признанные на территории Российской Федерации террористическими и/или в отношении которых судом принято вступившее в законную силу решение о запрете деятельности — см. полный список, а также деятельность которых запрещена по решению суда — см. полный список.
Площадь равностороннего треугольника
Площадь равностороннего треугольника равна половине произведения стороны треугольника и высоты, опущенной на эту сторону. В равностронннем треугольнике все стороны равны.
Формула площади равностороннего треугольника S через сторону и высоту имеет вид:
Калькулятор для вычисления:
Также площадь равностороннего треугольника равна произведению квадратного корня из трех, деленного на четыре, и квадрата его стороны. Формула площади равностороннего треугольника S через сторону имеет вид:
Калькулятор для вычисления:
Также площадь равностороннего треугольника равна квадрату высоты, деленной на квадратный корень из трех. Формула площади равностороннего треугольника S через высоту имеет вид:
Калькулятор для вычисления:
Для вычисления площади нужно знать высоту проведенную к стороне. Высота, половина стороны и сторона равностороннего треугольника образуют прямоугольный треугольник.
Вычислим площадь:
S = 1/2 * 10,4 * 12 = 62,4 кв. см
Как найти площадь треугольника. Формулы треугольника
Вы будете перенаправлены на Автор24
Понятие площади
Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.
Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.
Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице
Тогда площадь треугольника равняется
Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.
Как найти площадь треугольника через высоту и основание
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.
Математически это выглядит следующим образом
Следовательно, искомая площадь треугольника, по свойству 2, равняется
$S=S_ABH+S_CBH=\frac<1><2>h\cdot AH+\frac<1><2>h\cdot HC=\frac<1><2>h\cdot (AH+HC)=\frac<1><2>αh$
Готовые работы на аналогичную тему
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице
$S=\frac<1><2>\cdot 9\cdot 9=40,5$
Формула Герона
Рассмотрим следующий рисунок:
Из этих двух соотношений получаем равенство
По теореме 1, получим
Площадь равностороннего треугольника
Математически это выглядит следующим образом
Высота равностороннего треугольника является также и медианой, значит, по теореме Пифагора
Значит по теореме 1:
Используя теорему 3, получим
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 07.07.2022
Как найти площадь равностороннего треугольника — способы расчета фигуры
Треугольник – геометрическая фигура, сформированная 3 отрезками, соединенными между собой 3 точками. При этом все углы у нее расположены внутри. Равносторонний или равноугольный треугольник – многоугольник правильной формы с равными сторонами и углами (по 60°). В этой фигуре высота выступает одновременно и медианой, и биссектрисой. Площадь равностороннего треугольника можно просчитать через сторону, высоту, через сторону и высоту.
Геометрия – это раздел математики, который занимается изучением фигур в пространстве и на плоскости, а также вычислением их площади, объема и прочих показателей. Впервые как наука она появилась в Древней Греции. Изучением занимался ученый Евклид. Позже было создано еще несколько видов геометрии – проективная, начертательная, дифференциальная и аналитическая.
Геометрия окружает человека каждый день. Если оглянуться вокруг, то можно увидеть, что вокруг расположены не просто предметы, а геометрические фигуры. Например, монитор, кровать, стол и даже стены в комнате. Поэтому важно изучить хотя бы ее основы. Одной из самых популярных фигур, которые можно встретить в повседневной жизни, является треугольник.
Признаки и свойства
Треугольник представляет собой геометрическую фигуру, состоящую из трех точек, не располагающихся на одной прямой линии. Отрезки, которые из соединяют, называются стороны. Точки их соединения – это вершины. В геометрии принято обозначать их латинскими буквами. К примеру, так – А, В, С. Стороны указывают названиями двух точек (вершин) из которых они состоят – АВ, ВС, АС. В тех местах, где они соединяются, формируются углы. Нижний отрезок называют основанием.
Многоугольники классифицируют по нескольким признакам. Каждый из них имеет свои определенные свойства.
Классификация по углам (∠):
Виды треугольника по сторонам:
Для того чтобы рассчитать площадь равностороннего треугольника необходимо понимать свойства и признаки, которыми он обладает. Выделяют следующие основные признаки этой фигуры:
[stop]Если хотя бы один из этих признаков соблюдается, значит, треугольник является равносторонним.[/stop]
Дополнительно этот многоугольник обладает следующими свойствами:
Расчет через сторону
Существует множество способов вычисления площади (S) этой фигуры. Все они имеют свои преимущества и недостатки. Применяются в зависимости от условий, представленных задаче. Самый популярный способ найти искомое значение для равностороннего треугольника вычисляется через произведение половины сторон и синуса угла между ними, выглядит это следующим образом: 
В случае с равносторонним, этот способ упрощается в значительной степени. Для этого нужно обратиться к рассмотренным выше признакам и свойствам. Исходя из того, что все ∠ = 60 градусам. Синус 60 градусов, согласно таблице Брадиса, равняется 

Учитывая то, что все отрезки равны, то преобразованное выражение даст такой результат: 
Данная формула отлично подойдет в случае, если известна величина стороны. В таком виде вычислять показатель гораздо легче и быстрее.
Те, кто помнит формулу Герона, знают, как найти площадь. В процессе преобразования выражение изменится в представленное выше. Площадь по Герону рассчитывается так: 





Полученная формула площади и представленные ниже функции могут быть использованы только, в случае, если фигура является правильной, в ином случае не будет давать правильный ответ.
Расчет по высоте
Вычислить площадь равностороннего многоугольника также есть возможность, если известна его высота и сторона. Половина длины высоты (h) умножается на сторону, выбрана может быть любая h и сторона, ведь согласно свойствам, они все одинаковые: 
Если в задаче указана информация о том, что многоугольник с 3 углами является равносторонним и известна величина h, чему равна длина стороны неизвестно, то можно воспользоваться формулой, позволяющей ее определить. Найти сторону есть возможность, разделив двойную величину h на корень квадратный из трех, математически выглядит следующим образом: 
Для того чтобы не делать лишних подсчетов выводят формулу этого показателя сразу же через h. Квадрат h делится на корень квадратный из трех. Она будет выглядеть так: 
Расчет через окружности
В математике популярен также прием вычисления, рассматриваемого в статье значения, через помещение фигуры в окружность или наоборот. Такая окр-ть называется описанной. Если она находится внутри, то она называется вписанной. Именно в этом разделе возникает большинство вопросов, как найти площадь равностороннего многоугольника с тремя углами.
ОО обязательно должна проходить через все вершины, ВО должна проходить через стороны только в одной точке по касательной.
Преобразовав формулу 


Если же будет дан размер R ОО, то выражение будет выглядеть следующим образом: 
Использование этих свойств пригодится для расчета стороны. Для того чтобы ее определить нужно воспользоваться выражением 

Учитывая R описанной окр-ти определяют искомое значение при помощи возведения стороны в куб, после чего результат делится на R, увеличенный в 4 раза. Математически его записывают следующим образом: 
Процесс вычисления, чему равен показатель площади равностороннего треугольника через любую из предложенных формул не должен вызывать особых затруднений. Для того чтобы успешно справиться с этой задачей не нужно запоминать все указанные способы, достаточно запомнить основные общие формулы расчета, а также свойства и признаки этой фигуры.
[warning]Для проверки правильности расчетов можно воспользоваться несколькими способами, результаты должны совпасть.[/warning]
Как найти площадь равностороннего треугольника смотрите в видео:
Также смотрите в видео как найти площадь равностороннего треугольника, вписанного в окружность:
Применив логическое мышление, расчеты с легкостью преобразовываются в частные случаи, коих гораздо больше. Нецелесообразно забивать голову большим количеством нерелевантной информации, лучше развивать причинно-следственную связь для преобразования выражений.
Геометрия — это точная наука, которая не терпит отклонений и недочетов. Для ее изучения нужно запастись колоссальным терпением и быть очень внимательным. То, что на первый взгляд кажется непостижимым и непонятным, после освоения азов станет легким и доступным для понимания. Но все же особое внимание необходимо уделить изучению теорем и формул, так как они являются основой для вычислений таких важных показателей, как объем или площадь. Ее изучение и нужно начинать с таких простых и правильных фигур, как равносторонний треугольник. Он поможет понять основы и не потерять интерес к науке в целом.
Равносторонний треугольник формулы
Равносторонний треугольник – это треугольник, у которого все стороны равны.
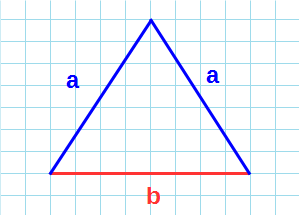
Другие виды треугольников:
Любой равносторонний треугольник характеризуется стороной a (см. рисунок). При решении задач могут понадобиться высота h, радиусы вписанной (r) и описанной (R) окружности. Именно эти характеристики используются в формулах равностороннего треугольника при вычислении площади, периметра, а также радиусов вписанной и описанной окружностей.
Формула радиуса вписанной окружности для равностороннего треугольника
Радиус вписанной окружности r можно вычислить, зная сторону равностороннего треугольника:
Формула радиуса описанной окружности для равностороннего треугольника
Радиус описанной окружности R можно вычислить, зная сторону равностороннего треугольника:
Формула периметра равностороннего треугольника
Периметр P равностороннего треугольника можно получить, зная его сторону:
Формулы площади равностороннего треугольника
Площадь равностороннего треугольника S можно вычислить, зная его сторону a:
Площадь равностороннего треугольника S также можно вычислить, зная его высоту h:
Если в задаче присутствует окружность, вписанная в треугольник, площадь равностороннего треугольника можно вычислить через радиус окружности r:
Если в задаче присутствует окружность, описанная вокруг треугольника, площадь равностороннего треугольника можно вычислить через радиус окружности R:
Поделитесь статьей с одноклассниками «РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК формулы площади, периметра и радиуса».
Площадь равностороннего треугольника
Вы будете перенаправлены на Автор24
На этой странице вы узнаете, как выглядит формула для нахождения площади равностороннего треугольника, а также сможете воспользоваться онлайн-калькулятором для её вычисления.
Для того чтобы найти площадь правильного треугольника, подставьте известные вам значения в поле ввода онлайн-калькулятора.
На странице приведены два онлайн-калькулятора: первый для расчёта площади равностороннего треугольника через заданную сторону, а второй — через высоту.
К каждому калькулятору дан пример использования.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника определяется по формуле:
$S = \sqrt3 \cdot \frac
$AB = BC = AC$ — длина стороны равностороннего треугольника.
Дано:
Как посчитать площадь треугольника
Что такое площадь треугольника
Треугольник — это многоугольник с тремя сторонами и тремя вершинами.
Площадь треугольника — это величина плоскости, заключенной между сторонами этой геометрической фигуры.У треугольника она равна произведению половины основания на высоту.
Математически это выглядит так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
где a — основание треугольника, а h — его высота.
Способы нахождения площади
Но существуют также и другие способы, по которым можно найти S этого многоугольника. Рассмотрим основные из них.
Через две стороны и угол
Если вам известны две стороны любого треугольника и угол между ними, найти площадь можно по формуле:
где a и b — стороны фигуры, а α — угол между ними.
Через радиус описанной окружности и три стороны
Если вам известен радиус окружности, которая описана вокруг вашего треугольника, а также все его стороны, можно вычислить S следующим образом:
где a, b и c — стороны фигуры, а R — радиус описанной окружности.
Через радиус вписанной окружности и три стороны
В случае, если вам известны все три стороны и радиус вписанной в треугольник окружности, можно найти его площадь по формуле:
где r — радиус вписанной окружности, \(\frac
Таким образом, формулу можно выразить всего двумя множителями:
где p — полупериметр треугольника.
Через сторону и два угла
Если в данной фигуры вам известна лишь одна сторона и две прилегающих к ней угла, ее S можно найти следующим образом:
Для прямоугольного треугольника
В случае треугольника с прямым углом формулы для нахождения площади будут немного отличаться. Найти S можно будет несколькими способами.
По двум сторонам
Если вам известны оба катета данной фигуры, рассчитать S можно умножив их друг на друга, а потом разделив на пополам:
где a и b — катеты прямоугольного треугольника.
Через гипотенузу и острый угол
Зная длину гипотенузы и величину одного из острых углов, мы можем найти один из его катетов по определению косинуса. И уже потом можем использовать формулу для нахождения площади треугольника через две стороны и синус угла между ними.
Начнем с поиска катета:
где c — гипотенуза треугольника, a — его катет, а α — угол между ними.
Через катет и прилежащий угол
В этом случае нужно будет использовать следующую формулу:
Через радиус вписанной окружности и гипотенузу
Зная радиус вписанной в данную фигуру окружности и гипотенузу, мы можем использовать следующее уравнение для расчета:
где r — радиус вписанной окружности, c — гипотенуза.
Через вписанную окружность
Радиус, опущенный в точку касания окружности и гипотенузы прямоугольного треугольника, делит эту гипотенузу на неравные отрезки. Если нам известны величины этих отрезков, мы можем найти площадь фигуры по формуле:
где \(с_1\) и \(с_2\) — неравные отрезки гипотенузы.
По формуле Герона
Если мы знаем длины всех сторон данного многоугольника, мы можем рассчитать S по формуле Герона:
где \(p=\frac
Для равнобедренного треугольника
Рассмотрим случаи нахождения площади, если у треугольника равные боковые стороны.
Через основание и сторону
В этом случае формула будет выглядеть следующим образом:
где a — одно из боковых ребер фигуры, а b — ее основание.
Через основание и противолежащий угол
Зная длину основания и противолежащий ему угол, мы можем использовать следующую формулу:
где b — основание многоугольника, β — противолежащий ему угол.
Через основание и высоту
Если нам известна величина основания равнобедренного треугольника, а также его высота, найдем S по приведенной ниже по элементарной формуле:
где b — основание фигуры, а h — высота, проведенная к этому основанию.
Через боковые стороны и угол между ними
Если мы знаем длину боковых сторон и угол между ними, найдем площадь, опираясь на расчеты:
где a — это боковое ребро, β — угол между равными ребрами.
Через основание и угол между боковыми сторонами
В этом случае нам сначала придется найти высоту по формуле:
где β — угол при вершине, а b — основание.
Далее подставляем значение в формулу
Для равностороннего треугольника
В треугольнике, у которого все стороны равны, способы нахождения S также имеют свою специфику.
Через радиус описанной окружности
Если вокруг данного многоугольника описали окружность и нам известен ее радиус, расчеты будут такими:
где R — радиус описанной окружности.
Через радиус вписанной окружности
В этом случае воспользуемся таким уравнением:
где r — радиус вписанной в многоугольник окружности.
Через сторону
Зная лишь одно ребро у равностороннего треугольника, мы можем найти S:
где a — сторона фигуры.
Через высоту
Если нам известна только высота, можем вычислить S таким образом:
Примеры решения задач
Разберемся с нахождением площади треугольника наглядно на примере некоторых случаев.
Задача 1
В треугольник вписана окружность с радиусом 6 см. Известно, что его стороны равны 10 см, 12 см и 14 см. Определить площадь фигуры.
Решение
Задача 2
Дан равносторонний треугольник, вокруг которого описали окружность с радиусом 3 см. Посчитать S данной фигуры.
Решение
Задача 3
Известно, что у равнобедренного треугольника основание равно 4 см, а стороны по 3 см. Нужно вычислить площадь фигуры.
Решение
Ответ: \(2\sqrt5 см^2.\)
Задача 4
Решение
Онлайн калькулятор. Площадь треугольника по трем сторонам. Формула Герона
Используя этот онлайн калькулятор, вы сможете найти площадь треугольника по трем сторонам используя формулу Герона.
Воспользовавшись онлайн калькулятором для вычисления площади треугольника, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти площадь треугольника по трем сторонам. Формула Герона.
Ввод данных в калькулятор для вычисления площади треугольника по трем сторонам. Формула Герона.
В онлайн калькулятор вводить можно числа или дроби 3, 0.4, 5/7. Более подробно читайте в правилах ввода чисел.
Если у вас возниели трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Дополнительные возможности калькулятора вычисления площади треугольника по трем сторонам
Теория. Площадь треугольника по трем сторонам. Формула Герона.
где p полупериметр
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Периметр и площадь треугольника
Периметр
Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:
где P — это периметр треугольника, a, b и c — его стороны.
Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.
Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
где P — это периметр равностороннего треугольника, a — любая из его сторон.
Площадь
Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:
Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:
В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:
Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2.
Общая формула площади треугольника:
где S — это площадь треугольника, a — его основание, ha — высота, опущенная на основание a.
Площадь равностороннего треугольника – формула через сторону и высоту
Многоугольник, который имеет три вершины и три стороны, называется треугольником. Треугольник называется равносторонним или правильным, если все его три стороны одинаковые, а все три угла равны 60°. О методах вычисления площади равностороннего треугольника поговорим в этой статье.
Определение
Правильным треугольником называют часть плоскости, ограниченную тремя одинаковыми отрезками. Их соединяют точки, которые не принадлежат одной прямой. Здесь все три угла одинаковые и равняются по 60 градусов. Поэтому для определения площади правильного треугольника можно будет пользоваться упрощенными формулами.
Равносторонний треугольник является частным случаем равнобедренного треугольника.
Значение площади правильного треугольника вычисляется путем подстановки параметров фигуры в классическую формулу.
Рис. 1. Правильный треугольник.
Нахождение площади правильного треугольника
Это свойство характерно для равнобедренных треугольников, но любой правильный треугольник и будет равнобедренным, просто любая из его сторон может считаться основанием, так как две другие стороны в любом случае будут равны.
В результате треугольник делиться на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для правильного треугольника.
Рис. 2. Рисунок к доказательству.
В прямоугольном треугольнике АВМ катет АМ можно выразить через синус угла АВМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет АМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.
Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.
Тогда формула будет выглядеть следующим образом:
Теперь вспомним классическую формулу площади треугольника:
$S= <1over2>h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. Формула площади равностороннего треугольника будет выглядеть следующим образом:
ВС заменили на а, так как все стороны равны между собой, а значение высоты мы находили ранее. Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.
Только в правильном треугольнике возможно нахождение площади через сторону.
По той же причине нельзя использовать эту формулу для равнобедренного или произвольного треугольника. Прежде чем использовать эту формулу необходимо доказать, что треугольник правильный или убедиться, что это условие прописано в исходных данных задачи.
Рис. 3. Произвольный треугольник.
Что мы узнали?
Площадь правильного треугольника можно вычислить через сторону, поскольку речь идет о фигуре с одинаковыми параметрами, или через высоту по классической формуле. Здесь углы также будут одинаковыми. При решении некоторых задач по геометрии стоит помнить о том, что высоты данной плоской фигуры, ограниченной тремя сторонами, равны между собой.
Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта «Образование».
Площадь правильного треугольника

Средняя оценка: 4.4
Всего получено оценок: 284.
Средняя оценка: 4.4
Всего получено оценок: 284.
Правильные треугольники – это особое явление в геометрии. Все углы треугольника абсолютно точно определены значением в 60 градусов. Из-за этого, помимо обычных для треугольников способов нахождения площади, существуют и способы нахождения именно площади правильного треугольника, не характерные для других фигур. Все способы будут рассмотрены в этой статье.
Формулы для нахождения площади треугольника.
Это свойство характерно для равнобедренных треугольников, но любой правильный треугольник и будет равнобедренным, просто любая из его сторон может считаться основанием, так как две другие стороны в любом случае будут равны.
В результате треугольник делиться на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для правильного треугольника.
В прямоугольном треугольнике АВМ катет АМ можно выразить через синус угла АВМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет АМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.
Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.
Тогда формула будет выглядеть следующим образом:
Теперь вспомним классическую формулу площади треугольника:
$S= <1\over2>h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. В заданном треугольнике это будет выглядеть следующим образом:
ВС заменили на а, так как все стороны равны между собой, а значение высоты мы находили ранее. Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.
Только в правильном треугольнике возможно нахождение площади полной поверхности через сторону.
По той же причине нельзя использовать эту формулу для равнобедренного или произвольного треугольника. Прежде чем использовать эту формулу необходимо доказать, что треугольник правильный или убедиться, что это условие прописано в исходных данных задачи.
Что мы узнали?
Мы узнали, как можно найти площадь правильного треугольника по стороне, разобрались как эту формулу можно просто и быстро вывести. Запомнив ход вывода можно пользоваться этим в дальнейшем, не запоминая точных значений, а просто проверяя себя, выводя формулу в черновике.
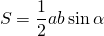

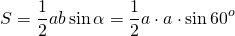
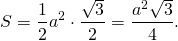








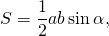
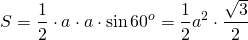
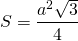













 , где
, где