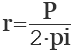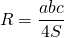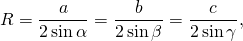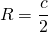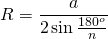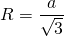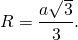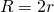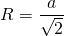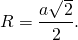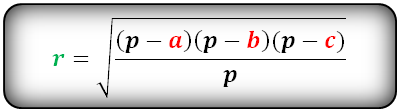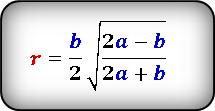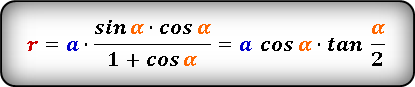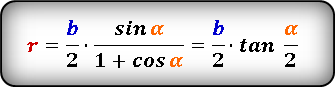Как найти радиус круга

Радиус круга

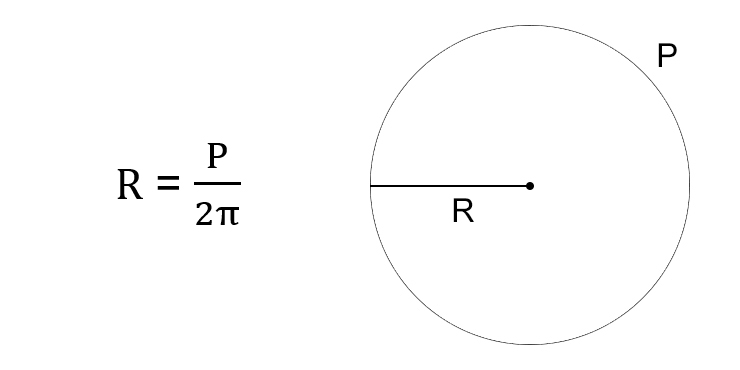
Предметы в форме круга, окружности встречаются нам ежедневно и повсюду: это и диск солнца или луны, колесо машины и ее руль, обручь, ось и т. д. Такая геометрическая фигура, как круг на плоскости была известна еще древним математикам, механикам. Как мы знаем, круг ограничивается окружностью, которая состоит из огромного множества точек, одинаково удаленных от центра точно на расстояние, называемое радиусом круга (окружности). Т.е. радиусом называют отрезок, соединяющий точки, расположенные на окружности, с центром круга. Если в задании известна длина окружности, то величина радиуса круга может быть вычислена по формуле:

R — радиус круга;
P — окружность круга.

Воспользовавшись онлайн калькулятором, вы можете быстро и правильно рассчитать искомую величину. Расчет величины радиуса необходим при изготовлении металлоконструкций, в строительстве и т.д.

Источник

Как определить радиус окружности, зная ее длину

Содержание статьи

«Учат в школе, учат в школе…»

По учебной программе шестого класса учащиеся общеобразовательных школ в курсе геометрии изучают круг и окружность как геометрическую фигуру, и все, что с этой фигурой связано. Ребята знакомятся с такими понятиями, как радиус и диаметр, длина окружности или периметр круга, площадь круга. Именно на этой теме они узнают про загадочное число Пи – это лудольфово число, как оно называлось раньше. Число Пи иррационально, так как его представление в виде десятичной дроби бесконечно. На практике используется его усеченный вариант из трех цифр: 3.14. Эта константа выражает отношение длины любой окружности к ее диаметру.
Шестиклассники решают задачи, выводя по одной данности и числа «Пи» остальные характеристики окружности и круга. В тетрадях и на классной доске они в масштабе вычерчивают абстрактные сферы и производят мало что говорящие вычисления.

А на практике

На практике такая задача может возникнуть в ситуации, когда, например, возникает необходимость проложить трассу определенной протяженности для проведения каких-либо состязаний со стартом и финишем в одном месте. Высчитав радиус, вы сможете на плане выбрать прохождение этой трассы, с циркулем в руке рассматривая варианты с учетом географических особенностей региона. Перемещая ножку циркуля – равноудаленного центра от будущей трассы, можно уже на этом этапе предусмотреть, где на участках будут подъемы, где спуски, учитывая естественные перепады рельефа. Также сразу можно определиться и с участками, где лучше разместить трибуны для болельщиков.

Радиус из окружности

Итак, предположим, что вам для проведения соревнований по автокроссу необходима круговая трасса длиной 10 000 м. Вот нужная формула для определения радиуса (R) окружности при известной её длине (C):
R=C/2п (п – число, равное 3.14).
Подставив имеющиеся значения, вы легко получаете результат:
R = 10 000:3.14 = 3 184. 71 (м) или 3 км 184 м и 71 см.

От радиуса к площади

Зная радиус окружности, легко можно определить площадь, которая будет изъята из ландшафта. Формула площади круга (S): S=пR2
При R = 3 184. 71 м она составит: S = 3.14 х 3 184. 71 х 3 184. 71 = 31 847 063 (кв. м) или почти 32 квадратных километров.

Подобные вычисления могут быть полезными при огораживании. Например, у вас имеется материал на ограду на столько-то погонных метров. Взяв эту величину за периметр круга, вы легко определите его диаметр (радиус) и площадь, а, следовательно, зримо представите величину будущего огороженного участка.

Источник

Радиус описанной и вписанной окружности: Формулы и примеры

Здравствуйте мои дорогие подписчики и гости сайта 9111.ru!

На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.

Что такое радиус

Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.

Вот так это выглядит графически.

Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.

Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.

Кстати, есть еще несколько значений слова РАДИУС:

Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

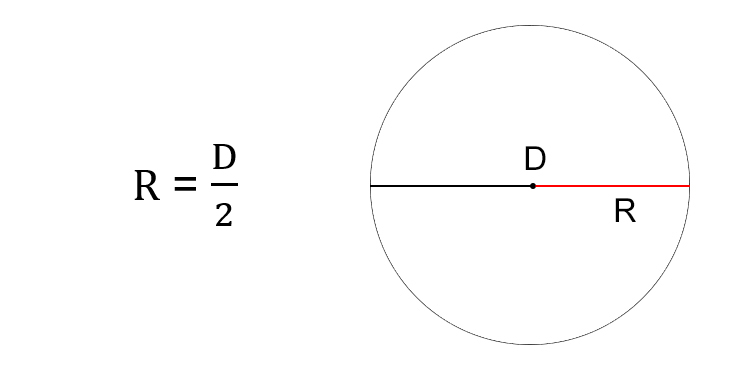
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.

Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.

Длина диаметра равна удвоенной длине радиуса.

Примеры задач

Длина окружности равняется 87,92 см. Найдите ее радиус.

Используем первую формулу (через периметр):

Найдите радиус круга, если его площадь составляет 254,34 см 2.

Воспользуемся формулой, выраженной через площадь фигуры:

Формулы для радиуса описанной окружности

Найти радиус описанной окружности треугольника по сторонам

Формула радиуса описанной окружности треугольника (R ) :

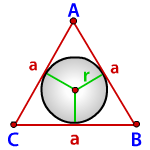
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте

Формула радиуса описанной окружности равностороннего треугольника через его сторону:

Формула радиуса описанной окружности равностороннего треугольника через высоту:

Найти радиус описанной окружности равнобедренного треугольника по сторонам

Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

Формула радиуса описанной окружности равнобедренного треугольника (R):

Найти радиус описанной окружности прямоугольного треугольника по катетам

Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.

Формула радиуса описанной окружности прямоугольного треугольника (R):

Радиус описанной окружности трапеции по сторонам и диагонали

Формула радиуса описанной окружности равнобокой трапеции, (R)

Найти радиус описанной окружности около квадрата

Радиус описанной окружности квадрата равен половине его диагонали

Формула радиуса описанной окружности квадрата (R):

Радиус описанной окружности прямоугольника по сторонам

Радиус описанной окружности прямоугольника равен половине его диагонали

Формула радиуса описанной окружности прямоугольника (R):

Радиус описанной окружности правильного многоугольника

Формула радиуса описанной окружности правильного многоугольника, (R):

Радиус описанной окружности правильного шестиугольника

Радиус описанной окружности правильного шестиугольника (R):

Формулы для радиуса вписанной окружности

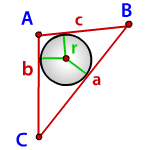
Радиус вписанной окружности в треугольник

Формула радиуса вписанной окружности в треугольник (r):

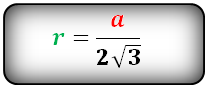
Радиус вписанной окружности в равносторонний треугольник

Формула для радиуса вписанной окружности в равносторонний треугольник (r):

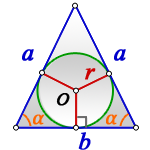
Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны (r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол (r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту (r ) :

Радиус вписанной окружности в прямоугольный треугольник

Формула радиуса вписанной окружности в прямоугольный треугольник (r):

Радиус вписанной окружности в равнобочную трапецию

Формула радиуса вписанной окружности равнобочной трапеции (r):

Радиус вписанной окружности в квадрат

Формула радиуса вписанной окружности в квадрат (r):

Радиус вписанной окружности в ромб

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

Формула радиуса вписанной окружности в ромб через диагонали (r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол (r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол (r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону (r ) :

2. Радиус вписанной окружности ромба, равен половине его высоты

Формула радиуса вписанной окружности в ромб (r ) :

Радиус вписанной окружности в правильный многоугольник

Формула радиуса вписанной окружности в правильный многоугольник, (r):

Радиус вписанной окружности в шестиугольник

Формула радиуса вписанной окружности в шестиугольник, (r):

Примеры задач

Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.

Сперва вычислим площадь треугольника. Для этого применим формулу Герона:

Остается только применить соответствующую формулу для вычисления радиуса круга:

Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.

Воспользуемся подходящей формулой, подставив в нее известные значения:

Всем спасибо и приятного просмотра! Если понравилась публикация подписывайтесь и ставьте палец вверх!

Источник

Нахождение радиуса описанной вокруг треугольника окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

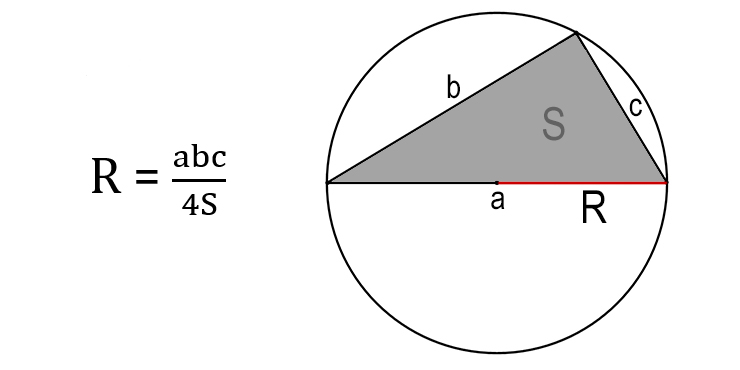
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

Источник

Как найти радиус окружности

Зачастую, когда школьник сдает выпускные экзамены в школе либо вступительные в какой-либо ВУЗ, ему необходимы определенные знания в области геометрии. Причем, задания бывают не такие уж сложные, просто нужно помнить базовые формулы, чтобы применить их в решении. Задачи, в которых необходимо найти радиус окружности, не являются исключением. В принципе, они достаточно просты в решении. В данной статье мы расскажем вам, как найти радиус окружности разными способами.

Когда вы получаете задание на контрольной или на экзамене, в котором надо найти радиус окружности, в первую очередь необходимо проанализировать имеющиеся данные. Потому что именно от них будет зависеть ход решения в целом. Так, например, найти рассматриваемую величину можно, используя такие параметры: длину окружности, ее площадь, диаметр и др. Мы рассмотрим самые простые и часто встречающиеся способы решения задач, в которых радиус окружности является неизвестным.

Все мы знаем, что радиусом окружности является длина от ее центра до какой-либо точки,которая расположена на самой окружности. В связи с этим, решения могут быть следующими:

Теперь вам не составит труда решить любую задачу с нахождением радиуса окружности. Главное – четко проанализировать исходные данные, а потом применить подходящую формулу, и можете считать себя великим математиком.

Поделиться советом: “Как найти радиус окружности”

Источник

Как найти радиус окружности. Вписанная и описанная окружность

Радиус – это отрезок, который соединяет любую точку на окружности с ее центром. Это одна из самых важных характеристик данной фигуры, поскольку на ее основе можно вычислить все другие параметры. Если знать, как найти радиус окружности, то можно рассчитать ее диаметр, длину, а также площадь. В том случае, когда данная фигура вписана или описана вокруг другой, то можно решить еще целый ряд задач. Сегодня мы разберем основные формулы и особенности их применения.

Известные величины

Если знать, как найти радиус окружности, который обычно обозначают буквой R, то его можно вычислить по одной характеристике. К таким величинам относят:

По длине окружности

Если в задаче известна величина C, то R = С / (2 * П). Эта формула является производной. Если мы знаем, что из себя представляет длина окружности, то ее уже не нужно запоминать. Предположим, что в задаче C = 20 м. Как найти радиус окружности в этом случае? Просто подставляем известную величину в вышеприведенную формулу. Отметим, что в таких задачах всегда подразумевается знание числа П. Для удобства расчетов примем его значение за 3,14. Решение в этом случае выглядит следующим образом: записываем, какие величины даны, выводим формулу и проводим вычисления. В ответе пишем, что радиус равен 20 / (2 * 3,14) = 3,19 м. Важно не забыть о том, что мы считали, и упомянуть название единиц измерения.

По диаметру

Сразу подчеркнем, что это самый простой вид задач, в которых спрашивается о том, как найти радиус окружности. Если такой пример попался вам на контрольной, то можете быть спокойны. Тут даже не нужен калькулятор! Как мы уже говорили, диаметр – это отрезок или, правильнее сказать, хорда, которая проходит через центр. При этом все точки окружности равноудалены. Поэтому данная хорда состоит из двух половинок. Каждая из них является радиусом, что следует из его определения как отрезка, который соединяет точку на окружности и ее центр. Если в задаче известен диаметр, то для нахождения радиуса нужно просто разделить эту величину на два. Формула выглядит следующим образом: R = D / 2. Например, если диаметр в задаче равен 10 м, то радиус – 5 метров.

По площади круга

Как найти радиус описанной окружности

Предположим, что a, b, c – это стороны треугольника. Если знать их величины, то можно найти радиус описанной вокруг него окружности. Для этого сначала нужно найти полупериметр треугольника. Чтобы было легче для восприятия, обозначим его маленькой буквой p. Он будет равен половине суммы сторон. Его формула: p = (a + b + c) / 2.

Рассмотрим пример задачи. У нас есть окружность, описанная вокруг треугольника. Длины ее сторон составляют 5, 6 и 7 см. Сначала вычисляем полупериметр. В нашей задаче он будет равен 9 сантиметрам. Теперь вычислим произведение длин сторон – 210. Подставляем результаты промежуточных расчетов в формулу и узнаем результат. Радиус описанной окружности равен 3,57 сантиметра. Записываем ответ, не забывая о единицах измерения.

Как найти радиус вписанной окружности

Предположим, что a, b, c – длины сторон треугольника. Если знать их величины, то можно найти радиус вписанной в него окружности. Сначала нужно найти его полупериметр. Для облегчения понимания обозначим его маленькой буквой p. Формула его вычисления выглядит следующим образом: p = ( a + b + c) / 2. Этот тип задачи несколько проще, чем предыдущий, поэтому больше не нужно никаких промежуточных расчетов.

Окружность и ее свойства

У каждой геометрической фигуры есть свои особенности. Именно от их понимания зависит правильность решения задач. Есть они и у окружности. Зачастую их используют при решении примеров с описанными или вписанными фигурами, поскольку они дают ясное представление о такой ситуации. Среди них:

Источник

Как найти радиус и диаметр окружности через площадь круга?

Нахождение радиуса и диаметра по площади круга.

Как найти радиус и диаметр окружности, если известна площадь круга?

S = πR² или S = 3,14R²

Если в задании нам известна площадь круга то мы можем легко вычислить радиус по формуле:

R = √(S / π) или R = √(S / 3,14)

Чтобы вычислить диаметр круга нужно просто результат (радиус) умножить на 2:

D = 2√(S / π) или D = 2√(S / 3,14)

Из этой формулы можно вывести формулу для вычисления радиуса круга через его площадь: R=√S/π.

Для того, чтобы вычислить радиус круга нужно извлечь корень квадратный ( √ ) из частного : площади круга, поделенной на число Пи.

Рассмотрим конкретный пример вычисления радиуса круга через его площадь:

Площадь круга равна 10 кв.см., найдем радиус круга: R=√10/3,14=1,78 см. Радиус круга, площадь которого равна 10 кв.см., равен 1,78 см.

То есть, для того, чтобы вычислить диаметр круга нужно извлечь корень квадратный ( √ ) из частного: площади круга, поделенной на число Пи, и полученный результат умножить на два.

Если мы вычислим диаметр круга с площадью 10 кв.см. по этой формуле, то получим результат 3,56 см.

Источник

Окружность

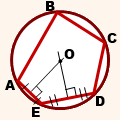
Точка О является центром окружности, R является радиусом окружности — расстоянием от какой-нибудь точки окружности до центра. По определению все радиусы замкнутой

кривой имеют одинаковую длину.

Концентрические окружности – это окружности, имеющие общий центр. Ортогональные окружности — это окружности, которые пересекаются под углом равным 90 градусов.

Плоскость, которую ограничивает окружность, называется кругом. Одна часть круга, которая ограничена двумя радиусами и дугой — это круговой сектор. Дуга сектора – это дуга, ограничивающая сектор.

Рис. 2

Взаимное расположение окружности и прямой (рис.2).

Окружность и прямая имеют две общие точки, если расстояние от прямой до центра окружности менее радиуса окружности. В таком случае прямая по отношению к окружности называется секущей.

Окружность и прямая имеют одну общую точку, если расстояние от прямой до центра окружности равно радиусу окружности. В таком случае прямая по отношению к окружности называется касательной к окружности. Их общая точка носит название точки касания окружности и прямой.

Основные формулы окружности:

Окружность и круг получили свое название в Древней Греции. Уже в древности человека интересовали круглые тела, поэтому окружность становилась венцом совершенства. То, что круглое тело могло двигаться само по себе, стало толчком к изобретению колеса. Казалось бы, что особенного в этом изобретении? Но представьте, если в одно мгновение колеса исчезнут из нашей жизни. В дальнейшем это изобретение и породило математическое понятие окружности.

Источник

Нахождение радиуса вписанной в треугольник окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса вписанной окружности

Произвольный треугольник

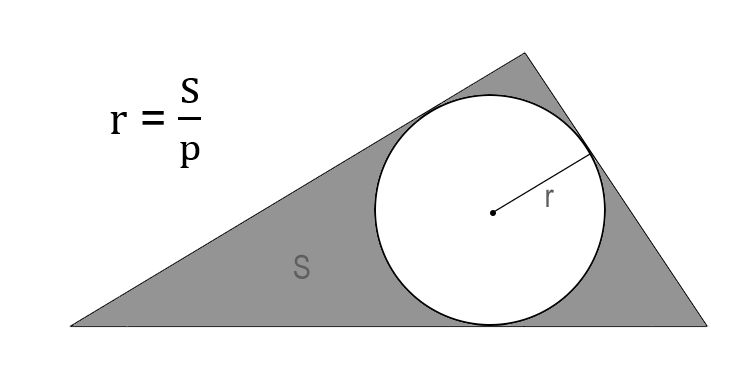
Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.

где a и b – катеты, c – гипотенуза треугольника.

Равнобедренный треугольник

Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:

где a – боковые стороны, b – основание треугольника.

Равносторонний треугольник

Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.

Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:

Остается только применить соответствующую формулу для вычисления радиуса круга:

Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.

Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:

Источник

Радиус окружности по хорде и дуге

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Сегмент

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Параметры сегмента по хорде и высоте

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Сегмент

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Параметры сегмента по хорде и высоте

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

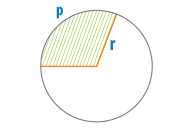
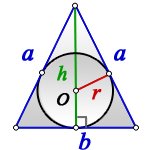
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии.

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.

Интересующие нас величины и их обозначения:

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.

1. Даны диаметр D и длина дуги L

; длина хорды ;
высота сегмента ; центральный угол .

2. Даны диаметр D и длина хорды X

; длина дуги ;
высота сегмента ; центральный угол .

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .

3. Даны диаметр D и центральный угол φ

; длина дуги ;
длина хорды ; высота сегмента .

4. Даны диаметр D и высота сегмента H

; длина дуги ;
длина хорды ; центральный угол .

6. Даны длина дуги L и центральный угол φ

; диаметр ;
длина хорды ; высота сегмента .

8. Даны длина хорды X и центральный угол φ

; длина дуги ;
диаметр ; высота сегмента .

9. Даны длина хорды X и высота сегмента H

; длина дуги ;
диаметр ; центральный угол .

10. Даны центральный угол φ и высота сегмента H

; диаметр ;
длина дуги ; длина хорды .

Внимательный читатель не мог не заметить, что я пропустил два варианта:

5. Даны длина дуги L и длина хорды X

7. Даны длина дуги L и высота сегмента H

Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?

Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.

Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:

длина окружности ;
площадь круга ;
площадь сектора ;
площадь сегмента ;

И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.

Источник

Радиус фигур

Радиус фигур – это отрезок, который соединяет в размещенной на плоскости окружности (в перпендикулярном сечении фигуры или ее основании) центральную ее точку с иными точками, которые на ней можно разместить. Он является важным параметром в описании свойств круга, сферы, цилиндра, конуса и иных фигур. Радиус равен половине значения диаметра. Зная радиус и число π, можно с легкостью вычислить значение площади круга (π r2) и длины окружности (2 π r).

В машиностроении и строительстве задействуется очень много деталей, имеющих цилиндрическую форму. Важным параметром для расчета тех или иных характеристик подобных элементов станков, механизмов и строительных конструкций является радиус.

После замера или вычисления радиуса часто требуется находить значения площади и объема (V=π х r2 х h) цилиндра. Расчет радиуса круга может быть необходим при проектировании конструкций с основанием в форме круга. Это, в частности, могут быть водонапорные и иные башни.

Перед конструкторами-проектировщиками в самых разных ситуациях могут стоять задачи вписывания сферы в цилиндр, или описывания сферы около цилиндра. При расчете требуется воспользоваться онлайн-калькулятором для определения R основания шара.

Источник

Радиус описанной окружности

Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.

Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):

где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.

у остроугольного треугольника — внутри треугольника;

у прямоугольного — на середине гипотенузы;

у тупоугольного — вне треугольника, напротив тупого угла.

Радиус описанной окружности для прямоугольного треугольника

Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:

Окружность, описанная около многоугольника

Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.

Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.

Радиус окружности, описанной около правильного многоугольника

Формула радиуса описанной окружности для правильного многоугольника

где a — длина стороны многоугольника, n — количество его сторон.

Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.

Радиус описанной окружности правильного треугольника

Формула радиуса описанной окружности для правильного треугольника

Если без иррациональности в знаменателе —

У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:

Радиус описанной окружности квадрата

Формула радиуса описанной окружности для квадрата

Если без иррациональности в знаменателе —

Радиус описанной окружности правильного шестиугольника

Формула радиуса описанной окружности для правильного шестиугольника

Источник

Формула, чему равен радиус круга?

Добрый вечер. Напишите пожалуйста формулу, чему равен радиус круга? Спасибо.

Здравствуйте. Как вы знаете, радиус круга – это расстояние до центра круга от точки, которая лежит на внешней окружности круга. Самый простой способ нахождения радиуса – разделить диаметр пополам.
Итак, вычислить длину окружности можно при помощи формулы:
,
Где – длина окружности, – радиус окружности, а – всегда равен 3,14, отсюд адиус находится:

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Источник

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Источник

Нахождение радиуса описанной вокруг правильного многоугольника окружности

В публикации представлена формула, с помощью которой можно найти радиус окружности, описанной около правильного многоугольника, а также приведен пример решения задачи для лучшего понимания представленного материала.

Формула расчета радиуса окружности

На рисунке изображен правильный шестиугольник с описанной вокруг него окружностью, но формула ниже подходит для любого правильного n-угольника.

где a – длина стороны.

Примечание: зная радиус описанного круга можно найти сторону равностороннего n-угольника (формула выводится из представленной выше):

Пример задачи

Дан правильный пятиугольник с длиной стороны 8 см. Вычислите радиус описанной около данной фигуры окружности.

Решение:
Применим соответствующую формулу, подставив в нее известное нам значение.

Источник

Радиус в физике – Как найти радиус (Формула), физика

Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

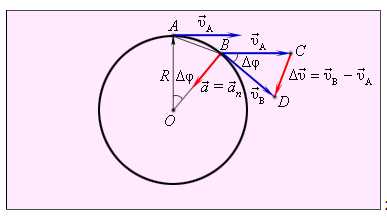
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Источник

Теорема описанной окружности — как построить, свойства

Описанная окружность — что из себя представляет

Решение задач по геометрии может быть проще, если при нахождении неизвестных пользоваться дополнительными сведениями и приемами. Одним из таких будет описание окружности вокруг фигуры.

Описанная окружность — окружность, которая описана вокруг многоугольника. Главным свойством описанной окружности будет тот факт, что она должна содержать все вершины многоугольника.

Точки окружности равноудалены от ее центра, а значит, также равноудалены будут и вершины многоугольника, вокруг которого описана окружность.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Вокруг чего можно описать

Окружность можно описать вокруг (или около):

Теорема, основные свойства, признаки

Правило об описанной окружности

Около любой из вышеперечисленных фигур можно описать окружность, причем только одну.

Доказательством теоремы будет тот факт, что точка пересечения серединных перпендикуляров через медианы у любой фигуры будет только одна. Это точка будет является центром окружности, а значит, никакая другая окружность, которая при этом также захватывает все вершины фигуры, не может быть описана вокруг нее.

Теорема синусов

Теорема синусов позволяет найти двойной радиус или диаметр окружности по расчету формулы:

a, b, c — стороны треугольника,

A, B, C — углы треугольника.

Соответственно, для того, чтобы найти радиус описанной окружности, необходимо знать величины любой стороны и противоположного ей угла.

Свойства описанной окружности:

Главным признаком описанной окружности будет ее расположение вокруг фигуры, причем ни одна из ее вершин не должна выходить за пределы кривой окружности.

Как найти радиус и диаметр описанной окружности, формула

Треугольник

Формула нахождения радиуса описанной окружности вокруг треугольника:

a, b и c — стороны треугольника,

Формула нахождения радиуса описанной окружности вокруг равностороннего треугольника по стороне:

а — сторона треугольника.

Формула нахождения радиуса описанной окружности вокруг равностороннего треугольника по высоте:

Формула нахождения радиуса описанной окружности вокруг равнобедренного треугольника по сторонам:

Формула нахождения радиуса описанной окружности вокруг прямоугольного треугольника по катетам и гипотенузе:

Трапеция

Формула нахождения радиуса описанной окружности вокруг трапеции по сторонам и диагонали:

a — боковые стороны трапеции,

b — верхнее основание,

с — нижнее основание,

р — полупериметр прямоугольного треугольника: \(p=\frac<\left(a+b+c\right)>2.\)

Правильный многоугольник

Формула нахождения радиуса описанной окружности вокруг правильного многоугольника:

а — сторона многоугольника,

N — количество сторон многоугольника.

Правильного шестиугольник

Формула нахождения радиуса описанной окружности вокруг правильного шестиугольника:

а — сторона шестиугольника,

d — диагональ шестиугольника.

Прямоугольник

Формула нахождения радиуса описанной окружности вокруг прямоугольника по стороне:

a и b — стороны прямоугольника,

Квадрат

Формула нахождения радиуса описанной окружности вокруг квадрата:

Так как диаметр является суммой двух радиусов, при помощи вышеперечисленных формул можно найти диаметр просто умножив полученный результат на 2.

Источник

Как найти радиус окружности

Как найти радиус окружности

Девять способов, которые помогут справиться с геометрическими задачами.

Выбирайте формулу в зависимости от известных величин.

Через площадь круга

Через длину окружности

Через диаметр окружности

Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

Через стороны и площадь вписанного треугольника

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

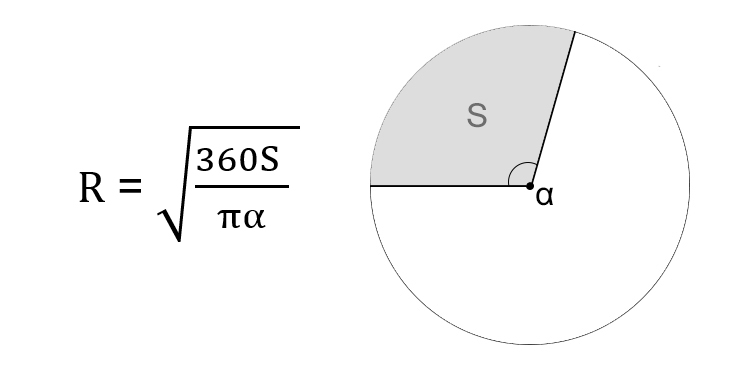
Через площадь сектора и его центральный угол

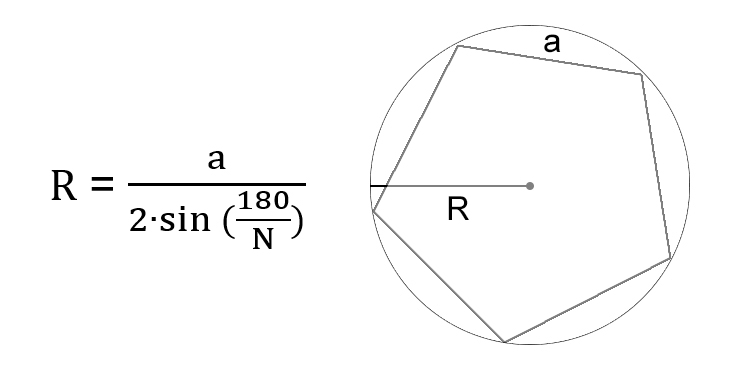
Через сторону вписанного правильного многоугольника

Источник

Люди, по какой формуле можно вычислить радиус?

Вопроса два.
1). Известны две величины. Это длинна дуги окружности и длинна хорды, соединяющей концы этой дуги. Нужно вычислить радиус.
2). Известны две величины. Это длинна хорды и длинна отрезка, перпендикулярно соединяющего середину хорды с краем окружности. Нужно опять вычислить радиус.
А то у меня формула что-то грешит совсем.

Keramamaster написал :
Что-то у меня не получается.

((100/2)*2 + 50*2)/100=(2500 + 2500)/100 = 50

Спасибо конечно, но мне, чайнику, проблематично интерпретировать эти формулы под вычисление именно радиуса.
Может вас не затруднит написать её в формате R(радиус)=»бла-бла-бла»

ну да, это очевидно, простая теореме Пифагора, там чисел нет, только неизвестные, могу развернуть, но автор не просил.
2О-это 2 умножить на отрезок.

Лида, вы заслуженный гений России!
Простите за жадность, но может еще формулу подкинете? вычисления R по длине дуги и хорды?

Vegazzz написал :
не усложняйте жизнь, длина дуги вещь не точная,т.е. сантиметром на полу ее не измеришь,

Согласен, но это с легкостью можно сделать с помощью курвиметра, по любой криволинейной поверхности.

Vegazzz написал :
сама задача п.1 имеет решение через тригометрическиую функцию синус

Мне нужна конечная формула, ее можно ввести в excel, а он сам посчитает что и как на основе всего двух данных: хорды и дуги.

Не только мне, но и всем тем, кто хочет радовать свой глаз точностью воплощения дизайн-проектов.

Keramamaster,постараюсь вечерком формулу начертить, только и вы колитесь, а то как мозаинки-проф.секркт, проф.секрет. для вас плитка очевидно. а я как баран сижу в своих мыслях и проблемах.
Не принимайте всерьез-конечно это шутка!

1). Известны две величины. Это длинна дуги окружности и длинна хорды, соединяющей концы этой дуги. Нужно вычислить радиус.

2). Известны две величины. Это длинна хорды и длинна отрезка, перпендикулярно соединяющего середину хорды с краем окружности. Нужно опять вычислить радиус.

И почему Нобель обделил своей премией матеметиков? Такой аццкий головняк эти формулы!
Спасибо всем! Только неужели в формулу для вычисления по окружности не надо вставлять число «Пи»? Может погрешность уменьшится?

Vegazzz написал :
. я как баран сижу в своих мыслях и проблемах.

Vegazzz, персонально благодарствую.
все когда-то случается впервые, скоро и у вас найдется индивидуальное решение

О чудо-форум! искал одно, а получил комплект! математику+русский. Низкий поклон

ЁмоЁ! Vegazzz, вы поломали мой нежный мозг
Ребус какой-то. Как бы это все привести в формат R=»бла-бла-бла»?
Ну честно, не силен я в пифагоровской науке

Keramamaster написал :
Ребус какой-то. Как бы это все привести в формат R=»бла-бла-бла»?

А всё потому, что Вы не даёте общей картины: что есть и что надо получить на выходе. Может, Вам совсем не длину дуги и хорды надо мерить, а что-то совсем другое. У меня, например, в голове не складывается прикладное применение этой задачи. Что это за окружность, доступа к которой нет (иначе можно было бы просто измерить диаметр), а есть лишь некий выступающий полупенёк (именно пенёк, а не часть трубы, иначе как Вы измерили расстояние до хорды?)? Причём не просто пенёк, а целый лес разновеликих полупеньков, поскольку Вам нужна некая формула для общего случая, чтоб быстренько обсчитывать все эти пеньки

Лида написал :
Что это за окружность, доступа к которой нет

Vegazzz написал :
догадываюсь, что керамомастер рисует большую дугу на полу, центр у нее неизвестно где, но надо найти.

во как!!это в мою копилку знаний в плане плитки.

А как же Вы тогда будете его использовать? И что толку от радиуса, который некуда приложить?

Vegazzz написал :
догадываюсь, что керамомастер рисует большую дугу на полу, центр у нее неизвестно где

А откуда известно в таком случае, что это именно окружность, а не некая кривуля?

Хороший вопрос про радиус, может еще один проф.секрет откроем.

Keramamaster написал :
Сейчас отдыхаю, но пока есть время, использую его для теоретичеких подкреплений для будущей практики.

Эта задача элементарно решается компьютерными программами Архикад или Автокад,,где рисуются сплайнами кривые по всей поверхности по которой надо вывести(можно задавать радиусы,а можно просто рисовать нужную кривую) и которую визуально можно видеть и корректировать,программа сама пересчитывает и выдает координаты,но лучше затем просто распечатать на принтере 1:1 и получите на выходе готовый шаблон.А в случае гидрорезки просто скинуть файл в формате DWG в фирму производящую гидрорезку и они в точности по Вашим чертежам произведут резку(со всеми ошибками,если их допустить,или без оных,если их не нет).А снятие размеров и дальнейший их перерасчет по формулам-это тупиковый путь,потому,что ошибки которые будут накапливаться при снятии размеров приведут к таким погрешностям,что без ручной доводки затем не обойтись.Это,если для этой цели использовать(ну в случае плитки).

Vegazzz написал :
во как!!это в мою копилку знаний в плане плитки.

Лида написал :
А как же Вы тогда будете его использовать? И что толку от радиуса, который некуда приложить?

Вот пример из моей практики. Тут и центр окружности за стенкой, и кривуля

Keramamaster написал :
Тут и центр окружности за стенкой, и кривуля

До меня поработали одни из лучших штукатуров. Сколько плитку после них не ложил, все углы в ноль сходились. Им доверял как себе и даже больше. Большая редкость.
А вообще вы правы, не нужна мне длина окружности, ну или не скоро понадобится.
Спасибо.

Keramamaster написал :
До меня поработали одни из лучших штукатуров. Сколько плитку после них не ложил, все углы в ноль сходились. Им доверял как себе и даже больше. Большая редкость.

Источник

Окружность

Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.

Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:

Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:

Построение окружности циркулем

Для построения окружности используют специальный прибор — циркуль:

Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:

Радиус, хорда и диаметр

Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:

Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.

Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.

Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:

Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:

Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:

Для обозначения дуг используется символ :

О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.

Хорда AB стягивает дуги AFB и AJB.

Источник

Длина окружности или периметр круга. как найти радиус круга, онлайн расчет

В публикации рассмотрены формулы, с помощью которых можно вычислить радиус круга (окружности), если известны его периметр или площадь, а также разобраны примеры решения задач.

Через площадь круга

Геометрия 6,7,8,9,10,11 класс, ЕГЭ, ГИА

Основная информация по курсу геометрии для обучения и подготовки в экзаменам, ГВЭ, ЕГЭ, ОГЭ, ГИАГеометрия 6,7,8,9,10,11 класс, ЕГЭ, ГИА

Код для вставки без рекламы с прямой ссылкой на сайт Код для вставки с рекламой без прямой ссылки на сайт

Код для вставки:

Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор.

Об этой статье

Эту страницу просматривали 657 571 раз.

Основные свойства окружности

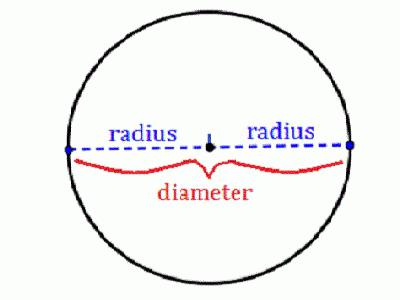
1. Диаметр окружности равен двум радиусам.

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Через диаметр окружности

Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.

Этимология

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

Площадь сегмента

Видео по теме

Подпишитесь на наши интересные статьи в соцетях!

Или подпишитесь на рассылку

Через площадь сектора и его центральный угол

Источник

Как найти радиус окружности

Слово переводится с латинского radius как «спица колеса, луч». Радиусом называется любой отрезок прямой, который соединяет центр окружности или сферы с любой из точек, лежащих на этой окружности или на поверхности данной сферы, также и длина этого отрезка является радиусом. Для обозначения радиуса в вычислениях и математических выражения используется латинская буква R.

Диаметр окружности представляет собой отрезок прямой, которыйпроходит через центр окружности и соединяет две наиболее удаленные между собой точки, лежащие на окружности. Длина этого отрезка тоже называется диаметром окружности. Радиус равен половине диаметра окружности, поэтому если известен диаметр данной окружности, чтобы найти ее радиус достаточно разделить его пополам. R = D/2, где D – диаметр окружности.

Круг – это геометрическая фигура, представляющая собой часть плоскости, ограниченная кривой являющейся окружностью. Если известна площадь круга, то найти радиус окружности можно из следующей формулы:R = v(S/?), где v — корень квадратный, S – площадь круга.

Источник

Нахождение радиуса описанной вокруг квадрата окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около квадрата. Также разберем примеры решения задач для закрепления изложенного материала.

Формулы вычисления радиуса описанной окружности

Через сторону квадрата

Радиус R окружности, описанной около квадрата, равняется длине его стороны a, умноженной на квадратный корень из двух и деленной на два.

Через диагональ квадрата

Радиус R описанной вокруг квадрата окружности равен половине его диагонали d.

Примеры задач

Задание 1

Длина стороны квадрата равняется 8 см. Найдите радиус описанной вокруг него окружности.

Применим первую формулу, рассмотренную выше:

Задание 2

Вычислите длину диагонали квадрата, если радиус описанной вокруг него окружности составляет 6 см.

Как мы знаем, радиус описанной окружности равняется половине диагонали квадрата. Следовательно, общая длина диагонали равняется 12 см (6 см ⋅ 2).

Источник

Вычислить радиус

Дата публикации: 21-09-2015 10:21:21 / Дата изменения: 28-09-2015 20:10:33

Вычислить радиус достаточно нетрудно. В интернете много сервисов предлагающих услуги по его расчету. Вот и сайт «Все обо Всем» решил создать свой собственный сервис для подобных расчетов. Но, прежде чем говорить о самом сервисе, давайте напомним, что такое радиус и как проводить вычисление радиуса в математике.

Вычислить радиус при помощи сервиса «Все обо всем».

Другие статьи на эту тему:

Вычислить диаметр.
Вычислить длину окружности.
Вычислить площадь круга.
Вычислить площадь шара.
Вычислить объем шара.

Радиус круга (шара) – это отрезок, который соединяет центр круга или шара с точкой на его поверхности. Мы начнем нашу статью с самого простого вида расчета радиуса – расчет радиуса по известной величине диаметра круга (шара). Позже, мы рассмотрим варианты вычисления радиуса по известным значениям длинны окружности, площади круга, площади шара и объема шара. Также в этой статье мы расскажем Вам о том, как вычислять значение радиуса при помощи сервиса калькулятор круга (калькулятор шара), который разработан в рамках сайта «Все обо всем».

Вычисление радиуса по диаметру.

Для начала вычисления нужно иметь представление о том, что такое диаметр круга или шара. Диаметр – это отрезок, который соединяет две точки, лежащие на окружности или поверхности шара и проходящий через его центр. Диаметр делит круг на два ровных полукруга. Для вычисления диаметра применяют следующую формулу: D=2r. Из этой формулы следует, что радиус равен r=D/2.

Вычислить радиус по длине окружности.

Дадим определение длине окружности. Длинна окружности – это кривая линия, все точки которой лежать на одинаковом и максимальном удалении от центра круга. Для расчета длинны окружности используют следующую формулу L=2Pr. В данной формуле P – константа, значение которой равно 3.14159. Следовательно, для вычисления значения радиуса по длине окружности необходимо использовать формулу r= L/2P.

Вычислить радиус по площади круга.

Вычислить радиус по площади шара.

Вычислить радиус по объему шара.

У многих посетителей нашего сайта возникает проблема с вычислением радиуса шара по известному показателю его объема. И это не удивительно, ведь здесь имеют место самые сложные вычисления. К счастью, наш сервис достаточно умен и проводит все расчеты в считанные секунды. Итак, давайте узнаем по какой формуле вычисляется объем шара? Формула имеет следующий вид: V=4/3(Pr 3 ). Формула не представляет из себя ничего сверх сложного, однако получить из нее значение радиуса не так уж и просто. Формула для расчета радиуса из объема шара имеет следующий вид: r=ᶟ√(V/(3/4P)). Радиус равен кубическому корню из объема шара деленного на три четвертых Пи.

Вот такая у нас получилась образовательная статья по вопросу вычисления радиуса, надеюсь, Вам было интересно. В ближайшее время Вас ожидает еще ряд статей на тему вычисления диаметра, длинны окружности, площади круга, площади шара и объема шара.

Другие статьи на эту тему:

Вычислить диаметр.
Вычислить длину окружности.
Вычислить площадь круга.
Вычислить площадь шара.
Вычислить объем шара.

Шитье. Как рассчитать радиус и нарисовать окружность без циркуля — 3 способа!

КАК РАССЧИТАТЬ РАДИУС ОКРУЖНОСТИ.

Для чего он нужен, этот расчет радиуса? Чтобы начертить окружность, нам надо знать радиус этой сомой окружности – то есть расстояние от одной ножки циркуля до другой.

Допустим нам надо нарисовать окружность донышка панамки, и все что мы знаем, это обхват головы ребеночка. Как широко надо раздвинуть ножки циркуля, чтобы в итоге получить окружность, совпадающую с размерами головы ребеночка?

Или нам нужно начертить окружность юбки-солнца, зная только то, что длина окружности должна идеально совпадать с обхватом нашей талии.

Сейчас, чтобы все было предельно ясно и понятно, разберем 2 конкретных случая, которые чаще всего встречаются в работе швей.

Это расчет радиуса донышка панамки. И расчет радиуса на выкройке юбки-солнца.

Ситуация первая – нужно рассчитать радиус и начертить окружность дня панамки для девочки.

Значит, чтобы узнать радиус – нам надо наш обхват головы ребеночка поделить на 6,28.

Берем мобильный телефон, находим в нем калькулятор и делим наши 42 см обхвата головы на 6,28 – получаем 6,68 см = то есть 6 см и 6 мм. Это и есть радиус.

Значит, нам надо раздвинуть ножки циркуля на расстояние 6 см 6 мм. И тогда нарисованная нами окружность будет равна 42 см – то есть ляжет ровненько по головке ребенка (только не забудьте ее обвесит отступив на 1 см для припусков на швы).

Ситуация вторая – нужно начертить окружность юбки-солнца. Все что мы знаем это обхват талии и длина юбки которую мы в итоге хотим получить.

В чертеже юбки солнца есть 2 окружности. Маленькая (внутренняя) должна лечь ровненько на нашу талию. То есть длина этой окружности должна совпасть с обхватом талии. Обхват талии 70 см, значит, и длина окружности должна быть 70 см (ну, разве что, там всякие сантиметры туда-сюда в виде припуска на швы, или еще какую дополнительную отделку в виде поясочка или кокеточки)

Значит нам нужно узнать, какого радиуса чертить круг, чтобы окружность в результате получилась длиной в эти нужные нам70 см.

На картинке ниже я все расписала и как рассчитать радиус маленькой окружности и как потом узнать радиус большой окружности.

И когда начерчена маленькая окружность. Все что нам нужно, это к маленькому радиусу прибавить желаемую длину юбки – и мы получаем большой радиус для большой окружности края юбки.

Вот с расчетами мы разобрались. Будем шить юбки и панамки – буду отправлять вас в эту статью.

Теперь давайте разберемся, как нарисовать окружность любого размера без циркуля.

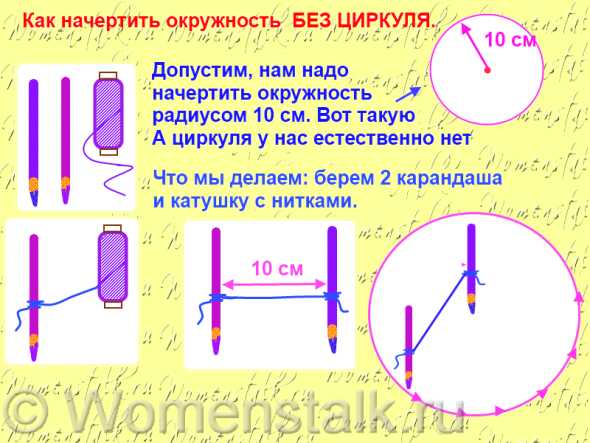
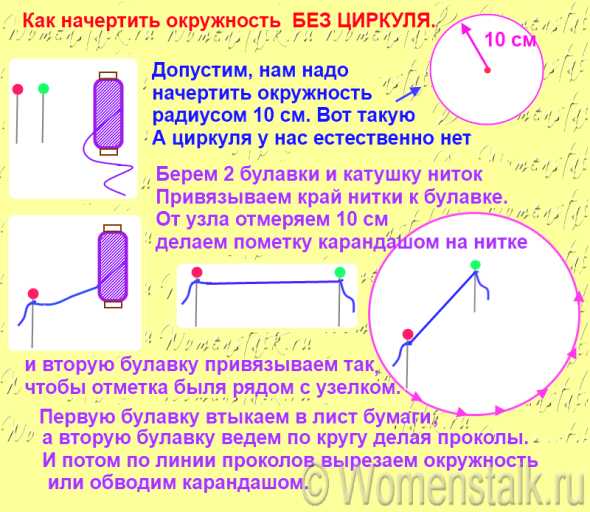
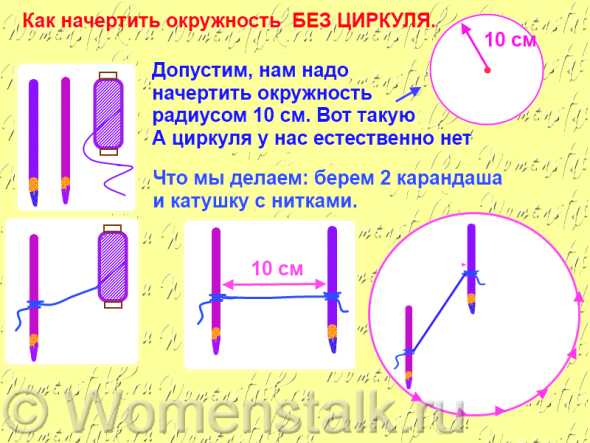
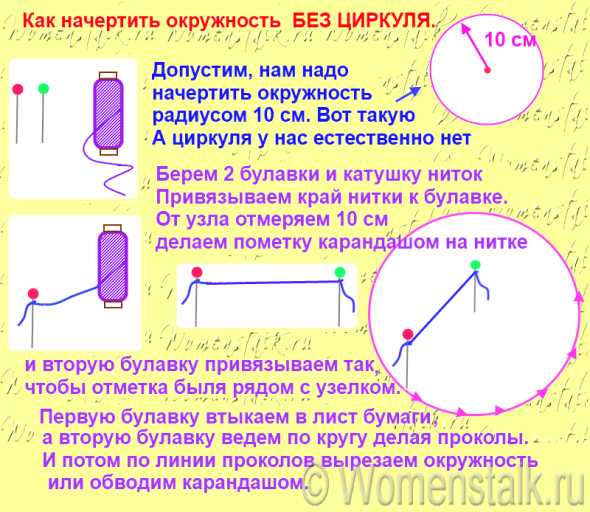
КАК НАРИСОВАТЬ ОКРУЖНОСТЬ БЕЗ ЦИРКУЛЯ.

Вот здесь ниже я проиллюстрировала тремя картинками три способа. Надеюсь что все понятно нарисовано и прописано.

Да это быстрый способ – но надо следить за тем, чтобы карандаши не откланялись в сторону. Угол наклона карандаша изменяем радиус. Или надо чтобы один человек ровно держал один карандаш, а другой ровно перпендикулярно чертил вторым карандашом.

Вообще-то, чем ниже привязана нитка тем точнее будет окружность. Поэтому некоторые пользуются маленькими булавочками. Погрешность при отклонении булавки в сторону небольшая, и при шитье ею можно принебречь.

И все-таки самый вернейший способ начертить точный круг без циркуля, это при помощи обычной линейки и карандаша. Вот как это выглядит:

И далее по кругу, двигаем сантиметр (как часовую стрелку в часах) и отмечаем точки на одном и том же расстоянии – то есть на одной и той же цифре сантиметровой ленты. Вместо ленты можно использовать бечевочку с нанесенной на ней отметкой – главное убедитесь что бечевочка нисколько не тянется.

Ольга Клишевская, специально для сайта “Женские разговоры”.

Думаю вам будет интересно:

Как рассчитать радиус окружности | ЧтоКак.ру

Чтобы рассчитать радиус окружности, достаточно знать величину радиуса данной окружности, а также необходимые постоянные значения величин. Рассмотрим два варианта вычисления длины окружности, в которых участвуют различные постоянные величины.

Для начала разберитесь в терминах и определениях, с которыми вам предстоит работать. Примите во внимание, что окружность – это это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы. Радиус – это не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек. Длина окружности – это величина отрезка АВ, состоящего из точек А, В, а также всех точек плоскости, из которых отрезок АВ виден под прямым углом, отличное от диаметра. Пи – иррациональное число, то есть никогда не заканчивающееся и не являющееся периодическим и составляющее длину полуокружности, радиус которой равен единице, число Пи примерно равняется 3,14.

Итак, согласно первому способу, вычислить радиус окружности можно, если известен радиус окружности. Для этого умножьте длину радиуса на число Пи, примерно равное 3,14 и на цифру 2. Другими словами, стандартная формула вычисления радиуса окружности выглядит так: L = 2 х П х R, где L – длина окружности, П – число Пи (

3,141592654), R – радиус окружности. Следует отметить, что из данной формулы можно вычислить, чему равен радиус: R = L / (2 x П).

Существует более краткая формула для того, чтобы узнать длину окружности. Формула выглядит так: L = R х alpha, где L – длина дуги окружности, R – радиус окружности, alpha – угол дуги в радианах. Окружность – это ничто иное, как замкнутая дуга, у которой угол составляет 2 х Пи радиан, то есть теоретически мы снова получаем формулу длины круга L = 2 х Пи х R, что свидетельствует о правильности данной формулы. Отсюда же следует, что число alpha также является постоянным значением и составляет 2 х Пи = 6,28. Таким образом, чтобы узнать длину окружности, умножьте радиус данной окружности на число 6,28.

Как рассчитать радиус и нарисовать окружность без циркуля.

Трудолюбивым — яркий свет горит по жизни, ленивым — тусклая свеча

calendar_today 7 июля 2012

visibility 14734 просмотра

Добрый день, дорогие начинающие швеи-самоучки. Сегодня я решила написать статью, которая нам поможет в будущем кроить детские панамки, взрослые пляжные шляпы, а также юбку-солнце, и естественно воланы. Как вы догадались, речь идет об умении рассчитать радиус окружности, и суметь нарисовать ее без циркуля. Потому что вполне возможно, что нам понадобится нарисовать окружности такого размера, для которого циркули и не продаются. Да и не у всех дома есть циркуль.

Итак, на повестке дня следующее:

КАК РАССЧИТАТЬ РАДИУС ОКРУЖНОСТИ.

Для чего он нужен, этот расчет радиуса? Чтобы начертить окружность, нам надо знать радиус этой сомой окружности – то есть расстояние от одной ножки циркуля до другой.

Допустим нам надо нарисовать окружность донышка панамки, и все что мы знаем, это обхват головы ребеночка. Как широко надо раздвинуть ножки циркуля, чтобы в итоге получить окружность, совпадающую с размерами головы ребеночка?

Или нам нужно начертить окружность юбки-солнца, зная только то, что длина окружности должна идеально совпадать с обхватом нашей талии.

Сейчас, чтобы все было предельно ясно и понятно, разберем 2 конкретных случая, которые чаще всего встречаются в работе швей.

Это расчет радиуса донышка панамки. И расчет радиуса на выкройке юбки-солнца.

Ситуация первая – нужно рассчитать радиус и начертить окружность дня панамки для девочки.

Значит, чтобы узнать радиус – нам надо наш обхват головы ребеночка поделить на 6,28.

Берем мобильный телефон, находим в нем калькулятор и делим наши 42 см обхвата головы на 6,28 – получаем 6,68 см = то есть 6 см и 6 мм. Это и есть радиус.

Значит, нам надо раздвинуть ножки циркуля на расстояние 6 см 6 мм. И тогда нарисованная нами окружность будет равна 42 см – то есть ляжет ровненько по головке ребенка (только не забудьте ее обвесит отступив на 1 см для припусков на швы).

Ситуация вторая – нужно начертить окружность юбки-солнца. Все что мы знаем это обхват талии и длина юбки которую мы в итоге хотим получить.

В чертеже юбки солнца есть 2 окружности. Маленькая (внутренняя) должна лечь ровненько на нашу талию. То есть длина этой окружности должна совпасть с обхватом талии. Обхват талии 70 см, значит, и длина окружности должна быть 70 см (ну, разве что, там всякие сантиметры туда-сюда в виде припуска на швы, или еще какую дополнительную отделку в виде поясочка или кокеточки)

Значит нам нужно узнать, какого радиуса чертить круг, чтобы окружность в результате получилась длиной в эти нужные нам70 см.

На картинке ниже я все расписала и как рассчитать радиус маленькой окружности и как потом узнать радиус большой окружности.

И когда начерчена маленькая окружность. Все что нам нужно, это к маленькому радиусу прибавить желаемую длину юбки – и мы получаем большой радиус для большой окружности края юбки.

Вот с расчетами мы разобрались. Будем шить юбки и панамки – буду отправлять вас в эту статью.

Теперь давайте разберемся, как нарисовать окружность любого размера без циркуля.

КАК НАРИСОВАТЬ ОКРУЖНОСТЬ БЕЗ ЦИРКУЛЯ.

Вот здесь ниже я проиллюстрировала тремя картинками три способа. Надеюсь что все понятно нарисовано и прописано.

Да это быстрый способ — но надо следить за тем, чтобы карандаши не откланялись в сторону. Угол наклона карандаша изменяем радиус. Или надо чтобы один человек ровно держал один карандаш, а другой ровно перпендикулярно чертил вторым карандашом.

Вообще-то, чем ниже привязана нитка тем точнее будет окружность. Поэтому некоторые пользуются маленькими булавочками. Погрешность при отклонении булавки в сторону небольшая, и при шитье ею можно принебречь.

И все-таки самый вернейший способ начертить точный круг без циркуля, это при помощи обычной линейки и карандаша. Вот как это выглядит:

И далее по кругу, двигаем сантиметр (как часовую стрелку в часах) и отмечаем точки на одном и том же расстоянии — то есть на одной и той же цифре сантиметровой ленты. Вместо ленты можно использовать бечевочку с нанесенной на ней отметкой — главное убедитесь что бечевочка нисколько не тянется.

Ольга Клишевская, специально для сайта «Женские разговоры».

Статью можно копировать только на личный компьютер или на страницы личного интернет-дневника С ОБЯЗАТЕЛЬНЫМ СОХРАНЕНИЕМ ВСЕХ ССЫЛОК ВНУТРИ СТАТЬИ.

Как рассчитать радиус окружности | Сделай все сам

Дабы рассчитать радиус окружности, довольно знать величину радиуса данной окружности, а также нужные непрерывные значения величин. Разглядим два варианта вычисления длины окружности, в которых участвуют разные непрерывные величины.

Инструкция

1. Для начала разберитесь в терминах и определениях, с которыми вам предстоит трудиться. Примите во внимание, что окружность – это это фигура, состоящая из всех точек плоскости, для всякой из которых отношение расстояний до 2-х данных точек равно данному числу, хорошему от единицы. Радиус – это не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек. Длина окружности – это величина отрезка АВ, состоящего из точек А, В, а также всех точек плоскости, из которых отрезок АВ виден под прямым углом, чудесное от диаметра. Пи – иррациональное число, то есть никогда не заканчивающееся и не являющееся периодическим и составляющее длину полуокружности, радиус которой равен единице, число Пи приблизительно равняется 3,14.

2. Выходит, согласно первому методу, вычислить радиус окружности дозволено, если вестим радиус окружности. Для этого умножьте длину радиуса на число Пи, приблизительно равное 3,14 и на цифру 2. Другими словами, стандартная формула вычисления радиуса окружности выглядит так: L = 2 х П х R, где L – длина окружности, П – число Пи (

3,141592654), R – радиус окружности. Следует подметить, что из данной формулы дозволено вычислить, чему равен радиус: R = L / (2 x П).

3. Существует больше короткая формула для того, дабы узнать длину окружности. Формула выглядит так: L = R х alpha, где L – длина дуги окружности, R – радиус окружности, alpha – угол дуги в радианах. Окружность – это ничто иное, как замкнутая дуга, у которой угол составляет 2 х Пи радиан, то есть теоретически мы вновь получаем формулу длины круга L = 2 х Пи х R, что свидетельствует о правильности данной формулы. Отсель же следует, что число alpha также является непрерывным значением и составляет 2 х Пи = 6,28. Таким образом, дабы узнать длину окружности, умножьте радиус данной окружности на число 6,28.

Видео по теме

Как определить радиус дуги или сегмента круга и найти центр

Первый метод определения радиуса дуги или сегмента круга

Изначально это выглядит так:

Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.

Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.

Решение подобной задачи достаточно подробно рассматривалось в статье «Расчет арочной перемычки», поэтому здесь лишь приведу основные формулы:

Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.

А теперь поговорим о недостатках.

Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад — для того, чтобы напомнить формулы — есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.

Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.

Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.

В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.

Второй метод определения радиуса дуги (метод последовательных приближений)

Итак продолжим рассмотрение имеющейся ситуации.

Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.

Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.

Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.

Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше — то искомый центр дуги выше на прямой.

Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.

Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.

Теоретически это выглядит примерно так:

Рисунок 463.2. Определение центра дуги методом последовательных приближений.

А на практике примерно так:

Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.

Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.

Источник