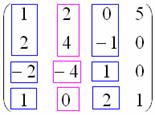
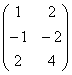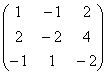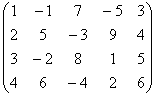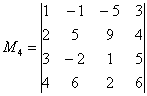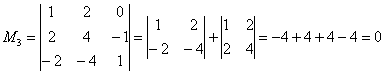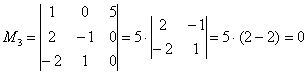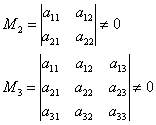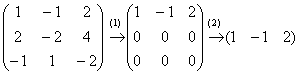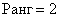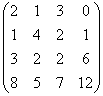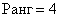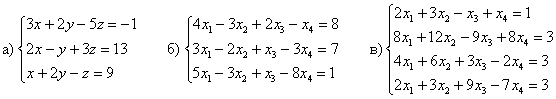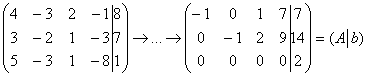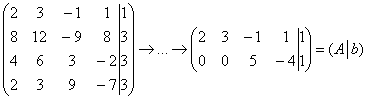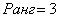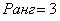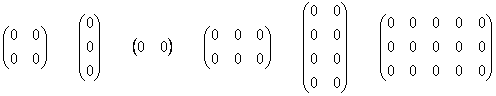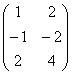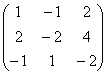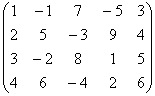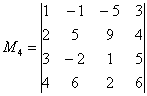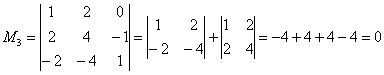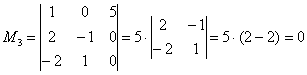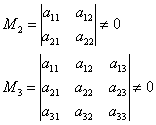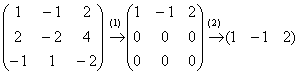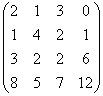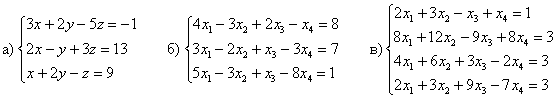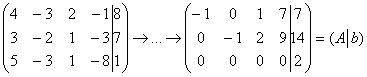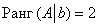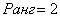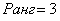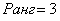Как найти ранг матрицы
Как найти ранг матрицы
Нахождение ранга матрицы — примеры решения
Что такое ранг матрицы — понятие, для чего используется
Возьмем случайную матрицу \(\underset
Минор k-го порядка матрицы A — это определитель k-го порядка с элементами, которые расположены на пересечении любых k строк и любых k столбцов.
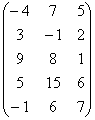
Всего из матрицы \(\underset
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Число r с такими характеристиками — ранг матрицы A.
Ранг матрицы — это наивысший порядок ее ненулевых миноров.
Устоявшегося обозначения ранга не существует, чаще всего его записывают как \(r (A)\) или rang A, где А — обозначение матрицы. Понятие ранга обычно используют в ситуациях, когда необходима проверка совместимости системы линейных уравнений.
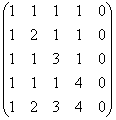
В случае, когда базисный минор матрицы \(\underset<3\times 4>A\) имеет порядок r \(\underset<3\times 4>A\) линейно зависимы. В случае, когда r = m, все строки являются базисными и линейно независимыми.
Из этого можно сделать следующие выводы:
Максимальное число линейно независимых столбцов матрицы равно максимальному количеству ее линейно независимых строк и равно ее рангу.
Ранг не меняется при транспонировании.
Как определить ранг матрицы, примеры
Нахождение ранга матрицы по определению
Определить ранг можно, перебрав все миноры.
Если из элементов матрицы можно составить ненулевой минор n-го порядка, то ранг равен n.
С учетом данной теоремы перебор производится по следующему алгоритму:
Нахождение ранга матрицы методом окаймляющих миноров
Этот метод дает возможность сократить вычисления.
Окаймляющий минор — минор (n+1)-го порядка матрицы А. Он окаймляет минор n-го порядка, если матрица, соответствующая минору (n+1)-го порядка, содержит матрицу, которая соответствует упомянутому минору n-го порядка. Таким образом, чтобы получить окаймляемый минор, надо взять окаймляющий его и вычеркнуть одну строку и один столбец.
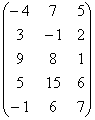
Вычислить ранг матрицы
В матрице есть элементы, отличные от нуля, значит, ее ранг больше единицы.
Раз ранг больше двух, нужно рассмотреть миноры 3-го порядка, содержащие вышеприведенный минор \(М_2.\)
Как мы видим, все миноры 3-го порядка нулевые, значит, наибольший ненулевой минор относится ко 2-му порядку.
Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
В большинстве случаев нахождение ранга перебором миноров требует долгих вычислений. Более простой способ решения этой задачи базируется на элементарных преобразованиях по методу Гаусса, сохраняющих ранг исходной матрицы A и приводящих ее к ступенчатому виду. К таким преобразованиям относятся:
Определитель r-го порядка \(\triangle_r^<(1)>\) в этом выражении отличается от \(\triangle_r\) тем, что вместо элементов q-й строки содержит соответствующие элементы строки \( r_
.\)
Так как p-я строка — не базисная, она может быть представлена в виде линейной комбинации r базисных строк, то \(\triangle_r^ <(1)>= 0\) и \(\triangle_r^ <(1)>= \triangle_r.\)
Как мы видим, при преобразовании \( r_ \rightarrow r_
+ \lambda r_
\) базисный минор ни при каких условиях не изменяется. Из этого делаем вывод, что r (A) = r (A′).
Матрицы A и B эквивалентны по рангу и обозначаются A ∼ B в том случае, когда B можно получить из A путем элементарных преобразований, перечисленных выше.
Вычислить ранг матрицы
Итак, исходная матрица 3-го порядка является невырожденной, поскольку ее определитель равен
Ранг матрицы
Формула
Формула ранга матрицы гласит, что он не должен превышать порядка этой же матрицы:
Как найти?
Чтобы найти ранг матрицы существует два метода:
Примеры решений
Пример решаем с помощью элементарных преобразований. Приводим матрицу к ступенчатой форме.
Прибавляем удвоенную первую строку ко второй:
В полученной матрице появилась нулевая строка, которую необходимо убрать из матрицы:
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Выполняем элементарные преобразования над матрицей, чтобы узнать количество линейно-независимых строк.
Вычитаем из второй строки, умноженной на четверку, первую строку, умноженную на пятерку:
Вычитаем из третьей строки, умноженной на четыре, первую строку, умноженную на девять:
Вычитаем из третьей строки вторую строку:
Замечаем, что последняя строка матрицы нулевая, значит её можно вычеркнуть:
Определение ранга матрицы. Вычисление ранга матрицы по определению.
Для работы с понятием ранга матрицы нам понадобятся сведения из темы «Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений». В первую очередь это касается термина «минор матрицы», так как ранг матрицы станем определять именно через миноры.
Поясним подробнее. Допустим, среди миноров второго порядка есть хотя бы один, отличный от нуля. А все миноры, порядок которых выше двух, равны нулю. Вывод: ранг матрицы равен 2. Или, к примеру, среди миноров десятого порядка есть хоть один, не равный нулю. А все миноры, порядок которых выше 10, равны нулю. Вывод: ранг матрицы равен 10.
В принципе, из самого определения ранга следует метод его нахождения. Процесс нахождения ранга матрицы по определению можно схематически представить так:
Что ждёт нас в конце этой процедуры? Возможно, что среди миноров k-го порядка найдётся хоть один, отличный от нуля, а все миноры (k+1)-го порядка будут равны нулю. Это значит, что k – максимальный порядок миноров, среди которых есть хотя бы один, не равный нулю, т.е. ранг будет равен k. Может быть иная ситуация: среди миноров k-го порядка будет хоть один не равный нулю, а миноры (k+1)-го порядка образовать уже не удастся. В этом случае ранг матрицы также равен k. Короче говоря, порядок последнего составленного ненулевого минора и будет равен рангу матрицы.
Перейдём к примерам, в которых процесс нахождения ранга матрицы по определению будет проиллюстрирован наглядно. Ещё раз подчеркну, что в примерах данной темы мы станем находить ранг матриц, используя лишь определение ранга. Иные методы (вычисление ранга матрицы методом окаймляющих миноров, вычисление ранга матрицы методом элементарных преобразований) рассмотрены в следующих темах.
Кстати, вовсе не обязательно начинать процедуру нахождения ранга с миноров самого малого порядка, как это сделано в примерах №1 и №2. Можно сразу перейти к минорам более высоких порядков (см. пример №3).
Если для формирования миноров третьего порядка мы станем выбирать столбец №2 или столбец №4, то такие миноры будут равными нулю (ибо они будут содержать нулевой столбец). Остаётся проверить лишь один минор третьего порядка, элементы которого расположены на пересечении столбцов №1, №3, №5 и строк №1, №2, №3. Запишем этот минор и найдём его значение:
Перейдём к минорам третьего порядка. Найдём, к примеру, минор, элементы которого расположены на пересечении строк №1, №3, №4 и столбцов №1, №2, №4:
Так как данный минор третьего порядка оказался равным нулю, то нужно исследовать иной минор третьего порядка. Либо все они окажутся равными нулю (тогда ранг будет равен 2), либо среди них найдётся хоть один, не равный нулю (тогда станем исследовать миноры четвёртого порядка). Рассмотрим минор третьего порядка, элементы которого расположены на пересечении строк №2, №3, №4 и столбцов №2, №3, №4:
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
Найти ранг матрицы: способы и примеры
Понятие ранга матрицы
Определение. Рангом матрицы называется максимальное число линейно независимых строк, рассматриваемых как векторы.
Теорема 1 о ранге матрицы. Рангом матрицы называется максимальный порядок отличного от нуля минора матрицы.
Понятие минора мы уже разбирали на уроке по определителям, а сейчас обобщим его. Возьмём в матрице сколько-то строк и сколько-то столбцов, причём это «сколько-то» должно быть меньше числа строк и стобцов матрицы, а для строк и столбцов это «сколько-то» должно быть одним и тем же числом. Тогда на пересечении скольки-то строк и скольки-то столбцов окажется матрица меньшего порядка, чем наша исходная матрица. Определитель это матрицы и будет минором k-го порядка, если упомянутое «сколько-то» (число строк и столбцов) обозначим через k.
Определение. Минор (r+1)-го порядка, внутри которого лежит выбранный минор r-го порядка, называется называется окаймляющим для данного минора.
Наиболее часто используются два способа отыскания ранга матрицы. Это способ окаймляющих миноров и способ элементарных преобразований (методом Гаусса).
При способе окаймляющих миноров используется следующая теорема.
Теорема 2 о ранге матрицы. Если из элементов матрицы можно составить минор r-го порядка, не равный нулю, то ранг матрицы равен r.
При способе элементарных преобразований используется следующее свойство:
— если путём элементарных преобразований получена трапециевидная матрица, эквивалентная исходной, то рангом этой матрицы является число строк в ней кроме строк, полностью состоящих из нулей.
Отыскание ранга матрицы способом окаймляющих миноров
Окаймляющим минором называется минор большего порядка по отношению к данному, если этот минорм большего порядка содержит в себе данный минор.
Например, дана матрица


окаймляющими будут такие миноры:

Алгоритм нахождения ранга матрицы следующий.
1. Находим не равные нулю миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы будет равен единице ( r =1 ).
2. Если существует хотя бы один минор второго порядка, не равный нулю, то составляем окаймляющие миноры третьего порядка. Если все окаймляющие миноры третьего порядка равны нулю, то ранг матрицы равен двум ( r =2 ).
3. Если хотя бы один из окаймляющих миноров третьего порядка не равен нулю, то составляем окаймляющие его миноры. Если все окаймляющие миноры четвёртого порядка равны нулю, то ранг матрицы равен трём ( r =2 ).
4. Продолжаем так, пока позволяет размер матрицы.
Пример 1. Найти ранг матрицы

Решение. Минор второго порядка 
Окаймляем его. Окаймляющих миноров будет четыре:




Таким образом, все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг данной матрицы равен двум ( r =2 ).
Пример 2. Найти ранг матрицы

Решение. Ранг данной матрицы равен 1, так как все миноры второго порядка этой матрицы равны нулю (в этом, как и в случаях окаймляющих миноров в двух следующих примерах, дорогим студентам предлагается убедиться самостоятельно, возможно, используя правила вычисления определителей), а среди миноров первого порядка, то есть среди элементов матрицы, есть не равные нулю.
Пример 3. Найти ранг матрицы

Решение. Минор второго порядка этой матрицы 
Пример 4. Найти ранг матрицы

Решение. Ранг данной матрицы равен 3, так как единственный минор третьего порядка этой матрицы равен 3.
Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
Уже на примере 1 видно, что задача определения ранга матрицы способом окаймляющих миноров требует вычисления большого числа определителей. Существует, однако, способ, позволяющий свести объём вычислений к минимуму. Этот способ основан на использовании элементарных преобразований матриц и ещё называется также методом Гаусса.
Под элементарными преобразованиями матрицы понимаются следующие операции:
1) умножение какой-либо строки или какого либо столбца матрицы на число, отличное от нуля;
2) прибавление к элементам какой-либо строки или какого-либо столбца матрицы соответствующих элементов другой строки или столбца, умноженных на одно и то же число;
3) перемена местами двух строк или столбцов матрицы;
4) удаление «нулевых» строк, то есть таких, все элементы которых равны нулю;
5) удаление всех пропорциональных строк, кроме одной.
Тогда ранг полученной матрицы будет равен числу строк в ней кроме строк, полностью состоящих из нулей.
Пример 5. Найти ранг матрицы


Вычитая из четвёртой строки третью, а затем переставив местами вторую и третью строки, получаем матрицу

Получили трапециевидную матрицу. Ранг полученной матрицы равен трём (r=3), так как после вычёркивания последней строки, полностью состоящей из нулей, в ней останется три строки.
Желающие могут проверить это решение способом окаймляющих миноров (минор третьего порядка, находящийся в левом верхнем углу, не равен нулю, а все миноры четвёртого порядка равны нулю).
Найти ранг матрицы самостоятельно, а затем посмотреть решение
Пример 6. Найти ранг матрицы

Пример 7. Найти ранг матрицы

Нахождение ранга матрицы
В данной статье пойдет речь о таком понятии, как ранг матрицы и необходимых дополнительных понятиях. Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.
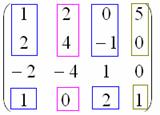
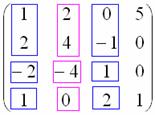
Минор матрицы
Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.
Минор k-ого порядка матрицы — определитель квадратной матрицы порядка k×k, которая составлена из элементов матрицы А, находящихся в заранее выбранных k-строках и k-столбцах, при этом сохраняется положение элементов матрицы А.
Проще говоря, если в матрице А вычеркнуть (p-k) строк и (n-k) столбцов, а из тех элементов, которые остались, составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы и есть минор порядка k матрицы А.
Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.
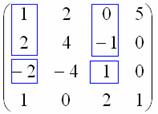
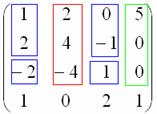
Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.
Другим минором 2-го порядка матрицы А является 0 0 1 1 = 0
Предоставим иллюстрации построения миноров второго порядка матрицы А:
Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:
Иллюстрация, как получается минор 3-го порядка матрицы А:
Для данной матрицы миноров выше 3-го порядка не существует, потому что
Сколько существует миноров k-ого порядка для матрицы А порядка p×n?
Число миноров вычисляют по следующей формуле:
После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.
Ранг матрицы: методы нахождения
Ранг матрицы — наивысший порядок матрицы, отличный от нуля.
Из определения ранга матрицы и минора матрицы становиться понятно, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы отличен от нуля.
Нахождение ранга матрицы по определению
Метод перебора миноров — метод, основанный на определении ранга матрицы.
Алгоритм действий способом перебора миноров:
Необходимо найти ранг матрицы А порядка p×n. При наличии хотя бы одного элемента, отличного от нуля, то ранг матрицы как минимум равен единице (т.к. есть минор 1-го порядка, который не равен нулю).
Далее следует перебор миноров 2-го порядка. Если все миноры 2-го порядка равны нулю, то ранг равен единице. При существовании хотя бы одного не равного нулю минора 2-го порядка, необходимо перейти к перебору миноров 3-го порядка, а ранг матрицы, в таком случае, будет равен минимум двум.
Аналогичным образом поступим с рангом 3-го порядка: если все миноры матрицы равняются нулю, то ранг будет равен двум. При наличии хотя бы одного ненулевого минора 3-го порядка, то ранг матрицы равен минимум трем. И так далее, по аналогии.
Найти ранг матрицы:
Поскольку матрица ненулевая, то ее ранг минимум равен единице.
Миноры 3-го порядка равны нулю, поэтому ранг матрицы равен двум.
Нахождение ранга матрицы методом окаймляющих миноров
Метод окаймляющих миноров — метод, который позволяет получить результат при меньшей вычислительной работе.
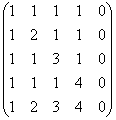
Найти ранг матрицы:
Записываем все окаймляющие миноры:
Чтобы обосновать метод окаймляющих миноров, приведем теорему, формулировка которой не требует доказательной базы.
Если все миноры, окаймляющие минор k-ого порядка матрицы А порядка p на n, равны нулю, то все миноры порядка (k+1) матрицы А равна нулю.
Чтобы найти ранг матрицы, необязательно перебирать все миноры, достаточно посмотреть на окаймляющие.
Если окаймляющие миноры равняются нулю, то ранг матрицы нулевой. Если существует хотя бы один минор, который не равен нулю, то рассматриваем окаймляющие миноры.
Если все они равны нулю, то Rank(A) равняется двум. При наличии хотя бы одного ненулевого окаймляющего минора, то приступаем к рассматриванию его окаймляющих миноров. И так далее, аналогичным образом.
Найти ранг матрицы методом окаймляющих миноров
Поскольку элемент а 11 матрицы А не равен нулю, то возьмем минор 1-го порядка. Начнем искать окаймляющий минор, отличный от нуля:
Нахождение ранга матрицы методом Гаусса (с помощью элементарных преобразований)
Вспомним, что представляют собой элементарные преобразования.
путем прибавления к элементам какой-либо строки (столбца) элементов, которые соответствуют другой стоки (столбца) матрицы, которые умножены на произвольное число k.
Нахождение ранга матрицы методом Гаусса — метод, который основывается на теории эквивалентности матриц: если матрица В получена из матрицы А при помощи конечного числа элементарных преобразований, то Rank(A) = Rank(B).
Справедливость данного утверждения следует из определения матрицы:
в случае прибавления к элементам некоторой строки или столбца матрицы соответствующих элементов другой строки или столбца, которые умножены на число k, не изменяет ее определителя.
Ранг матриц такого вида достаточно просто найти. Он равен количеству строк, в которых есть хотя бы один ненулевой элемент. А поскольку ранг при проведении элементарных преобразований не изменяется, то это и будет ранг матрицы.
Проиллюстрируем этот процесс:
1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0
Найти ранг матрицы А при помощи элементарных преобразований:
Поскольку элемент а 11 отличен от нуля, то необходимо умножить элементы первой строки матрицы А на 1 а 11 = 1 2 :
Прибавляем к элементам 2-ой строки соответствующие элементы 1-ой строки, которые умножены на (-3). К элементам 3-ей строки прибавляем элементы 1-ой строки, которые умножены на (-1):
Если проводить элементарные преобразования, то не допускаются приближенные значения!
Как найти ранг матрицы?
Знание ранга матрицы повысит ваш ранг =)
На сегодняшнем уроке мы познакомимся с понятием ранга алгебраической матрицы, научимся находить ранг матрицы методом окаймляющих миноров и методом Гаусса, а также рассмотрим важное практическое приложение темы: исследование системы линейных уравнений на совместность.
Что такое ранг матрицы?
В юмористическом эпиграфе статьи содержится большая доля истины. Само слово «ранг» у нас обычно ассоциируется с некоторой иерархией, чаще всего, со служебной лестницей. Чем больше у человека знаний, опыта, способностей, блата и т.д. – тем выше его должность и спектр возможностей. Выражаясь по молодёжному, под рангом подразумевают общую степень «крутизны».
И братья наши математические живут по тем же принципам. Выведем на прогулку несколько произвольных нулевых матриц:
Задумаемся, если в матрице одни нули, то о каком ранге может идти речь? Всем знакомо неформальное выражение «полный ноль». В обществе матриц всё точно так же:
Ранг нулевой матрицы 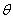
Примечание: нулевая матрица обозначается греческой буквой «тета»
В целях лучшего понимания ранга матрицы здесь и далее я буду привлекать на помощь материалы аналитической геометрии. Рассмотрим нулевой вектор 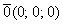
Теперь рассмотрим несколько ненулевых векторов-столбцов и векторов-строк: 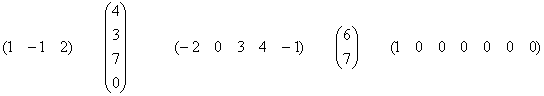
В каждом экземпляре есть хотя бы один ненулевой элемент, и это уже кое-что!
Ранг любого ненулевого вектора-строки (вектора-столбца) равен единице
И вообще – если в матрице произвольных размеров есть хотя бы один ненулевой элемент, то её ранг не меньше единицы.
Алгебраические векторы-строки и векторы-столбцы в известной степени абстрактны, поэтому снова обратимся к геометрической ассоциации. Ненулевой вектор 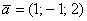
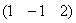
Теоретическая справка: в линейной алгебре вектор – это элемент векторного пространства (определяемое через 8 аксиом), который, в частности, может представлять собой упорядоченную строку 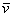
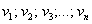
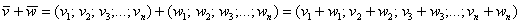
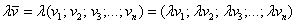
Рассмотрим матрицу 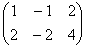
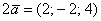
Перепишем координаты векторов в столбцы (транспонируем матрицу):
Что изменилось с точки зрения ранга? Ничего. Столбцы пропорциональны, значит, ранг равен единице. Кстати, обратите внимание, что все три строки тоже пропорциональны. Их можно отождествить с координатами трёх коллинеарных векторов плоскости, из которых только один полезен для построения «плоского» базиса. И это полностью согласуется с нашим геометрическим смыслом ранга.
Из вышеприведённого примера следует важное утверждение:
Ранг матрицы по строкам равен рангу матрицы по столбцам. Об этом я уже немного упоминал на уроке об эффективных методах вычисления определителя.
Примечание: из линейной зависимости строк следует линейная зависимость столбцов (и наоборот). Но в целях экономии времени, да и в силу привычки я почти всегда буду говорить о линейной зависимости строк.
Продолжим дрессировать нашего любимого питомца. Добавим в матрицу третьей строкой координаты ещё одного коллинеарного вектора 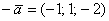
Помог ли он нам в построении трёхмерного базиса? Конечно, нет. Все три вектора гуляют туда-сюда по одной дорожке, и ранг матрицы равен единице. Можно взять сколько угодно коллинеарных векторов, скажем, 100, уложить их координаты в матрицу «сто на три» и ранг такого небоскрёба всё равно останется единичным.
Познакомимся с матрицей 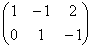
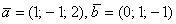
А чему равен ранг матрицы 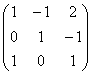
Как видите, линейная зависимость в рассмотренной матрице не очевидна, и сегодня мы как раз научимся выводить её «на чистую воду».
Думаю, многие догадываются, что такое ранг матрицы!
Рассмотрим матрицу 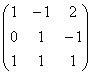
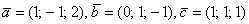
Как вы знаете, любой четвёртый, пятый, десятый вектор трёхмерного пространства будет линейно выражаться через базисные векторы. Поэтому, если в матрицу 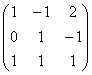
Аналогичные рассуждения можно провести для матриц бОльших размеров (понятно, уже без геометрического смысла).
Определение: ранг матрицы – это максимальное количество линейно независимых строк. Или: ранг матрицы – это максимальное количество линейно независимых столбцов. Да, их количество всегда совпадает.
Из вышесказанного также следует важный практический ориентир: ранг матрицы не превосходит её минимальной размерности. Например, в матрице 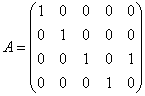
Обозначения: в мировой теории и практике не существует общепринятого стандарта для обозначения ранга матрицы, наиболее часто можно встретить: 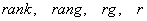
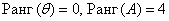
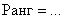
Как найти ранг матрицы с помощью миноров?
На уроках о вычислении определителя и нахождении обратной матрицы нам уже встречались миноры второго порядка, получаемые вычёркиванием строк и столбцов в матрице «три на три». Сейчас мы расширим понятие минора и дадим его определение… да не вздыхайте так тяжко, тут с картинками =)
Минором прямоугольной матрицы называется определитель, составленный из чисел, которые находятся на пересечении различных 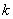
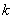
Заметьте, что сама матрица не обязана быть квадратной. Рассмотрим конкретный пример:
Как получить какой-нибудь минор 2-го порядка? Нужно выбрать две произвольные строки, например, 2-ю и 4-ю, два произвольных столбца, например, 3-й и 5-й, и числа, находящиеся на их пересечении 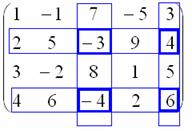
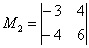
Получим какой-нибудь минор третьего порядка. Рассматриваем три произвольные строки, например, 1-ю, 3-ю и 4-ю, три произвольных столбца, например, 1-й, 2-й и 4-й и с их пересечения 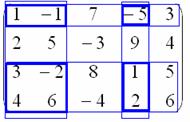
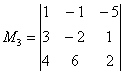
Что касается миноров 4-го порядка, то здесь выбор уже невелик: необходимо задействовать все 4 строки и четыре произвольных столбца, например, все столбцы, за исключением 3-го:
Алгоритм нахождения ранга матрицы с помощью миноров
В качестве примера возьмём ту же матрицу 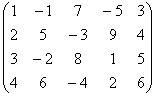
Дальше необходимо начать перебор и вычисление миноров 2-го порядка. Если ВСЕ миноры 2-го порядка окажутся нулевыми, то ранг матрицы равен единице. Но это крайне маловероятно, рано или поздно (чаще всего рано), встретится ненулевой минор 
На следующем шаге последовательно перебираем и рассчитываем миноры 3-го порядка. Если ВСЕ эти миноры равны нулю, то 
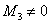
Перебор и вычисление миноров 4-го порядка. Если ВСЕ миноры 4-го порядка равны нулю, то 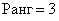
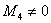
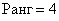
Таким образом, ранг матрицы равен максимальному порядку ненулевого минора.
Схему «перебора в лоб» часто критикуют, но как ни странно, во многих случаях она даёт неплохие результаты. Тем не менее, следует отметить длительность процесса и в целях сокращения количества вычислений разработан:
метод окаймляющих миноров
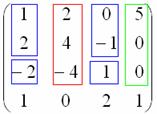
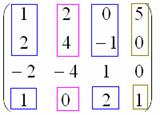
Алгоритм в общем виде, боюсь, будет мало кому понятен, гораздо проще разобрать его на конкретной задаче:
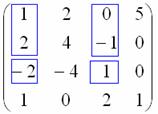
Найти ранг матрицы методом окаймляющих миноров
Решение: дана квадратная матрица «четыре на четыре» и, понятно, её ранг не больше четырёх.
Поскольку в матрице есть ненулевые элементы, то её ранг не менее единицы.
Проверку миноров 2-го порядка начинаем с так называемого углового минора 
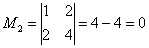
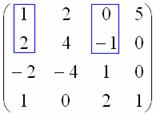
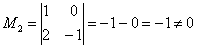




При необходимости (когда получились одни нули), следует продолжить перебор миноров по аналогичной схеме у:
1-й и 3-й строк;
1-й и 4-й строк;
2-й и 3-й строк;
2-й и 4-й строк;
3-й и 4-й строк – до тех пор, пока не повстречается минор, отличный от нуля.
Если все миноры 2-го порядка оказались нулевыми, то 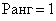
Но в нашем случае уже на втором шаге обнаружен «хороший» минор, и теперь мы переходим к рассмотрению миноров третьего порядка. Приделываем ноги младшему коллеге 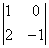
Вопрос «третьим будешь?» может быть адресован либо красному, либо зелёному товарищу:
Был бы пятый столбец – нашёлся бы ещё один друг.
Начнём с красного:
Не помогло. Теперь сообразим с зелёным:
Тоже плохо. Свешиваем ноги ниже и последовательно берём в компанию «малиновые» и «коричневые» числа:
Сначала «синие» с «малиновыми»: 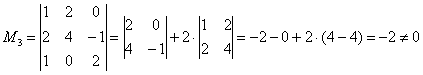
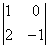
Миноров 3-го порядка на самом деле больше, и рассматриваемый метод в данном случае позволяет сократить вычисления, максимум, до четырёх определителей. Успех нас поджидал на 3-м шаге, и «хороший» ненулевой минор 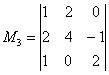
Теперь «синие» и «малиновые» столбцы должны входить во все миноры высших порядков. В данном случае это единственный минор 4-го порядка, совпадающий с определителем матрицы:

Если бы у бабушки нас в матрице был пятый столбец, то следовало бы вычислить ещё один минор 4-го порядка («синие», «малиновый» + 5-й столбец).
Вывод: максимальный порядок ненулевого минора равен трём, значит, 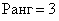
Возможно, не все до конца осмыслили данную фразу: минор 4-го порядка равен нулю, но среди миноров 3-го порядка нашёлся ненулевой – поэтому максимальный порядок ненулевого минора и равен трём.
Возникает вопрос, а почему бы сразу не вычислить определитель? Ну, во-первых, в большинстве заданий матрица не квадратная, а во-вторых, даже если у вас и получится ненулевое значение, то задание с высокой вероятностью забракуют, так как оно обычно подразумевает стандартное решение «снизу вверх». А в рассмотренном примере нулевой определитель 4-го порядка и вовсе позволяет утверждать, что ранг матрицы лишь меньше четырёх.
Должен признаться, разобранную задачу я придумал сам, чтобы качественнее объяснить метод окаймляющих миноров. В реальной практике всё проще:
Найти ранг матрицы методом окаймляющих миноров
Решение и ответ в конце урока.
Когда алгоритм работает быстрее всего? Вернёмся к той же матрице «четыре на четыре» 
И, если 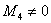
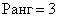
Размышление совсем не гипотетично – существует немало примеров, где всё дело и ограничивается только угловыми минорами.
Однако в ряде случаев более эффективен и предпочтителен другой способ:
Как найти ранг матрицы с помощью метода Гаусса?
Параграф рассчитан на читателей, которые уже знакомы с методом Гаусса и мало-мальски набили на нём руку.
С технической точки зрения метод не отличается новизной:
1) с помощью элементарных преобразований приводим матрицу к ступенчатому виду;
2) ранг матрицы равен количеству строк.
Совершенно понятно, что использование метода Гаусса не меняет ранга матрицы, и суть здесь предельно проста: согласно алгоритму, в ходе элементарных преобразований выявляются и удаляются все лишние пропорциональные (линейно зависимые) строки, в результате чего остаётся «сухой остаток» – максимальное количество линейно независимых строк.
Преобразуем старую знакомую матрицу с координатами трёх коллинеарных векторов:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку.
(2) Нулевые строки удаляем.
Таким образом, осталась одна строка, следовательно, 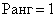
Напоминаю, что в самой по себе алгебраической матрице ничего менять нельзя, и преобразования выполняются только с целью выяснения ранга! Кстати, остановимся ещё раз на вопросе, почему нельзя? Исходная матрица 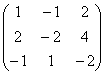
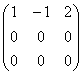
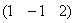
Перейдём к более содержательным заданиям, где помимо прочего познакомимся с важными вычислительными приёмами метода Гаусса:
Найти ранг матрицы с помощью элементарных преобразований
Решение: дана матрица «четыре на пять», значит, её ранг заведомо не больше, чем 4.
В первом столбце, отсутствует 1 или –1, следовательно, необходимы дополнительные действия, направленные на получение хотя бы одной единицы. За всё время существования сайта мне неоднократно задавали вопрос: «Можно ли в ходе элементарных преобразований переставлять столбцы?». Вот здесь – переставили первый-второй столбец, и всё отлично! В большинстве задач, где используется метод Гаусса, столбцы действительно переставлять можно. НО НЕ НУЖНО. И дело даже не в возможной путанице с переменными, дело в том, что в классическом курсе обучения высшей математике данное действие традиционно не рассматривается, поэтому на такой реверанс посмотрят ОЧЕНЬ криво (а то и заставят всё переделывать).
Второй момент касается чисел. В ходе решения полезно руководствоваться следующим эмпирическим правилом: элементарные преобразования по возможности должны уменьшать числа матрицы. Ведь с единицей-двойкой-тройкой работать значительно легче, чем, например, с 23, 45 и 97. И первое действие направлено не только на получение единицы в первом столбце, но и на ликвидацию чисел 7 и 11.
Сначала полное решение, потом комментарии:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3. И до кучи: к 4-й строке прибавили 1-ю строку, умноженную на –1.
(2) Последние три строки пропорциональны. Удалили 3-ю и 4-ю строки, вторую строку переместили на первое место.
(3) Ко второй строке прибавили первую строку, умноженную на –3.
В приведённой к ступенчатому виду матрице две строки.
Ответ:
Теперь ваша очередь мучить матрицу «четыре на четыре»:
Найти ранг матрицы методом Гаусса
Напоминаю, что метод Гаусса не предполагает однозначной жёсткости, и ваше решение, скорее всего, будет отличаться от моего решения. Краткий образец оформления задачи в конце урока.
Какой метод использовать для нахождения ранга матрицы?
На практике зачастую вообще не сказано, какой метод необходимо использовать для нахождения ранга. В такой ситуации следует анализировать условие – для одних матриц рациональнее провести решение через миноры, а для других значительно выгоднее применить элементарные преобразования:
Найти ранг матрицы
Решение: первый способ как-то сразу отпадает =)
Чуть выше я советовал не трогать столбцы матрицы, но когда есть нулевой столбец, либо пропорциональные/совпадающие столбцы, то всё же стОит провести ампутацию:
(1) Пятый столбец нулевой, удалим его из матрицы. Таким образом, ранг матрицы не больше четырёх. Первую строку умножили на –1. Это ещё одна фирменная фишка метода Гаусса, превращающая следующее действие в приятную прогулку:
(2) Ко всем строкам, начиная со второй, прибавили первую строку.
(3) Первую строку умножили на –1, третью строку разделили на 2, четвёртую строку разделили на 3. К пятой строке прибавили вторую строку, умноженную на –1.
(4) К пятой строке прибавили третью строку, умноженную на –2.
(5) Последние две строки пропорциональны, пятую удаляем.
В результате получено 4 строки.
Ответ:
Стандартная пятиэтажка для самостоятельного исследования:
Найти ранг матрицы
Краткое решение и ответ в конце урока.
Следует отметить, что словосочетание «ранг матрицы» не так часто встретишь на практике, и в большинстве задач можно вообще обойтись без него. Но существует одно задание, где рассматриваемое понятие является главным действующим лицом, и в заключение статьи мы рассмотрим это практическое приложение:
Как исследовать систему линейных уравнений на совместность?
Нередко помимо решения системы линейных уравнений по условию предварительно требуется исследовать её на совместность, то есть доказать, что какое-либо решение вообще существует. Ключевую роль в такой проверке играет теорема Кронекера-Капелли, которую я сформулирую в необходимом виде:
Если ранг матрицы системы равен рангу расширенной матрицы системы, то система совместна, причём, если данное число совпадает с количеством неизвестных, то решение единственно.
Таким образом, для исследования системы на совместность нужно проверить равенство 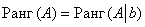
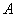
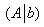
Исследовать систему на совместность и найти её решение, если система совместна
А когда системы уже прорешаны – просто вдвойне… нет – втройне =)
Решение: тем не менее, обратим внимание на строгую верхнюю строчку – по условию,
в первую очередь, требуется проверить систему на совместность. Как начать решение?
В любом случае записываем расширенную матрицу системы и с помощью элементарных преобразований приводим её к ступенчатому виду:
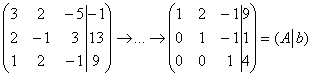
а) Пример № 1 статьи о методе исключения неизвестных:
Элементарные преобразования не меняют ранга матриц, поэтому в результате выполненных действий получены эквивалентные исходным матрица системы 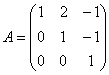
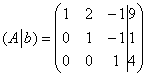
Обе матрицы имеют ступенчатый вид, причём в каждой матрице три стоки.
Вывод: 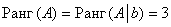
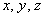
Что дальше? Дальше следует непосредственно решить систему. Если по условию не предложен способ, то, конечно же, раскручиваем обратный ход метода Гаусса. Если требуется решить систему методом Крамера или с помощью обратной матрицы, ну что поделать….
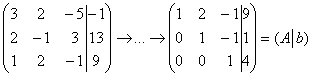
б) Пример № 1 статьи о несовместных системах и системах с общим решением:
В результате элементарных преобразований получена эквивалентная матрица системы 
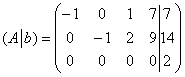
Приведём матрицу системы к ступенчатому виду, удалив нулевую строку:
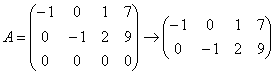
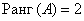
Расширенная же матрица системы имеет ступенчатый вид и количество её строк равно трём, а посему 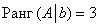
Вывод: 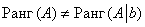
Следует заметить, что обоснование этого факта можно провести и через миноры:
Максимальный порядок ненулевого минора матрицы системы равен двум, например: 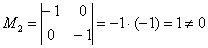
Максимальный порядок ненулевого минора расширенной матрицы системы равен трём, например:
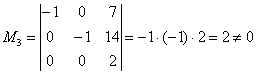
Таким образом, 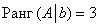
Вывод: 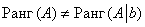
И обращаю внимание, что если по условию не требуется исследовать систему на совместность, то вполне достаточно ограничиться стандартным ответом (см. решение Примера 1).
в) Пример № 3 той же статьи:
В результате элементарных преобразований получена эквивалентная матрица системы 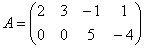
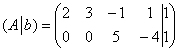
Обе матрицы имеют ступенчатый вид и в каждой из них две строки.
Вывод: 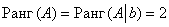
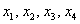
Далее находим общее решение по стандартной схеме.
Приведу также альтернативное доказательство с помощью миноров, которое встречается в некоторых методичках:
Максимальный порядок ненулевого минора матрицы системы равен двум, например: 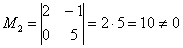
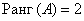
Максимальный порядок ненулевого минора расширенной матрицы системы также равен двум, например (обязательно включаем столбец свободных членов):
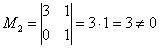
Второй абзац можно полностью заменить хитрой лаконичной фразой: «по этой же причине 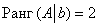
Вывод: 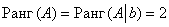
+ Образец исследования системы на совместность можно ещё посмотреть в начале
Примера № 1 урока о нахождении различных базисных решений системы.
…Всё-таки иногда удивительно обманываются ожидания – порой думаешь, что статья получится огромной, а она оказывается весьма компактной, а иногда, как сейчас – наоборот. Посмотрел статистику и жутко удивился добрым 20 тысячам символов. Поэтому всем высокого ранга и до скорых встреч!
Решения и ответы:
Пример 2: Решение: поскольку в матрице есть ненулевые элементы, то её ранг не меньше единицы. 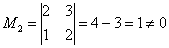
Рассмотрим миноры 3-го порядка, при этом в них обязательно должен содержаться ненулевой минор 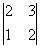
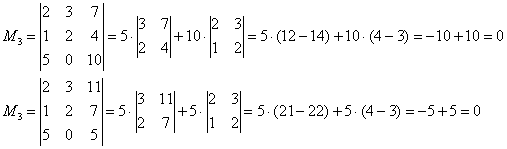
Максимальный порядок ненулевого минора равен двум.
Ответ:
Пример 4: Решение: с помощью элементарных преобразований приведем матрицу к ступенчатому виду: 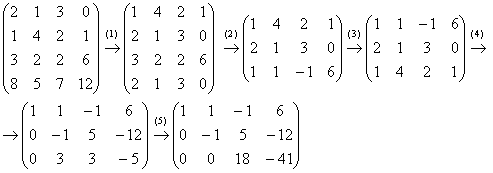
(1) Первую и вторую строки поменяли местами. К 4-й строке прибавили 3-ю строку, умноженную на –2.
(2) Вторая и 4-я строки одинаковы, 4-ю строку удалили. К третьей строке прибавили вторую строку, умноженную на –1.
(3) Первую и третью строки поменяли местами.
(4) Ко второй строке прибавили первую строку, умноженную на –2. К 3-й строке прибавили первую строку, умноженную на –1.
(5) К третьей строке прибавили вторую строку, умноженную на 3.
В результате получены 3 строки, значит, ранг матрицы равен 3.
Ответ:
Пример 6: Решение: ранг матрицы не превосходит минимальной размерности, то есть, трёх.
В матрице есть ненулевые элементы, значит, ранг не менее единицы. 
Максимальный порядок ненулевого минора равен трём
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Как найти ранг матрицы?
Знание ранга матрицы повысит ваш ранг =)
На сегодняшнем уроке мы познакомимся с понятием ранга алгебраической матрицы, научимся находить ранг матрицы методом окаймляющих миноров и методом Гаусса, а также рассмотрим важное практическое приложение темы: исследование системы линейных уравнений на совместность.
Что такое ранг матрицы?
В юмористическом эпиграфе статьи содержится большая доля истины. Само слово «ранг» у нас обычно ассоциируется с некоторой иерархией, чаще всего, со служебной лестницей. Чем больше у человека знаний, опыта, способностей, блата и т.д. – тем выше его должность и спектр возможностей. Выражаясь по молодёжному, под рангом подразумевают общую степень «крутизны».
И братья наши математические живут по тем же принципам. Выведем на прогулку несколько произвольных нулевых матриц:
Задумаемся, если в матрице одни нули, то о каком ранге может идти речь? Всем знакомо неформальное выражение «полный ноль». В обществе матриц всё точно так же:
Ранг нулевой матрицы 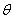
Примечание: нулевая матрица обозначается греческой буквой «тета»
В целях лучшего понимания ранга матрицы здесь и далее я буду привлекать на помощь материалы аналитической геометрии. Рассмотрим нулевой вектор 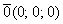
Теперь рассмотрим несколько ненулевых векторов-столбцов и векторов-строк: 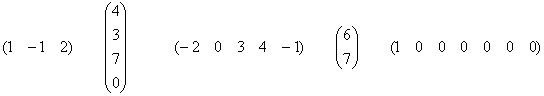
В каждом экземпляре есть хотя бы один ненулевой элемент, и это уже кое-что!
Ранг любого ненулевого вектора-строки (вектора-столбца) равен единице
И вообще – если в матрице произвольных размеров есть хотя бы один ненулевой элемент, то её ранг не меньше единицы.
Алгебраические векторы-строки и векторы-столбцы в известной степени абстрактны, поэтому снова обратимся к геометрической ассоциации. Ненулевой вектор 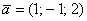
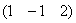
Теоретическая справка: в линейной алгебре вектор – это элемент векторного пространства (определяемое через 8 аксиом), который, в частности, может представлять собой упорядоченную строку 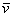
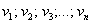
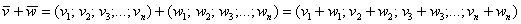
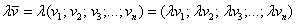
Рассмотрим матрицу 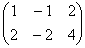
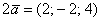
Перепишем координаты векторов в столбцы (транспонируем матрицу):
Что изменилось с точки зрения ранга? Ничего. Столбцы пропорциональны, значит, ранг равен единице. Кстати, обратите внимание, что все три строки тоже пропорциональны. Их можно отождествить с координатами трёх коллинеарных векторов плоскости, из которых только один полезен для построения «плоского» базиса. И это полностью согласуется с нашим геометрическим смыслом ранга.
Из вышеприведённого примера следует важное утверждение:
Ранг матрицы по строкам равен рангу матрицы по столбцам. Об этом я уже немного упоминал на уроке об эффективных методах вычисления определителя.
Примечание: из линейной зависимости строк следует линейная зависимость столбцов (и наоборот). Но в целях экономии времени, да и в силу привычки я почти всегда буду говорить о линейной зависимости строк.
Продолжим дрессировать нашего любимого питомца. Добавим в матрицу третьей строкой координаты ещё одного коллинеарного вектора 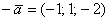
Помог ли он нам в построении трёхмерного базиса? Конечно, нет. Все три вектора гуляют туда-сюда по одной дорожке, и ранг матрицы равен единице. Можно взять сколько угодно коллинеарных векторов, скажем, 100, уложить их координаты в матрицу «сто на три» и ранг такого небоскрёба всё равно останется единичным.
Познакомимся с матрицей 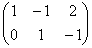
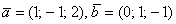
А чему равен ранг матрицы 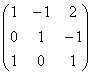
Как видите, линейная зависимость в рассмотренной матрице не очевидна, и сегодня мы как раз научимся выводить её «на чистую воду».
Думаю, многие догадываются, что такое ранг матрицы!
Рассмотрим матрицу 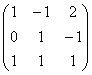
Как вы знаете, любой четвёртый, пятый, десятый вектор трёхмерного пространства будет линейно выражаться через базисные векторы. Поэтому, если в матрицу 
Аналогичные рассуждения можно провести для матриц бОльших размеров (понятно, уже без геометрического смысла).
Определение: ранг матрицы – это максимальное количество линейно независимых строк. Или: ранг матрицы – это максимальное количество линейно независимых столбцов. Да, их количество всегда совпадает.
Из вышесказанного также следует важный практический ориентир: ранг матрицы не превосходит её минимальной размерности. Например, в матрице 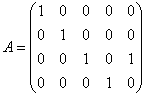
Обозначения: в мировой теории и практике не существует общепринятого стандарта для обозначения ранга матрицы, наиболее часто можно встретить: 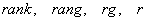
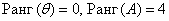
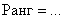
Как найти ранг матрицы с помощью миноров?
На уроках о вычислении определителя и нахождении обратной матрицы нам уже встречались миноры второго порядка, получаемые вычёркиванием строк и столбцов в матрице «три на три». Сейчас мы расширим понятие минора и дадим его определение… да не вздыхайте так тяжко, тут с картинками =)
Минором прямоугольной матрицы называется определитель, составленный из чисел, которые находятся на пересечении различных 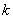
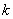
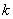
Заметьте, что сама матрица не обязана быть квадратной. Рассмотрим конкретный пример:
Как получить какой-нибудь минор 2-го порядка? Нужно выбрать две произвольные строки, например, 2-ю и 4-ю, два произвольных столбца, например, 3-й и 5-й, и числа, находящиеся на их пересечении 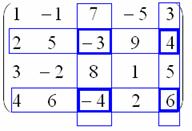
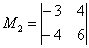
Получим какой-нибудь минор третьего порядка. Рассматриваем три произвольные строки, например, 1-ю, 3-ю и 4-ю, три произвольных столбца, например, 1-й, 2-й и 4-й и с их пересечения 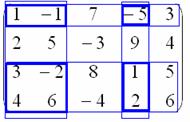
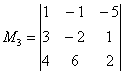
Что касается миноров 4-го порядка, то здесь выбор уже невелик: необходимо задействовать все 4 строки и четыре произвольных столбца, например, все столбцы, за исключением 3-го:
Алгоритм нахождения ранга матрицы с помощью миноров
В качестве примера возьмём ту же матрицу 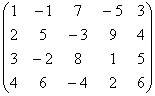
Дальше необходимо начать перебор и вычисление миноров 2-го порядка. Если ВСЕ миноры 2-го порядка окажутся нулевыми, то ранг матрицы равен единице. Но это крайне маловероятно, рано или поздно (чаще всего рано), встретится ненулевой минор 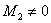
На следующем шаге последовательно перебираем и рассчитываем миноры 3-го порядка. Если ВСЕ эти миноры равны нулю, то 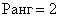
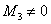
Перебор и вычисление миноров 4-го порядка. Если ВСЕ миноры 4-го порядка равны нулю, то 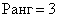
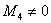
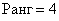
Таким образом, ранг матрицы равен максимальному порядку ненулевого минора.
Схему «перебора в лоб» часто критикуют, но как ни странно, во многих случаях она даёт неплохие результаты. Тем не менее, следует отметить длительность процесса и в целях сокращения количества вычислений разработан:
метод окаймляющих миноров
Алгоритм в общем виде, боюсь, будет мало кому понятен, гораздо проще разобрать его на конкретной задаче:
Найти ранг матрицы методом окаймляющих миноров
Решение: дана квадратная матрица «четыре на четыре» и, понятно, её ранг не больше четырёх.
Поскольку в матрице есть ненулевые элементы, то её ранг не менее единицы.
Проверку миноров 2-го порядка начинаем с так называемого углового минора 
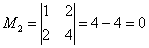
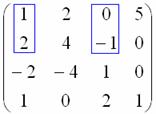
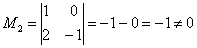




При необходимости (когда получились одни нули), следует продолжить перебор миноров по аналогичной схеме у:
1-й и 3-й строк;
1-й и 4-й строк;
2-й и 3-й строк;
2-й и 4-й строк;
3-й и 4-й строк – до тех пор, пока не повстречается минор, отличный от нуля.
Если все миноры 2-го порядка оказались нулевыми, то 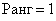
Но в нашем случае уже на втором шаге обнаружен «хороший» минор, и теперь мы переходим к рассмотрению миноров третьего порядка. Приделываем ноги младшему коллеге 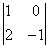
Вопрос «третьим будешь?» может быть адресован либо красному, либо зелёному товарищу:
Был бы пятый столбец – нашёлся бы ещё один друг.
Начнём с красного:
Не помогло. Теперь сообразим с зелёным:
Тоже плохо. Свешиваем ноги ниже и последовательно берём в компанию «малиновые» и «коричневые» числа:
Сначала «синие» с «малиновыми»: 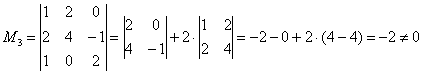
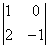
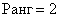
Миноров 3-го порядка на самом деле больше, и рассматриваемый метод в данном случае позволяет сократить вычисления, максимум, до четырёх определителей. Успех нас поджидал на 3-м шаге, и «хороший» ненулевой минор 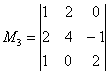
Теперь «синие» и «малиновые» столбцы должны входить во все миноры высших порядков. В данном случае это единственный минор 4-го порядка, совпадающий с определителем матрицы:

Если бы у бабушки нас в матрице был пятый столбец, то следовало бы вычислить ещё один минор 4-го порядка («синие», «малиновый» + 5-й столбец).
Вывод: максимальный порядок ненулевого минора равен трём, значит, 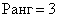
Возможно, не все до конца осмыслили данную фразу: минор 4-го порядка равен нулю, но среди миноров 3-го порядка нашёлся ненулевой – поэтому максимальный порядок ненулевого минора и равен трём.
Возникает вопрос, а почему бы сразу не вычислить определитель? Ну, во-первых, в большинстве заданий матрица не квадратная, а во-вторых, даже если у вас и получится ненулевое значение, то задание с высокой вероятностью забракуют, так как оно обычно подразумевает стандартное решение «снизу вверх». А в рассмотренном примере нулевой определитель 4-го порядка и вовсе позволяет утверждать, что ранг матрицы лишь меньше четырёх.
Должен признаться, разобранную задачу я придумал сам, чтобы качественнее объяснить метод окаймляющих миноров. В реальной практике всё проще:
Найти ранг матрицы методом окаймляющих миноров
Решение и ответ в конце урока.
Когда алгоритм работает быстрее всего? Вернёмся к той же матрице «четыре на четыре» 
И, если 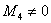
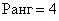
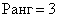
Размышление совсем не гипотетично – существует немало примеров, где всё дело и ограничивается только угловыми минорами.
Однако в ряде случаев более эффективен и предпочтителен другой способ:
Как найти ранг матрицы с помощью метода Гаусса?
Параграф рассчитан на читателей, которые уже знакомы с методом Гаусса и мало-мальски набили на нём руку.
С технической точки зрения метод не отличается новизной:
1) с помощью элементарных преобразований приводим матрицу к ступенчатому виду;
2) ранг матрицы равен количеству строк.
Совершенно понятно, что использование метода Гаусса не меняет ранга матрицы, и суть здесь предельно проста: согласно алгоритму, в ходе элементарных преобразований выявляются и удаляются все лишние пропорциональные (линейно зависимые) строки, в результате чего остаётся «сухой остаток» – максимальное количество линейно независимых строк.
Преобразуем старую знакомую матрицу с координатами трёх коллинеарных векторов:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку.
(2) Нулевые строки удаляем.
Таким образом, осталась одна строка, следовательно, 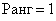
Напоминаю, что в самой по себе алгебраической матрице ничего менять нельзя, и преобразования выполняются только с целью выяснения ранга! Кстати, остановимся ещё раз на вопросе, почему нельзя? Исходная матрица 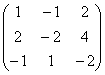
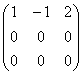
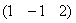
Перейдём к более содержательным заданиям, где помимо прочего познакомимся с важными вычислительными приёмами метода Гаусса:
Найти ранг матрицы с помощью элементарных преобразований
Решение: дана матрица «четыре на пять», значит, её ранг заведомо не больше, чем 4.
В первом столбце, отсутствует 1 или –1, следовательно, необходимы дополнительные действия, направленные на получение хотя бы одной единицы. За всё время существования сайта мне неоднократно задавали вопрос: «Можно ли в ходе элементарных преобразований переставлять столбцы?». Вот здесь – переставили первый-второй столбец, и всё отлично! В большинстве задач, где используется метод Гаусса, столбцы действительно переставлять можно. НО НЕ НУЖНО. И дело даже не в возможной путанице с переменными, дело в том, что в классическом курсе обучения высшей математике данное действие традиционно не рассматривается, поэтому на такой реверанс посмотрят ОЧЕНЬ криво (а то и заставят всё переделывать).
Второй момент касается чисел. В ходе решения полезно руководствоваться следующим эмпирическим правилом: элементарные преобразования по возможности должны уменьшать числа матрицы. Ведь с единицей-двойкой-тройкой работать значительно легче, чем, например, с 23, 45 и 97. И первое действие направлено не только на получение единицы в первом столбце, но и на ликвидацию чисел 7 и 11.
Сначала полное решение, потом комментарии:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3. И до кучи: к 4-й строке прибавили 1-ю строку, умноженную на –1.
(2) Последние три строки пропорциональны. Удалили 3-ю и 4-ю строки, вторую строку переместили на первое место.
(3) Ко второй строке прибавили первую строку, умноженную на –3.
В приведённой к ступенчатому виду матрице две строки.
Ответ:
Теперь ваша очередь мучить матрицу «четыре на четыре»:
Найти ранг матрицы методом Гаусса
Напоминаю, что метод Гаусса не предполагает однозначной жёсткости, и ваше решение, скорее всего, будет отличаться от моего решения. Краткий образец оформления задачи в конце урока.
Какой метод использовать для нахождения ранга матрицы?
На практике зачастую вообще не сказано, какой метод необходимо использовать для нахождения ранга. В такой ситуации следует анализировать условие – для одних матриц рациональнее провести решение через миноры, а для других значительно выгоднее применить элементарные преобразования:
Найти ранг матрицы
Решение: первый способ как-то сразу отпадает =)
Чуть выше я советовал не трогать столбцы матрицы, но когда есть нулевой столбец, либо пропорциональные/совпадающие столбцы, то всё же стОит провести ампутацию:
(1) Пятый столбец нулевой, удалим его из матрицы. Таким образом, ранг матрицы не больше четырёх. Первую строку умножили на –1. Это ещё одна фирменная фишка метода Гаусса, превращающая следующее действие в приятную прогулку:
(2) Ко всем строкам, начиная со второй, прибавили первую строку.
(3) Первую строку умножили на –1, третью строку разделили на 2, четвёртую строку разделили на 3. К пятой строке прибавили вторую строку, умноженную на –1.
(4) К пятой строке прибавили третью строку, умноженную на –2.
(5) Последние две строки пропорциональны, пятую удаляем.
В результате получено 4 строки.
Ответ:
Стандартная пятиэтажка для самостоятельного исследования:
Найти ранг матрицы
Краткое решение и ответ в конце урока.
Следует отметить, что словосочетание «ранг матрицы» не так часто встретишь на практике, и в большинстве задач можно вообще обойтись без него. Но существует одно задание, где рассматриваемое понятие является главным действующим лицом, и в заключение статьи мы рассмотрим это практическое приложение:
Как исследовать систему линейных уравнений на совместность?
Нередко помимо решения системы линейных уравнений по условию предварительно требуется исследовать её на совместность, то есть доказать, что какое-либо решение вообще существует. Ключевую роль в такой проверке играет теорема Кронекера-Капелли, которую я сформулирую в необходимом виде:
Если ранг матрицы системы равен рангу расширенной матрицы системы, то система совместна, причём, если данное число совпадает с количеством неизвестных, то решение единственно.
Таким образом, для исследования системы на совместность нужно проверить равенство 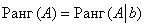
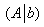
Исследовать систему на совместность и найти её решение, если система совместна
А когда системы уже прорешаны – просто вдвойне… нет – втройне =)
Решение: тем не менее, обратим внимание на строгую верхнюю строчку – по условию,
в первую очередь, требуется проверить систему на совместность. Как начать решение?
В любом случае записываем расширенную матрицу системы и с помощью элементарных преобразований приводим её к ступенчатому виду:
а) Пример № 1 статьи о методе исключения неизвестных:
Элементарные преобразования не меняют ранга матриц, поэтому в результате выполненных действий получены эквивалентные исходным матрица системы 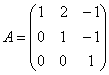
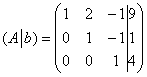
Обе матрицы имеют ступенчатый вид, причём в каждой матрице три стоки.
Вывод: 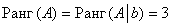
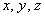
Что дальше? Дальше следует непосредственно решить систему. Если по условию не предложен способ, то, конечно же, раскручиваем обратный ход метода Гаусса. Если требуется решить систему методом Крамера или с помощью обратной матрицы, ну что поделать….
б) Пример № 1 статьи о несовместных системах и системах с общим решением:
В результате элементарных преобразований получена эквивалентная матрица системы 
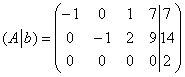
Приведём матрицу системы к ступенчатому виду, удалив нулевую строку:
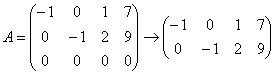
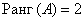
Расширенная же матрица системы имеет ступенчатый вид и количество её строк равно трём, а посему 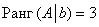
Вывод: 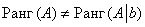
Следует заметить, что обоснование этого факта можно провести и через миноры:
Максимальный порядок ненулевого минора матрицы системы равен двум, например: 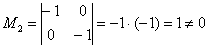
Максимальный порядок ненулевого минора расширенной матрицы системы равен трём, например:
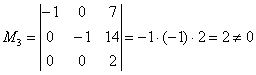
Таким образом, 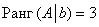
Вывод: 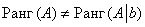
И обращаю внимание, что если по условию не требуется исследовать систему на совместность, то вполне достаточно ограничиться стандартным ответом (см. решение Примера 1).
в) Пример № 3 той же статьи:
В результате элементарных преобразований получена эквивалентная матрица системы 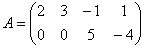
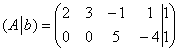
Обе матрицы имеют ступенчатый вид и в каждой из них две строки.
Вывод: 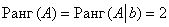
Далее находим общее решение по стандартной схеме.
Приведу также альтернативное доказательство с помощью миноров, которое встречается в некоторых методичках:
Максимальный порядок ненулевого минора матрицы системы равен двум, например: 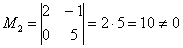
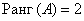
Максимальный порядок ненулевого минора расширенной матрицы системы также равен двум, например (обязательно включаем столбец свободных членов):
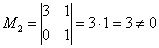
Второй абзац можно полностью заменить хитрой лаконичной фразой: «по этой же причине 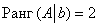
Вывод: 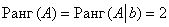
+ Образец исследования системы на совместность можно ещё посмотреть в начале
Примера № 1 урока о нахождении различных базисных решений системы.
…Всё-таки иногда удивительно обманываются ожидания – порой думаешь, что статья получится огромной, а она оказывается весьма компактной, а иногда, как сейчас – наоборот. Посмотрел статистику и жутко удивился добрым 20 тысячам символов. Поэтому всем высокого ранга и до скорых встреч!
Решения и ответы:
Пример 2: Решение: поскольку в матрице есть ненулевые элементы, то её ранг не меньше единицы. 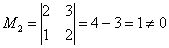
Рассмотрим миноры 3-го порядка, при этом в них обязательно должен содержаться ненулевой минор 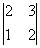
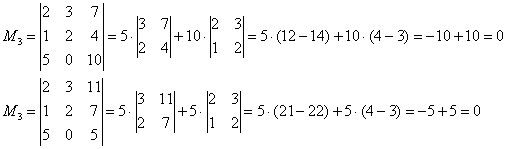
Максимальный порядок ненулевого минора равен двум.
Ответ:
Пример 4: Решение: с помощью элементарных преобразований приведем матрицу к ступенчатому виду: 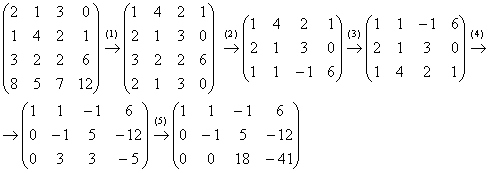
(1) Первую и вторую строки поменяли местами. К 4-й строке прибавили 3-ю строку, умноженную на –2.
(2) Вторая и 4-я строки одинаковы, 4-ю строку удалили. К третьей строке прибавили вторую строку, умноженную на –1.
(3) Первую и третью строки поменяли местами.
(4) Ко второй строке прибавили первую строку, умноженную на –2. К 3-й строке прибавили первую строку, умноженную на –1.
(5) К третьей строке прибавили вторую строку, умноженную на 3.
В результате получены 3 строки, значит, ранг матрицы равен 3.
Ответ:
Пример 6: Решение: ранг матрицы не превосходит минимальной размерности, то есть, трёх.
В матрице есть ненулевые элементы, значит, ранг не менее единицы. 
Максимальный порядок ненулевого минора равен трём
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys