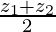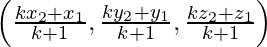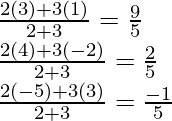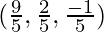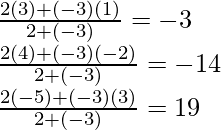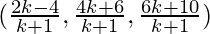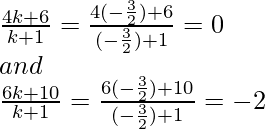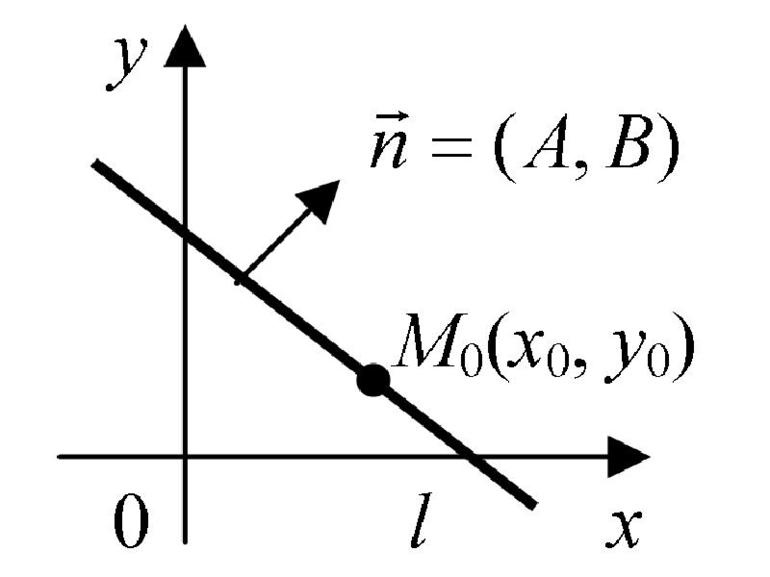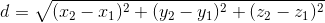Как найти расстояние между двумя точками
Как найти расстояние между двумя точками
Расстояния между двумя точками
На данной странице калькулятор поможет рассчитать расстояние между двумя точками онлайн в плоскости и пространстве. Для расчета задайте координаты.
Расстояния между двумя точками
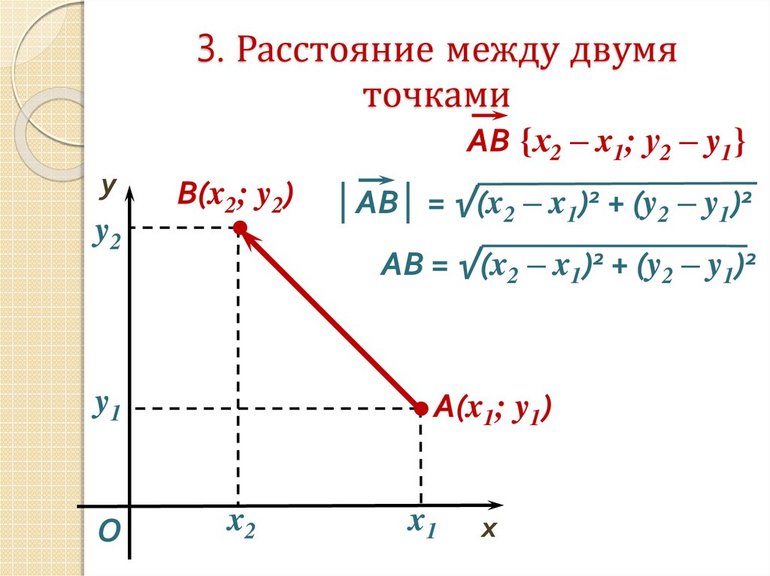
Формула вычисления расстояния между двумя точками A(xa; ya) и B(xb; yb) на плоскости:
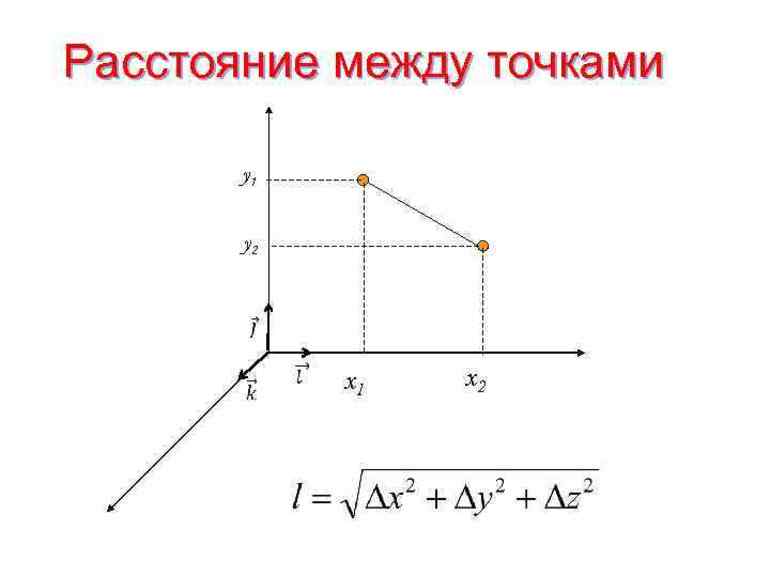
Формула вычисления расстояния между двумя точками A(xa; ya; za) и B(xb; yb; zb) в пространстве:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат x и y.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
Спомощью теоремы Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Расстояние между точками
На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.
Расстояние между двумя точками — это длина отрезка, соединяющего эти точки.
Расстояние между двумя точками на плоскости
Формула для нахождения расстояния между двумя точками A(xa, ya) и B(xb, yb) на плоскости:
Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее — нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.
Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB — его гипотенузой. Длины катетов AC и BC найти довольно просто:
Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:
Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:
Нахождение расстояния между двумя точками
В данной публикации мы рассмотрим, чему равно расстояние между двумя точками, и по какой формуле оно считается (на плоскости и в пространстве). Также разберем примеры решения задач по этой теме.
Расчет расстояния между двумя точками
Расстояние между двумя точками — это длина отрезка (d), который получится, если их соединить.
Если точки и расположены на плоскости, то расстояние между ними считается по формуле:
Если точки и находятся в трехмерном пространстве, расстояние вычисляется так:
Примеры задач
Решение:
Воспользуемся первой формулой, представленной выше:
Решение:
Применим соответствующую формулу, подставив в нее известные нам значения:
Расстояние от точки до точки: формулы, примеры, решения
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
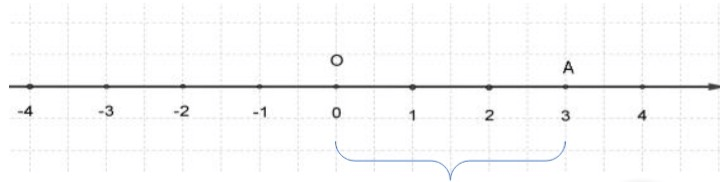
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A
Расстояние между точками на плоскости
— если точки А и В совпадают, то расстояние между ними равно нулю;
— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
Расстояние между точками в пространстве
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Используя полученные ранее выводы, запишем следующее:
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
Полученная формула действительна также для случаев, когда:
— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Решение
Решение
А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Решение
Как найти расстояние между двумя точками?
Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.
Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.
Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
\( c^2 = a^2 + b^2 \) где c — это гипотенуза, a и b — катеты.
Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.
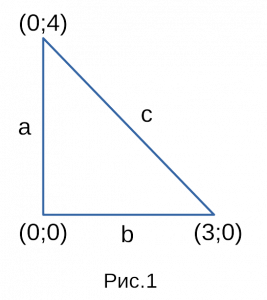
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.
Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. Взгляните на формулу,
которая получилась:
Подставляем наши координаты:
В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.
Расстояние между двумя точками.
Формулы вычисления расстояния между двумя точками:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Примеры задач на вычисление расстояния между двумя точками
Пример вычисления расстояния между двумя точками на плоскости
Пример вычисления расстояния между двумя точками в пространстве
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Как определить расстояние между двумя точками?
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения. Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе.
Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние от точки до точки: формулы, примеры, решения, формула расстояния между двумя точками
Расстояние между точками на координатной прямой
Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой xA: OA=xA
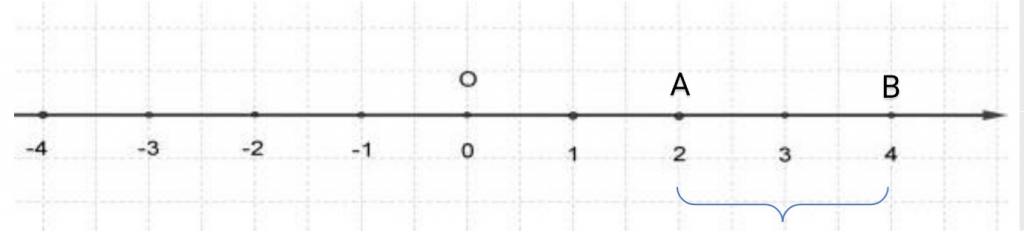
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B, лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты xA и xB : AB=xB-xA.
Расстояние между точками на плоскости
Исходные данные: точки A и B, лежащие на плоскости в прямоугольной системе координат Oxy с заданными координатами: A(xA, yA) и B(xB, yB). Проведем через точки А и B перпендикуляры к осям координат Ox и Oy и получим в результате точки проекции: Ax, Ay, Bx, By. Исходя из расположения точек А и B далее возможны следующие варианты:
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек: AB=(xB-xA)2+(yB-yA)2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: AB=(xB-xA)2+(yB-yA)2=02+02=0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс: AB=(xB-xA)2+(yB-yA)2=02+(yB-yA)2=yB-yA
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат: AB=(xB-xA)2+(yB-yA)2=(xB-xA)2+02=xB-xA
Расстояние между точками в пространстве
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: Ax, Ay, Az, Bx, By, Bz
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: AxBx, AyBy и AzBz
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: AB2=AxBx2+AyBy2+AzBz2
Используя полученные ранее выводы, запишем следующее: AxBx=xB-xA, AyBy=yB-yA, AzBz=zB-zA
Преобразуем выражение: AB2=AxBx2+AyBy2+AzBz2=xB-xA2+yB-yA2+zB-zA2==(xB-xA)2+(yB-yA)2+zB-zA2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом: AB=xB-xA2+yB-yA2+(zB-zA)2
Полученная формула действительна также для случаев, когда:
Расстояние между точками на координатной плоскости — формулы и расчеты
Аналитическая геометрия — важная ветвь математики, которая позволяет рассчитать любые характеристики расположения объектов в пространстве, например, углы и дистанции.
Формула расстояния между точками на координатной плоскости является основным инструментом, применяемым при решении ряда задач в двумерном пространстве.
Система координат
Прежде чем говорить о расстоянии между точками по координатам, следует ввести систему отчета, в которой каждый геометрический объект можно будет однозначно определять.
Для этой цели часто используют декартову систему координат. Она представляет собой взаимно перпендикулярные прямые, на каждой из которых отмечены единичные отрезки.
Именно в них определяется положение тел в пространстве, на плоскости или на прямой линии. Для названных трех случаев декартова система координат отличается количеством осей:
Единичные отрезки на координатных осях в общем случае могут иметь разную длину. Однако ввиду симметричности пространства и для удобства выполнения практических расчетов применяют, как правило, единичные отрезки равной длины. Каждому из них соответствует единичный вектор.
Понятие о векторе
Чтобы уметь вычислять расстояние от точки до точки по координатам, удобно пользоваться понятием вектора. Из школьного курса геометрии известно, что под ним принято понимать отрезок, имеющий некоторое определенное направление. Обозначают его в виде прямой линии конечной длины, на конце которой изображена стрелка.
Пользу использования указанного геометрического объекта трудно переоценить. Например, в физике все величины делятся на 2 большие группы:
К первым относятся масса, электрический заряд, энергия и другие. Вторая группа более обширная. Здесь следует назвать скорость, ускорение, силу тока, напряженности магнитного и электрического полей, силу любой природы и многие другие.
Характеристики объекта
Как любой геометрический объект, вектор обладает набором математических свойств, которые используются при решении задач. Основные из них:
Для всех свойств существуют определяющие их правила. Например, при осуществлении вычитания вектора a- из b- необходимо соединить концы этих объектов отрезком и направить его к концу a-, тогда получается результирующий вектор разницы.
Умножение a- и b- векторным способом является полезной операцией при определении площадей и объемов фигур. Для ее выполнения следует уметь работать с матрицами второго и третьего порядка, в частности, знать, как рассчитывается детерминант (определитель).
Универсальный способ
Речь идет о координатном представлении нульмерных, одномерных, двумерных и трехмерных геометрических фигур. Параметры точек, треугольников, квадратов, прямых, плоскостей и других более сложных объектов могут быть однозначно выражены в виде наборов чисел, привязанных к соответствующей координатной системе.
Поскольку существует задача определения расстояния от точки до точки по координатам, имеет смысл рассмотреть только указанный одномерный объект и вектор.
Точка на плоскости
Первое число здесь означает количество единичных отрезков, которые необходимо отсечь на оси x, второе значение — на оси y. Точка D лежит в начале координат, то есть на пересечении x и y. В общем случае удобно обозначить произвольную точку Q (x0; y0).
Направленный отрезок в двумерном пространстве
На плоскости координаты направленного отрезка так же, как и точки, представляют собой набор двух чисел. Оба обозначают число отрезков единичной длины, которые следует отложить на каждой оси, чтобы получить проекции вектора на x и y.
На плоскости и в трехмерном пространстве всего 2 точки однозначно определяют направленный отрезок. Если его начало переместить в пересечение осей x и y, его конец легко можно найти, вычитая соответствующие координаты точек друг из друга. Следующий простой пример демонстрирует сказанное.
Даны точки A (x1; y1), B (x2; y2), тогда AB- будет иметь координаты: AB- = B — A = (x2-x1; y2-y1).
Вторая точка показывает место расположения конца AB-.
Формула дистанции
Имея полученные представления и знания о свойствах точек и векторов, можно перейти к вопросу нахождения формулы расстояния. Согласно геометрическому определению, под дистанцией между двумя точками понимают длину отрезка, который их соединяет. Эта величина также равна модулю вектора, построенного на нульмерных объектах.
Длину направленного отрезка на плоскости определить просто: необходимо возвести в квадрат каждую его координату, сложить полученные значения, и взять квадратный корень из результирующей суммы. Для вектора a- (x; y) длина будет равна следующей величине: |a-| = (x 2 + y 2 )^0,5.
Возведение суммы в степень 0,5 эквивалентно взятию из нее квадратного корня. Поскольку определение координат вектора по соответствующим значениям точек известно, можно получить следующую простую формулу для A (x1; y1) и B (x2; y2): |AB-| = ((x2-x1)^2 + (y2-y1)^2)^0,5.
В трехмерном пространстве соответствующее выражение будет иметь подобную форму, только добавится третья координата z.
Расстояние между Q и прямой
Полученные знания можно с легкостью применять для решения разнообразных задач по геометрии. Часто приходится находить дистанцию между точкой и прямой. Определить эту величину можно, если знать направляющий вектор прямой. Предположим, что он имеет следующие координаты: a- (x1; y1). Прямая проходит через A (x2; y2). Точка задается так: Q (x0; y0).
В параметрическом виде прямая записывается следующим образом: (x;y) = (x2;y2) + t*(x1;y1).
Здесь t — параметр, который может принимать любое действительное число. Это выражение позволяет записать равенство (1): (x-x2)/x1 = (y-y2)/y1 (1).
Пусть точка P (x;y) является проекцией Q (x0;y0) на прямую, тогда расстояние PQ является искомой дистанцией, которую следует найти по условию задачи. Поскольку вектора PQ- и a- перпендикулярны друг другу, их скалярное произведение будет равно нулю (угол между векторами равен 90 градусов, его косинус равен нулю). Исходя из этих рассуждений, можно записать выражение (2): (x-x0)*x1 + (y-y0)*y1 = 0 (2).
Поскольку имеющиеся равенства (1) и (2) содержат 2 неизвестные переменные, объединение их в систему и решение ее позволит определить точку P (x;y). Зная ее координаты и используя формулу дистанции между двумя точками на плоскости, можно получить искомое расстояние PQ.
Пример задачи
Чтобы определить направляющий вектор, достаточно взять 2 любые точки на прямой. Подставляя в выражение произвольные значения x, можно определить эти точки A, B и вместе с ними направляющий вектор AB-:
Вектор QP-, который пересекает прямую под прямым углом, должен подчиняться следующему уравнению (свойство скалярного произведения):
В это выражение нужно подставить значение y из уравнения прямой.
Получается:
Рассчитанное значение округлено до сотых долей и выражается в единицах единичных векторов координатной системы.
При решении подобных задач для сокращения последующих вычислений рекомендуется проверять принадлежность точки прямой, для чего следует подставить координаты в уравнение. Если этот факт подтверждается, искомое расстояние равно нулю.
Углы треугольника
Польза от использования формулы дистанции между точками на плоскости наглядно показывается на примере решения задач на нахождение углов фигур. Пусть нужно определить все углы треугольника, который построен на вершинах A (x1;y1), B (x2;y2), C (x3;y3).
На первый взгляд сложная задача решается легко, если вспомнить о понятии векторного произведения. Например, для векторов AB- и AC- записывается оно так:
Произведение [AB-*AC-] является вектором, который находится как детерминант матрицы третьего порядка. Его модуль, а также длины |AB-| и |AC-| вычисляются по формуле расстояния между двумя точками.
Чтобы определить угол при вершине A треугольника, остается взять функцию арксинуса от отношения векторного произведения к произведению длин сторон AB и AC.
Конвертер величин
Калькулятор расстояния между двумя точками
Этот калькулятор определяет расстояние (называемое также метрикой) между двумя точками в одномерном, двумерном, трехмерном и четырехмерном евклидовом, чебышёвском и манхэттенском пространствах.
Введите значения для расчета и нажмите кнопку Рассчитать
Определения и формулы
Прямоугольная (декартова) система координат
Прямоугольная система координат носит имя французского философа и математика Рене Декарта, так как именно он ввел эту систему в своей работе «Геометрия» (фр. La Géométrie), опубликованной на французском языке в 1637 г. в Лейдене (Нидерланды) совестно с тремя другими книгами, включая «Рассуждения о методе» (фр. Discours de la méthode pour bien conduire sa raison, et chercher la verité dans les sciences), которая больше всего известна по знаменитой цитате «Je pense, donc je suis» — «Я мыслю, следовательно, я существую».
В прямоугольной системе координат каждая точка на плоскости однозначно определяется двумя числовыми координатами, которые являются расстояниями до точки от двух перпендикулярных осей, измеренными в одинаковых единицах. Ось x называется абсциссой, а ось y — ординатой. Эти два числа называется соответственно координатами x и y заданной точки.
Изобретение прямоугольной системы координат дало толчок к развитию аналитической геометрии — науки, использующей систему координат для построения фигур или тел. В аналитической геометрии кривые и формы описываются алгебраическими функциями, которые облегчают расчеты. Декартова система координат позволяет использовать относительно простые алгебраические уравнения для простых линий, плоскостей и трехмерных фигур. Числовое представление кривых и объемных фигур в аналитической геометрии удобно для их последующей компьютерной обработки.
Декартова система координат часто используются в реальных жизненных ситуациях — например, в вашем смартфоне двумерная система прямоугольных координат используется для показа изображений и отслеживания движений пальцев.
А трехмерная прямоугольная система координат с тремя осями может использоваться для описания положения точки на Земле или над Землей. Эта система вращается вместе с Землей. Начало такой системы координат (нулевая точка с координатами 0; 0; 0) находится в центре масс Земли. Ось z направлена от центра на Северный полюс. Ось x направлена от центра на экватор в точку его пересечения с нулевым меридианом и перпендикулярна оси z. Она указывает на долготу 0°и широту 0°. Ось y геоцентрической системы координат направлена от центра Земли вдоль линии, перпендикулярной осям z и x и, в соответствии с правилом правой руки, указывает на долготу 90° и широту 0°.
Поскольку метр вначале определялся как одни десятимиллионная часть расстояния от экватора до Северного полюса (10 000 км или ¼ длины окружности Земли, приблизительно равной 40 000 км), а километр является одной десятитысячной частью этого расстояния, километр представляется хорошим выбором единицы измерения для геоцентрической системы координат. Описанная выше система координат получила название привязанная к Земле геоцентрическая система координат.
Метрики и метрические пространства
Когда мы говорим о расстоянии в математике, мы всегда упоминаем метрику, которая также называется функцией расстояния. Метрикой называется функция, которая определяет расстояние между каждой парой элементов во множестве, которое является коллекцией объектов и само рассматривается как объект. Множество, в котором определена метрика, называется метрическим пространством. Метрическое пространство — математический объект, в котором расстояние между двумя точками точно определено и имеет смысл. Множество, в котором такая функция не определена, не является метрическим пространством.
Метрика, как числовая функция, удовлетворяет минимальным требованиям к расстоянию, которое мы обычно представляем себе как длину перемещения между двумя точками
Знакомое нам евклидово пространство с метрикой в форме евклидова расстояния, которое мы изучали в средней школе — это один из примеров метрического пространства. Другими примерами является метрические пространства с метриками расстояния городских кварталов (манхэттенское расстояние, метрика такси), чебышёвского расстояния и расстояния Минковского. Есть даже такая экзотическая метрика как метрика SNCF (Национальная компания французских железных дорог), в которой, если нужно добраться на поезде из точки А в точку В, наиболее эффективным способом будет добраться из точки А до Парижа, а оттуда добраться до точки В.
Метрики расстояния широко используются в алгоритмах машинного обучения для улучшения процессов классификации и информационного поиска. Например, они помогают классифицировать и узнавать изображения в системах распознавания изображений. Эта статья была написана во время пандемии COVID-19 и поэтому мы можем даже сказать, что использование метрик расстояния в системах распознавания лиц помогает отслеживать распространение вируса, так как эта технология обеспечивает быстрый неконтактный метод идентификации лиц, которые известны как носители вируса COVID-19, а также людей, которые были с ними в контакте.
Отметим, что, хотя мы говорим о расстоянии, «расстояние» в этом контексте означает не только то, как далеко друг от друга находится объекты в пространстве. Метрика расстояния между объектами — это одна из основных вычислимых функций, используемых в программах машинного обучения. В приложениях машинного обучения часто необходимо определить как близко друг к другу находятся два объекта данных. Например, апельсин похож на яблоко, потому что он сферический. В то же время апельсин похож на баскетбольный мяч, потому что они оранжевые. Цвет и форма — характеристики объектов, их можно выразить в цифровом виде и различие между ними будет являться «расстоянием» между объектами.
Для надежного сравнения предметов нужно описать их математически, в виде чисел, и тогда мы превратим нашу задачу в набор объектов, различные характеристики которых будут описываться числами. Затем, чтобы определить насколько они похожи, мы определим «расстояние» между ними. В нашем случае мера расстояния — это численная оценка, которая описывает относительное различие между объектами в наборе.
В компьютерной науке расстояния между объектами множества можно определять с использованием любых количественных мер или переменных, например, высоты, возраста, веса или температуры. Годится любая переменная, которую можно измерить и выразить числом. Например, если имеется набор нескольких объектов с различными температурами, мы можем сказать, что «расстояние» между объектами с разницей температур в 1 °С меньше, чем расстояние между объектами с разницей температур 2 °С. Или можно рассмотреть объекты с различными температурами и весами и измерить «расстояния» между ними с использованием этих двух количественных переменных для каждого объекта в наборе. Конечно, в этом контексте можно рассматривать и реальные расстояния между объектами, выраженные в единицах длины.
Евклидово расстояние
Евклидово расстояние между двумя точками в двумерном и трехмерном пространстве представляет собой прямую линию, соединяющую две точки. Это очевидный способ представить расстояние между двумя точками. Поскольку в евклидовом пространстве имеется функция, определяющая евклидово расстояния в виде прямой линии, евклидово пространство считается метрическим. Это исторически первое метрическое пространство в математике. Позднее, с развитием математической и физической наук появились другие метрические пространства. Евклидово расстояние, называется также расстоянием L², так как это частный случай расстояния Минковского второго порядка, которое мы рассмотрим ниже.
Для определения расстояния в двумерном пространстве можно использовать теорему Пифагора. Для точек p и q с координатами (x₁, y₁) и (x₂, y₂) в двумерном пространстве (на плоскости) евклидово расстояние определяется по формуле
В трехмерном пространстве евклидово расстояние между двумя точками p и q с координатами (x₁, y₁, z₁) и (x₂, y₂, z₂) определяется как
Конечно, трудно понять даже четырехмерное пространство, не говоря уже об n-мерном пространстве, потому что наши чувства слишком ограничены. Если, например, в трехмерном пространстве многогранник составляется из плоских многоугольников, то в четырехмерном пространстве политопы (многогранники в n-мерном пространстве) составляются из трехмерных многогранников. Например, «гиперграни» гиперповерхности четырехмерного куба, называемого тессерактом, представляют собой трехмерные кубы.
Интересно сравнить сечения двумерных, трехмерных и четырехмерных объектов. Если двумерный объект пересекает одномерная прямая, мы наблюдаем сечение, которое представляет собой отрезок этой линии. Если рассмотреть сечение плоскостью трехмерного объекта, например, куба, мы можем наблюдать один из нескольких многоугольников: треугольник, трапецию, пятиугольник и шестиугольник. Тип многоугольника зависит от количества пересекаемых поверхностей: если плоскость пересекает три поверхности куба, получается треугольник, если четыре — трапеция (помним, что квадрат и прямоугольник — частные случаи трапеции); пять пересекаемых граней куба дают пятиугольник и шесть — шестиугольник.
А что получится, если «разрезать» четырехмерный объект трехмерным объектом, например, если мы возьмем трехмерный куб и разрежем им четырехмерный куб, называемый тессерактом? Мы оставляем читателям возможность ответить на этот вопрос самостоятельно. Подсказка: при построении сечения четырехмерной сферы трехмерной сферой получается трехмерная сфера.
До начала XIX в. считалось, что единственным правильным способом определения расстояния является способ, которым пользовался Евклид. Однако в XIX веке математики начали исследовать другие версии геометрии, которые выглядели необычно. Конечно, в таких привычных областях техники как архитектура или геодезия без евклидовой геометрии не обойтись. В то же время, физики и математики поняли, что пришло время создания неевклидовых геометрий. Во многих случаях бывает удобно не применять евклидову геометрию и измерять расстояния иным образом.
Немецкий математик Герман Минковский ввел несколько других видов геометрии, основанных на различных методах измерения расстояния между точками пространства. Выступая перед делегатами съезда немецких естествоиспытателей и врачей в Кёльне, Минковский начал доклад ставшими знаменитыми словами, что «Отныне пространство само по себе и время само по себе должны сделаться всецело тенями и только особого рода их сочетание должно еще сохранить самостоятельность».
Ниже мы очень кратко рассмотрим несколько неевклидовых геометрий. Отметим, что мы не будем здесь затрагивать пространство-время Минковского и поговорим только о расстоянии Минковского.
Расстояние Чебышёва
Расстояние Чебышёва между двумя n-мерными точками или векторами — это максимальный модуль разности координат этих точек. Для прямоугольной системы координат расстояние Чебышёва между двумя точками можно определить как сумму абсолютных значений разностей их прямоугольных координат. Расстояние Чебышёва называется также максимальной метрикой и метрикой L∞. Метрика названа в честь русского математика Пафнутия Чебышёва, который известен работами по механике, статистике, аналитической геометрии и теории чисел.
Расстояние Чебышёва оценивает абсолютный максимум значения разности между координатами (или иными количественными свойствами) пары объектов. Расстояние Чебышёва между двумя точками p и q с координатами pi и qi равно
Например, рассмотрим две точки в трехмерном пространстве p (x₁,y₁,z₁) = p (2,3,4) и q (x₂,y₂,z₂) = q (5,9,11). Чебышёвское расстояние между этими точками p and q равно
Расстояние Чебышёва называют также метрикой шахматной доски, так как минимальное число ходов, которое нужно сделать королю, чтобы перейти из одного поля в другое, равно расстоянию Чебышёва между центрами полей при условии, что поля шахматной доски имеют единичную длину стороны квадрата и координатные оси выровнены с краями шахматной доски. Это связано с тем, что король может делать ход на соседнее поле в любом направлении: влево, вправо, вверх, вниз и по диагонали. Отметим, что расстояние Чебышёва для ходов по диагонали равно расстоянию для ходов по вертикали и горизонтали. Например, расстояние Чебышёва для перемещения короля e4—g6 равно 2.
Расстояние Чебышёва также широко применяется в программировании промышленных роботов, если их манипуляторы могут с одинаковой скоростью двигаться в восьми направления вдоль осей y и y, а также по диагонали.
Манхэттенское расстояние
Формула евклидова расстояния удобна для измерения теоретических расстояний. Однако в реальной жизни, например, в городе, в большинстве случаев невозможно двигаться от одной точки до другой по прямой. Заборы, здания, улицы не позволяют это сделать и приходится двигаться по улицам, которые часто бывают расположены в виде регулярной сетки. В городе удобнее пользоваться манхэттенским расстоянием, так как оно позволяет рассчитывать расстояние между двумя точками данных на регулярной координатной сетке, например, среди городских кварталов или на шахматной доске, где между двумя точками может быть много путей с одинаковым манхэттенским расстоянием. Оно называется манхэттенским, потому что большинство улиц на Манхэттене расположены в строгом порядке, за исключением, разве что, Бродвея, который появился до создания регулярной планировки улиц.
Манхэттенское расстояние известно также под названием «метрика такси», «расстояние городских кварталов». метрика L¹, расстояние L₁, метрика прямоугольного города и другими. Формула для манхэттенского расстояния между двумя точками p и q с координатами (x₁, y₁) и (x₂, y₂) имеет вид:
Обобщенная формула для манхэттенского расстояния в n-мерном векторном пространстве имеет вид:
Расстояние Минковского
Расстояние Минковского между двумя точками в n-мерном пространстве — обобщение манхэттенского, евклидова и чебышёвского расстояний:
где λ — порядок метрики Минковского. Для различных значений λ расстояние Минковского рассчитывается тремя способами:
Можно рассчитывать и с промежуточными значениями λ, например λ = 1,5, при которых получается нечто среднее между двумя метриками.
Расстояние между точками на координатной прямой
Расстояние между двумя точками на координатной прямой равно модулю разности их координат.
Формула расстояния между точками на координатной прямой:
где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.
Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.
Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:
Ответ. Расстояние между точками L и M равно 8.
Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).
Решение. Обозначим середину отрезка точкой C. Так как C — середина отрезка AB, то |AC| = |CB|. Значит, чтобы найти координату точки C, надо сначала вычислить длину отрезка AB и разделить её на 2, то есть, на две равные части AC и CB:
10 : 2 = 5, значит |AC| = |CB| = 5.
Как видно из чертежа, чтобы найти координату середины отрезка, надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:
Ответ. Координата середины отрезка C(0).
Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).
Ответ. Координата точки C — 16.
Онлайн калькулятор. Длина отрезка. Расстояние между точками.
Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния между точками.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния между точками и закрепить пройденный материал.
Калькулятор для вычисления расстояния между двумя точками
Выберите необходимую вам размерность:
Введите координаты точек.
Ввод данных в калькулятор для вычисления расстояния между точками
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления расстояния между точками
Теория. Расстояние между точками.
Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
В зависимости от размерности задачи расстояние между двумя точками можно найти используя следующие формулы:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Расстояние между двумя точками.
Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Формулы вычисления расстояния между двумя точками:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Пример вычисления расстояния между двумя точками на плоскости
Пример 1. Найти расстояние между точками A(-1, 3) и B(6,2).
Формула расстояния и ее использование в трехмерной геометрии
Формула расстояния определяет расстояние между любыми двумя точками в пространстве XYZ.
Формула:
Distance (d) =
Эта формула расстояния используется для вычисления расстояния между двумя точками в любом трехмерном пространстве. Когда мы знаем координаты двух точек на плоскости (в виде упорядоченной пары (x, y, z)), мы можем легко получить расстояние между двумя точками, подставив их в формулу расстояния.
Расстояние между двумя точками: формулы и решенные примеры
Distance (d) =
Пример 1. Найдите расстояние между точками P (1, –3, 4) и Q (- 4, 1, 2)?
Решение:
Using the formula to calculate the distance between point P and Q,
Distance (d) =
d =
Пример 2: показать, что точки P (–2, 3, 5), Q (1, 2, 3) и R (7, 0, –1) лежат на одной прямой?
Решение:
We know that points are said to be collinear if they lie on a line.
Hence P, Q and R are collinear.
Расстояние от точки до линии: значение, формулы и примеры
Distance (d) =
Where ‘s’ is the directing vector of line l.
Пример: найти расстояние от точки P (-6, 1, 21) до прямой 
Решение:
Расстояние от точки до плоскости: формулы, уравнения и примеры
Distance (d) =
Решение:
Distance (d) =
Расстояние между параллельными линиями: формулы и примеры
Distance (d) =
Если уравнение двух параллельных прямых задано как:
ax + by + d1 = 0 и ax + by + d2 = 0, то формула имеет вид
Distance (d) =
Where a and b are the coefficients of variables x and y in the line.
Пример 1. Найти расстояние между линиями y = 2x + 10 и y = 2x + 12? (Примечание: обе линии параллельны друг другу)
Решение:
The lines y = 2x + 10 and y = 2x + 12 are in form y = mx + c.
Using formula, the distance (d) =
Решение:
The lines given are 4x + 3y + 6 = 0 and 4x + 3y – 3 = 0. Both lines are in form ax + by + d = 0.
Using formula for this case, distance (d) will be calculated as:
Формула раздела: определение, векторная формула, случай и примеры
Случай 1: Координаты средней точки: если R является средней точкой PQ, тогда m: n = 1: 1, так что
x =
, y =
and z =
Это координаты средней точки отрезка, соединяющего P (x1, y1, z1) и Q (x2, y2, z2).
Случай 2: координаты точки R, которая делит PQ в соотношении k: 1, получаются, если k = 
Решение:
(i) Let P (x, y, z) be the point that divides the line segment joining A(1, – 2, 3)
and B (3, 4, –5) internally in the ratio 2 : 3. Therefore
Thus, the required point is
(ii) Let P (x, y, z) be the point which divides segment joining A (1, –2, 3) and
B (3, 4, –5) externally in the ratio 2 : 3. Then,
Therefore, the required point is (–3, –14, 19).
Пример 2: Используя формулу сечения, докажите, что три точки (- 4, 6, 10), (2, 4, 6) и (14, 0, –2) лежат на одной прямой?
Решение:
Let A (– 4, 6, 10), B (2, 4, 6), and C(14, 0, – 2) be the given points. Let the
point P divides AB in the ratio k: 1. Then coordinates of the point P are
Let us examine whether, for some value of k, the point P coincides with point C.
On putting 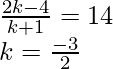
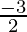
Therefore, C (14, 0, –2) is a point that divides AB externally in the ratio 3: 2 and is
same as P. Hence A, B, C are collinear.
Формула расстояния между точками на координатной плоскости является основным инструментом, применяемым при решении ряда задач в двумерном пространстве.
Система координат
Прежде чем говорить о расстоянии между точками по координатам, следует ввести систему отчета, в которой каждый геометрический объект можно будет однозначно определять. Для этой цели часто используют декартову систему координат. Она представляет собой взаимно перпендикулярные прямые, на каждой из которых отмечены единичные отрезки. Именно в них определяется положение тел в пространстве, на плоскости или на прямой линии.
Для названных трех случаев декартова система координат отличается количеством осей:
Единичные отрезки на координатных осях в общем случае могут иметь разную длину.
Однако ввиду симметричности пространства и для удобства выполнения практических расчетов применяют, как правило, единичные отрезки равной длины. Каждому из них соответствует единичный вектор.
Понятие о векторе
Чтобы уметь вычислять расстояние от точки до точки по координатам, удобно пользоваться понятием вектора.
Из школьного курса геометрии известно, что под ним принято понимать отрезок, имеющий некоторое определенное направление. Обозначают его в виде прямой линии конечной длины, на конце которой изображена стрелка.
Пользу использования указанного геометрического объекта трудно переоценить. Например, в физике все величины делятся на 2 большие группы:
К первым относятся масса, электрический заряд, энергия и другие. Вторая группа более обширная. Здесь следует назвать скорость, ускорение, силу тока, напряженности магнитного и электрического полей, силу любой природы и многие другие.
Характеристики объекта
Как любой геометрический объект, вектор обладает набором математических свойств, которые используются при решении задач. Основные из них:
Для всех свойств существуют определяющие их правила. Например, при осуществлении вычитания вектора a- из b- необходимо соединить концы этих объектов отрезком и направить его к концу a-, тогда получается результирующий вектор разницы.
Умножение a- и b- векторным способом является полезной операцией при определении площадей и объемов фигур. Для ее выполнения следует уметь работать с матрицами второго и третьего порядка, в частности, знать, как рассчитывается детерминант (определитель).
Универсальный способ
Речь идет о координатном представлении нульмерных, одномерных, двумерных и трехмерных геометрических фигур. Параметры точек, треугольников, квадратов, прямых, плоскостей и других более сложных объектов могут быть однозначно выражены в виде наборов чисел, привязанных к соответствующей координатной системе. Поскольку существует задача определения расстояния от точки до точки по координатам, имеет смысл рассмотреть только указанный одномерный объект и вектор.
Точка на плоскости
В общем случае удобно обозначить произвольную точку Q (x0; y0).
Направленный отрезок в двумерном пространстве
На плоскости и в трехмерном пространстве всего 2 точки однозначно определяют направленный отрезок. Если его начало переместить в пересечение осей x и y, его конец легко можно найти, вычитая соответствующие координаты точек друг из друга. Следующий простой пример демонстрирует сказанное.
Даны точки A (x1; y1), B (x2; y2), тогда AB- будет иметь координаты:
Вторая точка показывает место расположения конца AB-.
Формула дистанции
Имея полученные представления и знания о свойствах точек и векторов, можно перейти к вопросу нахождения формулы расстояния. Согласно геометрическому определению, под дистанцией между двумя точками понимают длину отрезка, который их соединяет. Эта величина также равна модулю вектора, построенного на нульмерных объектах.
Длину направленного отрезка на плоскости определить просто: необходимо возвести в квадрат каждую его координату, сложить полученные значения, и взять квадратный корень из результирующей суммы. Для вектора a- (x; y) длина будет равна следующей величине:
Возведение суммы в степень 0,5 эквивалентно взятию из нее квадратного корня.
Поскольку определение координат вектора по соответствующим значениям точек известно, можно получить следующую простую формулу для A (x1; y1) и B (x2; y2):
В трехмерном пространстве соответствующее выражение будет иметь подобную форму, только добавится третья координата z.
Расстояние между Q и прямой
Полученные знания можно с легкостью применять для решения разнообразных задач по геометрии. Часто приходится находить дистанцию между точкой и прямой. Определить эту величину можно, если знать направляющий вектор прямой. Предположим, что он имеет следующие координаты: a- (x1; y1). Прямая проходит через A (x2; y2). Точка задается так: Q (x0; y0).
В параметрическом виде прямая записывается следующим образом:
Здесь t — параметр, который может принимать любое действительное число. Это выражение позволяет записать равенство (1):
Пусть точка P (x;y) является проекцией Q (x0;y0) на прямую, тогда расстояние PQ является искомой дистанцией, которую следует найти по условию задачи. Поскольку вектора PQ- и a- перпендикулярны друг другу, их скалярное произведение будет равно нулю (угол между векторами равен 90 градусов, его косинус равен нулю). Исходя из этих рассуждений, можно записать выражение (2):
Поскольку имеющиеся равенства (1) и (2) содержат 2 неизвестные переменные, объединение их в систему и решение ее позволит определить точку P (x;y). Зная ее координаты и используя формулу дистанции между двумя точками на плоскости, можно получить искомое расстояние PQ.
Пример задачи
Применить полученные знания поможет простая геометрическая проблема. Имеется прямая, которая задана на плоскости в виде следующего общего выражения:
Пусть проекцией точки Q на прямую будет нульмерный объект P (x;y). Координаты P должны удовлетворять записанному уравнению.
Чтобы определить направляющий вектор, достаточно взять 2 любые точки на прямой. Подставляя в выражение произвольные значения x, можно определить эти точки A, B и вместе с ними направляющий вектор AB-:
Вектор QP-, который пересекает прямую под прямым углом, должен подчиняться следующему уравнению (свойство скалярного произведения):
В это выражение нужно подставить значение y из уравнения прямой.
Получается:
Рассчитанное значение округлено до сотых долей и выражается в единицах единичных векторов координатной системы.
При решении подобных задач для сокращения последующих вычислений рекомендуется проверять принадлежность точки прямой, для чего следует подставить координаты в уравнение. Если этот факт подтверждается, искомое расстояние равно нулю.
Углы треугольника
Польза от использования формулы дистанции между точками на плоскости наглядно показывается на примере решения задач на нахождение углов фигур. Пусть нужно определить все углы треугольника, который построен на вершинах A (x1;y1), B (x2;y2), C (x3;y3).
На первый взгляд сложная задача решается легко, если вспомнить о понятии векторного произведения. Например, для векторов AB- и AC- записывается оно так:
Произведение [AB-*AC-] является вектором, который находится как детерминант матрицы третьего порядка. Его модуль, а также длины |AB-| и |AC-| вычисляются по формуле расстояния между двумя точками.
Чтобы определить угол при вершине A треугольника, остается взять функцию арксинуса от отношения векторного произведения к произведению длин сторон AB и AC.
Расчет расстояния между точками
Точка — одна из простейших геометрических фигур. На практике очень часто приходится определять расстояние между точками.
Если две точки расположены на одной координатной прямой, расстояние между ними равняется модулю разности их координат. Расстояние между точками А и В с координатами х1 и х2 соответственно будет равно: |АВ| = |х2 — х1|.
Всякая точка на плоскости определяется двумя координатами (по оси Ох и Оу).
Чтобы вычислить расстояние между 2-мя точками, следует найти корень квадратный из суммы квадратов разностей координат по каждой оси.
Пусть заданы две точки на плоскости. Координаты первой точки (х1, у1), координаты второй (х2, у2). Тогда расстояние между ними рассчитаем по формуле:
d =
Любая точка в пространстве определяется тремя координатами. Пусть заданы две точки в пространстве. Координаты первой точки (х1, у1, z1), координаты второй (х2, у2, z2). Расстояние между двумя точками в 3-х мерном пространстве вычисляем используя координаты этих точек по формуле:
Быстро определить расстояние между точками можно с помощью онлайн калькулятора.
Расстояние между точками в координатах – Расстояние между двумя точками | Формулы и расчеты онлайн
формулы, примеры, решения, формула расстояния между двумя точками
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Yandex.RTB R-A-339285-1 Определение 1
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.
Расстояние между двумя точками.
Навигация по странице:
Определение. Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Формулы вычисления расстояния между двумя точками:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Примеры задач на вычисление расстояния между двумя точками
Пример вычисления расстояния между двумя точками на плоскости
Найти расстояние между точками A(-1, 3) и B(6,2).
AB = √(xb — xa) 2 + (yb — ya) 2 = √(6 — (-1)) 2 + (2 — 3) 2 = √7 2 + 1 2 = √50 = 5√2
Пример вычисления расстояния между двумя точками в пространстве
= √(6 — (-1)) 2 + (2 — 3) 2 + (-2 — 3) 2 = √7 2 + 1 2 + 5 2 = √75 = 5√3
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Формула расстояния между точками | Треугольники
Формула для нахождения расстояния между двумя точками A(x1;x2) B(x2;y2) на плоскости:
Сначала рассмотрим частные случаи.
К этой же формуле придём, если подставим координаты точек A и B в общую формулу:
2) Аналогично, если x1=x2:
Эту же формулу получим, подставив координаты A и B в общую формулу:
3) Если x1=x2 и y1=y2, AB=0. Формула для этого случая также верна.
4) Если x1≠x2, y1≠y2.
Проведём через точки A и B прямые, перпендикулярные координатным осям. Обозначим точку пересечения этих прямых через C.
Из прямоугольного треугольника ABC по теореме Пифагора
Что и требовалось доказать.
Онлайн расчет расстояния по координатам + формула
Расчет расстояния между координатами
Данный сервис позволяет рассчитать расстояние между двумя точками с известными географическими координатами.
Как известно, кратчайшим расстоянием между двумя точками на земной поверхности является длина дуги круга, проведенного на сфере по этим двум точкам. При расчете расстояния по географическим координатам делается предположение, что Земля не плоская, а круглая (если быть точнее, имеет форму, приближенную к сфере), то есть Земля — сфероид.
Для определения расстояния между двумя точками будет применяться формула расчета длины дуги, так называемая «модифицированная формула гаверсинусов».
Поскольку в расчете участвует радиус, а у Земли, как у не совсем правильной сферы, он разный, скажем на северном полюсе — 6335.437 км, а на экваторе — 6399.592 км. В связи с этим в расчете берется среднее значение радиуса Земли равное 6372.795 км, что позволяет получать результат с точность 99,5%.
В калькуляторе ниже для примера приводится расчет расстояния между координатами г.Москва и г.Санкт-Петербург.
Формула расчета расстояния по координатам
Формула расстояние d т.е.длины дуги, для сферы радиуса R и приведены в радианах
Больше матиматики …
На компьютерных системах с низкой точностью с плавающей запятой, эта формула может иметь большие ошибки округления, если расстояние не большое (если две точки находятся в 1 км друг от друга на поверхности Земли, косинус центрального угла выходит 0,99999999). Для современных 64-разрядных чисел с плавающей запятой, формула Теоремы косинусов, которая приведенна выше, не имеет серьезных ошибок округления для расстояний более нескольких метров на поверхности Земли. Эта формула лучше подходит для вычисления растояние по координатам на небольшые расстояния
Для получения более точных рузультатов на большых расстояниях стараются исполтзовать формулу посложнее, в которой сделано предположение, что сфера является эллипсоидом с одинаковыми большой и малой осями.
Более подробную информацию о выведении формулы расчета расстояния по координатам читайте здесь: http://en.wikipedia.org/wiki/Great_circle_distance
Расстояние между двумя точками.
Расстояние между двумя точками
Формулы вычисления расстояния между двумя точками:
) 2
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Пример вычисления расстояния между двумя точками на плоскости
Пример 1. Найти расстояние между точками A(-1, 3) и B(6,2).
Пример вычисления расстояния между двумя точками в пространстве
(6 — (-1)) 2 + (2 — 3) 2 + (-2 — 3) 2
Расстояние между двумя точками на прямой
Расстояние между двумя точками на координатной прямой равно модулю разности их координат.
Формула расстояния между точками на координатной прямой:
где A и B – это произвольные точки, расстояние между которыми надо найти, то есть найти длину отрезка AB, a и b – координаты точек.
Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.
Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.
Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:
|-3 — 5| = |-8| = 8 или |5 — (-3)| = |5 + 3| = 8
Ответ. Расстояние между точками L и M равно 8.
Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).
Решение. Обозначим середину отрезка точкой C. Так как C – середина отрезка AB, то |AC| = |CB|, значит чтобы найти координату точки C надо сначала вычислить длину отрезка AB и разделить её на 2, то есть на две равные части AC и CB:
10 : 2 = 5, значит |AC| = |CB| = 5
Как видно из чертежа, чтобы найти координату середины отрезка надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:
-5 + 5 = 0 или 5 — 5 = 0
Ответ. Координата середины отрезка C(0).
Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).
AB = |7 — 25| = |-18| = 18
7 + 9 = 16 или 25 — 9 = 16
Ответ. Координата точки C – 16.
Определение расстояний на поверхности Земли
Определение расстояний на поверхности Земли
Размеры и форма Земли
Форма Земли отличается от шара и имеет несколько сплющенную форму, близкую к сфероиду (эллипсоиду вращения), но истинная фигура Земли отличается и от сфероида, и от трехосного эллипсоида и не может быть представлена ни одной из известных математических фигур.
Поэтому, говоря о фигуре Земли, имеют в виду не физическую форму земной поверхности, с океанами и материками, с их возвышенностями и впадинами, а так называемую поверхность геоида.
Поверхность, нормалями к которой в любой из ее точек являются отвесные линии, называется уровенной поверхностью, или поверхностью равновесия. Уровенных поверхностей, как внутри Земли, так и охватывающих земную поверхность, или пересекающихся с ней, можно провести бесчисленное множество.
Та поверхность равновесия, которая совпадает в открытом океане с поверхностью покоящейся свободной воды, называется геоидом.
Для решения многих задач навигации и составления карт мелкого масштаба Землю принимают за сферу (шар).
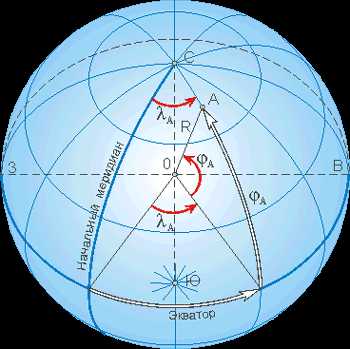
Положение точки па земной сфере определяется сферическими координатами: сферической широтой и сферической долготой (в картографии применяют термин «географические координаты«).
Сферическая широта точки А — угол φА между плоскостью экватора и направлением R на данную точку из центра земной сферы.
Сферическая долгота точки А — угол λА, заключенный между плоскостью нулевого (Гринвичского) меридиана и плоскостью меридиана данной точки.
Средний радиус Земли R = 6371210 м.
Экваториальный радиус Земли RЭ = 6378,245 м.
Полярный радиус Земли RП = 6356,830 м.
Длина дуги меридиана (дуги экватора, дуги окружности большого круга) в 1°, 1′ и 1″ равна соответственно:
111 197 м (111,2 км), 1852 м (1,852 км) и 30,9 м.
Законы сферической тригонометрии позволяют рассчитывать расстояния между точками, расположенными на сфере.
Кратчайшее расстояние между двумя точками на земной поверхности (если принять ее за сферу) определяется зависимостью:
где φА и φB — широты, λА, λB — долготы данных пунктов, d — расстояние между пунктами, измеряемое в радианах длиной дуги большого круга земного шара.
Расстояние между пунктами, измеряемое в километрах, определяется по формуле:
где R = 6371 км — средний радиус земного шара.
Таблица расстояний (с точностью 1 км), рассчитанными по этим формулам,
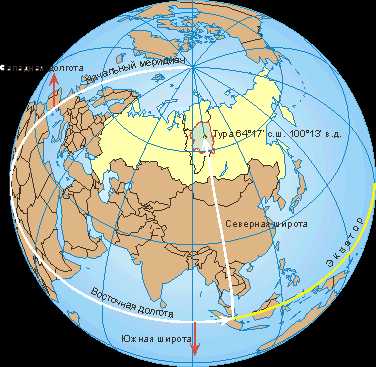
для пунктов Эвенкийского автономного округа (Эвенкийского муниципального района):
| уточнения внесены 25.03.2010 | Тура | Байкит | Ванавара |
| Красноярск | 1007 | 662 | 738 |
| Агата | 426 | ||
| Географический центр РФ, Виви | 364 | ||
| Ессей | 467 | ||
| Кислокан | 201 | ||
| Нидым | 21 | ||
| Ногинск | 439 | ||
| Тембенчи | 99 | ||
| Тура | 350 | 450 | |
| Тутончаны | 313 | ||
| Учами | 186 | ||
| Чиринда | 363 | ||
| Эконда | 293 | ||
| Юкта | 293 | ||
| Байкит | 350 | 352 | |
| Бурный | 197 | ||
| Кузьмовка | 236 | ||
| Куюмба | 82 | ||
| Мирюга | 220 | ||
| Ошарово | 177 | ||
| Полигус | 101 | ||
| Суломай | 274 | ||
| Суринда | 114 | ||
| Таимба | 203 | ||
| Усть-Камо | 121 | ||
| Ванавара | 450 | 352 | |
| Кербо | 242 | ||
| Муторай | 147 | ||
| Оскоба | 100 | ||
| Стрелка-Чуня | 159 | ||
| Тунгусский метеорит (эпицентр) | 64 | ||
| Чемдальск | 102 |
Для расчета расстояния между пунктами, расположенными в разных полушариях (северное-южное, восточное-западное), знаки (±) у соответствующих параметров (широт или долгот) должны быть разными.
Пример: (см. таблицу ниже)
для вычисления расстояния между Турой и Сиднеем (Австралия) применяем формулу:
cos(d) = sin(φА)·sin(−φB) + cos(φА)·cos(−φB)·cos(λА − λB) = −0,27462.
d = 1,848988
Расстояние L = d·R = 11 779,9 км.
Расстояние L = d·R = 8 334,92 км.
В таблице расстояния определены с точностью 1 км.
Расстояние от точки до точки: формулы, примеры, решения
Время чтения: 26 минут
На первый взгляд может показаться, что математика сложна и коварна, но это далеко не так. Если приложить усилия к её изучению, то можно удивиться тому, насколько быстро вы измените своё мнение о ней. Давайте же разберём одну из тем, которая поможет находить расстояние от точки до точки при различных условиях. После того как вы изучите данную статью, вы можете решить предоставленные задания, чтобы лучше закрепить пройденный материал.
Математические термины
Для начала введём некоторые определения.
Расстояние между точками – это измерение отрезка, находящегося между этими точками, составляющего длину расстояния.
Эти отрезки располагаются в определенном масштабе, потому как необходимо знать единицу длины для их измерения, без этого нельзя.
Функция – это связь величин, выражаемая в зависимости одной переменной Y, от второй переменной X.
Произвольная функция (точка) – это такая точка, которую можно расположить в любом месте.
Координатная прямая – это прямая, на которой изображают точку отсчёта 0 и единичные отрезки. Прямой также задают направление.
Действительные числа – это совокупность рациональных и иррациональных чисел.
Рациональное число – это такое число, которое может находиться в виде обыкновенной дроби, в отличие от иррационального числа.
Иррациональное число – это бесконечная непериодическая десятичная дробь. Такое число нельзя представить в виде обыкновенной дроби.
Модуль или же абсолютная величина – это обязательно неотрицательное число, которое является расстоянием определённых точек.
Как определить расстояние между точками, находящимися на координатной прямой
Чтобы найти расстояние от одной точки до другой, т.е. длину этого отрезка, нужно сравнить его с другим таким отрезком в заданном масштабе.
Действительные числа
Рассмотрим этот способ на примере:
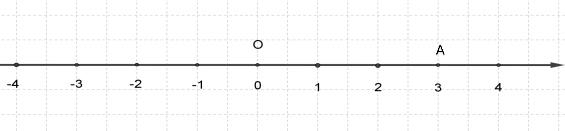
Здесь мы имеем координатную прямую OX, на которой отмечена точка A. Она произвольная, поэтому мы можем задать ей любое действительное число, пусть это будет 3.
Отрезок – это единица длины, поэтому все отрезки, что мы отложили от точки O нужно сложить, вследствие чего полученное количество единичных отрезков будет равняться длине отрезка OA. В данном случае здесь три отрезка, поэтому и ответ таков.
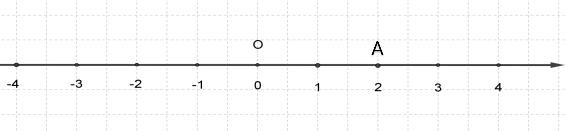
Ещё один пример, где точку отсчёта O и произвольную точку A соединяют 2 отрезка. Это значит, что расстояние длин всех единичных отрезков OA равно 2. Если же точка A будет иметь другое число, например: 6, то мы откладываем от точки O именно 6 единичных отрезков и получаем искомое расстояние.
Рациональные числа
С действительным числами всё понятно, а что делать с рациональными? Представим, что координаты точки A равны 5,5. Из этого следует, что нам нужно отложить из точки O сначала 5 единичных отрезков, то есть, целое число, а после прибавить 0,5. Иногда это кажется невозможным, ведь некоторые числа трудно представить в виде отрезка, из-за чего приходится искать самое приближенное значение числа.
Иррациональные числа
Иррациональным числам данный метод не подходит, потому как такие числа нельзя поставить на координатной прямой OX. Для примера приведём числа √5, √8, √17. Здесь можно перейти к отвлечённому представлению и посмотреть на эти числа таким образом:
Также можно сказать, что это подходит и к действительным числами. Если точка A будет находиться на начальной точке O, то и расстояние между ними будет равно 0. Здесь нужно уметь хорошо работать с рисунком, тогда всё будет понятно.
Важно помнить, что расстояние между точками не может быть отрицательным.
В данном случае у нас есть модуль числа A, что является расстоянием OA и это число 3.
Если на координатной прямой будут точки A и B, то их расстояние нужно определить по модулю разности этих координат. Получается, чтобы найти длину отрезка AB, необходимо из числа точки B отнять число точки A:
Как определить расстояние между двумя точками на плоскости
Представим прямоугольную систему координат и плоскость на ней, с находящимися там точками A и B. Далее проведём прямые от этих точек к осям Ox и Oy, как на изображении. В следствие этого образовались точки Ax и Ay, а также Bx и By.
Из этого можно вывести несколько вариантов:
В случае расположения точек A и B на прямой, которая в свою очередь перпендикулярна оси Ox – точки A и B совпадают, а модуль AB равен модулю AyBy. Как говорилось ранее, для нахождения длины промежутка (расстояния) между двумя точками, нужно найти разность модуля заданных координат, поэтому можно сказать, что:
|AB| = |AyBy| = |yB – yA|.
При этом совпадении их расстояние равняется 0.
Формула для нахождения расстояния между двумя точками на плоскости:
Теперь рассмотрим тот случай, когда прямая перпендикулярна оси Oy. Находится расстояние таким же образом, но уже с участием xB и xA: |AB| = |AxBx| = |xB – xA|.
Формула для нахождения расстояния между двумя точками на плоскости:
Теперь поговорим о прямоугольном треугольнике ABC. Чтобы найти расстояние на плоскости между точкой A и точкой B, необходимо воспользоваться формулой:
|AB| = √(xB – xA)² + (yB – yA)².
Эта формула доказывает правильность ранее написанных утверждений к тем заданиям, на графиках которых точки лежат на прямой, перпендикулярной Ox и Oy.
Если точки совпадают, к ним справедливо равенство:
|AB| = √(xB – xA)² + (yB – yA)² = √0² + 0² = 0.
По рисунку видно, что:
|AC| = |AxBx|, а также |BC|=|AyBy|. Далее вспомним теорему Пифагора и с её помощью запишем равенство:
Пример
Найдите расстояние между двумя точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (3, –1), а также B (X + 3, 7). Также надо найти значение действительного числа X, зная, что при них расстояние между точками будет равно 10.
Чтобы решить эту задачу, необходимо использовать формулу:
|AB| = √(xB – xA)² + (yB – yA)².
После этого действия подставляем вышеприведённые числа:
√(X + 3 – 3)² + (7 – ( – 1))² = √X² + 64.
Далее обратим внимание на то, что |AB| = 10 и составим равенство:
Расстояние между двумя координатами. Как вычислить расстояние между координатами gps
Время на чтение: 16 минут
§2. Координаты точки на плоскости
3. Расстояние между двумя точками.
Мы говорили уже, что это создает определенные преимущества. Так, мы можем рисунок, составленный из точек, передать по телеграфу, сообщить его вычислительной машине, которая совсем не понимает чертежей, а числа понимает хорошо.
В предыдущем пункте мы задали при помощи соотношений между числами некоторые множества точек на плоскости. Теперь попробуем последовательно переводить на язык чисел другие геометрические понятия и факты.
Мы начнем с простой и обычной задачи.
Найти расстояние между двумя точками плоскости.
Быть может, некоторым из читателей этот подход к решению задачи покажется странным и надуманным. Чего проще, скажут они, точки заданы, пусть даже координатами. Нарисуйте эти точки, возьмите линейку и измерьте расстояние между ними.
Этот способ иногда не так уж плох. Однако представьте себе опять, что вы имеете дело с вычислительной машиной. В ней нет линейки, и она не рисует, но зато считать она умеет настолько быстро, что это для неё вообще не составляет никакой проблемы. Заметьте, что наша задача поставлена так, чтобы правило вычисления расстояния между двумя точками состояло из команд, которые может выполнить машина.
Указание. Воспользуйтесь теоремой Пифагора.
Теперь напишите общую формулу для вычисления расстояния точки от начала координат.
Расстояние точки от начала координат определяется по формуле:
Очевидно, правило, выражаемое этой формулой, удовлетворяет поставленным выше условиям. В частности, им можно пользоваться при вычислении на машинах, которые способны умножать числа, складывать их и извлекать квадратные корни.
Теперь решим общую задачу
Даны две точки плоскости и найти расстояние между ними.
Пусть задана прямоугольная система координат.
Теорема 1.1. Для любых двух точек М 1 (х 1 ;у 1) и М 2 (х 2 ;у 2) плоскости расстояние d между ними выражается формулой
Доказательство. Опустим из точек М 1 и М 2 перпендикуляры М 1 В и М 2 А соответственно



Деление отрезка в данном отношении.
Пусть на плоскости дан произвольный отрезок М 1 М 2 и пусть М ─ любая точка этого
Теорема 1.2. Если точка М(х;у) делит отрезок М 1 М 2 в отношении l, то координаты этой определяются формулами
х = 

Доказательство. Докажем первую из формул (4). Вторая формула доказывается аналогично. Возможны два случая.
х = х 1 = 


Т.к. Р 1 Р = ôх – х 1 ô, РР 2 = ôх 2 – хô и числа (х – х 1) и (х 2 – х) имеют один и тот же знак (при х 1 х 2 отрицательны), то
х = 
х = 
Доказательство. Так как М 1 М = М 2 М, то l = 1 и по формулам (4) получаем формулы (5).
Теорема 1.3. Для любых точек А(х 1 ;у 1), В(х 2 ;у 2) и С(х 3 ;у 3), не лежащих на одной
прямой, площадь S треугольника АВС выражается формулой
S = ô(х 2 – х 1)(у 3 – у 1) – (х 3 – х 1)(у 2 – у 1)ô (6)
Доказательство. Площадь ∆ АВС, изображённого на рис. 1.7, вычисляем следующим
Вычисляем площади трапеций:
S ADEC =

S BCEF =
Х 1 у 3) = (х 3 (у 1 – у 2) + х 1 у 2 – х 1 у 1 + х 1 у 1 – х 2 у 1 + у 3 (х 2 – х 1)) = (х 1 (у 2 – у 1) – х 3 (у 2 – у 1) + +у 1 (х 1 – х 2) – у 3 (х 1 – х 2)) = ((х 1 – х 3)(у 2 – у 1) + (х 1 – х 2)(у 1 – у 3)) = ((х 2 – х 1)(у 3 – у 1) –
— (х 3 – х 1)(у 2 – у 1)).
Для другого расположения ∆ АВС формула (6) доказывается аналогично, но может получиться со знаком «-». Поэтому в формуле (6) ставят знак модуля.
Уравнение прямой линии на плоскости: уравнение прямой с главным коэффициентом, общее уравнение прямой, уравнение прямой в отрезках, уравнение прямой, проходящей через две точки. Угол между прямыми, условия параллельности и перпендикулярности прямых на плоскости.
2.1. Пусть на плоскости задана прямоугольная система координат и некоторая линия L.
Определение 2.1. Уравнение вида F(x;y) = 0, связывающее переменные величины x и y, называется уравнение линии L (в заданной системе координат), если этому уравнению удовлетворяют координаты любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой прямой.
Примеры уравнений линий на плоскости.
1) Рассмотрим прямую, параллельную оси Oy прямоугольной системы координат (рис. 2.1). Обозначим буквой A точку пересечения этой прямой с осью Ox, (a;o) ─ её ор-
Динаты. Уравнение x = a является уравнением данной прямой. Действительно, этому уравнению удовлетворяют координаты любой точки M(a;y) этой прямой и не удовлетворяют координаты ни одной точки, не лежащей на прямой. Если a = 0, то прямая совпадает с осью Oy, которая имеет уравнение x = 0.
4) Уравнение x 2 + y 2 = 0 определяет на плоскости единственную точку O(0;0).
5) Уравнение x 2 + y 2 = 25 ─ уравнение окружности радиуса 5 с центром в начале координат.
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
По формуле d = √((х А – х В) 2 + (у А – у В) 2) находим:
МА = √((-а + 2) 2 + (а – 1) 2).
√((-а + 2) 2 + (а – 1) 2) = а.
После возведения в квадрат и упрощения имеем: а 2 – 6а + 5 = 0. Решим уравнение, найдем а 1 = 1; а 2 = 5.
Получаем две точки М 1 (-1; 1) и М 2 (-5; 5), удовлетворяющие условию задачи.
6. Вычисление координат точки, которая находится на одинаковом заданном расстоянии от оси абсцисс (ординат) и от данной точки
Найти точку М такую, что расстояние ее от оси ординат и от точки А(8; 6) будет равно 5.
Из условия задачи следует, что МА = 5 и абсцисса точки М равна 5. Пусть ордината точки М равна b, тогда М(5; b) (рис. 6).
По формуле d = √((х А – х В) 2 + (у А – у В) 2) имеем:
МА = √((5 – 8) 2 + (b – 6) 2).
√((5 – 8) 2 + (b – 6) 2) = 5. Упростив его, получим: b 2 – 12b + 20 = 0. Корни этого уравнения b 1 = 2; b 2 = 10. Следовательно, есть две точки, удовлетворяющие условию задачи: М 1 (5; 2) и М 2 (5; 10).
Известно, что многие учащиеся при самостоятельном решении задач нуждаются в постоянных консультациях по приемам и методам их решения. Зачастую, найти путь к решению задачи без помощи преподавателя учащемуся не под силу. Необходимые консультации по решению задач учащийся и может получить на нашем сайте.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Расстояние между двумя точками плоскости.
Системы координат
Полученная формула позволяет находить расстояние между любыми двумя точками плоскости, если только известны координаты этих точек
Если некоторая точка плоскости в системе координат х0у имела координаты (х, у), то в новой системе координат х»0у» она будет иметь уже другие координаты (х», у»).
В качестве примера рассмотрим точку М, расположенную на оси 0х» и отстоящую от точки 0 на расстоянии, равном 1.
Очевидно, что в системе координат x0у эта точка имеет координаты (cos α , sin α ), а в системе координат х»0у» координаты (1,0).
Координаты любых двух точек плоскости А и В зависят от того, как в этой плоскости задана система координат. А вот расстояние между этими точками не зависит от способа задания системы координат. Это важное обстоятельство будет существенно использовано нами в следующем параграфе.
I. Найти расстояния между точками плоскости с координатами:
II. Найти периметр треугольника, стороны которого заданы уравнениями:
III. В системе координат х0у точки М и N имеют координаты (1, 0) и (0,1) соответственно. Найти координаты этих точек в новой системе координат, которая получается и результате поворота старых осей вокруг начальной точки на угол в 30° против часовой стрелки.
как найти расстояние между двумя точками??
Кратчайшее расстояние между двумя точками на земной поверхности (если принять ее за сферу) определяется зависимостью:
cos(d) = sin(φА) ·sin(φB) + cos(φА) ·cos(φB)·cos(λА − λB),
где φА и φB — широты, λА, λB — долготы данных пунктов, d — расстояние между пунктами, измеряемое в радианах длиной дуги большого круга земного шара.
Расстояние между пунктами, измеряемое в километрах, определяется по формуле:
где R = 6371 км — средний радиус земного шара.
Сферическая широта точки А — угол φА между плоскостью экватора и направлением R на данную точку из центра земной сферы.
Сферическая долгота точки А — угол λА, заключенный между плоскостью нулевого (Гринвичского) меридиана и плоскостью меридиана данной точки.
Опять же расстояние получится без учета пересеченности местности и эллипсоидности Земли.
Законы сферической тригонометрии позволяют рассчитывать расстояния между точками, расположенными на сфере.
Кратчайшее расстояние между двумя точками A и B на земной поверхности (если принять ее за сферу) определяется зависимостью:
где Фa и Фb — широты, Лa, Лb — долготы данных пунктов, d — расстояние между пунктами, измеряемое в радианах длиной дуги большого круга земного шара.
Расстояние между пунктами, измеряемое в километрах, определяется по формуле:
где R = 6371 км — средний радиус земного шара.
Переводим в радианы
Фa=51.1801*3.14/180=0.8928084111111111
Фb=41.89474*3.14/180=0.7308304644444444
Лa=71.44598*3.14/180=1.2463354288888889
Лb=12.4839*3.14/180=0.2177747
Расстояние авиаперелета: 4499 км.
Расстояние между Римом и Астаной по прямой (то есть расстояние авиаперелета) равно 4499 километров (2794 миль).
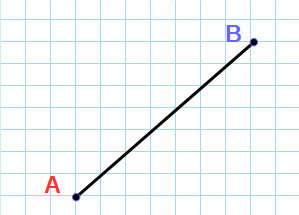
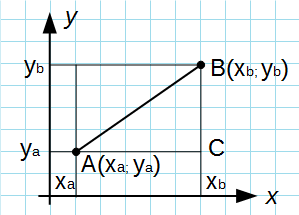





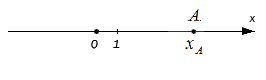
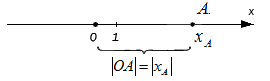
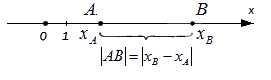
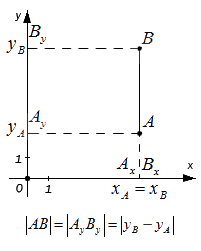
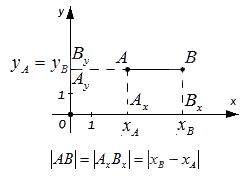
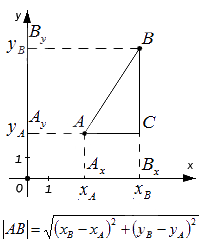
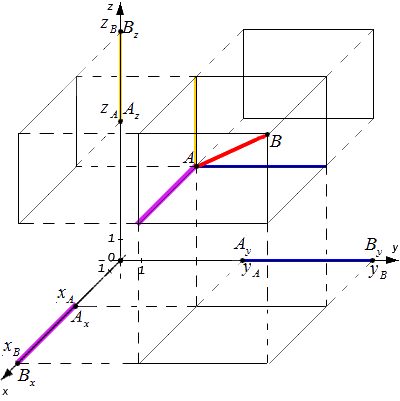

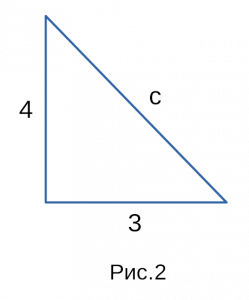
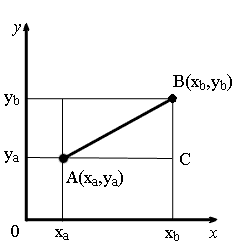















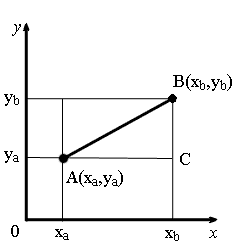

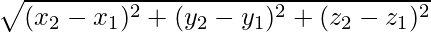
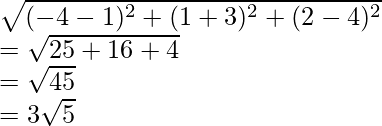
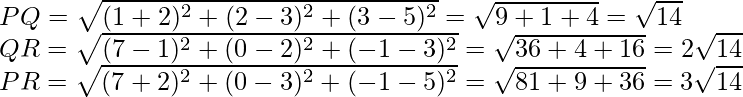
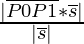


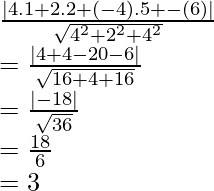
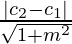
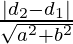
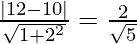
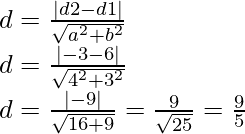

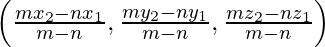
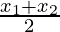 , y =
, y = 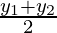 and z =
and z =