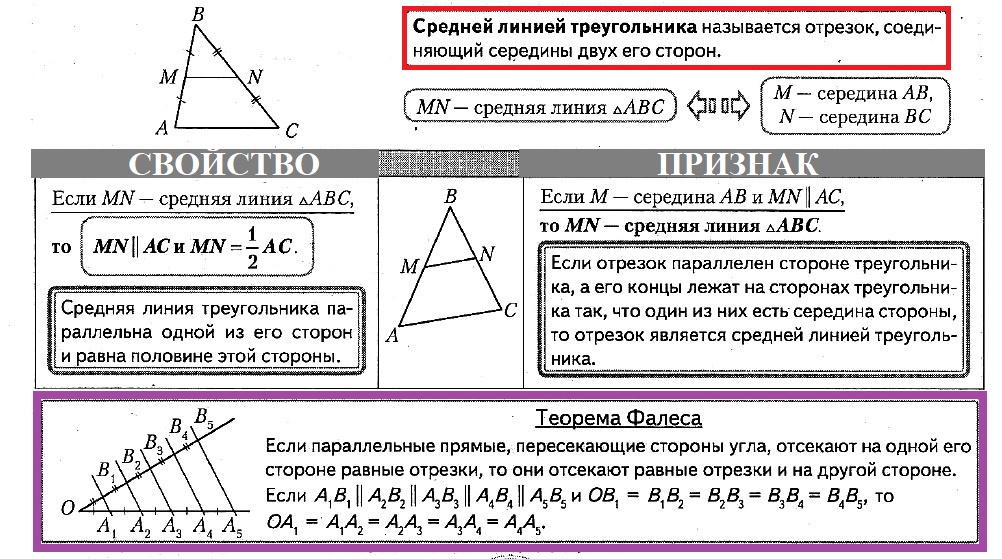
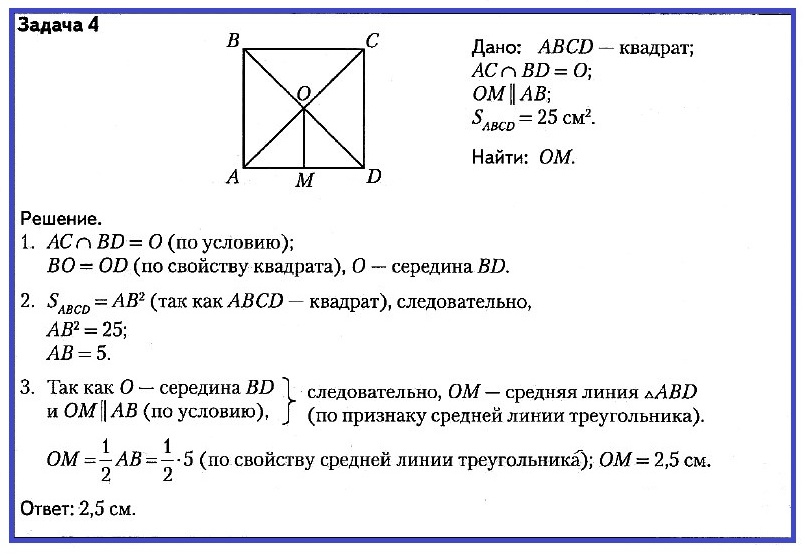
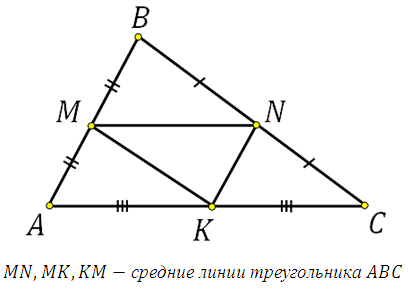
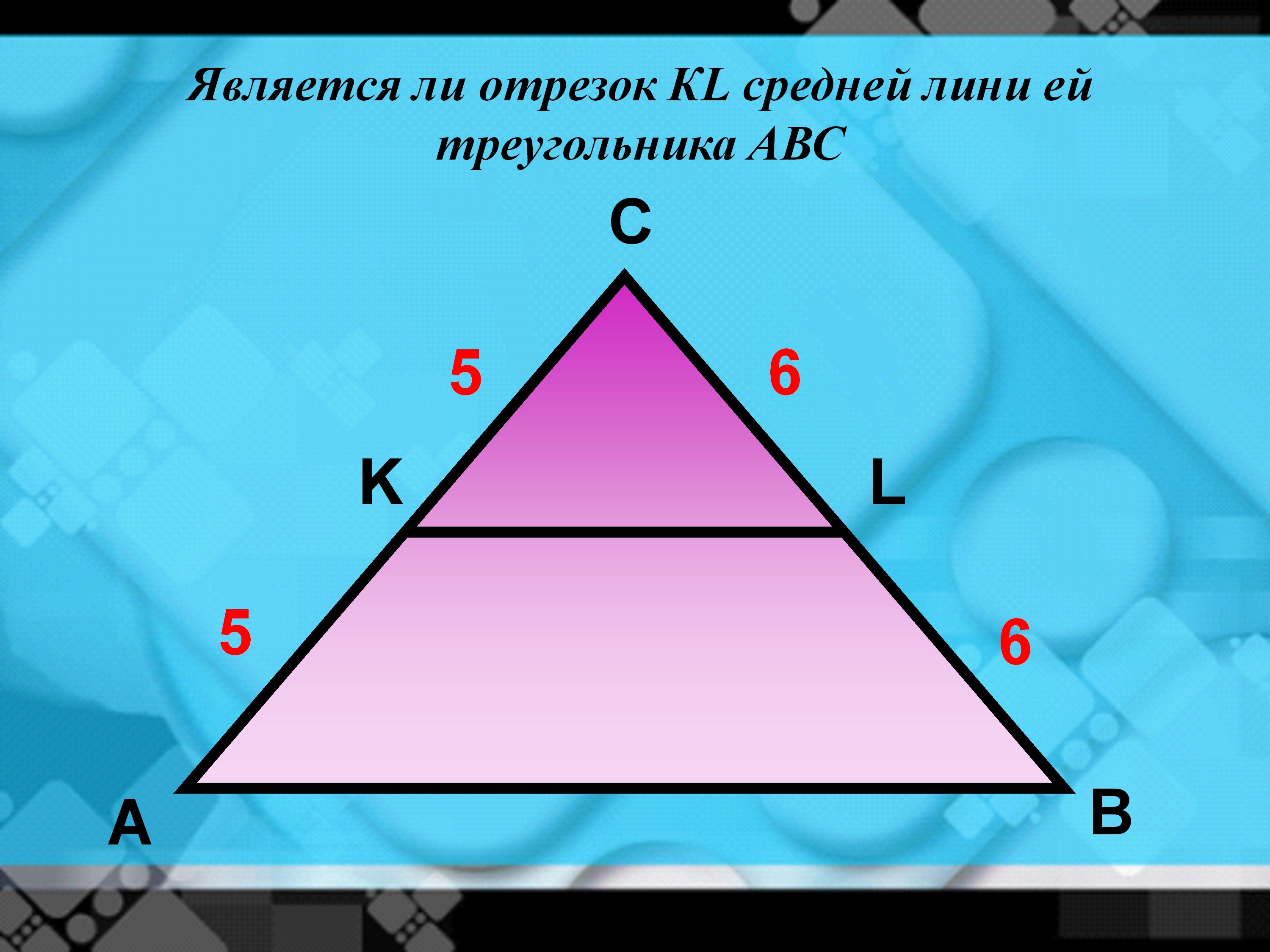
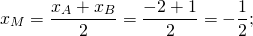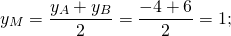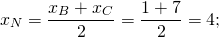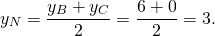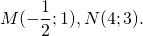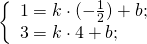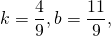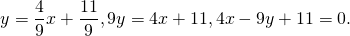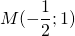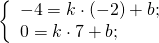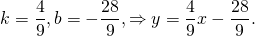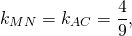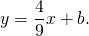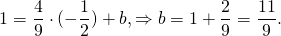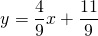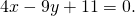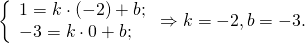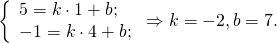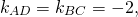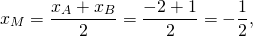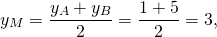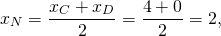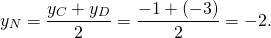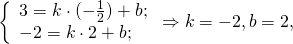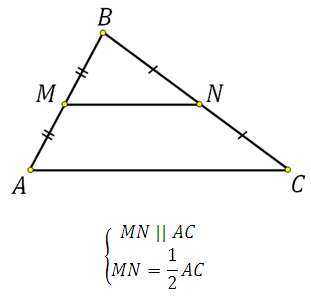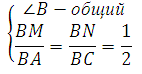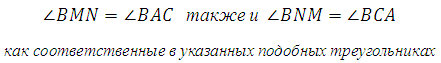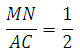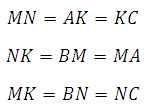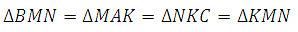Как найти среднюю линию треугольника

Как найти среднюю линию треугольника

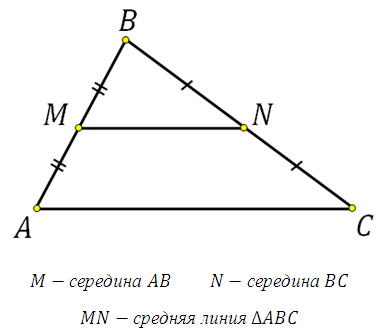
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника:
1. Средняя линия параллельна третьей стороне и равна ее половине.
2. Средняя линия трeугольника отсекает от него треугольник, подобный данному (с коэффициентом подобия 1/2 ).
3. Три средние линии треугольника делят его на 4 равных треугольника, подобных данному, с коэффициентом подобия 1/2.

Свойство средней линии треугольника является следствием теоремы Фалеса.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

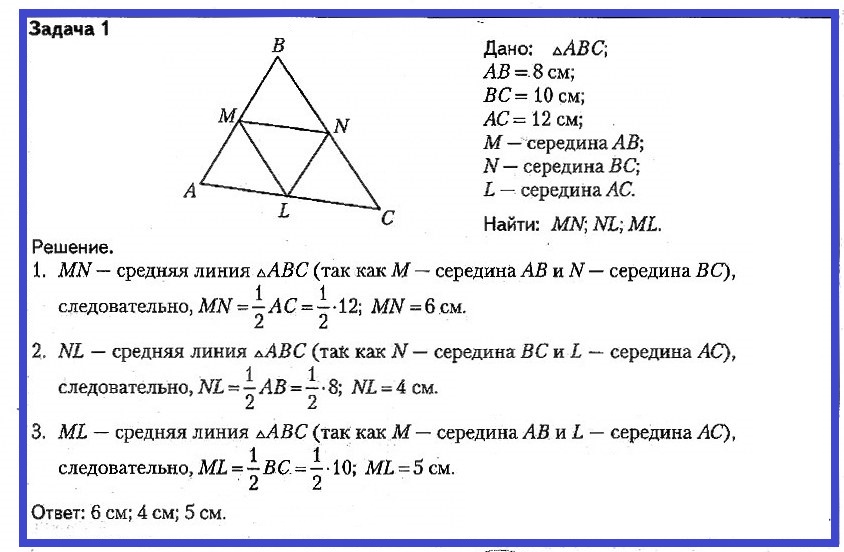
Задача № 1. Дано: ΔABC; AB = 8 см; BC = 10 см; AC = 12 см; M — середина AB; N — середина BC; L — середина AC. Найти: MN, NL, ML.

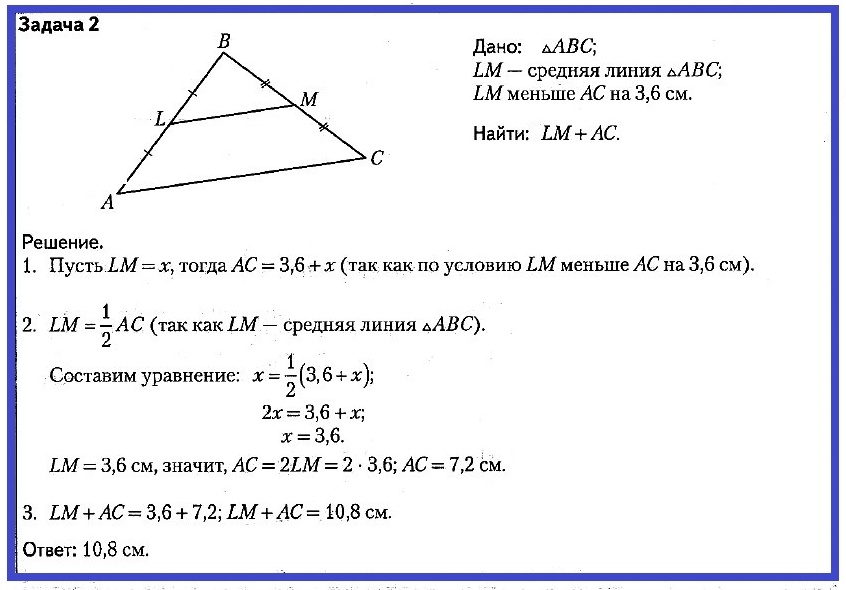
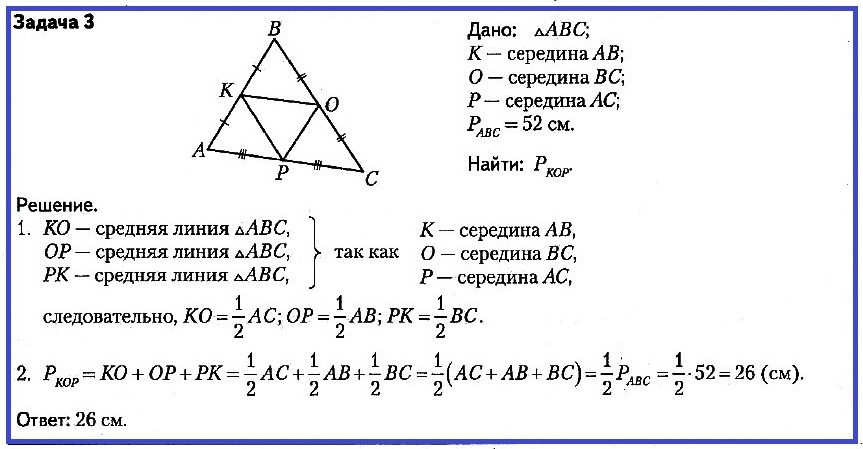
Задача № 3. ΔABC; K — середина AB; O — середина BC; P — середина AC; P_ABC = 52 см. Найти: P_КOР

Это конспект по теме «Средняя линия треугольника + Задачи по теме». Выберите дальнейшие действия:

Источник

Средняя линия треугольника — свойства, признаки и формулы

Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.

Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.

Определение и признаки средней линии треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.

Доказательство следует из теоремы Фалеса.

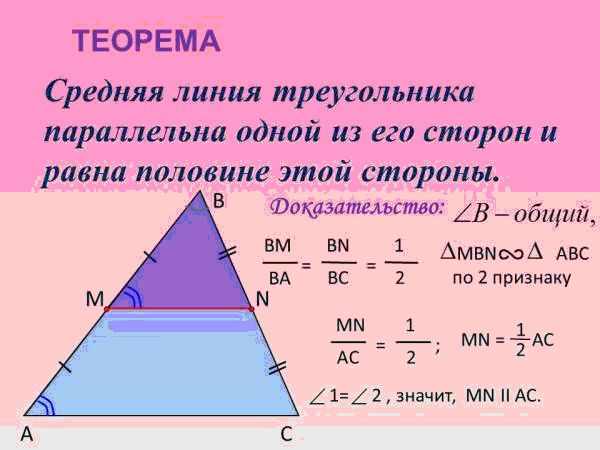
Теорема о средней линии треугольника

Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.

Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.

Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.

По определению, MN – средняя линия ΔABC.

Необходимо доказать, что MN II AC, MN = ½AC.

Доказательства

Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.

Следовательно, MN II AC.

Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.

Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.

Рассматриваются треугольники MBN и ABC. В них угол B является общим,

По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.

Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.

Формула MN = ½AC следует из условий

поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.

Рассматривается сумма векторов

Поскольку в результате образуется замкнутая ломаная, то

Отсюда следует, что

Из последнего равенства следуют условия теоремы.

Следствия из теоремы с доказательствами

Следствие №1

Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому

Из третьего признака подобия вытекает рассматриваемое свойство.

Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как

Следствие №2

Три средних линии треугольника разбивают его на четыре равных треугольника, подобные заданному, с коэффициентом подобия ½.

Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.

Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.

Таким образом: ∠BNM = ∠BCA = ∠MPA.

Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.

Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.

Равенство остальных пар треугольников доказывается аналогично.

По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.

Свойства средней линии треугольника

Теорема и следствия из неё составляют основные свойства средней линии треугольника.

Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.

Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.

Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.

Средняя линия прямоугольного треугольника

Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.

Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.

Пример решения задачи

Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.

Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.

Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.

Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.

Источник

Уравнение средней линии

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

М — середина отрезка AB, N — середина BC.

Составим уравнение прямой MN, например, в виде y=kx+b:

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

— середина отрезка AB. Составим уравнение прямой AC:

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

то есть уравнение прямой MN ищем в виде

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

Таким образом, уравнение прямой MN

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

Поскольку угловые коэффициенты прямых равны:

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Источник

Средняя линия треугольника. Определение

Средняя линия треугольника. Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была на блоге статья, в которой сии факты я предлагал просто запомнить, теперь подробнее…

Что такое средняя линия треугольника и каковы её свойства?

Средняя линия треугольника. Определение

Определение. Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.

Понятно, что средних линий в треугольнике три. Покажем их:

Без всяких доказательств вы уже, наверное, заметили, что все четыре образованные треугольника равны. Это так, но подробнее об этом поговорим далее.

Средняя линия треугольника. Теорема

Теорема. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.

1. Давайте рассмотрим треугольники BMN и BAC. По условию у нас BM=MA, BN=NC. Можем записать:

Следовательно треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А то что:

По признаку параллельности прямых MN||AC.

2. Также из подобия треугольников следует, что

То есть MN в два раза меньше. Доказано!

Средняя линия треугольника. Задача

Решим типичную задачу.

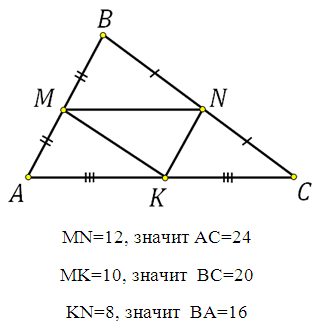
Задача. В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.

Решение. Конечно, прежде всего следует проверить существование треугольника MNK (а значит и существование треугольника АВС). Сумма двух меньших сторон должна быть более третьей стороны, записываем 10+8>12. Выполнятся, следовательно треугольник существует.

Таким образом периметр треугольника АВС равен 24+20+16=60.

*Теперь подробнее о треугольниках полученных при построении всех трёх средних линий. Их равенство легко доказывается. Посмотрите:

Равны они по трём сторонам. Конечно, и другие признаки здесь применимы. Получаем, что

Как это свойство используется в заданиях включённых в состав экзамена? Особо хочется заострить внимание на задачах по стереометрии. Есть такие типы, в которых речь идет о треугольной призме.

Например, сказано что плоскость проходит через середины сторон основания и она параллельна третьему ребру основания. Ставятся вопросы о изменении площади поверхности призмы, её объёма и другие.

Так вот. Зная и понимая информацию изложенную выше вы сразу же определите, что эта плоскость отсекает от основания указанной призмы одну четвёртую часть и задачу решите устно. Вот статья на блоге с такими задачами.

На этом всё! Всего доброго!

Скачать материал статьи

С уважением, Александр Крутицких.

Делитесь информацией сайта в социальных сетях!

Источник

Средняя линия треугольника

Средняя линия треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника. [1]

Свойства средней линии треугольника:

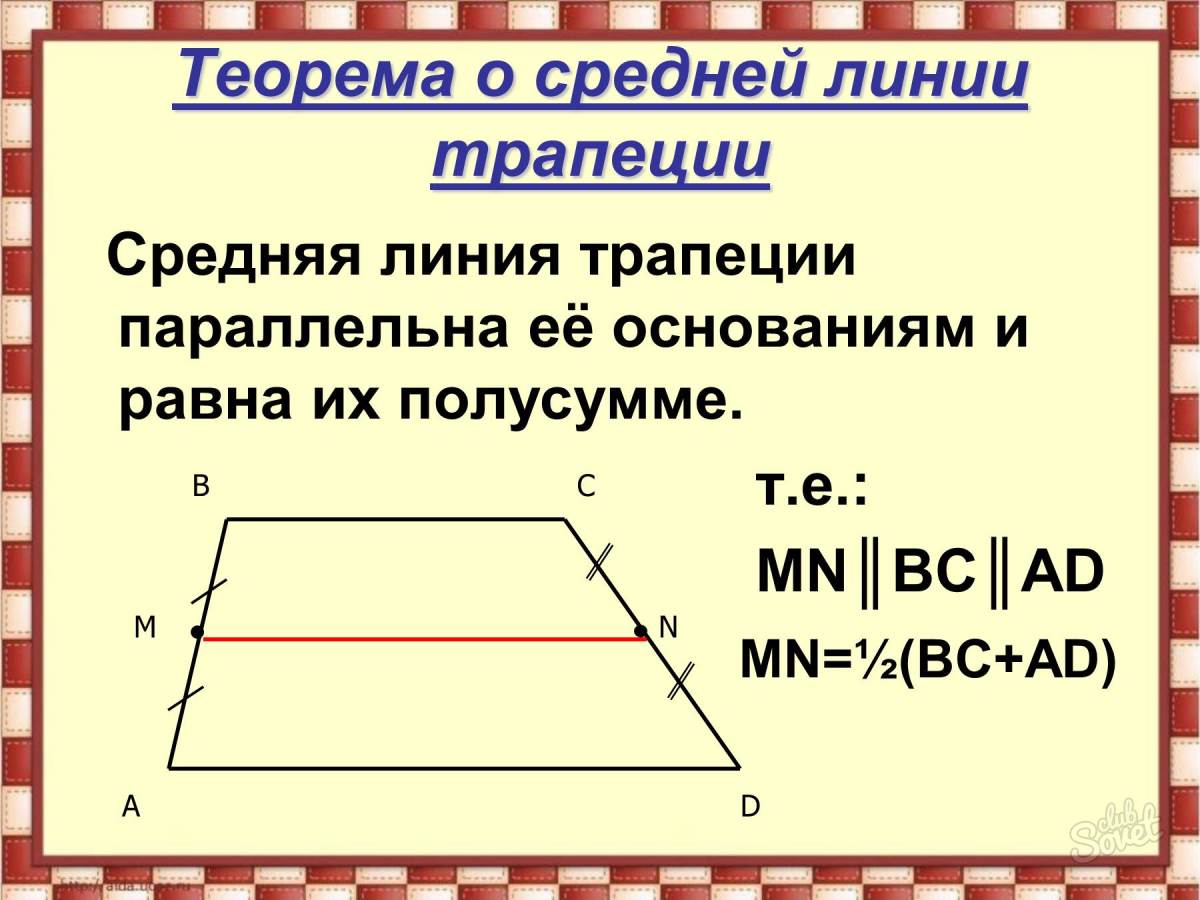
Средняя линия трапеции

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции.

Свойство средней линии трапеции: средняя линия параллельна основаниям трапециии равна их полусумме.

Примечания

Полезное

Смотреть что такое «Средняя линия треугольника» в других словарях:

Средняя линия — фигур в планиметрии отрезок, соединяющий середины двух сторон этой фигуры. Понятие употребляется для следующих фигур: треугольник, четырехугольник, трапеция. Содержание 1 Средняя линия треугольника 1.1 Свойства … Википедия

СРЕДНЯЯ ЛИНИЯ — (1) трапеции отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям и равна их полусумме; (2) треугольника отрезок, соединяющий середины двух сторон этого треугольника: третья сторона при этом… … Большая политехническая энциклопедия

СРЕДНЯЯ ЛИНИЯ — треугольника (трапеции) отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Большой Энциклопедический словарь

средняя линия — треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции). * * * СРЕДНЯЯ ЛИНИЯ СРЕДНЯЯ ЛИНИЯ треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Энциклопедический словарь

СРЕДНЯЯ ЛИНИЯ — треугольника отрезок, соединяющий середины двух сторон треугольника. Третья сторона треугольника при этом наз. основанием треугольника. С. л. треугольника параллельна основанию и равна половине его длины. Во всяком треугольнике С. л. отсекает от… … Математическая энциклопедия

СРЕДНЯЯ ЛИНИЯ — треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Естествознание. Энциклопедический словарь

Средняя линия — 1) С. л. треугольника, отрезок, соединяющий середины двух сторон треугольника (третью сторону называют основанием). С. л. треугольника параллельна основанию и равна его половине; площади частей треугольника, на которые делит его с. л.,… … Большая советская энциклопедия

Площадь треугольника — Стандартные обозначения Треугольник простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника … Википедия

Словарь терминов планиметрии — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Коллинеарные точки — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Источник

Как найти среднюю линию треугольника

Средняя линия треугольника

Цели урока

• Закрепить знания школьников о треугольниках;
• Познакомить учащихся с таким понятием, как средняя линия треугольника;
• Сформировать знания учеников о свойствах треугольников;
• Продолжать обучать детей применению свойств фигур при решении задач;
• Развивать логическое мышление, усидчивость и внимание учеников.

Задачи урока

• Формировать знания школьников о средней линии треугольников;
• Проверить знания учащихся по пройденным темам о треугольниках;
• Проверить умение учащихся решать задачи.
• Развивать у школьников интерес к точным наукам;
• Продолжать формировать умение учащихся излагать свои мысли и владеть математическим языком;

План урока

1. Средняя линия треугольника. Основные понятия.
2. Средняя линия треугольника, теоремы и свойства.
3. Повторение ранее изученного материала.
4. Основные линии треугольника и их свойства.
5. Интересные факты из области математики.
6. Домашнее задание.

Средняя линия треугольника

Средней линией треугольника называют такой отрезок, который соединяет середины двух сторон данного треугольника.

В каждом треугольнике есть три средние линии, которые образуют еще один новый треугольник, расположенный внутри.

Вершины вновь образованного треугольника находятся на срединах сторон данного треугольника.

В каждом треугольнике есть возможность провести три средние линии.

Теперь давайте более детально остановимся на этой теме. Посмотрите на рисунок треугольника вверху. Перед вами треугольник АВС, на котором проведении средние линии. Отрезки MN, MP и NP образуют внутри данного треугольника еще один треугольник MNP.

Свойства средней линии треугольника

Каждая средняя линия треугольника, соединяющая середины его сторон, обладает следующими свойствами:

1. Средняя линия треугольника параллельна его третей стороне и равна её половине.

Таким образом, мы видим, что сторона АС параллельна MN, которая в два раза меньше, чем сторона АС.

2. Средние линии треугольника делят его на четыре равных треугольника.

Если мы посмотрим на треугольник АВС, то увидим, что средние линии MN, MP и NP разделили его на четыре равных треугольника, и в итоге образовались треугольники MBN, PMN, NCP и AMP.

3. Средняя линия треугольника отсекает от данного треугольника подобный, площадь которого равняется одной четвертой исходного треугольника.

Так, например, в треугольнике АВС средняя линия MP отсекает от данного треугольника, образуя треугольник AMP, площадь которого равна одной четвертой треугольника АВС.

Треугольники

В предыдущих классах вы уже изучали такую геометрическую фигуру, как треугольник и знаете, какие бывают виды треугольников, чем они отличаются и какими свойствами обладают.

Треугольник относится к простейшим геометрическим фигурам, которые имеют три стороны, три угла и их площадь ограничена тремя точками и тремя отрезками, которые попарно соединяют эти точки.

Вот мы вспомнили определение треугольника, а сейчас давайте повторим все что вы знаете об этой фигуре, ответив на вопросы:

4. Какие виды треугольников вы уже изучили? Перечислите их.
5. Дайте определения каждому из видов треугольников.
6. Чему равна площадь треугольника?
7. Чему равна сумма углов этой геометрической фигуры?
8. Какие типы треугольников вам известны? Назовите их.
9. Какие вы знаете треугольники по типу равных сторон?
10. Дайте определение гипотенузы.
11. Сколько острых углов может быть в треугольнике?

Основные линии треугольника

К основным линиям треугольника относятся: медиана, биссектриса, высота и срединный перпендикуляр.

Медианой треугольника называют отрезок, который соединяет вершину треугольника с серединой противолежащей стороны данного треугольника.

Свойства медиан треугольника

1. Она делит треугольник на два других, равных по площади;
2. Все медианы данной фигуры пересекаются в одной точке. Эта точка делит их в отношении два к одному, начиная отсчет от вершины, и называется центром тяжести треугольника;
3. Медианы разделяют данный треугольник на шесть равновеликих.

Луч, который выходит из вершины и, проходя между сторонами угла, делит его пополам, называется биссектрисой этого угла.

А если отрезок биссектрисы угла соединяет его вершину с точкой, которая лежит на противолежащей стороне треугольника, то он называется биссектрисой треугольника.

Свойства биссектрис треугольника

1. Биссектрисой угла является геометрическое место точек, которые равноудалены от сторон данного угла.
2. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, которые являются пропорциональными прилежащим сторонам треугольника.
3. Центром окружности, вписанной в треугольник, является точка пересечения биссектрис данной фигуры.

Перпендикуляр, который проведен с вершины к фигуры к прямой, которая является противоположной стороной треугольника, называется его высотой.

Свойства высот треугольника

1. Высота, проведенная из вершины прямого угла, делит треугольник на два подобных.
2. Если треугольник является остроугольным, то его две высоты отсекают от данного треугольника ему подобные.

Срединным перпендикуляром треугольника называют прямую, которая проходит через середину отрезка, который расположен перпендикулярно к этому отрезку.

Свойства серединных перпендикуляров треугольника

1. Любая точка серединного перпендикуляра к отрезку, равноудалена от его концов. В этом случае будет верно и обратное утверждение.
2. Точка пересечения серединных перпендикуляров, которые проведены к сторонам треугольника, есть центром окружности, которая описана около этого треугольника.

Интересные факты из области математики

Будет ли для вас новостью узнать, что за расшифровку секретной переписки правительства Испании, Франсуа Виета хотели отправить на костер, так как считали, что узнать шифр мог только дьявол, а человеку это не по силам.

Известно ли вам, что первым человеком, который предложил нумеровать кресла, ряды и места, был Рене Декарт? Аристократы-театралы даже просили короля Франции дать за это Декарту награду, но, увы, король отказал, так как считал, что давать награды философу – это ниже его достоинства.

Из-за учащихся, которые могли запомнить теорему Пифагора, но не смогли ее понять, эту теорему называли «ослиным мостом». Это значило, что ученик «осел», который не смог преодолеть мост. В данном случае мостом считали теорему Пифагора.

Писатели сказочники посвящали свои произведения не только мифическим героям, людям и зверюшкам, но и математическим символам. Так, например, автор знаменитой «Красной Шапочки», написал сказку о любви циркуля и линейки.

Домашнее задание

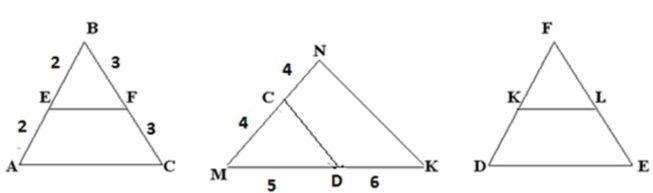
1. Перед вами изображены три треугольника, дайте ответ, являются ли проведенные в треугольниках линии средними?
2. Сколько средних линий можно построить в одном треугольнике?

3. Дан треугольник АВС. Найдите стороны треугольника АВС, если его средние линии имеют такие размеры: OF = 5,5 см, FN = 8 см, ON = 7 см.

Источник

Как найти среднюю линию треугольника

Здравствуйте!
Как найти среднюю линию треугольника? Какие есть задачи на среднюю линию?
Спасибо!

Прежде, чем разобраться, как найти среднюю линию треугольника, вспомним, что такое средняя линия треугольника.
Это понятие полностью описывается своим названием. Линия называется средней, значит, она соединяет середины чего-то. И это середины двух сторон треугольника. У треугольника три стороны, которые попарно можно соединить тремя линиями. Поэтому у треугольника можно провести три средние линии.
Средняя линия треугольника обладает очень интересным свойством — она равна половине той стороны, к которой к тому же проходит параллельно.
Рассмотрим пример нахождения средней линии треугольника

Пример.
У треугольника стороны соответственно равны 29 см, 46 см и 38 см. найдем стороны треугольника, у которого вершины лежат на серединах сторон заданного треугольника.

Решение.
Рассмотрим треугольник DHL.
По условию DH = 29 см, HL = 46 см, DL = 38 см.
Обозначим на сторонах треугольника DHL их середины точками R, T и P соответственно и соединим их отрезками. Получим треугольник RTP, стороны которого необходимо найти.
Поскольку точки R, T и P — середины сторон треугольника DHL, то согласно определения отрезки RT, TP и RP являются средними линиями данного треугольника.
Согласно свойству средней линии получим:
(см);
(см);
(см).

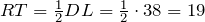
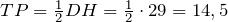
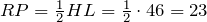
Ответ. 19 см, 14,5 см и 23 см.

Источник

Средняя линия прямоугольного треугольника – формула

Средняя линия прямоугольного треугольника – это прекрасная возможность для составителей задач. Большая часть обучающихся знают, что такое средняя линия и умело используют ее свойства в решении. Но как только этот отрезок появляется на чертеже прямоугольного треугольника, то сразу впадают в ступор из-за некоторой необычности рисунка, поэтому разберемся в теме подробнее.

Что такое прямоугольный треугольник?

В общем случае, треугольник это фигура, состоящая из стрех сторон и трех углов. В зависимости от величин углов, входящих в состав треугольника выделяют:

Прямоугольные треугольники интересны специальными формулами, которые значительно упрощают решение. Но средняя линия прямоугольного треугольника ни чем не отличается от средней линии произвольного. Почему задачи с этим отрезком вызывают затруднения?

Только из-за необычности чертежа

Рис. 1. Прямоугольный треугольник.

Средняя линия

Что такое средняя линия? Это один из характеризующих отрезков любого треугольника. Средняя линия соединяет середины смежных сторон многоугольника.

Средняя линия есть не только у треугольника. Она существует у каждой выпуклой фигуры. При этом свойства средних линий треугольников не всегда совпадают с свойствами средних линий трапеций. Поэтому будьте аккуратны, у каждой фигуры есть свои свойства и признаки.

Рис. 2. Средняя линия трапеции.

Свойства средней линии

Свойств у средней линии не так много, но все они более чем интересны.

Если формулировка «Средняя линия параллельна основанию» не совсем правильная, то почему же ее применяют в учебнике? Дело в том, что любое свойство должно быть коротким и ясным для простоты запоминания. Поэтому и сокращают некоторые высказывания. А основанием произвольного треугольника можно считать любую сторону, а значит неправильной формулировку назвать нельзя.

Задача

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. В получившемся прямоугольнике MNPA известно, что синус угла между диагоналями равен 0,5. А средние линии MN и NP равны 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Рис. 3. Рисунок к задаче.

В прямоугольнике две диагонали между собой равны. Одна из диагоналей MP это гипотенуза прямоугольного треугольника MNP. Катеты треугольника известны, значит можно найти гипотенузу через теорему Пифагора.

Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними.

В большом треугольнике 4 малых, а в прямоугольнике 2 малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольнику, нужно умножить площадь прямоугольника на 2.

$S=12,5*2=25$ – ответ получен.

Что мы узнали?

Мы узнали, что такое средняя линия прямоугольного треугольника. Поговорили о свойствах средней линии и решили небольшую задачу для закрепления материала.

Источник

Средняя линия треугольника и ее свойства

1) Средняя линия параллельна третьей стороне треугольника и равна ее половине;

2) Средняя лини отсекает треугольник, подобный исходному, с коэффициентом подобия .

Сумма внутренних углов треугольника

Сумма внутренних углов треугольника равна 180º.

Прямоугольный треугольник

2) Теорема, обратная теореме Пифагора: Если в некотором треугольнике квадрат длины одной стороны равен сумме квадратов длин двух других сторон, то этот треугольник – прямоугольный.

3) В прямоугольном треугольнике выполняются следующие соотношения между его сторонами и углами (рис.6.5): , , , . Эти соотношения также принято называть «решениями прямоугольного треугольника».

4) Проекции c₁,c₂ соответственно катетов a, bна гипотенузу обладают следующими свойствами (рис. 6.6): , , ,

5) Медиана, проведенная из вершины прямого угла на гипотенузу, равна половине гипотенузы: . Верно также и обратное утверждение: если в некотором треугольнике длина одной из медиан равна половине той стороны, которую она делит пополам, то этот треугольник является прямоугольным (рис. 6.7).

Четырехугольники

Параллелограмм и его свойства

1) Противоположные стороны параллелограмма равны;

2) Противоположные углы параллелограмма равны;

3) Сумма углов, прилежащих к любой из сторон параллелограмма, равна 180º;

4) Диагонали параллелограмма делятся точкой их пересечения пополам;

5) Точка пересечения диагоналей параллелограмма является его центром симметрии;

6) Сумма квадратов длин диагоналей параллелограмма равна удвоенной сумме квадратов длин его сторон: d 2 ₁ + d 2 ₂ = 2(a 2 + b 2 ) (рис. 6.8).

Ромб и его свойства

1) Все стороны ромба равны;

2) Диагонали ромба взаимно перпендикулярны и являются биссектрисами его внутренних углов;

3) Прямые, содержащие диагонали ромба, являются его осями симметрии (рис. 6.9).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1.Дан правильный треугольник ABC. На продолжении стороны АС за точку С взята точка D, а на продолжении стороны ВС за точку С – точка Е так, что BD=DE. Докажите, что AD=CE.

Решение.

На отрезке CE отметим точку F такую, что FE=BC (см. рис.). Треугольники BDC и EDF равны по первому признаку равенства треугольников. Отсюда CD=DF. Далее, поскольку DFC= DCF= ACB=60°, треугольник CDF – равносторонний. Поэтому CF=CD и AD=AC+CD=BC+CF=FE+CF=CE, что и требовалось доказать.

2.Медианой пятиугольника ABCDE назовем отрезок, соединяющий вершину с серединой противолежащей стороны (А – с серединой CD, В – с серединой DE и т.д.). Докажите, что если четыре медианы выпуклого пятиугольника перпендикулярны сторонам, к которым они проведены, то таким же свойством обладает и пятая медиана.

Решение.Условие перпендикулярности медианы пятиугольника и его противолежащей стороны равносильно тому, что диагонали, проведенные из соответствующей вершины, равны. Поэтому, если медианы, проведенные из вершин A, B, C и D, перпендикулярны противолежащим сторонам, то выполняются равенства AC=AD, BE=BD, CA=CE, DB=DA. Отсюда следует, что CE=BE, т.е. медиана, проведенная из вершины E, также перпендикулярна противолежащей стороне.

Решение.Треугольники ABG и DBC равны (AB =DB, BG = BC, углы ABG и DBC равны). Значит, AG=CD, и четырехугольник ADGC – трапеция с равными диагоналями. Но такая трапеция является равнобедренной: AD=CG. Но если диагонали квадратов равны, то равны и их стороны: AB=BC.

4.Разделите данный отрезок АВ на четыре равные части с помощью циркуля и линейки, проведя всего 6 линий (прямых и окружностей).

Решение. Проведем две окружности радиуса АВ с центрами в точках А и В. Через точки пересечения этих окружностей проведем прямую, которая пересекает отрезок АВ в точке С. Проведем теперь окружность с центром в точке С радиусом АВ. Эта окружность пересечет каждую из проведенных окружностей в двух точках. И, наконец, проведем через эти две пары точек две прямые — см. рис. 11. Таким образом, мы провели 6 линий: три окружности и три прямые. Докажем, что три проведенные прямые делят отрезок А В па четыре равные части. Как известно, геометрическим местом точек, равноудаленных от концов отрезка, является серединный перпендикуляр этого отрезка — прямая, проведенная через середину данного отрезка перпендикулярно к нему. Две точки пересечения двух первых построенных окружностей находятся на одинаковом расстоянии АВ от точек А и В, поэтому прямая, проходящая через них, является серединным перпендикуляром отрезка АВ и делит его на две равные части в точке С.

Аналогично точки пересечения третьей окружности с одной из первых двух находятся на одинаковом расстоянии А В и от середины С отрезка АВ, от конца. Аналогично точки пересечения третьей окружности с одной из первых двух находятся на одинаковом расстоянии А В и от середины С отрезка АВ, и от конца этого отрезка, поэтому прямая, проходящая через эти

точки пересечения, делит половину отрезка АВ еще раз пополам.

5.Дан равнобедренный треугольник с углом 20° при вершине. Докажите, что его боковая сторона больше удвоенного основания.

Решение. Пусть ABC — данный треугольник, AB = AC, CAB = 20°. Отложим на стороне АВ отрезок BE, равный отрезку ВС (см. рис.). Тогда CEB = ECB = 50°, ACE = 30°, а так как в треугольнике против большего угла лежит большая сторона, то АЕ > СЕ и СЕ > СВ. Следовательно, АВ = АЕ + ВЕ> 2СВ.

6.Отрезки АС и ВD пересекаются в точке О. Известно, что равны периметры треугольников АВС и АВD, а также равны периметры треугольников АСD и ВСD. Найдите длину АО, если ВО=10 см.

Решение: Из равенства периметров треугольников получаем, что

АС + ВС = АD + ВD и АD+АС=ВD+ВС.

Вычитая из первого равенства второе, получим, что ВС=АD, а тогда АС=ВD. Из равенства треугольников АВD и АВС получаем равенство углов АВD и ВАС. А тогда треугольник АОВ равнобедренный и АО=ВО=10 см.

7.На гипотенузе BCпрямоугольного треугольника ABC выбрана точка Kтак, что AB = AK. Отрезок AK пересекает биссектрису CL в ее середине. Найдите острые углы треугольника ABC.

Ответ.

Решение. Обозначим середину биссектрисы CLчерез P, а угол ABCчерезb; тогда . В прямоугольном треугольнике ACLотрезок AP является медианой, поэтому AP = CP = LP. Теперь из равнобедренных треугольников APLи ABKполучаем . С другой стороны, как внешний угол в . Значит, , откуда , или . Тогда .

8.Три стороны трапеции равны по 10 дм, а острый угол равен 60°. Найти длину отрезка, соединяющего центр вписанной окружности с вершиной меньшего основания.

Решение. Пусть в трапеции KNML (NM || KL) KN = NM = ML = 10 дм, . Заметим, что и, так как , то . Значит . Так как ON = OM– как радиусы, то – равнобедренный, т.е. , но тогда . Выходит, что – равносторонний и MO = MN = 10 дм.

9.В параллелограмме АСВМ АС = 16 м, СВ = 24 м, СЕ и CF — соответственно высоты, проведенные к сторонам AM и ВМ, ÐECF = 60°. Найти длину высоты СЕ.

Решение.

По условию в параллелограмме ACBMCE^AMи ÐECF =60º, тогда ÐACE =30º. Значит, AE=1/2 · AC = 8 (м).

Решение. Так как точка O – точка пересечения медиан, то , , .

Достроим Δ AOCдо параллелограмма AOCE. Известно, что в параллелограмме AC 2 +OE 2 = 2(AO 2 + OC 2 ), или , откуда находим .

11.Найти длину средней линии прямоугольной трапеции, вписанной в окружность, если расстояния от центра окружности до концов большей боковой стороны равны соответственно 6 и 8 дм.

Решение. Поскольку O – центр вписанной окружности, то MOи NO – биссектрисы углов KNMи LMN, тогда , т.е. ÐMON=90º, тогда, из ΔMON (дм).

Заметим, что высота OAΔOMNявляется одновременно и радиусом вписанной окружности, тогда , откуда OA = 4,8 (дм 2 ). Значит, KL=2·OA=9,6 (дм). По свойству описанного четырехугольника KN + LM=KL + MN=10+9,6=19,6 (дм), тогда (дм).

12.Сумма числа сторон выпуклого многоугольника и числа его диагоналей равна 21. Определить число сторон многоугольника.

Решение. Пусть x число сторон(а значит и вершин) многоугольника. Заметим, что из каждой вершины многоугольника можно провести (x— 3) диагонали, а из всех его вершин – в x раз больше. Тогда общее число диагоналей многоугольника будет равно . Согласно условию, имеем уравнение: . Решая его, найдем, что x=7.

13.Внутри угла в 60° дана точка М, удаленная от сторон угла на 2 и 11 единиц. Найти расстояние точки М от вершины угла.

Решение. Пусть AM = 2, MB = 11. Продолжим AM до пересечения в точке D со стороной DO данного угла. Δ OAD и ΔMBD – прямоугольные с общим углом ADOв 30º.

14.Диагональ параллелограмма делит его угол в отношении 1:3. Найти углы параллелограмма, если длины сторон относятся как 1:2.

Решение.

Построим луч BE так, чтобы ÐEBD = a. ТогдаÐABE = 2a = ÐAEB; BE = AE =ED = x.

Значит, ÐABD = 90º, ÐA = 60º, ÐABC = 120º.

Источник

Средняя линия прямоугольного треугольника

Средняя оценка: 4.2

Всего получено оценок: 75.

Средняя оценка: 4.2

Всего получено оценок: 75.

Прямоугольный треугольник стоит особняком от остальных треугольников. Прямой угол делает возможным применение других признаков равенства и подобия. Для углов в прямоугольном треугольнике можно без дополнительных построений использовать геометрические тождества, а любую из сторон можно найти по теореме Пифагора. Но среднюю линию прямоугольного треугольника определить трудно просто потому, что она редко упоминается в задачах, из-за чего мало кто может себе её визуально представить.

Что такое средняя линия прямоугольного треугольника?

Средняя линия – это отрезок, соединяющий середины сторон в треугольнике. В любом треугольнике можно провести три средних линии. При этом этот отрезок будет равен половине основания – это и считается формулой средней линии прямоугольного треугольника. Основанием считается сторона, с которой средняя линия не пересекается.

Причем, если средняя линия проводится в прямоугольном треугольнике, то каждый из четырех получившихся треугольников будет являться прямоугольным.

Все эти свойства можно использовать в ряде задач, что позволяет создавать интересные уникальные решения и доказательства.

Задача 1

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. При этом MN=NP=2.

Рис. 1. Рисунок к задаче

Задача 2

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. В получившемся прямоугольнике MNPA известно, что диагональ MP равна 5, а синус угла между диагоналями равен 0,48. Найти площадь большого прямоугольного треугольника.

Рис. 2. Рисунок к задаче

В прямоугольнике две диагонали между собой равны. Одна из диагоналей MP = 5, значит и вторая диагональ AN равна тоже 5.

Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними.

В большом треугольнике 4 малых, а в прямоугольнике 2 малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольника, нужно умножить площадь прямоугольника на 2.

$S=12*2=24$ – ответ получен.

Задача 3

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. Найти площадь прямоугольника MNPA, если известно, что площадь АВС равна 36.

Рис. 3. Рисунок к задаче

Аналогично с предыдущей задачей, можно вывести утверждение, что площадь треугольника равна двум площадям малого прямоугольника. Подставим в выражение цифры и выразим неизвестное. Площадь треугольника обозначим за S, прямоугольника s.

Что мы узнали?

Мы узнали, что такое средняя линия, поговорили о свойствах средней линии и выделили особенности средней линии в прямоугольном треугольнике. Также мы закрепили пройденный материал, подробно изучив алгоритм решения задач на заданную тему.

Источник

Средняя линия треугольника

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

ФГНОУ ВПО «Мордовский государственный педагогический институт имени М.Е.Евсевьева»

по геометрии для учащихся 8 класса

Выполнила: студентка группы МДМ-210

Тема урока: средняя линия треугольника

Тип урока: изучение нового материала

— образовательная: ввести понятие средней линии треугольника и изучить теорему о средней линии треугольника.

— развивающая: развивать логическое и пространственное воображение, интуицию учащихся; формировать умения чётко и ясно излагать свои мысли

-воспитательная: воспитывать интерес к геометрии, культуру устной речи, правильное и аккуратное оформление геометрических задач.

Методы обучения: индуктивно-репродуктивный,

Требования к знаниям и умениям учащихся:

Учащиеся должны знать: какой отрезок называют средней линией треугольника, сколько можно их построить

Учащиеся должны уметь: строить среднюю линию треугольника, доказывать теорему о средней линии треугольника, решать задачи на нахождение средней линии треугольника.

Оборудование урока: линейка

1.Геометрия. Учебник /Л.С.Атанасян «Просвещение»,2011

2.Дидактические материалы по геометрии, 8 класс /Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г., «Просвещение», 2010

1. Орг. момент (2 мин)

2. Актуализация знаний (7 мин)

3. Изучение нового материала (20 мин)

4. Первичное закрепление изученного (14 мин)

5. Подведение итогов урока и домашнее задание (2 мин)

Приветствие, проверка готовности учеников к уроку

Учитель: мы приступаем к изучению нового раздела, который называется «применение подобия к доказательству теорем и решению задач». И тема урока, первый пункт параграфа, средняя линия треугольника. Цель урока, вести определение средней линии треугольника, доказать свойства средней линии и рассмотреть задачи на применение свойств. Прежде чем перейти к изучению темы, вспомним признаки подобия треугольников. Итак, сформулируете первый признак подобия треугольников

Ученик: если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны

Учитель: сформулируете второй признак подобия треугольников

Ученик: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны

Учитель: сформулируете третий признак подобия треугольников

Ученик: если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны

Учитель: устно рассмотрим задачу представленную на доске

Запись на доске

Действия учителя и ученика

Доказать:

(ученики проговаривают решения устно)

Ученик: так как АМ равен 9,а МВ равен 3, то вся сторона АВ равна 12.

Так как КВ равна 5,а СК 15 то сторона СВ равна 20.

Так как длины сторон обоих треугольников известны то здесь можно применить правило отношение сторон (отношение сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой) то есть отношение АВ к ВМ равно 12 к 3,и равно 4.Аотношение ВС к ВК равно 20 к 5 и равно тоже 4.(учитель делает записи на доске под диктовку ученика) Коэффициенты подобия у нас получились одинаковые следовательно АВ относиться к ВМ как ВС к ВК.

Учитель: на основании подобий треугольников докажите что сторона МК параллельна стороне АС

3.ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Учитель: открываем тетради, записываем число и тему урока: СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА

Запись на доске (в тетради)

СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА

Учитель: итак, давайте построим треугольник и среднюю линию

Запись на доске (в тетрадях)

Действия учителя и ученика

Учитель: строим треугольник АВС, находим середину стороны АВ и середину стороны ВС, получили точку М и точку Р, получившиеся точки соединяем и получаем отрезок МР который будет, является средней линией треугольника АВС. Мы с вами построили среднюю линию на сторонах АВ и ВС

Учитель: можем ли мы еще с вами построить в этом же треугольники среднюю линию?

Ученик: да можем.

Учитель: и действительно можем. Находим середину стороны АС и получаем точку О, соединяем точку О с точкой Р и получаем еще одну среднюю линию треугольника РО

Учитель: наконец нам осталось соединить точку М с точкой О и получаем третью среднюю линию МО.

Учитель: что же называется средней линией треугольника? Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Учитель: сколько средний линей можно построить в треугольники?

Ученик: в треугольники можно построить 3 средние линии

Учитель: итак средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Учитель: так же, существует и теорема о средней линии треугольника. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Докажем теорему. Строим треугольник АВС и строим среднюю линию МН сторон АВ и ВС

(учитель строит на доске чертеж, а ученики в тетрадях)

Запись на доске (в тетрадях)

Действие учителя и ученика

Дано:

Доказать: 1)МН АС

2)МН= АС

3)Т.к. В- общий

то (по второму признаку подобия треугольников)

4)Т.к. а

то

5)Т.к. то

6) Т.к. то 1 = 2-как соответственные ч.тр.доказать

Учитель: пишем, дано треугольник АВС, МН – средняя линия. Доказать что МН параллельна третий стороне то есть АС и что МН равно АС.

Учитель: пишем. Первый шаг. Так как МН по условию задачи средняя линия то ВМ равно АВ и ВН равно ВС.

Второй шаг. Так как ВМ равно АВ и ВН равно ВС то составляем отношение (пропорцию) ВМ относиться к АВ как ВН к ВС и равно все это

Третий шаг. Так как ВМ относиться к ВА как ВН к ВС и равно все это угол В общий то треугольник АВС подобен треугольнику МВН по второму признаку подобия треугольников.

Четвертый шаг. Так как треугольники подобны а коэффициент подобия из отношений ВМ относиться к ВА как ВН к ВС мы выяснили равен то и отношения МН к АС равен .

умножить на АС

Все мы с вами доказали теорему, что и требовалось доказать

Учитель: подведем итоги, значит средняя линия это отрезок, соединяющий две его стороны и параллелен третей стороне, а также равен одна вторая основания треугольника.

(ученики задают вопросы, учитель отвечает)

4.ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО

(ученик рисует рисунок)

Запись на доске (и в тетрадях)

Деятельность учителя и ученика

Учитель: нам даны стороны большого треугольника АВС и требуется найти сторона маленького треугольника А1В1С1. Как найти стороны маленького треугольника?

Ученик: А1,В1,С1(по условию) середины сторон то А1С1 равна одна вторая АС, В1С1 равна одна вторая ВС, а А1В1 равна одна вторая АВ. Сторона АВ, ВС, АС нам известны значит мы можем найти А1С1,В1С1,А1В1.

Ученик: решение. Первый шаг. Так как А1,В1,С1 середины сторон то А1С1 равна одна вторая АС, В1С1равна одна вторая ВС, а А1В1 равна одна вторая АВ. Так как сторона АВ,ВС,АС нам известны значит мы можем найти А1С1,В1С1, А1В1. Находим периметр, он равен 10 см.

Учитель: следующая задача 565.Расстояние от точки пересечения диагоналей прямоугольника до прямой, содержащей его большую сторону, равно 2,5 см. Найти меньшую сторону прямоугольника. Итак, строим рисунок и находим меньшую сторону прямоугольника. Кто пойдет к доске?

(ученик рисует рисунок)

Запись на доске (и в тетрадях)

Деятельность учителя и ученика

Учитель: давайте вспомним, что называется прямоугольником?

Ученик: прямоугольником называется четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны

Учитель: перечислите основные свойства прямоугольника

Ученик: диагональ прямоугольника делит его на два равных треугольника

Ученик: диагонали прямоугольника в точке их пересечения делятся пополам

Учитель: зная основные свойства прямоугольника и его признаки. Как будем решать задачу, если нам дана только высота ОН

Учитель: хорошо оформим решения задачи

5.ПОДВЕДЕНИЕ ИТОГОВ УРОКА И ДОМАШНЕЕ ЗАДАНИЕ

Учитель: сегодня на уроке мы с вами изучи новую тему, средняя линия треугольника. Мы с вами доказали, что средняя линия параллельна одной из его сторон и равна половине этой стороны. Рассмотрели задачи, применяя определение и свойства средней линии. Домашнее задания номер 566 и 567

Источник

Средняя линия прямоугольного треугольника – формула

Средняя линия прямоугольного треугольника – это прекрасная возможность для составителей задач. Большая часть обучающихся знают, что такое средняя линия и умело используют ее свойства в решении. Но как только этот отрезок появляется на чертеже прямоугольного треугольника, то сразу впадают в ступор из-за некоторой необычности рисунка, поэтому разберемся в теме подробнее.

Что такое прямоугольный треугольник?

В общем случае, треугольник это фигура, состоящая из стрех сторон и трех углов. В зависимости от величин углов, входящих в состав треугольника выделяют:

Прямоугольные треугольники интересны специальными формулами, которые значительно упрощают решение. Но средняя линия прямоугольного треугольника ни чем не отличается от средней линии произвольного. Почему задачи с этим отрезком вызывают затруднения?

Только из-за необычности чертежа

Рис. 1. Прямоугольный треугольник.

Средняя линия

Что такое средняя линия? Это один из характеризующих отрезков любого треугольника. Средняя линия соединяет середины смежных сторон многоугольника.

Средняя линия есть не только у треугольника. Она существует у каждой выпуклой фигуры. При этом свойства средних линий треугольников не всегда совпадают с свойствами средних линий трапеций. Поэтому будьте аккуратны, у каждой фигуры есть свои свойства и признаки.

Рис. 2. Средняя линия трапеции.

Свойства средней линии

Свойств у средней линии не так много, но все они более чем интересны.

Если формулировка «Средняя линия параллельна основанию» не совсем правильная, то почему же ее применяют в учебнике? Дело в том, что любое свойство должно быть коротким и ясным для простоты запоминания. Поэтому и сокращают некоторые высказывания. А основанием произвольного треугольника можно считать любую сторону, а значит неправильной формулировку назвать нельзя.

Задача

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. В получившемся прямоугольнике MNPA известно, что синус угла между диагоналями равен 0,5. А средние линии MN и NP равны 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Рис. 3. Рисунок к задаче.

В прямоугольнике две диагонали между собой равны. Одна из диагоналей MP это гипотенуза прямоугольного треугольника MNP. Катеты треугольника известны, значит можно найти гипотенузу через теорему Пифагора.

Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними.

В большом треугольнике 4 малых, а в прямоугольнике 2 малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольнику, нужно умножить площадь прямоугольника на 2.

$S=12,5*2=25$ – ответ получен.

Что мы узнали?

Мы узнали, что такое средняя линия прямоугольного треугольника. Поговорили о свойствах средней линии и решили небольшую задачу для закрепления материала.

Источник

Свойства средней линии треугольника, с примерами

Рассмотрим треугольники (ABC) и (A_1B_1C_1) со сторонами (a,b,c) и (a_1, b_1, c_1) соответственно (см. рисунок выше).

Пусть треугольники (ABC) и (A_1B_1C_1) подобны, причём (dfrac = dfrac = dfrac = k). Обозначим буквами (S) и (S_1) площади этих треугольников соответственно.

Пусть (ABC) и (A_1B_1C_1) – треугольники такие, что (angle A =
angle A_1), (angle B = angle B_1). Тогда по теореме о сумме углов треугольника (angle C = 180^circ — angle A — angle B = 180^circ
— angle A_1 — angle B_1 = angle C_1), то есть углы треугольника (ABC) соответственно равны углам треугольника (A_1B_1C_1).

Рассмотрим два треугольника (ABC) и (A’B’C’), таких что (dfrac=dfrac), (angle BAC = angle A’). Докажем, что треугольники (ABC) и (A’B’C’) – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что (angle B = angle B’).

Рассмотрим треугольник (ABC»), у которого (angle 1 = angle A’), (angle 2 = angle B’). Треугольники (ABC») и (A’B’C’) подобны по первому признаку подобия треугольников, тогда (dfrac =
dfrac).

С другой стороны, по условию (dfrac = dfrac). Из последних двух равенств следует, что (AC = AC»).

Пусть стороны треугольников (ABC) и (A’B’C’) пропорциональны: (dfrac = dfrac = dfrac). Докажем, что треугольники (ABC) и (A’B’C’) подобны.

Через точку (B_1) проведем (lparallel OB). Пусть (lcap a=K). Тогда (ABB_1K) — параллелограмм, следовательно, (B_1K=AB=OA) и (angle
A_1KB_1=angle ABB_1=angle OAA_1); (angle AA_1O=angle KA_1B_1) как вертикальные. Значит, по второму признаку ( riangle
OAA_1= riangle B_1KA_1 Rightarrow OA_1=A_1B_1). Лемма доказана.

Перейдем к доказательству теоремы. Пусть (OA=AB=BC), (aparallel
bparallel c) и нужно доказать, что (OA_1=A_1B_1=B_1C_1).

Таким образом, по данной лемме (OA_1=A_1B_1). Докажем, что (A_1B_1=B_1C_1). Проведем через точку (B_1) прямую (dparallel OC), причем пусть (dcap a=D_1, dcap c=D_2).

Тогда (ABB_1D_1, BCD_2B_1) — параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2).

Таким образом, (angle A_1B_1D_1=angle C_1B_1D_2) как вертикальные, (angle
A_1D_1B_1=angle C_1D_2B_1) как накрест лежащие, и, значит, по второму признаку ( riangle A_1B_1D_1= riangle C_1B_1D_2
Rightarrow A_1B_1=B_1C_1).

Теорема Фалеса

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

Доказательство

Пусть параллельные прямые (pparallel qparallel rparallel s) разбили одну из прямых на отрезки (a, b, c, d). Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd) соответственно, где (k) – некоторое число, тот самый коэффициент пропорциональности отрезков.

Проведем через точку (A_1) прямую (pparallel OD) ((ABB_2A_1) — параллелограмм, следовательно, (AB=A_1B_2)). Тогда ( riangle OAA_1
sim riangle A_1B_1B_2) по двум углам. Следовательно, (dfrac=dfrac Rightarrow A_1B_1=kb).

Аналогично проведем через (B_1) прямую (qparallel OD Rightarrow
riangle OBB_1sim riangle B_1C_1C_2 Rightarrow B_1C_1=kc) и т.д.

Через точку (N) проведем прямую параллельно (AB). Пусть эта прямая пересекла сторону (AC) в точке (K). Тогда (AMNK) — параллелограмм ((AMparallel NK, MNparallel AK) по предыдущему пункту). Значит, (MN=AK).

Т.к. (NKparallel AB) и (N) – середина (BC), то по теореме Фалеса (K) – середина (AC). Следовательно, (MN=AK=KC=dfrac12 AC).

Следствие

Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом (frac12).

Матвокс ⋆ признак средней линии треугольника ⋆ энциклопедия математики

Skip to content

Если отрезок параллелен одной из сторон треугольника и соединяет середину одной стороны треугольника с точкой, лежащей на другой стороне треугольника, то это средняя линия треугольника.

Признак средней линии треугольника

Рассмотрим треугольник АВС.

Пусть точка К делит сторону АВ пополам:

И пусть через точку К проходит отрезок КЕ, параллельный стороне треугольника АС:

Докажем, что КЕ – средняя линия треугольника, т.е. докажем, что:

Доказательство признака средней линии треугольника. Шаг 1

Так как KE||AC и АК=КВ, то по теореме Фалеса если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Признак средней линии треугольника доказан.

Доказательство признака средней линии треугольника. Шаг 2

Privacy & Cookies Policy

Замечательные линии треугольника

Медиана треугольника – это отрезок, который связывает вершину треугольника с серединой одной из сторон данного треугольника.

Медиана делит треугольник на два треугольника, площади которых одинаковы.

Медианы треугольника пересекаются только в одной точке, которая разделяет каждую из них в отношении 2 : 1, отсчитывая от вершины. Такая точка именуется центром тяжести треугольника.

Весь треугольник разбивается своими медианами на шесть равных по значению треугольников.

Биссектриса угла – это исходящий из вершины угла луч, пролегающий между образующими сторонами и разделяющий его пополам.

Свойства биссектрисы треугольника

Высотой треугольника называется линия, проведенная из вершины треугольника к одной из сторон расположенной перпендикулярно.

Свойства высоты треугольника

Перпендикулярная линия высоты прямоугольного треугольника разделяет его на два подобных ему треугольника.

Две линии высоты остроугольного треугольника, отделяют от него подобные треугольники.

Перпендикулярная прямая, которая проходит через середину отрезка, называется – срединный перпендикуляр к отрезку.

Все точки серединного перпендикуляра к отрезку равноудалены от окончаний этого отрезка. Верно так же и обратное утверждение, что каждая точка, находящаяся на равных расстояниях от концов отрезка, расположена на серединном перпендикуляре к нему.

В точке пересечения серединных перпендикуляров, проведенных в направлении к одной из сторон треугольника, находится центр окружности, который описывает данный треугольник.

Отрезок, который соединяет две стороны треугольника в их серединах, называется – средняя линия треугольника.

Средняя линия, какого либо треугольника, всегда расположена параллельно одной из его сторон и является половиной этой стороны.

Длина средней линии треугольника

Средняя линия треугольника интересный характеризующий отрезок, так как обладает несколькими свойствами, позволяющими найти простое решение для казалось бы сложной задачи. Поэтому рассмотрим основные свойства средней линии и поговорим о том, как найти длину этого отрезка в треугольнике.

Треугольник это фигура, состоящая из трех сторон и трех углов. В зависимости от углов треугольники делятся на:

Рис. 1. Виды треугольников

Основными характеризующими отрезками треугольника являются:

Рис. 2. Высота, медиана и биссектриса в треугольнике

Для каждого из характеризующих отрезков существует своя точка пересечения. При соединении трех точек пересечения медиан, биссектрис и высот получается золотое сечение треугольника.

Однако существует и ряд дополнительных характеризующих отрезков:

Смежными сторонами треугольников называют стороны, которые имеют общую вершину. В геометрии существует понятие противоположных сторон, т.е. сторон, которые лежат друг напротив друга и не имеют общих вершин. Но это понятие для треугольников не применимо – любая пара сторон в треугольнике является смежной.

Свойств средней линии не так много, но все они имеют значение при решении задач. Дело в том, что задач на нахождение длины средней линии мало, а потому некоторые из них способны построить ученика в ступор при всей своей простоте.

Поэтому приведем и обсудим все свойства средней линии треугольника:

Рис. 3. Средние линии в треугольнике

Собственно формула длины средней линии вытекает из второго свойства:

$m=1over<2>*a$- где m – средняя линия, а- сторона противоположная средней линии.

Мы поговорили о второстепенных характеризующих отрезках, выделив среднюю линию. Привели свойства средних линий и поговорили о особенностях формулировки этих свойств. Рассказали, как выводится формула длины средней линии треугольника и как средняя линия разбивает треугольник. Все эти свойства используются при решении треугольников.

Средняя оценка: 4.3. Всего получено оценок: 185.

Как находить среднюю линию треугольника? Основные свойства, определения и способы :

Порой темы, которые объясняют в школе, могут быть не всегда понятны с первого раза. Особенно это касается такого предмета, как математика. Но все становится намного сложнее, когда эта наука начинает подразделяться на две части: алгебру и геометрию.

Каждый ученик может обладать способностью к одному из двух направлений, но особенно в начальных классах важно понять базу и алгебры, и геометрии. В геометрии одной из главных тем принято считать раздел о треугольниках.

Как находить среднюю линию треугольника? Давайте разбираться.

Основные понятия

Для начала чтобы разобраться, как находить среднюю линию треугольника, важно понимать, что же это.

Для проведения средней линии нет ограничений: треугольник может быть любым (равнобедренным, равносторонним, прямоугольным). И все свойства, которые относятся к средней линии, будут действовать.

Средняя линия треугольника является отрезком, соединяющим середины 2-х его сторон. Следовательно, любой треугольник может иметь 3 таких линии.

Свойства

Чтобы знать, как находить среднюю линию треугольника, обозначим ее свойства, которые необходимо запомнить, иначе без них будет невозможным решение задач с необходимостью обозначить длину средней линии, поскольку все полученные данные необходимо обосновать и аргументировать теоремами, аксиомами или свойствами.

Таким образом, чтобы ответить на вопрос: «Как найти среднюю линию треугольника АВС?», достаточно знать одну из сторон треугольника.

Приведем пример

Взгляните на рисунок. На нем представлен треугольник ABC со средней линией DE. Обратим внимание, что она параллельна основанию AC в треугольнике. Следовательно, каким бы ни было значение AC, средняя линия DE будет в два раза меньше. К примеру, AC=20, значит DE=10 и т. д.

Вот такими несложными способами можно понять, как находить среднюю линию треугольника. Запомните ее основные свойства и определение, и тогда у вас никогда не возникнет проблем с нахождением ее значения.

Президентский ФМЛ №239

Отрезок, соединяющий середины двух сторон треугольника, называется
средней линией треугольника.

Средняя линия треугольника параллельна стороне треугольника и равна
ее половине.

Третий признак средней линии неверен.

math-public/srednyaya_liniya_treugolnika.txt · Последние изменения: 2016/04/13 19:46 — labreslav

Средняя линия треугольника

Умение: проводить исследования несложных ситуаций (сравнение средней линии и основания треугольника), формулировать гипотезы исследования, понимать необходимость ее проверки, доказательства, совместно работать в группе.

Организационный этап. Мотивация.

— Здравствуйте ребята! Давайте начнем наш сегодняшний урок с доброжелательности. Повернемся к друг другу, улыбнемся. И с хорошим настроением отправимся в очередной путь по дороге к знаниям.

— А сопутствующими словами нам сегодня будут слова древнего мыслителя Конфуция:

Три пути ведут к знанию: Путь размышления – это путь самый благородный, Путь подражания – это путь самый легкий, И путь опыта – это путь самый горький.

— Сегодня мы продолжим знакомство с самой популярной в школьном курсе геометрической фигурой. Это самая простая замкнутая прямолинейная фигура, свойства которой человек узнал еще в глубокой древности, так как она имела широкое применение в практической жизни. Вы догадались, что это за фигура?

Актуализация опорных знаний.

— По каким признакам треугольники бывают подобными?- Как связаны соответствующие стороны и углы подобных треугольников?- Что такое коэффициент подобия, чему он равен?- Какие прямые называются параллельными?

«Открытие» нового знания. Создание проблемной ситуации.

— Ребята, сейчас поработаем в парах: на каждой парте лежит заготовка треугольника. Отметьте середины двух любых его сторон и проведите среднюю линию. Давайте посмотрим на расположение средней линии треугольника относительно третьей стороны.

— Какие результаты вы получили? Какой вывод можно сделать?

— Мы сейчас докажем теорему. Разобраться в логике доказательства вам помогут печатные заготовки, которые есть у каждого из вас, возьмите их.

— Итак, что нам дано? Что необходимо доказать?

Строят в тетрадях треугольники и поводят средние линии. Отвечают на вопросы.

Выслушиваются все варианты ответов учащихся. Важно выделить учеников, давших правильный ответ, поддержать того, кто не смог дать верный ответ.

Источник

Как найти среднюю линию треугольника

Диагональ трапеции делит её среднюю линию на отрезки, равные 4 см и 3 см. Найдите меньшее основание трапеции.

Пусть KN — средняя линия трапеции, где L — точка пересечения с диагональю.

Таким образом, длина меньшего основания равна 6 см.

Аналоги к заданию № 311411: 311475 341708 Все

Основания трапеции равны 3 и 13. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Пусть KN — средняя линия трапеции, где L — точка пересечения с диагональю.

Так как KN — средняя линия трапеции, то KL и LN средние линии треугольников ABC и СAD соответственно.

,

Аналоги к заданию № 311411: 311475 341708 Все

Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.

Так как KN — средняя линия трапеции, то KL и LN средние линии треугольников ABC и СAD соответственно.

,

На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Какие из следующих утверждений верны?

1) Площадь треугольника меньше произведения двух его сторон.

2) Средняя линия трапеции равна сумме её оснований.

3) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Проверим каждое из утверждений.

1) «Площадь треугольника меньше произведения двух его сторон» — верно, так как площадь треугольника равна где — угол между сторонами a и b треугольника. Синус угла всегда меньше единицы, поэтому площадь треугольника меньше произведения двух его сторон.

2) «Средняя линия трапеции равна сумме её оснований» — неверно, средняя линия трапеции равна полусумме его оснований.

3) «Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны» — верно, по признаку подобия треугольников.

Какие из следующих утверждений верны?

1) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.

2) Площадь трапеции равна произведению суммы оснований на высоту.

3) Площадь трапеции не превосходит произведения средней линии на высоту.

4) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.

Проверим каждое из утверждений.

1) «Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.» — неверно, площадь треугольника равна

2) «Площадь трапеции равна произведению суммы оснований на высоту.»— неверно, площадь трапеции равна произведению полусуммы оснований на высоту.

3) «Площадь трапеции не превосходит произведения средней линии на высоту.» — верно, площадь трапеции равна произведению средней линии на высоту.

4) «Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.» — верно, площадь треугольника равна

Какие из следующих утверждений верны?

1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.

2) В равнобедренном треугольнике имеется не менее двух равных углов.

3) Площадь трапеции не превосходит произведения средней линии на высоту.

4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.

Проверим каждое из утверждений.

1) «Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.» — верно, равные треугольники являются подобными.

2) «В равнобедренном треугольнике имеется не менее двух равных углов.»— верно, в равнобедренном треугольнике углы при основании равны.

3) «Площадь трапеции не превосходит произведения средней линии на высоту.» — верно, площадь трапеции равна произведению средней линии на высоту.

4) «Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.» — неверно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.

Какие из следующих утверждений верны?

1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

2) Средняя линия трапеции параллельна её основаниям.

3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны» — неверно: такого признака равенства треугольников нет.

2) «Средняя линия трапеции параллельна её основаниям» — верно, по теореме о средней линии трапеции она параллельна основаниям и равна их полусумме.

3) «Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов» — верно, для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.

Какие из следующих утверждений верны?

1. Площадь треугольника меньше произведения двух его сторон.

2. Средняя линия трапеции равна сумме её оснований.

3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Рассмотрим каждое из утверждений:

Какое из следующих утверждений верно?

1) Сумма острых углов прямоугольного треугольника равна 90 градусам.

2) Средняя линия трапеции равна сумме её оснований.

3) В любой четырёхугольник можно вписать окружность.

Проверим каждое из утверждений.

1) «Сумма острых углов прямоугольного треугольника равна 90 градусам.» — верно, сумма трех углов треугольника равна 180°, один из углов прямой, поэтому сумма острых углов прямоугольного треугольника равна 90°.

2) «Средняя линия трапеции равна сумме её оснований.» — неверно, средняя линия трапеции равна полусумме её оснований.

3) «В любой четырёхугольник можно вписать окружность.» — неверно, в четырёхугольник можно вписать окружность, только если равны суммы длин его противоположных сторон.

Какое из следующих утверждений верно?

1. Сумма острых углов прямоугольного треугольника равна 90 градусам.

2. Средняя линия трапеции равна сумме её оснований.

3. В любой четырёхугольник можно вписать окружность.

В ответ запишите номер выбранного утверждения.

Рассмотрим каждое из утверждений:

Какие из следующих утверждений верны?

1) Средняя линия трапеции равна сумме её оснований.

2) Диагонали ромба перпендикулярны.

3) Площадь треугольника меньше произведения двух его сторон.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

1) Средняя линия трапеции равна сумме её оснований. — неверно, Средняя линия трапеции равна полусумме её оснований.

2) Диагонали ромба перпендикулярны. — верно, по свойству ромба.

3) Площадь треугольника меньше произведения двух его сторон. — верно, так как площадь треугольника равна где — угол между сторонами a и b треугольника. Синус угла всегда меньше единицы, поэтому площадь треугольника меньше произведения двух его сторон.

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 16. Найдите её среднюю линию.

Пусть в равнобедренной трапеции ABCD с основаниями AD и BC диагонали AC и BD перпендикулярны и пересекаются в точке O.

Тогда в равнобедренных прямоугольных треугольниках AOD и BOC медианы равны половине основания. Значит, в этих треугольниках высота равна средней линии, и в трапеции ABCD высота равна средней линии.

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.

Тут показана не средняя линия.

Тимур, прочитайте решение.

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 19. Найдите её среднюю линию.

Пусть в равнобедренной трапеции ABCD с основаниями AD и BC диагонали AC и BD перпендикулярны и пересекаются в точке O.

Тогда в равнобедренных прямоугольных треугольниках AOD и BOC медианы равны половине основания. Значит, в этих треугольниках высота равна средней линии, и в трапеции ABCD высота равна средней линии.

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Введём обозначения, как показано на рисунке. MN — средняя линия, поэтому, откуда по теореме Фалеса Рассмотрим треугольник ABD MK — средняя линия, следовательно,

Основания трапеции равны 1 и 11. Найдите бóльший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Введём обозначения, как показано на рисунке. MN — средняя линия, AM = MB, откуда по теореме Фалеса AK = KC. Рассмотрим треугольник ACD. KN — средняя линия, следовательно,

Основания трапеции равны 10 и 11. Найдите бóльший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Введём обозначения, как показано на рисунке. MN — средняя линия, поэтому, откуда по теореме Фаллеса Рассмотрим треугольник MK — средняя линия, следовательно,

Какие из следующих утверждений верны?

1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

2) В тупоугольном треугольнике все углы тупые.

3) Средняя линия трапеции равна полусумме её оснований.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов» — верно, для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.

2) «В тупоугольном треугольнике все углы тупые» — неверно: в тупоугольном треугольнике один тупой и два острых угла.

3) «Средняя линия трапеции равна полусумме её оснований» — верно.

Какие из следующих утверждений верны?

1. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

2. В тупоугольном треугольнике все углы тупые.

3. Средняя линия трапеции равна полусумме её оснований.

Рассмотрим каждое из утверждений:

Найдите площадь трапеции, диагонали которой равны 16 и 12, а средняя линия равна 10.

Пусть — длина средней линии. Проведём высоту CH и проведём прямую CE, параллельную BD. Рассмотрим четырёхугольник следовательно, BCED — параллелограмм, откуда Рассмотрим треугольник ACE, Пусть p — полупериметр треугольника ACE. Найдём площадь треугольника ACE по формуле Герона:

Выразим площадь треугольника ACE как произведение основания AE на высоту CH, откуда найдём

Площадь трапеции равна произведению высоты на полусумму оснований:

Решение можно сократить, заметив, что треугольник ACE является прямоугольным, и его площадь равна площади трапеции ABCD. Действительно, в силу равенства

по теореме, обратной теореме Пифагора, заключаем, что треугольник ACE прямоугольный. Тогда площадь треугольника находится как полупроизведение катетов:

Далее, треугольник ACE имеет общую высоту с трапецией, а его основание AE есть сумма оснований трапеции. Таким образом, найденная площадь данного треугольника равна искомой площади трапеции.

Источник