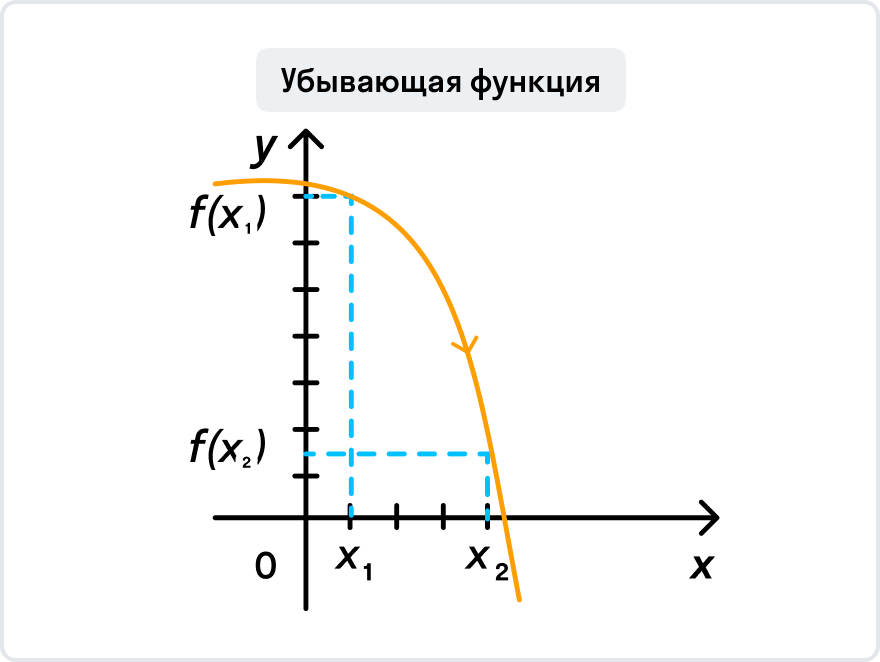
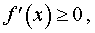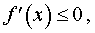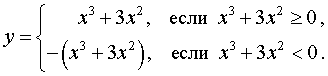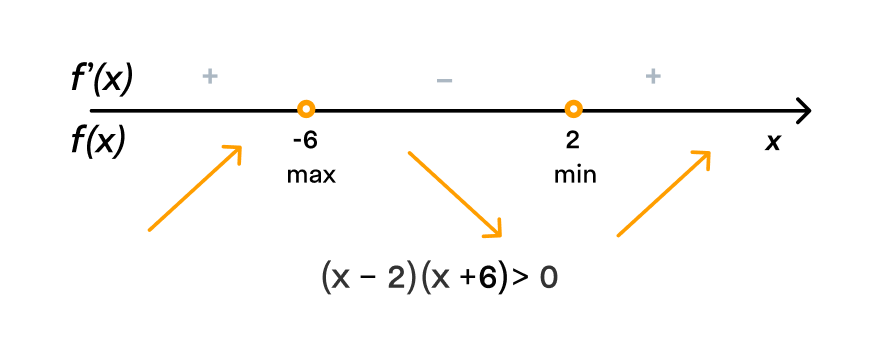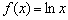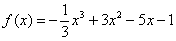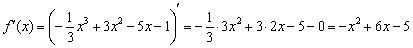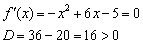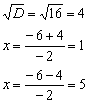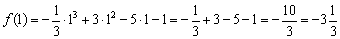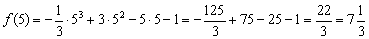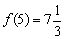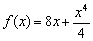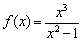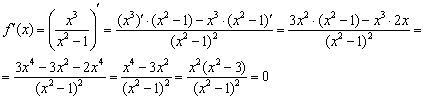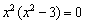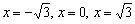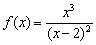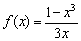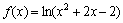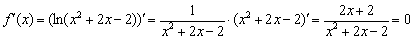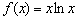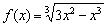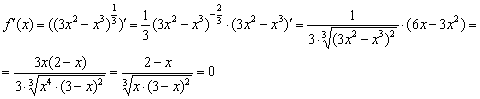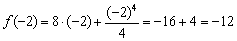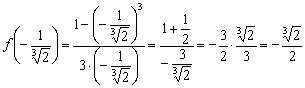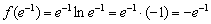Как найти точки экстремума функции
Как найти точки экстремума функции
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
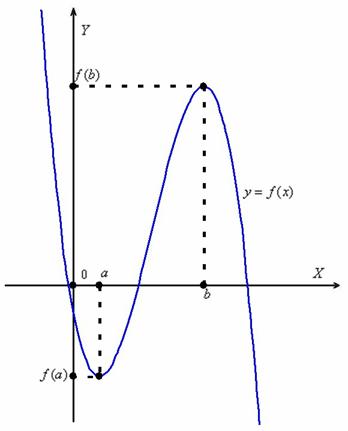
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
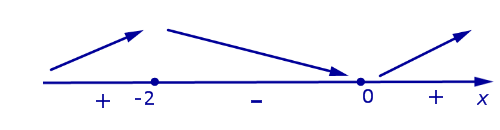
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.
\(- 9\): функция возрастает, а потом убывает – максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является \(-2\).
Исследование поведения функций с помощью производной
 Интервалы возрастания и убывания функции Интервалы возрастания и убывания функции |
 Достаточные условия для возрастания и убывания функции Достаточные условия для возрастания и убывания функции |
 Экстремумы (максимумы и минимумы) функции Экстремумы (максимумы и минимумы) функции |
 «Подозрительные» на наличие экстремума точки функции. Теорема Ферма «Подозрительные» на наличие экстремума точки функции. Теорема Ферма |
 Достаточные условия для существования экстремума функции Достаточные условия для существования экстремума функции |
 Пример исследования поведения функции Пример исследования поведения функции |
Интервалы возрастания и убывания функции
Для того, чтобы найти интервалы, на которых функция возрастает или убывает, часто используется метод, основанный на анализе знаков производной рассматриваемой функции. Суть этого метода состоит в следующем.
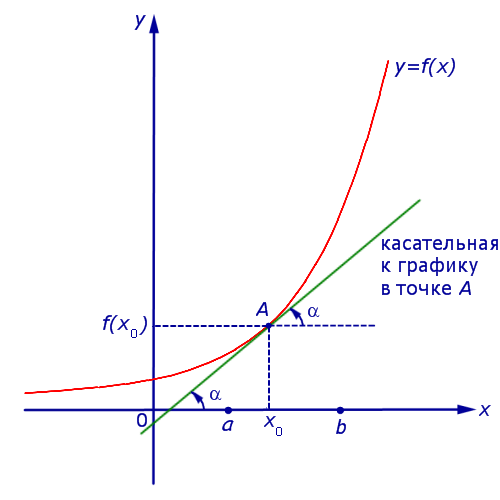
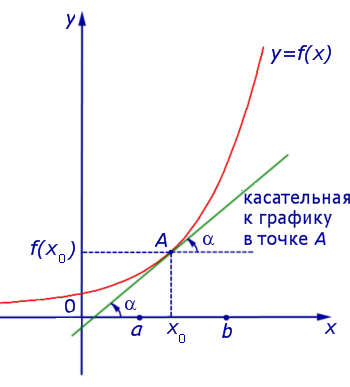
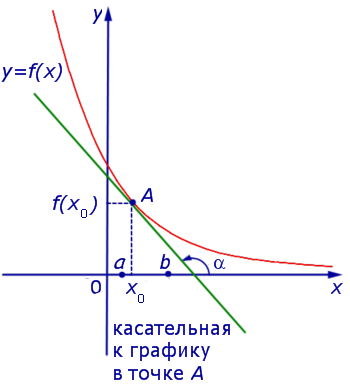
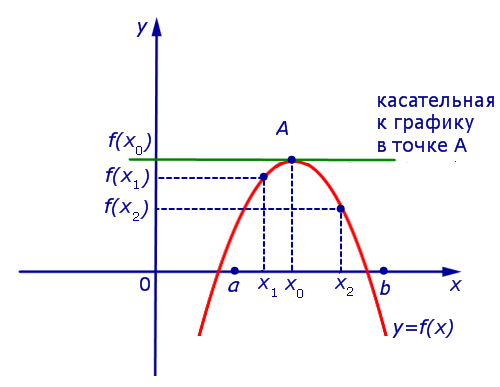
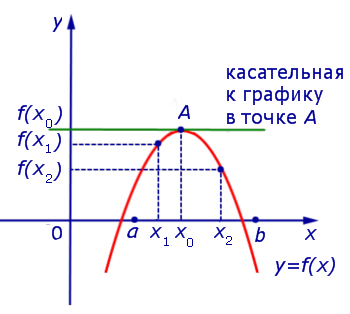
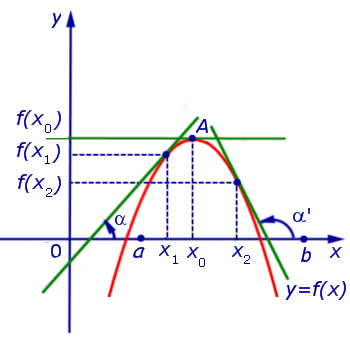
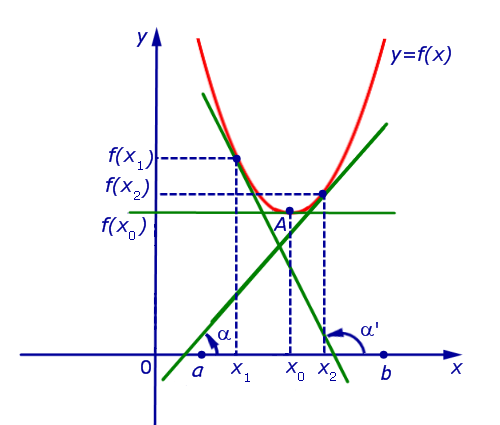
Если на интервале (a, b) функция y = f (x) строго возрастает и в каждой точке x0 интервала имеет производную, то, как показано на рисунке 1, а также на рисунке 2,
угол α наклона касательной к графику функции будет острым, откуда вытекает неравенство:
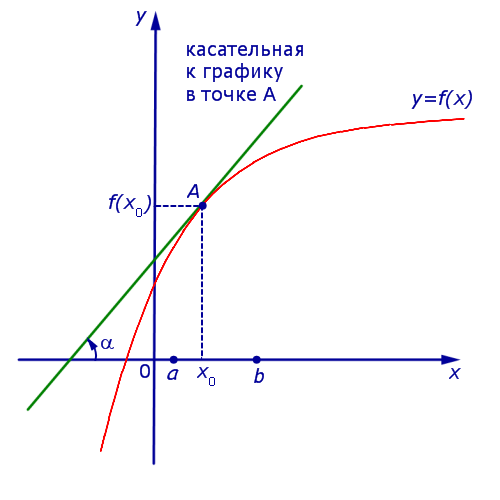
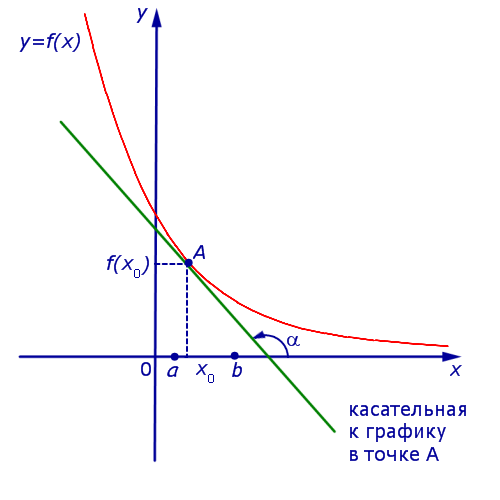
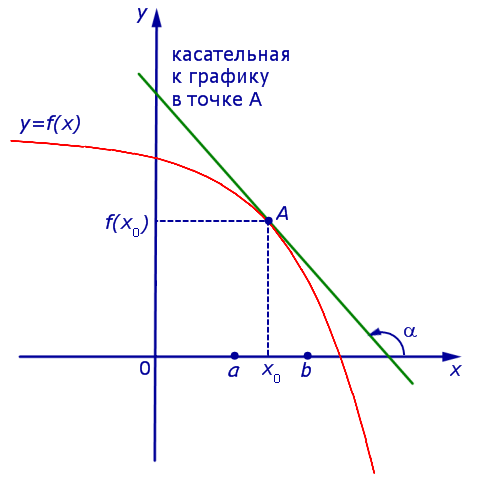
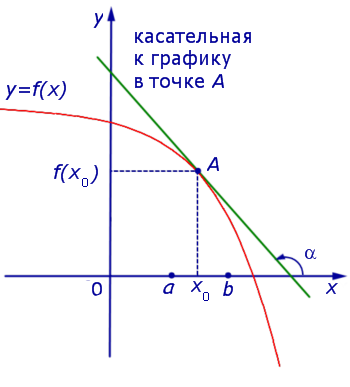
Если же на интервале (a, b) функция y = f (x) строго убывает и в каждой точке x0 интервала имеет производную, то, как показано на рисунках 3 и 4,
угол α наклона касательной к графику функции будет тупым, откуда вытекает неравенство:
а). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
б). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
в). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
г). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
Экстремумы (максимумы и минимумы) функции
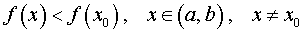
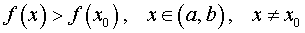
«Подозрительные» на наличие экстремума точки функции.
Теорема Ферма
Определение 4. Стационарной точкой функции называют такую точку, в которой производная функции равна нулю.
Определение 5. Критической точкой функции называют такую точку, в которой производная функции равна нулю или не существует.
Таким образом, если точка x0 является критической точкой функции, то точка x0 либо является стационарной точкой функции, либо производная функции в точке x0 не существует.
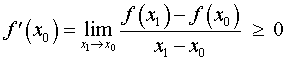
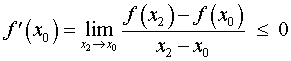
Достаточные условия для существования экстремума функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики и в нашем справочнике не приводится, сформулированы достаточные условия для экстремума функции.
а). Если для точек 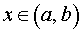
б). Если для точек 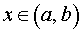
Пример исследования поведения функции
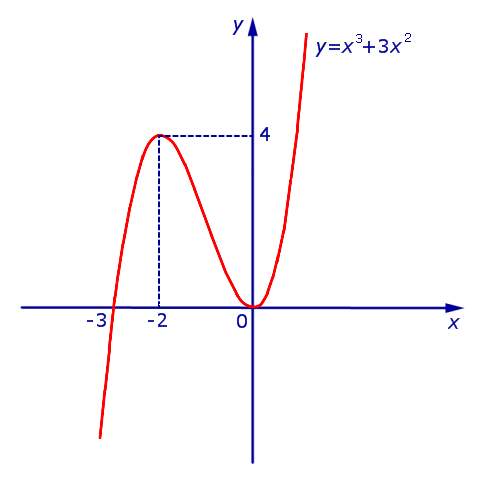
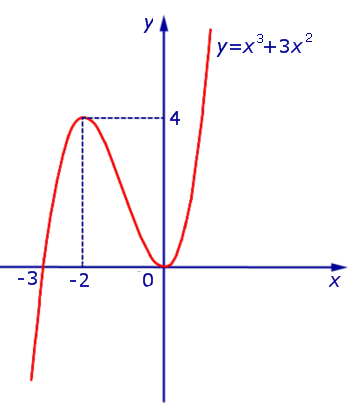
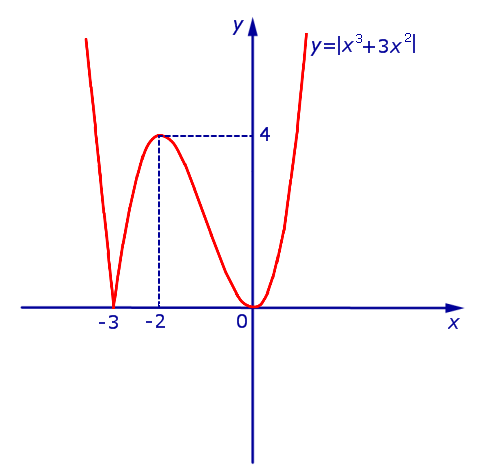
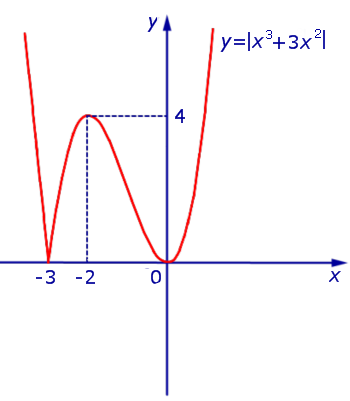
Пример. Найти интервалы возрастания, убывания и экстремумы функции
| y = | x 3 + 3x 2 | | (1) |
Решение. Исследуем сначала на возрастание, убывание и экстремумы функцию
| y1 = x 3 + 3x 2 | (2) |
и построим ее график. Для этого представим формулу (2) в виде
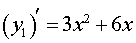 | (3) |
и разложим на множители правую часть формулы (3):
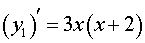 | (4) |
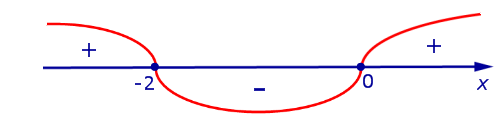
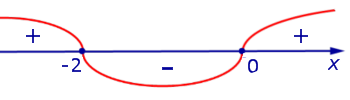
На рисунке 8 при помощи метода интервалов изобразим на числовой оси знаки производной (4)
Поскольку решением неравенства
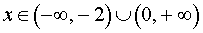 , , | (5) |
то в соответствии с утверждением 1 функция y1 возрастает на каждом из интервалов 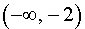
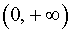
С другой стороны, поскольку решением неравенства
3x (x + 2) (– 2, 0),
Так как решениями уравнения
Заметим, что при анализе поведения функции по знакам ее производной, удобно использовать следующую диаграмму, на которой стрелками указаны интервалы возрастания и убывания функции (рис. 9).
В силу определения модуля, справедливо равенство
В точке x = – 3 производная функции y = | x 3 + 3x 2 | не существует. Во всех остальных точках числовой оси производная функции y = | x 3 + 3x 2 | существует.
Функция y = | x 3 + 3x 2 | возрастает на каждом из интервалов (– 3, – 2) и 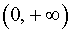
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок № 16. Экстремумы функции.
Перечень вопросов, рассматриваемых в теме
1) Определение точек максимума и минимума функции
2) Определение точки экстремума функции
3) Условия достаточные для нахождения точек экстремума функции
Глоссарий по теме
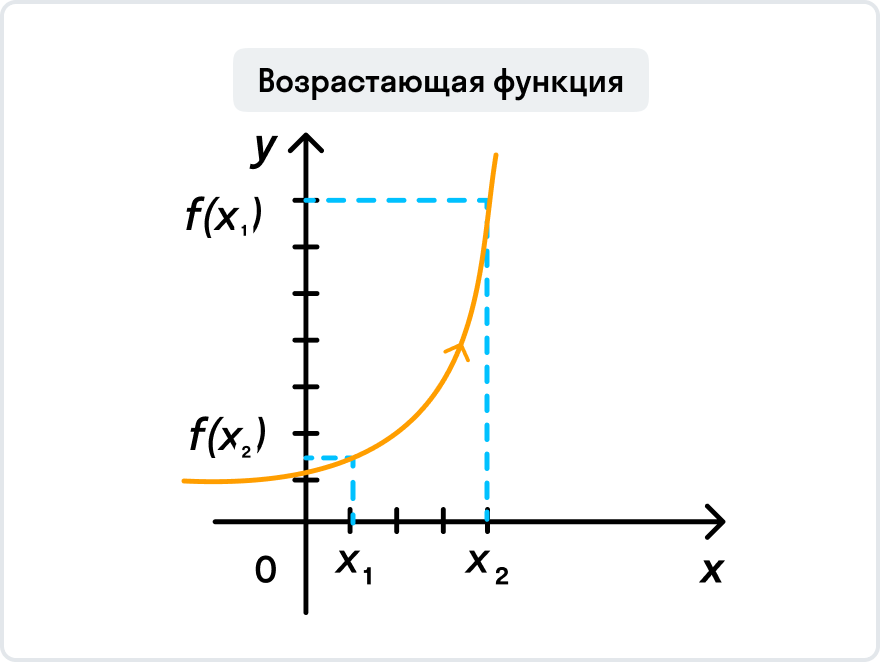
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, 

Максимум функции. Значение функции в точке максимума называют максимумом функции
Минимум функции. Значение функции в точке минимума называют минимумом функции
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, 

Алгоритм исследования функции на монотонность и экстремумы:
1) Найти область определения функции D(f)
3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
существует) точки функции y = f(x).
4) Отметить стационарные и критические точки на числовой
прямой и определить знаки производной на получившихся
5) Сделать выводы о монотонности функции и точках ее
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.
Точки максимума и минимума – точки экстремума.
Функция может иметь неограниченное количество экстремумов.
Критическая точка – это точка, производная в которой равна 0 или не существует.
Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
Алгоритм нахождения максимума/минимума функции на отрезке:
Примеры и разбор решения заданий тренировочного модуля
Решение: Найдем производную заданной функции: у’=2x-8
Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
№2. Найдите точку минимума функции у= 2х-ln(х+3)+9
Решение: Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 м\c
№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.
Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3
Возрастание и убывание функции на интервале, экстремумы
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Точки экстремума, экстремумы функции
Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.
Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Иначе говоря, получим их условия постановки знака:
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
После чего необходимо найти производную:
Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
Изображение на прямой имеет вид
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
Перейдем к вычислению минимумов:
Произведем вычисления максимумов функции. Получим, что
Второй признак экстремума функции
Для начала находим область определения. Получаем, что
Необходимо продифференцировать функцию, после чего получим
Третье достаточное условие экстремума
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.
Возрастание и убывание функции
Что такое функция
Как обычно, начнем мы с самого начала: с определения слова «функция».
Под функцией понимают правило, формулу, уравнение, которое описывает зависимость одной переменной от другой (например, у от х). Если изучить функцию, мы поймем:
как изменится одна переменная, если другая увеличится;
что произойдет с аргументом, если мы уменьшим функцию;
что будет, если мы отобразим эту зависимость графически.
Спойлер: если изобразить зависимость в координатной системе, мы получим график! Давайте рассмотрим некоторые виды функций и графики, которые им соответствуют.
Важное напоминание: функция — это зависимая переменная величина (чаще у), аргумент — независимая переменная (чаще х).
Возрастание и убывание функции
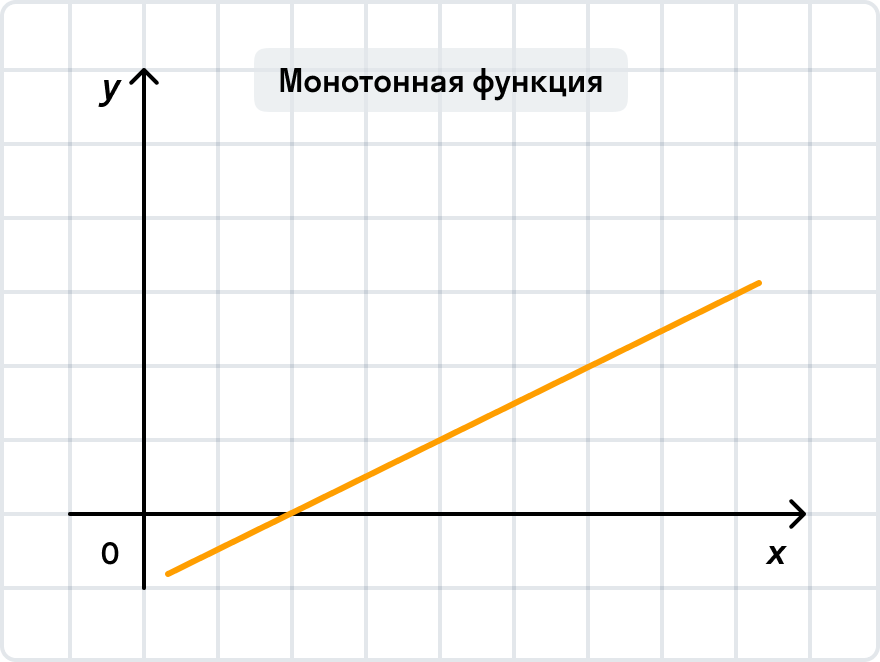
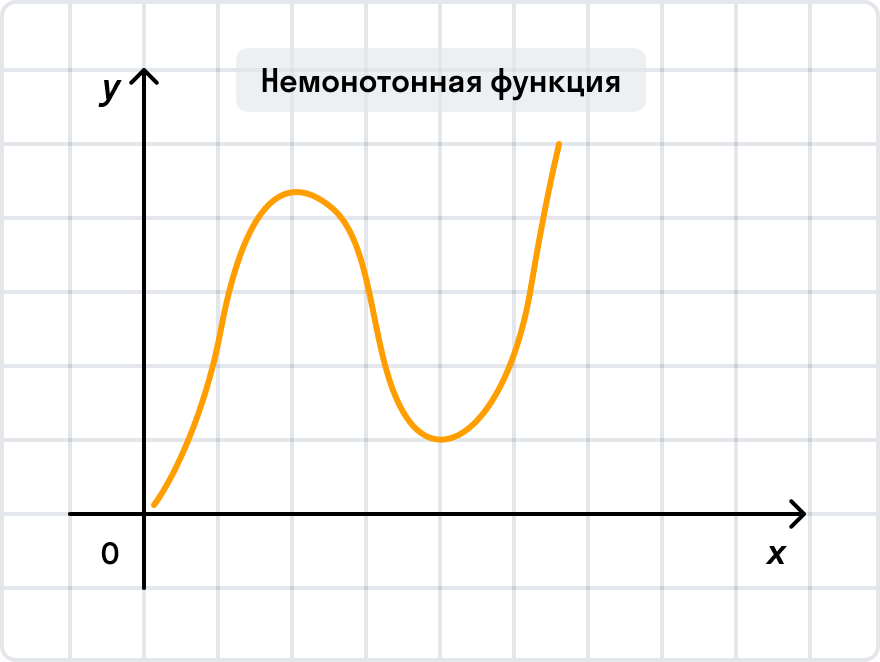
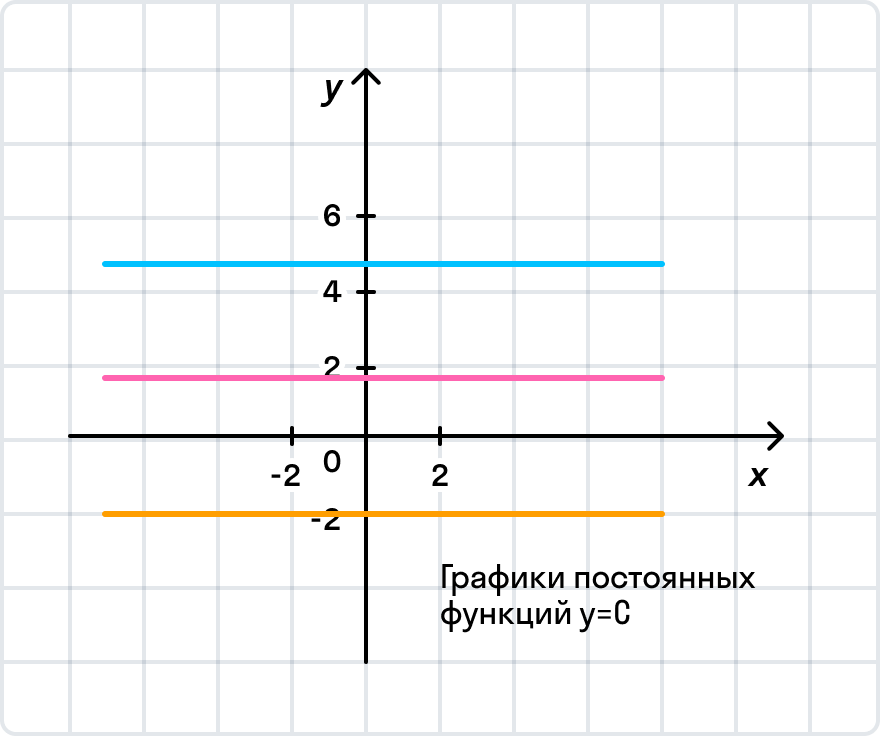
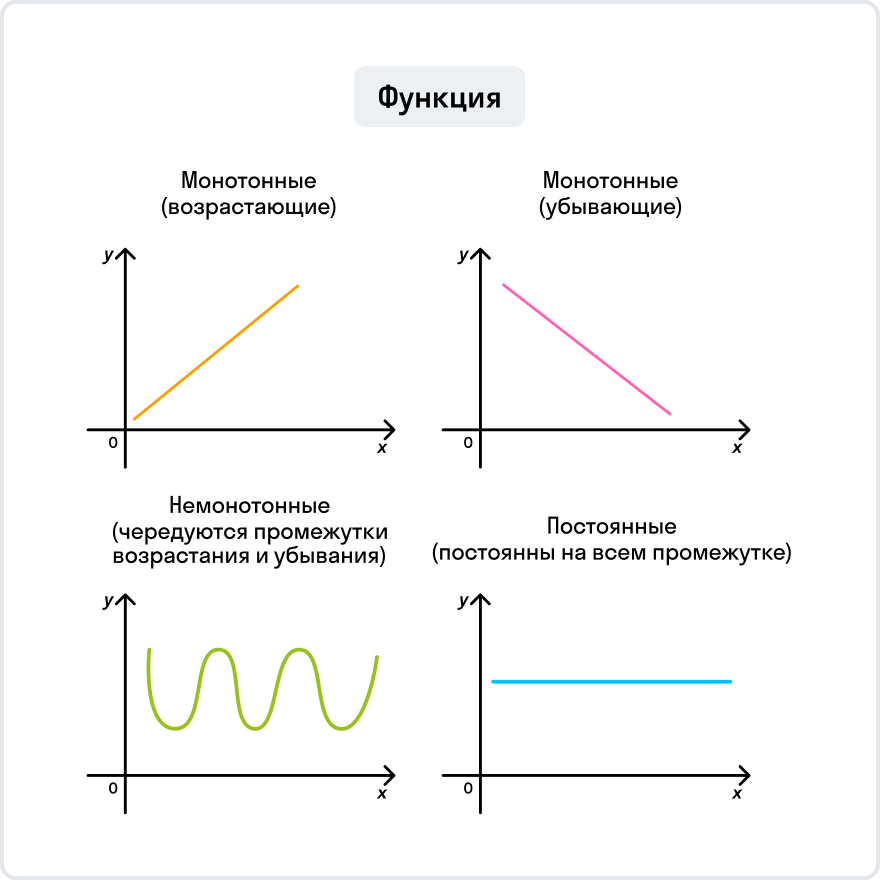
В исследовании функции особое значение уделяют ее поведению в системе координат — монотонности функции. Функции бывают монотонными, немонотонными и постоянными.
Теперь к теме раздела: приведем определение возрастающей и убывающей функции.
Проще говоря, здесь работает правило «чем больше, тем больше»: чем больше значение х, тем больше и значение у.
Теперь вы знаете, как понять, что функция возрастает или убывает. Давайте решим пару задач, чтобы разобраться во всем наглядно.
Задача 1
Определите, возрастающая или убывающая функция y = 2x + 3.
1) Найдем область определения функции: х ∈ R.
2) Найдем координаты нескольких точек, которые ей принадлежат.
х
у
Как вы уже заметили, значения х и у одновременно увеличиваются — функция возрастает на всем промежутке.
Задача 2
Определите, возрастающая или убывающая функция y = 1/2х.
1) Найдем область определения функции: х ≠ 0.
2) Найдем координаты нескольких точек, которые ей принадлежат.
х
у
х
у
Мы видим, что функция убывает при любом значении х ≠ 0. Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.
Возрастание и убывание функции на интервале
Мы еще не закончили с возрастающими и убывающими функциями — эх, если бы все было так просто! Дело в том, что нас, математиков, интересуют вот какие вопросы:
Как найти промежутки возрастания и убывания функции по графику?
Что делать, если просят определить характер на числовом промежутке?
Как определить поведение функции без построения?
Давайте разбираться! Сначала узнаем, как определить характер функции на промежутке:
Подставим значение х из промежутка в функцию.
Проанализируем полученные значения у.
Если при увеличении х увеличивается и у — это промежуток возрастания функции.
Если у уменьшается при увеличении х — это промежуток убывания функции.
Достаточно просто, правда? 🙂
Пример
Возьмем функцию y = 4x – 6 и определим ее характер на промежутке [0;2]. Подставим числа из промежутка вместо х в функцию:
Мы видим, что при возрастании х возрастает и значение у, т. е. на этом промежутке функция возрастает.
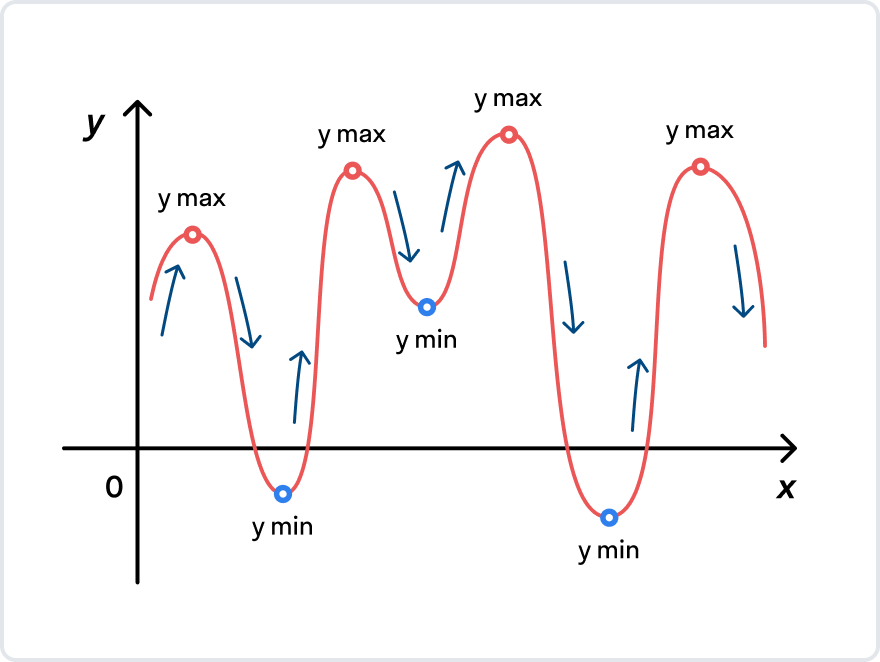
Точки экстремума, экстремумы функции
Не пугайтесь этих страшных слов! Сейчас разберем их подробнее — это проще, чем кажется.
На графике выше y min — минимальное значение функции, точка минимума.
На том же графике y мах — максимальное значение функции, точка максимума.
Иначе точки минимума и максимума в математике принято называть точками экстремума, а значения функции, которые соответствуют точкам экстремума — экстремумами функции.
В точках экстремума функция меняет свой характер. Обратите внимание на рисунок ниже: функция стремительно возрастала до точки максимума, но после нее начала также стремительно уменьшаться. И наоборот, после прохождения точки минимума функция снова начинает возрастать.
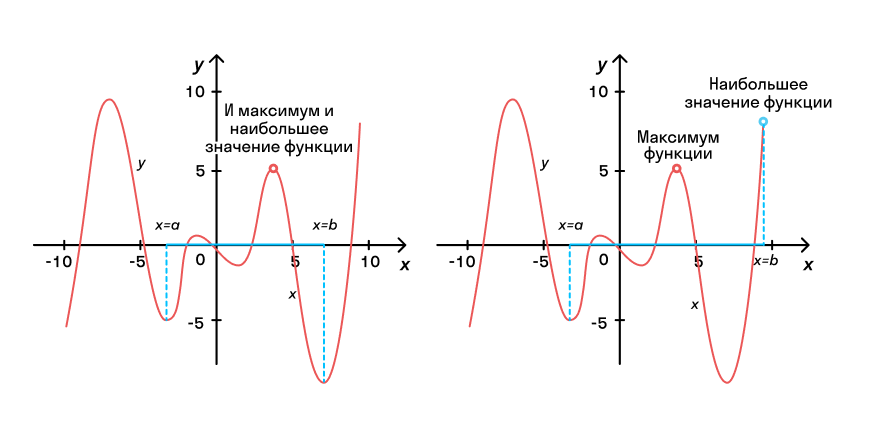
Здесь вам может стать интересно: наибольшее/наименьшее значение функции на промежутке — это то же самое или нет. Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.
Достаточные условия возрастания и убывания функции
У нас есть две новости: хорошая и не очень. Начнем с первой: если использовать достаточные условия возрастания/убывания, можно определить промежутки монотонности функции. И для этого даже не придется строить график! Но здесь нам пригодится производная.
Иначе говоря, производная функции показывает, как быстро увеличивается функция при бесконечно малом увеличении х.
К сожалению, в рамках этой статьи мы не будем долго останавливаться на производных. Как это сделать с помощью таблицы и правил дифференцирования, мы уже разбирали в статье «Таблица производных функций». Советуем почитать!
Достаточные признаки возрастания и убывания функции на интервале:
если производная функции y = f(x) положительна для любого x из интервала, то функция возрастает на этом интервале;
если производная функции y = f(x) отрицательна для любого x из интервала, то функция убывает на этом интервале.
Составим алгоритм действий, который поможет найти интервалы возрастания и убывания функции:
Найдем область определения функции.
Найдем производную функции.
Решим неравенства ƒ`(x) > 0 и ƒ`(x) 2 + 5х + 6
Решение
Область определения функции: х ∈ R
Найдем производную функции: y’ = 2х + 5
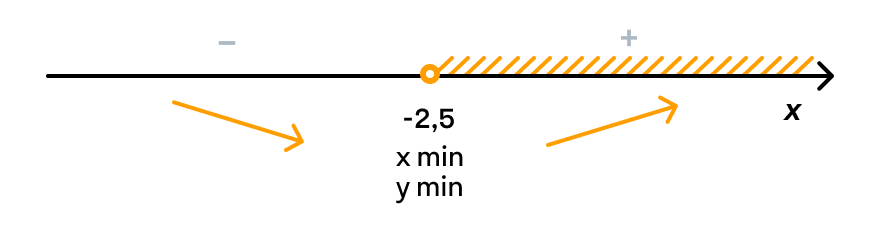
Решим неравенство: 2х + 5 > 0
Исследуем знаки производной с помощью числовой прямой.
Ответ: Функция убывает при х∈ (– ∞; –2,5], возрастает при х∈ [–2,5; +∞)
Задача 4
Определите интервалы возрастания и убывания функции у = х 3 – 18х.
Решение
Область определения функции: х ∈ R.
Найдем производную функции: y’ = 3x 2 + (–18).
Исследуем знаки производной с помощью числовой прямой. Чтобы определить знак на каждом промежутке, подставим произвольное значение из этого промежутка в выражение для производной.
Ответ: Функция убывает при х∈ [–3;3], возрастает при х∈ (–∞;—3] ∪ [3; +∞).
Первое достаточное условие экстремума
Пусть для функции у = f(x) определены следующие условия:
Функция непрерывна в окрестности точки x0 (нет разрыва).
ƒ′(x0) = 0 или ƒ′(x0) не существует;
Производная ƒ′(x) при переходе через точку x0 меняет свой знак.
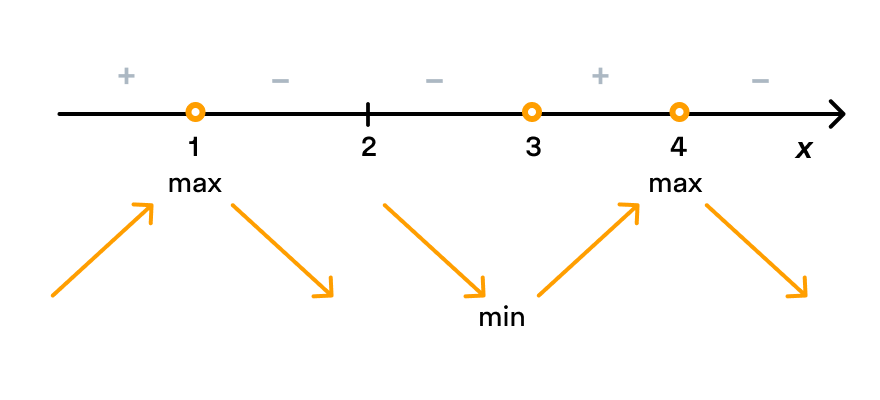
Тогда в точке x = x0 функция y = f(x) имеет экстремум, причем это минимум, если при переходе через точку x0 производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку x0 производная меняет свой знак с плюса на минус.
Если производная в точке x0 не меняет свой знак, то в этой точке нет экстремума.
Итак, точки 1 и 4 — точки максимума, точка 3 — точка минимума. В точке 2 экстремума нет.
Алгоритм для нахождения точек экстремума
Теперь разберемся, как найти точки экстремума функции. Для этого пройдем по этим шагам:
Найдем область определения функции.
Найдем производную функции на этой области.
Определим нули и точки, где функция не существует.
Определим знак производной на интервалах.
Выберем точки, где функция меняет знак.
Найдем точки минимума/максимума и экстремумы функции.
Задача 5
Найдите экстремумы функции у = –x 2 + 8x – 7.
Решение
Область определения функции: х ∈ R.
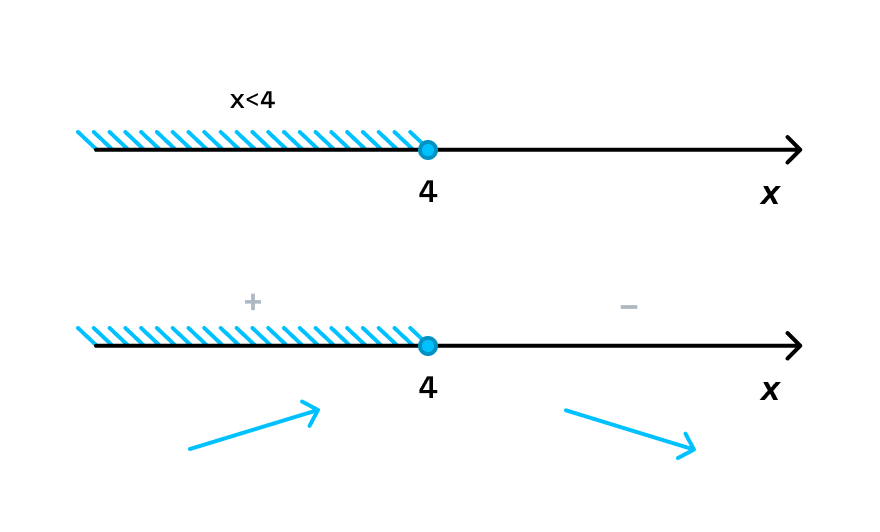
Производная функции: y’ = –2x + 8
Определим знак производной на числовой прямой. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
В точке х = 4 функция меняет свой знак с «+» на «–», значит, точка х = 4 — это точка максимума.
Ответ: у(4) = 9 — экстремум функции.
Задача 6
Найдите экстремумы функции у = ⅓ x 3 + 2x 2 – 12x + 6.
Решение
Область определения функции: х ∈ R.
Производная функции: y’ = x 2 + 4x – 12.
Определим знак производной на числовой прямой. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Так на интервале (–∞; –6) и (2; +∞) производная положительна — на них функция возрастает. На интервале (–6;2) производная отрицательна — функция убывает.
Ответ: x = 2 — точка минимума, у(2) = –7 ⅓ — экстремум функции; х = –6 — точка максимума, у(–6) = 78 — экстремум функции.
Как можно запомнить переход знаков для точек максимум или минимум:
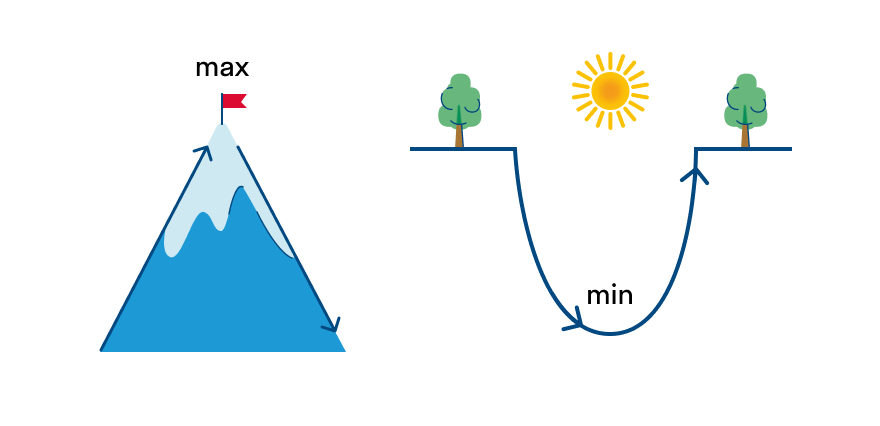
Когда функция возрастает, а потом убывает, мы будто поднимались на вершину горы — значит, посетили точку максимума.
Когда функция убывает, а потом возрастает, мы будто спускались в овраг и выбрались из него — а значит, были в точке минимума.
Второе достаточное условие экстремума
x0 — это точка экстремума функции f(x), если вторая производная функции в этой точке не равна нулю (f »(x) ≠ 0). Причем, если вторая производная больше нуля (f »(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f »(x) 3 + 2x 2 – 12x + 6:
Ее первая производная равна y’= x 2 + 4x – 12.
Определим нули производной — значение х, при котором производная обращается в ноль: x 2 + 4x – 12 = 0 при х = 2 и х = –6.
Возьмем вторую производную функции y’’= 2х + 4.
Подставим значения х = 2 и х = –6 во вторую производную и определим, являются ли эти точки максимумом или минимумом:
y’’(2) = 8, y’’ > 0, значит, х = 2 является точкой минимума,
В этом условии есть два важных замечания:
Если в точке x0 и первая, и вторая производные обращаются в ноль, то в этом случае нужно воспользоваться первым достаточным признаком экстремума функции, по второму признаку нельзя судить о наличии или отсутствии экстремумов.
Второй достаточный признак нельзя применять, когда в стационарной точке (нуле производной) первая производная не существует. Ведь тогда не существует и вторая производная.
Третье достаточное условие экстремума
Это условие не используется в школьной программе, так как требует большого количества вычислений и логических размышлений. Мы все равно познакомим вас с ним — возможно, вам захочется изучить это усaловие самостоятельно и блеснуть знаниями перед учителем. Что ж, мы только за!
Пусть функция y=f(x) имеет производные до n-ого порядка в ε-окрестности точки x0 и производные до n+1-го порядка в самой точке x0. Пусть ƒ′(x0) = ƒ n (x0) = ƒ m (x0) = … = ƒ (n) (x0) = 0 и ƒ (n+1) (x0) ≠ 0.
если n – четное, то x0 — точка перегиба;
если n – нечетное, то x0 — точка экстремума, причем
если ƒ (n+1) (x0) > 0, то x0 — точка минимума;
Возрастание, убывание и экстремумы функции
А сегодня в воздухе витает дух редкого единодушия, и я прямо чувствую, что все присутствующие горят желанием научиться исследовать функцию с помощью производной. Поэтому на экранах ваших мониторов незамедлительно появляется разумная добрая вечная терминология.
Зачем? Одна из причин самая что ни на есть практическая: чтобы было понятно, что от вас вообще требуется в той или иной задаче!
Монотонность функции. Точки экстремума и экстремумы функции
Рассмотрим некоторую функцию 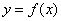
На всякий случай сразу избавимся от возможных иллюзий, особенно это касается тех читателей, кто недавно ознакомился с интервалами знакопостоянства функции. Сейчас нас НЕ ИНТЕРЕСУЕТ, как расположен график функции относительно оси 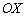
Функция возрастает на интервале, если для любых двух точек этого интервала, связанных отношением 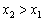
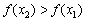
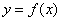
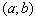
Аналогично, функция убывает на интервале, если для любых двух точек данного интервала, таких, что 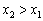
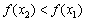
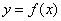
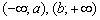
Если функция возрастает или убывает на интервале, то её называют строго монотонной на данном интервале. Что такое монотонность? Понимайте в буквальном смысле – однообразие.
Также можно определить неубывающую функцию (смягчённое условие 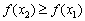
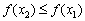
Теория рассматривает и другие подходы к определению возрастания/убывания функции, в том числе на полуинтервалах, отрезках, но чтобы не выливать на вашу голову масло-масло-масляное, договоримся оперировать открытыми интервалами с категоричными определениями – это чётче, и для решения многих практических задач вполне достаточно.
Таким образом, в моих статьях за формулировкой «монотонность функции» почти всегда будут скрываться интервалы строгой монотонности (строгого возрастания или строгого убывания функции).
Окрестность точки. Слова, после которых студенты разбегаются, кто куда может, и в ужасе прячутся по углам. …Хотя после поста Пределы по Коши уже, наверное, не прячутся, а лишь слегка вздрагивают =) Не беспокойтесь, сейчас не будет доказательств теорем математического анализа – окрестности мне потребовались, чтобы строже сформулировать определения точек экстремума. Вспоминаем:
Окрестностью точки называют интервал, который содержит данную точку, при этом для удобства интервал часто полагают симметричным. Например, точка 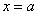
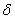

Собственно, определения:
Точка 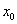
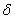
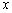
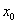
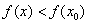
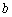
Точка 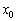
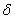
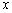
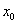
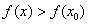
Примечание: требование симметричности окрестности вовсе не обязательно. Кроме того, важен сам факт существования окрестности (хоть малюсенькой, хоть микроскопической), удовлетворяющей указанным условиям
Точки 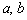
Как понимать слово «экстремум»? Да так же непосредственно, как и монотонность. Экстремальные точки американских горок.
Как и в случае с монотонностью, в теории имеют место и даже больше распространены нестрогие постулаты (под которые, естественно, подпадают рассмотренные строгие случаи!):
Точка 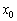
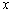
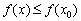
Точка 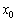
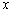
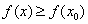
Заметьте, что согласно последним двум определениям, любая точка функции-константы (либо «ровного участка» какой-нибудь функции) считается как точкой максимума, так и точкой минимума! Функция 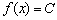
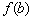
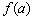
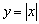
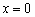
Да, кстати, о королевских особах:
– значение 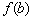
– значение 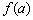
Общее название – экстремумы функции.
Пожалуйста, будьте аккуратны в словах!
Точки экстремума – это «иксовые» значения.
Экстремумы – «игрековые» значения.
! Примечание: иногда перечисленными терминами называют точки «икс-игрек», лежащие непосредственно на САМОМ ГРАФИКЕ функции.
Сколько может быть экстремумов у функции?
Ни одного, 1, 2, 3, … и т.д. до бесконечности. Например, у синуса бесконечно много минимумов и максимумов.
ВАЖНО! Термин «максимум функции» не тождественен термину «максимальное значение функции». Легко заметить, что значение 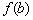
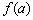
Чайникам на первых порах рекомендую создать и осмыслить небольшой терминологический конспект, чтобы не путать Иран с Ираком.
Подытожим наш небольшой экскурс в теорию контрольным выстрелом: что подразумевает задание «найдите промежутки монотонности и точки экстремума функции»?
Формулировка побуждает найти:
– интервалы возрастания/убывания функции (намного реже фигурирует неубывание, невозрастание);
– точки максимума и/или точки минимума (если таковые существуют). Ну и от незачёта подальше лучше найти сами минимумы/максимумы 😉
Как всё это определить? С помощью производной функции!
Как найти интервалы возрастания, убывания,
точки экстремума и экстремумы функции?
Многие правила, по сути, уже известны и понятны из урока о смысле производной.
Рассмотрим дифференцируемую на некотором интервале функцию 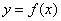
– если производная 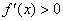
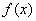
– если производная 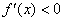
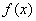
Примечание: справедливы и обратные утверждения.
Пусть точка 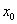
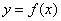
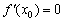
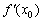
Но сначала потренируемся на кошках разделаемся с простейшими примерами. Почин положен в конце теоретической статьи о производной, и на очереди другие жертвы анализа. Заодно есть возможность провести маленькое самотестирование – насколько хорошо вы запомнили, как выглядят графики жизненно важных функций? В тяжелом случае, конечно же, следует открыть первый урок на соседней вкладке и щёлкать туда-сюда по мере комментариев.
Производная кубической функции 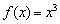
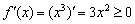
Действительно, кубическая парабола идёт «снизу вверх». Бесконечно близко около точки 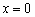
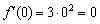
Функция 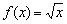
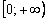
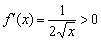
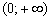
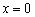
С геометрических позиций тут нет общей касательной. Однако в теории рассматриваются так называемые односторонние производные, и в указанной точке существует правосторонняя производная с правосторонней касательной. Желающие разобраться в этом подробнее могут покурить первый том матана.
Примечание: согласно информации первого параграфа, точка 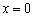
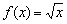
и слева и справа от данных точек. Так же не считаются точками экстремума крайние значения области определения арксинуса и арккосинуса (см. ниже).
Стандартная гипербола 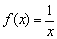
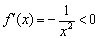
Здесь, к слову, точка 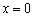
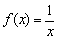
Экспоненциальная функция 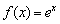
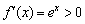
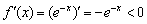
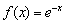
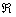
Что делает натуральный логарифм сегодня вечером?
Растёт:
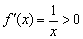
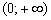
Начертите/распечатайте на соседних либо одном чертеже (иль просто представьте в уме) графики функции 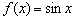
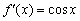
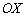
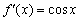
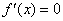
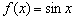
Аналогичная история с косинусом 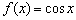
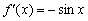
Производная тангенса 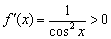
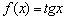
С котангенсом и его производной 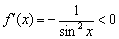
Арксинус на интервале 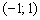
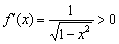
При 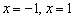
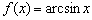
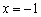
Думаю, вам не составит особого труда провести похожие рассуждения для арккосинуса и его производной.
Все перечисленные случаи, многие из которых представляют собой табличные производные, напоминаю, следуют непосредственно из определения производной.
Зачем исследовать функцию с помощью производной?
Чтобы лучше узнать, как выглядит график этой функции: где он идёт «снизу вверх», где «сверху вниз», где достигает минимумов максимумов (если вообще достигает). Не все функции такие простые – в большинстве случаев у нас вообще нет ни малейшего представления о графике той или иной функции.
Настала пора перейти к более содержательным примерам и рассмотреть алгоритм нахождения интервалов монотонности и экстремумов функции:
Найти интервалы возрастания/убывания и экстремумы функции
Решение:
1) На первом шаге нужно найти область определения функции, а также взять на заметку точки разрыва (если они существуют). В данном случае функция непрерывна на всей числовой прямой, и данное действие в известной степени формально. Но в ряде случаев здесь разгораются нешуточные страсти, поэтому отнесёмся к абзацу без пренебрежения.
2) Второй пункт алгоритма обусловлен
необходимым условием экстремума:
Если в точке 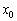
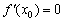
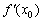
Смущает концовка? Экстремум функции «модуль икс».
Условие необходимо, но не достаточно, и обратное утверждение справедливо далеко не всегда. Так, из равенства 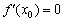
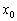
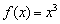
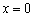
Но как бы там ни было, необходимое условие экстремума диктует надобность в отыскании подозрительных точек. Для этого следует найти производную и решить уравнение 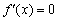
Получилось обычное квадратное уравнение:
Положительный дискриминант доставляет две критические точки:
Примечание: корни можно традиционно обозначить через 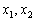
Итак, 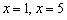
Но экстремумов в них может и не оказаться, поэтому нужно продолжить решение.
первое достаточное условие экстремума,
которое вкратце формулируется следующим образом: пусть функция дифференцируема в некоторой окрестности критической точки 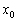
– если при переходе через точку 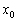
– если при переходе через точку 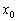
Тут всё очень и очень наглядно, представьте – функция росла-росла-росла, и после прохождения некоторого рубежа вдруг стала убывать. Максимум. Во втором случае график шёл-шёл-шёл «сверху вниз», а при переходе через точку 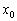
Исходя из вышесказанного, вытекает логичное решение: на числовой прямой нужно отложить точки разрыва функции, критические точки и определить знаки производной на интервалах, которые входят в область определения функции.
В рассматриваемом примере с непрерывностью на 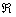
Напрашивается метод интервалов, который уже применялся для определения интервалов знакопостоянства функции. Так почему бы его не использовать для производной? Ведь производная тоже простая смертная функция, найдёшь её – и делай всё, что хочешь.
Внимание! Сейчас мы работаем с ПРОИЗВОДНОЙ, а не с самой функцией!
Перед нами парабола 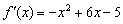

I) Берём какую-нибудь точку интервала 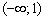
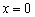
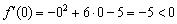
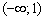
II) Выбираем точку 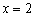
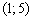
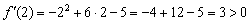
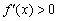
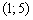
III) Вычислим значение производной в наиболее удобной точке 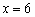
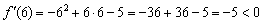
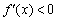
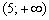
В результате получены следующие знаки производной:

Время собирать урожай!
На интервалах 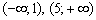
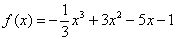
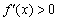
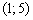
При переходе через точку 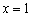
При переходе же через точку 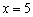
Ответ: функции возрастает на интервале 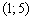
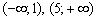
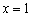
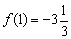
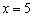
Остерегайтесь сокращенной записи 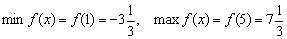
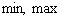
Пример так тщательно провёрнут через мясорубку, что грех не привести графическое изображение всех событий. Незнакомец теоретической части статьи снимает шляпу: 
Что произошло? На первом этапе мы нашли производную 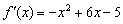
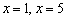
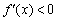
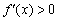
Помимо 1-го достаточного условия экстремума существует и 2-е достаточное условие, однако для исследования функций оно малоинформативно и больше используется в экстремальных задачах.
В начале первой статьи о графиках функции я рассказывал, как быстро построить параболу на примере 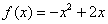
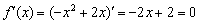
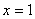
Найти промежутки монотонности и экстремумы функции
Это пример для самостоятельного решения. Полное решение и примерный чистовой образец оформления задачи в конце урока.
Наступил долгожданный момент встречи с дробно-рациональными функциями:
Исследовать функцию с помощью первой производной
Обратите внимание, как вариативно можно переформулировать фактически одно и то же задание.
Решение:
1) Функция терпит бесконечные разрывы в точках 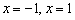
2) Детектируем критические точки. Найдём первую производную и приравняем её к нулю:
Решим уравнение 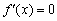
Таким образом, получаем три критические точки:
3) Откладываем на числовой прямой ВСЕ обнаруженные точки и методом интервалов определяем знаки ПРОИЗВОДНОЙ: 
Напоминаю, что необходимо взять какую-нибудь точку интервала, вычислить в ней значение производной 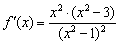
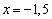
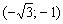
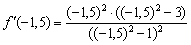
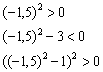
Два «плюса» и один «минус» дают «минус», поэтому 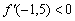
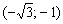
Действие, как вы понимаете, нужно провести для каждого из шести интервалов. Кстати, обратите внимание, что множитель числителя 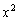
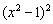
Итак, производная сообщила нам, что САМА ФУНКЦИЯ 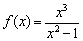
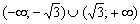
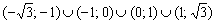
В точке 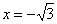
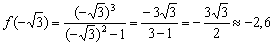
В точке 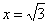
Подумайте, почему можно заново не пересчитывать второе значение 😉
При переходе через точку 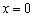
! Повторим важный момент: точки 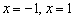
Ответ: функция возрастает на 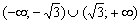
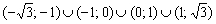
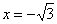
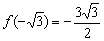
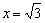
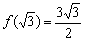
Знание интервалов монотонности и экстремумов вкупе с установленными асимптотами даёт уже очень хорошее представление о внешнем виде графика функции. Человек среднего уровня подготовки способен устно определить, что у графика функции 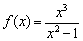
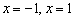
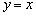
Постарайтесь ещё раз соотнести результаты исследования с графиком данной функции.
В критической точке 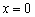
Найти экстремумы функции
Найти интервалы монотонности, максимумы и минимумы функции
…прямо какой-то Праздник «икса в кубе» сегодня получается.
Тааак, кто там на галёрке предложил за это выпить? =)
В каждой задаче есть свои содержательные нюансы и технические тонкости, которые закомментированы в конце урока.
Как отмечалось, в ходе выполнения задания всегда нужно внимательно следить за точками разрыва и интервалами, которые не входят в область определения функции. Казус состоит в том, что иногда производная может существовать на таких участках! Простейший пример: производная натурального логарифма 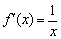
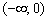
Типичный барьерный риф:
Найти интервалы монотонности и экстремумы функции
Приближаю оформление к боевым условиям и прекращаю нумерацию пунктов алгоритма.
Решение: в Примере 11 статьи об интервалах знакопостоянства была найдена область определения данной функции: 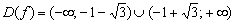
Вроде бы всё хорошо: у нас есть корень 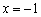
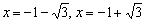
Но производная проявила своеволие – она в отличие от свого родителя определена и на интервале 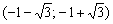
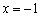

Функция убывает на интервале 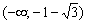
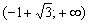
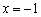
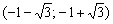
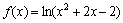
Ответ: функция убывает на интервале 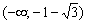
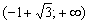
Будьте очень внимательны, если вам встретится логарифм или корень – в подобных примерах просто необходимо увАжить область определения функции!
Найти интервалы монотонности и экстремумы функции
Это приятный разгрузочный пример для самостоятельного решения.
И заключительный пример посвящен другому приключению непослушной дочери:
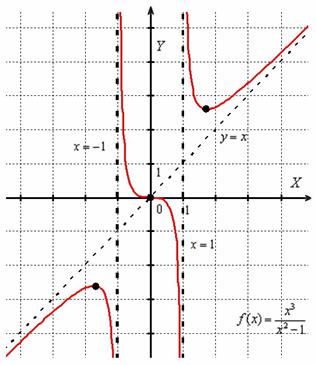
Найти точки экстремума функции
Решение: функция определена и непрерывна на всей числовой прямой.
Найдём критические точки:
На всякий случай детализирую преобразования знаменателя: 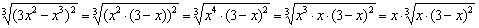
Таким образом, 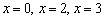
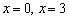
Определим знаки производной на полученных интервалах: 
Функция возрастает на интервале 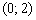
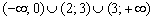
В точке 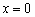
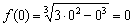
В точке 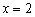
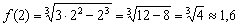
В точке 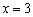
Ответ: 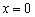
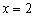
По условию требовалось найти точки экстремума и что-то добавлять излишне. Но в решении как бы невзначай вычислены и сами экстремумы 😉
Давайте посмотрим на на эту оригинальную картину: 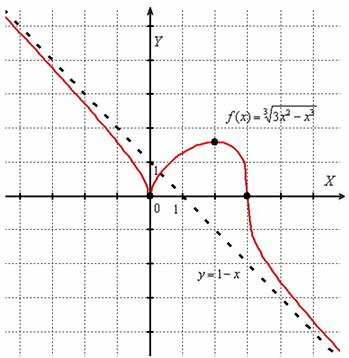
В точке 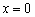
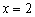
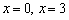
. да, родители и дети бывают разными. Но мама права в 95% случаев с погрешностью 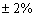
Решения и ответы:
Пример 2: Решение:
1) Функция определена и непрерывна на всей числовой прямой.
2) Найдём критические точки: 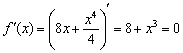
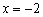
3) Методом интервалов определим знаки производной: 
Ответ: функция убывает на интервале 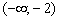
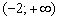
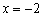
Пример 4: Решение:
1) Функция терпит бесконечный разрыв в точке 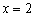
2) Найдём критические точки: 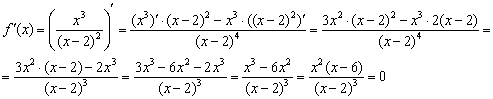
3) Методом интервалов определим знаки производной: 
В точке 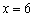
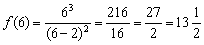
В точке 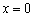
Ответ: в точке 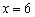
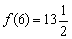
Примечание: обратите внимание, что информацию об интервалах монотонности раскрывать не обязательно, так как по условию требовалось найти только экстремумы функции
Пример 5: Решение:
1) Функция определена и непрерывна на всей числовой прямой кроме точки 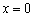
2) Найдём критические точки: 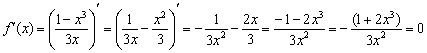
Примечание: в данном случае перед дифференцированием выгодно почленно разделить числитель на знаменатель
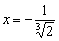
3) Определим знаки производной: 
Ответ: функция возрастает на 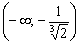
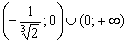
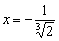
Пример 7: Решение:
Область определения: 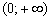
Найдём критические точки: 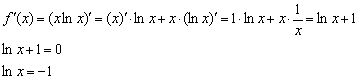
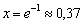
Определим знаки производной: 
Ответ: функция убывает на интервале 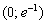
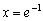
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys