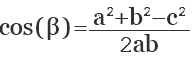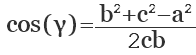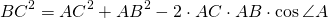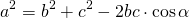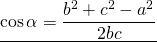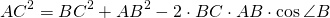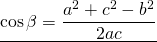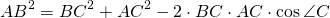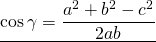Как найти углы треугольника если известны все стороны
Как найти углы треугольника если известны все стороны
Углы треугольника
Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.
α = 180°-β-γ
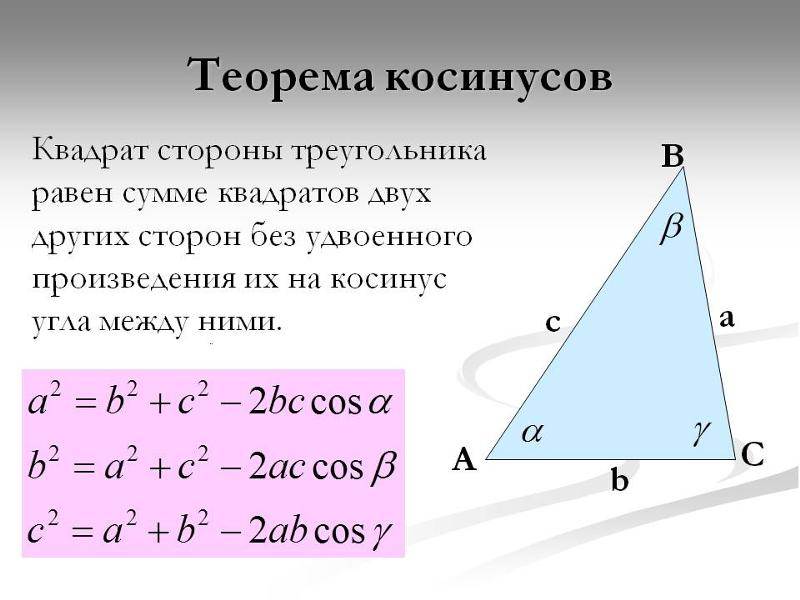
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.
a 2 = b 2 + c 2 + 2abc cos (α)
Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:
cos (α) = (b 2 + c 2 — a 2 ) / 2bc
,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.
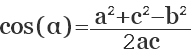
как найти угол треугольника если известны 3 стороны
Пусть задан треугольник со сторонами a, b и с. При этом сумма длин двух любых сторон треугольника должна быть больше длины третьей стороны, то есть a+b>c, b+c>a и a+c>b. И необходимо найти градусную меру всех углов этого треугольника. Пусть угол между сторонами a и b обозначен как α, угол между b и c как β, а угол между c и a как γ.
Теорема косинусов звучит так: квадрат длины стороны треугольника равен сумме квадратов двух других длин его сторон минус удвоенное произведение этих длин сторон на косинус угла между ними. То есть составьте три равенства: a²=b²+c²−2×b×c×cos(β); b²=a²+c²−2×a×c×cos(γ); c²=a²+b²−2×a×b×cos(α).
Из полученных равенств выразите косинусы углов: cos(β)=(b²+c²−a²)÷(2×b×c); cos(γ)=(a²+c²−b²)÷(2×a×c); cos(α)=(a²+b²−c²)÷(2×a×b). Теперь, когда известны косинусы углов треугольника, чтобы найти сами углы воспользуйтесь таблицами Брадиса или возьмите из этих выражений арккосинусы: β=arccos(cos(β)); γ=arccos(cos(γ)); α=arccos(cos(α)).
Например, пусть a=3, b=7, c=6. Тогда cos(α)=(3²+7²−6²)÷(2×3×7)=11/21 и α≈58,4°; cos(β)=(7²+6²−3²)÷(2×7×6)=19/21 и β≈25,2°; cos(γ)=(3²+6²−7²)÷(2×3×6)=-1/9 и γ≈96,4°.
Эту же задачу можно решить другим способом через площадь треугольника. Сначала найдите полупериметр треугольника по формуле p=(a+b+c)÷2. Затем посчитайте площадь треугольника по формуле Герона S=√(p×(p−a)×(p−b)×(p−c)), то есть площадь треугольника равна квадратному корню из произведения полупериметра треугольника и разностей полупериметра и каждой из сторон треугольника.
С другой стороны, площадь треугольника равна половине произведения длин двух сторон на синус угла между ними. Получается S=0,5×a×b×sin(α)=0,5×b×c×sin(β)=0,5×a×c×sin(γ). Теперь из этой формулы выразите синусы углов и подставьте полученное в 5 шаге значение площади треугольника: sin(α)=2×S÷(a×b); sin(β)=2×S÷(b×c); sin(γ)=2×S÷(a×c). Таким образом, зная синусы углов, чтобы найти градусную меру, используйте таблицы Брадиса или посчитайте арксинусы этих выражений: β=arccsin(sin(β)); γ=arcsin(sin(γ)); α=arcsin(sin(α)).
Например, пусть дан такой же треугольник со сторонами a=3, b=7, c=6. Полупериметр равен p=(3+7+6)÷2=8, площадь S=√(8×(8−3)×(8−7)×(8−6))=4√5. Тогда sin(α)=2×4√5÷(3×7)=8√5/21 и α≈58,4°; sin(β)=2×4√5÷(7×6)=4√5/21 и β≈25,2°; sin(γ)=2×4√5÷(3×6)=4√5/9 и γ≈96,4°.
По сторонам треугольника найти его углы
Чтобы по сторонам треугольника найти его углы, нужно применить теорему косинусов.
Рассмотрим треугольник ABC.
Обозначим BC=a, AC=b, AB=c,
Аналогично как следствие из теоремы косинусов находятся косинусы других углов треугольника:
Прежде чем рассмотреть на конкретных примерах, как по сторонам треугольника найти его углы, выясним, как по таблицам Брадиса по значению синуса или косинуса определить угол.
Формула найти угол треугольника
Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.
От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.
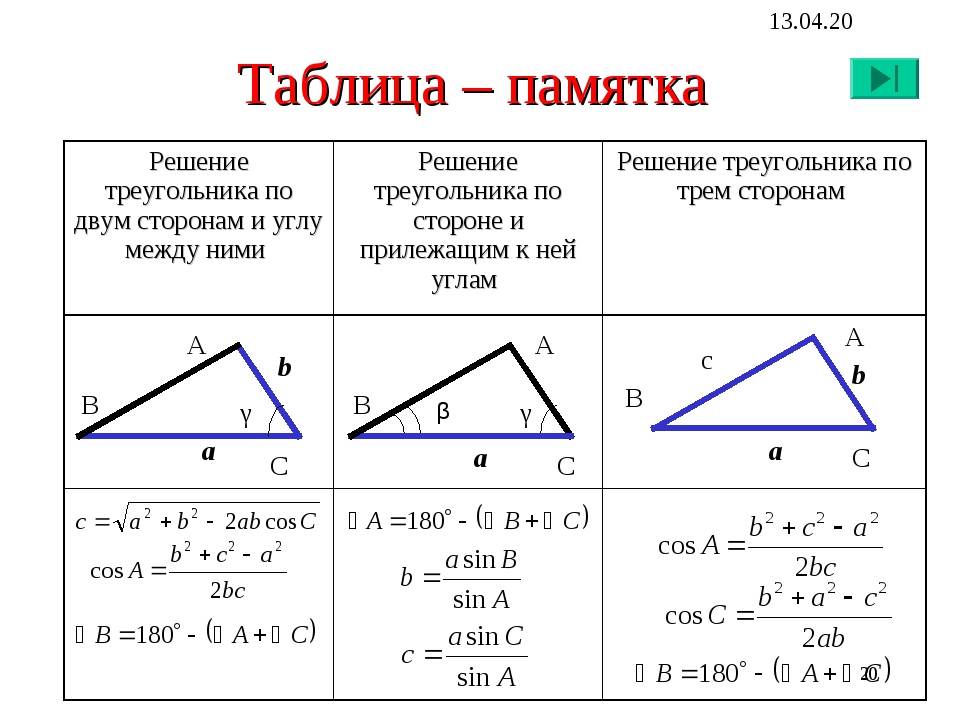
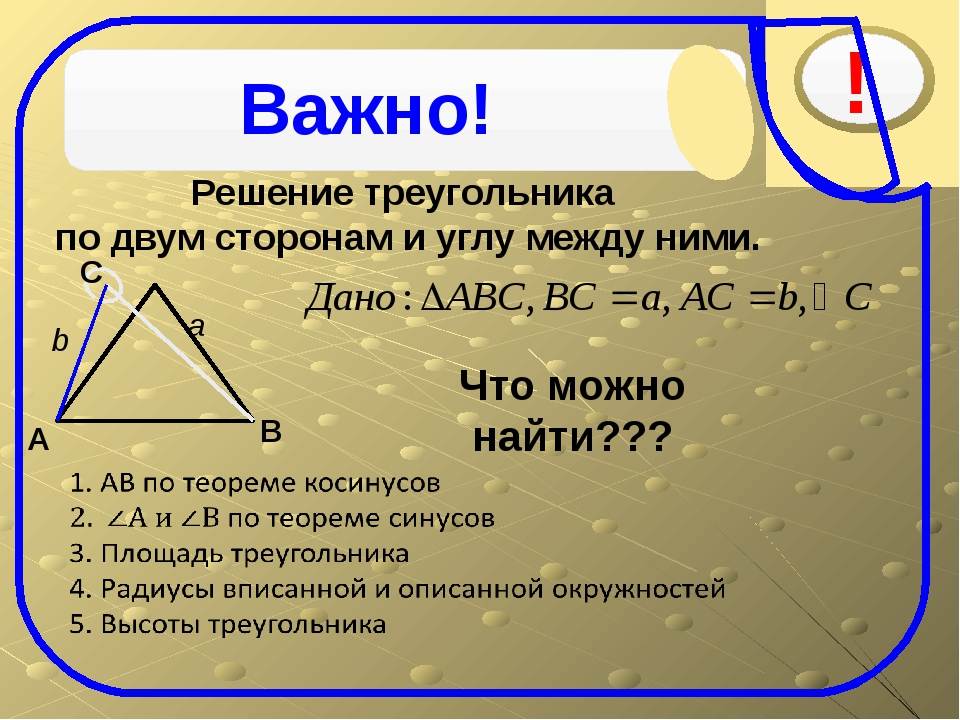
Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).
Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c»/> a»/> b»/>
В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.
Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)
Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
c – гипотенуза
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Решение прямоугольного треугольника по двум сторонам
Если известны катет a и гипотенуза c
Второй катет b определится по теореме Пифагора:
Угол A определится по формуле синуса:
Поскольку сумма всех углов треугольника равна 180 ° то второй острый угол определится так:
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и гипотенуза)
Если известны катеты a и b
Гипотенуза с определится по теореме Пифагора:
Угол A определится по формуле тангенса:
Поскольку сумма всех углов треугольника равна 180 ° то второй острый угол определится так:
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и катет)
Решение прямоугольного треугольника по стороне и острому углу
Если дан острый угол A, то B найдется по формуле:
Как найти углы прямоугольного треугольника
Онлайн калькулятор
Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
Введите их в соответствующие поля и получите результат.
Найти угол α зная угол β и наоборот
Формула
Найти углы прямоугольного треугольника зная катеты
Катет a =
Катет b =
Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?
Формулы
Пример
Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:
Найти углы прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет =
Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?
Расчет угла треугольника по трем сторонам
Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.
α = 180°-β-γ
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.
a 2 = b 2 + c 2 + 2abc cos (α)
Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:
cos (α) = (b 2 + c 2 — a 2 ) / 2bc
,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.
Он-лайн калькулятор плоских треугольников. Расчет треугольника по трем сторонам, двум сторонам и углу между, а так же двум углам и прилегающей к ним стороне.
Для начала выберете требующийся вам метод расчета треугольника нажав на одну из трех кнопок. Далее справа, в зависимости от метода расчета, введите длины сторон и величину углов. После следует нажать на кнопку “Рассчитать”.
Если вы заметили ошибку или у вас есть предложения по улучшению работы калькулятора расчета треугольника сообщите нам, пожалуйста, об этом. Написать можно прямо на этой странице ниже в комментариях или воспользовавшись формой контакты
В градусах 60минут. А у вашего сайты в градусе 100 минут.( считает минуты до ста и прибавляет градус). Могут быть большие погрешности. Исправьте пожалуйста
спасибо…
подумаем, как исправить 🙂
как скачать именно такой калькулятор для расчета треугольника спасибо отлично
боюсь, что никак
калькулятор работает только на сайте
Можно на телефоне воспользоватся функцией на телефоне в гугле “Добавить на главный экран” и у вас в понели телефона появится ярлык – ссылка, и вас будет перекижывать на этот сайт;) удачи!
Это десятичные градусы, после точки идут не минуты, а десятые градуса, так что всё правильно. Для расчёта здесь нужно перевести минуты в градусы, поделив на 60, и прибавить полученное к числу градусов, например, 60°30′ = 60,5°
Большое Человеческое Спасибо.
после запятой не минуты а сотые доли градуса, 60 умножте на то что после запятой и получите минуты.
Часто пользовался. Перестал работать… 🙁
спасибо что подсказали! сейчас должно работать..
В треугольнике только первый угол определяет по времени начертания и только одну сторону с ее углами. Сторона не определяют размеров углов /Шпаков А.А. Начальная методология. М., 458 с., 3013 г./..
На практике, нужно учитывать еще и толщину материала. К примеру, треугольник из рейки толщиной 30.
Цены бы небыло такой проге. 🙂
А как рассчитать длину катетов, в равнобедренном прямоугольном треугольнике, по длине гипотенузы?
площадь прямоугольного треугольника равна 64см2,найти его катеты если один из них в 2 раза больше другого
А как насчёт тройки a, b и альфа?
Спасибо огромное!! Очень помогли в работе. Удобный и понятный интерфейс
А где найти алгоритм для решения более сложной задачи- решить треугольник по углу пересечения биссектрис
Можно ли рассчитать треугольник с точностью хотя бы до тысячных. Решение с большими цифрами приводит к очень большой погрешности. Даже сумма углов треугольника не получается 180.
Не работает. При нажатии на кнопку “Рассчитать” просто ничего не происходит. “Опера”.
Да вроде работает.. и в опере..
Чет не работает. Никакой реакции на кнопку “Рассчитать” в режиме “2 угла(по 80*)+сторона(60)”
у меня работает.. все норм..
Большое спасибо за сайт! Очень помогает.
а как рассчитать углы в неправильном шестиугольнике по сторонам?
пробовала разбить его на треугольники, но получается известны только 2 стороны.
Спасибо.
Помогите расчитать объем бетона в кубах. длина 36.200мм ширина 8.800мм толщина по ширине с отметки А 150мм идет до отметки Б 60мм.
Здравствуйте! А можно сделать точность указание углов до тысячной доли?
Мне необходимо рассчитать секунды!
Спасибо большое! Економия времени и труда
И все таки в Опере не работает…
Спасибо! Не думал что так просто все можно подсчитать!
для прямоугольного треугольника калькулятор не работает. Проверяю стороны по теореме Пифагора расхождение сумм квадратов катетов и квадрата гипотенузы более чем в два раза!
У меня все нормально считает. В треугольнике прямой угол есть?
Делаю лестницы. Размеры 3-5-7 метров. Очень удобно считать наклон размеры стутенек. И изменять какие-то размеры без всяких заморочек. Спасибо
Спасибо, очень помогли.
помогите рассчитать гипотенузу в прямоугольном треугольнике, если угол А равен 10 градусам, а основание (прилегающий катет в) равно 12 метрам
не понимаю ничего…..прямоугольный треугольник один катет есть, угол есть какой длины другорй катет. помогите
Не самый лучший калькулятор.
Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
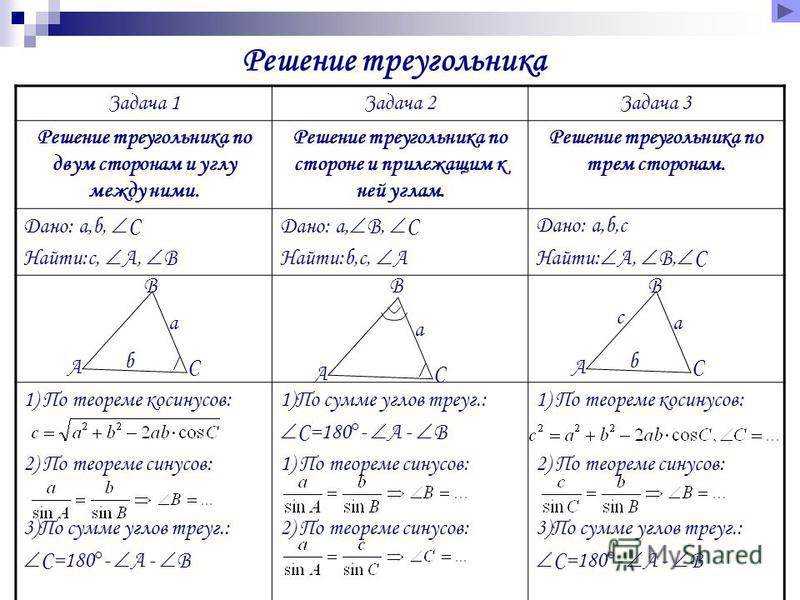
Решение треугольников.
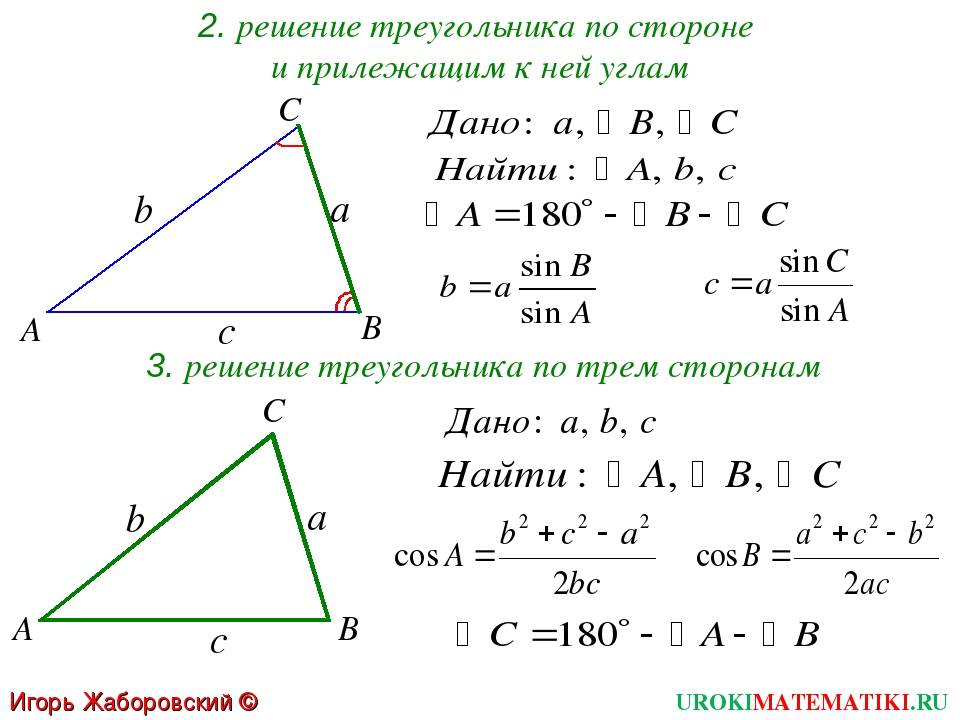
Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Эта математическая программа находит сторону \( c \), углы \( \alpha \) и \( \beta \) по заданным пользователем сторонам \( a, b \) и углу между ними \( \gamma \)
Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Введите стороны \( a, b \) и угол между ними \( \gamma \) Решить треугольник
Калькулятор сторон и углов треугольника
Подключиться к телеграм-каналу «Учи английский». Онлайн-курс английского языка для начинающих.
Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,
A = CAB, B = ABC, C = BCA − углы, противолежащие сторонам a, b, c соответственно.
Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле «Текст с картинки». Нажмите «Решить».
Калькулятор треугольника нужен, если требуется найти решение треугольников – длины сторон и величину углов треугольника.
Решить треугольник − найти все углы и стороны треугольника. Данный калькулятор предназначен для нахождения элементов треугольника.
Как решить треугольник
Здесь размещен онлайн-калькулятор, с помощью которого можно решить треугольник по трем, двум сторонам и углам, по теореме синусов и косинусов, то есть показывается, как находить углы в треугольнике.
Решение треугольников можно находить с помощью таблицы Брадиса. Здесь ответ вычисляется автоматически компьютерной программой онлайн, быстро и удобно.
Если нужны формулы и решения задач на теоремы косинусов и синусов с ответами, то можно найти подробное и точное решение, если использовать бесплатный калькулятор треугольника.
В решении подробно показывается, как найти третью сторону по двум сторонам и углу между ними или как определить неизвестные стороны треугольника, если известна одна сторона.
Примеры решений практических задач
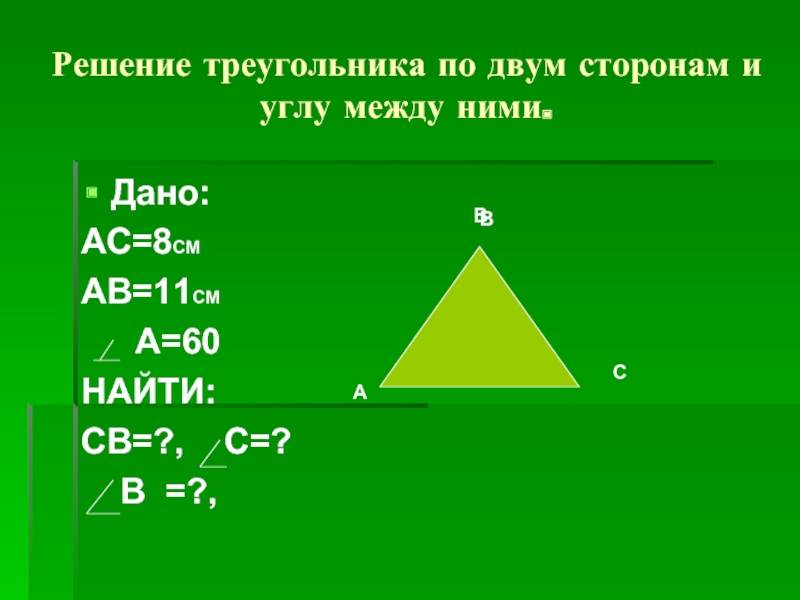
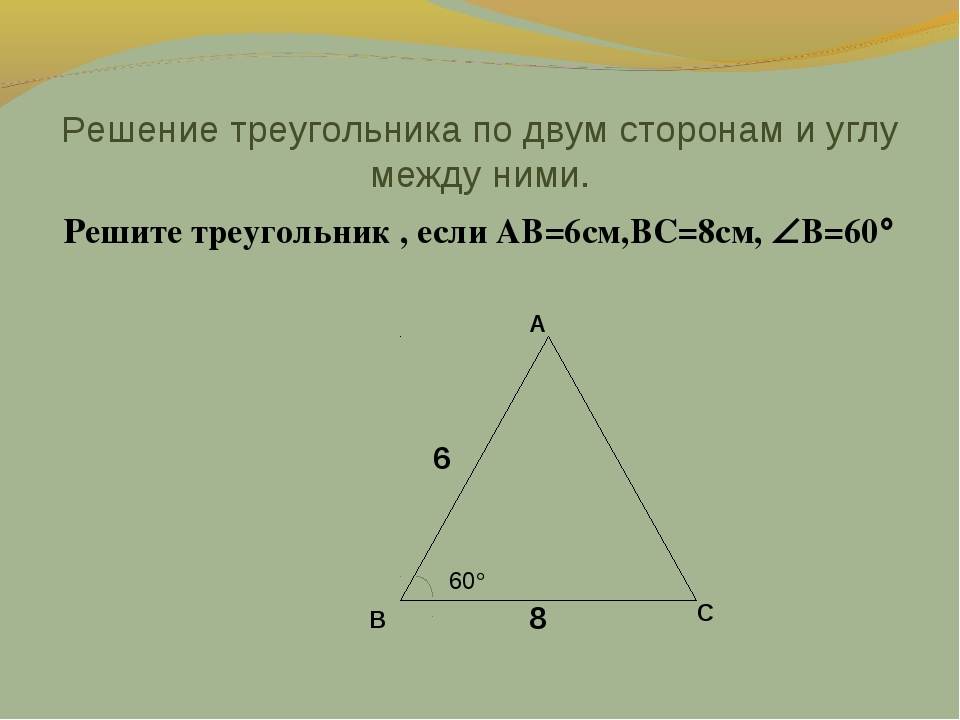
1) решить треугольник по двум сторонам и противолежащему углу, т.е. углу между ними. Даны стороны а = 12 см, b = 8 см, угол=60°. Для того, чтобы решить задачу, требуется указать в онлайн-форме на данной странице условия задачи. В поле для стороны «a» указывается 12, в поле для стороны «b» ставится 8, в поле для углов «A» указывается 60. Нажать «Решить».
В ходе решения задачи получаем ответ:
сторона c = 13,8 см;
угол B = 35,2644° = 35°15’52» = 35°16′ = 0,1959π = 0,6155 rad;
угол C = 84,7356° = 84°44’8» = 84°44′ = 0,4708π = 1,4789 rad;
Периметр = 33,8 см;
Полупериметр = 16,9 см;
Площадь = 47,7984 см 2 ;
Высота ha = 7,9664 см;
Высота hb = 11,9496 см;
Высота hc = 6,9273 см;
Медиана ma = 9,5513 см;
Медиана mb = 12,2958 см;
Медиана mc = 7,5107 см;
Радиус окружности R, описанной около треугольника = 6,9291 см;
Радиус окружности r, вписанной в треугольник = 2,8283 см.
Таким образом, был найден угол треугольника по двум сторонам и углу.
2) как найти угол треугольника, зная его стороны или решите треугольник по трем сторонам. Даны три стороны a = 2 см, b = 3 см, c = 4 см. В поле онлайн-формы «a» ставим 2, в поле «b» указываем 3, в поле «c» ставим 4. Далее следует нажать «Решить».
Используя теорему косинусов, получаем
угол A = 28,955° = 28°57’18» = 28°57′ = 0,1609π = 0,5054 rad;
угол B = 46,5675° = 46°34’3» = 46°34′ = 0,2587π = 0,8128 rad;
угол C = 104,4775° = 104°28’39» = 104°29′ = 0,5804π = 1,8235 rad;
Периметр = 9 см;
Полупериметр = 4,5 см;
Площадь = 2,9046 см 2 ;
Высота ha = 2,9046 см;
Высота hb = 1,9364 см;
Высота hc = 1,4523 см;
Медиана ma = 3,3912 см;
Медиана mb = 2,7839 см;
Медиана mc = 1,5811 см;
Радиус окружности R, описанной около треугольника = 2,0657 см;
Радиус окружности r, вписанной в треугольник = 0,6455 см.
Таким образом, были найдены все углы треугольника.
3) решить треугольник по двум углам и стороне. В треугольнике ABC сторона a = 5 см, два угла B = 30°, C = 45°.
Ответ:
сторона b = 2,59 см;
сторона c = 3,66 см;
угол A = 105° = 0,5833π = 1,8326 rad;
Периметр = 11,25 см;
Полупериметр = 5,625 см;
Площадь = 4,5785 см 2 ;
Высота ha = 1,8314 см;
Высота hb = 3,5355 см;
Высота hc = 2,5019 см;
Медиана ma = 1,9488 см;
Медиана mb = 4,1857 см;
Медиана mc = 3,537 см;
Радиус окружности R, описанной около треугольника = 2,588 см;
Радиус окружности r, вписанной в треугольник = 0,814 см.
Треугольники
Треугольник – многоугольник, который состоит из трех точек, соединенных тремя отрезками. Три точки в этом многоугольнике – вершины треугольника, а отрезки – стороны или ребра треугольника. На рисунке показан треугольник ΔABC, где A, B, C – его вершины, а AB, BC, AC – его стороны. Вершины треугольника дают треугольнику его обозначение. Угол при вершине A образуется сторонами AB и AC, обозначается как угол CAB.
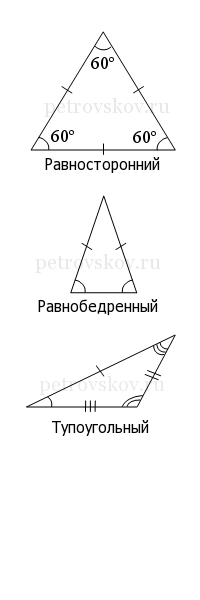
Треугольники бывают разными. Название треугольников зависит от длины его сторон и величины его углов.
Стороны треугольника
Равносторонний или правильный треугольник состоит из трех равных сторон и трех равных углов. Все три угла в равностороннем треугольнике равны 60 градусам. 
Если в треугольнике две стороны имеют одинаковую длину, то это равнобедренный треугольник.
В равнобедренном треугольнике две равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Теоремы равнобедренных треугольников:
1) углы при основании равны,
2) если в треугольнике два угла равны, то это равнобедренный треугольник,
3) медиана, которая проведена к основанию, является биссектрисой и высотой.
Равные стороны в треугольниках обозначают одним, двумя или тремя штрихами или черточками, равные углы – одной, двумя или тремя дуговыми линиями.
Углы треугольника
Треугольники бывают остроугольными, тупоугольными и прямоугольными.
Треугольник является прямоугольным, если один из трех углов треугольника равен 90 градусам. Сторона, которая расположена напротив угла в 90 градусов, называется гипотенузой. Гипотенуза – самая большая сторона в прямоугольном треугольнике. Две другие стороны называются катетами.
Тупоугольный треугольник – треугольник, в котором один из углов больше 90 градусов.
Остроугольный треугольник – треугольник, в котором все три угла меньше 90 градусов.
Свойства треугольников
В треугольнике только один угол может быть больше 90 градусов.
В треугольнике сумма углов равна 180 градусам.
Внешний угол треугольника – смежный угол при этой вершине.
Варианты, как найти внешний угол при вершине:
а) суммировать два внутренних угла, не смежных с ним,
б) вычислить разность между 180 и внутренним углом этой вершины.
Если сложить любые две стороны треугольника, то сумма длин этих сторон всегда больше длины третьей стороны.
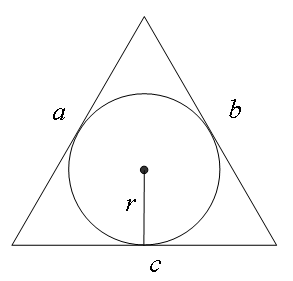
Радиус вписанной окружности
Окружность, вписанная в треугольник, – это круг, расположенный внутри треугольника. 
Радиус этого круга (r) – отрезок, проведенный из центра вписанной окружности перпендикулярно к одной из сторон треугольника.
Центр вписанной окружности – точка пересечения двух биссектрис и равноудален от каждой стороны треугольника.
Для вычисления радиуса вписанной окружности используются площадь и периметр треугольника
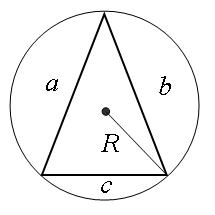
Радиус описанной окружности
Окружность, описанная около треугольника, проходит через 3 вершины треугольника. 
Для вычисления радиуса описанной окружности (R) используются площадь и длины всех сторон треугольника.
Как найти углы треугольника по сторонам
Внешние углы треугольника
Построим некоторый треуг-к, а потом продлим одну из его сторон. На рисунке мы продлили сторону АС. В результате образуется угол, который называют внешним углом треугольника:
В итоге мы доказали, что внешний угол треугольника равен сумме двух углов треуг-ка, которые с ним не смежны.
Задание. У ∆АВС ∠А = 50°, ∠В = 75°. Найдите величину внешнего угла, смежного с ∠С.
Решение. В данном случае, согласно доказанному нами правилу, достаточно просто сложить ∠А и ∠B:
Рассмотрим ещё несколько более тяжелых задач.
Задание. В ∆АВС проведены биссектрисы угловА и B. Они пересекаются в точке М. Известно, что ∠А = 58°, ∠B = 96°. Найдите ∠АМB.
Решение. Устно такую задачу не решить, поэтому построим рисунок:
АМ – это биссектриса, а она разбивает∠ВАС на два равных угла. Поэтому мы можем вычислить ∠ВАМ:
Отметим найденные углы на рисунке:
Обратите внимание на ∆АВМ, который выделен красным цветом. Теперь мы знаем два угла в нем
Значит, можно найти и третий! Запишем для ∆АВМ сумму его углов:
Задание. Построен внешний угол равнобедренного треугольника, который смежен с вершиной, лежащей против основания. Далее построили биссектрису этого внешнего угла. Докажите, что эта биссектриса будет параллельна основанию.
Решение. Выполним построение:
Пусть АС – это основание рав-бедр. ∆АВС. Тогда внешний угол должен быть проведен к вершине В, ведь именно она лежит против основания. Обозначим внешний угол как ∠СВD (для этого мы просто добавили точку Dна продолжение отрезка АВ). Далее проводим биссектрису ВК. Нам требуется доказать, что ВК||АС.
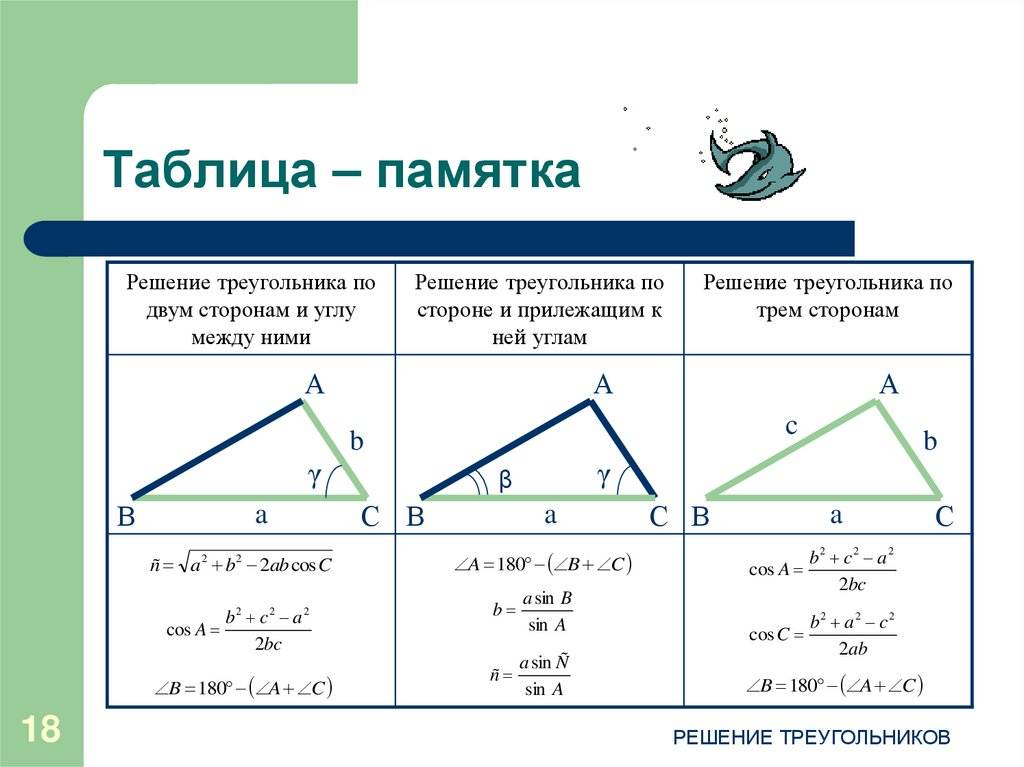
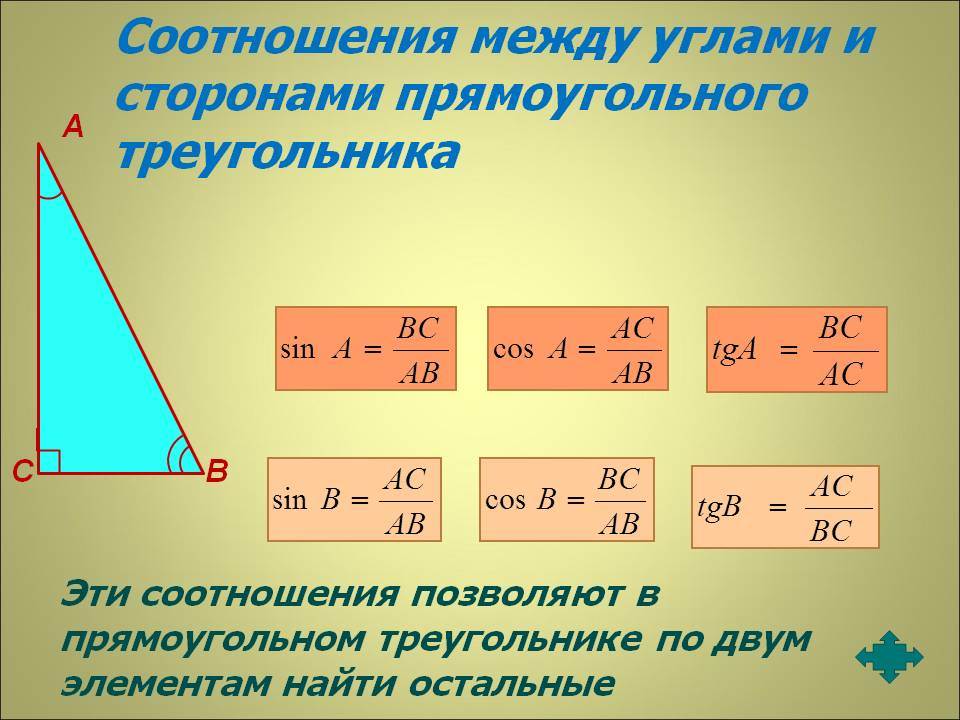
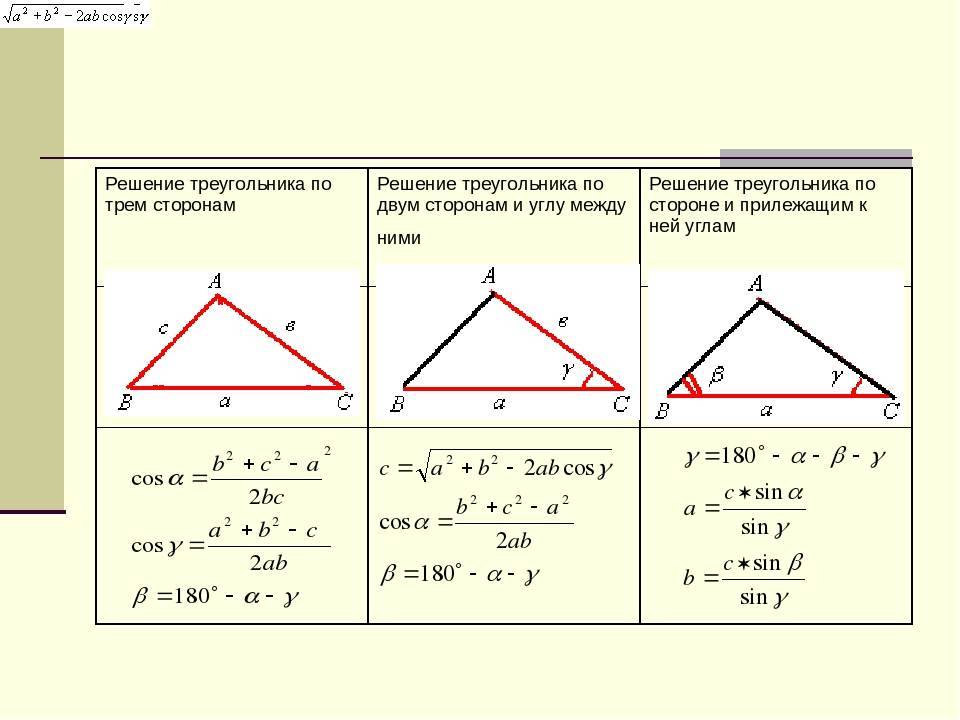
Поступим очень просто – обозначим неизвестную нам величину угла при основании как х. То есть
В результате мы получили, что и ∠С, и ∠CBK равны х, то есть они равны и друг другу. Однако эти углы являются накрест лежащими для прямых АС и ВК и секущей ВС. Из равенства накрест лежащих углов следует, что АС||ВК.
Задание. В ∆АВС проведена медиана АМ, причем ее длина равна ВМ. Найдите ∠А.
Решение. Напомним, что медиана – это прямая, разбивающая сторону на два равных отрезка. То есть ВМ = МС. По условию АМ = ВМ, значит, имеет место двойное равенство:
Посмотрите на рисунок – здесь есть сразу два рав-бедр. треуг-ка! Это ∆АВМ (с основанием АВ) и ∆АМС (с основанием АМС). Обозначим∠В как х, а ∠С – как у. Углы при основании рав-бедр. треуг-ков одинаковы, а потому
Неравенство треугольника
Следующая важная теорема называется неравенством треугольника:
Попробуем доказать неравенство треугольника. Возьмем произвольный ∆АВС и покажем, что сторона АВ меньше, чем величина ВС + АС. Для этого «дорисуем» к отрезку АС ещё один отрезок СD, равный BC, при этом АС и СD должны лежать на одной прямой:
Так как AD = АС + СD, то нам достаточно показать, что АВ
Получается, что в ∆АВD сторона АВ лежит против меньшего угла по сравнению со стороной АD. Значит, эта сторона должна быть меньше АD, что мы и пытаемся доказать.
Доказанная теорема означает, что не всякий треуг-к можно построить по его сторонам. Так, у нас никогда не получится построить треуг-к, у которого стороны равны 2, 3 и 7 см, так как одна из этих длин больше, чем сумма двух других:
Верно обратное утверждение – если все заданные длины удовлетворяют неравенству, то треуг-к построить можно.
Задание. Известны две стороны равнобедренного треугольника, они равны 25 и 10 см. Какая из них является основанием?
Решение. Рассмотрим сперва случай, когда основание равно 25 см. Тогда две другие стороны имеют длину 10 см. Их сумма (10 см + 10 см = 20 см) меньше основания. Такая ситуация невозможно из-за неравенства треуг-ка.
Ситуация же, при которой основание имеет длину 10 см, вполне допустима. Тогда две другие стороны равны 25 см, и для каждой стороны неравенство треуг-ка выполняется:
Прямоугольная фигура
С незапамятных времен человечество интересовалось свойствами геометрических объектов. Одним из них был прямоугольный треугольник, который еще в Древнем Египте считался священным, поскольку обладал характерными для него особенностями (речь идет о фигуре, соотношение сторон которой находится в отношении 3:4:5). Большие достижения в области изучения геометрических свойств рассматриваемой фигуры имели философы античной Греции, среди которых выделяется имя Пифагора.
Составляющие элементы и теорема Пифагора
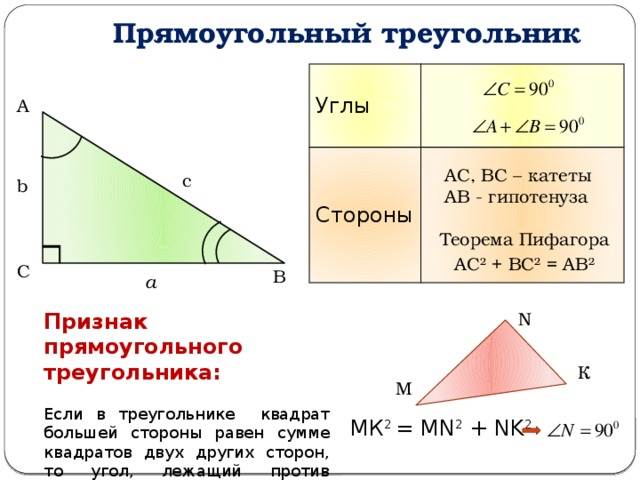
Поскольку речь идет о треугольнике, то для него также характерно наличие трех сторон и трех внутренних углов. Однако, в отличие от остальных фигур данного вида, прямоугольный треугольник имеет один угол равный 90 °. Остальные два угла всегда являются острыми, что следует из фиксированной суммы их значений (180 °).
Чтобы узнать, как называются стороны прямоугольного треугольника, следует рассмотреть его рисунок.
Стороны a и b образуют прямой угол. Они называются катетами. Сторона c, которая лежит против угла 90 °, ограничена двумя острыми углами. Она носит название гипотенузы. Эти названия стоит запомнить, поскольку на них основаны все свойства и теоремы для этого типа треугольника.
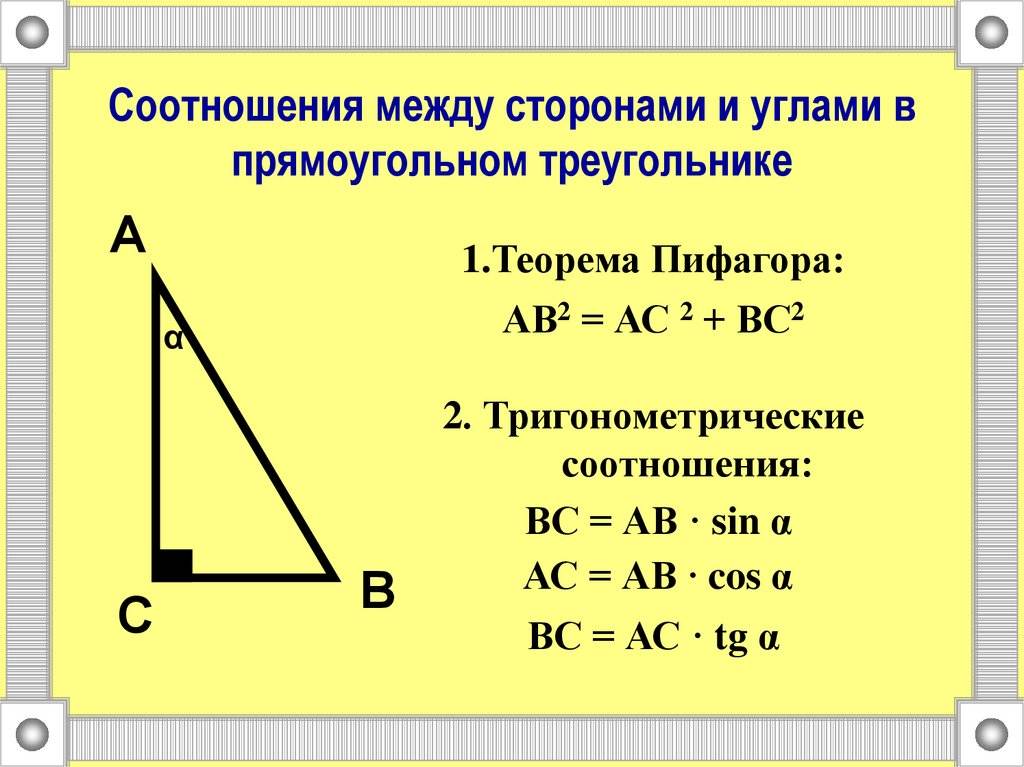
Существует два вида рассматриваемой фигуры:
Касательно равнобедренного прямоугольного геометрического объекта можно сказать, что его катеты друг другу равны, но они никогда не равны гипотенузе. Острые углы в таком треугольнике составляют по 45 °, что легко доказать, применяя теорему синусов, и учитывая, что сумма трех углов соответствует 180 °.
Теорема косинусов для рассматриваемого треугольника произвольной формы вырождается в простое равенство:
c 2 = a 2 + b 2 — 2*a*b*cosC ==>
Оно получается потому, что косинус прямого угла равен нулю согласно свойству этой тригонометрической функции. Формулировка «квадрат гипотенузы в точности соответствует сумме квадратов катетов данного треугольника» носит название известной теоремы Пифагора. Чтобы ее доказать, не прибегая к теореме косинусов, следует провести некоторые геометрические построения.
Основные свойства
Несмотря на общие свойства, которыми обладает прямоугольный треугольник, и которые характерны для любой фигуры с тремя вершинами и тремя сторонами, для него существуют также присущие только ему особенности. Основными из них являются следующие:
Кроме названных свойств, следует отметить, что рассматриваемый геометрический объект является источником определения тригонометрических выражений (синуса, косинуса, котангенса и тангенса). Так, синусом угла ∠ A будет отношения противолежащего ему катета a к гипотенузе c, то есть sinA = a/c. Косинусом этого угла будет отношения ближайшего или прилежащего к нему катета к стороне c: cosA = b/c. Составлены целые таблицы этих функций, которые активно используются при решении геометрических проблем.
Теорема о пересечении высот треугольника
Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.
Далее из \( \small AA_1⊥BC \) следует, что \( \small AA_1⊥B_2C_2 \) поскольку \( \small BC \ ǁ \ B_2C_2 \). Аналогично, \( \small BB_1⊥A_2C_2, \) \( \small CC_1⊥A_2B_2. \) Получили, что \( \small AA_1,\) \( \small BB_1, \) \( \small CC_1\) являются серединными перпендикулярами сторон \( \small B_2C_2, \) \( \small A_2C_2, \) \( \small A_2B_2, \) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.
Точка пересечения высот треугольника называется ортоцентром.
Высота треугольника по двум сторонам и радиусу описанной окружности
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:
Далее, из теоремы синусов имеем:
Подставляя (6) в (7), получим:
Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:
Пример 3. Известны стороны треугольника: \( \small b=7, \) \( \small c= 3 \) и радиус описанной окружности \( \small R=4. \) Найти высоту треугольника, отпущенная на сторону \( \small a. \)
Решение: Проверим сначала условие (9):
Условие (9) удовлетворяется, следовательно такой треугольник существует. Для нахождения выстоты треугольника воспользуется формулой (8). Имеем:
Ответ: \( \small 2\frac<5><8>. \)
Сравнение сторон и углов треугольника
Докажем следующую теорему:
Построим ∆АВС, в котором сторона АВ будет длиннее, чем АС. Нам надо доказать, что ∠С >∠B:
Выполним дополнительное построение – отметим на прямой АВ такую точку D, что AD = АС. Точка D будет располагаться на отрезке АВ, ведь АВ больше АС, а, значит, и больше АD. Также соединим C и D отрезком:
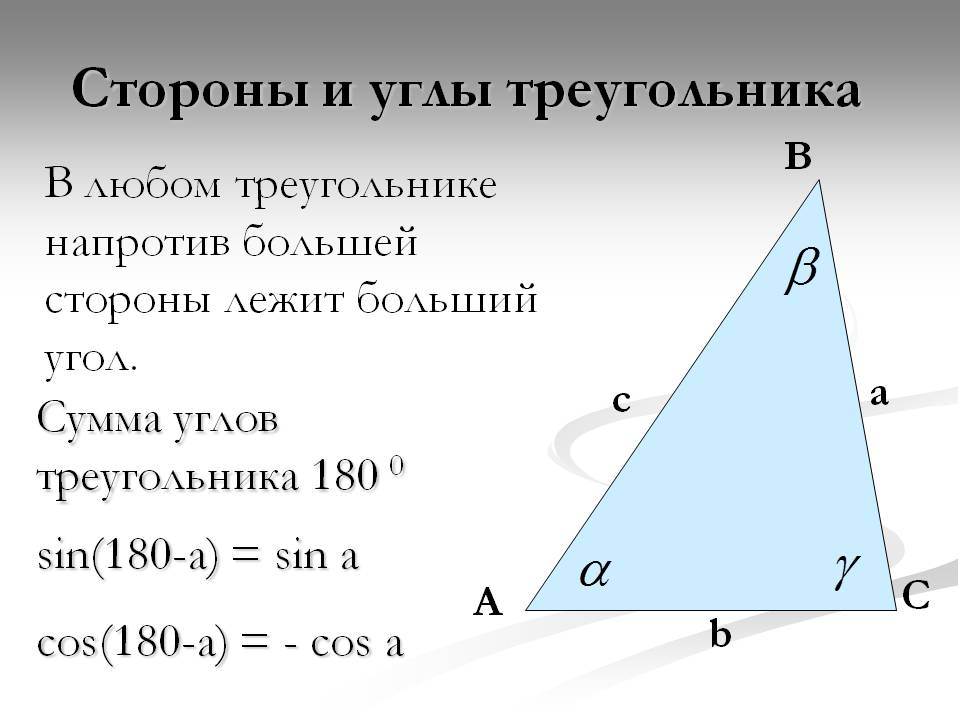
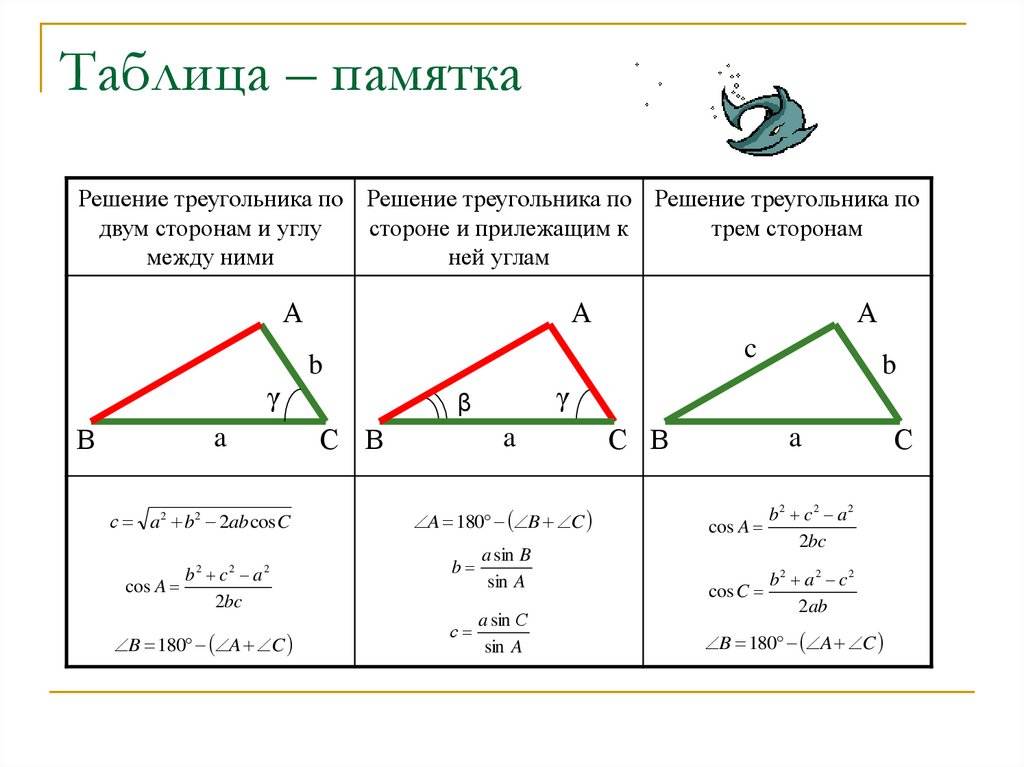
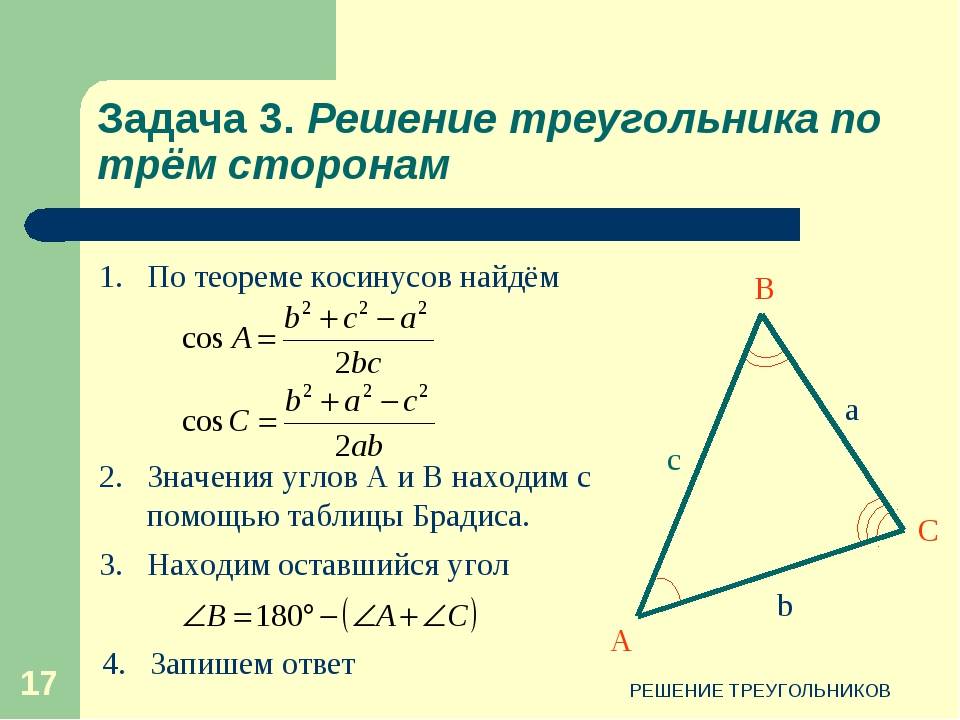
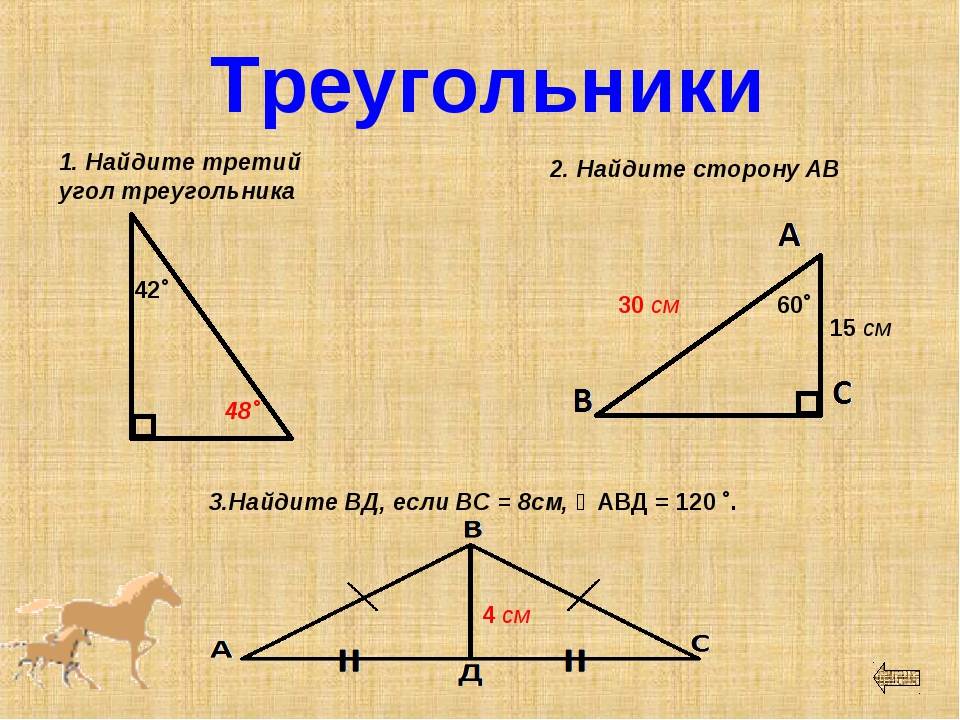
Теперь рассмотрим ∆ADC. Он является рав-бедр., ведь AD = AC. Из этого следует, что ∠ADC = ∠ACD.
Можно заметить, что ∠АDС является внешним углом для ∆BDC. Это значит, что
Мы доказали только первую часть теоремы. Теперь надо доказать обратное утверждение – против большего угла находится большая сторона треугольника. Предположим обратное, что существует ∆АВС, в котором ∠С>∠B, но не выполняется условие АВ >AC. Тогда либо АВ = ВС, либо АВ AC.
Задание. В ∆АВС известны углы:
Запишите стороны этого треуг-ка в порядке возрастания.
Решение. Всё очень просто – чем больше сторона, тем против большего угла она лежит. Поэтому самая большая сторона – это АВ, вторая по длине – АС, а наименьшая сторона – ВС. То есть BС
Доказанная теорема помогает сформулировать важный признак рав-бедр. треуг-ка:
Действительно, против равных углов должны лежать равные стороны, в противном случае сложится ситуация, когда в треуг-ке против сторон разной длины будут лежать равные углы, что невозможно.
Задание. В рав-бедр. ∆АВС основанием является АС. Из точек А и С проведены биссектрисы, которые пересеклись в точке О. Докажите, что ∆АОС также является рав-бедр.
Ясно, что ∠ВАС = ∠ВСА, так как это углы при основании рав-бедр. ∆АВС. С другой стороны, ∠ОАС равен половине ∠ВАС, ведь АО – биссектриса:
В итоге имеем, что ∠ОАС и ∠АСО равны. Но тогда в ∆АОС есть два одинаковых угла, а потому он является рав-бедр. (АО = ОС).
Сумма углов треугольника
Рассмотрим произвольный треугольник АВС. Точки А, В и С не лежат на одной прямой, а потому через В можно провести прямую a, параллельную АС. При этом прямые СВ и АВ окажутся секущими для двух параллельных прямых:
Равные углы (∠1 = ∠2, ∠3 = ∠4) отметим одним цветом. Также обозначим ∠АВС как ∠5:
В результате мы получили, что сумма углов треугольника АВС в точности равна 180°! В итоге мы можем сформулировать следующую теорему:
Задание. В треуг-ке один угол равен 50°, а второй – 60°. Чему равен третий угол этого треуг-ка?
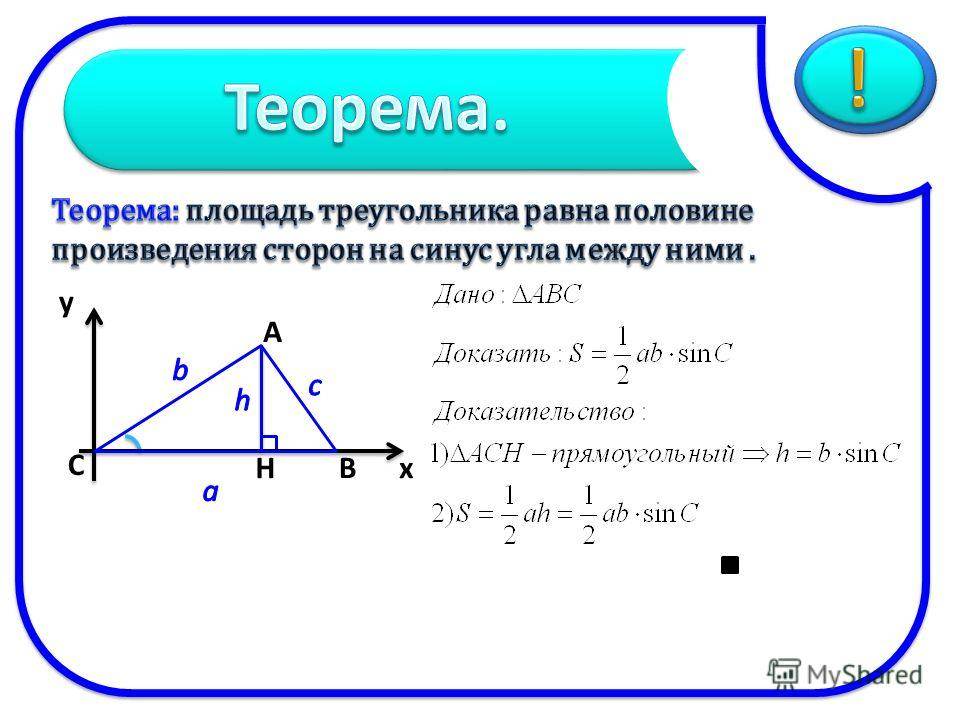
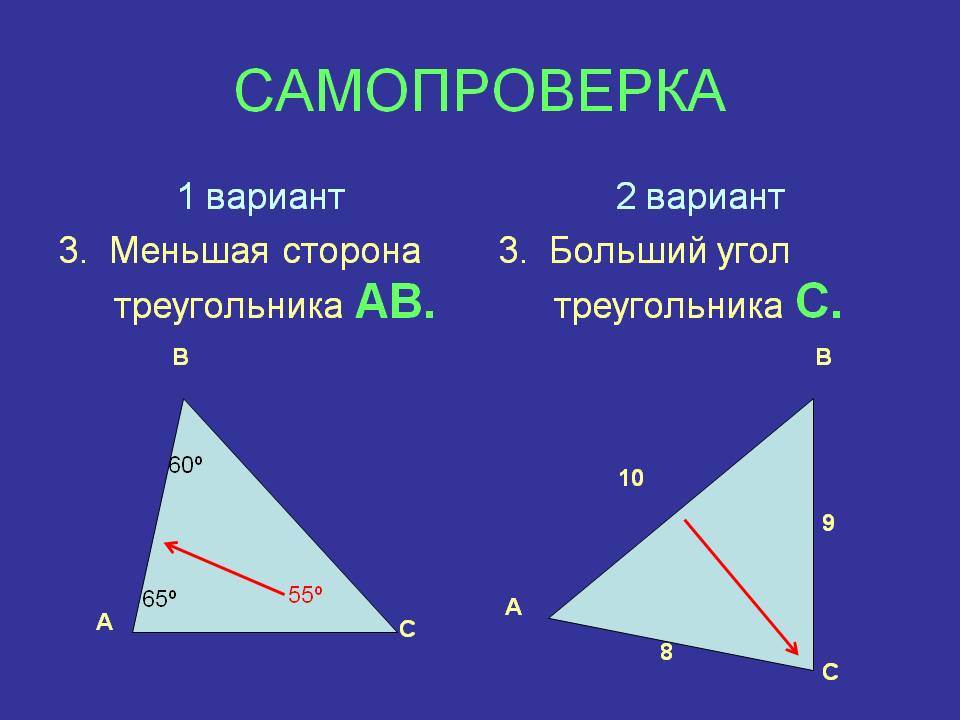
Решение. Обозначим углы треугольника как ∠1, ∠2 и ∠3.
Получили обыкновенное уравнение с одной переменной. Для его решения просто перенесем слагаемые 50° и 60° из левой части в правую:
Задание. Докажите, что у любого треуг-ка есть хотя бы один угол, который не превосходит 60°.
Решение. Докажем это утверждение методом «от противного». Пусть существует такой треуг-к, у которого каждый из углов больше 60°. Это можно записать в виде трех неравенств:
В итоге имеем, что в сумме эти углы больше 180°, а это невозможно. Это противоречие, следовательно, треуг-к с тремя углами, каждый из которых больше 60°, не существует.
Задание. Основанием рав-бедр. ∆АВС является сторона АС. Известно, что ∠В = 40°. Чему равны ∠А и ∠С этого треуг-ка?
Сначала необходимо вспомнить важное свойство – углы равнобедренного треугольника при его основании равны друг другу. В нашем случае это значит, что ∠А = ∠С:
Задание. Один из углов при основании рав-бедр. треуг-ка равен 50°. Найдите два других угла.
Решение. Построим рисунок по условию задачи:
Отдельного внимания заслуживает равносторонний треуг-к. Напомним, что у него равны все три стороны. Построим его:
Теперь подумаем о том, чему равны его углы. С одной стороны, мы можем рассматривать ∆АВС как рав-бедр. с основанием АС, ведь AB = BC. Тогда∠А = ∠С. Но с другой стороны, всё тот же ∆АВС мы можем одновременно считать и рав-бедр. с основанием АВ, ведь АС = ВС. Из этого следует, что ∠А = ∠С. В итоге получаем, что все три угла ∆АВС равны:
Итак, получили удивительный факт – в равностороннем треуг-ке все углы равны 60°!
Рассмотрим чуть более сложную задачу, где неизвестен ни один из углов треуг-ка, однако известны некоторые соотношения между ними.
Задание. Первый угол треуг-ка больше второго в 2 раза, а третий равен сумме первых двух углов. Чему равны углы треуг-ка?
Решение. Для большей наглядности примем первый угол треуг-ка за неизвестную величину, то есть за х. Тогда второй угол будет равен 2х, а третий окажется равным их сумме:
Как найти сторону треугольника?
Безусловно, чаще всего вопрос о том, как же найти неизвестную сторону треугольника возникает при проведении алгебраических или же геометрических расчетов, но иногда такая необходимость возникает и в обычной жизни, например, при построении каких-либо архитектурных чертежей или проведении расчетов.
В настоящий момент времени есть несколько различных способов решения такой задачи. И каждый способ отличается от предыдущего не только формулой, по которой производится расчет, но и исходными данными, которые необходимы для вычисления.
Способы нахождения сторон треугольника
Итак, самым простым и логичным ответом на вопрос: как находить стороны треугольника, является то, что необходимо найти решение по формуле. В зависимости от исходных данных, формулы могут быть самыми разными. Обычно необходимую сторону треугольника можно вычислить по:
Как видно, в любом, из двух названных случаях, все равно необходимо знать значения трех показателей. Без их знания никогда не будет возможным найти ответ на вопрос о том, как находить стороны треугольника.
Как найти неизвестную сторону треугольника
Итак, чтобы найти сторону треугольника которая не известна по условию при помощи первого способа необходимо использовать следующую формулу: с=v(а2+b2-2аb*cosC).
Что касается обозначений данной формулы, то а и b — это длины известных сторон, cosC угол, находящийся между ними.
На самом деле, для решения задачи о том, как найти неизвестную сторону в треугольнике, абсолютно нет никакой необходимости обладать какими-то особыми алгебраическими знаниями, вполне достаточно знать основы.
Но для того, чтобы полученные в ходе вычислений данные были точными, необходимо очень внимательно и правильно производить расчеты, лучше всего провести их два раза, а в случае несоответствия результатов друг другу, произвести расчет еще раз.
Треугольник, имеющий одинаковые стороны
Стандартные формула расчета поиска неизвестной стороны обычного треугольника были приведены выше. Но всегда необходимо помнить о том, что для того, чтобы найти боковую сторону равнобедренного треугольника, они не подходят. И поэтому для решения данного вопроса существуют специальные отдельные формулы, которые подходят лишь для данного треугольника.
Итак, в первую очередь, обязательно нужно помнить, что высота такого треугольника — это, в то же время, и его медиана. А боковая сторона, которую необходимо найти, будет являться его гипотенузой.
Как всем известно, еще со школьной программы, гипотенуза данного треугольника находится по теореме Пифагора.
И хотя, на первый взгляд, может показаться, что вычисление неизвестной стороны любого треугольника весьма сложное и трудоемкое занятие, это не совсем так. Сложным оно будет лишь в первый раз. Главное, правильно следовать формуле для каждой конкретной задачи, и проверять полученный результат несколько раз.
Решение прямоугольного треугольника
Решение прямоугольного треугольника по двум сторонам
Если известны катет a и гипотенуза c
Второй катет b определится по теореме Пифагора:
Угол A определится по формуле синуса:
Поскольку сумма всех углов треугольника равна 180 ° то второй острый угол определится так:
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и гипотенуза)
Если известны катеты a и b
Гипотенуза с определится по теореме Пифагора:
Угол A определится по формуле тангенса:
Поскольку сумма всех углов треугольника равна 180 ° то второй острый угол определится так:
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и катет)
Решение прямоугольного треугольника по стороне и острому углу
Если дан острый угол A, то B найдется по формуле:
Стороны можно найти по следующим формулам:
Вычислить, найти решение прямоугольного треугольника если известны катет a и противолежащий угол A
Здесь все углы мы найдем по формуле (7). Гипотенузу по формуле (14) и второй катет по формуле (16).
Углы равнобедренного треугольника
Треугольник с одинаковыми боковыми сторонами называется равнобедренным. В нем равны и углы при основании. Если они известны, то вычислить третий угол не составит труда. Как известно, сумма всех углов треугольника равна 180°. Если из 180° вычесть сумму двух одинаковых углов при основании (а), то найдем третий угол β:
β = 180°-2α
Если известна величина угла b, противолежащего основанию и требуется найти угол (а) при основании, необходимо из 180° вычесть известный угол β. Полученную величину делим на два, т.к. углы при основании равны.
α= (180°-β)/2
Если известны стороны равнобедренного треугольника, можно рассчитать все его углы. Чтобы найти угол при основании, проведем к основанию высоту, которая делит основание пополам, а треугольник — на два одинаковых прямоугольных треугольника. Гипотенузой вновь образованных треугольников будет боковая сторона равнобедренного треугольника (а), а одним из катетов — половина длины основания (b/2). Используя теорему косинусов определяем косинус угла (а), как отношение прилежащего к искомому углу катета (b/2) к гипотенузе (а) по формуле:
cosα= b/2a
Рассчитать угол при основании равнобедренного треугольника можно также через катеты образованного в нем прямоугольного треугольника (например, abc). Одним из его катетов (b) будет половина длины основания равнобедренного треугольника, другим катетом (а) — высота равнобедренного треугольника. Найти угол α при основании треугольника можно через тангенс угла, как отношение противолежащего ему катета (а) к прилежащему катету (b).
tg (α) = a/b
В таблицк тангенсов находим угол α в градусах. Т.к. Углы при основании равнобедренного треугольника равны, то найти третий угол не составит труда, зная, что сумма всех его углов равна 180°.
как найти угол треугольника если известны 3 стороны
Пусть задан треугольник со сторонами a, b и с. При этом сумма длин двух любых сторон треугольника должна быть больше длины третьей стороны, то есть a+b>c, b+c>a и a+c>b. И необходимо найти градусную меру всех углов этого треугольника. Пусть угол между сторонами a и b обозначен как α, угол между b и c как β, а угол между c и a как γ.
Теорема косинусов звучит так: квадрат длины стороны треугольника равен сумме квадратов двух других длин его сторон минус удвоенное произведение этих длин сторон на косинус угла между ними. То есть составьте три равенства: a²=b²+c²−2×b×c×cos(β); b²=a²+c²−2×a×c×cos(γ); c²=a²+b²−2×a×b×cos(α).
Из полученных равенств выразите косинусы углов: cos(β)=(b²+c²−a²)÷(2×b×c); cos(γ)=(a²+c²−b²)÷(2×a×c); cos(α)=(a²+b²−c²)÷(2×a×b). Теперь, когда известны косинусы углов треугольника, чтобы найти сами углы воспользуйтесь таблицами Брадиса или возьмите из этих выражений арккосинусы: β=arccos(cos(β)); γ=arccos(cos(γ)); α=arccos(cos(α)).
Например, пусть a=3, b=7, c=6. Тогда cos(α)=(3²+7²−6²)÷(2×3×7)=11/21 и α≈58,4°; cos(β)=(7²+6²−3²)÷(2×7×6)=19/21 и β≈25,2°; cos(γ)=(3²+6²−7²)÷(2×3×6)=-1/9 и γ≈96,4°.
Эту же задачу можно решить другим способом через площадь треугольника. Сначала найдите полупериметр треугольника по формуле p=(a+b+c)÷2. Затем посчитайте площадь треугольника по формуле Герона S=√(p×(p−a)×(p−b)×(p−c)), то есть площадь треугольника равна квадратному корню из произведения полупериметра треугольника и разностей полупериметра и каждой из сторон треугольника.
С другой стороны, площадь треугольника равна половине произведения длин двух сторон на синус угла между ними. Получается S=0,5×a×b×sin(α)=0,5×b×c×sin(β)=0,5×a×c×sin(γ). Теперь из этой формулы выразите синусы углов и подставьте полученное в 5 шаге значение площади треугольника: sin(α)=2×S÷(a×b); sin(β)=2×S÷(b×c); sin(γ)=2×S÷(a×c). Таким образом, зная синусы углов, чтобы найти градусную меру, используйте таблицы Брадиса или посчитайте арксинусы этих выражений: β=arccsin(sin(β)); γ=arcsin(sin(γ)); α=arcsin(sin(α)).
Например, пусть дан такой же треугольник со сторонами a=3, b=7, c=6. Полупериметр равен p=(3+7+6)÷2=8, площадь S=√(8×(8−3)×(8−7)×(8−6))=4√5. Тогда sin(α)=2×4√5÷(3×7)=8√5/21 и α≈58,4°; sin(β)=2×4√5÷(7×6)=4√5/21 и β≈25,2°; sin(γ)=2×4√5÷(3×6)=4√5/9 и γ≈96,4°.
Как найти углы треугольника если известны все стороны
От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.
Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).
Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c»/>
a»/>
b»/>
В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.
Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)
Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.
Как найти стороны прямоугольного треугольника
Определение
Тангенс острого угла α (tg α или tan α) – это отношение противолежащего катета (a) к прилежащему (b) в прямоугольном треугольнике.
Равнобедренный треугольник
Одно из свойств равнобедренного треугольника — два его угла равны. Для вычисление значений углов прямоугольного равнобедренного треугольника нужно знать, что:
Если известна величина одного из острых углов, второй можно найти по формуле: β=180º-90º-α, или α=180º-90º-β. Чаще всего это соотношение используется, если один из углов равен 60º или 30º.
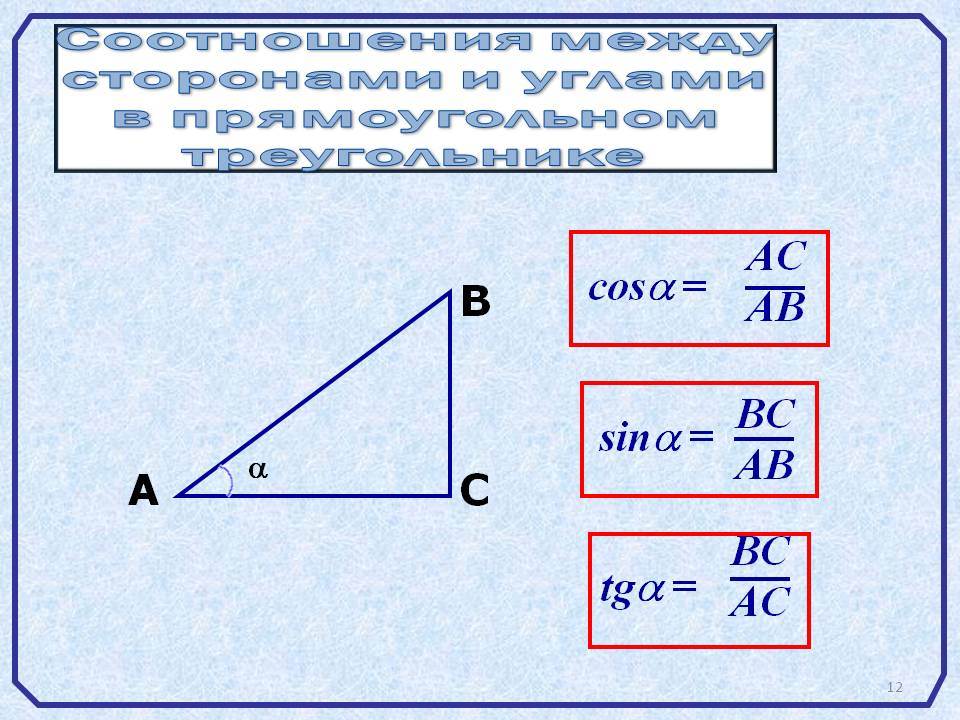
Определение тригонометрических функций.
Соотношения сторон и их связь с функциями:
Благодаря этим определениям легко вычислять значение функций для острых углов, т.е. в интервале 0 – 90° (0 – π/2 рад.).
Найти угол α зная угол β и наоборот
Формула
Задача
Тангенс — это отношение…
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).
Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Сумма углов треугольника
Есть два варианта нахождения общей суммы углов треугольника:
180*(n-2)- где n – количество сторон многоугольника.
Рис. 2. Рисунок к задаче
Пусть треугольник АВС – произвольный треугольник с основанием АС. Тогда построим прямую ВD, проходящую через точку В, параллельно основанию. Тогда получается две параллельные прямые: АС и ВD с двумя секущими АВ и ВС.
Тогда рассмотрим углы при секущих прямых. Сумма трех углов при вершине В будет равна 180 градусам, так как они представляют собой развернутый угол. Тогда внутренние углы треугольника будут равные накрест лежащим наружным углам. То есть сумма углов треугольника равняется градусной мере развернутого угла и равняется 180 градусам.
Важно понимать, что наружные углы нельзя называть внешними углами треугольника, так как внешние углы получаются с помощью продолжения одной из сторон треугольника, а прямая ВD продолжением стороны треугольника не является.
Общая формула суммы углов многоугольника получается с помощью разбиения фигуры на треугольники и подсчета сумм углов получившихся малых фигур.
Решение прямоугольного треугольника по двум сторонам
Если известны катет a и гипотенуза c
Второй катет b определится по теореме Пифагора:
Угол A определится по формуле синуса:
Поскольку сумма всех углов треугольника равна 180 ° то второй острый угол определится так:
Если известны катеты a и b
Гипотенуза с определится по теореме Пифагора:
Угол A определится по формуле тангенса:
Поскольку сумма всех углов треугольника равна 180 ° то второй острый угол определится так:
Свойства тангенса
Ниже в табличном виде представлены основные свойства тангенса с формулами.
Углы прямоугольного треугольника
Треугольник, у которого один угол прямой, называется прямоугольным треугольником. Как известно, сумма всех углов любого треугольника равна 180°. В нашем случае один угол равен 90°, тогда сумма остальных двух тоже равна 90°. Зная один из острых углов, второй находим путем вычитания из 90° величину известного угла.
α = 90°-β
Если известна величина двух катетов прямоугольного треугольника (а, b), находим угол, используя отношения тангенсов.
tg (α) = a/b
Т.е. тангенс угла α, противолежащий катету (стороне) треугольника а, прилежащий к катету (стороне) b равен отношению катета а к катету b (противолежащего к прилежащему). Величину угла в градусах найдем воспользовавшись таблицей тангенсов. Второй угол прямоугольного треугольника (β) определяем путем вычитания из 180° величину прямого угла 90° и величину найденного острого угла (α).
β = 180° — 90° — α
Если известен катет, противолежащий искомому углу (α), и гипотенуза прямоугольного треугольника ©, находим синус острого угла sin (α), как отношение этого катета к гипотенузе.
sin (α) = a/c
Стоит запомнить: в прямоугольном треугольнике напротив катета, в 2 раза меньшего гипотенузы, расположен угол в 30°.
Если известен катет, прилежащий искомому углу, и гипотенуза, можно вычислить косинус этого угла, как отношение прилежащего катета к гипотенузе. Затем в таблице косинусов находим величину угла.
Калькулятор расчета углов прямоугольного треугольника зная длину катетов
Калькулятор расчета углов прямоугольного треугольника зная длину катета и гипотенузы
Найти углы треугольника, если даны 3 стороны
Добавлено через 29 минут
помогите ПЛИЗ срочно.
Добавлено через 33 минуты
Если ввожу к примеру 1/2 то есть 0,5
выводит результат : 1
Добавлено через 18 секунд
как найти сам угол
Найти стороны треугольника, зная его углы и радиус описанной окружности
2)Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны.
Вычислить углы треугольника зная его стороны.
Задание написать прогу но вместо переменной использовать ссылку на неё.Вычислить углы треугольника.
Найти площадь равностороннего треугольника, если известна его стороны
1. Найти площадь равностороннего треугольника, если известна его стороны. 2. Написать программу.
Добавлено через 16 минут
Люди помогите плиз
Добавлено через 12 минут
Блин уже даже и мыслей нету как еще сделать, уже как только не пробивал.
atan2 даёт угол относительно центра координат, поэтому точки нужно смещать (например B2-A2). параметры функции (y, x)
Создать класс Triangle для представления треугольника. Поля данных должны включать углы и стороны.
Создать класс Triangle для представления треугольника. Поля данных должны включать углы и стороны.
Даны три стороны одного и три стороны другого треугольника. Я, чайник нужно в С++
Даны три стороны одного и три стороны другого треугольника. Эти треугольники равновеликие, т.е.
Для треугольника известны три стороны. Найти его площадь, если этот треугольник прямоугольный
Для треугольника известны три стороны. Найти его площадь, если этот треугольник прямоугольный. В.
С клавиатуры вводятся три числа, считая их сторонами треугольника найти углы этого треугольника
с клавиатуры вводятся три числа, считая их сторонами треугольника найти углы этого треугольника.
Как найти углы треугольника по сторонам
Треугольник – это примитивный многоугольник, ограниченный на плоскости тремя точками и тремя отрезками попарно соединяющими эти точки. Углы в треугольнике бывают острыми, тупыми и прямыми. Сумма углов в треугольнике величина непрерывная и равна 180 градусам.
Вам понадобится
Инструкция
1. Обозначим длины сторон треугольника a=2, b=3, c=4, а его углы u, v, w, всякий из которых лежит наоборот одной сторон. По теореме косинусов квадрат длины стороны треугольника равен сумме квадратов длин 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними. То есть a^2 = b^2 + c^2 – 2bc*cos(u). Подставим в это выражение длины сторон и получим: 4 = 9 + 16 – 24cos(u).
2. Выразим из полученного равенства cos(u). Получим следующее: cos(u) = 7/8. Дальше найдём собственно угол u. Для этого посчитаем arccos(7/8). То есть угол u = arccos(7/8).
3. Аналогичным образом, выражая другие стороны через остальные, найдём оставшиеся углы.
Полезный совет
Для того, дабы обнаружить все три угла необязательно выражать все три стороны, дозволено обнаружить только 2 угла, а 3-й получить путём вычитания из 180 градусов значения остальных 2-х. Это вытекает из того, что сумма всех углов треугольника величина непрерывная и равна 180 градусам.
Как найти сторону треугольника?
Как найти длину одной из сторон треугольника? Какие есть формулы?
Сейчас на примере я покажу, как нужно их применять.
Есть произвольный треугольник со стороной 18 см, один угол при нем равен 30 градусам, а площадь равна 36 см.кв. Нужно найти две другие стороны. Сделаем рисунок
Для решения задачи проведем к основанию (с=18см) высоту h и тем самым разделим наш треугольник на два прямоугольных.
Исходя из формулы площади, найдем высоту
S = 1/2h*c откуда h = 2S/c = 2*36/18 = 4 см
Теперь находим сторону b по синусу угла
sin = h/b (отношение противоположного катета к гипотенузе) откуда b = h/(sin 30) = 4/(1/2) = 8 см.
Можно по формуле Пифагора
и находим последнюю сторону нашего треугольника
а = кв.к из (c-x)*(c-x) + h*h = кв.к из 18*18-2*18*4*(кв.к3)+4*(кв.к3)*4*(кв.к3)+4*4
здесь стоит обратить внимание, что
4*(кв.к3)*4*(кв.к3)+4*4 = 4*4*3+4*4 = 4*4*4 = 4*2*2*2 = 8*8 = b*b
2*18*4*(кв.к3) = 2*18*4*2*(кв.к3/2) = 2*18*8*(кв.к3/2) = 2*с*b*cos30 и теперь можно записать
Теперь посчитаем и найдем сторону а = 11,772 см.
Существует целый ряд формул, с помощью которых можно найти сторону треугольника.
Рассмотрим 2 варианта:
1) Сторона треугольника через 2 других стороны и угол между ними.
В треугольнике ABC сторона AB = 6 см, сторона AC = 10 см, угол меду ними = 60º.
2) Сторона треугольника через два угла и сторону.
Здесь можно воспользоваться теоремой синусов.
Если даны углы α и β, а также сторона c, то две другие стороны можно найти по формулам:
b = c * (sinβ / sinγ).
c = 10 см, α = 30°, β = 45°.
a = 10 * (0,5 / 0,96) = 5,21 см.
b = 10 * (0,7 / 0,96) = 7,29 см.
Например, для нахождения катетов или гипотенузы можно воспользоваться теоремой Пифагора.
Есть еще формулы для равнобедренного треугольника (это треугольник у которого две стороны равны и углы при оснавании также равны между собой). Для такого треугольника основание можно рассчитать по формулам:
b = 2a*sin(x/2) = a*√(2-2cosx)
Для того чтобы найти равные стороны равнобедренного треугольника можно использовать вот эти формулы:
a = b/(2*sin(x/2)) = b/√(2-2cosx)
Для рассчетов по этим формулам нужно знать длину хотябы одной стороны и хотябы один угол. Так как зная величину одного любого угла в равнобедренном треугольнике можно найти все остальные углы исходя из теоремы о сумме углов треугольника (сумма всех углов любого треугольника равна 180°)
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины, углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
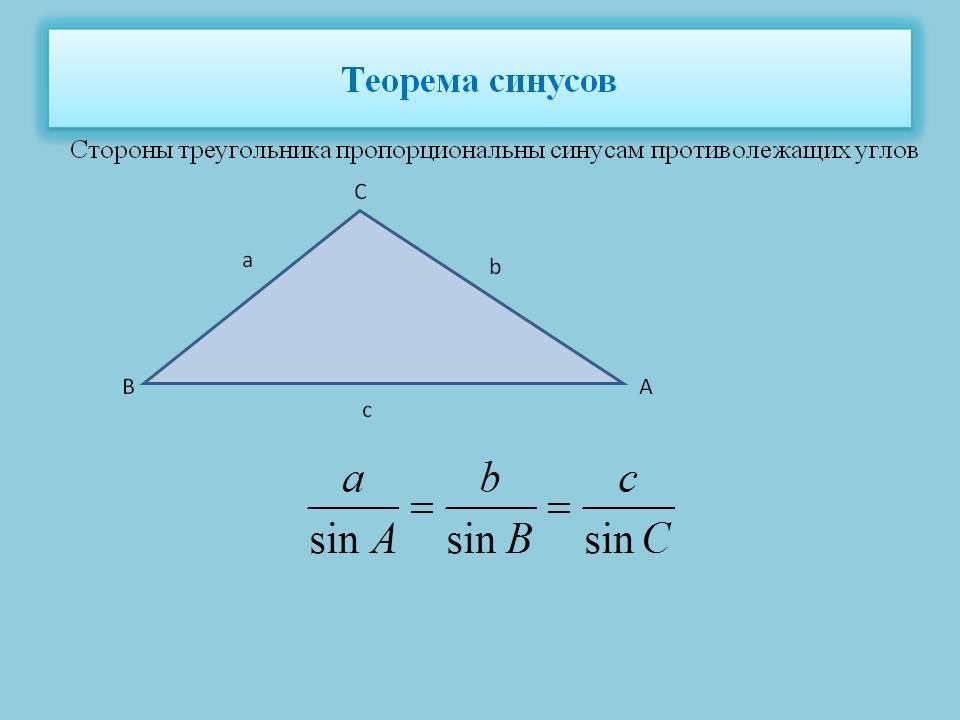
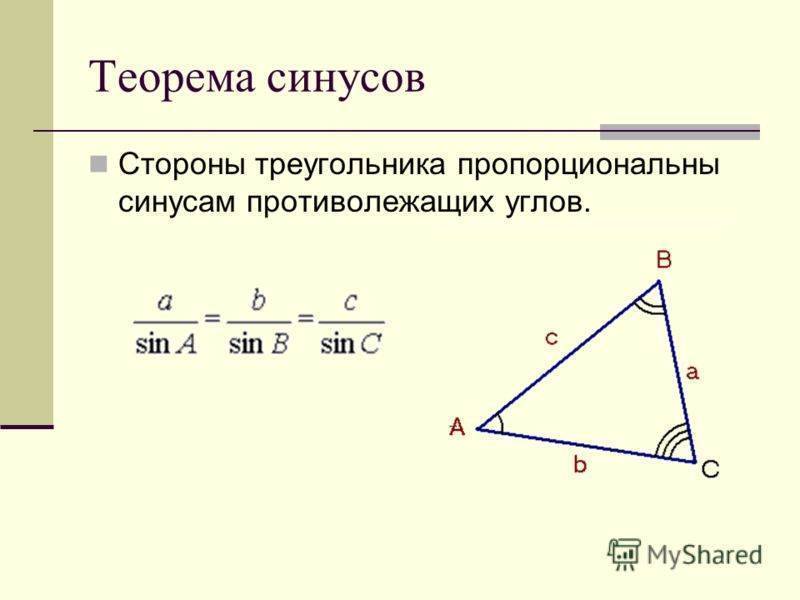
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
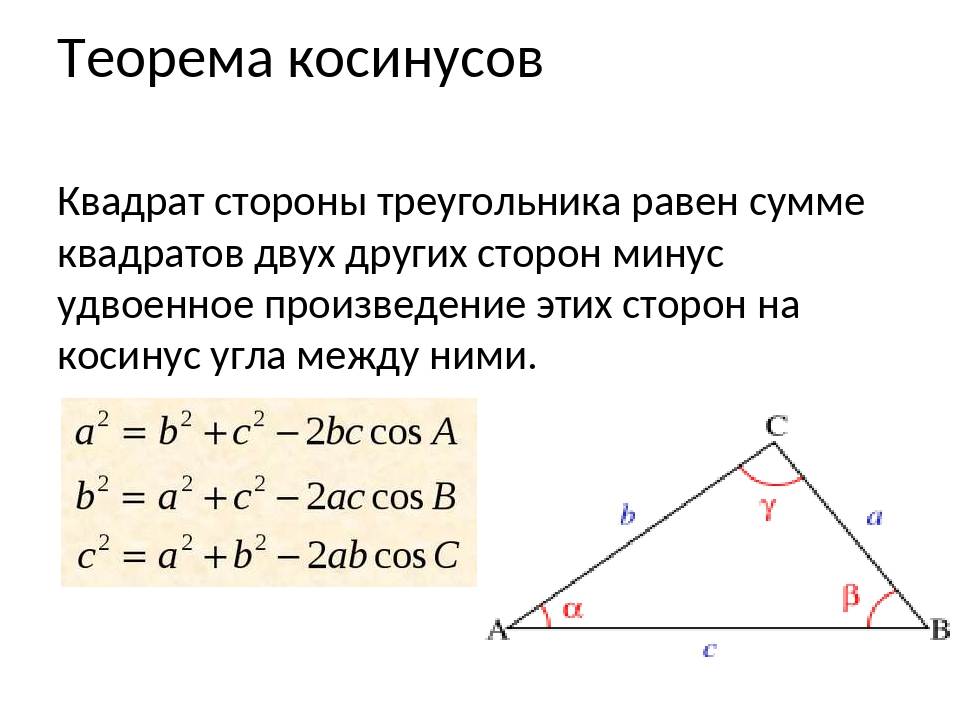
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Геометрия
План урока:
Сумма углов треугольника
Рассмотрим произвольный треугольник АВС. Точки А, В и С не лежат на одной прямой, а потому через В можно провести прямую a, параллельную АС. При этом прямые СВ и АВ окажутся секущими для двух параллельных прямых:
Известно, что секущие образуют пары накрест лежащие углы, причем они равны. Отметим на рисунке эти пары и обозначим их как ∠1, ∠2, ∠3 и ∠ 4.
Равные углы (∠1 = ∠2, ∠3 = ∠4) отметим одним цветом. Также обозначим ∠АВС как ∠5:
С одной стороны, углы 2, 4 и 5 вместе образуют развернутый угол, то есть их сумма равна 180°:
В результате мы получили, что сумма углов треугольника АВС в точности равна 180°! В итоге мы можем сформулировать следующую теорему:
Задание. В треуг-ке один угол равен 50°, а второй – 60°. Чему равен третий угол этого треуг-ка?
Решение. Обозначим углы треугольника как ∠1, ∠2 и ∠3.
Получили обыкновенное уравнение с одной переменной. Для его решения просто перенесем слагаемые 50° и 60° из левой части в правую:
Задание. Докажите, что у любого треуг-ка есть хотя бы один угол, который не превосходит 60°.
Решение. Докажем это утверждение методом «от противного». Пусть существует такой треуг-к, у которого каждый из углов больше 60°. Это можно записать в виде трех неравенств:
В итоге имеем, что в сумме эти углы больше 180°, а это невозможно. Это противоречие, следовательно, треуг-к с тремя углами, каждый из которых больше 60°, не существует.
Задание. Основанием рав-бедр. ∆АВС является сторона АС. Известно, что ∠В = 40°. Чему равны ∠А и ∠С этого треуг-ка?
Решение. Сначала необходимо вспомнить важное свойство – углы равнобедренного треугольника при его основании равны друг другу. В нашем случае это значит, что ∠А = ∠С:
Задание. Один из углов при основании рав-бедр. треуг-ка равен 50°. Найдите два других угла.
Решение. Построим рисунок по условию задачи:
Отдельного внимания заслуживает равносторонний треуг-к. Напомним, что у него равны все три стороны. Построим его:
Теперь подумаем о том, чему равны его углы. С одной стороны, мы можем рассматривать ∆АВС как рав-бедр. с основанием АС, ведь AB = BC. Тогда∠А = ∠С. Но с другой стороны, всё тот же ∆АВС мы можем одновременно считать и рав-бедр. с основанием АВ, ведь АС = ВС. Из этого следует, что ∠А = ∠С. В итоге получаем, что все три угла ∆АВС равны:
Итак, получили удивительный факт – в равностороннем треуг-ке все углы равны 60°!
Рассмотрим чуть более сложную задачу, где неизвестен ни один из углов треуг-ка, однако известны некоторые соотношения между ними.
Задание. Первый угол треуг-ка больше второго в 2 раза, а третий равен сумме первых двух углов. Чему равны углы треуг-ка?
Решение. Для большей наглядности примем первый угол треуг-ка за неизвестную величину, то есть за х. Тогда второй угол будет равен 2х, а третий окажется равным их сумме:
Внешние углы треугольника
Построим некоторый треуг-к, а потом продлим одну из его сторон. На рисунке мы продлили сторону АС. В результате образуется угол, который называют внешним углом треугольника:
На рисунке видно, что ∠ВСD является внешним. Но одновременно можно утверждать и ещё один факт – углы ∠АСВ и ∠ВСD являются смежными. Это позволяет нам дать следующее определение:
В итоге мы доказали, что внешний угол треугольника равен сумме двух углов треуг-ка, которые с ним не смежны.
Задание. У ∆АВС ∠А = 50°, ∠В = 75°. Найдите величину внешнего угла, смежного с ∠С.
Решение. В данном случае, согласно доказанному нами правилу, достаточно просто сложить ∠А и ∠B:
Рассмотрим ещё несколько более тяжелых задач.
Задание. В ∆АВС проведены биссектрисы угловА и B. Они пересекаются в точке М. Известно, что ∠А = 58°, ∠B = 96°. Найдите ∠АМB.
Решение. Устно такую задачу не решить, поэтому построим рисунок:
АМ – это биссектриса, а она разбивает∠ВАС на два равных угла. Поэтому мы можем вычислить ∠ВАМ:
Отметим найденные углы на рисунке:
Обратите внимание на ∆АВМ, который выделен красным цветом. Теперь мы знаем два угла в нем. Значит, можно найти и третий! Запишем для ∆АВМ сумму его углов:
Задание. Построен внешний угол равнобедренного треугольника, который смежен с вершиной, лежащей против основания. Далее построили биссектрису этого внешнего угла. Докажите, что эта биссектриса будет параллельна основанию.
Решение. Выполним построение:
Пусть АС – это основание рав-бедр. ∆АВС. Тогда внешний угол должен быть проведен к вершине В, ведь именно она лежит против основания. Обозначим внешний угол как ∠СВD (для этого мы просто добавили точку Dна продолжение отрезка АВ). Далее проводим биссектрису ВК. Нам требуется доказать, что ВК||АС.
Поступим очень просто – обозначим неизвестную нам величину угла при основании как х. То есть
В результате мы получили, что и ∠С, и ∠CBK равны х, то есть они равны и друг другу. Однако эти углы являются накрест лежащими для прямых АС и ВК и секущей ВС. Из равенства накрест лежащих углов следует, что АС||ВК.
Задание. В ∆АВС проведена медиана АМ, причем ее длина равна ВМ. Найдите ∠А.
Решение. Напомним, что медиана – это прямая, разбивающая сторону на два равных отрезка. То есть ВМ = МС. По условию АМ = ВМ, значит, имеет место двойное равенство:
Посмотрите на рисунок – здесь есть сразу два рав-бедр. треуг-ка! Это ∆АВМ (с основанием АВ) и ∆АМС (с основанием АМС). Обозначим∠В как х, а ∠С – как у. Углы при основании рав-бедр. треуг-ков одинаковы, а потому
Сравнение сторон и углов треугольника
Докажем следующую теорему:
Построим ∆АВС, в котором сторона АВ будет длиннее, чем АС. Нам надо доказать, что ∠С >∠B:
Выполним дополнительное построение – отметим на прямой АВ такую точку D, что AD = АС. Точка D будет располагаться на отрезке АВ, ведь АВ больше АС, а, значит, и больше АD. Также соединим C и D отрезком:
Теперь рассмотрим ∆ADC. Он является рав-бедр., ведь AD = AC. Из этого следует, что ∠ADC = ∠ACD.
Можно заметить, что ∠АDС является внешним углом для ∆BDC. Это значит, что
Мы доказали только первую часть теоремы. Теперь надо доказать обратное утверждение – против большего угла находится большая сторона треугольника. Предположим обратное, что существует ∆АВС, в котором ∠С>∠B, но не выполняется условие АВ >AC. Тогда либо АВ = ВС, либо АВ AC.
Задание. В ∆АВС известны углы:
Запишите стороны этого треуг-ка в порядке возрастания.
Решение. Всё очень просто – чем больше сторона, тем против большего угла она лежит. Поэтому самая большая сторона – это АВ, вторая по длине – АС, а наименьшая сторона – ВС. То есть BС
Доказанная теорема помогает сформулировать важный признак рав-бедр. треуг-ка:
Действительно, против равных углов должны лежать равные стороны, в противном случае сложится ситуация, когда в треуг-ке против сторон разной длины будут лежать равные углы, что невозможно.
Задание. В рав-бедр. ∆АВС основанием является АС. Из точек А и С проведены биссектрисы, которые пересеклись в точке О. Докажите, что ∆АОС также является рав-бедр.
Ясно, что ∠ВАС = ∠ВСА, так как это углы при основании рав-бедр. ∆АВС. С другой стороны, ∠ОАС равен половине ∠ВАС, ведь АО – биссектриса:
В итоге имеем, что ∠ОАС и ∠АСО равны. Но тогда в ∆АОС есть два одинаковых угла, а потому он является рав-бедр. (АО = ОС).
Неравенство треугольника
Следующая важная теорема называется неравенством треугольника:
Попробуем доказать неравенство треугольника. Возьмем произвольный ∆АВС и покажем, что сторона АВ меньше, чем величина ВС + АС. Для этого «дорисуем» к отрезку АС ещё один отрезок СD, равный BC, при этом АС и СD должны лежать на одной прямой:
Так как AD = АС + СD, то нам достаточно показать, что АВ
Получается, что в ∆АВD сторона АВ лежит против меньшего угла по сравнению со стороной АD. Значит, эта сторона должна быть меньше АD, что мы и пытаемся доказать.
Доказанная теорема означает, что не всякий треуг-к можно построить по его сторонам. Так, у нас никогда не получится построить треуг-к, у которого стороны равны 2, 3 и 7 см, так как одна из этих длин больше, чем сумма двух других:
Верно обратное утверждение – если все заданные длины удовлетворяют неравенству, то треуг-к построить можно.
Задание. Известны две стороны равнобедренного треугольника, они равны 25 и 10 см. Какая из них является основанием?
Решение. Рассмотрим сперва случай, когда основание равно 25 см. Тогда две другие стороны имеют длину 10 см. Их сумма (10 см + 10 см = 20 см) меньше основания. Такая ситуация невозможно из-за неравенства треуг-ка.
Ситуация же, при которой основание имеет длину 10 см, вполне допустима. Тогда две другие стороны равны 25 см, и для каждой стороны неравенство треуг-ка выполняется:
Как найти угол треугольника зная все его стороны?
Как найти угол треугольника по 3 сторонам?
Решить треугольник по трем сторонам — это значит по трем заданным сторонам треугольника найти его углы. Единственность решения задачи вытекает из признака равенства треугольников: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Как узнать угол равнобедренного треугольника если известны все его стороны?
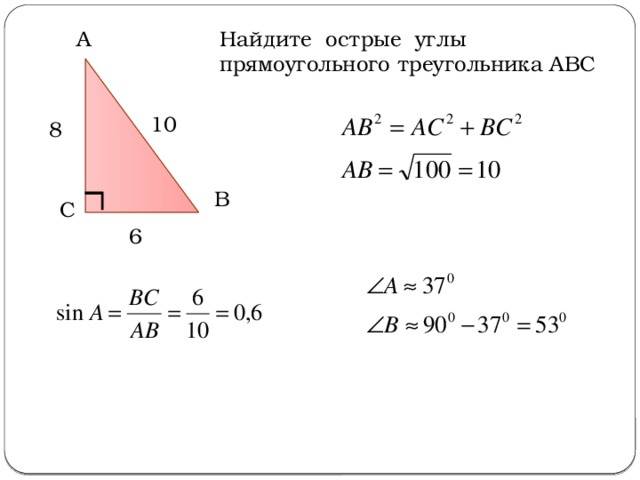
Как высчитать угол в прямоугольном треугольнике?
Как рассчитать угол в градусах?
Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.
Как найти третью сторону треугольника зная две другие?
Теорема косинусов в произвольном треугольнике гласит, что можно найти сторону в треугольнике, зная другие две стороны и угол между ними. Для того чтобы вычислить третью сторону треугольника нужно извлечь квадратный корень из разности от квадратов известных сторон их удвоенного произведения на косинус угла между ними.
Как найти угол треугольника если известны два других угла?
Как найти третий угол, если известны два других угла.
Просто надо вспомнить, теорему о внутренних углах треугольника и вычесть сумму двух известных углов из 180°. Например, пусть нам известно, что один из углов треугольника равен 70°, а второй 43°. Найдем третий угол.
Как найти основание равнобедренного треугольника?
Треугольник называется равнобедренным, если у него есть две равные стороны. Эти две равные стороны называются боковыми сторонами, а третья сторона – основание равнобедренного треугольника.
Чему равна сумма равнобедренного треугольника?
Сумма углов равнобедренного треугольника равна 180 градусам.
Сколько градусов в углах равностороннего треугольника?
Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
Как найти угол зная катеты и гипотенузу?
Если известна гипотенуза и катет, то угол будет равен арксинусу результата деления противолежащего катета на гипотенузу sin-1(b/c) либо арккосинусу результата деления прилежащего катета на гипотенузу cos-1(a/c).
Как рассчитать угол?
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.
Как рассчитать катет зная катет и угол?
Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла. Катет равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к первому катету угла.
Как рассчитать угол наклона конуса?
Как найти внешние углы?
Внешний угол равен разности между 180° и внутренним углом, он может принимать значения от 0 до 180° не включительно. Теорема о внешнем угле треугольника: Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом.
Как можно измерить угол без транспортира?
Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов.
Как найти стороны треугольника, если даны все углы
В первом случае известны такие данные в треугольнике, как величина угла и длина катетов, образующих этот угол. Сторону, противолежащую известному углу, необходимо находить по теореме косинусов, согласно которой необходимо длины известных сторон возвести в квадрат и сложить, затем отнять от полученной суммы произведение этих сторон, умноженное на два и на косинус известного угла.
Формула данного вычисления выглядит следующим образом:
h = √(e2+f2 – 2ef*cosA), где:
e и f – длины известных катетов;
h – неизвестный катет (или сторона);
A – угол, образованный известными катетами.
Во втором случае, когда известны два угла и катет между ними данного треугольника, нужно пользоваться теоремой синусов. Согласно данной теореме, если разделить синус угла на его длину противолежащего катета, то получится отношение, равное любому другому в этом треугольнике. Также, если вам неизвестен нужный катет, вы можете его легко найти, зная тот факт, что сумма углов треугольника равна стам восьмидесяти градусам.
Данное утверждение можно представить в виде формулы:
SinD/d = sinF/f = sinE/e, где:
D, F, E – величины противолежащих углов;
d, f, e – катеты, противолежащие соответствующим углам.
В третьем случае известны только углы данного треугольника, поэтому нельзя узнать длину всех сторон данного треугольника. Зато можно найти отношение этих сторон и методом подбора найти похожий треугольник. Отношение сторон данного треугольника находится с помощью составления системы из трех уравнений с тремя неизвестными.
Вот формула для составления:
d, f, e – неизвестные катеты треугольника;
D, F, E – углы, противолежащие неизвестным катетам.
Данное уравнение решается следующим образом:
d/sinD = f/sinF = e/sinE
(d*sinF*sinE-f* sinD* sinE-e* sinD* sinF)/ sinD* sinE* sinF.
Решение прямоугольного треугольника
Решение прямоугольного треугольника по двум сторонам
Если известны катет a и гипотенуза c
Второй катет b определится по теореме Пифагора:
Угол A определится по формуле синуса:
Поскольку сумма всех углов треугольника равна 180 ° то второй острый угол определится так:
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и гипотенуза)
Если известны катеты a и b
Гипотенуза с определится по теореме Пифагора:
Угол A определится по формуле тангенса:
Поскольку сумма всех углов треугольника равна 180 ° то второй острый угол определится так:
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и катет)
Решение прямоугольного треугольника по стороне и острому углу
Если дан острый угол A, то B найдется по формуле:
Стороны можно найти по следующим формулам:
Вычислить, найти решение прямоугольного треугольника если известны катет a и противолежащий угол A
Здесь все углы мы найдем по формуле (7). Гипотенузу по формуле (14) и второй катет по формуле (16).
Как найти углы треугольника если известны все стороны
Будем говорить, что данные компоненты (стороны, углы и др.) определяют фигуру однозначно, если другая фигура с такими же компонентами обязательно равна исходной. Например, для треугольника две стороны и угол между ними, сторона и два прилежащих к ней угла или три стороны по признакам равенства треугольников определяют всякий треугольник однозначно. Возможны и другие случаи однозначного определения треугольника: равнобедренный треугольник с данными основанием и опущенной на него высотой, треугольник с данными тремя медианами, треугольник с данными тремя высотами и т.п. Очень важно при решении планиметрической задачи определить однозначно фигуру и далее найти те ее неизвестные компоненты, которые необходимы для продолжения хода решения задачи.
где R – радиус описанной около треугольника окружности. Теорема косинусов
Следующий пример иллюстрирует применение теоремы синусов и косинусов для нахождения неизвестных сторон и углов некоторых однозначно определенных треугольников. Выполнить самостоятельно.
@ Как правило, при решении треугольников сначала стремятся определить три стороны, а затем находят необходимые компоненты. При известных трех сторонах треугольника для более точного изображения эскиза чертежа необходимо уметь определять вид треугольника (остроугольный, прямоугольный или тупоугольный).
Из формулы, следующей из теоремы косинусов, примененной к наибольшему углу, учитывая знак косинуса, можно получить соотношения между квадратами сторон, позволяющие определить вид треугольника.
По длинам трех сторон определить вид треугольника:
Указание : известно, что против большей стороны в треугольнике лежит больший угол, и обратно. Косинус большего угла можно найти по формуле, следующей из теоремы косинусов.
Ответ: а) и б) прямоугольные, в) тупоугольный, г) остроугольный, д) не существует.
Теперь приведем примеры решения некоторых заданий вступительных экзаменов в КубГУ.
Пример 6.2.4. (КубГУ, матем., 1979 г.)
И только лишь в случае, когда (т.е. ), мы получаем ранее указанный двузначный ответ.
Теперь для иллюстрации применения неравенства треугольника приведем решение одного несложного задания устных экзаменов на математический факультет КубГУ.
Указание : используйте рассуждения, подобные приведенным в начале доказательства предыдущего задания.
В заключение этого параграфа приведем три типовые задачи, в решении которых главную роль играет теорема косинусов.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение треугольников.
Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Эта математическая программа находит стороны \( b, c \), и угол \( \alpha \) по заданным пользователем стороне \( a \) и двум прилежащим к ней углам \( \beta \) и \( \gamma \)
Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Введите сторону \( a \) и два прилежащих к ней угла \( \beta \) и \( \gamma \) Решить треугольник