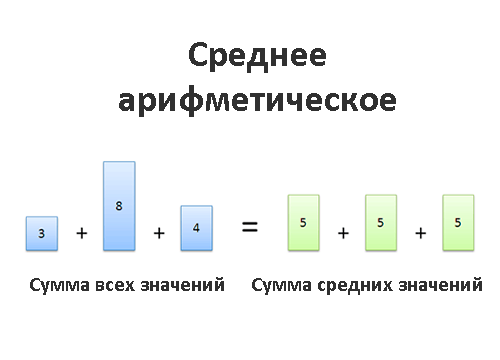
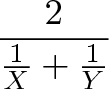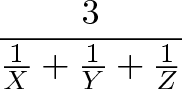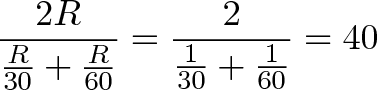Как посчитать среднее арифметическое
Как посчитать среднее арифметическое
Средняя арифметическая величина. Основные свойства средней арифметической
Средняя величина – обобщающая характеристика однотипных явлений по одному из варьирующих признаков.
Определить среднюю можно через исходное соотношение средней или ее логическую формулу:
Для изучения и анализа социально-экономических явлений применяются различные средние величины: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, кубическая, а также структурные средние – мода, медиана, квартили, децили.
Средние могут рассчитываться в двух вариантах: взвешенные и невзвешенные.
При расчете взвешенных средних величин веса, могут быть представлены как абсолютными величинами, так и относительными (в % или долях единицы).
Средней арифметической величиной называется такое значение признака в расчете на единицу совокупности, при вычислении которого общий объем признака в совокупности сохраняется неизменным.
Исходя из определения, формула средней арифметической величины имеет вид:
По данной формуле вычисляются средние величины первичных (объемных) признаков, если известны индивидуальные значения признака. Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения, или группировку, то расчет проводят по средней арифметической взвешенной
В качестве весов здесь выступают численность единиц совокупности в группе.
Пример. Имеются данные о средней заработной плате сотрудников двух предприятий за январь.
Средняя заработная плата, руб.
Численность работников, человек
Вычислить среднюю заработную плату сотрудников по двум предприятиям.
Определим исходные соотношения средней (ИСС) для показателя «средняя заработная плата».
Фонд заработной платы можно получить умножением средней заработной платы на численность работников. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
где xi – i –тый вариант осредняемого признака;
fi – вес i –ого варианта.
Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств знака и совокупности.
Среднее арифметическое в Excel
Среднее арифметическое значение — самый известный статистический показатель. В этой заметке рассмотрим его смысл, формулы расчета и свойства.
Средняя арифметическая как оценка математического ожидания
Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.
Формула матожидания имеет следующий вид:
где M(X) – математическое ожидание
xi – это случайные величины
То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.
Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.
Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.
Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.
где xi – значения переменной,
n – количество значений.
Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений).
Свойства средней арифметической (математического ожидания)
Теперь рассмотрим свойства средней арифметической, которые часто используются при алгебраических манипуляциях. Правильней будет вновь вернутся к термину математического ожидания, т.к. именно его свойства приводят в учебниках.
Матожидание в русскоязычной литературе обычно обозначают как M(X), в иностранных учебниках можно увидеть E(X). Встречается обозначение греческой буквой μ (читается «мю»). Для удобства предлагаю вариант M(X).
Итак, свойство 1. Если имеются переменные X, Y, Z, то математическое ожидание их суммы равно сумме их математических ожиданий.
M(X+Y+Z) = M(X) + M(Y) + M(Z)
Допустим, среднее время, затрачиваемое на мойку автомобиля M(X) равно 20 минут, а на подкачку колес M(Y) – 5 минут. Тогда общее среднее арифметическое время на мойку и подкачку составит M(X+Y) = M(X) + M(Y) = 20 + 5 = 25 минут.
Свойство 2. Если переменную (т.е. каждое значение переменной) умножить на постоянную величину (a), то математическое ожидание такой величины равно произведению матожидания переменной и этой константы.
К примеру, среднее время мойки одной машины M(X) 20 минут. Тогда среднее время мойки двух машин составит M(aX) = aM(X) = 2*20 = 40 минут.
Свойство 3. Математическое ожидание постоянной величины (а) есть сама эта величина (а).
Если установленная стоимость мойки легкового автомобиля равна 100 рублей, то средняя стоимость мойки нескольких автомобилей также равна 100 рублей.
Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
Автомойка за день в среднем обслуживает 50 автомобилей (X). Средний чек – 100 рублей (Y). Тогда средняя выручка автомойки в день M(XY) равна произведению среднего количества M(X) на средний тариф M(Y), т.е. 50*100 = 500 рублей.
Формула среднего значения в Excel
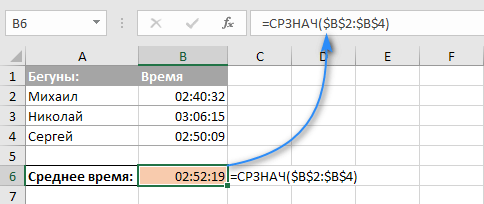
Среднее арифметическое чисел в Excel рассчитывают с помощью функции СРЗНАЧ. Выглядит примерно так.
У этой формулы есть замечательное свойство. Если в диапазоне, по которому рассчитывается формула, присутствуют пустые ячейки (не нулевые, а именно пустые), то они исключается из расчета.
Вызвать функцию можно разными способами. Например, воспользоваться командой автосуммы во вкладке Главная:
После вызова формулы нужно указать диапазон данных, по которому рассчитывается среднее значение.
Есть и стандартный способ для всех функций. Нужно нажать на кнопку fx в начале строки формул. Затем либо с помощью поиска, либо просто по списку выбрать функцию СРЗНАЧ (в категории «Статистические»).
Средняя арифметическая взвешенная
Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч.
Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:
Теперь преобразуем формулу до удобного вида.
Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.
Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.
где x – анализируемый показатель; f – вес.
Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую.
Формула средневзвешенного значение в Excel
Обычная функция среднего значения в Excel СРЗНАЧ, к сожалению, считает только среднюю простую. Готовой формулы для среднего взвешенного значения в Excel нет. Однако расчет несложно сделать подручными средствами.
Самый понятный вариант создать дополнительный столбец. Выглядит примерно так.
Имеется возможность сократить количество расчетов. Есть функция СУММПРОИЗВ. С ее помощью можно рассчитать числитель одним действием. Разделить на сумму весов можно в этой же ячейке. Вся формула для расчета среднего взвешенного значения в Excel выглядит так:
Интерпретация средней взвешенной такая же, как и у средней простой. Средняя простая – это частный случай взвешенной, когда все веса равны 1.
Физический смысл средней арифметической
Представим, что имеется спица, на которой в разных местах нанизаны грузики различной массы.
Как отыскать центр тяжести? Центр тяжести – это такая точка, за которую можно ухватиться, и спица при этом останется в горизонтальном положении и не будет переворачиваться под действием силы тяжести. Она должна быть в центре всех масс, чтобы силы слева равнялись силам справа. Для нахождения точки равновесия следует рассчитать среднее арифметическое взвешенное расстояний от начала спицы до каждого грузика. Весами будут являться массы грузиков (mi), что в прямом смысле слова соответствует понятию веса. Таким образом, среднее арифметическое расстояние – это центр равновесия системы, когда силы с одной стороны точки уравновешивают силы с другой стороны.
И последнее. В русском языке так сложилось, что под словом «средний» обычно понимают именно среднее арифметическое. То есть моду и медиану как-то не принято называть средним значением. А вот на английском языке слово «средний» (average) может трактоваться и как среднее арифметическое (mean), и как мода (mode), и как медиана (median). Так что при чтении иностранной литературы следует быть бдительным.
Средняя арифметическая
Самым распространенным видом средней является средняя арифметическая.
Средняя арифметическая простая
Простая среднеарифметическая величина представляет собой среднее слагаемое, при определении которого общий объем данного признака в совокупности данных поровну распределяется между всеми единицами, входящими в данную совокупность. Так, среднегодовая выработка продукции на одного работающего — это такая величина объема продукции, которая приходилась бы на каждого работника, если бы весь объем выпущенной продукции в одинаковой степени распределялся между всеми сотрудниками организации. Среднеарифметическая простая величина исчисляется по формуле:
Простая средняя арифметическая — Равна отношению суммы индивидуальных значений признака к количеству признаков в совокупности
Найти среднюю заработную плату
Решение: (3 + 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 тыс. руб.
Средняя арифметическая взвешенная
Если объем совокупности данных большой и представляет собой ряд распределения, то исчисляется взвешенная среднеарифметическая величина. Так определяют средневзвешенную цену за единицу продукции: общую стоимость продукции (сумму произведений ее количества на цену единицы продукции) делят на суммарное количество продукции.
Представим это в виде следующей формулы:
Взвешенная средняя арифметическая — равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков).Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.
| Заработная плата одного рабочего тыс.руб; X | Число рабочих F |
| 3,2 | 20 |
| 3,3 | 35 |
| 3,4 | 14 |
| 4,0 | 6 |
| Итого: | 75 |
Средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:
Ответ: 3,35 тыс.руб.
Средняя арифметическая для интервального ряда
При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.
Средние, вычисляемые из интервальных рядов являются приближенными.
Пример 3. Определить средний возраст студентов вечернего отделения.
| Возраст в годах !!х?? | Число студентов | Среднее значение интервала | Произведение середины интервала (возраст) на число студентов |
| до 20 | 65 | (18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20) | 1235 |
| 20 — 22 | 125 | (20 + 22) / 2 = 21 | 2625 |
| 22 — 26 | 190 | (22 + 26) / 2 = 24 | 4560 |
| 26 — 30 | 80 | (26 + 30) / 2 = 28 | 2240 |
| 30 и более | 40 | (30 + 34) / 2 = 32 | 1280 |
| Итого | 500 | 11940 |
Средние, вычисляемые из интервальных рядов являются приближенными. Степень их приближения зависит от того, в какой мере фактическое распределение единиц совокупности внутри интервала приближается к равномерному.
При расчете средних в качестве весов могут использоваться не только абсолютные, но и относительные величины (частость):
Средняя арифметическая обладает целым рядом свойств, которые более полно раскрывают ее сущность и упрощают расчет:
1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т.е.
2.Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:
3.Алгебраическая сумма отклонений индивидуальных значений признака от средней равна нулю:
6.Если все варианты ряда уменьшить или увеличить в раз, то средняя также уменьшится или увеличится в раз:
7.Если все частоты (веса) увеличить или уменьшить в раз, то средняя арифметическая не изменится:
Формула среднего арифметического значения в Excel — функции и примеры
В статье показано, как определить среднее значение в Excel для разных типов данных с помощью формул СРЗНАЧ или СРЗНАЧА. Вы также узнаете, как использовать функции СРЗНАЧЕСЛИ и СРЗНАЧЕСЛИМН для усреднения ячеек, соответствующих определенным критериям.
Средняя зарплата… Средняя продолжительность жизни… Ежедневно мы с вами слышим эти словосочетания, служащие для описания множества одним единственным числом. Но, как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека. Например, в какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).
В математике среднее называется средним арифметическим, и оно рассчитывается путем сложения группы чисел, а затем деления на количество этих чисел.
В приведенном выше примере средняя зарплата составляет: 195 000 рублей =(50000*9+1500000)/10. Вряд ли эта цифра соответствует реальной ситуации, но таковы расчёты среднего арифметического значения.
И всё же в большинстве случаев знать среднее весьма полезно.
Как посчитать среднее арифметическое в Экселе? Вам не нужно писать сложные математические выражения. Есть несколько функций «на все случаи жизни».
Функция СРЗНАЧ.
СРЗНАЧ применяется для возврата среднего арифметического указанных ячеек.
Использование функции СРЗНАЧ – на примерах.
Пример 1. Расчет среднего из нескольких чисел.
Вы можете указать числа непосредственно. Например,
=СРЗНАЧ(1;2;3;4) возвращает результат 2,5.
Чтобы вычислить среднее по столбцу, укажите ссылку на него целиком:
=СРЗНАЧ(A:A)
Чтобы получить по строке, введите ссылку на нее:
=СРЗНАЧ(1:1)
Чтобы вычислить в каком-то диапазоне, укажите его:
=СРЗНАЧ(A1:C20)
Чтобы вернуть среднее из несмежных ячеек, запишите каждую ячейку отдельно, например
=СРЗНАЧ(A1; C1; D1)
И, естественно, ничто не мешает вам включать числа, ссылки и диапазоны в одну формулу. Например, следующее выражение вычисляет среднее из 2 диапазонов и 1 отдельного значения:
=СРЗНАЧ(B3:B5; C7:D9; B11)
Примечание. Если вы хотите округлить полученное число до ближайшего целого, примените одну из функций округления, например:
Помимо чисел, вы можете использовать функцию СРЗНАЧ для вычисления среднего на основе других видов чисел, таких как проценты и время. Это показано в следующих примерах.
Пример 2. Расчет среднего процента.
Если у вас есть столбец с процентами на вашем листе, как вы получаете средний процент выполнения? Возьмём обычную формулу Excel для среднего 🙂
Примечание. Обратите внимание, что СРЗНАЧ учитывает и нулевые значения при расчете. А это существенно повлияет на итоговую цифру. Если вы предпочитаете исключать нули из расчета, возьмите вместо этого СРЗНАЧЕСЛИ, как будет показано чуть ниже. ССЫЛКА
Пример 3. Расчет среднего времени.
Этим совсем не так просто, как с обычными числами. Ведь время включает часы, минуты и секунды? Вычислять разные единицы времени вручную было бы очень сложно… но СРЗНАЧ отлично с этим справляется.
Важные особенности СРЗНАЧ!
Как вы только что видели, применять СРЗНАЧ очень просто. Тем не менее, у нее есть несколько особенностей, о которых вам нужно знать.
Чем отличается функция СРЗНАЧА?
СРЗНАЧА аналогична СРЗНАЧ в том, что она вычисляет среднее арифметическое чисел. Разница в том, что СРЗНАЧА включает в расчет все непустые ячейки, независимо от того, содержат ли они числа, текст, логические ИСТИНА и ЛОЖЬ, или пустые строки, возвращаемые другими формулами.
Она обрабатывает различные типы данных, такие как числа, текстовые строки и логические. Что нужно запомнить:
Например, =СРЗНАЧА(2;ЛОЖЬ) дает нам 1, что является средним между 2 и 0.
=СРЗНАЧА(2;ИСТИНА) возвращает 1,5, что является средним от 2 и 1.
На следующем скриншоте показаны два варианта расчёта для среднего значения в Excel, и разные результаты, которые они возвращают:
Поэтому, если вы не хотите включать в свои вычисления логические выражения и текстовые строки, используйте СРЗНАЧ, а не СРЗНАЧА.
СРЗНАЧЕСЛИ вычисляет среднее арифметическое всех ячеек, которые соответствуют заданным критериям.
СРЗНАЧЕСЛИ (диапазон; критерии; [диапазон_усреднения])
Она имеет следующие аргументы (первые 2 обязательны, последний – нет):
А теперь давайте посмотрим, как вы можете применить СРЗНАЧЕСЛИ на реальных рабочих листах, чтобы найти среднее ячеек, соответствующих вашим требованиям.
Точное соответствие критериям
В этом примере давайте усредним только продажи (B2: B8) для заказов на бананы (A2: A8):
Вместо того, чтобы вводить условие непосредственно в формулу, вы можете ввести его в отдельную ячейку ($B$10) и затем обратиться к ней. Это очень известный и всеми применяемый приём.
Примечание. Чтобы округлить возвращаемое число до определенного количества десятичных знаков, примените одну из функций округления Excel, или диалоговое окно «Формат ячеек», чтобы изменить только отображение числа на экране.
Например, чтобы округлить полученный выше результат до 2 десятичных знаков, вы можете заключить его в функцию ОКРУГЛ следующим образом:
Частичное соответствие критериям (с символами подстановки).
Вы можете применить символы подстановки в аргументе критерия для выбора ячеек на основе частичного совпадения:
) перед этим символом (то есть,
Предположим, что у вас есть 3 разных вида бананов, и вы хотите найти среднюю величину их продаж:
Если вашему ключевому слову может предшествовать и/или последовать какой-либо другой символ, добавьте звездочку * как перед словом, так и после него.
Чтобы найти среднее по всем товарам, за исключением каких-либо бананов, запишите следующую формулу:
Как применить числовые условия и логические операторы.
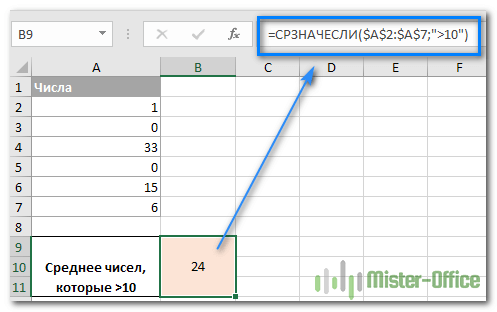
Довольно часто вам может потребоваться усреднить ячейки, в которых количество больше или меньше определенного числа. Например, есть перечень чисел в столбце A, и мы хотим найти среднее из тех из них, которые больше 10.
Правильный подход — заключить логический оператор и число в двойные кавычки.
Итак, мы получили вот что:
Другая весьма распространенная проблема – как найти среднее чисел, которые не равны нулю. Для этого вам понадобится оператор «не равно» в аргументе критерия:
Как вы, возможно, заметили, мы не задействуем третий аргумент [диапазон усреднения] ни в одном из приведенных выше выражений, поскольку мы хотим считать по начальному диапазону.
Для пустых или непустых ячеек
При выполнении анализа данных в Excel часто может потребоваться найти среднее чисел, которые соответствуют либо пустым, либо непустым областям.
Среднее, если пусто.
Чтобы включить пустые ячейки, которые не содержат абсолютно ничего (без формулы, без строки нулевой длины), введите «=» в аргументе.
Например, вычислим среднее ячеек C2: C8, если клетка в столбце B в той же строке абсолютно пуста:
Чтобы усреднить значения, соответствующие визуально пустым ячейкам, включая те, которые содержат пустые строки, возвращаемые другими функциями (например, с формулой вроде = «»), запишите «». Например:
Среднее, если не пустое.
Чтобы найти среднее, соответствующее непустым ячейкам, введите «<>».
Например, так вычисляем среднеарифметическое C2:C8, если соответствующая позиция в столбце B не пуста:
Использование ссылок и других функций в описании условий.
Вместо того, чтобы записывать параметры подсчета непосредственно в формуле, вы можете обратиться к определенной ячейке, в которую можно вводить различные значения, не изменяя саму формулу. Так значительно уменьшается риск случайной ошибки при корректировке.
Если ссылка является критерием точного соответствия, то просто укажите ее в аргументе:
Если в качестве условия вы берёте логическое выражение со ссылкой или c другой функцией, нужно заключить логический оператор в «двойные кавычки» и добавить амперсанд (&) для их объединения.
Например, чтобы рассчитать средние продажи (C2: C8), превышающие указанное в E4:
С датами в B2: B8, приведенное ниже возвращает среднюю величину продаж (C2: C8), которые произошли до текущей даты:
=СРЗНАЧЕСЛИ($B$2:$B$8; »
Вместо прямого указания даты можно взять соответствующую функцию. К примеру,
СРЗНАЧЕСЛИМН учитывает сразу несколько условий и возвращает среднеарифметическое ячеек, которые соответствуют всем указанным критериям.
СРЗНАЧЕСЛИМН(диапазон подсчёта, диапазон_критерия_1, критерий_1, [диапазон_критерия_2, критерий_2],…)
Она имеет следующие аргументы:
Функция СРЗНАЧЕСЛИМН доступна в Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010 и 2007.
Как уже упоминалось, СРЗНАЧЕСЛИМН находит среднее ячеек, которые соответствуют всем указанным вами критериям (логика «И»). По сути, вы применяете его совершенно аналогично СРЗНАЧЕСЛИ, за исключением того, что вы можете указать в ней несколько областей проверки и соответствующих условий.
Пример 1. Среднеарифметическое количество ячеек по нескольким параметрам (текст и число)
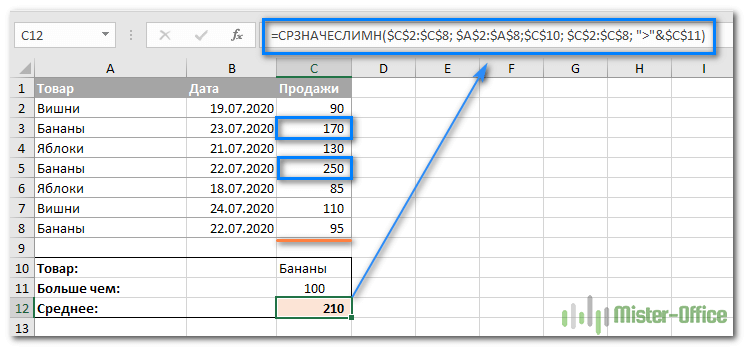
Предположим, что у вас есть список товаров в столбце A и суммы продаж в столбце B. Давайте выясним среднее продаж бананов, превышающее 100 единиц.
Собираем вышеперечисленные компоненты вместе. И если вы замените условия ссылками, вы получите нечто похожее на это:
Как видите, только две ячейки (С3 и С5) удовлетворяют обоим условиям, и поэтому только они и берутся для расчета.
Пример 2. Среднеарифметическое на основе критерия даты
В этом примере давайте посчитаем среднее количество товаров, доставленных до 22 июля 2020 года, статус которых определен (позиция в соответствующем столбце не пустая). С количеством, указанным в столбце D, датами в колонке В (критерий_1) и статусом в С (критерий_2), формула выглядит следующим образом:
В критерии1 вы вводите дату, которой предшествует оператор сравнения. В критерии2 вы вводите «<>», который указывает включать только непустые ячейки в пределах столбца «Статус».
Как усреднить числа по нескольким параметрам с помощью логики ИЛИ?
Поскольку СРЗНАЧЕСЛИМН работает с логикой «И», а СРЗНАЧЕСЛИ допускает только 1 критерий, нам придется составить нашу собственную формулу для усреднения с помощью логики «ИЛИ».
Другими словами, мы составим выражение для вычисления среднего арифметического в Excel, если выполняется любое из указанных требований.
Пример 1. Среднее с логикой ИЛИ на основе нескольких текстовых критериев
Предположим, вы хотите получить средние продажи (C2: C8) как для бананов, так и для яблок (A2: A8). Чтобы рассчитать это, вам понадобится формула массива, включающая несколько функций Excel:
Если товары, которые мы ищем, записать отдельно (скажем, в E1 и E2), то наш расчет будет выглядеть так:
Из всех формул усреднения Excel, которые обсуждались до сих пор, это самая хитрая (хотя осталось еще два примера 😉
Как это работает?
Для наших любопытных и вдумчивых читателей, которые хотят не только механически применять рекомендации, но и понимать, что же они делают, даем подробное объяснение логики расчетов.
В начале функция ЕСЛИ определяет, какие значения в исходном диапазоне соответствуют любому из указанных параметров, и передает их в СРЗНАЧ. Вот как:
ПОИСКПОЗ берёт исходные данные в A2:A8 в качестве условий поиска и сравнивает каждое из них с массивом поиска, представленным критериями в E1: E2.
3- й аргумент, установленный в 0, указывает искать точные совпадения:
Когда совпадение найдено, программа возвращает относительную позицию в массиве поиска, в противном случае ошибку #Н/Д!.
ЕЧИСЛО преобразует любые числа в ИСТИНА, а ошибки в ЛОЖЬ:
Этот массив отправляется на логическую проверку ЕСЛИ.
Она заменяет позиции, соответствующие ИСТИНА в приведённом выше массиве, фактическими значениями из B2: B8:
Этот окончательный массив передается в СРЗНАЧ, которая вычисляет, игнорируя логические значения.
Пример 2. Среднее с логикой ИЛИ на основе числовых критериев с операторами сравнения
Если вы хотите найти среднее арифметическое на основе нескольких числовых критериев и условий больше/меньше, чем в сочетании с логикой ИЛИ, то формула, рассмотренная в предыдущем примере, не будет работать. Ведь вы не можете поместить эти логические выражения в массив. Решение заключается в применении функции СУММ в формуле массива.
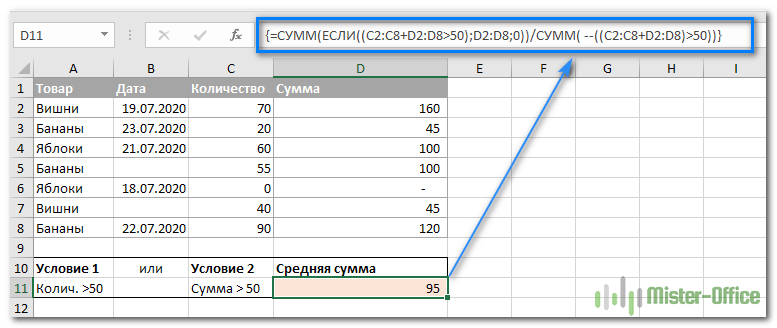
Предположим, у вас есть количество в столбце B и сумма в столбце C, и вы хотите усреднить суммы, которые больше 50 в столбце B или C. При этом вы хотите избежать дубликатов, то есть не считать строку дважды, если число больше 50 в обоих столбцах.
Вот рабочий пример:
Помните, что это формула массива, и поэтому вы должны нажать Ctrl + Shift + Enter и ввести ее правильно.
Как видите, выражение состоит из 2 частей. В первой части вы применяете функцию ЕСЛИ с оператором ИЛИ в аргументе (C2:C8> 50) + (D2:D8> 50). Как вы, вероятно, знаете, в формулах массива плюс (+) действует как оператор ИЛИ.
Итак, первая часть складывает числа в столбце C, если выполняется любое из условий.
Вторая часть возвращает количество таких ячеек, а затем вы делите сумму на количество, чтобы найти среднеарифметическое.
И, естественно, вы можете указать разные условия для каждого диапазона. Например, чтобы усреднить продажи, если столбец C больше 50 или столбец D больше 100, используйте следующие выражения: (C2: C8> 50) + (D2: D8> 100). Всё целиком будет выглядеть следующим образом:
Пример 3. Среднее с логикой ИЛИ на основе пустых/непустых ячеек
Средняя формула с несколькими условиями ИЛИ, соответствующими пустым и непустым ячейкам, очень похожа на ту, которую мы только что обсуждали.
Для непустых ячеек.
Следующая формула массива находит среднее количество (столбец B), если указана либо дата (столбец B), либо статус (столбец C), т. е. если столбцы B или C не пустые.
Чтобы сделать её более компактной, вы можете объединить диапазоны с помощью амперсанда (&):
Для пустых ячеек.
Чтобы усреднить числа в столбце D, соответствующие пустым ячейкам в B или C, замените непустой оператор (<> «») пустым оператором (= «»).
Объединение диапазонов при помощи амперсанда не будет работать в этом случае.
Вот как рассчитывается среднее в Excel.
Я благодарю вас за чтение и надеюсь еще не раз увидеть вас в нашем блоге!
Среднее арифметическое
Опубликовано 07.06.2020 · Обновлено 07.06.2021
Что такое Среднее арифметическое?
Среднее арифметическое – это простейшая и наиболее широко используемая мера среднего или среднего. Он просто включает в себя получение суммы группы чисел, а затем деление этой суммы на количество чисел, используемых в серии.
Например, возьмите 34, 44, 56 и 78. Сумма равна 212. Среднее арифметическое равно 212, деленному на четыре, или 53.
Как работает среднее арифметическое
Среднее арифметическое также сохраняет свое место в финансах. Например, оценки среднего дохода обычно представляют собой среднее арифметическое. Допустим, вы хотите узнать среднюю ожидаемую прибыль 16 аналитиков, работающих с определенной акцией. Просто сложите все оценки и разделите на 16, чтобы получить среднее арифметическое.
То же самое верно, если вы хотите рассчитать среднюю цену закрытия акции в течение определенного месяца. Допустим, в месяце 23 торговых дня. Просто возьмите все цены, сложите их и разделите на 23, чтобы получить среднее арифметическое.
Среднее арифметическое простое, и большинство людей даже с небольшими финансовыми и математическими навыками могут его вычислить. Это также полезная мера центральной тенденции, поскольку она дает полезные результаты даже при больших группировках чисел.
Ключевые моменты
Ограничения среднего арифметического
Среднее арифметическое не всегда идеально, особенно когда один выброс может сильно исказить среднее. Предположим, вы хотите оценить содержание группы из 10 детей. Девять из них получают пособие от 10 до 12 долларов в неделю. Десятый ребенок получает пособие в размере 60 долларов. Этот один выброс приведет к среднему арифметическому значению в 16 долларов. Это не очень представитель группы.
В данном конкретном случае лучшим показателем может быть среднее пособие, равное 10.
Среднее арифметическое также невелико при расчете эффективности инвестиционных портфелей, особенно когда оно включает в себя начисление сложных процентов или реинвестирование дивидендов и прибыли. Он также обычно не используется для расчета настоящих и будущих денежных потоков, которые аналитики используют при расчетах. Это почти наверняка приведет к неверным цифрам.
Важный
Для этих приложений аналитики обычно используют среднее геометрическое, которое рассчитывается иначе. Он берет произведение всех чисел в ряду и увеличивает его до значения, обратного длине ряда. Это легко вычислить в Microsoft Excel с помощью функции ГЕОМЕН. Среднее геометрическое отличается от среднего арифметического или среднего арифметического тем, как оно рассчитывается, поскольку оно учитывает сложение, которое происходит от периода к периоду. Из-за этого инвесторы обычно считают среднее геометрическое более точным показателем доходности, чем среднее арифметическое.
Средняя арифметическая
В экономических и статистических исследованиях наибольшее применение нашли средние арифметические величины. Средняя арифметическая (при степени k = 1) применяется в тех случаях, когда объем изучаемого признака образуется как сумма значений отдельных единиц анализируемой совокупности. Если средней арифметической величиной заменить каждый вариант усредняемого признака, итоговый показатель не изменяется.
Например, если заменить заработную плату отдельных работников предприятия средней заработной платой по данному предприятию за этот же период, то объем фонда заработной платы не будет изменяться.
Средняя арифметическая величина может быть простой и взвешенной.
Простая средняя арифметическая величина (X) рассчитывается с использованием следующей формулы:
где п — объем статистической совокупности (число единиц в статистической совокупности).
Применяют простую среднюю арифметическую величину, как правило, при определении среднего уровня абсолютных величин с тем условием, что используемые при расчете данные (абсолютные величины) не сгруппированы.
Рассмотрим расчет и применение средней арифметической величины на практическом примере.
Имеются данные о трудовом стаже рабочих цеха. Необходимо рассчитать средний стаж рабочих.
В таблице определено, что всего в цехе работает 12 рабочих (п) с различным трудовым стажем (л*,). Используя формулу (4.1), получаем, что средний стаж рабочих цеха составляет
В том случае, когда данные по абсолютным величинам сгруппированы и представлены в виде статистического ряда распределения, используется расчет средней арифметической взвешенной величины но формуле
где Xj — индивидуальное значение признака (варианта).
Для расчета также может быть использована еще одна формула, которая представляет собой модификацию формулы (4.2):
где dj — частость, соответствующая Хг
Средняя арифметическая обладает следующими свойствами:
1) если в формуле (4.2) все частоты разделить или умножить на одно и то же число, то величина средней арифметической не изменится
2) общий множитель индивидуальных значений признака может быть вынесен за скобку
3) средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних
4) если все варианты имеют одинаковое значение (Хх =Х2 =. = Xt =. = = Хп = С), то их средняя арифметическая равна этому значению
5) сумма отклонений индивидуальных значений признака от средней арифметической равна нулю
Расчет средней арифметической взвешенной специфичен для дискретного и интервального рядов распределения. Рассмотрим это на практическом примере.
На основании имеющихся данных составим дискретный ряд и рассчитаем значение арифметической взвешенной по дискретному ряду распределения на основании формул (4.2) и (4.3).
Стаж работы, лет
Численность рабочих, чел.
Доля рабочих в общей численности
Используя формулу (4.2), рассчитываем средний стаж рабочих:
Теперь рассчитаем аналогичный показатель (средний стаж рабочих) с использованием модифицированной формулы средней арифметической взвешенной (4.3):
Результаты расчетов одинаковы как для средней арифметической простой, так и для средней арифметической взвешенной, рассчитанной с использованием традиционной и модифицированной формул.
Далее рассмотрим расчет средней арифметической взвешенной величины на примере интервального ряда.
Имеется интервальный ряд распределения предприятий по объемам производства продукции. Необходимо рассчитать среднюю арифметическую взвешенную, которая будет характеризовать средний объем производства продукции.
Первоначально необходимо узнать срединное значение каждого интервала. Срединное значение каждого интервала рассчитывается как сумма границ интервала, деленная на два (это графа 4 в таблице). Для первого интервала срединное значение составит: (5 + 6,6) : 2 = 5,8. Аналогичным образом выполняется расчет и для всех последующих интервалов.
Группы предприятий по объему производства, млн руб.
Доля в общем количестве предприятий
по объему произвол-
Затем по формуле (4.2) или (4.3) определяем среднюю арифметическую:
Итак, средний объем производства продукции по совокупности предприятий составляет 9,7 млн руб.
В случае если в ряду распределения имеются открытые интервалы, при нахождении их срединного значения предполагается, что длина их равна длине предшествующего или последующего закрытого интервала.
Следует иметь в виду, что изложенный прием расчета средней арифметической по интервальному ряду распределения дает лишь приблизительный результат и используется в случаях, когда нет непосредственных данных о величине каждой варианты. Однако ошибка будет тем меньше, чем меньше длина интервалов и чем больше единиц совокупности в каждом из них.
При расчете средней арифметической взвешенной по данным, представленным в виде ряда распределения (дискретного или интервального), в качестве веса используется частота или частость. Но в экономико-статистических расчетах «вес» — понятие более широкое, чем число единиц совокупности в отдельных группах ряда распределения.
Расчет средней арифметической взвешенной величины используют, как правило, при расчете среднего уровня относительных величин (например, средняя производительность труда работников, средняя себестоимость единицы продукции, средняя рентабельность производства ассортимента продукции и т.п.).
Здесь особое значение приобретает обоснование того показателя, который используется в качестве веса признака (т.е. веса того признака, для которого производится расчет среднего уровня). Для правильного выбора веса необходимо четко понимать сущность изучаемого показателя и знать аналитическую форму его расчета.
На практических примерах рассмотрим специфику определения веса, необходимого для расчета среднего уровня ряда относительных экономических показателей.
Имеются данные о суммах инвестиций и доли в них собственных инвестиций предприятий в составе акционерного общества. Необходимо определить вес и рассчитать среднюю арифметическую взвешенную удельного веса собственных средств в общем объеме инвестиций по предприятиям акционерного общества (АО).
Предприятия в составе АО
Сумма инвестиций, млн руб.
Удельный вес собственных средств в сумме инвестиций, %
Прежде всего необходимо определить аналитическую формулу по показателю, для которого будет рассчитываться средняя взвешенная величина. В данном случае — это показатель удельного веса собственных средств предприятий в общей сумме инвестиций:
На основании аналитической формулы определяем, что для расчета удельного веса собственных средств предприятий в общем объеме инвестиций, рассчитываемом по всему акционерному обществу, в знаменателе необходимо указать сумму инвестиций по акционерному обществу, которая составит 87,5 млн руб. (15,5 + 40 + 32). Соответственно, в числителе необходимо отразить сумму собственных средств предприятий, которые были вложены в общий объем инвестиций.
Возвращаясь к аналитической формуле, мы видим, что если удельный вес — это отношение собственных средств к инвестированным всего, то, следовательно, собственные средства в стоимостном выражении — это сумма инвестиций, деленная на удельный вес собственных средств (если расчет ведется в процентах) или умноженная на удельный вес (если расчет ведется в коэффициентах):
II! = 15,5 млн руб.: 69,3% (или 15,5 млн руб. • 0,693) = 10,7 млн руб.;
П2 = 40 млн руб.: 57,4% (или 40 млн руб. • 0,574) = 23 млн руб.;
П3 = 32 млн руб.: 62,8% (или 32 млн руб. • 0,628) = 20,1 млн руб.
В данном случае вес (/)) средней арифметической взвешенной — это сумма инвестиций, а доля собственных средств предприятий — это индивидуальное значение признака (*,):
Таким образом, получаем, что среднее взвешенное значение удельного веса собственных средств предприятий акционерного общества в общем объеме инвестиций составляет 61,5%, соответственно, удельный вес привлеченных средств составит 38,5%.
Имеются данные по рентабельности реализованных видов продукции, выпущенных предприятием, и затрат, связанных с производством данных видов продукции.
эеделить среднюю рентабельность реализованной продукции.
Как вычислить среднее арифметическое в Excel
Вычисление среднего арифметического числа – довольно частая процедура, которую приходится делать пользователям Excel. Существует сразу несколько возможных методов, позволяющих это сделать в самых разных ситуациях, в том числе, и использование статистических функций. Давайте более детально разберемся, что делать для вычисления среднего арифметического числа в Excel?
Как найти среднее арифметическое чисел (математика)?
Чтобы определить среднее арифметическое нескольких чисел или ячеек, надо взять все значения в последовательности, выполнить между ними операцию сложения, а полученный результат разделить на их общее количество. Очень легко показать работу среднего арифметического на примере школьных отметок в табеле, поскольку показатель среднего балла знакомый каждому, кто учился в заведении среднего образования.
Предположим, у нас есть итоговая таблица, в которой приводятся оценки одного ученика за выполненные промежуточные контрольные работы: 3, 4, 3, 5, 5. Средним значением за четверть в этом случае будет 4 балла.
Среднее арифметическое Excel
Допустим, у нас есть таблица с набором определенных значений. Что они обозначают, не так важно в этой ситуации. Пусть это будет случайный набор цифр. Это никак не повлияет на логику рассуждения.

Нам необходимо нажать левой клавишей мыши по ячейке A2, тем самым активировав ее. После этого переходим в главное меню или обращаем внимание на ленту, находим там опцию «Редактирование», и в появившемся меню делаем левый клик мыши по кнопке «Сумма». При этом клик осуществляем не по самому значку, а по стрелочке, располагающейся рядом с ним. После этого появится еще одно меню, в котором будет набор разных функций. В нашем случае нас интересует «Среднее». После того, как нажать по ней, в выделенной ячейке будет автоматически записана формула.
Это еще не все. После этого нужно ввести аргумент функции, для чего достаточно просто выделить те ячейки, для которых и требуется определение среднего арифметического. После этого нажимаем клавишу «Enter».
Синтаксис СРЗНАЧ
Аргументы СРЗНАЧ
На практике формула вместе с введенным аргументом будет выглядеть следующим образом.
Такая формула осуществит расчет суммы значений от первого до десятого ряда, после чего поделит получившийся результат на 10.
Вычисление среднего арифметического с помощью Мастера функций
Мастер функций – это универсальная возможность Excel, позволяющая осуществлять самые сложные расчеты, при этом не зная названий формул. Достаточно просто выбрать правильную из списка, а потом вести правильные аргументы. Причем все они показываются в отдельном диалоговом окне с подсказками. Так что пользователь легко может разобраться, какая функция за что отвечает и какой она имеет синтаксис.
Рекомендуется поиграться с этим перечнем на досуге, чтобы получить представление о том, какие функции Excel были заложены разработчиками.
Чтобы вызвать мастер функций, необходимо нажать комбинацию клавиш Shift + F3 или найти возле строки ввода формул клавишу fx. После того, как это сделать, появится окошко, в котором нам нужно найти функцию «СРЗНАЧ». Значительно проще искать нужную нам функцию, если выбрать ее тип. В специальном выпадающем меню, расположенном в верхней части экрана, нужно выбрать пункт: «Статистические». Тогда перечень существенно сузится и будет проще выбирать.
Частный вариант – вызов функции вывода среднего арифметического из ленты. Для этого надо найти вкладку «Формулы», потом перейти в раздел «Другие функции», там навести мышью на пункт «Статистические». После всех этих операций появится функция СРЗНАЧ.
Панель формул
Каждый документ содержит панель формул, которая меняется в зависимости от того, какую ячейку выбрать. Если формула там есть, то она там будет записана. Если формула отсутствует, то там тогда будет отображаться просто значение ячейки (например, если там записан просто текст). На этом скриншоте видно конкретный пример, как может использоваться строка ввода формул. С ее помощью можно посмотреть на то, какая формула кроется за определенным числом (13,2) на примере, а также отредактировать аргументы. Или вообще убрать старую формулу и ввести новую. Или убрать все формулы, а оставить пустое значение или число. Возможностей у нее много достаточно. Можно выбрать любую, которая поможет выполнить поставленную задачу.
Ручной ввод функций
Функция СРЗНАЧ относится к простым. Ее легко запомнить, а также она содержит всего один аргумент. Поэтому мы ее введем вручную. В качестве примера будем использовать скриншот, приведенный выше. Как видим, можно использовать два разрозненных диапазона, не соединенных непосредственно между собой.
Мы введем ее вручную.
Очевидно, что в соответствующих местах нужно выставлять свои адреса. Если нужно, чтобы при копировании в другие ячейки они сохранялись, не стоит забывать делать ссылки абсолютными. Для этого их нужно выделять, а потом нажимать кнопку F4.
Настоятельно рекомендуется запоминать все функции, которые изучаете, потому что в будущем это позволит очень сильно сэкономить время.
Расчет среднего значения по условию
Может понадобиться находить среднее значение для определенных чисел только при условии, что они соответствуют конкретному критерию. Условие может быть любым, как текстовым, так и числовым. Также она может записываться как непосредственно в формулу, так и в другие ячейки.
Представим такую ситуацию: нам руководство поставило задачу определить среднее арифметическое для тех значений, которые равняются или больше 10.
Конечная формула будет следующей:
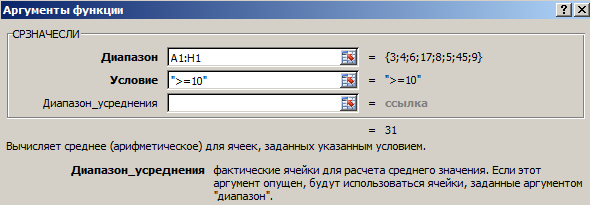
В результате, получится такое значение.

Разберем аргументы этой функции более подробно.
Мы опустили третий пункт, потому что в первом аргументе диапазон числовой, в то время как его лучше использовать лишь при текстовых критериях там.
Как найти среднее значение с учетом текста?
Если есть такая необходимость, критерий может быть записан в какой-то ячейке, а дальше просто достаточно дать ссылку на нее.
Теперь давайте отыщем среднее арифметическое, используя в качестве диапазона критерия набор текстовых значений из колонки А.
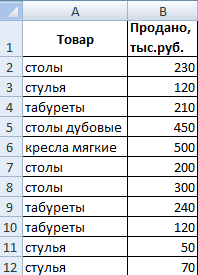
Важно! Указание диапазона усреднения является обязательным требованием к текстовым критериям.
Как рассчитать средневзвешенную цену в Excel?
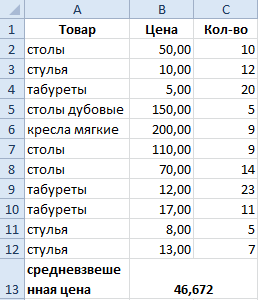
Чтобы узнать средневзвешенную цену в этом случае, необходимо использовать формулу.
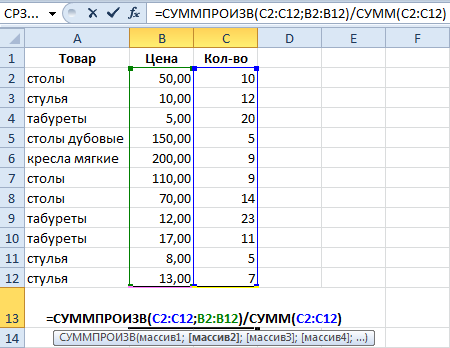
Далее происходит операция деления общей выручки товара на количество единиц. Вот таким образом и получилось найти средневзвешенную стоимость – показатель, который определяет то, насколько значимым оказывается конкретный товар в общей выручке.
Среднее квадратическое отклонение: формула в Excel
Когда заходить речь о среднем арифметическом, обязательно где-то рядом находится еще одно понятие – среднеквадратическое отклонение (или просто стандартное отклонение). Но чтобы понять, что это такое, необходимо сначала разобраться, что такое дисперсия.
Этот термин означает степень разброса значений. Все-таки разница между набором значений 4 и 6 со средним арифметическим 5 и 1 и 9 с тем же средним значением колоссальна. В первом случае дисперсия минимальная, а во втором значения находятся в очень большом разбросе.
Формула расчета дисперсии довольно сложная, но ее можно легко рассчитать с помощью стандартных инструментов Excel. Для этого есть две функции: ДИСП.В и ДИСП.Г
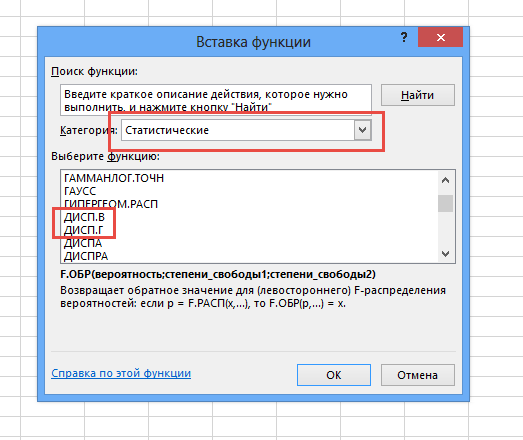
На практике это значение само по себе используется редко. Оно может применять для проверки правильности статистической гипотезы или определения коэффициентов корреляции. В разрезе нашей статьи дисперсия используется для определения среднеквадратического отклонения, которое образуется по простой формуле. Нужно из полученного значения дисперсии извлечь квадратный корень.
Есть два вида стандартного отклонения в Excel – по генеральной совокупности и выборочной.
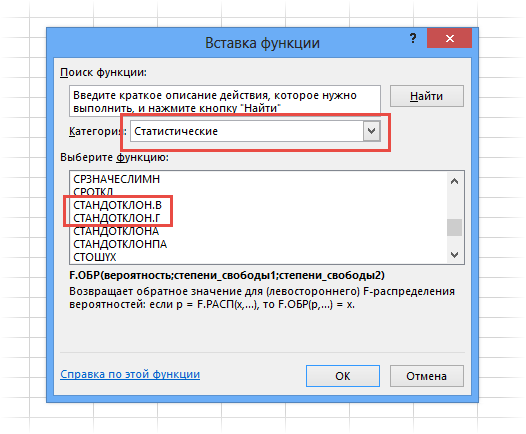
Формула дисперсии нам не нужна для расчета стандартного отклонения (за тем лишь исключением, если по каким-то причинам она уже известна, тогда можно просто извлечь из нее корень). Как видим из скриншота выше, есть две формулы стандартного отклонения в Excel.
Здесь, как видим, нужно разобраться еще в двух терминах: генеральная и выборочная совокупность. Первый – это весь диапазон анализируемых данных (общество, например), а второй – это часть этого диапазона, которая должна представлять генеральную совокупность (например, конкретная группа людей, которая соответствует ей по демографическим, социально-экономическим показателям).
Для стандартного отклонения характерна привязка к масштабу данных. Чтобы получить полное представление о том, насколько сильный разброс значений, наличия одних лишь абсолютных значений недостаточно. Необходимо еще получить относительные.
Для этого используется коэффициент вариации. Чтобы его вычислить, необходимо разделить стандартное отклонение на среднее значение. Его можно использовать, если значение не равно нулю и он оказывается полезным в тех ситуациях, когда имея информацию о среднем значении, можно понимать, насколько сильно отклонение.
Таким образом, получение среднего арифметического в Excel может осуществляться целым рядом способов. Это одна из самых главных формул, используемых в электронных таблицах. Поэтому ее знать обязательно наизусть. Тем более, что запомнить ее несложно, название интуитивно понятное, а аргумент всего один (хотя если нужно проанализировать несколько диапазонов, то количество параметров будет большим).
Среднее арифметическое
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами.
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
При стремлении количества элементов множества чисел стационарного случайного процесса к бесконечности среднее арифметическое стремится к математическому ожиданию случайной величины.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным.
В теории вероятностей случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными вероятностями.
Для определения средних или наиболее типичных значений совокупности используются показатели центра распределения. Основные из них — математическое ожидание, среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее степенное, взвешенные средние, центр сгиба, медиана, мода.
Что такое среднее арифметическое? Как найти среднее арифметическое?
Формула среднего арифметического чисел?
Среднее арифметическое нескольких чисел — это сумма этих чисел, делённая на их количество.
x ср — среднее арифметическое
n — количество чисел.
Например, нам нужно найти среднее арифметическое чисел 3, 4, 5 и 6.
Для этого нам нужно их сложить и полученную сумму разделить на 4:
(3 + 4 + 5 + 6) : 4 = 18 : 4 = 4,5.
Мне, как математику, интересны вопросы по данному предмету.
Начну с истории вопроса. Над средними величинами задумывались с древних времмен. Среднее арифметическое, среднее геометоическое, среднее гармоническое. Эти понятия предложены в древней Греции пифагорийцами.
А теперь интересующий нас вопрос. Что же понимается под средним арифметичским нескольких чисел:
Итак, для нахождения среднего арифметического чисел нужно прибавить все числа и разделить полученную сумму на количество слагаемых.
Имеет место формула:
Пример. Найти среднее арифметическое чисел: 100, 175, 325.
Воспользуемся формулой нахождения среднего арифметического трех чисел (то есть вместо n будет 3; нужно сложить все 3 числа и разделить полученную сумму на их количество, т.е. на 3). Имеем: х=(100+175+325)/3=600/3=200.
Как правильно вычислить среднее значение
Как найти среднее арифметическое
Например, перед вами ряд чисел «1, 2, 3, 4, 5, 6». Как следует из определения, чтобы узнать среднее арифметическое, нужно сложить все данные вам числа, а потом разделить получившийся результат на количество этих чисел. В приведённом примере — на шесть. Вот как это выражается формулой:
Допустим, вам нужно определить среднее арифметическое для чисел 4, 5 и 6. Складываем 4 + 5 + 6 = 15. Теперь делим 15 на 3 и получаем 5. Это и будет среднее арифметическое.
Таким же образом оно подсчитывается для десятичных и обыкновенных дробей.
Пример расчёта среднего арифметического для обыкновенных дробей будет выглядеть так:
А это пример, как найти среднее арифметическое для десятичных дробей:
Видео
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Какие способы вычисления среднего бывают?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
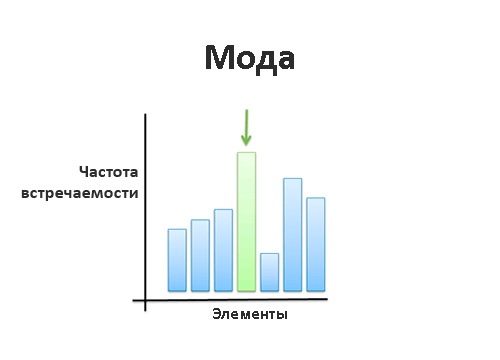
Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.
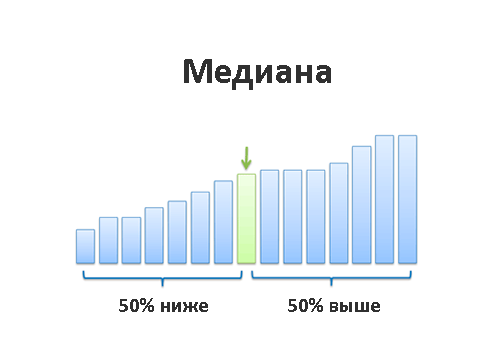
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.
Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:
И вот какие значения у нас получились:
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.
Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.
Вычисляем среднее арифметическое на SQL
И чтобы ее использовать достаточно написать вот такой запрос:
Вычисляем моду на SQL
В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.
Вычисляем медиану на SQL
Выглядит все это так:
Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.
Better Explained: Как правильно посчитать среднюю температуру по больнице
Среднее значение кажется очень простым термином. Именно простота делает его таким лукавым. Давайте поговорим о том, какие средние значения бывают, и как их использовать правильно.
Простой пример: Утром вы ведёте машину до работы со скоростью 30 км/ч, потому что вы не хотите на работу, а обратно едете уже со скоростью 60 км/ч, потому что спешите попасть домой. Какова средняя скорость вашего передвижения в этот день?
Подсказка: Нет, не 45 км/ч.
А пока вот вам небольшая табличка.
Но что всё это значит?
Давайте начнём сначала. Что вообще мы понимаем под словом «среднее»? Для большинства из нас это «какое-то число посередине» либо некое сбалансированное по каким-то критериям число.
Можно предложить более универсальную интерпретацию понятия «среднее значение». Среднее значение какого-либо ряда значений — это то, которым можно заменить любую единицу ряда и получить тот же результат. Условно говоря, я могу выбросить все представленные данные, кроме среднего значения, и общий смысл не изменится.
Одна из целей получения среднего значения — это понять суть выборки данных с помощью репрезентативного образца. Но сам процесс вычисления среднего значения зависит от того, каким образом взаимодействуют элементы группы данных. Давайте посмотрим, как это происходит.
Среднее арифметическое
Среднее арифметическое знакомо нам всем со школы:
среднее арифметическое = сумма всех величин/количество величин
Задачка: вы весите 75 кг и зашли в лифт с подростком весом 50 кг и толстяком весом 175 кг. Каков средний вес вашей группы?
На самом деле вопрос стоит так: Если заменить вашу весёлую компанию тремя клонированными людьми с одинаковым весом, каким весом должен обладать каждый такой клон?
В этом случае мы просто заказываем на фабрике по производству клонов человека трёх экземпляров весом в 100 килограмм каждый (Помним: (75+50+175)/3) и довольно потираем руки.
Преимущества среднего арифметического:
Недостатки среднего арифметического:
Среднее арифметическое срабатывает в 80% случаев. К сожалению, 20% оставшихся случаев и вынуждают нас искать альтернативы для подсчёта среднего значения.
Медиана
Медиана — это та самая грань, которая отделяет наибольшие значения от наименьших. То самое «число посередине». Постойте-постойте, а разве среднее арифметическое делает не то же самое?
Вот вам простой пример. Какое число находится в середине этого ряда?
1, 2, 3, 4, 100
Число «3» находится в середине ряда. И хотя среднее арифметическое (22) является «средним», оно никак не отражает распределения этих чисел. Интуитивно (и абсолютно правильно!) мы считаем, что в середине этого ряда всё-таки 3, а не 22. Здесь среднее значение увеличилось благодаря резко отклоняющемуся от общей массы значению, 100.
Медиана решает эту проблему. Медиана делит наш числовой ряд на две равные части, причём первая половина имеет значения меньше либо равные медиане, а вторая — больше либо равные. Если в середине числового ряда оказывается два числа, мы просто берём среднее арифметическое этих двух чисел, чтобы получить медиану. В числовом ряду 1, 2, 3, 4 медианой станет число 2,5. Именно медиана позволяет выбивающимся из общей массы числам вроде 100 в нашем примере выше не влиять на общее впечатление о числовом ряде.
Преимущества медианы:
Недостатки медианы:
Такие средние значения, как цены на недвижимость или, например, уровень дохода часто вычисляются именно по медиане, потому что нам важна именно средняя стоимость большей части домов в конкретном районе или средний уровень доходов большей части населения. В таком случае Билл Гейтс с годовым доходом в несколько миллиардов не испортит нам всю статистику. Видите, как много зависит от того, как мы работаем с имеющимися данными?
Само слово может звучать странно, но оно означает всего лишь наиболее часто встречающийся в группе элемент. На практике обычно мода определяется путём опросов и сбора мнений. Да, действительно порой бывают случаи, когда лучшим способом получить наиболее репрезентативный образец данных является сбор откликов.
Ну, скажем, вы планируете вечеринку, и вам нужно выбрать день для её проведения. Дни недели — такой же числовой ряд, что и любой другой. Это всего лишь числа от 1 до 7. Среднее арифметическое и медиана тут не помогут (Лиза и Паша могут в пятницу, а Коля и Петя — в воскресенье; поэтому назначим субботу). Что делать в таком случае? Конечно, выбрать тот день, который выберет большинство.
Как правило, мода используется для получения наиболее репрезентативного значения в нечисловых рядах. Популярные цвета в сезоне, хиты продаж, рейтинги фильмов и музыки, лучшие кафе и закусочные определяются именно по моде.
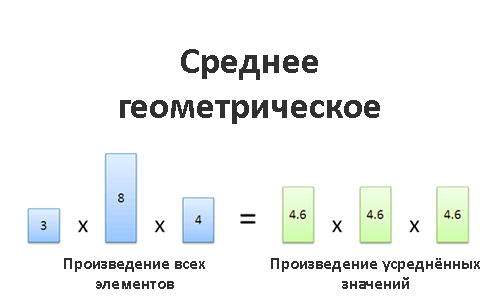
Среднее геометрическое
Наш «усреднённый элемент» зависит от того, что мы делаем с уже существующими элементами группы данных. В большинстве случаев элементы просто складываются, и среднее арифметическое прекрасно работает. Но иногда нам нужно что-то большее. Например, когда мы работаем с инвестициями, площадью и объёмом. В таких случаях данные взаимодействуют между собой именно путём умножения (ожидаемая доходность, объём или площадь фигуры вычисляются с помощью умножения), и это меняет наш подход к выявлению средних значений.
Вот пример. Какой инвестиционный портфель вы предпочтёте? Иными словами, какой из них принесёт большую прибыль в течение типичного года?
Выглядят они похоже. Наша повседневная логика, построенная на привычке к среднему арифметическому, говорит нам, что оба портфеля достаточно рискованны, и оба в среднем приведут к убыткам или нулевой прибыли. Поэтому, наверное, мы выберем портфель Б, поскольку в успешный год он принесёт больше прибыли.
И это неверно! На фондовом рынке с таким подходом мы с вами точно бы прогорели. Проценты с инвестиций умножаются, а не складываются. Мы не можем просто взять и использовать среднее арифметическое, нам нужно найти действительный коэффициент окупаемости. Коэффициент окупаемости считается достаточно просто: берём условные 100% нашего текущего капитала в качестве единицы. Далее представляем колебания доходности-убытка, представленные в описании портфелей, добавляя к нашей единице или вычитая из неё процентные показатели. Затем перемножаем полученные колебания и получаем коэффициент. Для расчёта среднегодового значения коэффициента окупаемости делим полученный коэффициент на 4 (поскольку элементов в нашем числовом ряду четыре).
Коэффициент окупаемости: 1,1 * 0,9 * 1,1 * 0,9 = 0,98 (2% убытка)
Среднегодовое значение: (0,98)^(1/4) = 0,5% годового убытка
Коэффициент окупаемости: 1,3 * 0,7 * 1,3 * 0,7 = 0,83 (17% убытка)
Среднегодовое значение: (0,83)^(1/4) = 4,6% годового убытка
Выбор между 2% или 17%? Огромная разница! Конечно, разумный человек отказался бы от обоих портфелей, но из двух зол лучше выбрать Портфель А. И именно здесь среднее арифметическое не работает.
Несколько примеров, где работает среднее геометрическое:
Среднее геометрическое помогает найти «типичный элемент» среди группы элементов, взаимодействующих друг с другом путём умножения. И, как видим, у него множество практических применений.
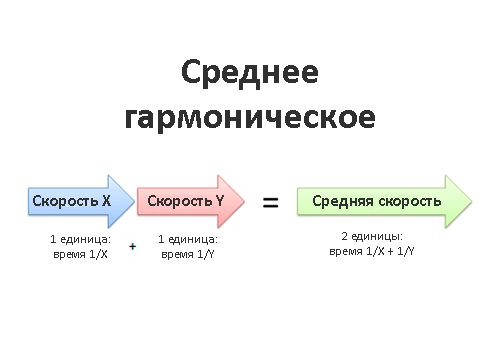
Среднее гармоническое
Среднее гармоническое представить сложнее, чем предыдущих представителей «средних», но оно не менее полезно. Между прочим, само понятие «гармоники» в математике связано с обратными числами (1/2, 1/3 и т.д.). Среднее гармоническое помогает нам вычислить среднее арифметическое в рядах чисел, заданных обратными значениями. Это случается чаще, чем вы можете подумать.
Например, если я еду со скоростью 30 км/ч, это значит, что я получаю определённый результат (30 км) за какую-либо единицу времени (1 час). Когда мы хотим узнать среднее значение для нескольких скоростей (Х и Y), нужно думать о результате и единицах измерения, а не об исходных цифрах.
средняя скорость = общий результат/общая единица измерения
Возьмём двух работников: Х и Y. Оба работают в одном проекте и выполняют одинаковое количество работы, но скорость их работы разная. Какова средняя скорость их работы?
Скажем, работник Х кладёт 30 кирпичей в час, а работник Y — 60 кирпичей в час. Значит, на один кирпич у каждого работника уходит:
Складываем результаты и единицы измерения:
Общий результат: 2 кирпича (Х и Y уложили по одному) Общая единица времени: 1/X + 1/Y (у каждого уходит разное количество времени)
Средней скоростью обоих работников будет:
Если бы у нас было 3 работника (X, Y и Z), их средняя скорость вычислялась бы по формуле:
Здорово же иметь одну формулу вместо того, чтобы каждый раз заниматься долгими вычислениями. Даже вычисляя среднюю скорость 5 нерадивых работников стало бы головной болью. Помните наш первый пример про скорость, с которой вы едете на работу и домой? Чтобы найти среднюю скорость вашего передвижения в тот день, мы просто используем формулу.
При этом нам даже не нужно знать, где находится дом или офис! Теперь вместо X и Y у нас не кирпичи, а количество километров за единицу времени. Вне зависимости от расстояния результат один и тот же: допустим, некое количество километров R мы проходим на скорости X, а другое количество километров R — на скорости Y. Средняя скорость при этом будет вычисляться так же, как вычисляется средняя скорость прохождения 1 км на скорости X и одного километра на скорости Y:
Ключевая идея: Среднее гармоническое используется тогда, когда один и тот же объём работы выполняется на разных скоростях.
Ещё более ключевая идея: Помните, что среднее значение — это один элемент, способный передать суть целой группы элементов. В нашем примере с работой и офисой в среднем туда-обратно мы едем на скорости 40 км/ч (вместо 30 км/ч туда и 60 км/ч обратно). Важно помнить, что средней скоростью мы заменяем каждую «стадию».
Ещё несколько примеров из жизни среднего гармонического:
В чём здесь фокус?
Среднее гармоническое действительно не самая очевидная вещь. Дело в том, что если бы у вас было две разных установки, одна из которых работает со скоростью 10 деталей/час, а другая — 20 деталей/час, конечно, их средняя производительность составляла бы 15 деталей/час. В этом случае вы имеете полное право просто сложить их производительность и вычислить среднее арифметическое, ведь установки работают независимо друг от друга.
Если не верите в среднее гармоническое, можно устроить себе обратную проверку. Мы утверждаем, что наша универсальная установка по заготовке и полировке деталей справляется с 7,14 деталями в час. Проверим: мы знаем, что за час машина либо обрабатывает 25 деталей, либо полирует 10. Получаем:
Подготовка: 7,14/25 = 0,29 часов Полировка: 7,14/10 = 0,71 часов
Да-да, 0,29 + 0,71 = 1, цифры работают: для полного цикла изготовления 7,14 деталей действительно требуется один час.
В качестве заключения
Даже такая простая на первый взгляд идея, как «среднее значение», имеет множество применений. Мы здесь рассмотрели лишь самые основные и не затронули средневзвешенное, центр тяжести, математическое ожидание и многое другое. Но мы поняли главные принципы:
Среднее арифметическое. Среднее значение величины
Урок 37. Математика 5 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности
Конспект урока «Среднее арифметическое. Среднее значение величины»
– Паша, привет. Чем занимаешься?
– Привет, Саша. Да вот читаю журнал. Представляешь, в России за год каждый человек съедает по 4,3 килограмма шоколада. Это же сколько шоколадок получается?
– Интересно, а как считали? Вот, например, я очень люблю шоколад и могу съесть много, а мой сосед Ваня вообще не ест шоколад, у него аллергия. И как тогда получили столько шоколада? Это что, у каждого жителя России спрашивали, сколько шоколада он ест? У меня никто не спрашивал. Какое-то это неправильное число, и вообще непонятно, откуда его взяли.
– Может, сходим к Электроше и у него узнаем, как получили это число?
– Мы к тебе с новым вопросом. Вот смотри, в журнале мы прочитали, что каждый житель России за год съедает 4,3 килограмма шоколада. И нам интересно, а как это считают? Ведь если, например, Ваня не может есть шоколад из-за аллергии, то за год он никак не съест так много.
– Сейчас я вам всё объясню. Но сначала давайте порешаем устно.
Вернёмся к вашей задаче.
В таких случаях речь идёт о среднем количестве шоколада, который съедают жители России. Получают это число так: общее количество всего шоколада, который съели за год, делят на общее количество людей, которые живут в России.
Аналогичным способом можно посчитать, например, средний возраст ребят вашего класса.
Или, например, таким же способом можно узнать среднюю скорость набора текста на компьютере.
В масштабах страны среднее арифметическое используют тогда, когда говорят, например, о том, что пшеницы собрано пятнадцать тонн с гектара или о среднем размере пенсии.
Для таких задач ввели специальную величину – среднее арифметическое.
Дадим определение. Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на количество слагаемых.
Попробуем найти среднее арифметическое чисел: 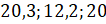
Сложим их, разделим на 3 и получим, что среднее арифметическое равно 17,5.
Вам всё понятно?
– Тогда, Саша, задание для тебя.
Найдите среднее арифметическое чисел: 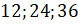
Сложим все числа. Так как всего чисел 3, значит, и делить будем на 3. Получим, что среднее арифметическое чисел 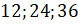
Очень часто, когда мы слышим, что автомобиль ехал со средней скоростью 90 километров в час, речь идёт именно о среднем арифметическом скоростей.
Давайте попробуем найти среднюю температуру за 3 жарких летних дня. По показаниям синоптиков, температура в первый день поднималась до 25 градусов выше нуля, во второй – до 23, а в третий – до 27 градусов выше нуля. Чтобы найти среднюю температуру, нам надо найти среднее арифметическое трёх чисел. Сложим их и разделим на 3. Получим, что средняя температура за 3 дня составляла 25 градусов выше нуля.
Давайте решим вот такую задачу.
Автомобиль 3 часа ехал со скоростью 56 километров в час. Затем 2 часа – со скоростью 57 километров в час. Определите среднюю скорость движения автомобиля.
– Ой, Электроша, а мы не знаем, как такое решать. Ты можешь помочь?
– Конечно. Давайте вспомним формулу, по которой мы можем найти скорость. Паша, ты помнишь?
– Скорость равна отношению длины всего пути ко времени, потраченному на этот путь 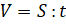
– Правильно. Давайте посчитаем, чему равно общее расстояние, которое проехал автомобиль.
– Хорошо. Перемножим 3 и 56, получим, что со скоростью 56 километров в час автомобиль проехал 168 километров. Со скоростью 57 километров в час автомобиль проехал 114 километров. То есть всего автомобиль проехал 282 километра.
А время, которое автомобиль был в пути, найти несложно. Оно равно 5.
– Остаётся только поделить путь на время, и получим, что средняя скорость автомобиля равна 56,4 километра в час.
– Вам стало понятно, ребята?
– Тогда вот для вас ещё одно задание. Среднее арифметическое пяти чисел равно 25,7. Первые четыре числа равны 13,9; 7,2; 20,4; 9,5. Найдите пятое число.
– Саша, это задание для тебя.
Обозначим пятое число за х.
– У нас известно среднее арифметическое пяти чисел.
Тогда мы можем определить сумму этих чисел. Зная сумму и первые четыре числа, пятое определить несложно. Получим, что пятое число равно 77,5.
Вот вам ещё одно задание. Одно число больше второго в 5 раз. Среднее арифметическое чисел равно 6. Найдите эти числа.
– Паша, это задание для тебя.
Обозначим одно число за х, получим, что второе число равно 5х.
Раз среднее арифметическое двух чисел равно 6, значит, сумма искомых чисел равна 12. Получаем уравнение: 6х = 12. Отсюда х = 2. Это первое число, и второе число равно 10.
Определение среднего значения, вариации и формы распределения. Описательные статистики
Способы представления числовых и категорийных данных в виде таблиц и диаграмм являются существенной, но не основной частью анализа данных. Ведущая роль принадлежит методам исследования числовых данных и их свойств. В этой заметке рассмотрены способы определения среднего значения, вариации и формы распределения генеральной совокупности. [1]
В большинстве случаев данные концентрируются вокруг некоей центральной точки. Таким образом, чтобы описать любой набор данных, достаточно указать средне значение. Рассмотрим последовательно три числовые характеристики, которые используются для оценки среднего значения распределения: среднее арифметическое, медиана и мода.
Среднее арифметическое
Среднее арифметическое (часто называемое просто средним) — наиболее распространенная оценка среднего значения распределения. Она является результатом деления суммы всех наблюдаемых числовых величин на их количество. Для выборки, состоящей из чисел Х1, Х2, …, Хn, выборочное среднее (обозначаемое символом 

где 
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Рассмотрим вычисление среднего арифметического значения пятилетней среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска (рис. 1).
Рис. 1. Среднегодовая доходность 15 взаимных фондов с очень высоким уровнем риска
Выборочное среднее вычисляется следующим образом:
Это хороший доход, особенно по сравнению с 3–4% дохода, который получили вкладчики банков или кредитных союзов за тот же период времени. Если упорядочить значения доходности, то легко заметить, что восемь фондов имеют доходность выше, а семь — ниже среднего значения. Среднее арифметическое играет роль точки равновесия, так что фонды с низкими доходами уравновешивают фонды с высокими доходами. В вычислении среднего задействованы все элементы выборки. Ни одна из других оценок среднего значения распределения не обладает этим свойством.
Когда следует вычислять среднее арифметическое. Поскольку среднее арифметическое зависит от всех элементов выборки, наличие экстремальных значений значительно влияет на результат. В таких ситуациях среднее арифметическое может исказить смысл числовых данных. Следовательно, описывая набор данных, содержащий экстремальные значения, необходимо указывать медиану либо среднее арифметическое и медиану. Например, если удалить из выборки доходность фонда RS Emerging Growth, выборочное среднее доходности 14 фондов уменьшится почти на 1% и составит 5,19%.
Медиана
Медиана представляет собой срединное значение упорядоченного массива чисел. Если массив не содержит повторяющихся чисел, то половина его элементов окажется меньше, а половина — больше медианы. Если выборка содержит экстремальные значения, для оценки среднего значения лучше использовать не среднее арифметическое, а медиану. Чтобы вычислить медиану выборки, ее сначала необходимо упорядочить.
Эта формула неоднозначна. Ее результат зависит от четности или нечетности числа n:
Чтобы вычислить медиану выборки, содержащей данные о доходности 15 взаимных фондов с очень высокий уровнем риска, сначала необходимо упорядочить исходные данные (рис. 2). Тогда медиана будет напротив номера среднего элемента выборки; в нашем примере №8. В Excel есть специальная функция =МЕДИАНА(), которая работает и с неупорядоченными массивами тоже.
Рис. 2. Медиана 15 фондов
Таким образом, медиана равна 6,5. Это означает, что доходность одной половины фондов с очень высоким уровнем риска не превышает 6,5, а доходность второй половины — превышает ее. Обратите внимание на то, что медиана, равная 6,5, ненамного больше среднего значения, равного 6,08.
Если удалить из выборки доходность фонда RS Emerging Growth, то медиана оставшихся 14 фондов уменьшится до 6,2%, то есть не так значительно, как среднее арифметическое (рис. 3).
Рис. 3. Медиана 14 фондов
Мода
Термин был впервые введен Пирсоном в 1894 г. Мода — это число, которое чаще других встречается в выборке (наиболее модное). Мода хорошо описывает, например, типичную реакцию водителей на сигнал светофора о прекращении движения. Классический пример использования моды — выбор размера выпускаемой партии обуви или цвета обоев. Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика»). Мультимодальность распределения дает важную информацию о природе исследуемой переменной. Например, в социологических опросах, если переменная представляет собой предпочтение или отношение к чему-то, то мультимодальность может означать, что существуют несколько определенно различных мнений. Мультимодальность также служит индикатором того, что выборка не является однородной и наблюдения, возможно, порождены двумя или более «наложенными» распределениями. В отличие от среднего арифметического, выбросы на моду не влияют. Для непрерывно распределенных случайных величин, например, для показателей среднегодовой доходности взаимных фондов, мода иногда вообще не существует (или не имеет смысла). Поскольку эти показатели могут принимать самые разные значения, повторяющиеся величины встречаются крайне редко.
Квартили
Квартили — это показатели, которые чаще всего используются для оценки распределения данных при описании свойств больших числовых выборок. В то время как медиана разделяет упорядоченный массив пополам (50% элементов массива меньше медианы и 50% — больше), квартили разбивают упорядоченный набор данных на четыре части. Величины Q1, медиана и Q3 являются 25-м, 50-м и 75-м перцентилем соответственно. Первый квартиль Q1 — это число, разделяющее выборку на две части: 25% элементов меньше, а 75% — больше первого квартиля.
Третий квартиль Q3 — это число, разделяющее выборку также на две части: 75% элементов меньше, а 25% — больше третьего квартиля.
Для расчета квартилей в версиях Excel до 2007 г. использовалась функция =КВАРТИЛЬ(массив;часть). Начиная с версии Excel2010 применяются две функции: [2]
Эти две функции дают немного различные значения (рис. 4). Например, при вычислении квартилей выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска Q1 = 1,8 или –0,7 для КВАРТИЛЬ.ВКЛ и КВАРТИЛЬ.ИСКЛ, соответственно. Кстати функция КВАРТИЛЬ, использовавшаяся ранее соответствует современной функции КВАРТИЛЬ.ВКЛ. Для расчета квартилей в Excel с помощью вышеприведенных формул массив данных можно не упорядочивать.
Рис. 4. Вычисление квартилей в Excel
Подчеркнем еще раз. Excel умеет рассчитывать квартили для одномерного дискретного ряда, содержащего значения случайной величины. Расчет квартилей для распределения на основе частот приведен ниже в разделе Вычисление описательных статистик для распределения на основе частот.
В отличие от среднего арифметического среднее геометрическое позволяет оценить степень изменения переменной с течением времени. Среднее геометрическое — это корень n-й степени из произведения n величин (в Excel используется функция =СРГЕОМ):

Похожий параметр – среднее геометрическое значение нормы прибыли – определяется формулой:

где Ri – норма прибыли за i-й период времени.
Например, предположим, что объем вложенных средств в исходный момент времени равен 100 000 долл. К концу первого года он падает до уровня 50 000 долл., а к концу второго года восстанавливается до исходной отметки 100 000 долл. Норма прибыли этой инвестиции за двухлетний период равна 0, поскольку первоначальный и финальный объем средств равны между собой. Однако среднее арифметическое годовых норм прибыли равно 

Интересные факты. Во-первых, среднее геометрическое всегда будет меньше среднего арифметического тех же чисел. За исключением случая, когда все взятые числа равны друг другу. Во-вторых, рассмотрев свойства прямоугольного треугольника, можно понять, почему среднее называется геометрическим. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу, а каждый катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу (рис. 5). Это даёт геометрический способ построения среднего геометрического двух (длин) отрезков: нужно построить окружность на сумме этих двух отрезков как на диаметре, тогда высота, восставленная из точки их соединения до пересечения с окружностью, даст искомую величину:
Рис. 5. Геометрическая природа среднего геометрического (рисунок из Википедии)
Второе важное свойство числовых данных — их вариация, характеризующая степень дисперсии данных. Две разные выборки могут отличаться как средними значениями, так и вариациями. Однако, как показано на рис. 6 и 7, две выборки могут иметь одинаковые вариации, но разные средние значения, либо одинаковые средние значения и совершенно разные вариации. Данные, которым соответствует полигон В на рис. 7, изменяются намного меньше, чем данные, по которым построен полигон А.
Рис. 6. Два симметричных распределения колоколообразной формы с одинаковым разбросом и разными средними значениями
Рис. 7. Два симметричных распределения колоколообразной формы с одинаковыми средними значениями и разным разбросом
Существует пять оценок вариации данных:
Размах
Размахом называется разность между наибольшим и наименьшим элементами выборки:
Размах позволяет измерить общий разброс данных. Хотя размах выборки является весьма простой оценкой общего разброса данных, его слабость заключается в том, что он никак не учитывает, как именно распределены данные между минимальным и максимальным элементами. Этот эффект хорошо прослеживается на рис. 8, который иллюстрирует выборки, имеющие одинаковый размах. Шкала В демонстрирует, что если выборка содержит хотя бы одно экстремальное значение, размах выборки оказывается весьма неточной оценкой разброса данных.
Рис. 8. Сравнение трех выборок, имеющих одинаковый размах; треугольник символизирует опору весов, и его расположение соответствует среднему значению выборки
Межквартильный размах
Межквартильный, или средний, размах — это разность между третьим и первым квартилями выборки:
Эта величина позволяет оценить разброс 50% элементов и не учитывать влияние экстремальных элементов. Межквартильный размах выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска, можно вычислить, используя данные на рис. 4 (например, для функции КВАРТИЛЬ.ИСКЛ): Межквартильный размах = 9,8 – (–0,7) = 10,5. Интервал, ограниченный числами 9,8 и –0,7, часто называют средней половиной.
Следует отметить, что величины Q1 и Q3, а значит, и межквартильный размах, не зависят от наличия выбросов, поскольку при их вычислении не учитывается ни одна величина, которая была бы меньше Q1 или больше Q3. Суммарные количественные характеристики, такие как медиана, первый и третий квартили, а также межквартильный размах, на которые не влияют выбросы, называются устойчивыми показателями.
Дисперсия и стандартное отклонение
Хотя размах и межквартильный размах позволяют оценить общий и средний разброс выборки соответственно, ни одна из этих оценок не учитывает, как именно распределены данные. Дисперсия и стандартное отклонение лишены этого недостатка. Эти показатели позволяют оценить степень колебания данных вокруг среднего значения. Выборочная дисперсия является приближением среднего арифметического, вычисленного на основе квадратов разностей между каждым элементом выборки и выборочным средним. Для выборки Х1, Х2, … Хn выборочная дисперсия (обозначаемая символом S 2 задается следующей формулой:
В общем случае выборочная дисперсия — это сумма квадратов разностей между элементами выборки и выборочным средним, деленная на величину, равную объему выборки минус один:
где 
Наиболее практичной и широко распространенной оценкой разброса данных является стандартное выборочное отклонение. Этот показатель обозначается символом S и равен квадратному корню из выборочной дисперсии:
В Excel до версии 2007 для расчета стандартного выборочного отклонения использовалась функция =СТАНДОТКЛОН(), с версии 2010 используется функция =СТАНДОТКЛОН.В(). Для расчета этих функций массив данных может быть неупорядоченным.
Ни выборочная дисперсия, ни стандартное выборочное отклонение не могут быть отрицательными. Единственная ситуация, в которой показатели S 2 и S могут быть нулевыми, — если все элементы выборки равны между собой. В этом совершенно невероятном случае размах и межквартильный размах также равны нулю.
Числовые данные по своей природе изменчивы. Любая переменная может принимать множество разных значений. Например, разные взаимные фонды имеют разные показатели доходности и убытков. Вследствие изменчивости числовых данных очень важно изучать не только оценки среднего значения, которые по своей природе являются суммарными, но и оценки дисперсии, характеризующие разброс данных.
Дисперсия и стандартное отклонение позволяют оценить разброс данных вокруг среднего значения, иначе говоря, определить, сколько элементов выборки меньше среднего, а сколько — больше. Дисперсия обладает некоторыми ценными математическими свойствами. Однако ее величина представляет собой квадрат единицы измерения — квадратный процент, квадратный доллар, квадратный дюйм и т.п. Следовательно, естественной оценкой дисперсии является стандартное отклонение, которое выражается в обычных единицах измерений — процентах дохода, долларах или дюймах.
Стандартное отклонение позволяет оценить величину колебаний элементов выборки вокруг среднего значения. Практически во всех ситуациях основное количество наблюдаемых величин лежит в интервале плюс-минус одно стандартное отклонение от среднего значения. Следовательно, зная среднее арифметическое элементов выборки и стандартное выборочное отклонение, можно определить интервал, которому принадлежит основная масса данных.
Стандартное отклонение доходности 15 взаимных фондов с очень высоким уровнем риска равно 6,6 (рис. 9). Это значит, что доходность основной массы фондов отличается от среднего значения не более чем на 6,6% (т.е. колеблется в интервале от 

Рис. 9. Стандартное выборочное отклонение
Обратите внимание на то, что в процессе суммирования квадратов разностей элементы выборки, лежащие дальше от среднего значения, приобретают больший вес, чем элементы, лежащие ближе. Это свойство является основной причиной того, что для оценки среднего значения распределения чаще всего используется среднее арифметическое значение.
Коэффициент вариации
В отличие от предыдущих оценок разброса, коэффициент вариации является относительной оценкой. Он всегда измеряется в процентах, а не в единицах измерения исходных данных. Коэффициент вариации, обозначаемый символами CV, измеряет рассеивание данных относительно среднего значения. Коэффициент вариации равен стандартному отклонению, деленному на среднее арифметическое и умноженному на 100%:
где S — стандартное выборочное отклонение, 
Коэффициент вариации позволяет сравнить две выборки, элементы которых выражаются в разных единицах измерения. Например, управляющий службы доставки корреспонденции намеревается обновить парк грузовиков. При погрузке пакетов следует учитывать два вида ограничений: вес (в фунтах) и объем (в кубических футах) каждого пакета. Предположим, что в выборке, содержащей 200 пакетов, средний вес равен 26,0 фунтов, стандартное отклонение веса 3,9 фунтов, средний объем пакета 8,8 кубических футов, а стандартное отклонение объема 2,2 кубических фута. Как сравнить разброс веса и объема пакетов?
Форма распределения
Третье важное свойство выборки — форма ее распределения. Это распределение может быть симметричным или асимметричным. Чтобы описать форму распределения, необходимо вычислить его среднее значение и медиану. Если эти два показателя совпадают, переменная считается симметрично распределенной. Если среднее значение переменной больше медианы, ее распределение имеет положительную асимметрию (рис. 10). Если медиана больше среднего значения, распределение переменной имеет отрицательную асимметрию. Положительная асимметрия возникает, когда среднее значение увеличивается до необычайно высоких значений. Отрицательная асимметрия возникает, когда среднее значение уменьшается до необычайно малых значений. Переменная является симметрично распределенной, если она не принимает никаких экстремальных значений ни в одном из направлений, так что большие и малые значения переменной уравновешивают друг друга.
Рис. 10. Три вида распределений
Данные, изображенные на шкале А, имеют отрицательную асимметрию. На этом рисунке виден длинный хвост и перекос влево, вызванные наличием необычно малых значений. Эти крайне малые величины смещают среднее значение влево, и оно становится меньше медианы. Данные, изображенные на шкале Б, распределены симметрично. Левая и правая половины распределения являются своими зеркальными отражениями. Большие и малые величины уравновешивают друг друга, а среднее значение и медиана равны между собой. Данные, изображенные на шкале В, имеют положительную асимметрию. На этом рисунке виден длинный хвост и перекос вправо, вызванные наличием необычайно высоких значений. Эти слишком большие величины смещают среднее значение вправо, и оно становится больше медианы.
Если на вкладе Данные в области Анализ у вас не отображается пиктограмма Анализ данных, нужно предварительно установить надстройку Пакет анализа (см., например, Представление числовых данных в виде таблиц и диаграмм).
Рис. 11. Описательные статистики пятилетней среднегодовой доходности фондов с очень высоким уровнями риска, вычисленные с помощью надстройки Анализ данных программы Excel
Excel вычисляет целый ряд статистик, рассмотренных выше: среднее, медиану, моду, стандартное отклонение, дисперсию, размах (интервал), минимум, максимум и объем выборки (счет). Кроме того, Excel вычисляет некоторые новые для нас статистики: стандартную ошибку, эксцесс и асимметричность. Стандартная ошибка равна стандартному отклонению, деленному на квадратный корень объема выборки. Асимметричность характеризует отклонение от симметричности распределения и является функцией, зависящей от куба разностей между элементами выборки и средним значением. Эксцесс представляет собой меру относительной концентрации данных вокруг среднего значения по сравнению с хвостами распределения и зависит от разностей между элементами выборки и средним значением, возведенных в четвертую степень.
Вычисление описательных статистик для генеральной совокупности
Среднее значение, разброс и форма распределения, рассмотренные выше, представляют собой характеристики, определяемые по выборке. Однако, если набор данных содержит числовые измерения всей генеральной совокупности, можно вычислить ее параметры. К числу таких параметров относятся математическое ожидание, дисперсия и стандартное отклонение генеральной совокупности.
Математическое ожидание равно сумме всех значений генеральной совокупности, деленной на объем генеральной совокупности:
где µ — математическое ожидание, Xi — i-е наблюдение переменной X, N — объем генеральной совокупности. В Excel для вычисления математического ожидания используется та же функция, что и для среднего арифметического: =СРЗНАЧ().
Дисперсия генеральной совокупности равна сумме квадратов разностей между элементами генеральной совокупности и мат. ожиданием, деленной на объем генеральной совокупности:
где σ 2 – дисперсия генеральной совокупности. В Excel до версии 2007 для вычисления дисперсии генеральной совокупности используется функция =ДИСПР(), начиная с версии 2010 =ДИСП.Г().
Стандартное отклонение генеральной совокупности равно квадратному корню, извлеченному из дисперсии генеральной совокупности:
В Excel до версии 2007 для вычисления стандартного отклонения генеральной совокупности используется функция =СТАНДОТКЛОНП(), начиная с версии 2010 =СТАНДОТКЛОН.Г(). Обратите внимание на то, что формулы для дисперсии и стандартного отклонения генеральной совокупности отличаются от формул для вычисления выборочной дисперсии и стандартного отклонения. При вычислении выборочных статистик S 2 и S знаменатель дроби равен n – 1, а при вычислении параметров σ 2 и σ — объему генеральной совокупности N.
Эмпирическое правило
В большинстве ситуаций крупная доля наблюдений концентрируется вокруг медианы, образуя кластер. В наборах данных, имеющих положительную асимметрию, этот кластер расположен левее (т.е. ниже) математического ожидания, а в наборах, имеющих отрицательную асимметрию, этот кластер расположен правее (т.е. выше) математического ожидания. У симметричных данных математическое ожидание и медиана совпадают, а наблюдения концентрируются вокруг математического ожидания, формируя колоколообразное распределение. Если распределение не имеет ярко выраженной асимметрии, а данные концентрируются вокруг некоего центра тяжести, для оценки изменчивости можно применять эмпирическое правило, которое гласит: если данные имеют колоколообразное распределение, то приблизительно 68% наблюдений отстоят от математического ожидания не более чем на одно стандартное отклонение, приблизительно 95% наблюдений отстоят от математического ожидания не более чем на два стандартных отклонения и 99,7% наблюдений отстоят от математического ожидания не более чем на три стандартных отклонения.
Таким образом, стандартное отклонение, представляющее собой оценку среднего колебания вокруг математического ожидания, помогает понять, как распределены наблюдения, и идентифицировать выбросы. Из эмпирического правила следует, что для колоколообразных распределений лишь одно значение из двадцати отличается от математического ожидания больше, чем на два стандартных отклонения. Следовательно, значения, лежащие за пределами интервала µ ± 2σ, можно считать выбросами. Кроме того, только три из 1000 наблюдений отличаются от математического ожидания больше чем на три стандартных отклонения. Таким образом, значения, лежащие за пределами интервала µ ± 3σ практически всегда являются выбросами. Для распределений, имеющих сильную асимметрию или не имеющих колоколообразной формы, можно применять эмпирическое правило Бьенамэ-Чебышева.
Более ста лет назад математики Бьенамэ и Чебышев независимо друг от друга открыли полезное свойство стандартного отклонения. Они обнаружили, что для любого набора данных, независимо от формы распределения, процент наблюдений, лежащих на расстоянии не превышающем k стандартных отклонений от математического ожидания, не меньше (1 – 1/k 2 )*100%.
Например, если k = 2, правило Бьенамэ-Чебышева гласит, что как минимум (1 – (1/2) 2 ) х 100% = 75% наблюдений должно лежать в интервале µ ± 2σ. Это правило справедливо для любого k, превышающего единицу. Правило Бьенамэ-Чебышева носит весьма общий характер и справедливо для распределений любого вида. Оно указывает минимальное количество наблюдений, расстояние от которых до математического ожидания не превышает заданной величины. Однако, если распределение имеет колоколообразную форму, эмпирическое правило более точно оценивает концентрацию данных вокруг математического ожидания.
Вычисление описательных статистик для распределения на основе частот
Если исходные данные недоступны, единственным источником информации становится распределение частот. В таких ситуациях можно вычислить приближенные значения количественных показателей распределения, таких как среднее арифметическое, стандартное отклонение, квартили.
Если выборочные данные представлены в виде распределения частот, приближенное значение среднего арифметического можно вычислить, предполагая, что все значения внутри каждого класса сосредоточены в средней точке класса:
где 
Для вычисления стандартного отклонения по распределению частот также предполагается, что все значения внутри каждого класса сосредоточены в средней точке класса.
Чтобы понять, как определяются квартили ряда на основе частот, рассмотрим расчет нижнего квартиля на основе данных за 2013 г. о распределении населения России по величине среднедушевых денежных доходов (рис. 12).
Рис. 12. Доля населения России со среднедушевыми денежными доходами в среднем за месяц, рублей
Для расчета первого квартиля интервального вариационного ряда можно воспользоваться формулой: [3]
где Q1 – величина первого квартиля, хQ1 – нижняя граница интервала, содержащего первый квартиль (интервал определяется по накопленной частоте, первой превышающей 25%); i – величина интервала; Σf – сумма частот всей выборки; наверное, всегда равна 100%; SQ1–1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль; fQ1 – частота интервала, содержащего нижний квартиль. Формула для третьего квартиля отличается тем, что во всех местах вместо Q1 нужно использовать Q3, а вместо ¼ подставить ¾.
В нашем примере (рис. 12) нижний квартиль находится в интервале 7000,1 – 10 000, накопленная частота которого равна 26,4%. Нижняя граница этого интервала – 7000 руб., величина интервала – 3000 руб., накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль – 13,4%, частота интервала, содержащего нижний квартиль – 13,0%. Таким образом: Q1 = 7000 + 3000 * (¼ * 100 – 13,4) / 13 = 9677 руб.
Ловушки, связанные с описательными статистиками
В этой заметке мы рассмотрели, как описать набор данных с помощью различных статистик, оценивающих его среднее значение, разброс и вид распределения. Следующим этапом является анализ и интерпретация данных. До сих пор мы изучали объективные свойства данных, а теперь переходим к их субъективной трактовке. Исследователя подстерегают две ошибки: неверно выбранный предмет анализа и неправильная интерпретация результатов.
Анализ доходности 15 взаимных фондов с очень высоким уровнем риска является вполне беспристрастным. Он привел к совершенно объективным выводам: все взаимные фонды имеют разную доходность, разброс доходности фондов колеблется от –6,1 до 18,5, а средняя доходность равна 6,08. Объективность анализа данных обеспечивается правильным выбором суммарных количественных показателей распределения. Было рассмотрено несколько способов оценки среднего значения и разброса данных, указаны их преимущества и недостатки. Как же выбрать правильную статистику, обеспечивающую объективный и беспристрастный анализ? Если распределение данных имеет небольшую асимметрию, следует ли выбирать медиану, а не среднее арифметическое? Какой показатель более точно характеризует разброс данных: стандартное отклонение или размах? Следует ли указывать на положительную асимметрию распределения?
С другой стороны, интерпретация данных является субъективным процессом. Разные люди приходят к разным выводам, истолковывая одни и те же результаты. У каждого своя точка зрения. Кто-то считает суммарные показатели среднегодовой доходности 15 фондов с очень высоким уровнем риска хорошими и вполне доволен полученным доходом. Другим может показаться, что эти фонды имеют слишком низкую доходность. Таким образом, субъективность следует компенсировать честностью, нейтральностью и ясностью выводов.
Этические проблемы
Анализ данных неразрывно связан с этическими вопросами. Следует критически относиться к информации, распространяемой газетами, радио, телевидением и Интернетом. Со временем вы научитесь скептически относиться не только к результатам, но и к целям, предмету и объективности исследований. Лучше всего об этом сказал известный британский политик Бенджамин Дизраэли: «Существуют три вида лжи: ложь, наглая ложь и статистика».
Как было отмечено в заметке Искусство графического представления данных этические проблемы возникают при выборе результатов, которые следует привести в отчете. Следует публиковать как положительные, так и отрицательные результаты. Кроме того, делая доклад или письменный отчет, результаты необходимо излагать честно, нейтрально и объективно. Следует различать неудачную и нечестную презентации. Для этого необходимо определить, каковы были намерения докладчика. Иногда важную информацию докладчик пропускает по невежеству, а иногда — умышленно (например, если он применяет среднее арифметическое для оценки среднего значения явно асимметричных данных, чтобы получить желаемый результат). Нечестно также замалчивать результаты, которые не соответствуют точке зрения исследователя.
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 178–209
[2] Функция КВАРТИЛЬ оставлена для совмещения с более ранними версиями Excel