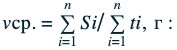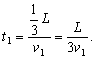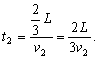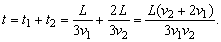Как посчитать среднюю скорость

29.08.202229.08.2022 admin 0 Комментариев

Как посчитать среднюю скорость

Способы нахождения средней скорости в физике

Основные понятия и законы кинематики

Кинематика — раздел механики, описывающий механическое движение тел без рассмотрения причин, из-за которых происходит движение.

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Для описания движения нужна система отсчета, относительно которой мы будем описывать движение.

Система отсчета — это система координат, связанная с телом отсчета и прибор для измерения времени.

Тело отсчета — это тело, относительно которого рассматривают положение других тел.

Материальная точка — это тело, размеры которого можно не учитывать при решении задачи.

Траектория — это мысленная линия в пространстве, которую при движении описывает материальная точка.

Траектория движения делится на два типа:

Путь — это длина траектории, которую описывает тело или материальная точка за данный промежуток времени.

Перемещение S → — это вектор, соединяющий начальное положение тела или материальной точки с ее конечным положением.

Скорость — это векторная физическая величина, характеризующаяся направлением и быстротой перемещения материальной точки.

Определение средней скорости

Рассчитать среднюю скорость можно по следующей формуле:

Определение средней путевой скорости

Средняя путевая скорость — это отношение пути или длины траектории, пройденного телом, к интервалу времени, за которое этот путь был пройден.

Формула средней путевой скорости выглядит так:

Примеры решения задач

Автомобиль первый час ехал со скоростью 100 км/ч, после чего сделал остановку. Следующие два часа автомобиль ехал со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость на протяжении всего пути автомобиля.

В условии сказано о трех участках пути.

ϑ с р → = S 1 → + S 2 → + S 3 → t 1 + t 2 + t 3

Участки пути мы можем вычислить и посчитать следующим образом:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

ϑ с р = 100 + 180 + 160 1 + 2 + 2 = 440 5 = 88 к м ч

Ответ: средняя скорость составляет 88 км/ч.

Автомобиль проехал по дороге расстояние 140 км за время, равное 2 часам, затем сделал остановку. После остановки автомобиль проехал 60 км за 3 часа. Какова средняя скорость автомобиля за весь путь?

ϑ с р → = ∆ S → ∆ t ϑ с р → = S 1 → + S 2 → t 1 + t 2 ϑ с р → = 140 + 60 2 + 3 = 40 к м ч

Ответ: средняя скорость автомобиля составляет 40 км/ч.

Человек занимается бегом и за 2 часа пробежал 5 км, а за следующий час пробежал 3 км. Определите среднюю скорость бегуна.

Искать среднюю скорость будем как во второй задаче.

Источник

Вычисление средней скорости движения в физике: расчёты и формулы

Содержание:

Под средней скоростью движения какого-либо тела понимают отношение пройденного расстояния к временному промежутку, который был затрачен на его преодоление. Определение средней скорости может понадобиться в случае, когда в процессе перемещения тела на разных участках его скорость изменялась. Неважно в каком направлении совершалось движение и изменялось ли оно с течением времени. Характер движения может быть сложным или простым. Средняя скорость является скалярной величиной, поэтому алгоритм вычисления всегда будет примерно одинаковым.

Как найти среднюю скорость тела?

Пример. Автомобиль всего проехал 1 километр и 200 метров. После каждых 400 м он изменял скорость движения. Первые 400 метров он двигался со скоростью 20 км/ч, потом со скоростью 40 км/ч, 50 км/ч и последний участок проехал на скорости 35 км/ч. Определение средней скорости движения производим так:

В любом другом случае вычисление средней скорости в физике производят более сложным путем по формуле:

Пример задачи на вычисление средней скорости в физике

Сначала найдем путь, который был пройден за каждый из промежутков времени:

S₁ = 1 х 7 = 7 км

S₂ = 2 х 4 = 8 км

Далее пишется вышеприведенная формула в более привычном виде, как обычно, подставляются необходимые данные и определяется средняя скорость:

Средняя скорость при равноускоренном движении

На практике очень часто встречаются задачи, когда вычисление средней скорости необходимо производить для случая, когда тело, двигаясь с какой-то начальной скоростью, с течением времени начало ускоряться и в конце пути достигло какой-то новой скорости. Тогда следует использовать формулу, которая выражает среднюю скорость через величину ускорения:

vcp. = v0 + \frac < at > < 2 >, где:

Пример. Двигаясь с начальной скоростью 160 м/с, самолет в течение двух минут ускорял свое движение на 1,5 м/с2. Какова его средняя скорость за этот промежуток времени?

vcp. = 160 + \frac < 1,5 * 120 > < 2 >= 250 м/с

Источник

Средняя скорость движения

Пример 1
Автомобиль проехал первую треть всего пути со скоростью 60 км/ч, а оставшееся расстояние со скоростью 40 км/ч. Найдите среднюю скорость движения автомобиля.

Решение
Обозначим длину всего пути S, скорость на 1-м участке V₁, а скорость на 2-м участке V₂. Тогда время, затраченное на прохождение первого участка будет
t₁ = S / 3 / V₁ = S / 3 / 60 = S / 180
а на прохождение второго участка
t₂ = S * 2 / 3 / V₂ = S * 2 / 3 / 40 = S / 60
Отсюда общее время прохождения пути будет
t = t₁ + t₂ = S / 180 + S / 60 = (S + 3 * S) / 180 = S * 4 / 180 = S / 45
Используя формулу средней скорости, получим
V = S / t = S / (S / 45) = 45

Ответ
Средняя скорость автомобиля 45 км/ч

Ответ
Скорость автомобиля на третьем участке 72 км/ч

Источник

Скорость время расстояние

Онлайн калькулятор поможет Вам рассчитать время пути из пункта А в пункт Б и среднюю скорость движения.

Смотрите также

в описании к калькулятору добавьте, что из-за особенностей Javascript он не принимает «,» даже не представляю сколько людей погорело у вас тут.

Спасибо.
Поддержку «,» добавили.

Два пешехода вышли навстречу друг другу. Скорость первого составляет 3 м/мин, а второго — 4 м/мин. Через
сколько минут они встретятся, если расстояние между ними 1680 метров?

Медвежат отвезли за 600 км от населенного пункта. Через 18 дней (432часа) они вернулись в посёлок. Вопрос: Это реально? И с какой скоростью они могли передвигаться в сутки?

За какое время пройдёт машина расстояние 10 метров со скоростью 170км/ч

От города A до города B расстояние 40 км. Два велосипедиста выехали из A и B навстречу друг другу, один со скоростью 10 км/ч, а другой — 15 км/ч. Муха вылетела с первым из A со скоростью 100 км/ч, долетела до второго, села ему на лоб и полетела обратно к первому, села ему на лоб, вернулась ко второму и так далее, пока они не столкнулись лбами и не раздавили ими муху. Сколько километров пролетела муха?

Если пешеход вышел в деревню со скоростью 4.8 км/ч,возвращался со скоростью 6 км/ч и вернулся на час раньше. Какое расстояние от села до деревни?

Источник

Средняя скорость пути

Известно, что средняя скорость V равна пути S, деленному на время t средней скорости. Средняя скорость не всегда находится так легко. В случае, если автомобиль движется равномерно с постоянной скоростью, например 45 км/час, то, очевидно, средняя скорость и постоянная скорость одинаковы, т. е. 45 км/час. Если же автомобиль трогается с места (начальная скорость равна 0) и развивает скорость постепенно, то среднюю скорость можно найти следующим способом: нужно записать сумму всех скоростей и поделить ее на число отсчетов скоростей. Важно — временные интервалы должны быть одинаковые (например: записывать скорость каждые 5 секунд, или каждые 7 минут).

Калькулятор средней скорости пути

Складывая скорости, введенные вами, мы находим их сумму. Разделив эту сумму на количество равных временных отсчетов, мы узнаем среднюю скорость.

Единицы скорости

Скорость обычно определяют как путь, пройденный за единицу времени. Поэтому, если скорость автомобиля 90 км/час, то он за минуту должен пройти 1,5 км, а в секунду 1500 : 60, или 25 м. Следовательно, скорость 90 км/час может быть выражена различными способами в зависимости от выбора единиц времени и пути:

90 км/час = 1.5 км/мин =25 м/сек.

Поскольку скорость может быть выражена в различных единицах, то надо внимательно следить за выбором единиц в формуле S=vt. Если скорость выбираем в км/час, то время надо брать в часах, если — в м/сек, то время должно быть выражено в секундах.

Источник

Как найти среднюю скорость автомобиля после поездки в разных режимах?

Автор: Дмитрий Сапко

Для вычисления средней скорости поездки на современной машине достаточно подготовиться заранее, сбросив показатели суточного пробега на нуль, а также обнулив средние данные расхода и скорости. После этого вы сможете не засекать никакого времени, а также не продумывать формулы по расчету средней скорости поездки. Тем не менее, такой вариант не всегда подходит, да и не все автомобили оснащены хорошим бортовым компьютером. Потому следует разобраться с тем, как определять среднюю скорость и прочие параметры.

Находим среднюю скорость и средний расход поездки по факту

Если замеры средней скорости поездки важны для вас в коммерческих целях или в качестве отчетности для фирмы, в которой вы работаете, то проще всего купить GPS-навигатор, который обладает функцией учета скорости и времени, проведенного в дороге. Этот прибор полностью заменит бортовой компьютер и сможет без применения различных формул показать вам среднюю скорость поездки.

В иных случаях можно пользоваться более грубыми методами определения. Для замеров вам потребуется секундомер, который будет определять рабочее время поездки. То есть, для нас важна каждая секунда, которую автомобиль проводит в дороге. Время, проведенное на заправках или в придорожных кафе зачастую в расчет не входит. Задачи для точного замера следующие:

Предположим, на поездку у вас ушло ровно 5 часов, а пройденное по спидометру расстояние оказалось 300 километров. Это значит, что средняя скорость вашего автомобиля во время движения составила 60 км/ч. Если вы будете практиковать определение средней скорости для каждой дальней поездки, то будете удивлены низкими показателями.

Часто создается впечатление, что средняя скорость должна быть около 120 километров в час, но на деле оказывается меньше 60. Подобным образом вы сможете просчитать средний расход топлива. Нужно затраченные литры поделить на сотни километров пройденного расстояния. К примеру, если вы проехали 300 километров, то делать сумму литров нужно на 3.

Какой должна быть средняя скорость машины в поездке?

Многие задаются вопросом, а какой же на самом деле должна быть средняя скорость автомобиля. Просчитав удивительный факт того, что средняя скорость авто в трассовом режиме составила всего 80 километров в час, водитель начинает сомневаться в том, что он эффективно использует ресурс транспортного средства. На самом деле, такая скорость вполне допустима.

Оптимальной скоростью при движении по трассе является 90 км/ч, но далеко не всегда получает держать крейсерскую скорость постоянно. Иногда происходят ситуации, которые заставляют в течение нескольких минут ехать медленно. К примеру, можно тянуться за фурой, ожидая возможности обгона. Оптимальная средняя скорость на трассе будет зависеть от таких факторов:

Это лишь базовые факторы, которые влияют на среднюю скорость машины при трассовой поездке. На практике при отсутствии нарушений ПДД средняя скорость автомобиля на трассе составляет 75-80 километров в час. Достичь средней скорости в 90 км/ч можно только на определенном отрезке трассы. Потому не огорчайтесь, увидев небольшие значения на экране бортового компьютера.

Первым фактором, который нужно оценивать при выборе скоростного режима на трассе, является безопасность. Именно этот важный критерий иногда становится жертвой нехватки времени или желания показать достойные цифры средней скорости. На деле такие цели никогда не приводят к хорошим последствиям, потому всегда выбирайте безопасные режимы поездки.

Главным критерием выбора скоростного режима являются далеко не возможности машины, а ваши соображения о безопасности и уверенности поездки. Если вы считаете, что ехать со скоростью 90 км/ч при данных условиях опасно, то лучше выбрать более комфортный и уверенный режим. Тем не менее, существуют определенные рекомендации от производителей.

Первое, о чем стоит вспомнить в таком контексте разговора, является средний расход. Если вы будете поддерживать скорость машины на уровне 90 километров в час, то расход будет максимально близким к паспортным показателям расхода на трассе. Многие водители переживают по поводу того, что их машина на трассе расходует больше топлива, чем указано в документах. Происходит это по таким причинам:

Именно по этим причинам средние показатели расхода часто оказываются на порядок больше паспортных замеров. При определении расхода в трассовом режиме для технических характеристик машины производитель выполняет тестирование транспорта не треке, где машина едет с постоянной одной рекомендованной скоростью. Именно это позволяет достичь столь занимательных цифр расхода топлива.

Для получения максимальных выгод в расходе топлива и прочих характеристиках вашего автомобиля экспериментируйте и пробуйте разные режимы поездки. Не лишни будет и почитать отзывы о том, как люди эксплуатируют ваш тип транспорта. Это поможет максимально упростить эксплуатацию машины, сделать меньшим расход топлива и предсказать любые особенности поведения транспортного средства. Помните, что скорость должна быть оправданной. Предлагаем подборку видео ДТП, случившихся в частности из-за высокой скорости:

Подводим итоги

Если вы решили учитывать особенности вашей эксплуатации транспорта, следует начать с учета средней скорости при движении, а также средних показателей расхода. Если вы сможете учитывать эти показатели постоянно, вы также сможете улучшать средний расход, ведь в данном случае проснется спортивный интерес. Занимаетесь ли вы учетом средних показателей эксплуатации вашего авто?

Источник

Как высчитывается средняя скорость. Как найти среднюю скорость

Средняя скорость — машина

Средняя скорость машин ЕС-1030 по Гибсону составляет 100 тыс. операций в секунду.

Под средней скоростью машины понимают среднюю линейную скорость одной из точек ведущего вала машины во время ее установившегося движения.

Для того чтобы средняя скорость машины могла оставаться постоянной, необходимо, чтобы при этой скорости имело место равновесие между работой движущих сил и работой сопротивлений. Но это равновесие может нарушаться по различным причинам.

Для установления козфициента нагрузки двигателя определим среднюю скорость машины v — кгк, момент трения по формуле ( 55), угловую скорость машины ( см. фиг.

Очевидно, что такая система позволяет на уровне программирования заботиться о том, чтобы информация была заранее считана в быстрые регистры операндов и арифметическое устройство не ожидало ее поступления из памяти. Средняя скорость машины CDC-6600 оценивается в 3 5 млн. операций в секунду, однако, как утверждают разработчики, при оптимальном программировании она может быть значительно повышена.

Сравнение формул ( 52) и ( 58) дает следующий вывод: коэфициент нагрузки двигателя на повороте при бортовых фрикционах в два раза меньше, чем при простом дифе-ренциале. Это снижение нагрузки достигается за счет снижения потери в тормозе, а также вследствие понижения средней скорости машины на повороте. Зависимость между коэ-фициентами нагрузки двигателя и параметром поворота показана на диаграмме фиг.

Если бы движение машины было равномерно, если бы она шла всегда одинаково быстро, то оценка 40 км в час полностью характеризовала бы ее скорость — одну и ту же в любой момент движения. Но машина движется неравномерно; за час скорость ее много раз резко меняется, и когда нам говорят, что машина прошла в час 40 км, то это дает нам представление лишь о некоторой средней скорости машины за этот час и ничего не говорит о скорости ее в тот или другой определенный момент, в том или другом определенном месте ее пути. Час — это слишком большой промежуток времени, за который скорость движения машины может меняться много раз.

Средняя скорость машины при выполнении арифметики тем самым приблизительно равна 10000 операций в секунду. При выполнении логических программ быстродействие резко возрастает. В минимальном комплекте в состав процессора входит оперативная память объемом 8192 байта. Правда, объем памяти при необходимости может быть расширен до 64 Кбайт.

На маршруте ABCDE длиной 147 км Турист может сам выбирать способ передвижения. На обратном пути из пункта Е в пункт А он поступил по-другому: до пункта D дошел пешком, преодолев расстояние в 24 км, в пункте D пересел на лошадь и добрался до пункта В за 3 ч 20 мин, а от пункта Л до пункта А доехал на машине за 1 ч 12 мин. Определите скорость передвижения туриста на машине и на лошади, если средние скорости машины и лошади были постоянными при движении от А к S и обратно.

Находим среднюю скорость и средний расход поездки по факту

Для чего это нужно

Такие расчеты полезны всем. Мы все время планируем свой день и перемещения. Имея дачу за городом, есть смысл узнать среднюю путевую скорость при поездках туда.

Это упростит планирование проведения выходных. Научившись находить эту величину, мы сможем быть более пунктуальными, перестанем опаздывать.

Вернемся к примеру, предложенному в самом начале, когда часть пути автомобиль проехал с одной скоростью, а другую — с иной. Такой вид задач очень часто используется в школьной программе. Поэтому, когда ваш ребенок попросит вас помочь ему с решением подобного вопроса, вам будет просто это сделать.

Сложив длины участков пути, вы получите общее расстояние. Поделив же их значения на указанные в исходных данных скорости, можно определить время, потраченное на каждый из участков. Сложив их, получим время, потраченное на весь путь.

Часто водителю необходимо отыскать такой важный показатель, как средняя скорость автомобиля после той или иной поездки. Иногда эта цифра будет важным фактом для водителя транспорта компании, а в иных случаях — просто интересное число для владельца транспортного средства. В любом случае, расчет средней скорости важен для многих водителей. В современных автомобилях, оснащенных эффективными компьютерными системами управления, достаточно просто выбрать нужный режим отображения информации на экране компьютера, чтобы узнать среднюю скорость за определенный промежуток времени или пробег.

Средняя скорость — движение — автомобиль

Средняя скорость движения автомобиля зависит от максимальной скорости, которую он может развить на дорогах различного качества, и от интенсивности разгона. Кроме того, на среднюю скорость автомобиля существенное влияние оказывают его тормозные свойства.

Средние скорости движения автомобилей приведены для дорог с усовершенствованным типом покрытия в хорошем состоянии.

Средняя скорость движения автомобиля составляет v км / час.

Средняя скорость движения автомобиля зависит от многих факторов: на нее влияют, с одной стороны, конструктивные особенности автомобиля, а с другой — дорожные условия. При испытаниях ее стремятся поддерживать максимально возможной. Чтобы полнее выяснить причины, вызывающие ограничение скорости, принято определять среднюю скорость чистого движения и среднюю техническую скорость.

Стремление повысить среднюю скорость движения автомобилей ( автопоездов) при одновременном увеличении их полной массы приводит к повышению мощности двигателя, что, в свою очередь, вызывает повышенные требования к трансмиссии автомобиля. Это непосредственно относится и к ведущему мосту, назначение которого состоит в изменении крутящего момента двигателя при передаче его к ведущим колесам таким образом, чтобы вместе с коробкой передач обеспечить согласование скоростной характеристики двигателя с динамической характеристикой автомобиля.

График, для определения нагрузочного режима трансмиссии автомобиля ( по нормали.

Угловую скорость рассчитываемых подшипников определяют по средней скорости движения автомобиля аа ср — с учетом соответствующего передаточного числа между валами коробки передач.

Именно эта скорость имеется в виду, когда, например, говорят о средней скорости движения автомобиля или средней скорости поезда.

За эквивалентное число оборотов пэкв принимается число оборотов подшипника ( вала), соответствующее средней скорости движения автомобиля на основной ( прямой) передаче.

Зависимость коэффициента сцепления от различных факторов.

В практике управления автомобилем важно знать н только максимальную скорость движения автомобиля на отдельных участках маршрута, но и среднюю скорость на всем маршруте. Возможность определения средней скорости движения автомобиля имеет практическое значение для осуществления планирования перевозок грузов и пассажиров на автомобильном транспорте.
. Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости

В итоге следует ожидать повышения средней скорости движения автомобиля. Для того чтобы оценить степень влияния удельной мощности на среднюю скорость вследствие сокращения именно этого этапа цикла, рассмотрим процесс разгона автомобиля с учетом переключения передач.

Постоянная скорость

Самый простой случай в физике — равномерное движение. Скорость постоянна, не меняется на протяжении всего пути. Есть даже скоростные константы, сведенные в таблицы, — неизменные величины. К примеру, звук распространяется в воздухе со скоростью 340,3 м/с.

А свет — абсолютный чемпион в этом плане, он обладает самой большой в нашей Вселенной скоростью — 300 000 км/с. Эти величины не меняются от начальной точки движения до конечной. Они зависят только от среды, в которой движутся (воздух, вакуум, вода и пр.).

Равномерное движение часто встречается нам и в повседневной жизни. Так работает конвейер на заводе или фабрике, фуникулер на горных трассах, лифт (за исключением очень коротких периодов пуска и остановки).

График такого движения очень прост и представляет собой прямую линию. 1 секунда — 1 м, 2 секунды — 2 м, 100 секунд — 100 м. Все точки находятся на одной прямой.

Частные случаи нахождения средней скорости

2. Два одинаковых интервала движения.
Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила: м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Главная&nbsp>&nbsp Wiki-учебник&nbsp>&nbsp Физика&nbsp>&nbsp7 класс&nbsp>

Как же рассчитать скорость

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы
, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать
, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

Можно записать использовать и такой вид вычислений:

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей
.

Не упустите

Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:

Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.

Вот так легко запоминается формула «скорость, время, расстояние»

Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено

Уровень B

1. О какой скорости – средней или мгновенной – идет речь в следующих случаях:

а) пуля вылетает из винтовки со скоростью 800 м/с;

б) скорость движения Земли вокруг Солнца 30 км/с;

в) на участке дороги установлен ограничитель максимальной скорости – 60 км/ч;

г) мимо вас проехал автомобиль со скоростью 72 км/ч;

д) автобус преодолел расстояние между Могилевом и Минском со скоростью 50 км/ч?

2. Путь в 63 км от одной станции до другой электропоезд проходит за 1 ч 10 мин со средней скоростью 70 км/ч. Какое время занимают остановки?

3. Самоходная косилка имеет ширину захвата 10 м. Определите площадь поля, скошенного за 10 мин, если средняя скорость косилки 0,1 м/с.

4. На горизонтальном участке пути автомобиль ехал со скоростью 72 км/ч в течение 10 мин, а затем проехал подъем со скоростью 36 км/ч за 20 мин. Чему равна средняя скорость на всем пути?

5. Велосипедист первую половину времени при переезде из одного пункта в другой ехал со скоростью 12 км/ч, а вторую половину времени (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость движения велосипедиста.

6. Школьник проехал 1/3 всего времени на автобусе со скоростью 60 км/ч, еще 1/3 всего времени на велосипеде со скоростью 20 км/ч, остальное время прошел со скоростью 7 км/ч. Определите среднюю скорость движения школьника.

7. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью 12 км/ч, а вторую половину (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость его движения.

8. Из одного пункта в другой мотоциклист двигался со скоростью 60 км/ч, обратный путь им был пройден со скоростью 10 м/с. Определите среднюю скорость мотоциклиста за все время движения.

9. Школьник проехал 1/3 пути на автобусе со скоростью 40 км/ч, еще 1/3 пути на велосипеде со скоростью 20 км/ч, последнюю треть пути прошел со скоростью 10 км/ч. Определите среднюю скорость движения школьника.

10. Пешеход часть пути прошел со скоростью 3 км/ч, затратив на это 2/3 времени своего движения. Оставшееся время он прошел со скоростью 6 км/ч. Определите среднюю скорость.

11. Скорость поезда на подъеме 30 км/ч, а на спуске – 90 км/ч. Определите среднюю скорость на вcем участке пути, если спуск в два раза длиннее подъема.

12. Половину времени при переезде из одного пункта в другой автомобиль двигался с постоянной скоростью 60 км/ч. С какой постоянной скоростью он должен двигаться оставшееся время, если средняя скорость движения равна 65 км/ч?

Аналог средней температуры в механике

В каких случаях каверзно сформулированные условия задачи подталкивают нас к поспешному необдуманному ответу? Если говорится о «частях» пути, но не указывается их протяжённость, это настораживает даже мало искушённого в решении подобных примеров человека. А вот если в задаче прямо указывается на равные промежутки, например, «первую половину пути поезд следовал со скоростью…», или «первую треть пути пешеход прошагал соскоростью…», и далее подробно расписывается, как объёкт передвигался на оставшихся равных участках, то есть известно соотношение S 1 = S 2 = … = S n
и точные значения скоростей v 1, v 2, … v
n
, наше мышление нередко даёт непростительную осечку. Считается среднее арифметическое скоростей, то есть все известные значения v
складываются и делятся на n
. В итоге ответ получается неверный.

Формула скорости математика 4 класс

С какой скоростью черепах ползла после камня, если она проползла 33 см?

3. Поезд шёл до станции 7 ч со скоростью 63 км/ч, а после станции поезд проехал ещё 4 ч. С какой скоростью поезд проедет путь от станции, если всего он прошёл 741 км?

Составные задачи на расстояние.

Травоядный динозавр сначала бежал 3 ч со скоростью 6 км/ч, а потом он бежал ещё 4 ч со скоростью 5 км/ч. Какое расстояние пробежал травоядный динозавр?

Рассуждаем так. Это задача в одном направлении.

Слова « скорость », «время», «расстояние» запишем зеленой ручкой.

Скорость (V) Время (t) Расстояние (S)

Составим план решения этой задачи. Чтобы узнать какое расстояние пробежал динозавр, надо знать, какое расстояние он пробежал, потом и какое расстояние он пробежал сначала.

Чтобы найти расстояние, надо скорость умножить на время.

6· 3 = 18 (км) — расстояние, которое пробежал динозавр сначала. Чтобы найти расстояние, надо скорость умножить на время.

5 4 = 20 (км) — расстояние, которое пробежал динозавр потом.

Составим выражение:6 3 + 5 4 = 38(км)

Ответ: 38 км пробежал травоядный динозавр.

1. Ракета сначала летела 28 с со скоростью 15 км/с, а оставшийся путь летела 53 с со скоростью 16 км/с. Какое расстояние пролетела ракета?

2. Утка сначала плыла 3 ч со, скоростью 19 км/ч, а потом она плыла ещё 2 ч со скоростью 17 км/ч. Какое расстояние проплыла утка?

3. Кит полосатик сначала плыл 2 ч со скоростью 22 км/ч, а потом он плыл ещё 2 ч со скоростью 43 км/ч. Какое расстояние проплыл кит полосатик?

4. Теплоход до пристани шёл 3 ч со скоростью 28 км/ч, а после пристани плыл ещё 2 ч со скоростью 32 км/ч. Какое расстояние проплыл теплоход?

Задачи на нахождение времени совместной работы.

Привезли 240 саженцев елей. Первый лесник может посадить эти ели за 4 дня, а второй за 12 дней. За сколько дней оба лесника могут выполнить задание, работая вместе?

240: 4 = 60 (саж,) за 1 день сажает первый лесник.

240: 12 — 20 (саж.) за 1 день сажает второй лесник.

60 + 20 = 80 (саж.) за 1 день сажают оба лесника. 240:80 = 3(дн.)

Ответ: за 3 дня лесники посадят саженцы, работая вместе.

1. В мастерской 140 мониторов. Один мастер отремонтирует их за 70 дней, а другой, за 28 дней. За сколько дней оба мастера отремонтируют эти мониторы, если будут работать вместе?

2. Было 600 кг горючего. Один трактор израсходовал его за 6 дней, а другой – за 3 дня. За сколько дней тракторы израсходуют это горючее, работая вместе?

3. Надо перевезти 150 пассажиров. Один катер перевезёт их за 15 рейсов, а другой за 10 рейсов. За сколько рейсов эти катера перевезу всех пассажиров, работая вместе?

4. Один ученик может сделать 120 снежинок 60 мин, а другой — за 30 мин. Сколько потребуется времени ученикам, если они будут работать вместе?

5. Один мастер может изготовить 90 шайбочек за 30 мин, другой—‘за 15 мин. За какое время они изготовят 90 шайбочек при совместной работе?

Источник

Как найти среднюю скорость: разные методологии и проблемы

Далее мы изучим больше методов, как найти среднюю скорость, так как это основная цель поста.

Какая формула для средней скорости

Основная формула, используемая для расчета V_{средний} включает как смещение во времени.

Общая используемая формула имеет следующий вид:

Он используется при решении основных задач, связанных со средней скоростью.

V = Δs / Δt

Где,

Δs = смещение

Δt = затраченное время

Теперь давайте посмотрим, как найти среднюю скорость с помощью расстояния и времени.

Как найти среднюю скорость в зависимости от расстояния и времени

Прежде всего, мы должны рассчитать общую длину пути, по которому прошел объект, а затем мы должны проверить продолжительность времени, необходимого для достижения пункта назначения. Позже, чтобы найти среднюю скорость этого движения, нам нужно использовать ранее рассчитанные расстояние и время с помощью формулы.

Теперь давайте продолжим изучение, чтобы узнать больше подходов к нахождению средней скорости.

Как найти среднюю скорость за интервал

V = общее расстояние / общее время или

Теперь давайте посмотрим, как рассчитать V_{средний} между двумя точками.

Средняя скорость между двумя точками

Среднюю скорость между двумя точками можно найти по простой формуле.

В общем, мы знаем, что Vavg тела равно среднему арифметическому начальных и конечных точек, приведенному ниже.

Vavg = [Начальная скорость (i) + Конечная скорость (v)] / 2

Пора узнать, как найти V_{средний} на графике.

Как найти среднюю скорость на графике

Переменные, взятые на графике, имеют характерную природу, все факторы, такие как изменение положения (между начальной и конечной точками), характер графика, т. Е. Является ли он линейным или нет, имеет значение.

При таком подходе мы можем рассчитать среднюю скорость по графику.

Как найти среднюю скорость на линейном графике

Линейный график иногда называют прямолинейным графиком.

Если мы хотим узнать среднюю скорость на линейном графике, тогда мы должны взять как начальную, так и конечную скорости и разделить ее на число 2. Это похоже на среднее значение, которое мы используем в математике для решения определенных задач.

Теперь давайте узнаем условие вычисления средней скорости на нелинейном графике.

Как найти среднюю скорость на нелинейном графике

Нелинейный граф также можно рассматривать как искривленный граф.

В нелинейном графике, что мы можем сделать, чтобы вычислить V_{средний} мы можем рассмотреть область под графиком, которая состоит из смещения (интегрировать его), а затем разделить на время.

Таким образом мы можем вычислить V_{средний} в нелинейном графике.

Пример задачи средней скорости

Пример 1

Представьте, что человек едет на своей машине в какой-то пункт назначения, но в течение первых 15 секунд положение машины меняется с x₁ = 80 м до x₂= 100 м. Какова средняя скорость автомобиля?

Решение: учитывая исходное положение x₁= 80m

Точно так же конечная позиция x₂ = 100m

Изменение водоизмещения автомобиля рассчитывается следующим образом:

Δt = 15 с

По формуле мы имеем

v = Δx / Δt

v = 20/15

v = 1.33 м / с

Таким образом, средняя скорость автомобиля составляет 1.33 м / с.

Из поставленной выше задачи мы узнали еще об одном подходе к нахождению средней скорости

Часто задаваемые вопросы | FAQs

Что такое средняя скорость?

Это векторная величина, определяемая как деление ∆x на ∆t. Где ∆x обозначает смещение, а ∆t обозначает общее время, затрачиваемое телом на завершение движения. Иногда может быть положительным или отрицательным, все зависит от направления смещения. Обозначается с помощью единицы СИ м / с.

Чем средняя скорость отличается от других скоростей?

Есть два основных типа скоростей, с которыми мы обычно сталкиваемся в физике.

Чем средняя скорость отличается от мгновенной скорости в конкретный интервал времени?

Если мы возьмем конкретный временной интервал, тогда будет разница в измерении средней и мгновенной скорости.

Основное различие заключается в том, что для определенного периода интервала мгновенная скорость измеряется смещением и временем в определенной точке (s, t), а средняя скорость считается общим изменением положения во времени в определенном временном интервале.

Сохраняется ли средняя скорость в движении?

Скорость не остается неизменной в конкретном движении, она продолжает изменяться.

Мы выяснили, что скорость является переменной, зависящей от многих факторов. Он не остается постоянным, но продолжает изменять свое значение с помощью перемещения и времени этого объекта. Исходя из этого, мы можем сказать, что средняя скорость движения не остается неизменной.

Каковы два основных способа вычисления средней скорости?

Есть много приложений, с помощью которых мы можем легко измерить среднюю скорость.

Второй метод основан на использовании формулы, известной как уравнение средней скорости.

Это простое уравнение для измерения средней скорости.

Как найти смещение со средней скоростью?

Есть много способов найти смещение в кинематике.

Почему различаются средняя скорость и средняя скорость?

Оба термина означают совершенно разные друг от друга, когда мы изучаем их в физике.

Разница между средней скоростью и средней скоростью

Основные различия между этими двумя величинами приведены ниже:

Я Рагхави Ачарья, я закончил аспирантуру по физике со специализацией в области физики конденсированного состояния. Очень хорошо разбираюсь в Latex, gnu-plot и octave. Я всегда считал физику увлекательной областью изучения, и мне нравится изучать различные области этого предмета. В свободное время я занимаюсь цифровым искусством. Мои статьи направлены на то, чтобы донести до читателей представления о физике в очень упрощенной форме. Давайте подключимся через LinkedIn: https://www.linkedin.com/in/raghavi-cs-260a801b1 EMAIL ID: raghavics6@gmail.com

Последние посты

Иногда мы используем будущее совершенное простое время, чтобы описать событие или действие, которое будет завершено в определенное время в будущем. Примеры будущего совершенного простого времени:

О НАС

Мы группа профессионалов из разных областей и областей, т.е. инженерии, передовой науки и исследований, технологий. Мы вместе работаем над созданием платформы, основанной на знаниях, которая будет содержать огромное количество академических и профессиональных предметов из всех областей и отраслей.

Источник

Как найти среднюю скорость с несколькими скоростями?

Средняя скорость = 2ab / (a + b)

Точно так же, как вы находите среднюю скорость по времени и скорости? Самая распространенная формула для средней скорости: пройденное расстояние, разделенное на затраченное время. Другая формула: если у вас есть начальная и конечная скорость, сложите их вместе и разделите на 2.

Похожие страницы:Блог

Какие есть 3 вида налогов?

Как найти среднюю точку между двумя точками?

Как вы делаете кадровые прогнозы?

Как найти начальную скорость, зная только время?

Как найти среднюю скорость с 3 скоростями?

Во-вторых, по какой формуле найти среднее значение? Среднее значение равно сумме набора чисел, разделенной на количество, которое является количеством добавляемых значений.. Например, вы хотите получить среднее значение 13, 54, 88, 27 и 104. Найдите сумму чисел: 13 + 54 + 88+ 27 + 104 = 286. В нашем наборе данных пять чисел, поэтому разделите 286 на 5, чтобы получить 57.2.

Какая средняя скорость и напишите формулу?

Средняя скорость рассчитывается по формуле S = d / t, где S — средняя скорость, d — общее расстояние, t — общее время. Проблемы: 1). Автомобиль проезжает расстояние 70 км за 2 часа.

то какая средняя скорость по математике? Средняя скорость объекта равна общее расстояние, пройденное объектом, деленное на время, затраченное на преодоление этого расстояния. Это скалярная величина, что означает, что она определяется только величиной.

Что является примером средней скорости? Средняя скорость рассчитывается путем деления общего пройденного расстояния на временной интервал. Например, тот, кто за 40 минут проехал 20 миль на север, а затем 20 миль на юг (чтобы оказаться в том же месте), имеет среднюю скорость 40 миль, разделенных на 40 минут, или 1 милю в минуту (60 миль в час).

Как рассчитать среднюю скорость?

Средняя скорость рассчитывается по формуле разделение вашего смещения (вектор, указывающий от вашего начального положения до вашего конечного положения) на общее время; средняя скорость рассчитывается путем деления общего пройденного расстояния на общее время.

Каковы 3 способа расчета среднего? 4.2.

Выделяют три основных типа среднего: среднее, медиана и мода. Каждый из этих методов работает немного по-разному и часто приводит к немного отличающимся типичным значениям. Среднее значение является наиболее часто используемым средним значением. Чтобы получить среднее значение, вы складываете все значения и делите эту сумму на количество значений.

Как найти среднемесячное значение?

Разделите текущую сумму на общее количество дней в месяц, который прошел до сих пор. Затем умножьте на общее количество дней в месяце.

Как решить проблемы со средней скоростью? Как рассчитать среднюю скорость

Как вы рассчитываете скорость на примере?

Рассчитайте его скорость. Скорость = Расстояние / время = 15/2 = 7.5 миль в час. Пример 3. Автомобиль преодолевает расстояние за 4 часа, если он движется со скоростью 40 миль в час.

Как найти среднюю скорость и среднюю скорость?

Величина средней скорости всегда меньше или равна средней скорости, потому что перемещение всегда меньше или равно пройденному расстоянию. Средняя скорость вычисляется по формула V = D/t, где V равно средней скорости, D равно полному смещению и t равно общему времени.

Как вы рассчитываете скорость?

Пример средней скорости? Например, у человека, которому требуется 40 минут, чтобы проехать 20 миль на север, а затем 20 миль на юг (чтобы оказаться в одном и том же месте), средняя скорость составляет 40 миль, разделенных на 40 минут, или 1 милю в минуту (60 миль в час). Однако средняя скорость включает полное перемещение, а не расстояние.

Как получить в среднем 2 числа?

Что такое среднее математическое? Среднее математическое вычисляется путем взятия суммы группы значений и деления ее на количество значений в группе. Он также известен как среднее арифметическое.

Как написать среднюю формулу в Excel?

Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter.
.
Пример.

Данные
=СРЕДНЕЕ(A2:C2)	Среднее число в ячейках от A2 до C2.	19

Как рассчитать средние затраты? Чтобы получить среднее значение, сложите сумму денег, потраченную за 12 месяцев подряд, затем разделите на 12. Это даст среднее значение того, сколько было потрачено в месяц.

Как рассчитать среднее значение за 3 месяца?

Чтобы рассчитать 3-точечные скользящие средние из списка чисел, выполните следующие действия:

Как я могу рассчитать среднее значение? Среднее значение равно сумме набора чисел, разделенной на количество, которое является количеством добавляемых значений.. Например, вы хотите получить среднее значение 13, 54, 88, 27 и 104. Найдите сумму чисел: 13 + 54 + 88+ 27 + 104 = 286. В нашем наборе данных пять чисел, поэтому разделите 286 на 5, чтобы получить 57.2.

Источник

Как высчитывается средняя скорость Как найти среднюю скорость

Как найти среднюю скорость. Пошаговая инструкция

Есть средние величины, неправильное определение которых вошло в анекдот или в притчу. Любые неверно произведённые расчёты комментируются расхожей общепонятной ссылкой на такой заведомо абсурдный результат. У каждого, к примеру, вызовет улыбку саркастического понимания фраза «средняя температура по больнице». Однако те же знатоки нередко, не задумываясь, складывают скорости на отдельных отрезках пути и делят подсчитанную сумму на число этих участков, чтобы получить столь же бессмысленный ответ. Напомним из курса механики средней школы, как найти среднюю скорость правильным, а не абсурдным способом.

Аналог «средней температуры» в механике

Простые «формулы» расчёта величин при равномерном движении

И для всего пройденного пути, и для отдельных его участков в случае усреднения скорости справедливы соотношения, написанные для равномерного движения:

То есть для нахождения искомой величины v с использованием соотношения (3) нам нужно точно знать две другие. Именно решая вопрос, как найти среднюю скорость движения, мы прежде всего должны определить, каков весь пройденный путь S и каково всё время движения t.

Математическое обнаружение скрытой ошибки

Явное подтверждение ошибки «в числах»

Для того чтобы «на пальцах» подтвердить, что определение среднего арифметического — ошибочный путь при расчёте v_ср, конкретизируем пример, заменив абстрактные буквы числами. Для поезда возьмём скорости 40 км/ч и 60 км/ч (ошибочный ответ — 50 км/ч). Для пешехода — 5, 6 и 4 км/ч (среднее арифметическое — 5 км/ч). Нетрудно убедиться, подставив значения в соотношения (4) и (5), что верными ответами будут для локомотива 48 км/ч и для человека — 4,(864) км/ч (периодическая десятичная дробь, результат математически не слишком красивый).

Когда среднее арифметическое «не подводит»

Если задача формулируется так: «За равные промежутки времени тело двигалось сначала со скоростью v₁, затем v₂, v₃ и так далее», быстрый ответ на вопрос, как найти среднюю скорость, может быть найден неправильным способом. Предоставим читателю самостоятельно в этом убедиться, просуммировав в знаменателе равные промежутки времени и воспользовавшись в числителе v_ср соотношением (1). Это, пожалуй, единственный случай, когда ошибочный метод приводит к получению корректного результата. Но для гарантированно точных расчётов нужно пользоваться единственно правильным алгоритмом, неизменно обращаясь к дроби v_ср = S : t.

Алгоритм на все случаи жизни

Для того чтобы наверняка избежать ошибки, при решении вопроса, как найти среднюю скорость, достаточно запомнить и выполнить простую последовательность действий:

В статье рассмотрены простейшие случаи, когда исходные данные приводятся для равных долей времени или равных участков пути. В общем случае соотношение хронологических промежутков либо пройденных телом расстояний может быть самым произвольным (но при этом математически определённым, выраженным конкретным целым числом или дробью). Правило обращения к соотношению v_ср = S : t абсолютно универсально и никогда не подводит, сколь бы сложные на первый взгляд алгебраические преобразования ни приходилось выполнять.

Напоследок отметим: для наблюдательных читателей не осталась незамеченной практическая значимость использования верного алгоритма. Правильно рассчитанная средняя скорость в приведённых примерах оказалась несколько ниже «средней температуры» на трассе. Поэтому ложный алгоритм для систем, фиксирующих превышения скорости, означал бы большее число ошибочных постановлений ГИБДД, высылаемых в «письмах счастья» водителям.

Физика

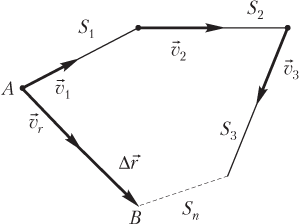
Средняя скорость перемещения является векторной физической величиной, которую определяют по формуле

где Δ r → — вектор перемещения; ∆ t — интервал времени, за которое это перемещение произошло.

Средняя путевая скорость является скалярной физической величиной и вычисляется по формуле

Здесь S 1 = v 1 t 1 — первый участок пути; v 1 — скорость прохождения первого участка пути (рис. 1.18); t 1 — время движения на первом участке пути и т.п.

Пример 7. Одну четверть пути автобус движется со скоростью 36 км/ч, вторую четверть пути — 54 км/ч, оставшийся путь — со скоростью 72 км/ч. Рассчитать среднюю путевую скорость автобуса.

Решение. Общий путь, пройденный автобусом, обозначим S :

S 1 = S /4 — путь, пройденный автобусом на первом участке,

S 2 = S /4 — путь, пройденный автобусом на втором участке,

S 3 = S /2 — путь, пройденный автобусом на третьем участке.

Время движения автобуса определяется формулами:

t 1 = S 1 v 1 = S 4 v 1 ;

на втором участке ( S 2 = S /4) —

t 2 = S 2 v 2 = S 4 v 2 ;

на третьем участке ( S 3 = S /2) —

Общее время движения автобуса составляет:

Вычисление средней путевой скорости автобуса произведем по формуле

v s = S общ t общ = S S ( 1 4 v 1 + 1 4 v 2 + 1 2 v 3 ) =

Расчет дает значение средней путевой скорости:

v s = 4 ⋅ 36 ⋅ 54 ⋅ 72 54 ⋅ 72 + 36 ⋅ 72 + 2 ⋅ 36 ⋅ 54 = 54 км/ч.

Пример 8. Пятую часть времени городской автобус тратит на остановки, остальное время он движется со скоростью 36 км/ч. Определить среднюю путевую скорость автобуса.

Решение. Общее время движения автобуса на маршруте обозначим t :

t 1 = t /5 — время, затраченное на остановки,

t 2 = 4 t /5 — время движения автобуса.

Путь, пройденный автобусом:

так как скорость автобуса v 1 на данном временном интервале равна нулю ( v 1 = 0);

где v 2 — скорость автобуса на данном временном интервале ( v 2 = = 36 км/ч).

Общий путь автобуса составляет:

Вычисление средней путевой скорости автобуса произведем по формуле

Расчет дает значение средней путевой скорости:

v s = 4 5 ⋅ 36 = 30 км/ч.

Пример 9. Уравнение движения материальной точки имеет вид x ( t ) = (9,0 − 6,0 t + 2,0 t 2 ) м, где координата задана в метрах, время — в секундах. Определить среднюю путевую скорость и величину средней скорости перемещения материальной точки за первые три секунды движения.

Решение. Для определения средней скорости перемещения необходимо рассчитать перемещение материальной точки. Модуль перемещения материальной точки в интервале времени от t 1 = 0 с до t 2 = 3,0 с вычислим как разность координат:

x ( t 1 ) = 9,0 − 6,0 t 1 + 2,0 t 1 2 = 9,0 − 6,0 ⋅ 0 + 2,0 ⋅ 0 2 = 9,0 м;

x ( t 2 ) = 9,0 − 6,0 t 2 + 2,0 t 2 2 = 9,0 − 6,0 ⋅ 3,0 + 2,0 ⋅ ( 3,0 ) 2 = 9,0 м.

Подстановка значений в формулу для вычисления модуля перемещения дает:

| Δ r → | = | x ( t 2 ) − x ( t 1 ) | = 9,0 − 9,0 = 0 м.

Таким образом, перемещение материальной точки равно нулю. Следовательно, модуль средней скорости перемещения также равен нулю:

| v → r | = | Δ r → | t 2 − t 1 = 0 3,0 − 0 = 0 м/с.

Для определения средней путевой скорости нужно рассчитать путь, пройденный материальной точкой за интервал времени от t 1 = 0 с до t 2 = 3,0 с. Движение точки является равнозамедленным, поэтому необходимо выяснить, попадает ли точка остановки в указанный интервал.

Для этого запишем закон изменения скорости материальной точки с течением времени в виде:

где v x = −6,0 м/с — проекция начальной скорости на ось Ox ; a x = = 4,0 м/с 2 — проекция ускорения на указанную ось.

Найдем точку остановки из условия

τ ост = v 0 a = 6,0 4,0 = 1,5 с.

Точка остановки попадает во временной интервал от t 1 = 0 с до t 2 = 3,0 с. Таким образом, пройденный путь вычислим по формуле

где S 1 = | x ( τ ост ) − x ( t 1 ) | — путь, пройденный материальной точкой до остановки, т.е. за время от t 1 = 0 с до τ ост = 1,5 с; S 2 = | x ( t 2 ) − x ( τ ост ) | — путь, пройденный материальной точкой после остановки, т.е. за время от τ ост = 1,5 с до t 1 = 3,0 с.

Рассчитаем значения координат в указанные моменты времени:

x ( t 1 ) = 9,0 − 6,0 t 1 + 2,0 t 1 2 = 9,0 − 6,0 ⋅ 0 + 2,0 ⋅ 0 2 = 9,0 м;

x ( τ ост ) = 9,0 − 6,0 τ ост + 2,0 τ ост 2 = 9,0 − 6,0 ⋅ 1,5 + 2,0 ⋅ ( 1,5 ) 2 = 4,5 м;

x ( t 2 ) = 9,0 − 6,0 t 2 + 2,0 t 2 2 = 9,0 − 6,0 ⋅ 3,0 + 2,0 ⋅ ( 3,0 ) 2 = 9,0 м.

Значения координат позволяют вычислить пути S 1 и S 2 :

S 1 = | x ( τ ост ) − x ( t 1 ) | = | 4,5 − 9,0 | = 4,5 м;

S 2 = | x ( t 2 ) − x ( τ ост ) | = | 9,0 − 4,5 | = 4,5 м,

а также суммарный пройденный путь:

S = S 1 + S 2 = 4,5 + 4,5 = 9,0 м.

Следовательно, искомое значение средней путевой скорости материальной точки равно

v s = S t 2 − t 1 = 9,0 3,0 − 0 = 3,0 м/с.

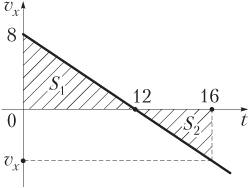
Пример 10. График зависимости проекции скорости материальной точки от времени представляет собой прямую линию и проходит через точки (0; 8,0) и (12; 0), где скорость задана в метрах в секунду, время — в секундах. Во сколько раз средняя путевая скорость за 16 с движения превышает величину средней скорости перемещения за то же время?

Решение. График зависимости проекции скорости тела от времени показан на рисунке.

Для графического вычисления пути, пройденного материальной точкой, и модуля ее перемещения необходимо определить значение проекции скорости в момент времени, равный 16 с.

Существует два способа определения значения v x в указанный момент времени: аналитический (через уравнение прямой) и графический (через подобие треугольников). Для нахождения v x воспользуемся первым способом и составим уравнение прямой по двум точкам:

где ( t 1 ; v x 1 ) — координаты первой точки; ( t 2 ; v x 2 ) — координаты второй точки. По условию задачи: t 1 = 0, v x 1 = 8,0, t 2 = 12, v x 2 = 0. С учетом конкретных значений координат данное уравнение принимает вид:

При t = 16 с значение проекции скорости составляет

Данное значение можно получить также из подобия треугольников.

где S 1 = 1 2 ⋅ 8,0 ⋅ 12 = 48 м — путь, пройденный материальной точкой за интервал времени от 0 с до 12 с; S 2 = 1 2 ⋅ ( 16 − 12 ) ⋅ | v x | = 1 2 ⋅ 4,0 ⋅ 8 3 = = 16 3 м — путь, пройденный материальной точкой за интервал времени от 12 с до 16 с.

Суммарный пройденный путь составляет

S = S 1 + S 2 = 48 + 16 3 = 160 3 м.

Средняя путевая скорость материальной точки равна

v s = S t 2 − t 1 = 160 3 ⋅ 16 = 10 3 м/с.

S = | S 1 − S 2 | = | 48 − 16 3 | = 128 3 м.

Величина средней скорости перемещения составляет

| v → r | = | Δ r → | t 2 − t 1 = 128 3 ⋅ 16 = 8 3 м/с.

Искомое отношение скоростей равно

Средняя путевая скорость материальной точки в 1,25 раза превышает модуль средней скорости перемещения.

Задания №11. Текстовые задачи на среднюю скорость

При решении задач на среднюю скорость важно знать:

Средняя скорость – есть отношение всего пройденного пути ко всему затраченному времени.

Если половину всего времени + показать

Действительно, если обозначить все время за t, то

ср

Если половину всего пути + показать

ср

Задачи на среднюю скорость могут встретиться в категории В11 ЕГЭ по математике.

Задача 1.

Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость на всем пути, нужно весь путь разделить на все время движения. Пусть t часов – полное время движения автомобиля, тогда средняя скорость равна:
км/ч.

Задача 2.

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость на всем пути, нужно весь путь разделить на все время движения. Тогда

км/ч.

Задача 3.

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость на всем пути, нужно весь путь разделить на все время движения. Пусть S км – весь путь автомобиля, тогда средняя скорость равна:

км/ч.

Задача 4.

Путешественник переплыл море на яхте со средней скоростью 21 км/ч. Обратно он летел на спортивном самолете со скоростью 567 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ ч.

Пусть путь, что проделал путешественник –

Время, затраченное на путь в один конец, – ч, время, затраченное на путь в другой конец, – ч.

км/ч.

Смотрите фрагмент видеолекции «Текстовые задачи», имеющий непосредственное отношение к рассматриваемой теме:

Чтобы не потерять страничку, вы можете сохранить ее у себя:

после слова “Решение” у вас большие пробелы, а между задачами пробела вообще нет, всё сливается…
А ещё я бы сделал слово “Решение” курсивом или полужирным 😉

Да, да, спасибо. Одна из первых написанных статей. Тогда еще стиля не было продумано никакого… Подправила!

Физика всегда мне плохо давалась… Первые две формулы сложно понять…

Да как бы физика здесь и не причем… Главное запомнить – ср. скорость – весь путь поделить на все время!
Разбираем первую формулу:
Весь путь состоит из двух участков. Скорость на первом – , на втором – Время, затраченное на первый участок пути – (у нас весь путь разделен на равные временные промежутки, их 2), на второй – Значит, весь путь –
А все время –
Оттуда и дробь выскакивает (первая формула)…
Разобраться придется, формулы-то и не особо используются в задачах… Не всегда у нас весь путь делится на 2 равных временных промежутка, может и из трех состоять и так далее… А если вовсе не на равные временные промежутки путь разделен, а на равные по длине… (там уже другие формулы)… а если разделен путь на неравные по длине участки…
Не будем же мы запоминать формулы на все случаи жизни? Суть надо понять!
А видеолекцию смотрим? Не помогает?

Задачи на среднюю скорость

Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:

*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.

Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:

Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трёх участках пути. СК будем искать по формуле:

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Сказано о трёх участках пути. Формула:

Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:

Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

*Есть задача про путешественника, который пересёк море. С решением у ребят возникают проблемы. Если вы не видите его, то пройдите регистрацию на сайте! Кнопка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После регистрации войдите на сайт и обновите данную страницу.

Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

В данной рубрике продолжим рассматривать задачи, не пропустите! Успехов вам!

Как найти среднюю скорость автомобиля после поездки в разных режимах?

Находим среднюю скорость и средний расход поездки по факту

Какой должна быть средняя скорость машины в поездке?

Оптимальная скорость для автомобиля — второй фактор выбора режима поездки

Подводим итоги

Средняя скорость автомобиля — важный показатель, который может объяснить повышенный расход и задержки по времени, которые вы испытываете в той или иной поездке. Нужно уметь рассчитывать среднюю скорость и знать параметры эксплуатации своего транспорта для выбора оптимальных режимов поездки. Такие знания никогда вам не помешают, а также помогут понять многие тонкости эксплуатации автомобиля.

Как высчитывается средняя скорость Как найти среднюю скорость

Средняя скорость

Средняя скорость – не самое сложное понятие в кинематике. Однако для многих учащихся простота этого понятия оказывается обманчивой.
Известно, что средняя скорость – это величина, равная отношению пути, пройденного телом, ко времени, за которое пройден этот путь: 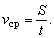Краткость и простота определения скрывают от некоторых учеников важные для решения задач вопросы и ответы на них.
1. Какое время следует учитывать при расчете средней скорости, если тело в пути делало остановки?
В определении указано: “. ко времени, за которое пройден этот путь”, то есть ко всему промежутку времени с момента, когда тело тронулось в этот путь (представьте, что Вы включили секундомер), до момента, когда тело преодолело этот путь (только в этот момент Вы останавливаете секундомер!). О том, что время на остановки не следует учитывать, в определении ничего не сказано (поэтому секундомер на промежуточных остановках не выключайте!). Таким образом, при расчете средней скорости следует учитывать всё время, которое ушло на преодоление пути (в том числе и время, потраченное на остановки).

2. Как правильно рассчитать среднюю скорость тела, которое начало движение в пункте А, окончило его в пункте В, но по дороге из А в В поворачивало назад (может быть ни один раз!), а затем вновь продолжало движение к пункту В?
В определении указано “. равная отношению пути, пройденного телом. ”, значит, при расчете средней скорости определяющим является не расстояние между точками (пунктами) начала и окончания движения, а реальный путь, которое прошло тело.

Пример 1. Найти среднюю скорость человека на пути от дома до станции, расстояние между которыми l =800 м, если, пройдя четверть пути, он вернулся домой (например, проверить, хорошо ли закрыта дверь) и через 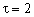мин продолжил путь на станцию. Скорость движения человека постоянна и равна v =4 км/ч.

Решение. Началом движения человека, конечно, следует считать момент времени, когда он первый раз вышел из дома. Четверть пути составляет расстояние l_1/4 =l : 4 =800 : 4 =200 м. При возвращении домой человек прошел путь 2l_1/4 =400 м. После этого он вышел из дома второй раз и дошел до станции. Путь, пройденный человеком с начала движения, составит:

Время t, которое затрачено на преодоление этого пути, складывается из времени пребывания дома 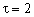и времени Т, в течение которого человек двигался по маршруту “из дома–к дому–на станцию”. Поскольку скорость движения человека постоянна (v =4 км/ч) и проделанный путь известен, то время движения составляет:

1,2 км : 4 км/ч =0,3 ч =18 мин.
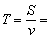
Тогда все время, затраченное человеком, составляет:

t = 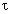+ T = 2 + 18 =20 мин =1/3 ч.
Найдем среднюю скорость:

1,2 км : ч =3,6 км/ч.

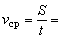
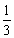
Среднюю скорость движения человек оценивает довольно часто, но судит о ней, глядя на часы. Торопящийся человек соотносит расстояние, которое ещё осталось преодолеть, и время, отпущенное ему на это, после чего делает вывод (хотя числовое значение средней скорости вряд ли при этом находится): “Ну, теперь можно идти помедленнее” или “Придется еще поднажать, иначе не успею”.

Вернемся к рассмотренному примеру. Будем считать, что скорость v =4 км/ч выбрана человеком не случайно. проходя от дома до станции ежедневно, человек замечает, что расстояние l ==800 м, он проходит за время t =12 мин =0,2 ч:

= 0,8 км : 0,2 ч =4 км/ч.

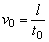
Пример 2. Человек обычно доходит из дома до станции за время t =12 мин, проходя расстояние l =800 м. Однажды, пройдя четверть пути, он вспоминает, что не выключил электроприборы, и возвращается домой, выключает электроприборы, затрачивая время 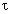= 2 мин, и снова идет на станцию. С какой наименьшей скоростью надо двигаться человеку, после того как он повернул домой, чтобы успеть на станцию в обычное время (и не опоздать на электричку).

1. Обычно человек двигается со скоростью

м/мин =4 км/ч.

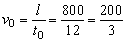
2. Пройдя с такой скоростью четверть пути, он затратил время 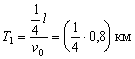: 4 км/ч =0,05 ч =3 мин. Значит, в его распоряжении осталось время Т₂ =t – T₁ =12 – 3 =9 мин.

3. За время Т₂ человек должен преодолеть путь до дома, а затем снова до станции:
м =1 км и, кроме того, часть времени ( 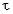= 2 мин) потратить дома. Поэтому путь S человеку придется преодолевать за время

ч,

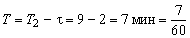
то есть со скоростью, не меньшей, чем

1 км : ч = км/ч = км/ч » 8,6 км/ч.

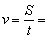
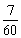
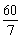
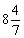
Проверьте, что добежав до дома со скоростью 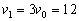км/ч, а затем шагая со скоростью v₂ =2v =8 км/ч, человек придет на станцию вовремя.
Ответ: человеку необходимо двигаться со скоростью, не меньшей, чем 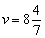км/ч. Обратите внимание, что средняя скорость за время (t =12 минут) от начала движения до его окончания составляет

м/мин =100 м/мин =6 км/ч.

км/ч.

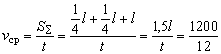
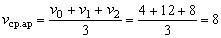
Это значение не равно значению средней скорости v_ср. Убедитесь в этом и не совершайте в дальнейшем распространенную ошибку: не пытайтесь искать среднюю скорость как среднее арифметическое значение (оно не имеет физического смысла!).

Пример 3. Автомобиль проезжает первую треть пути равномерно со скоростью v₁ =108 км/ч, а остальные две трети пути – со скоростью v₂ =72 км/ч. Найти среднюю скорость автомобиля.
Решение. Неверно считать, что средняя скорость совпадает со средним арифметическим значением v₁ и v₂, которое составляет

км/ч.

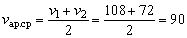
1. Найдем время t₁ движения со скоростью v₁, полагая, что весь путь равен L [км]. Из условия ясно, что

2. Время t₂ движения на оставшемся участке пути составляет

3. Итак, время на продолжение пути L составляет

4. По определению средней скорости

км/ч.

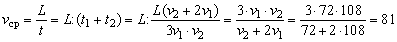
Ответ : средняя скорость v_ср =81 км/ч.

Значение средней скорости совпадает со средним арифметическим значением скорости только в одном частном случае, когда тело двигается с различными скоростями так, что между последовательными моментами изменения (переключения) скорости проходит одинаковое время Т. Таким образом, тело двигается со скоростью v₁ в течение времени t₁=T, со скоростью v₂ в течение времени t₂=T, со скоростью v₃ в течение времени t₃=T и т.д. Если на протяжении пути скорость изменялась n раз, то пройденный путь

Время t, за которое пройден путь, составляет

Не запрещено для этого частного случая двигаться со скоростью v =0, т.е. делать остановки. Но время остановки должно составлять t =T.

Пример 4. Вертолет пролетает без остановок равномерно и прямолинейно над пунктами А, В, С (в указанном порядке) и возвращается в А. Пункты А, В, С являются как бы вершинами треугольника. Расстояние между А и В составляет L_AB =150 км, между В и С L_BC =200 км, между С и А L_CA =100 км. Время, за которое вертолет пролетает от одного пункта до другого, составляет полчаса. Найти среднюю скорость движения вертолета на маршруте АВСА. Изменится ли средняя скорость, если L_CA =200 км и всё расстояние вертолет преодолеет за 1 ч?

Решение. 1. Находим скорость движения вертолета на каждом участке:

км/ч;

км/ч.

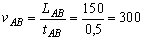
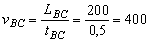
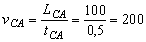
2. Поскольку t =0,5 ч одинаково для всех участков движения, то

км/ч.

Источник

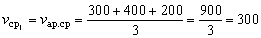
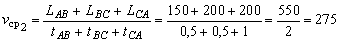
Средняя скорость (примеры решения)

Средняя скорость это общее расстояние, пройденное этим объектом, деленное на общее время, затраченное на преодоление указанного расстояния.

Средняя скорость объекта говорит вам о средней скорости, с которой он преодолеет расстояние, то есть объект имеет скорость 30 км/час, его положение будет меняться в среднем на 30 км каждый час.

Средняя скорость-это скорость, то есть величина, деленная на время, затраченное на получение этой величины. Единицей измерения скорости в СИ являются метры в секунду.

Что такое средняя скорость

Средняя скорость рассчитывается по формуле S = d/t, где S равна средней скорости, d равно общему расстоянию, а t равно общему времени.

Чтобы узнать о средней скорости и средней скорости, сначала должны знать некоторые термины и их значения.

Пройденное расстояние, как ясно видно из названия, — это общее расстояние, пройденное объектом.

Время, необходимое объекту для перемещения на заданное расстояние.

Смещение это кратчайшее расстояние между начальной точкой, в которой находился объект, и конечной точкой, в которой объект оказался.

Скорость это расстояние, пройденное объектом за единицу времени. Скорость-это скалярная величина. Это означает, что у него нет определенного направления. Скорость относится к тому, как быстро движется объект, или, по сути, к скорости, с которой преодолевается расстояние.

Скорость

Скорость это полное перемещение объекта в заданном направлении в единицу времени. Скорость-это векторная величина. Это означает, что он имеет определенное направление.

Скорость относится к скорости перемещения объекта во времени. Представьте себе человека, который проходит некоторое расстояние, прежде чем вернуться в исходное положение.

Поскольку скорость-это скорость перемещения, это движение приводит к нулевой скорости. Если человек хочет максимизировать свою скорость, он должен максимизировать смещение от своего первоначального положения.

Поскольку скорость является векторной величиной, при ее оценке мы должны отслеживать направление.

Основное различие между скоростью и скоростью заключается в том, что скорость не учитывает направление, поскольку она является скалярной величиной.

А скорость зависит от пройденного расстояния, в то время как скорость является векторной величиной, которая учитывает направление, а скорость зависит от перемещения.

Примеры определения средней скорости

1). Автомобиль преодолевает расстояние в 70 км за 2 часа. Какова средняя скорость?

Ответ: средняя скорость = расстояние/время

Таким образом, средняя скорость автомобиля составляет 70 км/2 часа = 35 км/час

2). Человек может ходить со скоростью 1,5 метра в секунду. Как далеко он пройдет за 4 минуты?

Ответ: средняя скорость = расстояние/время

Расстояние = средняя скорость(время)

Расстояние = 1,5(4) (60)

Расстояние = 360 метров.

Решение а) Время t₁ для преодоления расстояния d со скоростью 60 км/ч определяется как

Время t₂ для преодоления расстояния 2d со скоростью 80 км/ч определяется как

Средняя скорость = расстояние/время = (d + 2d) / (d/60) + (2d/80) = 3d / (80d + 2d×60)/ (60×80)

= 3 d/(200d/4800) = 3d (4800)/200d = 72 км/ч

Средняя скорость объекта

Средняя скорость объекта может быть определена как смещение относительно исходного положения, деленное на время. Другими словами, это скорость, с которой объект совершает перемещения со временем.

Как и средняя скорость, единица измерения СИ составляет метры в секунду. Можно также сказать, что средняя скорость-это отношение общего перемещения объекта к общему времени, за которое должно произойти это действие.

Направление средней скорости-это направление перемещения. Даже если скорость объекта колеблется и его величина меняется, его направление все равно будет таким же, как и направление перемещения.

Величина средней скорости всегда либо меньше, либо равна средней скорости, поскольку смещение всегда меньше или равно пройденному расстоянию.

Средняя скорость рассчитывается по формуле V = D/t, где V равна средней скорости, D равно полному перемещению, а t равно общему времени.

Примеры определения средней скорости объекта

V = 1 километр в минуту

Решение: Начальное расстояние, пройденное человеком, x_i = 7 м,

Конечное пройденное расстояние, x_f = 18 м,

Начальный интервал времени t_i = 4 с,

Конечный интервал времени t_f = 6 с,

Средняя скорость V = x_i − x_f / t_i − t_f = 18-7 / 6-4 = 11 / 2 = 5.5 м/с.

Различия и сходства между средней скоростью и средней скоростью

Оба этих термина имеют в среднем некоторую продолжительность по времени. Единица СИ и другие стандартные единицы измерения как средней скорости, так и средней скорости одинаковы.

Формула, используемая для расчета средней скорости и средней скорости, практически одинакова,

с той лишь небольшой разницей, что в первом случае следует упомянуть направление.

Средняя скорость является скаляром и не зависит от наличия или отсутствия направления, в то время как средняя скорость, являющаяся вектором, нуждается в направлении.

Средняя скорость зависит от расстояния, то есть общей длины, пройденной во время измерения, в то время как средняя скорость зависит от перемещения, то есть от прямого расстояния от исходного положения до конечного положения.

Примеры определения со средней скоростью так и со средней скоростью

Пример 1. Автомобиль проедет по прямой дороге на восток 120 метров за 5 секунд, затем проедет на запад 60 метров за 1 секунду. Определите среднюю скорость и среднюю скорость.

Расстояние = 120 метров + 60 метров = 180 метров

Смещение = 120 метров – 60 метров = 60 метров, на восток.

Прошедшее время = 5 секунд + 1 секунда = 6 секунд.

Средняя скорость = Пройденное расстояние / время = 180 метров / 6 секунд = 30 метров/сек.

Средняя скорость = Перемещение / прошедшее время = 60 метров / 6 секунд = 10 метров/сек.

Пример 2. Бегун бегает по прямоугольной дорожке длиной = 50 метров и шириной = 20 метров. Он дважды объезжает прямоугольную дорожку и, наконец, возвращается в исходную точку.

Если общее время, необходимое ему для пробежки по трассе, составляет 100 секунд, определите среднюю скорость и среднюю скорость.

Окружность прямоугольника, которая представляет собой расстояние, пройденное за один раунд = 2(50 метров) + 2(20 метров) = 100 метров + 40 метров = 140 метров.

Обегает прямоугольник дважды = 2(140 метров) = 280 метров.

Расстояние = 280 метров.

Смещение = 0 метров. (С тех пор, как бегун вернулся в исходную точку)

Средняя скорость равна пройденному расстоянию / времени = 280 метров / 100 секунд = 2,8 метра/сек.

Средняя скорость равна перемещению / затраченному времени = 0/100 секунд = 0.

Пример 3. Человек начинает ходить из точки на круговом поле радиусом 0,5 км и через 1 час оказывается в той же точке, откуда он изначально начал.

(а) Какова средняя скорость за все время его путешествия? Какова средняя скорость этого человека для того же самого?

Решение: а) Если этот человек обойдет круговое поле и вернется в ту же точку, он преодолел расстояние, равное окружности круга.

Таким образом, средняя скорость, с которой он путешествовал = Расстояние / время = окружность / время = Pi (0,5) (2) / 1 час = 3,14 км/час (приблизительно)

б) Если он ходит по кругу и возвращается в ту же точку, с которой начал по кругу, то изменение его положения равно нулю.

Поскольку изменение его положения равно нулю, смещение также равно нулю. Это означает, что средняя скорость также равна нулю.

Часто задаваемые вопросы и ответы?

Что такое средняя скорость движения?

Скорость движения при этом не обязана быть постоянной. Здесь – средняя скорость, – весь путь, пройденный телом, – время прохождения пути. Единица измерения скорости – м/с (метр в секунду).

Средняя скорость – скалярная величина.

Как найти среднюю скорость?

Чтобы найти среднюю скорость, надо:

1) найти весь пройденный путь;

2) найти все время движения;

3) весь пройденный путь разделить на все время движения: На примерах посмотрим, как находить среднюю скорость.

1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч.

Что называется средней скоростью за промежуток времени?

Δ s = | Δ x 1 | + | Δ x 2 | + … ( 2). Средней скоростью ( ⟨ v ⟩ ) материальной точки за промежуток времени Δ t называют физическую величину, которая равна отношению перемещения, которое совершило тело к этому промежутку времени.

Как найти среднюю скорость имея только две скорости?

Сложите значения двух скоростей.

Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.

Таким образом, если автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч, средняя скорость автомобиля на всем протяжении пути составила 50 км/ч.

Чему равна средняя скорость движения?

Скажем, если половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч (а не 100 км/ч).

В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках.