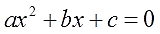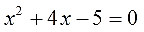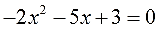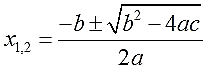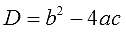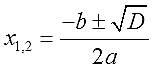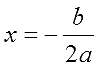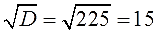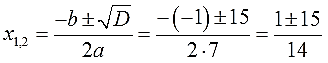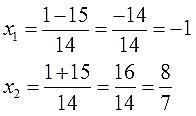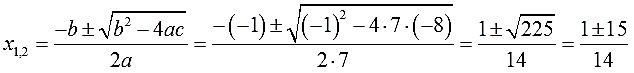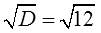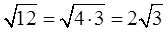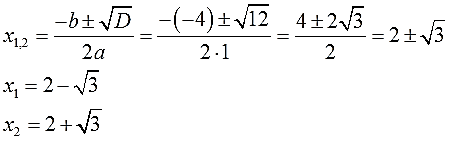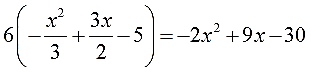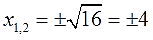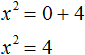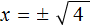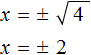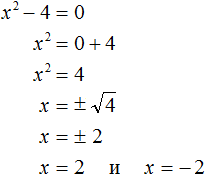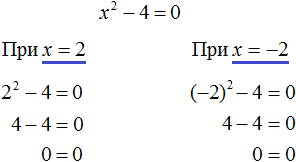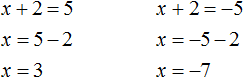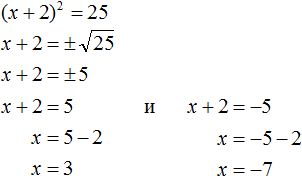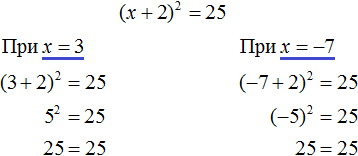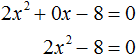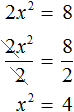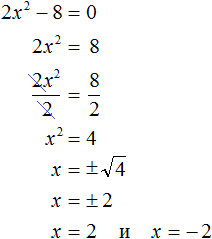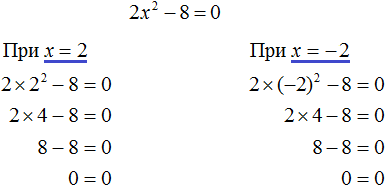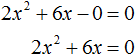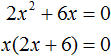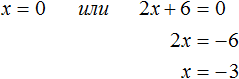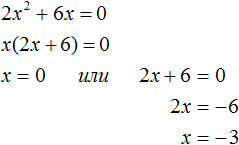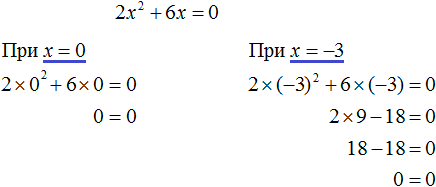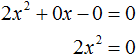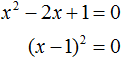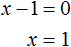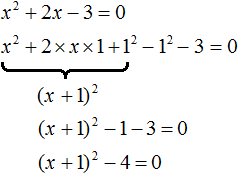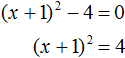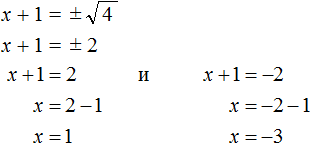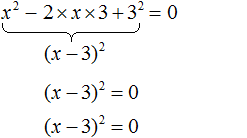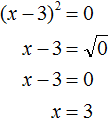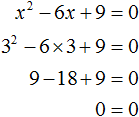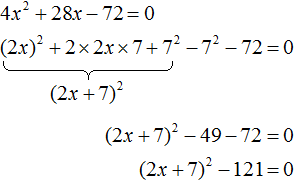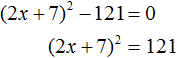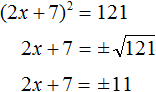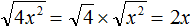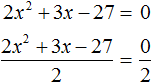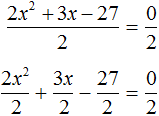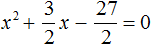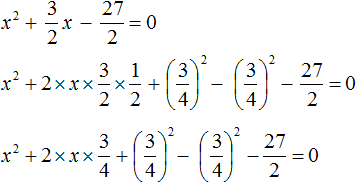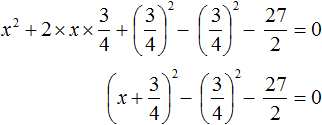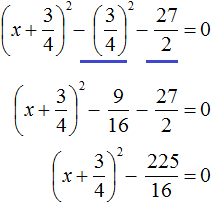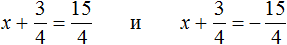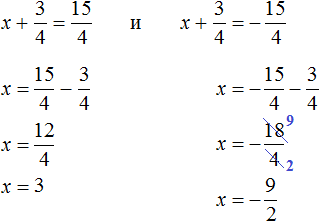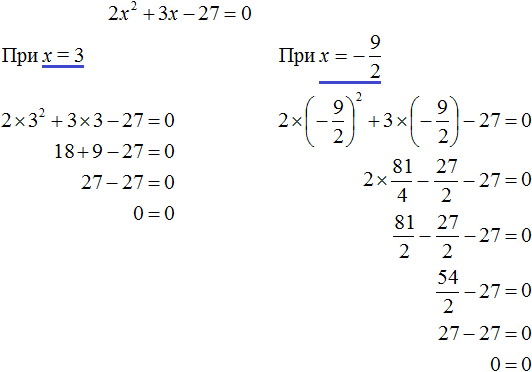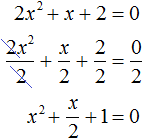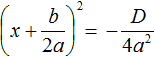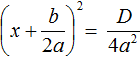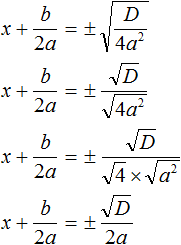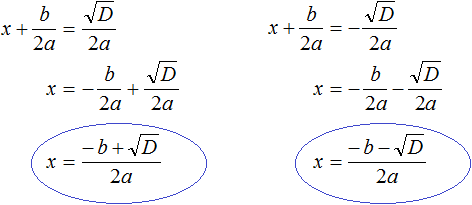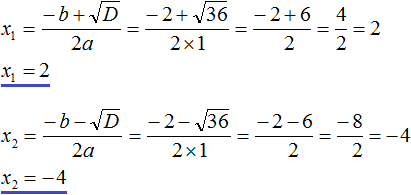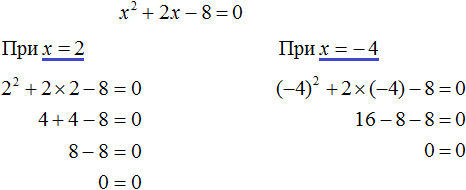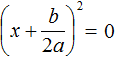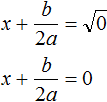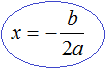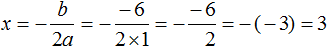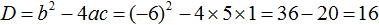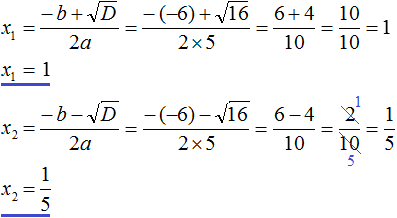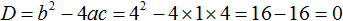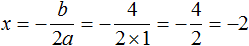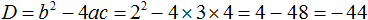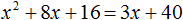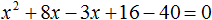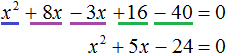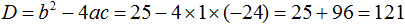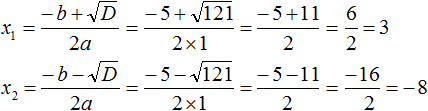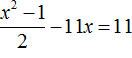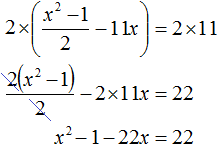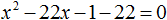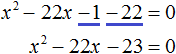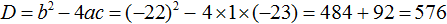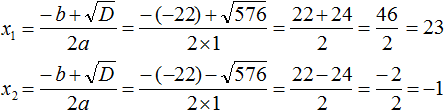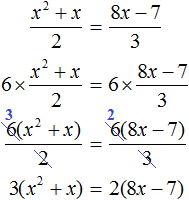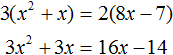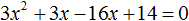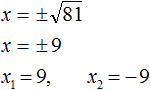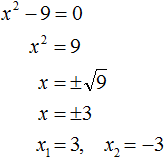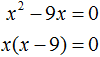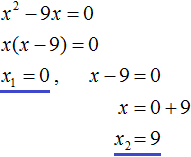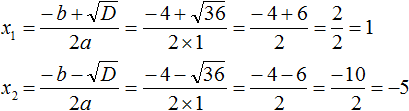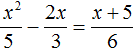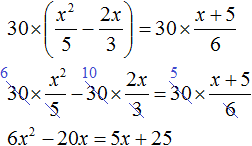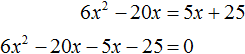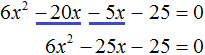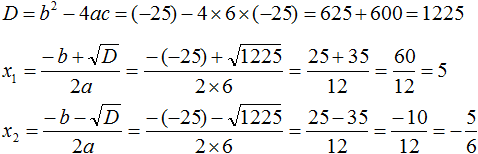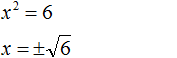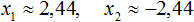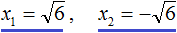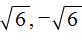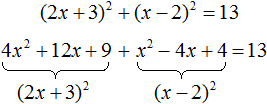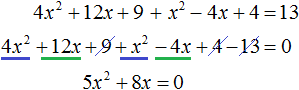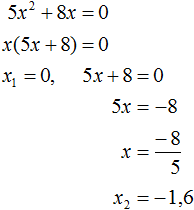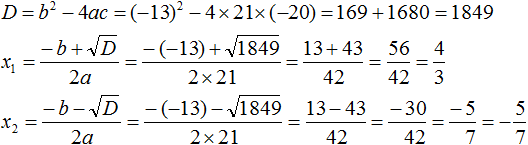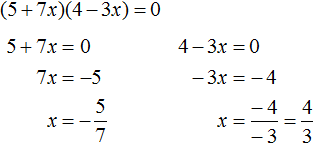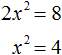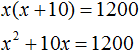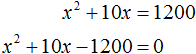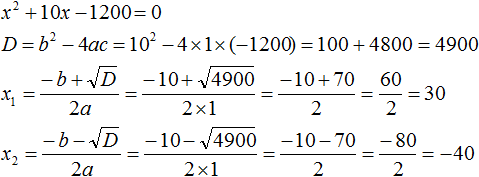Как решать квадратные уравнения через дискриминант
Как решать квадратные уравнения через дискриминант
Квадратные уравнения (8 класс)
Уравнение называют квадратным, если его можно записать в виде \(ax^2+bx+c=0\), где \(x\) неизвестная, \(a\), \(b\) и \(с\) коэффициенты (то есть, некоторые числа, причем \(a≠0\)).
В первом примере \(a=3\), \(b=-26\), \(c=5\). В двух других \(a\),\(b\) и \(c\) не выражены явно. Но если эти уравнения преобразовать к виду \(ax^2+bx+c=0\), они обязательно появятся.
Коэффициент \(a\) называют первым или старшим коэффициентом, \(b\) – вторым коэффициентом, \(c\) – свободным членом уравнения.
Виды квадратных уравнений
Если в квадратном уравнении присутствуют все три его члена, его называют полным. В ином случае уравнение называется неполным.
Как решать квадратные уравнения
Итак, стандартный алгоритм решения полного квадратного уравнения:
Преобразовать уравнение к виду \(ax^2+bx+c=0\).
Выписать значения коэффициентов \(a\), \(b\) и \(c\).
Пока не отработали решение квадратных уравнений до автоматизма, не пропускайте этот этап! Особенно обратите внимание, что знак перед членом берется в коэффициент. То есть, для уравнения \(2x^2-3x+5=0\), коэффициент \(b=-3\), а не \(3\).
Решите квадратное уравнение \(2x(1+x)=3(x+5)\)
Решение:
Теперь переносим все слагаемые влево, меняя знак.
Уравнение приняло нужный нам вид. Выпишем коэффициенты.
Найдем дискриминант по формуле \(D=b^2-4ac\).
Решите квадратное уравнение \(x^2+9=6x\)
Решение:
Тождественными преобразованиями приведем уравнение к виду \(ax^2+bx+c=0\).
Найдем дискриминант по формуле \(D=b^2-4ac\).
В обоих корнях получилось одинаковое значение. Нет смысла писать его в ответ два раза.
Решите квадратное уравнение \(3x^2+x+2=0\)
Решение:
Уравнение сразу дано в виде \(ax^2+bx+c=0\), преобразования не нужны. Выписываем коэффициенты.
Найдем дискриминант по формуле \(D=b^2-4ac\).
Обратите внимание, в первом уравнении у нас два корня, во втором – один, а в третьем – вообще нет корней. Это связано со знаком дискриминанта (подробнее смотри тут ).
Пример. Решить уравнение \(x^2-7x+6=0\).
Решение: Согласно обратной теореме Виета, корнями уравнения будут такие числа, которые в произведении дадут \(6\), а в сумме \(7\). Простым подбором получаем, что эти числа: \(1\) и \(6\). Это и есть наши корни (можете проверить решением через дискриминант).
Ответ: \(x_1=1\), \(x_2=6\).
Квадратные уравнения
Числа называются коэффициентами квадратного уравнения.
Квадратное уравнение может иметь два действительных корня, один действительный корень или ни одного.
Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.
Дискриминант уравнения равен > 0. Уравнение имеет два корня.
Дискриминант уравнения равен > 0.
Уравнение имеет два корня.
Полезная теорема для решения квадратных уравнений – теорема Виета.
Квадратное уравнение можно решить несколькими способами. Можно вычислять дискриминант, или воспользоваться теоремой Виета, а иногда можно просто угадать один из корней. Или оба корня.
Неполные квадратные уравнения
Квадратное уравнение, в котором один из коэффициентов b или с (или они оба) равны нулю, называется неполным. В таких случаях искать дискриминант не обязательно. Можно решить проще.
Проще всего разложить левую часть уравнения на множители по формуле разности квадратов. Получим:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
3) Вот похожее уравнение:
.
Его левую часть можно разложить на множители, вынеся за скобки. Получим:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Разложение квадратного трехчлена на множители
Запомните эту формулу. Она необходима для решения квадратичных и дробно-рациональных неравенств.
Например, наше уравнение
.
Полезные лайфхаки для решения квадратных уравнений.
1) Намного проще решать квадратное уравнение, если коэффициент а, который умножается на х², положителен. Кажется, что это мелочь, да? Но сколько ошибок на ЕГЭ возникает из-за того, что старшеклассник игнорирует эту «мелочь».
Намного проще умножить его на – 1, чтобы коэффициент а стал положительным. Получим:
.
Дискриминант этого уравнения равен
.
2)Прежде чем решать квадратное уравнение, посмотрите на него внимательно. Может быть, можно сократить обе его части на какое-нибудь не равное нулю число?
Вот, например, уравнение
.
Можно сразу посчитать дискриминант и корни. А можно заметить, что все коэффициенты и делятся на 17. Поделив обе части уравнения на 17, получим:
3)Работать с дробными коэффициентами неудобно. Например, уравнение
.
Вы уже догадались, что надо сделать. Умножить обе части уравнения на 100! Получим:
Квадратные уравнения — 32 примера
Почему нужно обязательно научиться щёлкать квадратные уравнения как орешки?
Потому что решение многих уравнений сводится к решению квадратных! И будет обидно, например, на ЕГЭ решить более сложное уравнение и споткнуться на квадратном.
Изучи эту статью реши вместе с Алексеем все 32 примера и про квадратные уравнения ты будешь знать всё!
От дискриминанта, до теоремы Виета или метода выделения полного квадрата.
Квадратное уравнение — коротко о главном
Определения
Квадратное уравнение – это уравнение вида \(a<
^<2>>+bx+c=0\), где \(x\) – неизвестное, \(a\), \(b\) — коэффициенты квадратного уравнения, \(c\) – свободный член.
Полное квадратное уравнение – уравнение, в котором коэффициенты \(a\), \(b\), \(\displaystyle c\) не равны нулю.
Приведенное квадратное уравнение – уравнение, в котором коэффициент \(a=1\), то есть: \(
^<2>+bx+c=0\).
Неполное квадратное уравнение – уравнение, в котором коэффициент \(b\) и/или свободный член \(c\) равны нулю:
Алгоритм решения неполных квадратных уравнений
Неполное квадратное уравнение вида \(a<
Неполное квадратное уравнение вида \(a<
1) Вынесем общим множитель \(\displaystyle x\) за скобки: \(x\left( ax+b \right)=0\),
2) Произведение равно нулю, если хотя бы один из множителей равен нулю. Следовательно, уравнение имеет два корня: \(\left[ \begin
Неполное квадратное уравнение вида \(a<
Данное уравнение всегда имеет только один корень: \(x=0\).
Алгоритм решения полных квадратных уравнений вида \(a<
Решение с помощью дискриминанта
1) Приведем уравнение к стандартному виду: \(a<
2) Вычислим дискриминант по формуле: \(D=<^<2>>-4ac\), который указывает на количество корней уравнения:
3) Найдем корни уравнения:
Избавимся от знаменателя и домножим каждый член уравнения на \(4x\)
Перенесем все в левую часть и расположим члены в порядке убывания степеней икса
Теперь можно с уверенностью сказать, что данное уравнение является квадратным!
Пример 2
Домножим левую и правую часть на \(8x\):
Это уравнение, хотя в нем изначально был \(<
Пример 3
Страшно? Четвертая и вторая степени… Однако, если произвести замену \(t=<
Пример 4
Вроде бы есть \(<
Видишь, \(<
Определи сам, какое из следующих уравнений является квадратным:
Ответы:
Два вида квадратных уравнений
Все квадратные уравнения можно разделить на два вида:
Полные квадратные уравнения – уравнения, в которых коэффициенты \(a\) и \(b\), а также свободный член с не равны нулю (как в примере \(1\)).
Кроме того, среди полных квадратных уравнений выделяют приведенные – это уравнения, в которых коэффициент \(a=1\) (уравнение из примера один является не только полным, но еще и приведенным!)
Неполные квадратные уравнения – уравнения, в которых коэффициент \(b\) и или свободный член с равны нулю.
Неполные они потому, что в них не хватает какого-то элемента. Но в уравнении всегда должен присутствовать икс в квадрате. Иначе это будет уже не квадратное, а какое-то другое уравнение.
Зачем придумали такое деление?
Такое деление обусловлено методами решения. Рассмотрим каждый из них подробнее.
Решение неполных квадратных уравнений
Для начала остановимся на решении неполных квадратных уравнений – они гораздо проще!
Неполные квадратные уравнения бывают \(3\) типов:
Теперь рассмотрим решение каждого из этих подтипов.
Решение неполных квадратных уравнений первого типа
Поскольку мы знаем, как извлекать квадратный корень, то давайте выразим из этого уравнения
Эти формулы не нужно запоминать. Главное, ты должен знать и помнить всегда, что \(<
Давай попробуем решить несколько примеров.
Пример 5
Решите уравнение \(2<
Теперь осталось извлечь корень из левой и правой части. Ведь ты помнишь как извлекать корни?
Ответ: \(-3;\text< >3.\)
Никогда не забывай про корни с отрицательным знаком.
Пример 6
Решите уравнение \(5<
Ответ: \(-4;\text< >4.\)
Пример 7
Решите уравнение \(18<
Ой! Все ли здесь правильно?
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Решение неполных квадратных уравнений второго типа
Вынесем общим множитель \(\displaystyle x\) за скобки:
\(x\left( ax+b \right)=0\).
Произведение равно нулю, если хотя бы один из множителей равен нулю. А это значит, что уравнение имеет решение, когда:
Таким образом, данное квадратное уравнение имеет два корня. Здесь нет никаких ограничений, так как корень мы не извлекали.
Пример 8
Решите уравнение \(6<
Вынесем общий множитель \(\displaystyle x\) за скобки:
\(x\left( 6x+15 \right)=0\)
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Решение неполных квадратных уравнений третьего типа
Самый простой тип неполных квадратных уравнений (хотя они все простые, не так ли?). Очевидно, что данное уравнение всегда имеет только один корень:
Здесь обойдемся без примеров.
Решение полных квадратных уравнений
Напоминаем, что полное квадратное уравнение, это уравнение вида уравнение \(a<
Решение полных квадратных уравнений немного сложнее (совсем чуть-чуть), чем приведенных.
Запомни, любое квадратное уравнение можно решить с помощью дискриминанта! Даже неполное.
Остальные способы помогут сделать это быстрее, но если у тебя возникают проблемы с квадратными уравнениями, для начала освой решение с помощью дискриминанта.
Решение квадратных уравнений с помощью дискриминанта
Шаг 1. Привести уравнение к стандартному виду: \(a<
Если уравнение уже дано в таком виде, то этот шаг делать не нужно. Главное правильно определить коэффициенты \(a\) и \(b\) и свободный член \(c\).
Шаг 2. Вычислить дискриминант по формуле: \( \displaystyle D=<^<2>>-4ac\)
Решение квадратных уравнений этим способом очень простое, главное запомнить последовательность действий и пару формул.
Если \(D>0\), то уравнение имеет \(\displaystyle 2\) корня.
Нужно особое внимание обратить на шаг \(\displaystyle 2\). Дискриминант (\(\displaystyle D\)) указывает нам на количество корней уравнения:
В частном случае, которым является квадратное уравнение, \(f\left( x \right)=0\). А это значит, что корни квадратного уравнения, это точки пересечения с осью абсцисс (ось \(x\)).
Парабола может вообще не пересекать ось \(x\), либо пересекать ее в одной (когда вершина параболы лежит на оси \(x\)) или двух точках.
Кроме того, за направление ветвей параболы отвечает коэффициент \(a\). Если \(a>0\), то ветви параболы направлены вверх, а если \(a Пример 9
Уравнение представлено в стандартном виде, поэтому Шаг 1 пропускаем.
Шаг 2.
\(D>0\), а значит уравнение имеет два корня.
Шаг 3.
Ответ: \(-2;\text< >0,75\)
Пример 10
Решите уравнение \(4<
Уравнение представлено в стандартном виде, поэтому Шаг 1 пропускаем.
Шаг 2.
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Пример 11
Решите уравнение \(3<
Уравнение представлено в стандартном виде, поэтому Шаг 1 пропускаем.
Шаг 2.
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Решение квадратных уравнений с помощью теоремы Виета
Познакомили поэта с теоремою Виета.
Оба корня он сложил, минус \(p\) он получил.
А корней произведенье дает \(q\) из уравнения.
Если ты помнишь, то есть такой тип уравнений, которые называются приведенными (когда коэффициент а равен \(1\)):
Такие уравнения очень просто решать, используя теорему Виета:
Сумма корней приведенного квадратного уравнения \(<
^<2>>+px+q=0\) равна \(-p\), а произведение корней равно \(q\).
Использовать теорему Виета очень легко: нужно всего лишь подобрать такую пару чисел, произведение которых равно свободному члену уравнения, а сумма – второму коэффициенту, взятому с обратным знаком.
Рассмотрим несколько примеров.
Пример 12
Решите уравнение \(<
Это уравнение подходит для решения с использованием теоремы Виета, т.к. \(a=1\).
Сумма корней уравнения равна \(-p\), т.е. получаем первое уравнение:
А произведение равно \(q\):
Составим и решим систему:
Подберем такие пары чисел, произведение которых равно \(12\), и проверим, равна ли их сумма \(7\):
\(3\) и \(4\) являются решением системы:
Таким образом, \(3\) и \(4\) – корни нашего уравнения.
Ответ: \(3\); \(4\).
Пример 13
Уравнение приведенное, а значит:
Подберем такие пары чисел, произведение которых равно \(40\), а затем определим, какой корней должен иметь отрицательный знак:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Пример 14
Решите уравнение \(<
Уравнение приведенное, а значит:
Сумма корней отрицательна, а это значит что, по крайней мере, один из корней отрицателен. Но поскольку их произведение положительно, то значит оба корня со знаком минус.
Подберем такие пары чисел, произведение которых равно \(77\):
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Пример 15
Решение:
Подберем такие пары чисел, которые в произведении дают \(6\), а затем проверим, равна ли их сумма \(-5\):
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Пример 16
Решение:
Свободный член уравнения отрицательный, а значит и произведение корней – отрицательное число. Это возможно только если один из корней отрицательный, а другой – положительный. Поэтому сумма корней равна разности их модулей.
Подберем такие пары чисел, которые в произведении дают \(24\), и разность которых равна \(2\):
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Пример 17
Решение:
Уравнение приведенное, а значит:
Подберем такие пары чисел, произведение которых равно \(40\), а затем определим, какой корней должен иметь отрицательный знак:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Пример 18
Решите уравнение \(<
Решение:
Уравнение приведенное, а значит:
Сумма корней отрицательна, а это значит что, по крайней мере, один из корней отрицателен. Но поскольку их произведение положительно, то значит оба корня со знаком минус.
Подберем такие пары чисел, произведение которых равно \(77\):
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Согласись, это очень удобно – придумывать корни устно, вместо того, чтобы считать этот противный дискриминант. Старайся использовать теорему Виета как можно чаще.
Но теорема Виета нужна для того, чтобы облегчить и ускорить нахождение корней. Чтобы тебе было выгодно ее использовать, ты должен довести действия до автоматизма.
А для этого порешай-ка еще примеров. Но не жульничай: дискриминант использовать нельзя! Только теорему Виета!
Тренировка теоремы Виета
Решения
Пример 19
По теореме Виета:
Как обычно, начинаем подбор с произведения:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Пример 20
И снова наша любимая теорема Виета: в сумме должно получиться \(-13\), а произведение равно \(36\).
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Пример 21
\(\displaystyle 24
Хм… А где тут что?
Надо перенести все слагаемые в одну часть:
\(\displaystyle 24
Сумма корней равна \(\displaystyle 24\), произведение \(\displaystyle 22\).
Так, стоп! Уравнение-то не приведенное. Но теорема Виета применима только в приведенных уравнениях. Так что сперва нужно уравнение привести. Если привести не получается, бросай эту затею и решай другим способом (например, через дискриминант). Напомню, что привести квадратное уравнение – значит сделать старший коэффициент равным \(\displaystyle 1\):
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Пример 22
\(\displaystyle <
Свободный член отрицательный. Что в этом особенного? А то, что корни будут разных знаков. И теперь во время подбора проверяем не сумму корней, а разность их модулей: эта разность равна \(\displaystyle 11\), а произведение \(\displaystyle 26\).
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Задание 5. \(\displaystyle 2<
Что нужно сделать первым делом? Правильно, привести уравнение:
\(\displaystyle 2<
Снова: подбираем множители числа \(\displaystyle 28\), и их разность должна равняться \(\displaystyle 3\):
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Выводы:
Метод выделения полного квадрата
Если все слагаемые, содержащие неизвестное \(x\), представить в виде слагаемых из формул сокращенного умножения – квадрата суммы или разности – то после замены переменных можно представить уравнение в виде неполного квадратного уравнения типа \(a<
\(\displaystyle \Leftrightarrow <<\left( x+3 \right)>^<2>>=1\Leftrightarrow x+3=\pm 1\Leftrightarrow \left[ \begin
Пример 23
Решение:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Пример 24
Решите уравнение: \(3<
Решение:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
В общем виде преобразование будет выглядеть так:
Ничего не напоминает? Это же дискриминант! Вот именно, формулу дискриминанта так и получили.
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
Выделение полного квадрата — это самое сложное и важное умение, относящееся к формулам сокращенного умножения.
Этот навык поможет вам решать квадратные уравнения, раскладывать выражение на множители, разобраться с с уравнением окружности в задаче с параметром (18-я задача), которая дает целых 4 первичных балла.
В общем, метод выделения полного квадрата — бесценный навык и вы сможете приобрести его посмотрев это видео.
Выделение полного квадрата (разбор 8 примеров)
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий курсов
Добавить комментарий Отменить ответ
3 комментария
Некоторые комментарии прошлых лет к этой статье:
Михаил
15 апреля 2019
Здравствуйте, большое спасибо за материалы! Могу ошибаться, но в части про определение квадратного уравнения в примере 2 для самостоятельной работы допущена опечатка, конкретнее в ответах написано, что уравнение квадратное, хотя таким не является. Мы обе части уравнения умножаем на 7x после чего в левой сокращаются иксы, а в правой семерки и получаем 42 = x^2. На сколько понял такой вид не является квадратным. И еще раз спасибо за материалы! Очень доступно описано то, обо что я бился головой не один день
Александр (админ)
15 апреля 2019
Пожалуйста, Михаил. Очень рады, что понравился наш материал. По поводу вопроса. Я вижу в уравнении, которое ты привел переменную в квадрате, тот самый икс в квадрате. (42 = x^2). А по нашему вольному определению, данному вначале этого текста, уравнение является квадратным, если у него есть переменная в квадрате и нет переменных в 3-й и более степеней.
Алексей
23 августа 2019
Здравствуйте! Скажите почему в неполных квадратных уравнениях (в 3 типе) нельзя перенести второе слагаемое вправо, а затем поделить на x. Получиться что x не равен 0. Но это не так! Мы ведь можем левую и правую часть подвергать любым операциям или это кроме операций с переменной (умножать на ее, делить и т.д.) Или в конце просто сделать проверку?
Алексей Шевчук
25 августа 2019
Алексей, всё верно, на переменную умножать, делить и т.д. нельзя, если мы не уверены, что она не равна нулю. Если это сделать, то даже проверка не поможет найти упущенные корни. Пример, когда можно делить: (x^2+1)*x = 5*(x^2+1) здесь можно поделить на скобку (x^2+1), так как она равной нулю быть не может. Но для того, чтобы схема решения была универсальной, даже в таких задачах лучше всё переносить в одну сторону и раскладывать на множители — так меньше вероятность ошибки, и не придётся каждый раз анализировать, можно на неё делить или нет.
Квадратное уравнение
Загляни сюда, – вдруг узнаешь себя!
Надеюсь, вы внимательно изучили таблицу, приведенную выше. Если все еще есть вопросы, – давайте разбираться.
Во первых, почему рассматриваются только случаи при ? Просто потому, что при
у нас уже будет не квадратное уравнение, а линейное.
Формулу дискриминанта знают практически все, но почему же тогда возникают все же сложности с решением уравнений?
Начнем с того, что иногда происходит путаница с коэффициентами ,
и
. Ни в коем случае мы не считаем, что
– это тот коэффициент, что стоит на первом месте! Но – тот, что при
. Давайте договоримся, что будем приводить всякое квадратное уравнение к стандартному виду, ставя на первое место слагаемое, содержащее
, на последнее – свободный от
член (если таковой имеется). Например, уравнение
будем переписывать так
.
И, наконец, замечу, находятся и такие товарищи, которые, встречая, например, уравнение , спешат выносить
за скобку, путая это уравнение с неполным. Нет, это обычное полное квадратное уравнение, которое после переноса
влево примет вид
, – решаем мы его через дискриминант.
Поэтому, давайте договоримся всякое уравнение приводить к такому виду, чтобы справа стоял только ноль и ничего больше.
Плавно перешли к неполным квадратным уравнениям. Если мы будем придерживаться последного совета, то мы не сможем спутать неполное уравнение с полным уж это точно. Справа будет два слагаемых (вырожденный случай – одно), а не три как у полного уравнения. Можно, конечно, и такие уравнения решать через дискриминант,но проще поступить иначе.
В общем, каждое отдельно взятое квадратное уравнение мы решам одним из трех способов, – выбор не велик.
Заметим, также, что в случае полного квадратного уравнения в зависимости от того, какой дискриминант мы получаем, – на выходе разное количество корней. Если 0″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»54″ style=»vertical-align: 0px;»/>, то будем иметь два корня, если
, то имеем один корень (или два совпавших), наконец, если
, то корней нет.
Как решать квадратные уравнения?
Что такое квадратное уравнение? Виды квадратных уравнений. Примеры.
Обычно квадратные уравнения — одна из самых любимых учениками тем школьной математики. Почему? Потому, что алгоритм решения любого квадратного уравнения достаточно прост и универсален. Работает безотказно. Однако простора для дурацких ошибок при решении квадратных уравнений тоже хватает, да… Так что будем разбираться, что к чему.)
Начнём с названия.
Ключевым словом в понятии квадратное уравнение является слово «квадратное». Что оно означает? Оно означает то, что в уравнении обязательно должен присутствовать икс в квадрате. В любом случае. Также в уравнении могут быть (или не быть — как уж повезёт) просто икс (в первой степени) и просто число (свободный член). Но это ещё не всё. При этом в уравнении не должно быть иксов в кубе, в четвёртой и любых других степенях, больших двойки.
В самом общем виде квадратное уравнение выглядит так:
Здесь a, b, c — какие-то числа. Любые.) Числа b и c могут быть совсем-совсем любыми, а вот а — любым числом, кроме нуля. Почему — объясню чуть ниже.
А ещё бывают и такие квадратные уравнения, где чего-то не хватает. Что у нас произойдёт, если, например, обнулить коэффициент b (b=0)? У нас исчезнет икс в первой степени.
Получится, к примеру, что-то типа:
А если c=0? Тогда у нас пропадёт свободный член:
А если уж оба коэффициента a и b станут равны нулю, то тогда совсем всё просто получится:
Такие квадратные уравнения, где какого-то из членов не хватает, называются (вы не поверите) неполными.)
Таким образом, квадратные уравнения бывают двух основных видов — полные и неполные.
Общая формула корней квадратного уравнения.
Квадратные уравнения решаются достаточно просто. По одной единственной универсальной формуле. Всего одной!
И теперь у меня для вас есть две новости — хорошая и плохая. С какой начнём? Принято с плохой начинать? Что ж, ладно…
Новость плохая. Строгий аналитический вывод общей формулы корней квадратного уравнения достаточно громоздок и основан на процедуре выделения полного квадрата. В большинстве школьных учебников вывод общей формулы корней всё-таки приводят, но я считаю что эта процедура — очередной вынос мозга простому среднестатистическому школьнику. Поэтому в данном уроке я его (вывод) всё-таки опущу.)
Новость хорошая. Запоминать аналитический вывод формулы корней квадратного уравнения в общем виде и не требуется. Вообще! Гораздо важнее запомнить саму формулу и научиться её применять на практике. Вот мы и попрактикуемся. И уравнения порешаем.)
Достаю, достаю! Из широких штанин… О-па! Вот она, формула!)
Вот такая формула. Да, я не спорю, довольно громоздкая. Но и уравнение мы решаем всё-таки квадратное, а не более простое линейное…
Как вы видите, для поиска корней квадратного уравнения нам необходимы только коэффициенты a, b, c. И всё. Больше ничего. Аккуратно подставляем все коэффициенты в формулу и считаем наши корни.
Что такое дискриминант? Формула и смысл дискриминанта.
Выражение b 2 -4ac, стоящее в формуле под знаком квадратного корня, называется дискриминант. До боли знакомое и родное слово для большинства старшеклассников. Слова «решаем через дискриминант» звучат обнадёживающе и вселяют оптимизм!)
Обычно дискриминант обозначается буковкой D:
Тогда, с учётом данного обозначения, общая формула корней станет выглядеть вот так:
Сам по себе дискриминант, как правило, прост и безотказен в обращении. Но… В чём его смысл? Почему для, скажем, —b или 2a не вводятся какие-то специальные термины и обозначения? Буквы — они и в Африке буквы… А тут — такое красивое слово! Дискриминант…
А дело вот в чём. При решении любого квадратного уравнения по общей формуле возможны всего три ситуации.
1. Дискриминант положительный (D>0).
Это означает, что из него можно извлечь корень. Красиво корень извлекается или некрасиво — вопрос другой. Главное, что извлекается в принципе.
Тогда наше квадратное уравнение всегда имеет два различных корня.
Два — потому, что общая формула в этой ситуации разбивается на два отдельных случая. А именно — какой знак, плюс или минус, берётся перед радикалом. Каждый случай даёт свой корень.
2. Дискриминант равен нулю (D=0)
Как вы думаете, чему в этом случае будет равен корень из дискриминанта? Нулю, конечно же! А поскольку от прибавления/вычитания нуля в числителе ничего не меняется, то наше уравнение имеет один корень:
Вообще, строго говоря, это не один корень, а два одинаковых. Но в упрощённом виде, когда нам надо просто решить уравнение и получить ответ, принято говорить об одном решении. Поэтому в ответе не заморачиваются и пишут просто одинокий икс, безо всякой индексации х1,2 .
Однако в более солидных темах (например, в решении неравенств методом интервалов ) этот пунктик, с двумя одинаковыми (или, по-научному, кратными) корнями, настолько важен, что я буду про него напоминать снова и снова.
3. Дискриминант отрицательный (D
Из отрицательных чисел извлекать квадратный корень в средней школе не учат. Это означает, что уравнение не имеет корней. Ну и ладно. На нет, как говорится, и суда нет.
Как решать квадратные уравнения?
Начнём с полных квадратных уравнений.
Полные квадратные уравнения
Полное квадратное уравнение (любое!) решается всегда в четыре основных этапа.
1. Приводим уравнение к стандартному виду:
Всё просто: выстраиваем левую часть уравнения по убыванию степеней икса. На первом месте пишем слагаемое с иксом в квадрате, на втором месте — с иксом в первой степени и, наконец, свободный член. Справа — обязательно должен быть ноль! Если справа тусуются ещё какие-то члены, то переносим их в левую часть и приводим подобные.
Конечно, если уравнение уже дано в стандартном виде, то первый этап делать не нужно.)
Как только уравнение представлено в стандартном виде, приступаем ко второму этапу.
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
Если опыта пока что мало, во избежание досадных ошибок бывает очень полезным выписать их отдельно.
3. Считаем дискриминант по формуле D = b 2 -4ac.
Внимание! На данном этапе сразу же извлекаем корень из дискриминанта! Если красиво извлекается, конечно.)
4. Подставляем все значения в общую формулу, считаем корни уравнения и записываем ответ.
Вот и весь алгоритм. Простой и безотказный. Ну что, тренируемся на кошках?
Например, надо решить вот такое уравнение:
Работаем прямо по пунктам.
1. Приводим уравнение к стандартному виду.
Уравнение уже дано нам в стандартном виде. Стало быть, уже готово к решению. Слева — полный набор членов, выстроенных по убыванию степеней, а справа — ноль. Посему переходим сразу ко второму этапу.
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
3. Считаем дискриминант по формуле D = b 2 -4ac.
Аккуратно подставляем наши коэффициенты a, b и с в формулу дискриминанта. Подставляем со своими знаками! Частенько именно в знаках коэффициентов народ и путается. Точнее, не столько в самих знаках, сколько в подстановке отрицательных значений в формулу дискриминанта. Вот и не ленимся, аккуратно пишем все знаки и скобочки. Трудов много не отнимет, зато гарантированно убережёт от досадных промахов:
Извлекаем корень из дискриминанта:
Отлично, корень извлекается чисто. Теперь переходим к последнему, самому главному этапу — считаем наши корни.
4. Подставляем все значения в общую формулу, аккуратно считаем корни уравнения и записываем ответ.
Опять же, аккуратно подставляем все числа в формулу, со всеми знаками и скобочками:
Вот и всё. Это ответ.)
Кстати сказать, если вы просто решаете квадратное уравнение, то нет особой нужды отдельно считать дискриминант. Можно работать напрямую с общей формулой, просто аккуратно подставляя в неё коэффициенты a, b и с.
В нашем случае можно было бы сразу записать:
Но такое оформление чревато тем, что, впопыхах, можно где-нибудь потерять минус. Оно вам надо? Посему лучше считайте дискриминант отдельно — ошибок меньше будет. Естественно, посчитав дискриминант, не забывайте про корень.) Специально акцентирую внимание на этом моменте, потому что сам дискриминант народ обычно считает правильно, а вот корень извлечь частенько забывает… К тому же, привыкнув к отдельному поиску дискриминанта, вы быстрее запомните его общую формулу — в более серьёзных заданиях пригодится. Например, в задачах с параметрами. Такие задачи — высший пилотаж на ЕГЭ!
Естественно, бывают и сюрпризы. Не без этого… И к ним (к сюрпризам) тоже надо быть готовым, да. Чтобы не растеряться, в случае чего…) Рассмотрим первый сюрприз. Самый безобидный.
Например, дано нам такое уравнение:
Как обычно, работаем прямо по алгоритму.
1. Приводим уравнение к стандартному виду.
Уравнение пока не готово к решению. Справа нужен ноль, а у нас справа тусуется 4х. Не беда: переносим 4х влево и выстраиваем члены по убыванию степеней:
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
3. Считаем дискриминант по формуле D = b 2 -4ac.
А вот и первый сюрприз.) Дискриминант не является точным квадратом целого числа! И корень из дискриминанта извлекается плохо:
Что делать? Не решается уравнение? Ну да, как же!
Ничего страшного.) Работаем прямо с корнем. Естественно, если есть возможность, то выносим всё, что извлекается, за знак корня:
4. Подставляем все значения в общую формулу, аккуратно считаем корни уравнения и записываем ответ.
Корни нашего уравнения получились иррациональными. Ну и ничего страшного. Бывает.) Такой уж пример.
Открою небольшой секрет. Обычно задания на квадратные уравнения составляются так, чтобы корень из дискриминанта извлекался ровно и, тем самым, корни в ответе получались красивыми — либо целыми, либо рациональными. И народ постепенно привыкает к таким простым примерам наивно полагая, что дискриминант всегда обязан получаться точным квадратом. Не обязан! Более того, суровая реальность такова, что некрасивый дискриминант (а вместе с ним и лохматые иррациональные корни) — скорее правило, чем исключение! И если вы захотите задать какое-нибудь квадратное уравнение, выбрав в нём коэффициенты a, b и с случайным образом, то с вероятностью 99% корни вашего квадратного уравнения будут числами иррациональными.
Но иррациональных корней вовсе не надо бояться.) Ибо они — точно такие же числа, как и все остальные. Кстати говоря, в более серьёзных заданиях (неравенствах, задачах с параметрами) иррациональные корни встречаются сплошь и рядом. И с ними надо обязательно уметь работать — сравнивать, изображать на числовой оси и т.д. И мы тоже поработаем! В соответствующих уроках.)
Как видите, процедура решения полных квадратных уравнений проблем не вызывает. Всё просто, быстро, не больно.) Главное — аккуратно подставляйте коэффициенты в формулу дискриминанта и общую формулу корней. И считайте себе.) И что, думаете, ошибиться нельзя? Ну да, как же…
Вот краткий перечень глупых ошибок при решении квадратных уравнений:
2. Забывают извлечь корень из дискриминанта.
3. При работе с общей формулой корней в знаменатель дроби частенько подставляется не 2а, как положено, а просто двойка. Привыкает, видите ли, народ к простым уравнениям, с первым коэффициентом единичкой (а=1). Внимательнее надо быть, да.)
Например, дано такое уравнение:
Уравнение, в принципе, уже дано нам в стандартном виде. Слева — квадратный трёхчлен, построенный по убыванию степеней, справа — ноль.
Наши коэффициенты будут:
Можно приступать к решению. Только это… коэффициенты — дробные. Неудобно как-то…
Согласен, неудобно! Всё-таки лучше, когда уравнение безо всяких дробей, в линеечку.) Вот и избавимся сначала от дробей. На что надо домножить обе части уравнения, чтобы и двойка сократилась и тройка? На 6! Вот и домножаем. Слева получим:
А что будет справа? Справа будет ноль. Ноль на что ни умножай — всё равно ноль будет. Хорошее число.)
-2х 2 + 9х — 30 = 0
И опять не бросаемся решать, считать дискриминант и прочее. Минус перед иксом в квадрате — нехорош. Забыть его очень легко. Посему избавимся от этого минуса умножением обеих частей на (-1). Проще говоря, поменяем слева все знаки:
Ну вот. А теперь — по накатанной колее. Выписываем коэффициенты:
Вот так штука! А дискриминант-то отрицательный! Не можем мы корень из отрицательного числа извлечь. И сами корни посчитать, стало быть, тоже не можем, да. Стало быть, ответ — решений нет.
Это был второй сюрприз. Надеюсь, теперь отрицательный дискриминант в каком-нибудь примере вас нисколько не смутит.)
Это всё что касается полных квадратных уравнений. Теперь переходим к неполным.)
Неполные квадратные уравнения
Неполными, напоминаю, называются квадратные уравнения, где чего-то не хватает — или bx или с. Или обоих членов сразу.
Неполные квадратные уравнение также можно решать через дискриминант, по общей формуле. Надо только правильно догадаться, чему равняются коэффициенты a, b и с.
Во втором уравнении всё аналогично, только нулю будет равно не с, а b!
Но неполные уравнения можно решать гораздо проще. Безо всяких дискриминантов и безо всяких формул! Зачем же из пушки по воробьям…
Например, такое уравнение:
Что здесь можно сделать в левой части? Сильнее всего напрашивается вынести икс за скобки и разложить левую часть на множители. Давайте вынесем:
И что дальше? А то, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю! Вот и приравниваем (в уме!) каждый из множителей к нулю и получаем:
И все дела! Это и будут корни нашего уравнения. Оба годятся.) При подстановке каждого из них в исходное уравнение мы получим железное равенство 0=0. Как видите, решение куда проще, чем через дискриминант!
Теперь рассмотрим другое уравнение:
Остаётся корень извлечь из 16 и — ответ готов:
И так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки и разложения на множители, либо же переносом свободного члена вправо с последующим извлечением корня. Спутать эти два способа — надо очень хорошо постараться.) Ибо в первом случае вам пришлось бы корень из икса извлекать, что как-то не очень, а во втором случае выносить за скобки нечего…
Подытожим тему практическими советами.
1. Перед решением любого квадратного уравнения приводим его к стандартному виду, выстраиваем левую часть по убыванию степеней.
2. Если в уравнении имеются дробные коэффициенты, избавляемся от дробей умножением всего уравнения на нужный множитель.
3. Если коэффициент перед иксом в квадрате отрицательный, избавляемся от минуса умножением всего уравнения на (-1).
Ну что, наш урок окончен. Теперь можно и порешать.)
Независимо от того, в каком классе проходят уроки алгебры – математическом или обычном – квадратное уравнение изучается почти сразу после освоения всех видов своего простого линейного аналога, будучи «следующим уровнем сложности». Вычисление и поиск верного ответа не представляют трудностей, достаточно запомнить алгоритм решения и следовать ему.
Наравне с выражениями с комплексными числами и функциями с двумя переменными, алгебра поначалу заставит ученика изрядно поломать голову вне зависимости от возраста и склада ума.;
Примеры с переменной в квадрате – хорошие задания для тренировки навыков счета. В математических дисциплинах квадратное уравнение нередко выступает промежуточным шагом к доказательству теорем.
Дискриминант
Изучаемое выражение имеет стандартный вид:
Все три слагаемых имеют коэффициенты, способные принимать любые значения, но при переменной в квадрате он не должен равняться 0, иначе уравнение перестает быть квадратным.
Например, уравнение 2x 2 + 2 = 0 идентично выражению 2x 2 + 0x + 2 = 0.
Части равенства справа от знака равенства переносятся влево с противоположным знаком:
Разобрать квадратное уравнение поможет дискриминант (D). Этот вспомогательный показатель через сложные расчеты позволит найти корни выражения или обнаружить невозможность решения.
Вывод формулы выполняется благодаря манипуляции с числовыми показателями:
Определение дискриминанта подскажет количество корней:
Как решать
квадратные уравнения
В предыдущих уроках мы разбирали «Как решать линейные уравнения», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.
Что называют квадратным уравнением
Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.
Если максимальная степень, в которой стоит неизвестное — « 2 », значит, перед вами квадратное уравнение.
Примеры квадратных уравнений
Чтобы найти « a », « b » и « c » нужно сравнить свое уравнение с общим видом квадратного уравнения « ax 2 + bx + c = 0 ».
Давайте потренируемся определять коэффициенты « a », « b » и « c » в квадратных уравнениях.
Как решать квадратные уравнения
В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней.
Чтобы решить квадратное уравнение нужно:
Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.
Уравнение « x 2 − 3x − 4 = 0 » уже приведено к общему виду « ax 2 + bx + c = 0 » и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения.
Определим коэффициенты « a », « b » и « c » для этого уравнения.
Подставим их в формулу и найдем корни.
x 2 − 3x − 4 = 0
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
x1;2 =
| −(−3) ± √ (−3) 2 − 4 · 1· (−4) |
| 2 · 1 |
x1;2 =
| 3 ± √ 9 + 16 |
| 2 |
x1;2 =
| 3 ± √ 25 |
| 2 |
x1;2 =
| 3 ± 5 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 4 | x2 = −1 |
Ответ: x1 = 4 ; x2 = −1
Обязательно выучите наизусть формулу для нахождения корней.
С её помощью решается любое квадратное уравнение.
Рассмотрим другой пример квадратного уравнения.
В данном виде определить коэффициенты « a », « b » и « c » довольно сложно. Давайте вначале приведем уравнение к общему виду « ax 2 + bx + c = 0 ».
Теперь можно использовать формулу для корней.
x1;2 =
| −(−6) ± √ (−6) 2 − 4 · 1 · 9 |
| 2 · 1 |
x1;2 =
| 6 ± √ 36 − 36 |
| 2 |
x1;2 =
| 6 ± √ 0 |
| 2 |
x1;2 =
| 6 ± 0 |
| 2 |
x =
| 6 |
| 2 |
x = 3
Ответ: x = 3
Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.
Рассмотрим пример квадратного уравнения, у которого нет корней.
5x 2 + 2x = − 3
5x 2 + 2x + 3 = 0
x1;2 =
| −2 ± √ 2 2 − 4 · 3 · 5 |
| 2 · 5 |
x1;2 =
| −2 ± √ 4 − 60 |
| 10 |
x1;2 =
| −2 ± √ −56 |
| 10 |
Ответ: нет действительных корней.
Итак, мы получили ситуацию, когда под корнем стоит отрицательное число. Это означает, что в уравнении нет корней. Поэтому в ответ мы так и записали «Нет действительных корней».
Что означают слова «нет действительных корней»? Почему нельзя просто написать «нет корней»?
На самом деле корни в таких случаях есть, но в рамках школьной программы они не проходятся, поэтому и в ответ мы записываем, что среди действительных чисел корней нет. Другими словами «Нет действительных корней».
Неполные квадратные уравнения
Иногда встречаются квадратные уравнения, в которых отсутсвуют в явном виде коэффициенты « b » и/или « c ». Как например, в таком уравнении:
Такие уравнения называют неполными квадратными уравнениями. Как их решать рассмотрено в уроке «Неполные квадратные уравнения».
Формула корней квадратного уравнения
Дискриминант и решение квадратного уравнения
Если выражение справа неотрицательное, то:
И решение нашего уравнения:
Количество корней квадратного уравнения
Общий алгоритм решения квадратного уравнения
Ниже представлен полный алгоритм решения квадратного уравнения на множестве действительных чисел.
В зависимости от выполнения условий (в ромбах), в алгоритме происходит ветвление. Всего на ветках «вырастает» 11 листьев – 11 возможных решений.
Если условие в ромбе выполняется, выход обозначен синей веткой, не выполняется – красной. Над некоторыми ветками для наглядности представлены текущие значения параметров.
В простейшем (в математике говорят, «тривиальном») случае, при всех нулевых коэффициентах, уравнение имеет бесконечное множество решений.
Три ветки заканчиваются пустым множеством, с отсутствием решений.
Четыре ветки дают по одному корню, и три ветки дают по два корня.
Примеры
Пример 1. Решите уравнение, вычислив дискриминант:
$$D = 53^2-4 \cdot 7 \cdot (-24) = 2809+672 = 3481 = 59^2$$
$x \in \varnothing$, решений нет
Пример 2. Решите уравнения:
$$ \Rightarrow 4x^2-7x-6 = 3(x^2-4) \Rightarrow x^2-7x+6 = 0$$
$$ D = 7^2-4 \cdot 6 = 49-24 = 25 = 5^2$$
$$ x = \frac<7 \pm 5> <2>= \left[ \begin
$$ x = \frac<5 \pm 1> <2>= \left[ \begin
Пример 3*. Решите уравнение:
Корни каждого из уравнений:
Корни каждого из уравнений:
$$ D = 4^2-4 \cdot (-4) = 16+16 = 32, \sqrt
Квадратные уравнения. Полное квадратное уравнение. Неполное квадратное уравнение. Дискриминант.
Как решить квадратное уравнение?
Как выглядит формула квадратного уравнения?
Какие бывают квадратные уравнения?
Что такое полное квадратное уравнение?
Что такое неполное квадратное уравнение?
Что такое дискриминант?
Сколько корней имеет квадратное уравнение?
Эти вопросы вас больше не будут мучить, после изучения материала.
Формула квадратного уравнения:
где x — переменная,
a,b,c — числовые коэффициенты.

Пример полного квадратного уравнения:
Решение полных квадратных уравнений сводится к нахождению дискриминанта:
Если D>0, то уравнение имеет два корня и находим эти корни по формуле:

Если D=0, уравнение имеет один корень

Записываем сначала, чему равны числовые коэффициенты a, b и c.
Дискриминант больше нуля, следовательно, у нас два корня, найдем их:

Рассмотрим неполное квадратное уравнение:
ax 2 +bx=0, где числовой коэффициент c=0.
Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.
ax 2 +bx=0
x(ax+b)=0
x1=0 x2=-b/a
Пример №1:
3x 2 +6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x1=0
3x+6=0
3x=-6
Делим все уравнение на 3, чтобы получить у переменной x коэффициент равный 1.
x=(-6)/3
x2=-2
Рассмотрим неполное квадратное уравнение:
ax 2 +c=0, где числовой коэффициент b=0.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Квадратное уравнение
Что такое квадратное уравнение и как его решать?
Мы помним, что уравнение это равенство, содержащее в себе переменную, значение которой нужно найти.
Если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение называют уравнением второй степени или квадратным уравнением.
Например, следующие уравнения являются квадратными:
Все тождественные преобразования, которые мы применяли при решении обычных линейных уравнений, можно применять и при решении квадратных.
Итак, в уравнении x 2 − 4 = 0 перенесем член −4 из левой части в правую часть, изменив знак:
У нас переменная x всё ещё во второй степени, поэтому решение необходимо продолжить.
Обычно записывают так: перед квадратным корнем ставят знак «плюс-минус», затем находят арифметическое значение квадратного корня. В нашем случае на этапе когда записано выражение 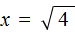
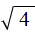
Затем найти арифметическое значение квадратного корня
Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно:
В обоих случаях левая часть равна нулю. Значит уравнение решено верно.
Решим ещё одно уравнение. Пусть требуется решить квадратное уравнение (x + 2) 2 = 25
Решим оба уравнения. Это обычные линейные уравнения, которые решаются легко:
Запишем полностью решение уравнения (x + 2) 2 = 25
Бывает и так, что квадратное уравнение имеет только один корень или вовсе не имеет корней. Такие уравнения мы рассмотрим позже.
Квадратное уравнение бывает дано в разном виде. Наиболее его распространенная форма выглядит так:
Это так называемый общий вид квадратного уравнения. В таком уравнении все члены собраны в общем месте (в одной части), а другая часть равна нулю. По другому такой вид уравнения называют нормальным видом квадратного уравнения.
В квадратном уравнении желательно упорядочивать члены так, чтобы они располагались в таком же порядке как у нормального вида квадратного уравнения.
Если какой-то из коэффициентов равен нулю (то есть отсутствует), то уравнение значительно уменьшается и принимает более простой вид. Такое квадратное уравнение называют неполным. Например, неполным является квадратное уравнение 2x 2 + 6x = 0, в нём имеются коэффициенты a и b (числа 2 и 6 ), но отсутствует свободный член c.
Рассмотрим каждый из этих видов уравнений, и для каждого из этих видов определим свой способ решения.
Для дальнейшего упрощения уравнения воспользуемся ранее изученными тождественными преобразованиями. В данном случае можно разделить обе части на 2
Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно:
В обоих случаях левая часть равна нулю, значит уравнение решено верно.
Также, неполным будет квадратное уравнение, если коэффициент c равен нулю.
Получилось уравнение x(2x + 6) = 0 в котором нужно найти x, при котором левая часть станет равна нулю. Заметим, что в этом уравнении выражения x и (2x + 6) являются сомножителями. Одно из свойств умножения говорит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
В нашем случае равенство будет достигаться, если x будет равно нулю или (2x + 6) будет равно нулю. Так и запишем для начала:
Видим, что второй корень равен −3.
Выполним проверку. Подставим корни 0 и −3 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 0 и −3 левая часть равна нулю, то это будет означать, что уравнение решено верно:
Проще говоря, если в квадратном уравнении вида ax 2 + bx + c = 0 числа b и с равны нулю, то корень такого уравнения равен нулю.
Отметим, что когда употребляются словосочетания « b равно нулю » или « с равно нулю «, то подразумевается, что параметры b или c вовсе отсутствуют в уравнении.
Значит корнем уравнения x 2 − 2x + 1 = 0 является единица. Других корней у данного уравнения нет. В данном случае мы решили квадратное уравнение, имеющее только один корень. Такое тоже бывает.
В данном случае левая часть уже не является квадратом суммы или разности. Поэтому нужно искать другие пути решения.
Заметим, что левая часть уравнения представляет собой квадратный трехчлен. Тогда можно попробовать выделить полный квадрат из этого трёхчлена и посмотреть что это нам даст.
Выделим полный квадрат из квадратного трёхчлена, располагающего в левой части уравнения:
В получившемся уравнении перенесем −4 в правую часть, изменив знак:
Выделим полный квадрат из левой части:
Далее воспользуемся квадратным корнем и узнáем чему равно x
Значит корнем уравнения x 2 − 6x + 9 = 0 является 3. Выполним проверку:
Выделим полный квадрат из левой части:
Перенесём −121 из левой части в правую часть, изменив знак:
Воспользуемся квадратным корнем:
Получили два простых уравнения: 2x + 7 = 11 и 2x + 7 = −11. Решим их:
Пример 5. Решить уравнение 2x 2 + 3x − 27 = 0
Это уравнение немного посложнее. Когда мы выделяем полный квадрат, первый член квадратного трёхчлена мы представляем в виде квадрата какого-нибудь выражения.
Если обе части исходного уравнения умножить или разделить на одно и то же число, то полýчится уравнение равносильное исходному. Это правило сохраняется и для квадратного уравнения.
Перепишем левую часть в виде трёх дробей со знаменателем 2
Сократим первую дробь на 2. Остальные члены левой части перепишем без изменений. Правая часть по-прежнему станет равна нулю:
Выделим полный квадрат.
При представлении члена 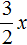


Свернём полученный полный квадрат:
Приведём подобные члены:
Перенесём дробь 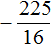
Воспользуемся квадратным корнем. Выражение 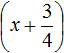
Для вычисления правой части воспользуемся правилом извлечения квадратного корня из дроби:
Тогда наше уравнение примет вид:
Полýчим два уравнения:
Значит корнями уравнения 2x 2 + 3x − 27 = 0 являются числа 3 и 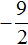
Корень 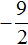
Выполним проверку. Подставим найденные корни в исходное уравнение:
В обоих случаях левая часть равна нулю, значит уравнение 2x 2 + 3x − 27 = 0 решено верно.
Такой вид квадратного уравнения называют приведённым квадратным уравнением.
Любое квадратное уравнение вида ax 2 + bx + c = 0 можно сделать приведённым. Для этого нужно разделить обе его части на коэффициент, который располагается перед x². В данном случае обе части уравнения ax 2 + bx + c = 0 нужно разделить на a
Пример 6. Решить квадратное уравнение 2x 2 + x + 2 = 0
Сделаем данное уравнение приведённым:
Выделим полный квадрат:
Получили уравнение 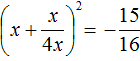
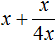
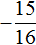
Формулы корней квадратного уравнения
Выделять полный квадрат для каждого решаемого квадратного уравнения не очень удобно.
Можно ли создать универсальные формулы для решения квадратных уравнений? Оказывается можно. Сейчас мы этим и займёмся.
Итак, выделим полный квадрат из левой части уравнения ax 2 + bx + c = 0. Сначала сделаем данное уравнение приведённым. Разделим обе его части на a
Теперь в получившемся уравнении выделим полный квадрат:
Перенесем члены 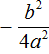

Приведём правую часть к общему знаменателю. Дроби, состоящие из букв, привóдят к общему знаменателю методом «крест-нáкрест». То есть знаменатель первой дроби станóвится дополнительным множителем второй дроби, а знаменатель второй дроби станóвится дополнительным множителем первой дроби:
В числителе правой части вынесем за скобки a
Сократим правую часть на a
Поскольку все преобразования были тождественными, то получившееся уравнение 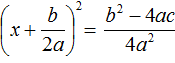
D = b 2 − 4ac = 1 2 − 4 × 2 × 2 = 1 − 16 = −15.
Видим, что D (оно же b 2 − 4ac ) является отрицательным числом. Тогда нет смысла решать уравнение 2x 2 + x + 2 = 0, выделяя в нём полный квадрат, потому что когда мы дойдем до уравнения вида 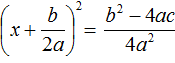
Станóвится понятно почему древние люди считали выражение b 2 − 4ac различителем. Это выражение подобно индикатору позволяет различить уравнение имеющего корни от уравнения, не имеющего корней.
В этом случае говорят, что у исходного уравнения корней нет, поскольку квадрат любого числа не должен быть отрицательным.
В этом случае уравнение будет иметь два корня. Для их вывода воспользуемся квадратным корнем:
Получили уравнение 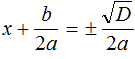
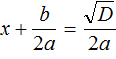
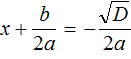
Очерёдность применения формул не важнá.
Прежде чем использовать формулы корней квадратного уравнения, нужно найти дискриминант этого уравнения.
D = b 2 − 4ac = 2 2 − 4 × 1 × (−8) = 4 + 32 = 36
Дискриминант больше нуля. Значит уравнение имеет два корня. Теперь можно воспользоваться формулами корней квадратного уравнения:
Наконец, рассмотрим случай когда дискриминант квадратного уравнения равен нулю. Вернёмся к уравнению 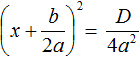
И в этом случае квадратное уравнение будет иметь только один корень. Воспользуемся квадратным корнем:
Далее выражаем x
D = b 2 − 4ac = (−6) 2 − 4 × 1 × 9 = 36 − 36 = 0
Значит корнем уравнения x 2 − 6x + 9 = 0 является число 3.
Для квадратного уравнения, имеющего один корень также применимы формулы 

Применим эти две формулы для предыдущего уравнения. В обоих случаях получим один и тот же ответ 3
Если квадратное уравнение имеет только один корень, то желательно применять формулу 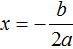


Пример 3. Решить уравнение 5x 2 − 6x + 1 = 0
Найдём дискриминант квадратного уравнения:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Значит корнями уравнения 5x 2 − 6x + 1 = 0 являются числа 1 и 
Ответ: 1; 
Пример 4. Решить уравнение x 2 + 4x + 4 = 0
Найдём дискриминант квадратного уравнения:
Дискриминант равен нулю. Значит уравнение имеет только один корень. Он вычисляется по формуле
Пример 5. Решить уравнение 3x 2 + 2x + 4 = 0
Найдём дискриминант квадратного уравнения:
Дискриминант меньше нуля. Значит корней у данного уравнения нет.
Ответ: корней нет.
Пример 6. Решить уравнение (x + 4) 2 = 3x + 40
Приведём данное уравнение к нормальному виду. В левой части располагается квадрата суммы двух выражений. Раскрóем его:
Перенесём все члены из правой части в левую часть, изменив их знаки. В правой части останется ноль:
Приведём подобные члены в левой части:
В получившемся уравнении найдём дискриминант:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Ответ: 3 ; −8.
Пример 7. Решить уравнение
В получившемся уравнении перенесём 22 из правой части в левую часть, изменив знак. В правой части останется 0
Приведём подобные члены в левой части:
В получившемся уравнении найдём дискриминант:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Ответ: 23; −1.
Пример 8. Решить уравнение
В получившемся уравнении раскроем скобки в обеих частях:
Теперь перенесём все члены из правой части в левую часть, изменив у них знаки. В правой части останется 0
Приведём подобные члены в левой части:
В получившемся уравнении найдём дискриминант:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Значит корнями уравнения 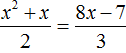
Примеры решения квадратных уравнений
Пример 1. Решить уравнение x 2 = 81
Это простейшее квадратное уравнение, в котором надо определить число, квадрат которого равен 81. Таковыми являются числа 9 и −9. Воспользуемся квадратным корнем для их вывода:
Пример 2. Решить уравнение x 2 − 9 = 0
Это неполное квадратное уравнение. Для его решения нужно перенести член −9 в правую часть, изменив знак. Тогда получим:
Ответ: 3, −3.
Пример 3. Решить уравнение x 2 − 9x = 0
Это неполное квадратное уравнение. Для его решения сначала нужно вынести x за скобки:
Левая часть уравнения является произведением. Произведение равно нулю, если хотя один из сомножителей равен нулю.
Левая часть станет равна нулю, если отдельно x равно нулю, или если выражение x − 9 равно нулю. Получится два уравнения, одно из которых уже решено:
Пример 4. Решить уравнение x 2 + 4x − 5 = 0
Это полное квадратное уравнение. Его можно решить методом выделения полного квадрата или с помощью формул корней квадратного уравнения.
Решим данное уравнение с помощью формул. Сначала найдём дискриминант:
D = b 2 − 4ac = 4 2 − 4 × 1 × (−5) = 16 + 20 = 36
Дискриминант больше нуля. Значит уравнение имеет два корня. Вычислим их:
Пример 5. Решить уравнение
Умнóжим обе части на наименьшее общее кратное чисел 5, 3 и 6. Это позвóлит избавиться от дробей в обеих частях:
В получившемся уравнении перенесём все члены из правой части в левую часть, изменив знак. В правой части останется ноль:
Приведём подобные члены:
Решим получившееся уравнение с помощью формул:
Пример 6. Решить уравнение x 2 = 6
В данном примере как и в первом нужно воспользоваться квадратным корнем:
Однако, квадратный корень из числа 6 не извлекается. Он извлекается только приближённо. Корень можно извлечь с определённой точностью. Извлечём его с точностью до сотых:
Но чаще всего корень оставляют в виде радикала:
Ответ:
Пример 7. Решить уравнение (2x + 3) 2 + (x − 2) 2 = 13
Раскроем скобки в левой части уравнения:
В получившемся уравнении перенесём 13 из правой части в левую часть, изменив знак. Затем приведём подобные члены:
Получили неполное квадратное уравнение. Решим его:
Пример 8. Решить уравнение (5 + 7x)(4 − 3x) = 0
Данное уравнение можно решить двумя способами. Рассмотрим каждый из них.
Первый способ. Раскрыть скобки и получить нормальный вид квадратного уравнения.
Приведём подобные члены:
Перепишем получившееся уравнение так, чтобы член со старшим коэффициентом располагался первым, член со вторым коэффициентом — вторым, а свободный член располагался третьим:
Чтобы старший член стал положительным, умнóжим обе части уравнения на −1. Тогда все члены уравнения поменяют свои знаки на противоположные:
Решим получившееся уравнение с помощью формул корней квадратного уравнения:
Произведение равно нулю, если хотя бы один из сомножителей равен нулю. В данном случае равенство в уравнении (5 + 7x)(4 − 3x) = 0 будет достигаться, если выражение (5 + 7x) равно нулю, или же выражение (4 − 3x) равно нулю. Наша задача выяснить при каких x это происходит:
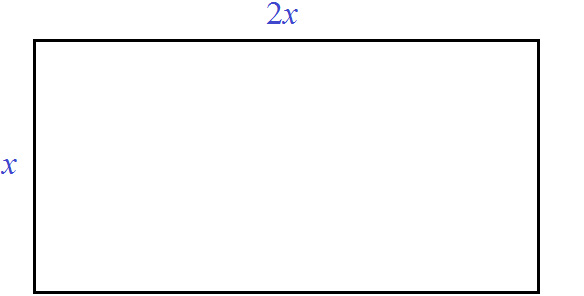
Примеры решения задач
Сделаем примерный рисунок этой комнаты, который иллюстрирует вид сверху:
Поверхность комнаты (её пол) является прямоугольником. Для вычисления площади прямоугольника, нужно длину данного прямоугольника умножить на его ширину. Сделаем это:
Получилось уравнение. Если решить его, то можно найти длину и ширину комнаты.
Первое что можно сделать это выполнить умножение в левой части уравнения:
В результате этого преобразования переменная x перешла во вторую степень. А мы говорили, что если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение является уравнением второй степени или квадратным уравнением.
Для решения нашего квадратного уравнения воспользуемся изученными ранее тождественными преобразованиями. В данном случае можно разделить обе части на 2
Пример 2. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м 2
Решение
Решим данное уравнение. Для начала раскроем скобки в левой части:
Перенесём 1200 из правой части в левую часть, изменив знак. В правой части останется 0
Решим получившееся уравнение с помощью формул:
x + 10 = 30 + 10 = 40 м
Значит длина участка составляет сорок метров, а ширина тридцать метров. Эти значения удовлетворяют условию задачи, поскольку если перемножить длину и ширину (числа 40 и 30 ) получится 1200 м 2
40 × 30 = 1200 м 2
Теперь ответим на вопрос задачи. Какова длина изгороди? Чтобы её вычислить нужно найти периметр участка.
Периметр прямоугольника это сумма всех его сторон. Тогда:
P = 2(a + b) = 2 × (40 + 30) = 2 × 70 = 140 м.
Ответ: длина изгороди огородного участка составляет 140 м.