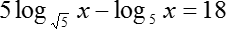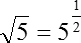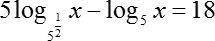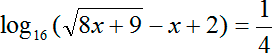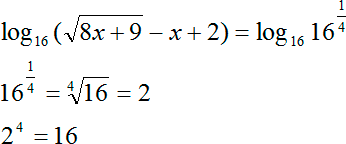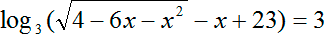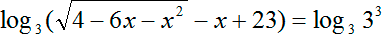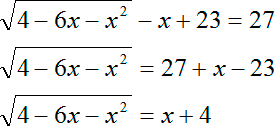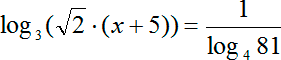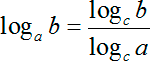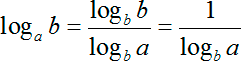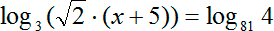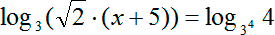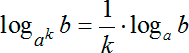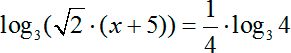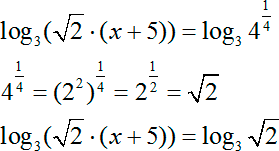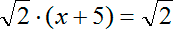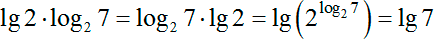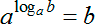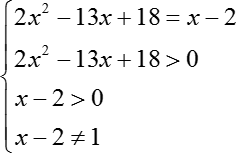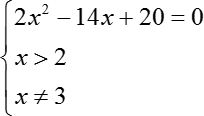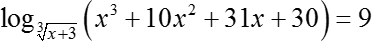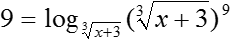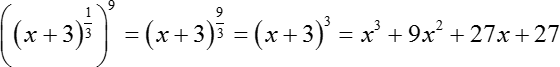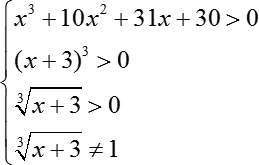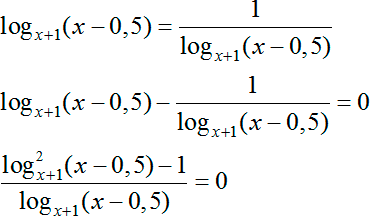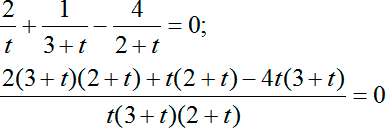Как решать логарифмические уравнения примеры
Как решать логарифмические уравнения примеры
Логарифмические уравнения
Алгоритм решения логарифмических уравнений
Как решать логарифмические уравнения
Уравнения, содержащие в том или ином виде логарифмы от некоторого выражения, зависящего от \(х\), называются логарифмическими.
Давайте сразу же рассмотрим пример, так будет легче всего разобраться.
Опять имеем два логарифма с одинаковым основанием \(3\). Избавляемся от логарифмов, приравнивая аргументы:
Кажется, что все очень просто. Но есть несколько непростых нюансов, которые необходимо обсудить. Давайте посмотрим еще один пример:
Мы решили уравнение, но я хочу позанудствовать и проверить, действительно ли получившийся корень является корнем исходного уравнения. Для этого подставим его в логарифмическое уравнение:
Мы получили слева и справа два одинаковых логарифма, вот только эти логарифмы НЕ СУЩЕСТВУЮТ, потому что нельзя взять логарифм от отрицательного числа.
Тут самое время вспомнить про область допустимых значений (ОДЗ). В логарифмах нужно всегда внимательно следить за тем, чтобы не нарушались ограничения, которые вытекают из определения логарифма. Рассмотрим логарифм от некоторой функции:
Область допустимых значений (ОДЗ) для него будет задаваться системой неравенств:
Следующая трудность при решении логарифмических уравнений возникает, когда у нас сравниваются логарифмы с разными основаниями:
Запишем ОДЗ: \(x>0\). У логарифма слева основание \(2\), а у логарифма справа основание \(4\). Чтобы воспользоваться способом решения, аналогичным первым трем примерам, необходимо привести логарифмы к одинаковому основанию.
Вспоминаем, что в самом начале к уравнению мы записывали ОДЗ \(х>0\). Тогда корень \(x=-3\) не удовлетворяет ОДЗ. Обратите внимание, что без учета ОДЗ в этом случае, мы бы получили неправильный ответ.
Подробнее про свойства логарифмов можно посмотреть тут. Логарифмические уравнения с разными основаниями встречаются в ЕГЭ регулярно, поэтому важно уметь применять все свойства логарифмов.
Рассмотрим еще один пример.
Как видим, в примере есть только логарифм в левой части равенства, а справа стоит просто число 2. Давайте постараемся привести к такому же виду, как и в прошлых примерах. То есть сделаем так, чтобы справа появился логарифм с основанием 5.
Подведем итоги. В большинстве случаев, для того, чтобы решить простейшее логарифмическое уравнение, необходимо привести логарифмы слева и справа к одинаковому основанию. Затем приравнять подлогарифмические выражения и решить получившееся уравнения. При этом ни в коем случае не забываем про ОДЗ. На ЕГЭ, если вы вдруг запишите в ответ хотя бы один корень, не удовлетворяющий ОДЗ, то вам поставят за это задание 0 баллов.
Для того, чтобы закрепить материал, решим еще одно логарифмическое уравнение:
Здесь все несколько сложнее, чем в предыдущих примерах. Для того чтобы представить наше уравнение в виде (*), нужно избавиться от множителя \(2\) перед первым логарифмом, кроме этого, нам мешается отдельное слагаемое \(4\), и в придачу ко всем этим неприятностям у логарифмов разные основания!
Логарифмические уравнения
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
При этом 0,\;a> 0,\;a\neq 1′ alt=’b> 0,\;a> 0,\;a\neq 1′/>.
Обратим внимание на область допустимых значений логарифма:
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,\;a> 0,\;a\neq 1′ alt=’b> 0,\;a> 0,\;a\neq 1′/>.
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
4. Решите уравнение:
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
0\\ x^<2>-4> 0\\ x^<2>+x=x^<2>-4 \end
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
0\\ x> 0\\ x\neq 1 \end
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′/>.
ОДЗ уравнения: 0′ alt=’x> 0′/>
Вернемся к переменной х:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
Логарифмическое уравнение: основные формулы и приемы
Этим видео я начинаю длинную серию уроков про логарифмические уравнения. Сейчас перед вами сразу три примера, на основе которых мы будем учиться решать самые простые задачи, которые так и называются — простейшие.
lg ( x + 3) = 3 + 2 lg 5
Напомню, что простейшим логарифмическим уравнением называется следующее:
При этом важно, чтобы переменная х присутствует только внутри аргумента, т. е. только в функции f ( x ). А числа а и b являются именно числами, а ни в коем случае не функциями, содержащими переменную х.
Основные методы решения
В результате я часто наблюдаю очень обидные ошибки, когда, например, эти буквы меняются местами. Данную формулу нужно либо понять, либо зубрить, причем второй способ приводит к ошибкам в самые неподходящие и самые ответственные моменты: на экзаменах, контрольных и т. д.
Именно поэтому всем своим ученикам я предлагаю отказаться от стандартной школьной формулы и использовать для решения логарифмических уравнений второй подход, который, как вы уже наверняка догадались из названия, называется канонической формой.
И вот тут мы вспоминаем наше замечательное правило, что любое число b может быть представлено в виде логарифма по основанию а от а в степени b :
Как запомнить эту формулу? Да очень просто. Давайте запишем следующую конструкцию:
b = b · 1 = b · log a a
Разумеется, что при этом возникают все ограничения, которые мы записали вначале. А теперь давайте воспользуемся основным свойством логарифма, и внесем множитель b в качестве степени а. Получим:
b = b · 1 = b · log a a = log a a b
В результате исходное уравнение перепишется в следующем виде:
log a f ( x ) = log a a b → f ( x ) = a b
Вот и все. Новая функция уже не содержит логарифма и решается стандартными алгебраическими приемами.
Конечно, кто-то сейчас возразит: а зачем вообще было придумывать какую-то каноническую формулу, зачем выполнять два дополнительных ненужных шага, если можно было сразу перейти от исходной конструкции к итоговой формуле? Да уже хотя бы затем, что большинство учеников не понимают, откуда берется эта формула и, как следствие, регулярно допускают ошибки при ее применении.
А вот такая последовательность действий, состоящая из трех шагов, позволяет вам решить исходное логарифмическое уравнение, даже если вы не понимаете, откуда берется та самая итоговая формула. Кстати, канонической формулой называется именно эта запись:
log a f ( x ) = log a a b
Удобство канонической формы состоит еще и в том, что ее можно применять для решения очень широкого класса логарифмических уравнений, а не только простейших, которые мы рассматриваем сегодня.
Примеры решения
А теперь давайте рассмотрим реальные примеры. Итак, решаем:
Давайте перепишем его следующим образом:
Многие ученики торопятся и пытаются сразу возвести число 0,5 в степень, которая пришла к нам из исходной задачи. И действительно, когда вы уже хорошо натренируетесь в решении подобных задач, вы можете сразу выполнять этот шаг.
Однако если сейчас вы только приступаете к изучению этой темы, лучше никуда не торопиться, чтобы не допускать обидных ошибок. Итак, перед нами каноническая форма. Имеем:
Это уже не логарифмическое уравнение, а линейное относительно переменной х. Чтобы решить его, давайте для начала разберемся с числом 0,5 в степени −3. Заметим, что 0,5 — это 1/2.
Все десятичные дроби переводите в обычные, когда вы решаете логарифмическое уравнение.
Переписываем и получаем:
3 x − 1 = 8
3 x = 9
x = 3
Все, мы получили ответ. Первая задача решена.
Вторая задача
Переходим ко второй задаче:
Как видим, это уравнение уже не является простейшим. Уже хотя бы потому, что слева стоит разность, а не один-единственный логарифм по одному основанию.
Следовательно, нужно каким-то образом избавиться от этой разности. В данном случае все очень просто. Давайте внимательно посмотрим на основания: слева стоит число под корнем:
Общая рекомендация: во всех логарифмических уравнениях старайтесь избавиться от радикалов, т. е. от записей с корнями и переходить к степенным функциям, просто потому что показатели этих степеней легко выносятся за знак логарифма и в конечном счета такая запись существенно упрощает и ускоряет вычисления. Вот давайте так и запишем:
Теперь вспоминаем замечательное свойство логарифма: из аргумента, а также из основания можно выносить степени. В случае с основаниями происходит следующее:
log a k b = 1/ k loga b
Другими словами, число, которое стояло в степени основания, выносится вперед и при этом переворачивается, т. е. становится обратным числом. В нашем случае стояла степень основания с показателем 1/2. Следовательно, мы можем вынести ее как 2/1. Получим:
Обратите внимание: ни в коем случае нельзя избавляться от логарифмов на этом шаге. Вспомните математику 4—5 класса и порядок действий: сначала выполняется умножение, а лишь затем — сложение и вычитание. В данном случае мы из 10 элементов вычитаем один такой же:
Теперь наше уравнение выглядит как надо. Это простейшая конструкция, и мы решаем его с помощью канонической формы:
Вот и все. Вторая задача решена.
Третий пример
Переходим к третьей задаче:
lg ( x + 3) = 3 + 2 lg 5
Напомню следующую формулу:
Вот именно этими свойствами мы сейчас и воспользуемся для решения задачи, поскольку она не является простейшей, которую мы записали в самом начале нашего урока.
Для начала заметим, что множитель 2, стоящий перед lg 5, может быть внесен и станет степенью основания 5. Кроме того, свободное слагаемое 3 также представимо в виде логарифма — это очень легко наблюдать из нашей записи.
Судите сами: любое число можно представить в виде log по основанию 10:
3 = log10 10 3 = lg 10 3
Перепишем исходную задачу с учетом полученных изменений:
lg ( x − 3) = lg 1000 + lg 25
lg ( x − 3) = lg 1000 · 25
lg ( x − 3) = lg 25 000
Перед нами снова каноническая форма, причем мы получили ее, минуя стадию преобразований, т. е. простейшее логарифмическое уравнение у нас нигде не всплывало.
Именно об этом я и говорил в самом начале урока. Каноническая форма позволяет решать более широкий класс задач, нежели стандартная школьная формула, которую дают большинство школьных учителей.
Ну и все, избавляемся от знака десятичного логарифма, и получаем простую линейную конструкцию:
x + 3 = 25 000
x = 24 997
Все! Задача решена.
Замечание по поводу области определения
Тут бы хотелось привести важное замечание по поводу области определения. Наверняка сейчас найдутся ученики и учителя, которые скажут: «Когда мы решаем выражения с логарифмами, необходимо обязательно помнить, что аргумент f ( x ) должен быть больше нуля!» В связи с этим возникает логичный вопрос: почему ни в одной из рассмотренных задач мы не требовали, чтобы это неравенство выполнялось?
Не переживайте. Никаких лишних корней в этих случаях не возникнет. И это еще одна замечательная хитрость, которая позволяет ускорить решение. Просто знайте, что если в задаче переменная х встречается лишь в одном месте (а точнее — в одном-единственном аргументе одного-единственного логарифма), и больше нигде в нашем случае нет переменной х, то записывать область определения не нужно, потому что она будет выполняться автоматически.
Судите сами: в первом уравнении мы получили, что 3х − 1, т. е. аргумент должен быть равен 8. Это автоматически означает, что 3х − 1 будет больше нуля.
Вот и все, что нужно знать для решения простейших задач. Уже одно это правило вместе с правилами преобразования позволит вам решать очень широкий класс задач.
Но давайте будем честными: для того, чтобы окончательно разобраться с этим приемом, чтобы научиться применять каноническую форму логарифмического уравнения, недостаточно просто посмотреть один видеоурок. Поэтому прямо сейчас скачайте варианты для самостоятельного решения, которые прилагаются к данному видеоуроку и начните решать хотя бы одну из этих двух самостоятельных работ.
Времени у вас уйдет буквально несколько минут. А вот эффект от такого обучения будет намного выше по сравнению с тем, если бы вы просто просмотрели данный видеоурок.
Надеюсь, этот урок поможет разобраться вам с логарифмическими уравнениями. Применяйте каноническую форму, упрощайте выражения с помощью правил работы с логарифмами — и никакие задачи вам будут не страшны. А у меня на сегодня все.
Учет области определения
Теперь поговорим об области определения логарифмической функции, а также о том, как это влияет на решение логарифмических уравнений. Рассмотрим конструкцию вида
Такое выражение называется простейшим — в нем лишь одна функция, а числа а и b — это именно числа, а ни в коем случае не функция, зависящая от переменной х. Решается оно очень просто. Достаточно лишь использовать формулу:
Данная формула является одним из ключевых свойств логарифма, и при подстановке в наше исходное выражение мы получим следующее:
log a f ( x ) = log a a b
Далее, поскольку и слева, и справа стоит логарифмы по одному и тому же основанию, мы избавляемся от них:
Это уже знакомая формула из школьных учебников. У многих учеников наверняка возникнет вопрос: поскольку в исходном выражении функция f ( x ) стоит под знаком log, на нее накладываются следующие ограничения:
Это ограничение действует потому, что логарифм от отрицательных чисел не существует. Так, может быть, вследствие этого ограничения следует ввести проверку на ответы? Быть может, их нужно подставлять в исходник?
Нет, в простейших логарифмических уравнениях дополнительная проверка излишня. И вот почему. Взгляните на нашу итоговую формулу:
Дело в том, что число а в любом случае больше 0 — это требование тоже накладывается логарифмом. Число а является основанием. При этом на число b никаких ограничений не накладывается. Но это и неважно, потому что в какую бы степень мы бы не возводили положительное число, на выходе мы все равно получим положительное число. Таким образом, требование f (х) > 0 выполняется автоматически.
Что действительно стоит проверять, так это область определения функции, стоящей под знаком log. Там могут встречаться довольно непростые конструкции, и в процессе решения за ними обязательно нужно следить. Давайте посмотрим.
Первый шаг: преобразуем дробь справа. Получим:
Избавляемся от знака логарифма и получаем обычное иррациональное уравнение:
Из полученных корней нас устраивает только первый, так как второй корень меньше нуля. Единственным ответом будет число 9. Все, задача решена. Никаких дополнительных проверок того, что выражение под знаком логарифма больше 0, не требуется, потому что оно не просто больше 0, а по условию уравнения оно равно 2. Следовательно, требование «больше нуля», выполняется автоматически.
Здесь все то же самое. Переписываем конструкцию, заменяя тройку:
Избавляемся от знаков логарифма и получаем иррациональное уравнение:
Возводим обе части в квадрат с учетом ограничений и получаем:
4 − 6 x − x 2 = ( x − 4) 2
4 − 6 x − x 2 = x 2 + 8 x + 16
x 2 + 8 x + 16 −4 + 6 x + x 2 = 0
2 x 2 + 14 x + 12 = 0 |:2
Решаем полученное уравнение через дискриминант:
Но x = −6 нас не устраивает, потому что если мы подставим это число в наше неравенство, то получим:
−6 + 4 = −2 x = −1 нам подходит:
Единственным ответом в нашем случае будет x = −1. Вот и все решение. Давайте вернемся в самое начало наших вычислений.
Основной вывод из этого урока: проверять ограничения для функции в простейших логарифмических уравнениях не требуется. Потому что в процессе решения все ограничения выполняются автоматически.
Однако это ни в коем случае не означает, что о проверке можно вообще забыть. В процессе работы над логарифмическим уравнением вполне может перейти в иррациональное, в котором будут свои ограничения и требования к правой части, в чем мы сегодня и убедились на двух различных примерах.
Смело решайте такие задачи и будьте особо внимательные, если в аргументе стоит корень.
Логарифмические уравнения с разными основаниями
Продолжаем изучать логарифмические уравнения и разберем еще два довольно интересных приема, с помощью которых модно решать более сложные конструкции. Но для начала вспомним, как решаются простейшие задачи:
В этой записи а и b являются именно числами, а в функции f ( x ) должна присутствовать переменная х, и только там, т. е. х должен находиться только в аргументе. Преобразовывать такие логарифмические уравнения мы будем с помощью канонической формы. Для этого заметим, что
Причем a b — это именно аргумент. Давайте перепишем это выражение следующим образом:
log a f ( x ) = log a a b
Мы именно этого и добиваемся, чтобы и слева, и справа стоял логарифм по основанию а. В этом случае мы можем, образно говоря, зачеркнуть знаки log, а с точки зрения математики мы можем сказать, что мы просто приравниваем аргументы:
В результате мы получим новое выражение, которое будет решаться намного проще. Давайте применим это правило к нашим сегодняшним задачам.
Итак, первая конструкция:
Прежде всего, отмечу, что справа стоит дробь, в знаменателе которой находится log. Когда вы видите такое выражение, не лишним будет вспомнить замечательное свойство логарифмов:
Другими словами, в сравнении с исходным заданием, мы поменяли местами аргумент и основание логарифма. Взамен нам пришлось перевернуть дробь.
Вспоминаем, что любую степень можно выносить из основания по следующему правилу:
Дробный множитель нельзя оставлять спереди, потому что в этом случае мы не сможем представить данную запись как каноническую форму (ведь в канонической форме перед вторым логарифмом никакой дополнительный множитель не стоит). Следовательно, давайте внесем дробь 1/4 в аргумент в виде степени:
Теперь мы приравниваем аргументы, основания которых одинаковые (а основания у нас действительно одинаковые), и записываем:
Вот и все. Мы получили ответ к первому логарифмическому уравнению. Обратите внимание: в исходной задаче переменная х встречается лишь в одном log, причем стоит в его аргументе. Следовательно, проверять область определения не требуется, и наше число х = −4 действительно является ответом.
Теперь переходим ко второму выражению:
lg 56 = lg 2 log2 7 − 3lg ( x + 4)
Здесь помимо обычных логарифмов, нам придется работать с lg f ( x ). Как решать такое уравнение? Неподготовленному ученику может показаться, что это какая-то жесть, но на самом деле все решается элементарно.
Внимательно посмотрите на слагаемое lg 2 log2 7. Что мы можем о нем сказать? Основания и аргументы log и lg совпадают, и это должно наводить на некоторые мысли. Давайте еще раз вспомним, как выносятся степени из-под знака логарифма:
Другими словами, то, что являлось степенью при числе b в аргументе, становится множителем перед самим log. Давайте применим эту формулу для выражения lg 2 log2 7. Пусть вас не пугает lg 2 — это самое обычное выражение. Можно переписать его следующим образом:
Для него справедливы все правила, которые действуют для любого другого логарифма. В частности, множитель, стоящий спереди, можно внести в степень аргумента. Давайте запишем:
Очень часто ученики в упор не видят это действие, потому что нехорошо вносить один log под знак другого. На самом деле ничего криминального в этом нет. Более того, мы получаем формулу, которая легко считается, если помнить важное правило:
Эту формулу можно рассматривать и как определение, и как одно из его свойств. В любом случае, если вы преобразуете логарифмическое уравнение, эту формулу вы должны знать точно так же, как и представление любого числа в виде log.
Возвращаемся к нашей задаче. Переписываем его с учетом того факта, что первое слагаемое справа от знака равенства будет равно просто lg 7. Имеем:
lg 56 = lg 7 − 3lg ( x + 4)
Давайте перенесем lg 7 влево, получим:
lg 56 − lg 7 = −3lg ( x + 4)
Вычитаем выражения слева, потому что они имеют одно и то же основание:
lg (56/7) = −3lg ( x + 4)
Теперь давайте внимательно посмотрим на уравнение, которое мы получили. Оно практически является канонической формой, однако справа присутствует множитель −3. Давайте внесем его в аргумент правого lg:
lg 8 = lg ( x + 4) −3
Перед нами каноническая форма логарифмического уравнения, поэтому мы вычеркиваем знаки lg и приравниваем аргументы:
Вот и все! Мы решили второе логарифмическое уравнение. При этом никаких дополнительных проверок не требуется, потому что в исходной задаче х присутствовал лишь в одном аргументе.
Перечислю еще раз ключевые моменты этого урока.
Главная формула, которая изучается во всех уроках на этой странице, посвященной решению логарифмических уравнений — это каноническая форма. И пусть вас не пугает то, что в большинстве школьных учебников вас учат решать подобные задачи по-другому. Данный инструмент работает очень эффективно и позволяет решать гораздо более широкий класс задач, нежели простейшие, которые мы изучали в самом начале нашего урока.
Кроме того, для решения логарифмических уравнений полезно будет знать основные свойства. А именно:
В заключении хотел бы добавить, что проверять область определения в каждом из этих случае не требуется, потому что везде переменная х присутствует только в одном знаке log, и при этом находится в его аргументе. Как следствие, все требования области определения выполняются автоматически.
Задачи с переменным основанием
Сегодня мы рассмотрим логарифмические уравнения, которые для многих учеников кажутся нестандартными, а то и вовсе нерешаемыми. Речь идет об выражениях, в основании которых стоят не числа, а переменные и даже функции. Решать такие конструкции мы будем с помощью нашего стандартного приема, а именно через каноническую форму.
Для начала вспомним, как решаются простейшие задачи, в основании которых стоят обычные числа. Итак, простейшей называется конструкция вида
Для решения таких задач мы можем использовать следующую формулу:
Переписываем наше исходное выражение и получаем:
log a f ( x ) = log a a b
Затем мы приравниваем аргументы, т. е. записываем:
Таким образом мы избавляемся от знака log и решаем уже обычную задачу. При этом полученные при решении корни и будут корнями исходного логарифмического уравнения. Кроме того, запись, когда и слева, и справа стоит по одному и тому же логарифму с одним и тем же основанием, как раз и называется канонической формой. Именно к такой записи мы будем пытаться свести сегодняшние конструкции. Итак, поехали.
log x − 2 (2 x 2 − 13 x + 18) = 1
Что мы видим? Перед нами каноническая форма логарифмического уравнения, поэтому мы смело можем приравнять аргументы. Получим:
2 x 2 − 13 x + 18 = x − 2
Но на этом решение не заканчивается, потому что данное уравнение не равносильно исходному. Ведь полученная конструкция состоит из функций, которые определены на всей числовой прямой, а наши исходные логарифмы определены не везде и не всегда.
Поэтому мы должны отдельно записать область определения. Давайте не будем мудрить и для начала запишем все требования:
Во-первых, аргумент каждого из логарифмов должен быть больше 0:
2 x 2 − 13 x + 18 > 0
Во-вторых, основание должно быть не только больше 0, но и отлично от 1:
В итоге получим систему:
Но вы не пугайтесь: при обработке логарифмических уравнений такую систему можно существенно упростить.
Судите сами: с одной стороны, от нас требуется, чтобы квадратичная функция была больше нуля, а с другой стороны — эта квадратичная функция приравнивается к некому линейному выражению, от которого также требуется, чтобы оно было больше нуля.
В таком случае, если мы требуем, чтобы x − 2 > 0, то автоматически будет выполняться и требование 2 x 2 − 13 x + 18 > 0. Поэтому мы можем смело зачеркнуть неравенство, содержащее квадратичную функцию. Таким образом, количество выражений, которое содержится в нашей системе, уменьшится до трех.
Разумеется, с тем же успехом мы могли бы зачеркнуть и линейное неравенство, т. е. вычеркнуть x − 2 > 0 и потребовать, чтобы 2 x 2 − 13 x + 18 > 0. Но согласитесь, что решить простейшее линейное неравенство гораздо быстрее и проще, чем квадратичное, пусть даже при условии, что в результате решения всей этой системы мы получим одни и те же корни.
В общем, по возможности старайтесь оптимизировать вычисления. И в случае с логарифмическими уравнениями вычеркивайте самые сложные неравенства.
Давайте перепишем нашу систему:
Вот такая система из трех выражений, с двумя из которых мы, по сути, уже разобрались. Давайте отдельно выпишем квадратное уравнение и решим его:
2 x 2 − 14 x + 20 = 0
x 2 − 7 x + 10 = 0
Перед нами приведенный квадратный трехчлен и, следовательно, мы можем воспользоваться формулами Виета. Получим:
А теперь возвращаемся к нашей системе и обнаруживаем, что х = 2 нас не устраивает, потому что от нас требуется, чтобы х был строго больше, чем 2.
А вот х = 5 нас вполне устраивает: число 5 больше, чем 2, и при этом 5 не равно 3. Следовательно, единственным решением данной системы будет являться х = 5.
Все, задача решена, в т. ч. с учетом ОДЗ. Переходим ко второму уравнению. Здесь нас ждут более интересные и содержательные выкладки:
Первый шаг: как и в прошлый раз, приводим все это дело к канонической форме. Для этого число 9 мы можем записать следующим образом:
Основание с корнем можно не трогать, а вот аргумент лучше преобразовать. Давайте перейдем от корня в степень с рациональным показателем. Запишем:
Давайте я не буду переписывать все наше большое логарифмическое уравнение, а просто сразу приравняю аргументы:
x 3 + 10 x 2 + 31 x + 30 = x 3 + 9 x 2 + 27 x + 27
Перед нами вновь приведенный квадратный трехчлен, воспользуемся формулами Виета и запишем:
Итак, мы получили корни, но никто нам не гарантировал, что они подойдут к исходному логарифмическому уравнению. Ведь знаки log накладывают дополнительные ограничения (здесь мы должны были бы записать систему, но из-за громоздкости всей конструкции я решил посчитать область определения отдельно).
В первую очередь, вспоминаем, что аргументы должны быть больше 0, а именно:
Это и есть требования, накладываемые областью определения.
Сразу заметим, что поскольку мы приравниваем первые два выражения системы друг к другу, то любое из них мы можем вычеркнуть. Давайте вычеркнем первую, потому что она выглядит более угрожающе, нежели вторая.
Кроме того, заметим, что решением второго и третьего неравенства будут одни и те множества (куб какого-то числа больше нуля, если само это число больше нуля; аналогично и с корнем третьей степени — эти неравенства полностью аналогичны, поэтому одно из них мы можем вычеркнуть).
А вот с третьим неравенством такое не пройдет. Избавимся от знака радикала, стоящего слева, для чего возведем обе части в куб. Получим:
Итак, мы получаем следующие требования:
Какой из наших корней: x 1 = −3 или x 2 = −1 отвечает этим требованиям? Очевидно, что только х = −1, потому что х = −3 не удовлетворяет первому неравенству (ибо неравенство у нас строгое). Итого возвращаясь к нашей задаче, мы получаем один корень: х = −1. Вот и все, задача решена.
Еще раз ключевые моменты данной задачи:
Накладывать последние требования на итоговые ответы можно по-разному. Например, можно решать целую систему, содержащую все требования к области определения. С другой стороны, можно сначала решить саму задачу, а затем вспомнить про область определения, отдельно проработать ее в виде системы и наложить на полученные корни.
Какой способ выбирать при решении конкретного логарифмического уравнения, решать только вам. В любом случае ответ получится один и тот же.
Решение логарифмических уравнений — заключительный урок
Заключительные видео из длинной серии уроков про решение логарифмических уравнений. В этот раз мы будем работать в первую очередь с ОДЗ логарифма — именно из-за неправильного учета (или вообще игнорирования) области определения возникает большинство ошибок при решении подобных задач.
В этом коротком видеоуроке мы разберем применение формул сложения и вычитания логарифмов, а также разберемся с дробно-рациональными уравнениями, с которыми у многих учеников также возникают проблемы.
О чем пойдет речь? Главная формула, с которой я хотел бы разобраться, выглядит так:
Это стандартный переход от произведения к сумме логарифмов и обратно. Вы наверняка знаете эту формулу с самого начала изучения логарифмов. Однако тут есть одна заминка.
Однако, как только вместо f и g появляются функции, возникает проблема расширения или сужения области определения в зависимости от того, в какую сторону преобразовывать. Судите сами: в логарифме, записанном слева, область определения следующая:
А вот в сумме, записанной справа, область определения уже несколько иная:
Данный набор требований является более жестким, чем исходный. В первом случае нас устроит вариант f g fg > 0 выполняется).
Итак, при переходе от левой конструкции к правой возникает сужение области определения. Если же сначала у нас была сумма, а мы переписываем ее в виде произведения, то происходит расширение области определения.
Другими словами, в первом случае мы могли потерять корни, а во втором — получить лишние. Это необходимо учитывать при решении реальных логарифмических уравнений.
Итак, первая задача:
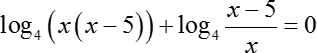
Слева мы видим сумму логарифмов по одному и тому же основанию. Следовательно, эти логарифмы можно сложить:
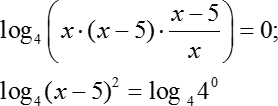
Как видите, справа мы заменил ноль по формуле:
Давайте еще немного преобразуем наше уравнение:
Перед нами каноническая форма логарифмического уравнения, мы можем зачеркнуть знак log и приравнять аргументы:
Обратите внимание: откуда взялся модуль? Напомню, что корень из точного квадрата равен именно модулю:
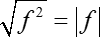
Затем решаем классическое уравнение с модулем:
| f | = g ( g > 0) ⇒ f = ± g
x − 5 = ±1 ⇒ x 1 = 5 − 1 = 4; x 2 = 5 + 1 = 6
Вот два кандидат на ответ. Являются ли они решением исходного логарифмического уравнения? Нет, ни в коем случае!
Оставить все просто так и записать ответ мы не имеем права. Взгляните на тот шаг, когда мы заменяем сумму логарифмов одним логарифмом от произведения аргументов. Проблема в том, что в исходных выражениях у нас стоят функции. Следовательно, следует потребовать:
х(х − 5) > 0; (х − 5)/х > 0.
Когда же мы преобразовали произведение, получив точный квадрат, требования изменились:
Когда это требование выполняется? Да практически всегда! За исключением того случая, когда х − 5 = 0. Т.е. неравенство сведется к одной выколотой точке:
Как видим, произошло расширение области определения, о чем мы и говорили в самом начале урока. Следовательно, могут возникнуть и лишние корни.
Как же не допустить возникновения этих лишних корней? Очень просто: смотрим на наши полученные корни и сравниваем их с областью определения исходного уравнения. Давайте посчитаем:
Решать будем с помощью метода интервалов:
х (х − 5) = 0 ⇒ х = 0; х = 5
Отмечаем полученные числа на прямой. Все точки выколотые, потому что неравенство строгое. Берем любое число, больше 5 и подставляем:
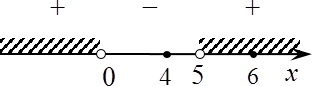
На интересуют промежутки (−∞; 0) ∪ (5; ∞). Если мы отметим наши корни на отрезке, то увидим, что х = 4 нас не устраивает, потому что этот корень лежит за пределами области определения исходного логарифмического уравнения.
Возвращаемся к совокупности, вычеркиваем корень х = 4 и записываем ответ: х = 6. Это уже окончательный ответ к исходному логарифмическому уравнению. Все, задача решена.
Переходим ко второму логарифмическому уравнению:
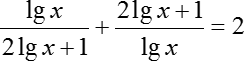
Решаем его. Заметим, что первое слагаемое представляет собой дробь, а второе — ту же самую дробь, но перевернутую. Не пугайтесь выражения lgx — это просто десятичный логарифм, мы можем записать:
Поскольку перед нами две перевернутые дроби, предлагаю ввести новую переменную:
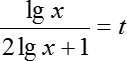
Следовательно, наше уравнение может быть переписано следующим образом:
( t 2 − 2 t + 1)/ t = 0;
Как видим, в числителе дроби стоит точный квадрат. Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля:
Решаем первое уравнение:

Приводим это уравнение к канонической форме:
В итоге мы получили единственный корень, который, по идее, является решением исходного уравнения. Однако давайте все-таки подстрахуемся и выпишем область определения исходного уравнения:
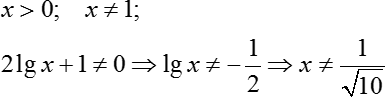
Следовательно, наш корень удовлетворяет всем требованиям. Мы нашли решение исходного логарифмического уравнения. Ответ: x = 0,1. Задача решена.
Ключевой момент в сегодняшнем уроке один: при использовании формулы перехода от произведения к сумме и обратно обязательно учитывайте, что область определения может сужаться либо расширяться в зависимости от того, в какую сторону выполняется переход.
Как понять, что происходит: сужение или расширение? Очень просто. Если раньше функции были вместе, а теперь стали по отдельности, то произошло сужение области определения (потому что требований стало больше). Если же сначала функции стояли отдельно, а теперь — вместе, то происходит расширение области определения (на произведение накладывается меньше требований, чем на отдельные множители).
С учетом данного замечания хотел бы отметить, что второе логарифмическое уравнение вообще не требует данных преобразований, т. е. мы нигде не складываем и не перемножаем аргументы. Однако здесь я хотел бы обратить ваше внимание на другой замечательный прием, который позволяет существенно упростить решение. Речь идет о замене переменной.
Однако помните, что никакие замены не освобождает нас от области определения. Именно поэтому после того были найдены все корни, мы не поленились и вернулись к исходному уравнению, чтобы найти его ОДЗ.
Часто при замене переменной возникает обидная ошибка, когда ученики находят значение t и думают, что на этом решение закончено. Нет, ни в коем случае!
Именно в этом состоит смысл введения новой переменной. Мы разбиваем исходное уравнение на два промежуточных, каждое из которых решается существенно проще.
Как решать «вложенные» логарифмические уравнения
Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого логарифма. Оба уравнения мы будем решать с помощью канонической формы.
Заметьте: a b — это аргумент. Точно так же в исходном уравнении аргументом является функция f ( x ). Затем мы переписываем уравнение и получаем вот такую конструкцию:
log a f ( x ) = log a a b
Уже затем мы можем выполнить третий шаг — избавится от знака логарифма и просто записать:
В результате мы получим новое уравнение. При этом никаких ограничений на функцию f ( x ) не накладывается. Например, на ее месте также может стоять логарифмическая функция. И тогда мы вновь получим логарифмическое уравнение, которое снова сведем к простейшему и решим через каноническую форму.
Впрочем, хватит лирики. Давайте решим настоящую задачу. Итак, задача № 1:
Итак, переписываем наше логарифмическое уравнение с учетом того, что двойка, которая стоит справа, на самом деле тоже является логарифмом. Получим:
Переходим к последнему шагу нашей схемы — избавляемся от канонической формы. Можно сказать, просто зачеркиваем знаки log. Однако с точки зрения математики «зачеркнуть log» невозможно — правильнее сказать, что мы просто просто приравниваем аргументы:
Отсюда легко находится 3 log2 x :
Мы вновь получили простейшее логарифмическое уравнение, давайте снова приведем его к канонической форме. Для этого нам необходимо провести следующие изменения:
Почему в основании именно двойка? Потому что в нашем каноническом уравнении слева стоит логарифм именно по основанию 2. Переписываем задачу с учетом этого факта:
Снова избавляемся от знака логарифма, т. е. просто приравниваем аргументы. Мы вправе это сделать, потому что основания одинаковые, и больше никаких дополнительных действий ни справа, ни слева не выполнялось:
Вот и все! Задача решена. Мы нашли решение логарифмического уравнения.
Обратите внимание! Хотя переменная х и стоит в аргументе (т. е. возникают требования к области определения), мы никаких дополнительных требований предъявлять не будем.
Как я уже говорил выше, данная проверка является избыточной, если переменная встречается лишь в одном аргументе лишь одного логарифма. В нашем случае х действительно стоит лишь в аргументе и лишь под одним знаком log. Следовательно, никаких дополнительных проверок выполнять не требуется.
Тем не менее, если вы не доверяете данному методу, то легко можете убедиться, что х = 2 действительно является корнем. Достаточно подставить это число в исходное уравнение.
Давайте перейдем ко второму уравнению, оно чуть интересней:
Если обозначить выражение внутри большого логарифма функцией f ( x ), получим простейшее логарифмическое уравнение, с которого мы начинали сегодняшний видеоурок. Следовательно, можно применить каноническую форму, для чего придется представить единицу в виде log2 2 1 = log2 2.
Переписываем наше большое уравнение:
Изваляемся от знака логарифма, приравнивая аргументы. Мы вправе это сделать, потому что и слева, и справа основания одинаковые. Кроме того, заметим, что log2 4 = 2:
log1/2 (2 x − 1) + 2 = 2
Переписываем наше уравнение и избавляемся от знака log, приравнивая аргументы:
Опять же мы сразу получили ответ. Никаких дополнительных проверок не требуется, потому что в исходном уравнении лишь один логарифм содержит функцию в аргументе.
Следовательно, никаких дополнительных проверок выполнять не требуется. Мы можем смело утверждать, что х = 1 является единственным корнем данного уравнения.
А вот если бы во втором логарифме вместо четверки стояла бы какая-то функция от х (либо 2х стояло бы не в аргументе, а в основании) — вот тогда потребовалось бы проверять область определения. Иначе велик шанс нарваться на лишние корни.
Однако по мере решения логарифмического уравнения мы избавляемся от всех знаков log и получаем простенькие конструкции. Здесь уже никаких ограничений не выставляется, потому что линейная функция определена при любом значении х.
Именно эта проблема, когда итоговая функция определена везде и всегда, а исходная — отнюдь не везде и не всегда, и является причиной, по которой в решении логарифмических уравнениях очень часто возникают лишние корни.
Но повторю еще раз: такое происходить лишь в ситуации, когда функция стоит либо в нескольких логарифмах, либо в основании одного из них. В тех задачах, которые мы рассматриваем сегодня, проблем с расширением области определения в принципе не существует.
Случаи разного основания
Этот урок посвящен уже более сложным конструкциям. Логарифмы в сегодняшних уравнениях уже не будут решаться «напролом» — сначала потребуется выполнить некоторые преобразования.
Начинаем решение логарифмических уравнений с совершенно разными основаниями, которые не являются точными степенями друг друга. Пусть вас не пугают подобные задачи — решаются они ничуть не сложнее, чем самые простые конструкции, которые мы разбирали выше.
Но прежде, чем переходить непосредственно к задачам, напомню о формуле решения простейших логарифмических уравнений с помощью канонической формы. Рассмотрим задачу вот такого вида:
Важно, что функция f ( x ) является именно функцией, а в роли чисел а и b должны выступать именно числа (без всяких переменных x ). Разумеется, буквально через минуту мы рассмотрим и такие случаи, когда вместо переменных а и b стоят функции, но сейчас не об этом.
Как мы помним, число b нужно заменить логарифмом по тому же самому основанию а, которое стоит слева. Это делается очень просто:
Разумеется, под словом «любое число b » и «любое число а» подразумеваются такие значения, которые удовлетворяют области определения. В частности, в данном уравнении речь идет лишь основание a > 0 и a ≠ 1.
Однако данное требование выполняется автоматически, потому что в исходной задаче уже присутствует логарифм по основанию а — оно заведомо будет больше 0 и не равно 1. Поэтому продолжаем решение логарифмического уравнения:
log a f ( x ) = log a a b
Подобная запись называется канонической формой. Ее удобство состоит в том, что мы сразу можем избавиться от знака log, приравняв аргументы:
Именно этот прием мы сейчас будем использовать для решения логарифмических уравнений с переменным основанием. Итак, поехали!
log2 ( x 2 + 4 x + 11) = log0,5 0,125
Что дальше? Кто-то сейчас скажет, что нужно вычислить правый логарифм, либо свести их к одному основанию, либо что-то еще. И действительно, сейчас нужно привести оба основания к одному виду — либо 2, либо 0,5. Но давайте раз и навсегда усвоим следующее правило:
Если в логарифмическом уравнении присутствуют десятичные дроби, обязательно переведите эти дроби из десятичной записи в обычную. Такое преобразование может существенно упростить решение.
Подобный переход нужно выполнять сразу, еще до выполнения каких-либо действий и преобразований. Давайте посмотрим:
Что нам дает такая запись? Мы можем 1/2 и 1/8 представить как степень с отрицательным показателем:
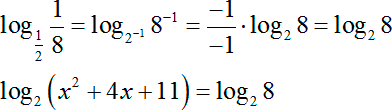
Перед нами каноническая форма. Приравниваем аргументы и получаем классическое квадратное уравнение:
x 2 + 4 x + 11 = 8
Перед нами приведенное квадратное уравнение, которое легко решается с помощью формул Виета. Подобные выкладки в старших классах вы должны видеть буквально устно:
Вот и все! Исходное логарифмическое уравнение решено. Мы получили два корня.
Напомню, что определять область определения в данном случае не требуется, поскольку функция с переменной х присутствует лишь в одном аргументе. Поэтому область определения выполняется автоматически.
Итак, первое уравнение решено. Переходим ко второму:
log0,5 (5 x 2 + 9 x + 2) = log3 1/9
Как и в прошлый раз, рекомендую избавиться от десятичных дробей:
log1/2 (5 x 2 + 9 x + 2) = log3 9 −1
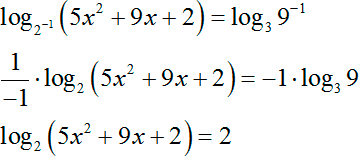
И вот сейчас мы выполнили очень важный шаг в решении логарифмического уравнения. Возможно, кто-то что-то не заметил, поэтому давайте я поясню.
Взгляните на наше уравнение: и слева, и справа стоит знак log, но слева стоит логарифм по основанию 2, а справа стоит логарифм по основанию 3. Тройка не является целой степенью двойки и, наоборот: нельзя записать, что 2 — это 3 в целой степени.
Следовательно, это логарифмы с разными основаниями, которые не сводятся друг к другу простым вынесением степеней. Единственный путь решения таких задач — избавиться от одного из этих логарифмов. В данном случае, поскольку мы пока рассматриваем довольно простые задачи, логарифм справа просто сосчитался, и мы получили простейшее уравнение — именно такое, о котором мы говорили в самом начале сегодняшнего урока.
Давайте представим число 2, которое стоит справа в виде log2 2 2 = log2 4. А затем избавимся от знака логарифма, после чего у нас остается просто квадратное уравнение:
log2 (5 x 2 + 9 x + 2) = log2 4
5 x 2 + 9 x + 2 = 4
5 x 2 + 9 x − 2 = 0
Перед нами обычное квадратное уравнение, однако оно не является приведенным, потому что коэффициент при x 2 отличен от единицы. Следовательно, решать мы его будем с помощью дискриминанта:
D = 81 − 4 5 (−2) = 81 + 40 = 121
x 1 = (−9 + 11)/10 = 2/10 = 1/5
Вот и все! Мы нашли оба корня, а значит, получили решение исходного логарифмического уравнения. Ведь в исходной задачи функция с переменной х присутствует лишь в одном аргументе. Следовательно, никаких дополнительных проверок на область определения не требуется — оба корня, которые мы нашли, заведомо отвечают всем возможным ограничениям.
На этом можно было бы закончить сегодняшний видеоурок, но в заключении я хотел бы сказать еще раз: обязательно переводите все десятичные дроби в обычные при решении логарифмических уравнений. В большинстве случаев это существенно упрощает их решение.
Редко, очень редко попадаются задачи, в которых избавление от десятичных дробей лишь усложняет выкладки. Однако в таких уравнениях, как правило, изначально видно, что избавляться от десятичных дробей не надо.
В большинстве остальных случаев (особенно если вы только начинаете тренироваться в решении логарифмических уравнений) смело избавляйтесь от десятичных дробей и переводите их в обычные. Потому что практика показывает, что таким образом вы значительно упростите последующее решение и выкладки.
Тонкости и хитрости решения
Сегодня мы переходим к более сложным задачам и будем решать логарифмическое уравнение, в основании которого стоит не число, а функция.
И пусть даже эта функция линейна — в схему решения придется внести небольшие изменения, смысл которых сводится к дополнительным требованиям, накладываемым на область определения логарифма.
Сложные задачи
Этот урок будет довольно длинным. В нем мы разберем два довольно серьезных логарифмических уравнения, при решении которых многие ученики допускают ошибки. За свою практику работы репетитором по математике я постоянно сталкивался с двумя видами ошибок:
Это последний урок, посвященный логарифмическим уравнениям. Он будет длинным, мы разберем сложные логарифмические уравнения. Устраивайтесь поудобней, заварите себе чай, и мы начинаем.
Первое уравнение выглядит вполне стандартно:
Сразу заметим, что оба логарифма являются перевернутыми копиями друг друга. Вспоминаем замечательную формулу:
Однако у этой формулы есть ряд ограничений, которые возникают в том случае, если вместо чисел а и b стоят функции от переменной х:
Эти требования накладываются на основание логарифма. С другой стороны, в дроби от нас требуется 1 ≠ a > 0, поскольку не только переменная a стоит в аргументе логарифма ( следовательно, a > 0), но и сам логарифм находится в знаменателе дроби. Но log b 1 = 0, а знаменатель должен быть отличным от нуля, поэтому a ≠ 1.
Но вот беда: второе требование ( b ≠ 1) отсутствует в первом неравенстве, посвященном левому логарифму. Другими словами, при выполнении данного преобразования мы должны отдельно проверить, что аргумент b отличен от единицы!
Вот давайте и проверим. Применим нашу формулу:
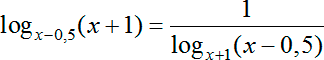
А теперь, прежде чем идти дальше, выпишем все требования области определения, накладываемые на исходную задачу:
1 ≠ х − 0,5 > 0; 1 ≠ х + 1 > 0
Вот мы и получили, что уже из исходного логарифмического уравнения следует, что и а, и b должны быть больше 0 и не равны 1. Значит, мы спокойно можем переворачивать логарифмическое уравнение:
Предлагаю ввести новую переменную:
В этом случае наша конструкция перепишется следующим образом:
Заметим, что в числителе у нас стоит разность квадратов. Раскрываем разность квадратов по формуле сокращенного умножения:
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Но в числителе стоит произведение, поэтому приравниваем к нулю каждый множитель:
Давайте приведем каждое из этих уравнений к канонической форме:
Избавляемся от знака логарифма в первом случае и приравниваем аргументы:
Такое уравнение не имеет корней, следовательно, первое логарифмическое уравнение также не имеет корней. А вот со вторым уравнением все намного интересней:
Решаем пропорцию — получим:
Напоминаю, что при решении логарифмических уравнений гораздо удобней приводить все десятичные дроби обычные, поэтому давайте перепишем наше уравнение следующим образом:
x 2 + x − 1/2 x − 1/2 − 1 = 0;
x 2 + 1/2 x − 3/2 = 0.
Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:
Получили два корня — они являются кандидатами на решение исходного логарифмического уравнения. Для того чтобы понять, какие корни действительно пойдут в ответ, давайте вернемся к исходной задаче. Сейчас мы проверим каждый из наших корней на предмет соответствия области определения:
1,5 ≠ х > 0,5; 0 ≠ х > −1.
Эти требования равносильны двойному неравенству:
Отсюда сразу видим, что корень х = −1,5 нас не устраивает, а вот х = 1 вполне устраивает. Поэтому х = 1 — окончательное решение логарифмического уравнения.
Переходим ко второй задаче:
На первый взгляд может показаться, что у всех логарифмов разные основания и разные аргументы. Что делать с такими конструкциями? В первую очередь заметим, что числа 25, 5 и 625 — это степени 5:
25 = 5 2 ; 625 = 5 4
А теперь воспользуемся замечательным свойством логарифма. Дело в том, что можно выносить степени из аргумента в виде множителей:
На данное преобразование также накладываются ограничения в том случае, когда на месте b стоит функция. Но у нас b — это просто число, и никаких дополнительных ограничений не возникает. Перепишем наше уравнение:
Получили уравнение с тремя слагаемыми, содержащими знак log. Причем аргументы всех трех логарифмов равны.
Самое время перевернуть логарифмы, чтобы привести их к одному основанию — 5. Поскольку в роли переменной b выступает константа, никаких изменений области определения не возникает. Просто переписываем:
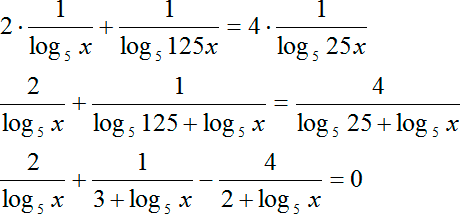
Как и предполагалось, в знаменателе «вылезли» одни и те же логарифмы. Предлагаю выполнить замену переменной:
В этом случае наше уравнение будет переписано следующим образом:
Выпишем числитель и раскроем скобки:
2 ( t + 3) ( t + 2) + t ( t + 2) − 4 t ( t + 3) = 2 ( t 2 + 5 t + 6) + t 2 + 2 t − 4 t 2 − 12 t = 2 t 2 + 10 t + 12 + t 2 + 2 t − 4 t 2 − 12 t = − t 2 + 12
Возвращаемся к нашей дроби. Числитель должен быть равен нулю:
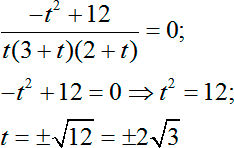
А знаменатель — отличен от нуля:
Последние требования выполняются автоматически, поскольку все они «завязаны» на целые числа, а все ответы — иррациональные.
Итак, дробно-рациональное уравнение решено, значения переменной t найдены. Возвращаемся к решению логарифмического уравнения и вспоминаем, что такое t :
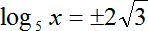
Приводим это уравнение к канонической форме, получим число с иррациональной степенью. Пусть это вас не смущает — даже такие аргументы можно приравнять:
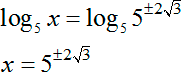
У нас получилось два корня. Точнее, два кандидата в ответы — проверим их на соответствие области определения. Поскольку в основании логарифма стоит переменная х, потребуем следующее:
С тем же успехом утверждаем, что х ≠ 1/125, иначе основание второго логарифма обратится в единицу. Наконец, х ≠ 1/25 для третьего логарифма.
Итого мы получили четыре ограничения:
1 ≠ х > 0; х ≠ 1/125; х ≠ 1/25
А теперь вопрос: удовлетворяют ли наши корни указанным требованиям? Конечно удовлетворяют! Потому что 5 в любой степени будет больше нуля, и требование х > 0 выполняется автоматически.
Итак, мы получили окончательный ответ. Ключевых моментов в данной задаче два:
В общем, при решении сложных логарифмических уравнений обязательно выписывайте исходную область определения. А у меня на сегодня все.:)
Алгебра
План урока:
Задание. Укажите корень логарифмического уравнения
Задание. Решите урав-ние
В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид
Задание. Найдите решение логарифмического уравнения
Задание. Решите урав-ние
Задание. Решите урав-ние
Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:
Уравнения вида logaf(x) = logag(x)
Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.
Задание. Решите урав-ние
Задание. Найдите корень урав-ния
Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид
С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.
Задание. Решите урав-ние
Получили квадратное уравнение, которое решаем с помощью дискриминанта:
Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:
Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:
Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log3 (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).
Уравнения, требующие предварительных преобразований
Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду logaf(x) = logag(x).
Задание. Решите урав-ние
с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:
Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:
Задание. Решите урав-ние
Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем
Задание. Решите урав-ние
Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log5 5. Тогда урав-ние можно преобразовать:
Задание. Решите урав-ние
Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что
Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что
Задание. Решите урав-ние
Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log25x 4 к основанию 5, используя известную нам формулу
Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:
Логарифмические уравнения с заменой переменных
Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.
Задание. Решите уравнение методом замены переменной
Задание. Найдите решение уравнения методом замены переменной
Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:
Логарифмирование уравнений
Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.
Задание. Укажите корни урав-ния
Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:
Возвращаемся от переменной t к переменной х:
Переход от логарифмических неравенств к нелогарифмическим
Рассмотрим график логарифмической функции у = logax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства
Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.
Задание. Найдите решение логарифмического неравенства
Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 logas:
Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 loga s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение
Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:
Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).
Решение логарифмических уравнений на ЕГЭ
Сегодня в этой статье мы с тобой обсудим, как решать простые логарифмические уравнения.
Для этого тебе понадобятся некоторые минимальные знания:
Обрати внимание: статья написана для учеников разного уровня подготовки, от ничего не знающих до суперпродвинутых.
Знаний, полученных в этой статье с лихвой хватит, чтобы решить любую задачу ЕГЭ по этой теме.
Логарифмические уравнения — коротко о главном
Определение логарифмических уравнений
Логарифмическое уравнение — уравнение, в котором неизвестные переменные находятся внутри логарифмов.
Простейшим логарифмическим уравнением является уравнение вида \( \displaystyle lo<
Процесс решения любого логарифмического уравнения сводится к приведению логарифмического уравнения к виду \( \displaystyle lo<
ОДЗ (Область допустимых значений) для логарифмического уравнения:
5 основных методов решения логарифмических уравнений:
1 метод. Использование определения логарифма:
2 метод. Использование свойств логарифма:
3 метод. Введение новой переменной (замена):
Замена \( \displaystyle lo<
t\)позволяетсвести логарифмическое уравнение к более простому алгебраическому уравнению относительно t.
4 метод. Переход к новому основанию:
5 метод. Логарифмирование:
Берется логарифм от правой и левой частей уравнения.
\( \displaystyle \left\< \begin
Что такое логарифмические уравнения
Это уравнения, в которых неизвестные переменные (ну мы такие жуткие случаи, когда переменных несколько, рассматривать не будем, для нас переменная всегда будет одна и называть мы ее будем «икс») находятся внутри логарифмов.
А вот уравнение \(\displaystyle 1+2x=lo<
Я думаю, тебе вполне ясно, почему?
Верно, все потому, что \(\displaystyle 2x\) не находится внутри никакого логарифма.
Такие уравнения называются смешанными и требуют индивидуального подхода.
Как же решать логарифмические уравнения?
3 основных способа решения логарифмических уравнений
На самом деле существует целая масса подходов: это и разложение на множители, и потенцирование, и замена, и работа с основаниями…
Но все методы решения логарифмических уравнения роднит одно: их цель свести логарифмические уравнения к простейшему виду:
а затем уже решать уравнение без логарифмов:
\( f\left( x \right)=g\left( x \right).\)
То есть правило такое:
Если уравнение сведено к такому, что слева и справа от знака «равно» стоят логарифмы с одним основанием, то логарифмы мы «зачеркиваем» и решаем оставшееся уравнение.
то после нахождения корней логарифмического уравнения, мы обязаны сделать проверку. Я не поленюсь и повторю еще раз:
В логарифмических уравнениях мы всегда делаем проверку получения корней.
Те учащиеся, которые игнорируют это требование, как правило допускают глупейшие и непростительные ошибки.
Cогласись, обидно решить правильно уравнение, а потом не сделать самую малость: проверку, и записать лишние корни, и записать из-за этого неправильный ответ!
Теперь давай потренируемся на решении простейших примеров (все примеры взяты из банка задач ЕГЭ), чтобы понять 6 основных способов решения логарифмических уравнений.
Примеры
Давай разбираться с каждым способом и примером по-отдельности.
Способ 1. Правило умножения на единицу
Пример №1
Слева у нас стоит выражение с логарифмом, а справа – нет.
Нужно сделать так, чтобы справа тоже было выражение с логарифмом по основанию \( \displaystyle 2\), а затем просто откинуть логарифмы.
Как этого добиться? Я люблю применять волшебное правило:
Правило умножения на единицу!
Вот в чем его соль: я умножу \( \displaystyle 7\) на \( \displaystyle 1\)
\( \displaystyle 7\cdot 1\)
Однако, мне же нужен логарифм! Что я знаю:
Мне же нужно основание \( \displaystyle 2\), поэтому я возьму \( \displaystyle a=2\), тогда
\( \displaystyle 7=7\cdot 1=7\cdot
Полдела сделано! Теперь мне нужно засунуть \( \displaystyle 7\) внутрь логарифма.
Это я сделаю, воспользовавшись следующим правилом:
Применительно к моей ситуации это даст:
Тогда мое исходное логарифмическое уравнение станет вот таким:
\( \displaystyle lo<
Ура! Избавляемся от логарифмов! Получим простейшее уравнение:
Но это еще не конец! Обещанная проверка:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Пример №2
Задача полностью аналогичная предыдущей: воспользуюсь правилом умножения на единицу для числа \( 2\):
Тогда исходное уравнение станет вот таким:
Делаем проверку:
Верно!
Пример №3
А здесь о нас с тобой уже заранее позаботились! Зачеркиваем логарифмы и получим:
Пример №4
Опять воспользуемся волшебным правилом!
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Способ 2. Правило «превращения единицы»
Разберем это правило на пятом примере логарифмического уравнения:
Пример № 5
Воспользуемся правилом «превращения единицы», которым мы уже пользовались в правиле «умножения на единицу»! Смотри как оно работает:
Тогда исходное уравнение станет вот таким:
Что дальше? Если ты видишь с одной стороны уравнения сумму (или разность, но лучше сумму!) логарифмов с одним основанием, то пользуйся вот такой формулой (тебе уже известной!)
Применительно к моей ситуации это даст:
Ну все, слева и справа у нас – логарифмы и ничего более. Убираем их.
\( 7-x=5\left( 3-x \right)\)
Кстати, а ты понял, откуда у нас взялся ноль справа? Ты асболютно прав:
Способ 3. Использование свойств логарифма
Пример № 6
Здесь у нас есть два возможных пути:
Первый – это как всегда правило умножения на единицу (ты можешь попытаться его проделать самостоятельно, ты ведь знаешь, как решать показательные уравнения?),
Второй – воспользоваться одним из свойств логарифма:
Но читать я ее буду справа налево:
Теперь разберемся с числом
Здесь нам понадобится еще одно хорошо известное тебе свойство:
Что она даст в нашем случае? Так как \( \displaystyle 8=<<2>^<3>>\), то
Тогда левая часть уравнения примет вид:
\( \displaystyle \frac<1><3>\cdot \left( 8
\( \displaystyle 8
Ну что же, во всех предыдущих примерах, так уж выходило (абсолютно случайно, кстати), что логарифмические уравнения имели корни, притом единственные, и все они нам подходили.
Так бывает далеко не всегда, увы! Но прежде чем я приведу тебе соответствующие примеры, я еще раз хочу напомнить тебе, какие формулы очень нужны для решения логарифмических уравнений:
6 главных формул необходимых для решения логарифмических уравнений:
Не так уж и много, правда?
Но тем не менее, эти формулы нам ЖИЗНЕННО НЕОБХОДИМЫ! Без них мы не сможем решить даже простейший пример.
Ну а далее обещанные примеры, где все не очень хорошо с корнями!
А теперь разбираем!
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Я надеюсь, что только что приведенные примеры навсегда отучат тебя пропускать проверку при решении логарифмических уравнений. Она необходима!
Логарифмическое уравнение с переменным основанием
Теперь я бы хотел рассмотреть с тобой еще один (чуть более сложный) вид логарифмических уравнений. Это будут уравнения с переменным основанием.
До этого же мы рассматривали только случаи, когда основания были постоянными: \( \displaystyle 2,3,10\) и т. д. Но ничто не мешает им быть некоторыми функциями от \( \displaystyle x\), например \( \displaystyle 2x+1,
Но не стоит пугаться!
Если при решении логарифмических неравенств переменное основание доставляет довольно много неудобств, то на сложности решения уравнения это практически никак не сказывается.
Пример №1
Действуем как и раньше: применяем метод «умножь на единицу» к числу \( \displaystyle 2\):
Тогда исходное уравнение преобразуется к виду:
Применю формулу разности квадратов:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
Как видишь, в случае уравнений нет никакой принципиальной разницы, переменные у нас основания или нет. В этом плане можно сказать, что решить логарифмическое уравнение как правило намного проще, чем решить логарифмическое неравенство!
Давай теперь попробуем решить еще вот такой «странный» пример.
Пример №2
Будем действовать как всегда – превратим правую часть в логарифм, вот такой хитрый:
Тогда исходное логарифмическое уравнение будет равносильно вот такому уравнению (правда снова логарифмическому):
Данное уравнение я буду решать снова по разности квадратов:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Я намеренно привел достаточно сложный пример, чтобы показать тебе, что не стоит пугаться больших и страшных логарифмов: достаточно знать несколько формул (которые я уже привел тебе выше) и из любой (практически) ситуации можно найти выход.
Ну вот, я привел тебе основные методы решения логарифмических уравнений (методы «без изысков»), которые позволят тебе справиться с большинством примеров ( в первую очередь на ЕГЭ). Теперь пришло твое время показать, чему ты научился. Попробуй самостоятельно решить следующие логарифмические уравнения, а затем мы с тобой сверим результат.
А теперь попробуй порешать логарифмические уравнения самостоятельно:
Разбор 7 примеров решения логарифмических уравнений
Рассмотренные в этой работы приемы, конечно, не исчерпывают всевозможные способы решения логарифмических уравнений. В некоторых случаях нам нужно очень «извернуться», чтобы придумать способ найти корни у каверзного уравнения.
Однако, каким бы сложным не было начальное уравнение, в результате оно сведется к уравнению того вида, которые мы с тобой только что научились решать!
Ответы на примеры для самостоятельной работы
Достаточно простая задачка. Воспользуемся свойством:
Тогда мы получим:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
2. \( \displaystyle \lg \left( <
Тоже ничего сверхъестественного: неохота мне делить, поэтому я перенесу слагаемое с «минусом» вправо: теперь слева и справа у меня стоят десятичные логарифмы, и я от них избавляюсь:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Здесь нужно немного поработать: ясно, что \( \displaystyle 25=<<5>^<2>>,
\frac<1><5>=<<5>^<-1>>\), снова воспользуюсь (не правда ли очень полезной?) формулой:
Что мне нужно сделать, прежде чем применить формулу сложения логарифмов?
Да, мне нужно избавиться от множителя \( \displaystyle 1.5\). Есть два пути: первый – в лоб занести его в логарифм по формуле:
В принципе, этот метод имеет право на существование, но что в нем плохо? Плохо иметь дело с выражением вида \( \displaystyle <
Так что можно сделать еще? Как можно избавиться от такой «нецелости»?
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Как и в предыдущем примере перепишем
Я опять не хочу никаких вычитаний ( и последующих делений) и поэтому перенесу полученное выражение вправо:
Теперь убираю логарифмы слева и справа:
Мы получили иррациональное уравнение, которое, как я надеюсь, ты уже умеешь решать. Я лишь напомню, что мы возводим обе стороны в квадрат:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
5. \( \displaystyle lo<
Все прозрачно: применяем формулу суммы логарифмов слева:
Тогда убираем логарифмы с двух сторон:
Ответ: \( \displaystyle x=7\);
6. \( \displaystyle lo<
Все проще некуда: уравнение уже приведено к простейшему виду. Нам осталось только приравнять
Опять воспользуемся формулой разности квадратов. Она позволяет при решении уравнений вида \( \displaystyle a<
^<2>>=b
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
7. \( \displaystyle lo<
Этот пример я оставил нам на десерт. Хотя в нем тоже нет ничего очень уж сложного.
Ноль представим как
Тогда мы с тобой получим вот такое логарифмическое уравнение:
И мы снимаем первую «шкурку» — внешние логарифмы.
Единицу представим как
Тогда наше уравнение примет вид:
Теперь мы снимаем «вторую шкурку» и добираемся до сердцевины:
Ответ: \( \displaystyle x=4\).
Четыре продвинутых метода решения логарифмических уравнений
Теперь, после ознакомления с логарифмическими уравнениями, ты овладел необходимым минимумом знаний, необходимых для решения простейших примеров.
Теперь я могу перейти к разбору четырех продвинутых методов решения логарифмических уравнений:
Метод введения новой переменной (или замены) – один из наиболее часто употребляемых на практике. Им решается большинство «трудных» задач, связанных с решением логарифмических (и не только) уравнений.
Метод логарифмирования служит для решения смешанных показательно-логарифмических уравнений, в конечном счете сводя задачу к выбору хорошей замены переменной ( то есть к первому методу).
Метод перехода к новому основанию пригоден для решения некоторых уравнений, в которых встречаются логарифмы с разными основаниями.
Мини-максный метод применяется для решения уравнений, которые не могут быть решены методом логарифмирования обеих частей.
Метод введения новой переменной
Я начну с рассмотрения первого метода. Как ты уже понял из названия, суть этого метода – ввести такую замену переменной, что твое логарифмическое уравнение чудесным образом преобразится в такое, которое ты уже с легкостью можешь решить.
Все что тебе останется после решения этого самого «упрощенного уравнения» — это сделать «обратную замену» : то есть вернуться от замененного к заменяемому. Давай проиллюстрируем только что сказанное на очень простом примере:
В этом примере замена прямо напрашивается сама собой! Ведь ясно, что если мы заменим \( \displaystyle lgx\) на \( \displaystyle t\), то наше логарифмическое уравнение превратится в рациональное:
Его ты без проблем решишь, сведя к квадратному:
\( \displaystyle \left( 2+t \right)+2\left( 4-t \right)=\left( 4-t \right)\left( 2+t \right)\)
Упрощая полученное выражение, мы окончательно получим:
Теперь делаем обратную замену: \( \displaystyle t=lgx\), тогда из \( \displaystyle 1=lgx\) следует, что \( \displaystyle x=10\), а из \( \displaystyle 2=lgx\) получим \( \displaystyle x=100\)
Теперь, как и раньше, пришла очередь проверки:
Пусть вначале \( \displaystyle x=10\), так как \( \displaystyle \lg 10=1\), то \( \displaystyle \frac<1><4-1>+\frac<2><2+1>=\frac<1><3>+\frac<2><3>=1\), верно!
Теперь \( \displaystyle x=100,\lg 100=2\), тогда \( \displaystyle \frac<1><4-2>+\frac<2><2+2>=\frac<1><2>+\frac<2><4>=1\), все верно!
Таким образом, числа \( \displaystyle 10\) и \( \displaystyle 100\) являются корнями нашего исходного уравнения.
Ответ: \( \displaystyle 10,100\).
Вот еще один пример с очевидной заменой:
1. \( \displaystyle 3\log _<2>^<2>x-7<<\log >_<2>>x+2=0\)
В самом деле, сразу же давай заменим
Тогда наше исходное логарифмическое уравнение превратится в квадратное:
Проверку проведи самостоятельно, убедись, что в данном случае оба найденных нами числа являются корнями.
Мне кажется, что основную идею ты уловил. Она не нова и распространяется не только на логарифмические уравнения.
Другое дело, что иногда довольно сложно сразу «увидеть» замену. Здесь требуется некоторый опыт, который придет к тебе после некоторых усилий с твоей стороны.
А пока что потренируйся в решении следующих примеров:
Готов? Давай проверим, что у тебя получилось:
Вначале решим второй пример.
Он как раз демонстрирует тебе, что не всегда замену удается сделать, что говорится, «в лоб». Прежде нам нужно немного преобразовать наше уравнение: применить формулу разности логарифмов в числителе первой дроби, и вынести степень в числителе второй.
Сделав это, ты получишь:
Теперь замена стала очевидной, не так ли?
Давай сделаем ее: \( \displaystyle t=lo<
при \( \displaystyle t\ne 1,t\ne 0.\)
Решив последнее уравнение, ты найдешь его корни:
Самостоятельно сделай проверку и удостоверься в том, что \( \displaystyle <
Теперь давай попробуем решить третье уравнение
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Метод перехода к новому основанию
Давай рассмотрим следующее уравнение:
Что мы видим? Два логарифма будто бы «противоположны» друг другу. Что нужно делать? Все легко: нам достаточно прибегнуть к одной из двух формул:
В принципе, мне ничего не мешает воспользоваться любой из этих двух формул, но из-за структуры уравнения, мне удобнее будет применить первую: я избавлюсь от переменного основания логарифма во втором слагаемом, заменив его на \( \displaystyle \frac<1><<<\log >_<5>>x>\).
Теперь легко заметить, что задача свелась к предыдущей: к выбору замены. Заменив \( \displaystyle t=<<\log >_<5>>x\), я получу следующее уравнение:
(при \( \displaystyle t\ne 0\))
Отсюда \( \displaystyle <
Вот еще один пример, в котором разумно будет перейти к новому основанию:
Однако, как ты можешь легко проверить, если мы с тобой перейдем к новому основанию сразу, это не даст должного эффекта. Что нам нужно сделать в этом случае?
А давай все упростим донельзя, а дальше будь что будет.
Вот, что я хочу сделать: представить \( \displaystyle 16\), как \( \displaystyle <<2>^<4>>\), \( \displaystyle 64\) как \( \displaystyle <<2>^<6>>\), вынести эти степени перед логарифмами, а также вынести квадрат у икса в первом логарифме. Дальше уже посмотрим.
\( \displaystyle 4\cdot \left( 0.5 \right)\cdot <<\log >_
Что делать дальше?
Есть негласное правило: делай основание логарифма как можно проще!
Запомни, с основанием бывает намного сложнее подружиться, чем с выражением, стоящим под знаком логарифма!
Следуя этому правилу, я заменю \( \displaystyle \log_
Ну а дальнейшие шаги тебе уже знакомы. Заменяй и ищи корни!
В результате ты отыщешь два корня исходного уравнения: \( \displaystyle <
Пришла пора тебе показать, чему ты научился! Постарайся вначале самостоятельно решить следующие (не самые легкие) примеры:
1. Здесь все достаточно стандартно: я буду стараться свести мое исходное уравнение к такому, чтобы была удобна замена \( \displaystyle t=<<\log >_<2>>x\).
Что мне для этого потребуется? Во-первых, преобразовать первое выражение слева (вынести четвертую степень двойки перед логарифмом) и вынести степень двойки из основания второго логарифма. Тогда я получу:
Осталось всего ничего: «перевернуть» первый логарифм!
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
2. Здесь я тоже буду стараться «подогнать» мое уравнение под приемлемую замену. Какую же? Пожалуй, мне подойдет \( \displaystyle t=<<\log >_<5>>x\).
Так давай не будем терять времени и приступим к преобразованиям!
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
3. Здесь сразу даже не совсем очевидно, что мы будем заменять. Есть одно золотое правило – не знаешь, что делать – делай то, что можно! Вот им я и воспользуюсь!
Теперь я «переверну» все логарифмы и применю к первому – формулу логарифма разности, а к двум последним – логарифм суммы:
Здесь я также пользовался тем, что \( \displaystyle <<\log >_
Ну вот, теперь нам можно применить подходящую замену:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Этот примерчик позаковырестее, однако, я постараюсь решить его вообще не прибегая к замене переменной!
Давай опять, будем делать, что можно: а можно для начала разложить логарифм слева по формуле для логарифма отношения, а также вынести двойку вперед у логарифма в скобках. В итоге у меня получится:
Что будем делать дальше? Непонятно. А что делать можно? Можно перенести \( \displaystyle <<\log >_
Ну а теперь та самая формула, которую мы уже применяли! Так как \( \displaystyle <<\log >_
\( \displaystyle <<\log >_
Как решать такие уравнения, ты уже знаешь. Корень находится без труда, и он равен \( \displaystyle 2\). Напоминаю тебе о проверке!
Ну вот, теперь ты, как я надеюсь, научился решать достаточно сложные задачи, которые « в лоб» не одолеешь! Но логарифмические уравнения бывают еще более коварными! Вот например такие:
Здесь уже, увы, предыдущий способ решения не даст ощутимых результатов. Как ты думаешь, почему? Да, никакой «обратности» логарифмов здесь уже не наблюдается. Этот наиболее общий случай, конечно, тоже поддается решению, но мы уже применяем вот такую формулу:
Уж этой формуле все равно, имеется у вас «противоположность» или нет. Ты можешь спросить, а чему выбирать основание \( \displaystyle c\)? Мой ответ – это не имеет никакого значения. Ответ в итоге не будет зависеть от этого \( \displaystyle c\). Традиционно используют либо натуральный, либо десятичный логарифм. Хотя это и не принципиально. Я, например, буду применять десятичный:
\( \displaystyle lgx\left( \lg 2+\lg 3 \right)=\lg 2\lg 3\)
\( \displaystyle lgxlg6=\lg 2\lg 3\)
Отставлять ответ в таком виде – форменное безобразие! Давайте я вначале запишу по определению, что
Теперь пришло время воспользоваться: внутри скобок – основным логарифмическим тождеством, а снаружи (в степени) – превратить отношение в один логарифм: \( \displaystyle <<10>^<\lg 2>>=2,\frac<\lg 3><\lg 6>=<<\log >_<6>>3\), тогда окончательно получим вот такой «странный» ответ: \( \displaystyle x=<<2>^<<<\log >_<6>>3>>\).
Дальнейшие упрощения, увы, нам уже недоступны.
Давай сделаем проверку вместе:
Верно! Кстати, еще раз вспомни, из чего следует предпоследнее равенство в цепочке!
В принципе, решение этого примера тоже можно свести к переходу к логарифму по новому основанию, только тебя должно уже пугать то, что получится в итоге. Давай попробуем поступить разумнее: как можно лучше преобразуем левую часть.
+23x+21=\left( 3x+7 \right)\left( 2x+3 \right)\)
Кстати, а как по-твоему я получил последнее разложение? Верно, я применил теорему о разложении квадратного трехчлена на множители, а именно:
Если \( \displaystyle <
Ну вот, теперь я перепишу мое исходное уравнение вот в таком виде:
\left( 3x+7 \right)\left( 2x+3 \right)=4\)
\left( 3x+7 \right)=3\)
А вот решить такую задачу нам уже вполне по силам!
Так как \( \displaystyle <<\log >_<2x+3>>
\left( 2x+3 \right)\), то введем замену \( \displaystyle t=<<\log >_<3x+7>>
Тогда мое исходное уравнение примет вот такой простой вид: \( \displaystyle \frac<2>
Его корни равны: \( \displaystyle <
\left( 2x+3 \right)=1\), откуда \( \displaystyle 3x+7=2x+3,<
\left( 2x+3 \right)=2\), откуда \( \displaystyle <<\left( 3x+7 \right)>^<2>>=\left( 2x+3 \right)\) – данное уравнение корней не имеет.
Тебе осталось сделать проверку!
Следующее уравнение попробуй решить самостоятельно. Не торопись и будь внимателен, тогда удача будет на твоей стороне!
\( \displaystyle <<\log >_<5>>\left( 5+3x \right)=<<\log >_<5>>3\cdot <<\log >_<3>>\left( 2x+10 \right)\)
Готов? Давай посмотрим, что у нас получилось.
На самом деле, пример решается в два действия:
2. Теперь справа у меня стоит выражение \( \displaystyle \frac<<<\log >_<3>>\left( 2x+10 \right)><<<\log >_<3>>5>\), которое равно \( \displaystyle <<\log >_<5>>\left( 2x+10 \right)\)
Таким образом, исходное уравнение свелось к простейшему:
\left( 5+3x \right)=<<\log >_<5>>\left( 2x+10 \right)\)
Проверка говорит о том, что данное число в самом деле является корнем уравнения.
Метод логарифмирования (для решения смешанных уравнений)
Ну и напоследок я очень кратко остановлюсь на методах решения некоторых смешанных уравнений. Само собой, я не берусь охватить все смешанные уравнения, а покажу приемы решения самых простых.
Такое уравнение может быть решено методом логарифмирования. Все, что тебе нужно сделать, это взять логарифм от обеих частей. Ясно, что поскольку у нас уже есть логарифм по основанию \( \displaystyle 3\), то логарифмировать я буду по тому же основанию:
Теперь я вынесу степень из выражения слева:
И разложу выражение на множители по формуле разности квадратов:
Проверка как всегда на твоей совести.
Последний пример данной статьи попробуй решить самостоятельно!
Проверяем: берем логарифм по основанию \( \displaystyle 10\) от обеих частей уравнения:
Выношу степень слева и раскалываю по формуле суммы справа:
Замена \( \displaystyle t=lgx\)
Угадываем один из корней: \( \displaystyle <
\( \displaystyle 2<
Проверку проведи, по-возможности, сам (хотя в данном случае, особенно с последними двумя корнями, она будет непростой).
Мини-максный метод решения смешанных уравнений (для суперпродвинутых)
В дополнение к уже изложенному материалу, я предлагаю нам с тобой рассмотреть еще один способ решения смешанных уравнений, содержащих логарифмы.
Однако здесь я буду рассматривать такие уравнения, которые не могут быть решены рассмотренным ранее методом логарифмирования обеих частей. Данный способ имеет название мини-максного.
Данный метод применим не только при решении смешанных уравнений, но также оказывается полезным при решении некоторых неравенств.
Итак, вначале введем следующие основные определения, которые необходимы для применения мини-максного метода.
Определение 1:
\( \displaystyle f(x)\) монотонно возрастает на\( \displaystyle [a,b]\), если для любых \( \displaystyle <
_<1>>,< _<2>>\) из этого промежутка из того, что \( \displaystyle < _<1>> < _<2>>\) следует, что \( \displaystyle f(< _<1>>)>f(< _<2>>).\)
Определение 2:
\( \displaystyle f(x)\) монотонно убывает на\( \displaystyle [a,b]\), если для любых \( \displaystyle <
_<1>>,
<
Функция на рисунке слева – монотонно возрастающая, а справа – монотонно убывающая. Теперь обратимся к логарифмической функции \( \displaystyle f(x)=lo<
На рисунке приведены примеры монотонно возрастающей и монотонно убывающей логарифмической функции.
Опишем непосредственно сам мини-максный метод
Я думаю, что ты понимаешь, от каких слов произошло такое название? Верно, от слов минимум и максимум. Кратко метод можно представить в виде:
\( \displaystyle \left\< \begin
Наша самая главная цель – это найти вот эту самую константу \( \displaystyle A\), чтобы далее свести уравнение к двум более простым. Для этого могут быть полезны свойства монотонности логарифмической функции, сформулированные выше.
Теперь давай рассмотрим конкретные примеры:
С другой стороны, по определению корня:
Таким образом, константа \( \displaystyle A\) найдена и равна \( \displaystyle 0\). Тогда исходное уравнение равносильно системе:
Первое уравнение имеет корни \( \displaystyle <
Таким образом, общий корень равен \( \displaystyle 2\), и данный корень будет корнем исходного уравнения. На всякий случай сделай проверку, чтобы убедиться в этом.
Ответ: \( \displaystyle 2\)
2. \( \displaystyle <<\left( 4<
Давай сразу задумаемся, что здесь написано? Я имею в виду общую структуру. Здесь сказано, что сумма двух квадратов равна нулю. Когда это возможно? Только тогда, когда оба этих числа по отдельности равны нулю. Тогда перейдем к следующей системе:
Общих корней у первого и второго уравнений нет, тогда и исходное уравнение корней не имеет.
Ответ: нет решений.
Давай вначале рассмотрим правую часть – она попроще. По определению синуса:
Теперь вернемся к левой части: рассмотрим выражение, стоящее под знаком логарифма:
Попытка найти корни у уравнения \( \displaystyle <
Так как \( \displaystyle y=<<\log >_<3>>t\) – функция возрастающая, то из \( \displaystyle <<\left( x+3 \right)>^<2>>+9\ge 9\) cледует, что \( \displaystyle <<\log >_<3>>\left( <<\left( x+3 \right)>^<2>>+9 \right)\ge <<\log >_<3>>9=2\).
Тогда наше исходное уравнение равносильно следующей системе:
Я не знаю, знаком ты или нет с решением тригонометрических уравнений, поэтому я сделаю так: решу первое уравнение (оно имеет максимум два корня), а потом результат подставлю во второе:
\( \displaystyle <
Теперь я подставлю его во второе уравнение:
Ответ: \( \displaystyle x=-3\)
Ну как, теперь тебе стала ясна техника применения мини-максного метода? Тогда постарайся решить следующий пример самостоятельно.
\( \displaystyle 1+\left| <<\log >_<4>>\left( 9<
Готов? Давай проверим:
Левая часть – сумма двух неотрицательных величин (единицы и модуля) а потому, левая часть не меньше единицы, причем она равна единице только тогда, когда
\( \displaystyle \left| <<\log >_<4>>\left( 9<
В то же время правая часть – это модуль (значит, больше нуля) произведения двух косинусов (значит не более единицы), тогда:
\( \displaystyle \left| <<\log >_<4>>\left( 9<
Тогда исходное уравнение равносильно системе:
\( \displaystyle \left\< \begin
Я опять предлагаю решить первое уравнение и результат подставить во второе:
Данное уравнение корней не имеет.
Тогда исходное уравнение также не имеет корней.
Ответ: решений нет.
Бонус: Подборка из 6 вебинаров по решению задачи ЕГЭ №13
И если ты воспринимаешь информацию визуально, посмотри подборку из 6 вебинаров по решению задачи ЕГЭ №13 — там также попадаются логарифмические уравнения и даже смешанные.
Вот в качестве примера один из них:
Очень сложная смешанная задача (тригонометрическая, показательная, логарифмическая)
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий курсов
Добавить комментарий Отменить ответ
8 комментариев
Если под корнем сумма числа и корня (a+b^0,5)^0,5 и разность квадратов является полным квадратом, то можно разложить на сумму двух корней по формуле Эйлера. а^2 —b = n. [(a + n)/2]^0,5 + [(a — n)/2]^0,5. В примере будет 25 —24 = 1 =1^2. Следовательно, выражение под корнем можно превратить в квадрат суммы (разности). Получим по формуле Эйлера.
[(5 + 1)/2]^0,5 + [(5 — 1)/2]^0,5 = 3^0,5 + 2^0,5 и то же, но с минусом. У Вас всё верно, но мне не понравился логарифм с экзотическим основанием. Достаточно десятичных. Получим sinx = плюс, минус lg3 : lg[3^0,5 +2^0,5].
x =(73,43; —73,43; 106,57; —106,57) градусов. Первый ответ надо отбросить.
Здраствуйте, во втором примере мини-максного метода логарифм по основанию 5 равняется нулю, не значит ли, что аргумент необходимо приравнивать к 1, а не 0?
Здравствуйте, хороший материал, но есть и такие уравнения 8=5lg(6*100/x)
Спасибо большое за Вашу работу.
Спасибо, Нина! Очень приятно слышать!
Спасибо Вам и низкий поклон за грамотную и, что немаловажно, в доступной форме подачу относительно сложного материала. Приятно встречать на просторах интернета умных людей!
Василий, спасибо огромное за теплые слова. Очень приятно слышать.
Некоторые комментарии прошлых лет к этой статье:
Ольга
04 апреля 2018
Спасибо, очень понравилось объяснение. Опечатка только в первом примере, вместо корня результат проверки в ответе указан.
Александр (админ)
04 апреля 2018
Спасибо за наблюдательность, Ольга! Да, действительно, опечатка. Поправили.
Александр (админ)
04 апреля 2018
И за теплые слова тоже спасибо! )
Антон
11 апреля 2018
Спасибо огромное, вы меня прям спасли!
Александр (админ)
11 апреля 2018
Скорая помощь на марше! 🙂 Пожалуйста, Антон. Мы рады, что тебе понравилось. Оказывается математика может быть простой, правда? )
Люба
01 мая 2018
Спасибо огромное, за очень простое и понятное объяснение
Александр (админ)
01 мая 2018
Пожалуйста, Люба. Держи в курсе как пройдет экзамен. Можно прямо здесь написать помог тебе наш сайт или нет к нему подготовиться )
Сергей
07 мая 2018
Спасибо вашему сайту. Добавил в закладки. По поводу 7-го примера для самостоятельного решения. Мне кажется, вы забыли дописать квадрат над «х»
Александр (админ)
12 мая 2018
Спасибо, Сергей за внимательность! Проверим обязательно.
Александр
12 мая 2018
в объяснении 5 примера есть опечатка, там стоит 3 — х, а должно быть 7 — х. А так спасибо вам)
Александр (админ)
12 мая 2018
И вам спасибо, Александр! Опечатку устраним. Будем рады, если вы найдете еще. ))
Кирилл
09 января 2019
Александр, спасибо большое за хорошее, подробное и понятное объяснение! Очень приятно осознавать, что есть такие доброжелательные люди)
Александр (админ)
09 января 2019
Пожалуйста, Кирилл. Очень приятно слышать. За объяснение надо благодарить нашего репетитора Алексея Шевчука. Это он их писал. Но я ему передам. )
Марина Варновская
23 января 2019
Большое спасибо! Все очень толково. Хотелось бы еще скачать материал.
Александр (админ)
23 января 2019
Спасибо, Марина. По поводу возможности скачивания — пока не получается. Сейчас весь учебник сделан так, что скачать текст и скопировать невозможно. Нужно либо делать сканы всего текста и выкладывать их на скачивание, либо делать текст и отдельные картинки. И то и другое — большие трудозатраты и деньги. Пока мы этого сделать не можем. Но мы думаем над этим.
Рашид
25 января 2019
Спасибо вам большое за этот проект!) Все очень понятно и доходчиво изложено, а то что все изученное можно закрепить примерами, так это вообще отдельный плюс) Обязательно куплю полную версию и посоветую друзьям 🙂
Александр (админ)
25 января 2019
И тебе спасибо, Рашид. Очень рады, что понравилось!
Виктор
27 января 2019
Спасибо большое за столь подробный разбор примеров. Но ни в одном не нашел случая, чтобы решить данное уравнение: log7log4(x-2)=0, с виду оно кажется в миллион раз проще, чем те, которые я уже решал. Но с ним у меня есть некие трудности. Не могли бы Вы мне, как решаются такие примеры? Как довести его до обычного простого уравнения, где нужно только убрать логарифмы и решить. Заранее спасибо!
Алексей Шевчук
04 февраля 2019
Виктор, сделай замену log4(x-2) = y, тогда задача сведётся к двум простым логарифмическим уравнениям.
Александр (админ)
31 января 2019
И тебе спасибо, Даагмар!
Алия
13 февраля 2019
Здравствуйте. Мне непонятен один момент во втором уравнении метода Мини-максный. Почему больше или равно 9, а не нулю?
Алексей Шевчук
13 февраля 2019
Алия, там больше или равно 9, потому что первая скобка в квадрате, и она точно не отрицательна. Потом мы сравниваем логарифм от этого выражения с логарифмом от 9.
Галина
27 июля 2019
Спасибо, за статью.
Александр (админ)
28 июля 2019
Пожалуйста, Галина! Рады, что понравилось!
Океан
30 октября 2019
Спасибо вам, уже пару раз пользуюсь вашим сайтом, он просто превосходный, помогает на контрольный работах. Спасибо вам большое
Александр (админ)
30 октября 2019
Рад слышать, Океан, что сайт помогает на контрольных. Желаю вам подготовиться с помощью наших сайтов youclever.org и 100gia.ru ко всем экзаменам! 🙂
Star
09 апреля 2020
Спасибо Вам огромное.
Александр (админ)
09 апреля 2020
Пожалуйста, Star, заходите еще и удачи на экзаменах!
admin
28 апреля 2020
spasibckii
Александр (админ)
28 апреля 2020
Пожалуйста 🙂
Виталий Торопов
24 мая 2020
Проверку делать не обязательно, можно воспользоваться ОДЗ.
Алексей Шевчук
05 июня 2020
Виталий, конечно. Либо проверка, либо ОДЗ.
Асад
24 июня 2020
Спасибо большое, очень понятно и внятно объяснили. Лучше чем многие видео на ютубе.
Александр (админ)
24 июня 2020
Спасибо, Асад! Очень приятно слышать такое сравнение )