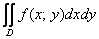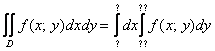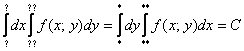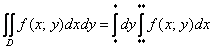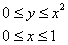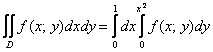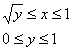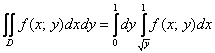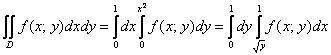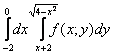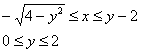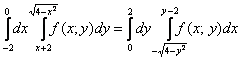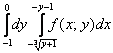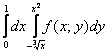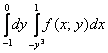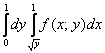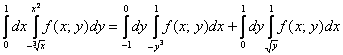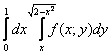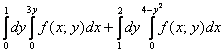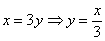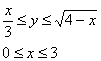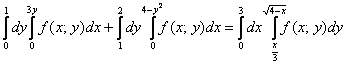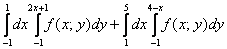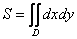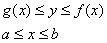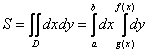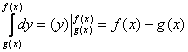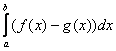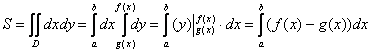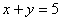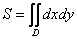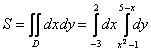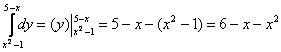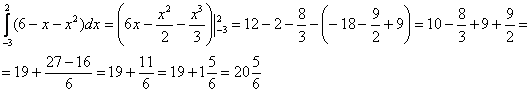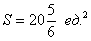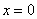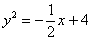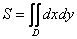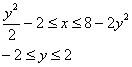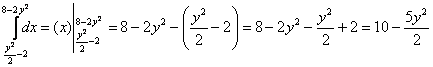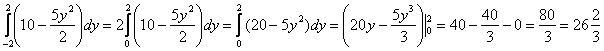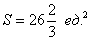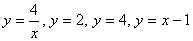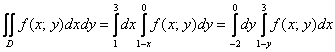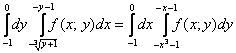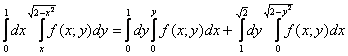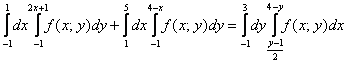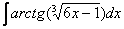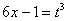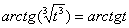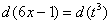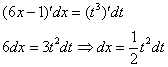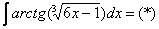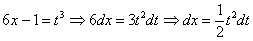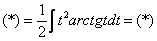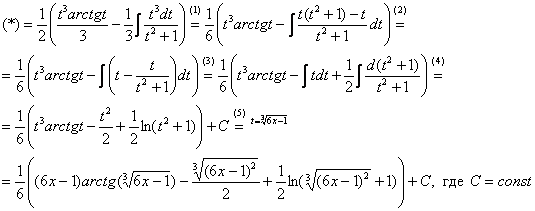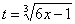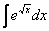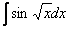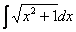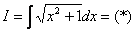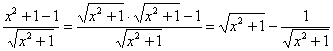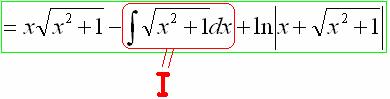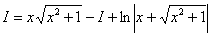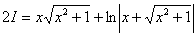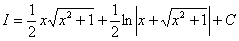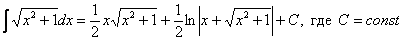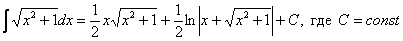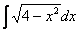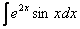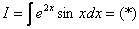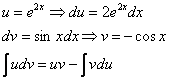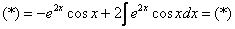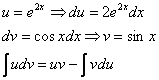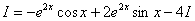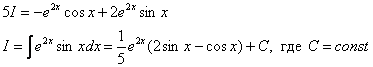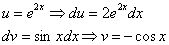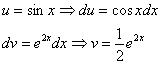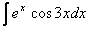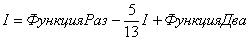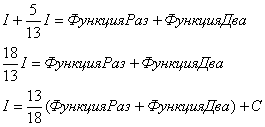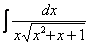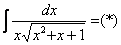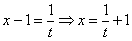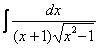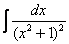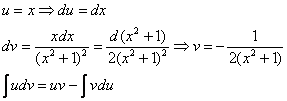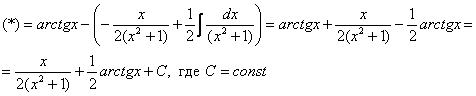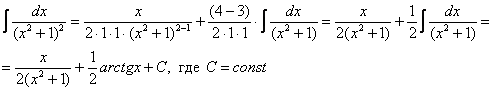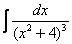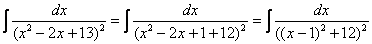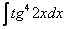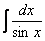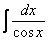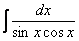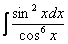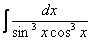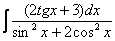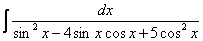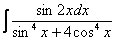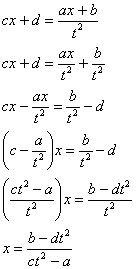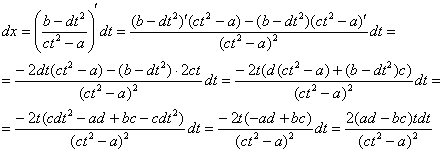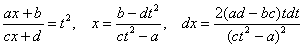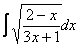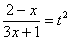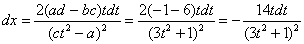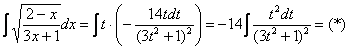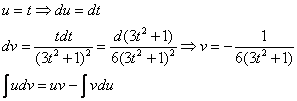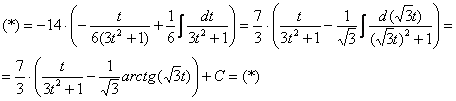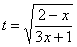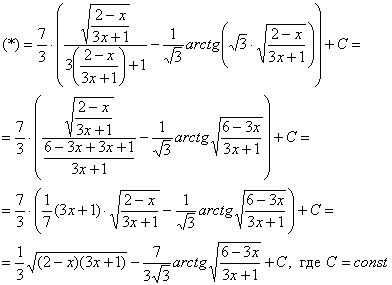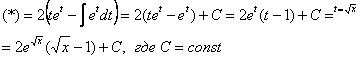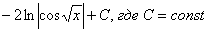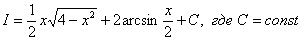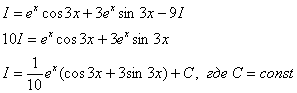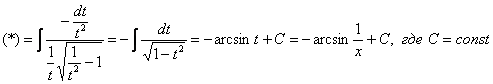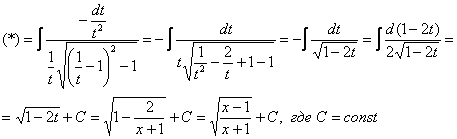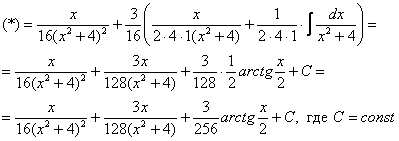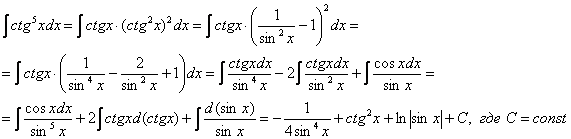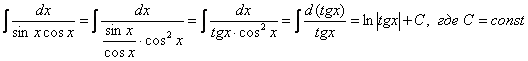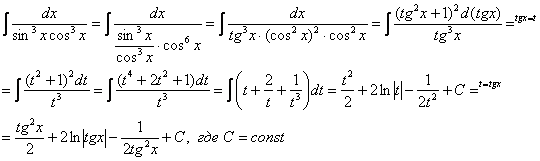Как считать интегралы
Как считать интегралы
Двойные интегралы для чайников
Данный урок открывает обширную тему кратных интегралов, с которыми студенты обычно сталкиваются на втором курсе. Двойными и тройными интегралами можно запугать обывателя не хуже, чем дифференциальными уравнениями, поэтому сразу же разберёмся с вопросом: сложно или нет? Конечно, некоторым будет сложно, и, если честно, я немного слукавил с названием статьи – для того, чтобы научиться решать двойные интегралы, необходимо обладать некоторыми навыками. Во-первых, если речь идёт об интегралах, то, очевидно, придётся интегрировать. Логично. Следовательно, для освоения примеров нужно уметь находить неопределённые интегралы и вычислять определённые интегралы хотя бы на среднем уровне. Хорошая новость состоит в том, что сами по себе интегралы в большинстве случаев достаточно просты.
Кому придётся туговато? Понятное дело. Тем, кто много пил пиво в течение первых семестров. Однако нормальных студентов тоже обнадёжу – на сайте есть все материалы, чтобы восполнить пробелы или недопонимание. Просто вам придётся потратить больше времени. Ссылки на темы, которые следует изучить или повторить, будут прилагаться по ходу статьи.
На вводном уроке поэтапно и подробно будут разобраны следующие базовые моменты:
– Понятие двойного интеграла
– Область интегрирования. Порядок обхода области интегрирования. Как изменить порядок обхода?
– Как вычислить площадь плоской фигуры с помощью двойного интеграла?
После того, как вы ХОРОШО поймёте все азы, можно будет перейти к статье Как вычислить двойной интеграл? Примеры решений. Кроме того, существует распространенная задача о вычислении двойного интеграла в полярных координатах и типовое приложение о нахождении центра тяжести плоской ограниченной фигуры.
Для желающих освоить тему в максимально сжатые сроки есть компактный pdf-курс Кратные и криволинейные интегралы (3-й семестр).
И мы немедленно приступаем. Начнём с насущного вопроса – что это такое?
Понятие двойного интеграла
Двойной интеграл в общем виде записывается следующим образом:
Разбираемся в терминах и обозначениях: 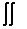
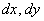
Что значит вычислить двойной интеграл?
Вычислить двойной интеграл – это значит найти ЧИСЛО. Самое обычное число: 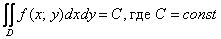
И крайне желательно найти его правильно =)
Результат (число 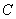
Многие помнят, что «обычный» определённый интеграл – тоже число. Здесь всё так же. У двойного интеграла существует и отличный геометрический смысл, но об этом позже, всему своё время.
Как вычислить двойной интеграл?
Для того чтобы вычислить двойной интеграл, его нужно свести к так называемым повторным интегралам. Сделать это можно двумя способами. Наиболее распространён следующий способ:
Вместо знаков вопроса необходимо расставить пределы интегрирования. Причём одиночные знаки вопроса 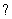
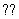
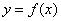
Откуда взять пределы интегрирования? Они зависят от того, какая в условии задачи дана область 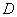
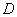
После того, как переход к повторным интегралам осуществлён, следуют непосредственно вычисления: сначала берётся внутренний интеграл 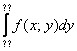
Грубо говоря, задача сводится к вычислению двух определённых интегралов. Как видите всё не так сложно и страшно, и если вы совладали с «обыкновенным» определённым интегралом, что мешает разобраться с двумя интегралами?!
Второй способ перехода к повторным интегралам встречается несколько реже: 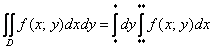
Что поменялось? Поменялся порядок интегрирования: теперь внутренний интеграл берётся по «икс», а внешний – по «игрек». Пределы интегрирования, обозначенные звёздочками – будут другими! Одиночные звёздочки внешнего интеграла – это числа, а двойные звёздочки внутреннего интеграла – это обратные функции 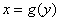
Какой бы мы ни выбрали способ перехода к повторным интегралам, окончательный ответ обязательно получится один и тот же:
Пожалуйста, запомните это важное свойство, которое можно использовать, в том числе, для проверки решения.
Алгоритм решения двойного интеграла:
Систематизируем информацию: в каком порядке нужно решать рассматриваемую задачу?
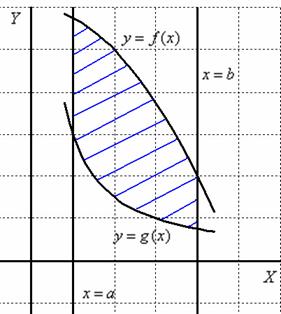
1) Выполнить чертёж. Без него решить задачу практически невозможо. За исключением каких-то совсем простых случаев и за исключением вундеркиндов, умеющих играть в шахматы «вслепую». На чертеже следует изобразить область 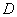
2) Расставить пределы интегрирования и перейти к повторным интегралам.
3) Взять внутренний интеграл
4) Взять внешний интеграл и получить ответ (число).
Область интегрирования. Порядок обхода области интегрирования.
Как изменить порядок обхода?
В данном параграфе мы рассмотрим важнейший вопрос – как перейти к повторным интегралам и правильно расставить пределы интегрирования. Как было сказано выше, сделать это можно так: 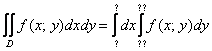
И так:
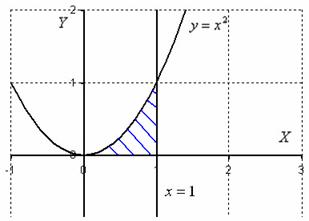
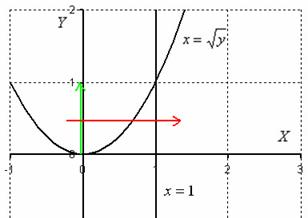
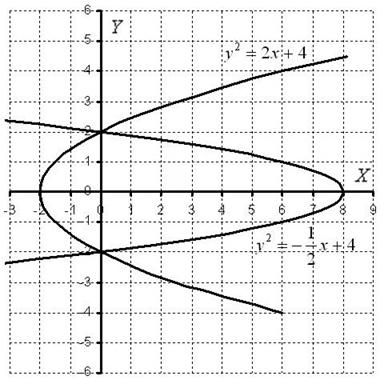
На практике эта вроде бы несложная задача вызывает наибольшие затруднения, и студенты часто путаются в расстановке пределов интегрирования. Рассмотрим конкретный пример:
Дан двойной интеграл 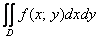
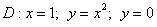
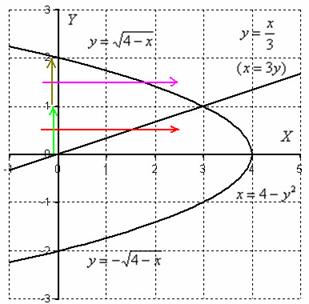
Решение: Изобразим область интегрирования на чертеже:
Обычная плоская фигура и ничего особенного.
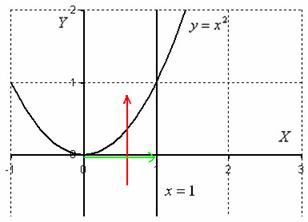
Теперь я выдам каждому из вас орудие труда – палку-копалку лазерную указку. Задача состоит в том, чтобы просканировать лучом лазера каждую точку заштрихованной области:
Луч лазера проходит область интегрирования строго снизу вверх, то есть указку вы ВСЕГДА держите ниже плоской фигуры. Луч входит в область через ось абсцисс, которая задаётся уравнением 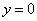
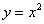
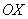
Итак, что получилось:
«игрек» изменяется от 0 до 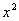
«икс» изменяется от 0 до 1.
В задачах вышесказанное записывают в виде неравенств:
Данные неравенства называют порядком обхода области интегрирования или просто порядком интегрирования
После того, как мы разобрались с порядком обхода, можно перейти от двойного интеграла к повторным интегралам:
Половина задачи решена. Теперь необходимо перейти к повторным интегралам вторым способом. Для этого следует найти обратные функции. Кто ознакомился со вторым параграфом урока Объем тела вращения, тому будет легче. Смотрим на функции, которыми задается область 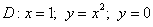
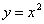
Если 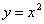
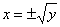
обратная функция 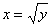
обратная функция 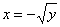
Нередко возникают сомнения, вот, к примеру, функция 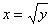
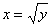
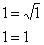
Получено верное равенство, значит, функция 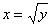
Более того, данную проверку (мысленно или на черновике) желательно проводить всегда, после того, как вы перешли к обратным функциям. Времени займет всего ничего, а от ошибки убережёт наверняка!
Обходим область интегрирования вторым способом:
Теперь лазерную указку держим слева от области интегрирования. Луч лазера проходит область строго слева направо. В данном случае он входит в область через ветвь параболы 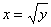
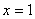
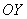
Таким образом:
«икс» изменяется от 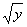
«игрек» изменяется от 0 до 1.
Порядок обхода области следует записать в виде неравенств:
И, следовательно, переход к повторным интегралам таков:
Ответ можно записать следующим образом:
Еще раз напоминаю, что окончательный результат вычислений не зависит от того, какой порядок обхода области мы выбрали (поэтому поставлен знак равенства). Но, до конечного результата ещё далеко, сейчас наша задача – лишь правильно расставить пределы интегрирования.
Дан двойной интеграл 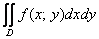
Это пример для самостоятельного решения. Грамотно постройте чертёж и строго соблюдайте направления обхода (откуда и куда светить лазерной указкой). Примерный образец чистового оформления в конце урока.
Чаще всего типовое задание встречается немного в другой формулировке:
Построить область интегрирования и изменить порядок интегрирования
Решение: По условию дан первый способ обхода области. Решение опять начинается с чертежа. Здесь область 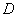
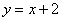
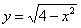
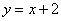
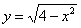
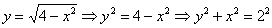
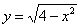
Смотрим на пределы внешнего интеграла: «икс» изменяется от –2 до 0.
Выполним чертёж: 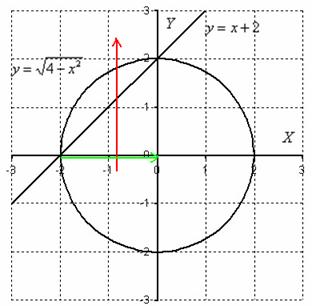
Для наглядности я указал стрелками первый способ обхода области, который соответствует повторным интегралам условия: 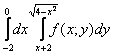
Теперь нужно изменить порядок обхода области, для этого перейдем к обратным функциям (выразим «иксы» через «игреки»): 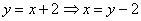
Недавно мы преобразовали функцию 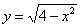
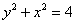
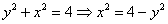
В результате получаем две обратные функции:
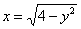
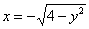
Опять же, если возникают сомнения, возьмите любую точку окружности и выясните, где лево, а где право.
Изменим порядок обхода области:
Согласно второму способу обхода, лазерный луч входит в область слева через левую полуокружность 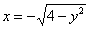
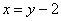
Таким образом, порядок обхода области:
В общем-то, можно записать ответ:
Построить область интегрирования и изменить порядок интегрирования
Это пример для самостоятельного решения. Пример не очень сложный, но обратите внимание, что порядок обхода изначально задан вторым способом! Что делать в подобных случаях? Во-первых, возникает трудность с чертежом, поскольку чертить график обратной функции наподобие 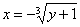
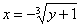
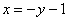
Анализируем исходные пределы интегрирования: входим слева в область через 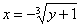
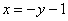
Похожий пример я еще разберу подробнее чуть позже.
Даже если вы всё отлично поняли, пожалуйста, не торопитесь переходить непосредственно к вычислениям двойного интеграла. Порядок обхода – вещь коварная, и очень важно немного набить руку на данной задаче, тем более, я еще не всё рассмотрел!
В предыдущих четырёх примерах область интегрирования находилась целиком в 1-й, 2-й, 3-й и 4-й координатных четвертях. Всегда ли это так? Нет, естественно.
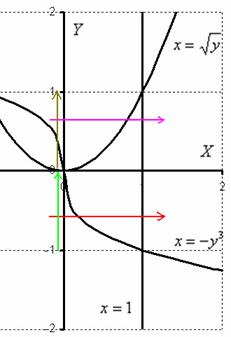
Изменить порядок интегрирования
Решение: Выполним чертёж, при этом, график функции 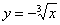
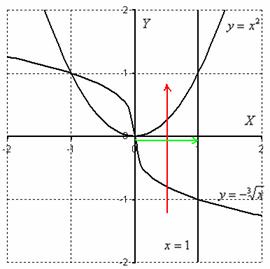
Порядок обхода области, который соответствует повторным интегралам 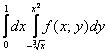
Перейдем к обратным функциям:
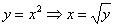
Изменим порядок обхода области. Как вы помните, при втором способе обхода, область нужно сканировать лазерным лучом слева направо. Но тут наблюдается интересная вещь:
Как поступать в подобных случаях? В таких случаях следует разделить область интегрирования на две части и для каждой из частей составить свои повторные интегралы:
1) Если «игрек» изменяется от –1 до 0 (зеленая стрелка), то луч входит в область через кубическую параболу 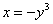
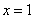
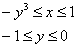
И соответствующие повторные интегралы:
2) Если «игрек» изменяется от 0 до 1 (коричневая стрелка), то луч входит в область через ветвь параболы 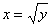
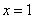
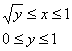
И соответствующие повторные интегралы:
У определенных и кратных интегралов есть весьма удобное свойство аддитивности, то есть, их можно сложить, что в данном случае и следует сделать:
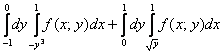
Ответ записываем так:
Какой порядок обхода выгоднее? Конечно тот, который был дан в условии задачи – вычислений будет в два раза меньше!
Изменить порядок интегрирования
Это пример для самостоятельного решения. В нём присутствуют полуокружности, разборки с которыми были подробно рассмотрены в Примере 3. Примерный образец оформления решения в конце урока.
А сейчас обещанная задача, когда изначально задан второй способ обхода области:
Изменить порядок интегрирования
Решение: Когда порядок обхода задан вторым способом, то перед построением чертежа целесообразно перейти к «обычным» функциям. В данном примере присутствуют два пациента для преобразования: 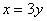
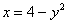
С линейной функцией всё просто:
График функции 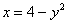
Выразим «игрек» через «икс»: 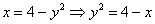
Получаем две ветви параболы: 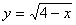
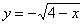
Еще раз обращаю внимание на тот факт, что на данном чертеже получилось несколько плоских фигур, и очень важно выбрать нужную фигуру! В выборе искомой фигуры как раз помогут пределы интегрирования исходных интегралов: 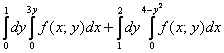
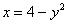
Стрелочки, которыми обозначен обход фигуры, в точности соответствуют пределам интегрирования интегралов 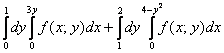
Довольно быстро вы научитесь проводить такой анализ мысленно и находить нужную область интегрирования.
Когда фигура найдена, заключительная часть решения, в общем-то, очень проста, меняем порядок обхода области: 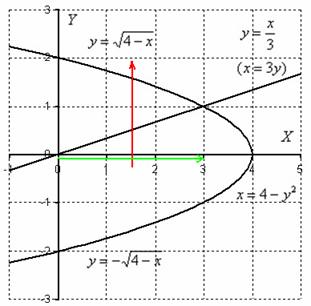
Обратные функции уже найдены, и требуемый порядок обхода области:
Ответ:
Заключительный пример параграфа для самостоятельного решения:
Изменить порядок интегрирования
Полное решение и ответ в конце урока.
Как вычислить площадь плоской фигуры с помощью двойного интеграла?
Начинаем рассматривать собственно процесс вычисления двойного интеграла 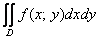
Двойной интеграл 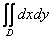
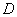
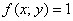
Сначала рассмотрим задачу в общем виде. Сейчас вы немало удивитесь, насколько всё действительно просто! Вычислим площадь плоской фигуры 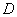
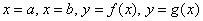
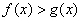
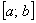
Изобразим область 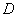
Выберем первый способ обхода области:
Таким образом:
И сразу важный технический приём: повторные интегралы можно считать по отдельности. Сначала внутренний интеграл, затем – внешний интеграл. Данный способ настоятельно рекомендую начинающим в теме чайникам.
1) Вычислим внутренний интеграл, при этом интегрирование проводится по переменной «игрек»:
Неопределённый интеграл тут простейший, и далее используется банальная формула Ньютона-Лейбница, с той лишь разницей, что пределами интегрирования являются не числа, а функции. Сначала подставили в «игрек» (первообразную функцию) верхний предел, затем – нижний предел
2) Результат, полученный в первом пункте необходимо подставить во внешний интеграл:
Более компактная запись всего решения выглядит так:
Полученная формула 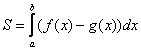
То есть, задача вычисления площади с помощью двойного интеграла мало чем отличается от задачи нахождения площади с помощью определённого интеграла! Фактически это одно и тоже!
Соответственно, никаких трудностей возникнуть не должно! Я рассмотрю не очень много примеров, так как вы, по сути, неоднократно сталкивались с данной задачей.
С помощью двойного интеграла вычислить площадь плоской фигуры 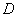
Решение: Изобразим область 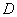
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
Выберем следующий порядок обхода области: 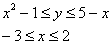
Здесь и далее я не буду останавливаться на том, как выполнять обход области, поскольку в первом параграфе были приведены очень подробные разъяснения.
Таким образом:
Как я уже отмечал, начинающим лучше вычислять повторные интегралы по отдельности, этого же метода буду придерживаться и я:
1) Сначала с помощью формулы Ньютона-Лейбница разбираемся с внутренним интегралом:
2) Результат, полученный на первом шаге, подставляем во внешний интеграл:
Пункт 2 – фактически нахождение площади плоской фигуры с помощью определённого интеграла.
Ответ:
Вот такая вот глупая и наивная задача.
Любопытный пример для самостоятельного решения:
С помощью двойного интеграла вычислить площадь плоской фигуры 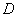
Примерный образец чистового оформления решения в конце урока.
В Примерах 9-10 значительно выгоднее использовать первый способ обхода области, любознательные читатели, кстати, могут изменить порядок обхода и вычислить площади вторым способом. Если не допустите ошибку, то, естественно, получатся те же самые значения площадей.
Но в ряде случаев более эффективен второй способ обхода области, и в заключение курса молодого ботана рассмотрим ещё пару примеров на эту тему:
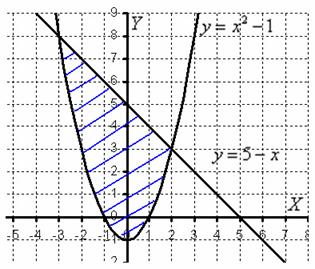
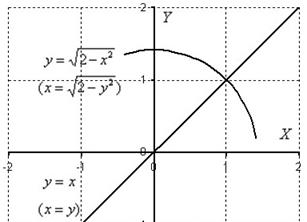
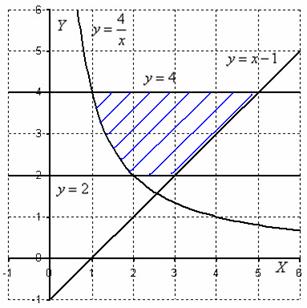
С помощью двойного интеграла, вычислить площадь плоской фигуры 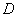
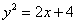
Решение: нас с нетерпением ждут две параболы, которые лежат на боку.
Как проще всего сделать чертёж?
Представим параболу 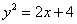
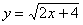
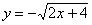
Аналогично, представим параболу 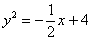
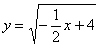
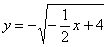
Далее рулит поточечное построение графиков, в результате чего получается вот такая причудливая фигура:
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
Что будет, если мы выберем первый способ обхода области? Во-первых, данную область придётся разделить на две части. А во-вторых, мы будем наблюдать сию печальную картину: 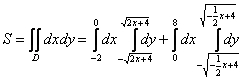
Поэтому из недоразумения, которое дано в условии, выразим обратные функции: 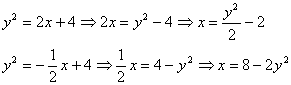
Обратные функции в данном примере обладают тем преимуществом, что задают сразу всю параболу целиком без всяких там листьев, желудей веток и корней.
Согласно второму способу, обход области будет следующим:
Таким образом: 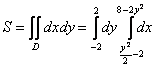
Как говорится, ощутите разницу.
1) Расправляемся с внутренним интегралом:
Результат подставляем во внешний интеграл:
2)
Интегрирование по переменной «игрек» не должно смущать, была бы буква «зю» – замечательно бы проинтегрировалось и по ней. Хотя кто прочитал второй параграф урока Как вычислить объем тела вращения, тот уже не испытывает ни малейшей неловкости с интегрированием по «игрек».
Также обратите внимание на первый шаг: подынтегральная функция 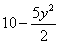
Что добавить…. Всё!
Ответ:
Для проверки своей техники интегрирования можете попробовать вычислить 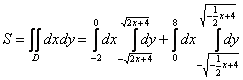
С помощью двойного интеграла, вычислить площадь плоской фигуры 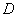
Это пример для самостоятельного решения. Интересно отметить, что если вы попробуете использовать первый способ обхода области, то фигуру придётся разделить уже не на две, а на три части! И, соответственно, получится три пары повторных интегралов. Бывает и такое.
Мастер класс подошел к завершению, и пора переходить на гроссмейстерский уровень – Как вычислить двойной интеграл? Примеры решений. Постараюсь во второй статье так не маньячить =)
Решения и ответы:
Пример 2: Решение: Изобразим область 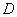
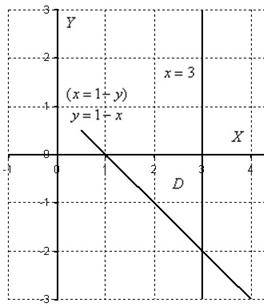
Выберем следующий порядок обхода области: 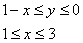
Таким образом: 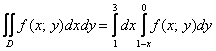
Перейдём к обратным функциям: 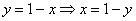
Изменим порядок обхода области: 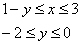
Таким образом: 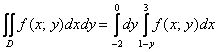
Ответ:
Пример 4: Решение: Перейдём к прямым функциям: 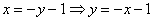
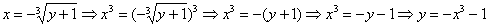
Выполним чертёж: 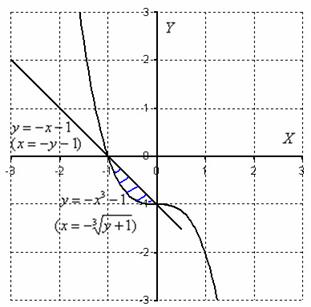
Изменим порядок обхода области: 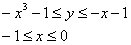
Ответ:
Пример 6: Решение: Выполним чертеж:
Перейдем к обратным функциям: 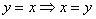
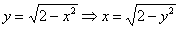
Изменим порядок интегрирования, разделив область интегрирования на две части. При этом порядок обхода области:
1) 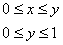
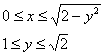
Ответ:
Пример 8: Решение: Изобразим область интегрирования на чертеже: 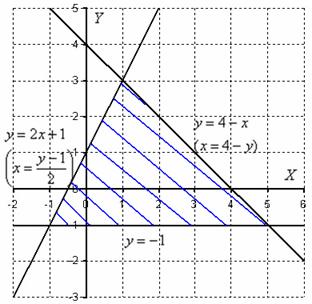
Перейдём к обратным функциям: 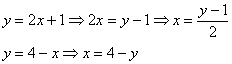
Изменим порядок обхода области: 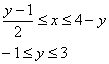
Ответ:
Пример 10: Решение: Изобразим область 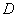
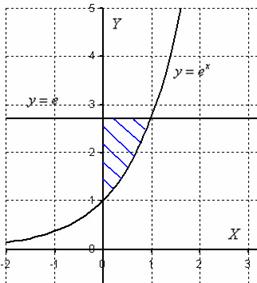
Площадь фигуры вычислим с помощью двойного интеграла по формуле: 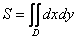
Выберем следующий порядок обхода области: 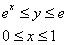
Таким образом: 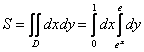
1) 
2) 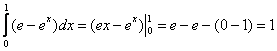
Ответ:
Пример 12: Решение: Изобразим данную фигуру на чертеже:
Площадь фигуры вычислим с помощью двойного интеграла по формуле: 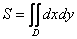
Перейдём к обратным функциям: 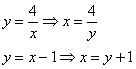
Порядок обхода области: 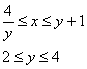
Таким образом: 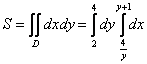
1) 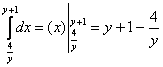
2) 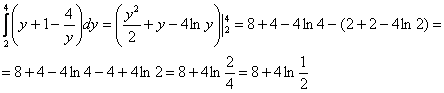
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Сложные интегралы
Данная статья завершает тему неопределенных интегралов, и в неё включены интегралы, которые я считаю достаточно сложными. Урок создан по неоднократным просьбам посетителей, которые высказывали пожелания, чтобы на сайте были разобраны и более трудные примеры.
Предполагается, что читатель сего текста хорошо подготовлен и умеет применять основные приемы интегрирования. Чайникам и людям, которые не очень уверенно разбираются в интегралах, следует обратиться к самому первому уроку – Неопределенный интеграл. Примеры решений, где можно освоить тему практически с нуля. Более опытные студенты могут ознакомиться с приемами и методами интегрирования, которые в моих статьях еще не встречались.
Какие интегралы будут рассмотрены?
Сначала мы рассмотрим интегралы с корнями, для решения которых последовательно используется замена переменной и интегрирование по частям. То есть, в одном примере комбинируются сразу два приёма. И даже больше.
Затем мы познакомимся с интересным и оригинальным методом сведения интеграла к самому себе. Данным способом решается не так уж мало интегралов.
Третьим номером программы пойдут интегралы от сложных дробей, которые пролетели мимо кассы в предыдущих статьях.
В-четвертых, будут разобраны дополнительные интегралы от тригонометрических функций. В частности, существуют методы, которые позволяют избежать трудоемкой универсальной тригонометрической подстановки.
И в заключение рассмотрим интеграл от корня из дроби, в числителе и знаменателе которой находятся линейные функции.
Конечно, название урока не совсем точно, будут и не сказать, что сильно сложные интегралы. Тем не менее, крепких орешков предостаточно. Запланировано довольно много примеров, поэтому поехали.
Последовательная замена переменной и интегрирование по частям
Найти неопределенный интеграл
Подынтегральная функция представляет собой арктангенс, под которым находится кубический корень. Первая же мысль, которая приходит в голову – избавиться бы от этого корня. Данный вопрос решается путем замены переменной, сама техника замены специфична, и она подробно рассмотрена на уроке Интегралы от иррациональных функций. Проведем замену:
После такой замены у нас получится вполне симпатичная вещь:
Осталось выяснить, во что превратится 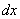
И само собой раскрываем дифференциалы:
На чистовике решение кратко записывается примерно так:
Проведем замену:
В результате замены получен знакомый тип интеграла, который интегрируется по частям:
(1) Выносим 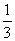
(2) В подынтегральной функции почленно делим числитель на знаменатель.
(3) Используем свойство линейности неопределенного интеграла. В последнем интеграле сразу подводим функцию под знак дифференциала.
(4) Берём оставшиеся интегралы. Обратите внимание, что в логарифме можно использовать скобки, а не модуль, так как 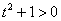
(5) Проводим обратную замену, выразив из прямой замены 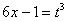
Студенты-мазохисты могут продифференцировать ответ и получить исходную подынтегральную функцию, как только что это сделал я. Нет-нет, я-то в правильном смысле выполнил проверку =)
Как видите, в ходе решения пришлось использовать даже больше двух приемов решения, таким образом, для расправы с подобными интегралами нужны уверенные навыки интегрирования и не самый маленький опыт.
На практике, конечно же, чаще встречается квадратный корень, вот три примера для самостоятельного решения:
Найти неопределенный интеграл
Найти неопределенный интеграл
Найти неопределенный интеграл
Данные примеры однотипны, поэтому полное решение в конце статьи будет только для Примера 2, в Примерах 3-4 – одни ответы. Какую замену применять в начале решений, думаю, понятно. Почему я подобрал однотипные примеры? Часто встречаются в своем амплуа. Чаще, пожалуй, только что-нибудь вроде 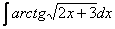
Но не всегда, когда под арктангенсом, синусом, косинусом, экспонентой и др. функциями находится корень из линейной функции, приходится применять сразу несколько методов. В ряде случаев удается «легко отделаться», то есть сразу после замены получается простой интеграл, который элементарно берётся. Самым легким из предложенных выше заданий является Пример 4, в нём после замены получается относительно несложный интеграл.
Методом сведения интеграла к самому себе
Остроумный и красивый метод. Немедленно рассмотрим классику жанра:
Найти неопределенный интеграл
Под корнем находится квадратный двучлен, и при попытке проинтегрировать данный пример чайник может мучаться часами. Такой интеграл берётся по частям и сводится к самому себе. В принципе не сложно. Если знаешь как.
Обозначим рассматриваемый интеграл латинской буквой 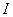
Интегрируем по частям:
(1) Готовим подынтегральную функцию для почленного деления.
(2) Почленно делим подынтегральную функцию. Возможно, не всем понятно, распишу подробнее:
(3) Используем свойство линейности неопределенного интеграла.
(4) Берём последний интеграл («длинный» логарифм).
Теперь смотрим на самое начало решения: 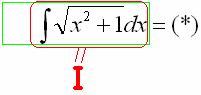
И на концовку:
Что произошло? В результате наших манипуляций интеграл свёлся к самому себе!
Приравниваем начало и конец:
Переносим 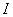
А двойку сносим в правую часть. В результате:
Или:
Константу 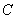
Примечание: Более строго заключительный этап решения выглядит так: 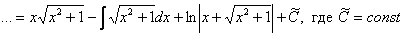
Таким образом: 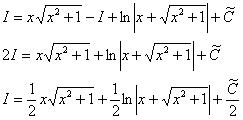
Константу 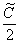
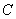
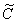
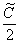
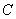
В результате:
Подобный трюк с переобозначением константы широко используется в дифференциальных уравнениях. И там я буду строг. А здесь такая вольность допускается мной только для того, чтобы не путать вас лишними вещами и акцентировать внимание именно на самом методе интегрирования.
Найти неопределенный интеграл
Еще один типовой интеграл для самостоятельного решения. Полное решение и ответ в конце урока. Разница с ответом предыдущего примера будет!
Если под квадратным корнем находится квадратный трехчлен, то решение в любом случае сводится к двум разобранным примерам.
Например, рассмотрим интеграл 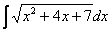
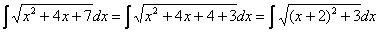
Далее проводится линейная замена, которая обходится «без всяких последствий»: 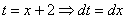
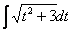
Или такой пример, с квадратным двучленом: 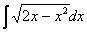
Выделяем полный квадрат: 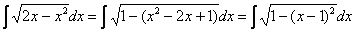
И, после линейной замены 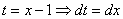
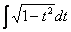
Рассмотрим еще два типовых примера на приём сведения интеграла к самому себе:
– интеграл от экспоненты, умноженной на синус;
– интеграл от экспоненты, умноженной на косинус.
В перечисленных интегралах по частям придется интегрировать уже два раза:
Найти неопределенный интеграл
Подынтегральная функция – экспонента, умноженная на синус.
Дважды интегрируем по частям и сводим интеграл к себе:

В результате двукратного интегрирования по частям интеграл свёлся к самому себе. Приравниваем начало и концовку решения:
Переносим 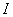
Готово. Попутно желательно причесать правую часть, т.е. вынести экспоненту за скобки, а в скобках расположить синус с косинусом в «красивом» порядке.
Теперь вернемся к началу примера, а точнее – к интегрированию по частям:
За 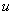
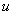
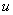
Почему такое возможно? Потому что экспонента превращается сама в себя (и при дифференцировании, и при интегрировании), синус с косинусом взаимно превращаются друг в друга (опять же – и при дифференцировании, и при интегрировании).
То есть, за 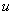
Найти неопределенный интеграл
Это пример для самостоятельного решения. Перед тем как решать, подумайте, что выгоднее в данном случае обозначить за 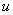
И, конечно, не забывайте, что большинство ответов данного урока достаточно легко проверить дифференцированием!
Примеры были рассмотрены не самые сложные. На практике чаще встречаются интегралы, где константа есть и в показателе экспоненты и в аргументе тригонометрической функции, например: 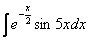
На завершающем этапе часто получается примерно следующее:
Даже в конце решения следует быть предельно внимательным и грамотно разобраться с дробями:
Интегрирование сложных дробей
Потихоньку подбираемся к экватору урока и начинаем рассматривать интегралы от дробей. Опять же, не все они суперсложные, просто по тем или иным причинам примеры были немного «не в тему» в других статьях.
Продолжаем тему корней
Найти неопределенный интеграл
В знаменателе под корнем находится квадратный трехчлен плюс за пределами корня «довесок» в виде «икса». Интеграл такого вида решается с помощью стандартной замены.
Решаем:
Замена тут проста:
Смотрим на жизнь после замены:
(1) После подстановки приводим к общему знаменателю слагаемые под корнем.
(2) Выносим 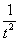
(3) Числитель и знаменатель сокращаем на 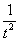
(4) Полученный интеграл, как вы помните из урока Интегрирование некоторых дробей, решается методом выделения полного квадрата. Выделяем полный квадрат.
(5) Интегрированием получаем заурядный «длинный» логарифм.
(6) Проводим обратную замену. Если изначально 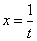
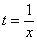
(7) Заключительное действие направлено на прическу результата: под корнем снова приводим слагаемые к общему знаменателю и выносим из-под корня 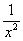
Найти неопределенный интеграл
Это пример для самостоятельного решения. Здесь к одинокому «иксу» добавлена константа, и замена почти такая же: 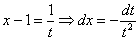
Единственное, что нужно дополнительно сделать – выразить «икс» из проводимой замены:
Полное решение и ответ в конце урока.
Иногда в таком интеграле под корнем может находиться квадратный двучлен, это не меняет способ решения, оно будет даже еще проще. Почувствуйте разницу:
Найти неопределенный интеграл
Найти неопределенный интеграл
Краткие решения и ответы в конце урока. Следует отметить, что Пример 11 является в точности биномиальным интегралом, метод решения которого рассматривался на уроке Интегралы от иррациональных функций.
Интеграл от неразложимого многочлена 2-й степени в степени
(многочлен в знаменателе)
Более редкий, но, тем не менее, встречающий в практических примерах вид интеграла.
Найти неопределенный интеграл
В знаменателе подынтегральной функции находится неразложимый на множители квадратный двучлен. Подчеркиваю, что неразложимость на множители является существенной особенностью. Если многочлен раскладывается на множители, то всё намного понятнее, например:
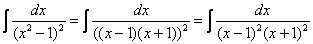
Но вернёмся к примеру со счастливым номером 13 (честное слово, не подгадал). Этот интеграл тоже из разряда тех, с которыми можно изрядно промучиться, если не знаешь, как решать.
Решение начинается с искусственного преобразования:
Как почленно разделить числитель на знаменатель, думаю, уже все понимают.
Полученный интеграл берётся по частям:
Для интеграла вида 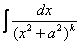
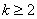
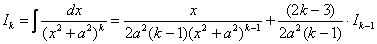
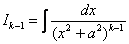
Убедимся в справедливости данной формулы для прорешанного интеграла 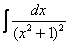
В данном случае: 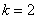
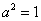
Как видите, ответы совпадают.
Найти неопределенный интеграл
Это пример для самостоятельного решения. В образце решения дважды последовательно использована вышеупомянутая формула.
Если под степенью находится неразложимый на множители квадратный трехчлен, то решение сводится к двучлену путем выделения полного квадрата, например:
Далее следует «безболезненная» линейная замена 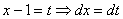
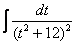
Что делать, если дополнительно в числителе есть многочлен? В этом случае используется метод неопределенных коэффициентов, и подынтегральная функция раскладывается в сумму дробей. Но в моей практике такого примера не встречалось ни разу, поэтому я пропустил данный случай в статье Интегралы от дробно-рациональной функции, пропущу и сейчас. Если такой интеграл все-таки встретится, смотрите учебник – там всё просто. Не считаю целесообразным включать материал (даже несложный), вероятность встречи с которым стремится к нулю.
Интегрирование сложных тригонометрических функций
Прилагательное «сложный» для большинства примеров вновь носит во многом условный характер. Начнем с тангенсов и котангенсов в высоких степенях. С точки зрения используемых методов решения тангенс и котангенс – почти одно и тоже, поэтому я больше буду говорить о тангенсе, подразумевая, что продемонстрированный прием решения интеграла справедлив и для котангенса тоже.
На уроке Интегралы от тригонометрических функций мы разобрали интеграл от тангенса в квадрате. На уроке Как вычислить площадь фигуры? в примере 10 фигурировал тангенс в кубе. В том примере для нахождения интеграла от тангенса в кубе мы применяли тригонометрическую формулу 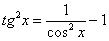
Найти неопределенный интеграл
Идея решения подобных интегралов состоит в том, чтобы с помощью формулы 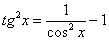
(1) Готовим подынтегральную функцию к применению формулы.
(2) Для одного из множителей используем формулу 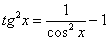
(3) Раскрываем скобки и сразу же используем свойство линейности неопределенного интеграла.
(4) В первом интеграле используем метод подведения функции под знак дифференциала. Во втором интеграле еще раз используем формулу 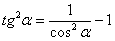
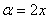
(5) Берём все три интеграла и получаем ответ.
Найти неопределенный интеграл
Это пример для самостоятельного решения. Для котангенса существует аналогичная формула: 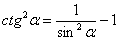
Если возникли затруднения или недопонимание, следует вернуться к уроку Интегралы от тригонометрических функций.
На вышеупомянутом уроке мы рассматривали универсальную тригонометрическую подстановку для решения определенного вида интегралов от тригонометрических функций. Недостаток универсальной тригонометрической подстановки заключается в том, что при её применении часто возникают громоздкие интегралы с трудными вычислениями. И в ряде случаев универсальной тригонометрической подстановки можно избежать!
Рассмотрим еще один канонический пример, интеграл от единицы, деленной на синус:
Найти неопределенный интеграл
Здесь можно использовать универсальную тригонометрическую подстановку и получить ответ, но существует более рациональный путь. Я приведу полное решение с комментами к каждому шагу:
(1) Используем тригонометрическую формулу синуса двойного угла 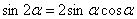
(2) Проводим искусственное преобразование: В знаменателе делим и умножаем на 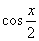
(3) По известной формуле в знаменателе превращаем дробь в тангенс.
(4) Подводим функцию под знак дифференциала.
(5) Берём интеграл.
Пара простых примеров для самостоятельного решения:
Найти неопределенный интеграл
Указание: Самым первым действием следует использовать формулу приведения 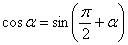
Найти неопределенный интеграл
Ну, это совсем простой пример.
Полные решения и ответы в конце урока.
Думаю, теперь ни у кого не возникнет проблем с интегралами:
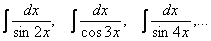
В чём состоит идея метода? Идея состоит в том, чтобы с помощью преобразований, тригонометрических формул организовать в подынтегральной функции только тангенсы и производную тангенса 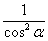
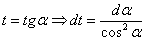
Аналогичные рассуждения, как я уже оговаривался, можно провести для котангенса.
Существует и формальная предпосылка для применения вышеуказанной замены:
Сумма степеней косинуса и синуса – целое отрицательное ЧЁТНОЕ число, например:
для интеграла 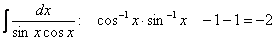
! Примечание: если подынтегральная функция содержит ТОЛЬКО синус или ТОЛЬКО косинус, то интеграл берётся и при отрицательной нечётной степени (простейшие случаи – в Примерах № 17, 18).
Рассмотрим пару более содержательных заданий на это правило:
Найти неопределенный интеграл
Сумма степеней синуса и косинуса 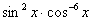
(1) Преобразуем знаменатель.
(2) По известной формуле получаем 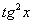
(3) Преобразуем знаменатель.
(4) Используем формулу 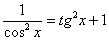
(5) Подводим функцию под знак дифференциала.
(6) Проводим замену 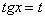
Далее берётся простой интеграл и проводится обратная замена.
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Держитесь, начинаются чемпионские раунды =)
Зачастую в подынтегральной функции находится «солянка»:
Найти неопределенный интеграл
В этом интеграле изначально присутствует тангенс, что сразу наталкивает на уже знакомую мысль:
Искусственное преобразование в самом начале и остальные шаги оставлю без комментариев, поскольку обо всем уже говорилось выше.
Пара творческих примеров для самостоятельного решения:
Найти неопределенный интеграл
Найти неопределенный интеграл
Да, в них, конечно, можно понизить степени синуса, косинуса, использовать универсальную тригонометрическую подстановку, но решение будет гораздо эффективнее и короче, если его провести через тангенсы. Полное решение и ответы в конце урока
У многих читателей могло сложиться впечатления, что я немного подустал. Отнюдь. За окном февральский ветер – самая атмосфера для лекций. Естественно, данная страничка создана не за один день, я успел несколько раз побриться, регулярно кушаю и так далее. К тому же, загружать студентов – удовольствие бесконечное =). …Шутка! На самом деле моя миссия – разгружать посетителей сайта. Вагонами.
Переходим к заключительному пункту познавательного путешествия в мир сложных интегралов:
Интеграл от корня из дроби
Интеграл, который мы рассмотрим, встречается достаточно редко, но я буду очень рад, если единственный пример данного параграфа вам поможет.
Корнями всё начиналось, корнями и закончится. Рассмотрим неопределенный интеграл: 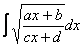
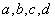
В подынтегральной функции у нас находится корень, а под корнем – дробь, в числителе и знаменателе которой располагаются линейные функции.
Метод стар – нужно избавиться от корня. Стар и уныл, но сейчас станет веселее, поскольку придется проводить громоздкую замену.
Замена, с помощью которой мы гарантированно избавимся от корня, очевидна: 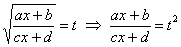
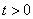
Теперь нужно выразить «икс» и найти, чему равен дифференциал 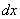
Выражаем «икс»:
Теперь найдем дифференциал:
Зачем были эти нелепые скучные телодвижения?
Я вывел готовые формулы, которыми можно пользовать при решении интеграла вида 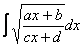
Формулы замены таковы:
Это было ни в коем случае не хвастовство, просто я не смог быстро найти эти формулы в близлежащей литературе и Сети – оказалось проще вывести. Да и может быть кто-нибудь для реферата возьмет.
Опять – двадцать пять, заключительный пример:
Найти неопределенный интеграл
Проведем замену:
В данном примере: 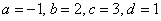
Таким образом:
Еще куда ни шло, могло всё оказаться значительно хуже. Такой интеграл, кстати, уже фигурировал в Примере 13. Интегрируем по частям:
Проведем обратную замену. Если изначально 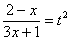
Некоторым страшно, а я это продифференцировал, ответ верный!
Иногда встречаются интегралы вида 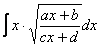
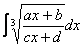
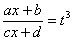
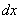
Теперь вам практически любой интеграл по силам, успехов!
Решения и ответы:
Пример 2: Решение: 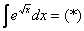
Проведем замену: 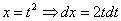
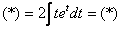
Интегрируем по частям: 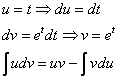
Пример 3: Ответ:
Пример 4: Ответ:
Пример 6: Решение: 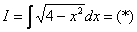
Интегрируем по частям: 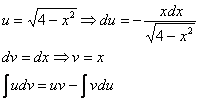

Таким образом: 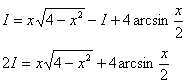
В результате:
Пример 8: Решение:
Дважды интегрируем по частям и сводим интеграл к себе: 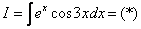
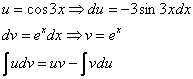
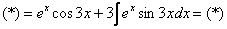
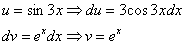
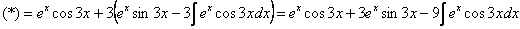
Таким образом:
Пример 10: Решение: 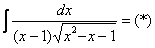
Проведем замену: 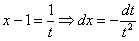
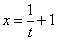
Пример 11: Решение: 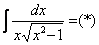
Замена: 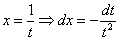
Пример 12: Решение: 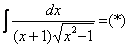
Замена: 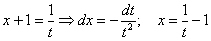
Пример 14: Решение: 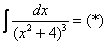
Дважды используем рекуррентную формулу 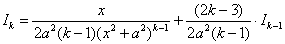
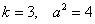
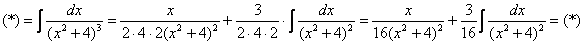
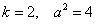
Пример 16: Решение:
Пример 18: Решение: 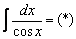
Используем формулу приведения: 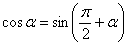
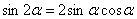
Пример 19: Решение:
Пример 21: Решение:
–3 – 3 = –6 – целое отрицательное ЧЁТНОЕ число
Пример 23: Решение:
Пример 24: Решение:
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys