Как сделать икосаэдр оригами
Как сделать Икосаэдр
Котаэдр с Икосаэдром:
Икосаэдр (двадцатигранник, скручено удлинённая пятиугольная бипирамида) — многогранник, гранями которого являются двадцать правильных треугольников. Также является одним из пяти правильных многогранников (Платоновы тела). У икосаэдра 20 граней, 12 вершин и 30 рёбер. Двойственным многогранником является додекаэдр. Икосаэдр имеет икосаэдрическую симметрию.
Икосаэдр много где встречается:
Двадцатигранные игральные кости.
Головка бактериофага в виде вытянутого икосаэдра.
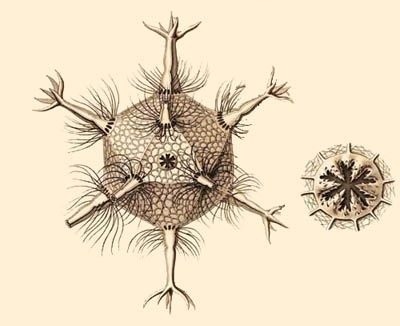
Радиолярия Circogonia icosahedra.
Террариум для растений
Музей американского искусства «Хрустальные мосты».
Тюрьма G-Man’a из Half-Life: Alyx
В комменты пишите, где ещё встречается икосаэдр.
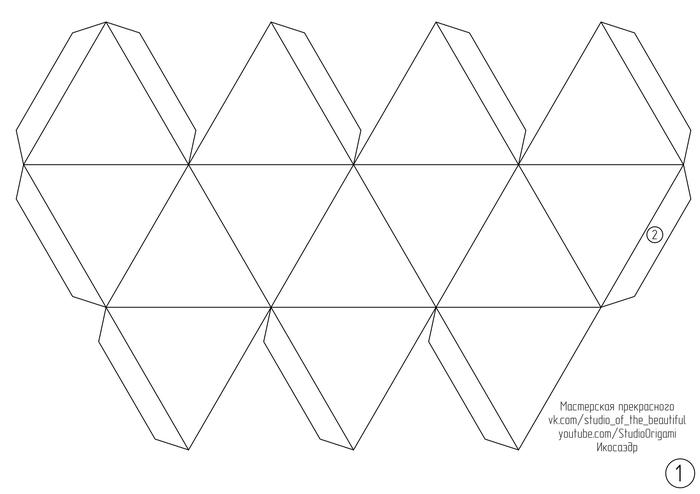
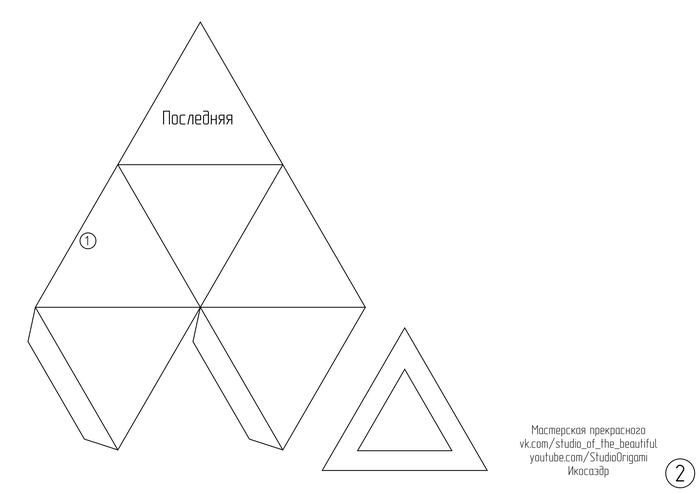
А теперь сама инструкция для сборки икосаэдра. Для развёртки икосаэдра необходимо 2 листа двухстороннего цветного картона формата А4 (или плотной бумаги). Длина ребра у икосаэдра получается 7 см. Развёртку икосаэдра в формате pdf Вы можете скачать по ссылке или картинкой ниже:
Если у Вас нет принтера, то Вы можете сами нарисовать развёртку икосаэдра с помощью карандаша, линейки и циркуля, смотря видеоинструкцию ниже:
Найдены возможные дубликаты
Рукодельники
27.8K постов 43.7K подписчиков
Правила сообщества
В сообществе запрещена торговля, обсуждение цен, ссылки на страницы с продажами, контакты автора в комментариях. Обязательна информация о материалах и инструментах в текстовом виде.
1. Будьте вежливы, старайтесь писать грамотно.
2. В публикациях используйте четкие и красивые фотографии.
3. Автор поста с тегом [моё] может оставить ссылку на свой профиль, группу или канал на других источниках, при условии, что ссылки (активные и не активные) не ведут на прямые продажи. Допускается не больше четырёх ссылок и только в конце поста (п. 8.5 основных правил).
-ссылки рекламного характера/спам;
-ссылки, ведущие на магазины с указанием стоимости товара/услуги;
-ссылки, ведущие на призывы, покупки, продажи, подписки, репосты, голосование и тому подобное.
(нарушение основных правил сайта, п.8.1 и п. 8.2).
При переходе по ссылке запрещено наличие активных (кликабельных) ссылок, ведущих на вышеперечисленное в п.3, содержание таких ключевых слов как «товар», «услуга», «купить», «продам», «в наличии», «под заказ» и т.п.
3.1 Размещение контактов автора (самим автором или другими пользователями) в комментариях запрещено и подлежит удалению (п. 9.1 и 9.3 основных правил).
4. Обязательным для авторов является наличие технических характеристик изделия в публикациях (материалы, техники, авторские приемы, размеры, времязатраты и прочее) в текстовом виде.
Также помечайте свою работу тегом «Рукоделие с процессом» или «Рукоделие без процесса».
5. Пост-видео, пост-фото без текстового описания переносится в общую ленту. Даже если в видео показан подробный процесс изготовления, делайте краткое описание для тех, у кого нет возможности/желания смотреть видео.
Администрация оставляет за собой право решать, насколько описание соответствует п. 5.
6. Посты с нарушениями без предупреждения переносятся в общую ленту.
За неоднократные нарушения автор получает бан.
Автор может размещать новую публикацию в сообществе, не допуская полученных ранее замечаний.
1. Соединение пяти тетраэдров.
2. Соединение шести тетраэдров
3. Малый икосо-икосо-додекаэдр
4. Большой додекаэдр
5. Малый звёздчатый додекаэдр
6. Малый икосо-геми-додекаэдр
8. Пятая звёздчатая форма икосаэдра
9. Шестая звёздчатая форма икосаэдра
10. Большой кубо-кубо-октаэдр
12. Большой звёздчатый додекаэдр
моё любимое ругательство: ах ты ж дважды косо скрученный ромбоикосододекаэдр))
Прибавление в мастерской
Всем привет, сегодня речь пойдет о появлении в моем «арсенале» нового помощника. Наверное пост не в тему, так как работы как таковой тут немного, но все же не могу не поделиться.
По счастливой случайности стал обладателем сего чудо инструмента :
Давно мечтал заиметь себе в мастерскую такие слесарные тисы, но при виде цены на рынке или в магазине всегда откладывал покупку в долгий ящик. А на днях дед откопал в своих закромах сей инструмент, чему я был не сказанно рад, когда он мне сообщил такую приятную новость))))
Итак, что имеем, все в рабочем состоянии за исключением некоторых нюансов, вал с резьбой немного загнут, и нет накладок на губках тисов, плюсом также была проблема с отломленными болтами которые крепят накладки.
В итоге вооружившись шуриком со сверлом начал добывать заводские отверстия для крепления накладок. Изначально резьба была М8 поэтому высверлив свелом немного меньшего диаметра старые отломленные болты и пробежавшись метчиком резьба была спасена, благо с шагом резьбы угадал и не пришлось ничего мудрить поэтому первая проблема решилась на ура
Теперь пришла очередь проделать отверстия в нужном месте для закрепления. Квадрат этот имел уже несколько отверстий меньшего диаметра, но к сожалению ни одно из них по месту не подошло, поэтому пришлось сверлить самому, а от мелких отверстий решил избавиться при помощи сварки
Накладки с правильными отверстиями
Также рассверли на глубину 5мм сверлом на 12мм, чтобы шляпы болтов сравнялись с пооскостью
При помощи лепесткового диска выравнил все огрехи:
Затем уже перешел к заключительной части работы, заварил ненужные отверстия, сделал насечки для более надежной фиксации заготовки. В итоге накладки обрели следующий вид
Осталось поставить все на свои места
Определил тисам место на верстаке, прикрутил, теперь можно работать
Всем спасибо за просмотр. До новых встреч!!
Отливаем печурку в бетоне
Сверлильный станок своими руками из того что было
Приветствую всех. Потихоньку познаю столярное дело. Как начинал, описывал в предыдущих постах. Даже несколько заказов на стулья появилось, чему несказанно рад. Но сегодня не об этом. Т.к. объем увеличился, начал думать об облегчении некоторых действий. Решил сделать сверлильный станок, потому как на сотом отверстии рука начинает отваливать, да и идеальные 90 градусов не получает. А с таким устройством будет гораздо все проще. Да и может кому пригодится. Ничего сложного и материалы доступные, а вообще делал из того что было))
А было немного фанеры 10ки, оставшиеся неиспользованные напрявляйки от ящика, какая то древняя пружина, даже не знаю от чего, и соответственно обрезки бруса. Насмотревшись ютуба начал думать над конструкцией. Решил придумывать на ходу. Как говорится главное начать.
Начал с центральной части, которая должна двигаться. По идее можно все из фанеры сделать. взять 20ку и не париться, а если есть циркулярка то процесс упрощается в разы. У меня же только ручной инструмент. Но что имеем. Так что, для утолщения я использовал брус, но можно без него. Взял охапку дров и сделал из этого бутерброд. Брус если что 40*30.
Далее взял напрявляйки (350мм длинной) и закрепил на этом бутерброде.
Основа готова. И тут у меня опять ступор. Нужно же что бы это все дело само поднималось, соответственно нужна пружина, а куда и как её закрепить, это вопрос. Пораскинув мозгами, придумал ее сделать скрытой, ну почти)) Сделал небольшую канавку и закрепил пружину там. Как и куда она потом крепиться будет ещё не представлял, но чем то чувствовал, что именно так нужно.
Вот теперь центр готов. Нужно делать стойки, на чем все это дело двигаться будет. Опять делал бутерброды из фанеры и бруса, но тут брус 50*50мм для большей устойчивости.
Закрепил направляющие и понял где нужно будет крепить пружину. Все проверил, механизм имеет право на жизнь и даже все работает))
Далее отрезал по размера этого устройства заднюю стенку из фанеры и закрепил. Получилось достаточно жесткая конструкция. Начал думать как закрепить дрель в этом устройстве. Отпилил из фанеры переднюю панель. Ширину взял всего устройства 190мм, а высоту по центральной части т.е. 350мм. Держатель дрели делал из склейки фанеры, т.е. 20мм.
Все закрепил. Получилось довольно таки не плохо, но что бы все это работало с комфортом нужна ручка. Опять же фанера, и немного кожи молодого дерматина, оставшиеся с другого проекта. Форму накидал на глаз.
Далее собрал подставку из двух брусков 50*50 и фанеры сверху. Получилось как то так. Но все работает, и уже не раз выручало.
во все конструкции допустил одну ошибку. Нужно было получше продумать как будет фиксироваться дрель. Мне пришлось ее зафиксировать саморезами. Но мне дрель не жалко было. Она два года валялась как не рабочая, но когда задумал это станок, решил сделать её ревизию. Оказалось что просто тупит кнопка, и на малых оборотах просто не срабатывает. А работать ей вручную не удобно, тяжелая. Да и шуруповерт мастхев.
В общем вот такое устройство. Спасибо что дочитали до конца. Надеюсь кому пригодится. Буду рад ответить на вопросы в комментариях.
Как сделать икосаэдр оригами
Рассылка Пикабу: отправляем лучшие посты за неделю 🔥
О сообществе
Умеешь делать что-то своими руками? Поделись этим умением со всеми!
А если у вас есть вопросы по поводу рукоделия, технологий, материалов и т.п. можете смело оставлять их в сообществе.
В сообществе запрещена торговля, обсуждение цен, ссылки на страницы с продажами, контакты автора в комментариях. Обязательна информация о материалах и инструментах в текстовом виде.
1. Будьте вежливы, старайтесь писать грамотно.
2. В публикациях используйте четкие и красивые фотографии.
3. Автор поста с тегом [моё] может оставить ссылку на свой профиль, группу или канал на других источниках, при условии, что ссылки (активные и не активные) не ведут на прямые продажи. Допускается не больше четырёх ссылок и только в конце поста (п. 8.5 основных правил).
-ссылки рекламного характера/спам;
-ссылки, ведущие на магазины с указанием стоимости товара/услуги;
-ссылки, ведущие на призывы, покупки, продажи, подписки, репосты, голосование и тому подобное.
(нарушение основных правил сайта, п.8.1 и п. 8.2).
При переходе по ссылке запрещено наличие активных (кликабельных) ссылок, ведущих на вышеперечисленное в п.3, содержание таких ключевых слов как «товар», «услуга», «купить», «продам», «в наличии», «под заказ» и т.п.
3.1 Размещение контактов автора (самим автором или другими пользователями) в комментариях запрещено и подлежит удалению (п. 9.1 и 9.3 основных правил).
4. Обязательным для авторов является наличие технических характеристик изделия в публикациях (материалы, техники, авторские приемы, размеры, времязатраты и прочее) в текстовом виде.
Также помечайте свою работу тегом «Рукоделие с процессом» или «Рукоделие без процесса».
5. Пост-видео, пост-фото без текстового описания переносится в общую ленту. Даже если в видео показан подробный процесс изготовления, делайте краткое описание для тех, у кого нет возможности/желания смотреть видео.
Администрация оставляет за собой право решать, насколько описание соответствует п. 5.
6. Посты с нарушениями без предупреждения переносятся в общую ленту.
За неоднократные нарушения автор получает бан.
Автор может размещать новую публикацию в сообществе, не допуская полученных ранее замечаний.
Как сделать тетраэдр из бумаги: развертка для склеивания
Икосаэдр – понятие, свойства и структура двадцатигранника
Используя 30 квадратных листов бумаги (размер каждой стороны 7,5 см), можно сделать довольно крепкую версию одной из разновидности этого геометрического чуда совсем без склеивания. Если в запасе есть материал разного цвета, то получится яркий и красивый макет с разноцветными блоками. Инструкция по изготовлению звездчатого икосаэдра поэтапно:
Всего таких блоков нужно сделать 30. Например, по 10 разного цвета.
Сборка элементов
Теперь самое время собирать блоки вместе. Поверхность звездчатого икосаэдра состоит из нескольких пирамид.
Чтобы было проще, нужно представить этот сложный куб, над которым идёт работа, в виде единственного додекаэдра (12-гранный правильный пятиугольник — ещё одно тело Платона), где каждая из его двадцати вершин будет заменена пирамидой.
Все 30 единиц пойдут на формирование этих 20 пирамид. Ход работы по сборке икосаэдра. Схема поэтапно:
В итоге получится красивая объёмная фигура, а если она сделана из цветной бумаги, то ещё и красочная. Безусловно, если нужно сэкономить время и силы, можно сильно упростить задачу и найти готовый шаблон модели, распечатать развёртку икосаэдра на бумаге и вырезать, оставляя припуски, а затем склеить.
Основные виды
Вообще, эта геометрическая фигура — одно из платоновых тел, известных с древних времён. Их всего пять: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Их определение довольно простое: все они представляют собой многогранники, состоящие из конгруэнтных (одинаковых по форме и размеру) регулярных (все углы равны, как и все стороны) полигональных граней, встречающихся в каждой вершине.
Обычный икосаэдр представлен в двух основных видах, обладающих одинаковыми признаками. У каждого есть 30 рёбер и 20 равносторонних треугольных граней, которые собираются по 5 штук, образуя 12 вершин. Оба имеют икосаэдрическую симметрию, центром которой является точка пересечения всех осевых линий, и называются:
Звездчатые формы образуются, когда грани или края многогранника расширяют до тех пор, пока они не встретятся, чтобы сформировать новую фигуру. Это делается таким образом, что сохраняются центр,оси и плоскости симметрии родительской фигуры.
К слову, большой икосаэдр можно отнести к этому виду. У других «звёздочек» есть более одной грани в каждой плоскости или они образуют соединения более простых многогранников. Это не строго икосаэдры, но их часто так называют.
В таблице представлены несколько разновидностей звездчатых тел.
| Вид икосаэдра | Рисунок |
| выпуклый | |
| малый триамбический | |
| медиальный (большой) триамбический | |
| соединение пяти октаэдров | |
| соединение из пяти тетраэдров | |
| финальный |
Ромбический икосаэдр – выпуклый многогранник, состоящий из двадцати конгруэнтных ромбических граней, четыре или пять из которых встречаются в каждой вершине. Напоминает сплюснутую сферу.
По специальным формулам икосаэдра определяют его размер, площадь и объём. А также есть специальные координаты — декартовы и сферические, с помощью которых описывают расположение вершин многогранника. Построение такой фигуры, чтобы избежать утомительных расчётов, можно проводить с помощью квадратных матриц по системе равносторонних линий. Другие интересные факты:
Икосаэдр имеет три специальных ортогональных проекции, центрированных на грани, ребре и вершине. Фигура также может быть представлена в виде сферической мозаики и спроецирована на плоскость через стереографическую проекцию.
Природные формы и использование
Многие микроорганизмы, в том числе вирусы, имеют икосаэдрические оболочки. Их структуры построены из повторяющихся идентичных белковых субъединиц, и икосаэдр является самой лёгкой формой для их сборки.
Используется обычный тип многогранника, поскольку он может быть построен из одного базового белка, который будет использоваться снова и снова. Это очень упрощает жизнь и экономит место в вирусном геноме.
А также были обнаружены различные органеллы бактериальной клетки с икосаэдрической формой. В 1904 году Эрнст Геккель описал ряд видов радиолярий, чей скелет имеет форму и свойства многогранника. Икосаэдрическое двойникование также происходит в кристаллах, особенно в наночастицах.
К другим примерам того, как природа использует такую структуру для достижения многих целей, можно отнести инклюзионные тела — компартменты, которые образуются внутри клеток, обычно во время некоторых фаз роста или в определённых условиях окружающей среды.
Использование икосаэдров для разделения пространства и контроля доступа очень эффективно и, по-видимому, предпочтительно, когда ресурсы организмов ограничены.
В древности игральные кости имели столько сторон, сколько граней в икосаэдре. Такие двадцатигранные кубики могли быть пронумерованы от 0 до 9 дважды или от 1 до 20.
Форма правильных многогранников часто используется для создания различных предметов в компьютерных играх и головоломках. В виртуальном мире, кстати, часто можно встретить и другие геометрические тела.
Например, в «Супер Марио Галактике» планеты имеют форму, похожую на ромбоусечённый икосододекаэдр — архимедово тело.
Японский картограф Содзи Садао и американский архитектор Ричард Бакминстер Фуллер разработали карту мира в виде развёрнутого икосаэдра. Этот же многогранник лежит в основе геодезических сеток, которыми пользуются метеорологи и климатологи.










Оригами додекаэдр
Одной из простейших бумажных кусудам считается додекаэдр-оригами. Но это не значит, что он выглядит неэффектно, особенно когда речь идёт о звёздчатой разновидности.
Декоративный многогранник, подобно другим своим родственникам – кусудамам, отлично подходит для праздничного украшения помещений или в качестве оригинального подарка.
Мини-додекаэдры можно использовать как модные украшения, сделав из них серьги или кулон.
Ажурная модель
Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.
Пошаговая инструкция:
Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.
Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.
Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.
За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.
Подробная сборка ажурного додекаэдра представлена и в видео-МК:
Кусудама из правильных пятиугольников
Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.
Пошаговая инструкция:
Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.
Додекаэдр-звезда
Правильные звёздчатые многогранники относятся к самым красивым геометрическим фигурам. С момента своего открытия в XVI веке, они считались символом совершенства Вселенной.
Малый звёздчатый додекаэдр впервые построил немецкий астроном и математик Иоганн Кеплер – создатель знаменитой теории о строении Солнечной системы.
Многогранник имеет собственное имя: Арур Кэли, в честь английского учёного, сделавшего огромный вклад в развитие линейной алгебры.
Малый звёздчатый додекаэдр-оригами представляет собой фигуру из 12 граней-пентаграмм, с пятью пентаграммами, сходящимися к вершинам. Он состоит из 30 модулей, которые складываются из квадратов, размером 8х8 см. Лучше всего использовать профессиональную бумагу-оригами, которая позволит создавать чёткие грани и жёсткие узлы, не позволяющие конструкции распадаться или деформироваться.
Интересные факты о додекаэдре
Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.
Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.
Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.
Игрушки древних римлян
На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины.
Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной.
Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.
Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.
В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр.
Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее.
В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.
Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.






Конструкция развертки
Высокое качество обработки обеспечивает конструкция развертки – большое количество режущих кромок обеспечивающих небольшой припуск при снятии металла. Процесс резания осуществляется при вращении и одновременном поступательном движении инструмента вдоль оси обрабатываемого отверстия.
Выше приведены рисунки четырёх типов разверток:
Инструмент имеет от 6 до 16 зубьев неравномерно (как правило) распределенных по окружности для повышения качества обработки. Рассмотрим конструкцию на примере ручной развертки цельной с хвостовиком цилиндрической формы. Инструмент состоит из трех основных частей – рабочей, шейки и хвостовика. В свою очередь рабочая часть развертки состоит из направляющей, режущей и калибрующих частей, а также обратного конуса. Основную часть процесса выполняет режущая часть, которая у ручного инструмента значительно длиннее, чем у машинного.
Как сделать правильный икосаэдр | Сделай все сам
Положительным многогранником именуется рельефный многогранник, если все его грани представляют собой равные между собой, положительные многоугольники, при этом в всей его вершине сходится идентичное число ребер.
Инструкция
1. Для построения икосаэдр а воспользуемся построением куба. Обозначим одну из его граней SPRQ.
2. Проведите два отрезка AA1 и BB1, так, дабы они соединяли середины ребер куба, то есть as = AP = A1R = A1Q = BS = BQ.
3. На отрезках AA1 и BB1 отложите равные между собой отрезки CC1 и DD1 длиной n так, дабы их концы находились на равных расстояниях от ребер куба, т.е. BD = B1D1 = AC = A1C1.
4. Отрезки CC1 и DD1 – это ребра строящегося икосаэдр а. Возведя отрезки CD и C1D, вы получите одну из граней икосаэдр а – CC1D.
Совет 2: Как сделать икосаэдр из бумаги
Икосаэдр – это верный многоугольник. Такая геометрическая фигура имеет 30 ребер, 20 треугольных граней и 12 вершин, являющихся местом стыка пяти ребер.
Собрать икосаэдр из бумаги достаточно трудно, но дюже увлекательно. Его дозволено сделать из гофрированной, упаковочной либо цветной бумаги, фольги.
Применяя разные материалы, вы можете придать еще крупную эффектность и красоту своему икосаэдру.
Вам понадобится
Совет 3: Как сделать положительный октаэдр
Октаэдр – один из четырех верных многогранников, которым люди придавали магическое значение еще в античные времена. Данный многогранник символизировал воздух. Демонстрационную модель октаэдра дозволено сделать из плотной бумаги либо проволоки.
Вам понадобится










Разнообразие фигур
На основе пяти приведенных видов, используя умение и фантазию, умельцы легко конструируют множество различных моделей из бумаги. Многогранник может совершенно отличаться от вышеописанных пяти фигур, формируясь одновременно из различных по форме граней, например из квадратов и треугольников. Так получаются архимедовы тела. А если одну или несколько граней пропустить, то получится открытая фигура, просматриваемая как снаружи, так и внутри. Для изготовления объемных моделей используются специальные выкройки, вырезаемые из достаточно плотной, хорошо держащей форму, бумаги. Делают и особенные многогранники из бумаги. Схемы таких изделий предусматривают наличие дополнительных, выступающих модулей. Разберем способы, как сконструировать очень красивую фигуру на примере додекаэдра (фото 3).