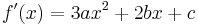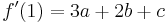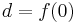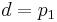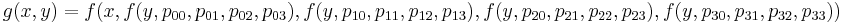Как сделать интерполяцию пример

Бикубическая интерполяция, теория и практическая реализация

Терминология

Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Кубическая интерполяция

Чтобы лучше понять принцип бикубической интерполяции, предлагаю рассмотреть принцип кубической интерполяции.

Если значения функции f(x) и ее производной известны в точках x=0 и x=1, тогда функция может быть интерполирована на интервале [0, 1] используя полином третьего порядка. Формула для вычисления может быть легко получена.

Полином третьего порядка и его производная: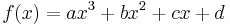

Значения полинома и его производной в точках x=0 и x=1

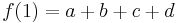
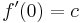
Эти четыре тождества могут быть записаны как: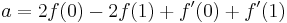

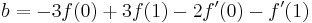
Итак мы получили нашу интерполяционную формулу

На практике алгоритм используют для интерполяции функции, имея некие известные значения в заданных точках. В этом случае мы не можем знать производную функции. Мы могли бы принять производную в заданных точках, как 0, однако для получения более гладких и правдоподобных графиков функций мы примем за производную уклон линии между предыдущей и следующей точкой. Таким образом для расчетов нам понадобится 4 точки. Предположим, мы имеем 4 значения функции в точках p0, p1, p2 и p3, расположенных соответственно на x=-1, x=0, x=1 и x=2. Подставим полученные значения f(0), f(1), f(2) и f(3):

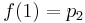
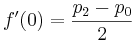
Сопоставив эти данные с полученными ранее формулами мы имеем: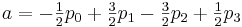

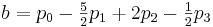
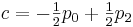
Результат:

Рассмотрим реализацию этого алгоритма на PHP:

Бикубическая интерполяция

Бикубическая интерполяция представляет собой кубическую интерполяцию в двух измерения. На самом деле мы можем интерполировать и в большем количестве измерений, но в рамках данной статьи, рассмотрим только этот пример.
Представим, что нам известно 16 точек p_ij, с точкой начала координат в (i-1, j-1), где i,j изменяются от 0 до 3. Тогда, мы сможем интерполировать поверхность на участке [0,0] х [1,1], для этого интерполируем 4 колонки и потом интерполируем полученные результаты в горизонтальном направлении:

Реализация метода на PHP, совмещенная с первой функцией:

Все было бы здорово, если бы не одна проблема — производительность. Для того чтобы интерполировать даже относительно небольшой объем данных требуются серьезные вычислительные ресурсы. Для оптимизации быстродействия существует следующий подход.
Рассмотрим нашу формулу в виде многомерного полинома: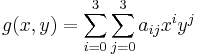

В развернутом виде будет что-то вроде:

Теперь необходимо вычислить коэффициенты a_ij. Здесь особо хотелось бы отметить, что вычислив единожды коэффициенты мы можем использовать их для интерполяции всех значений на участке от [0,0] до [1,1]

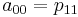
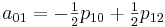
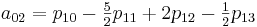
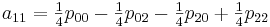
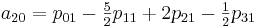
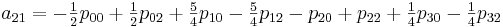
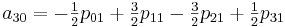
Для реализации этого метода создадим следующий класс:

Практическое применение

Рассмотрим применение бикубической интерполяции на следующем примере:
Исходные данные: массив данных 7 х 7 точек
Требуется: Представить поверхность в виде изображения 300 х 300 пикселей.

В коде постарался максимально возможно прокомментировать каждый шаг, думаю все будет понятно

Отдельно вынес файл для создания карты цветов

Источник

Интерполяция данных: соединяем точки так, чтобы было красиво

Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:

Немного матчасти

Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P₁&nbsp. &nbspP_n, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти n&nbsp–&nbsp1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:

Функции f_i могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками P_i) называется сплайном.

В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.

Ставим опыты

Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
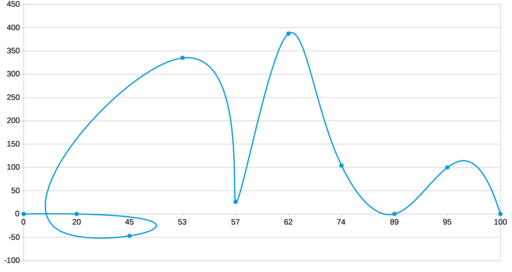
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):

Результат линейной интерполяции этих точек выглядит так:

Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.

Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a;&nbspb], это означает, что на [a;&nbspb] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз P_i, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.

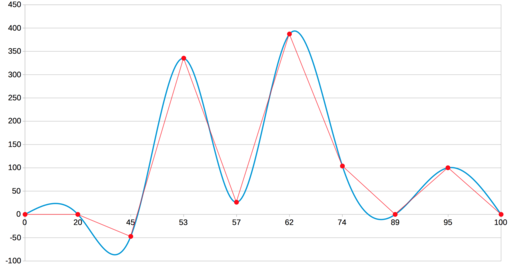
Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:

Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.

Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n&nbsp–&nbsp1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
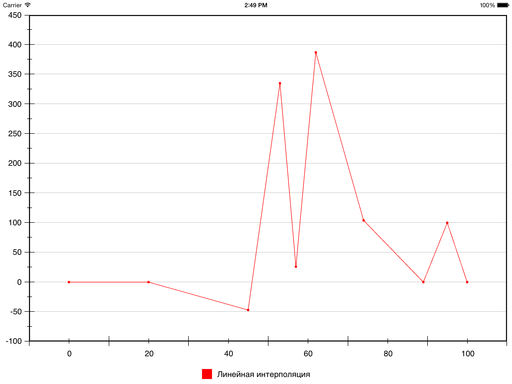
Но вот что получается:

Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.

В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k&nbsp+&nbsp1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k&nbsp–&nbsp1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:

Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k&nbsp=&nbsp1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k&nbsp–&nbsp1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k&nbsp=&nbsp3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (P_i), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
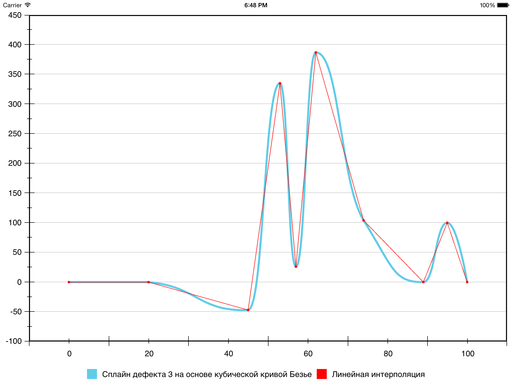
Вот что получится на нашем тестовом наборе:

Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.

Думаем и экспериментируем

Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:

Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:

Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C₁ (1) и C_{n&nbsp–&nbsp1} (2) совпадают с точками P₁ и P_n соответственно).
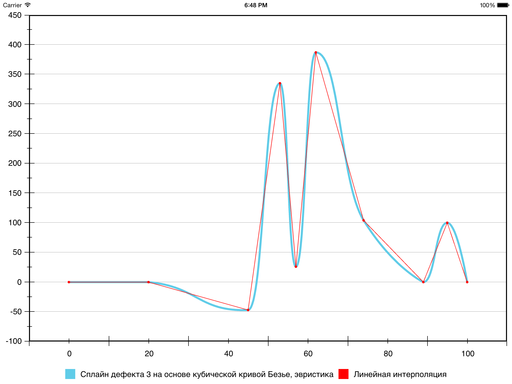
В этом случае получается вот такая кривая:

Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.

Эвристика для вычисления расстояний будет такой:

Результат получается такой:

В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:

Результат следующий:

На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.

А как люди-то делают?

Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.

MS Excel

Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.

LibreOffice Calc

В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.

Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат 🙂

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).

amCharts, ещё одна популярная JS-библиотека

Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.

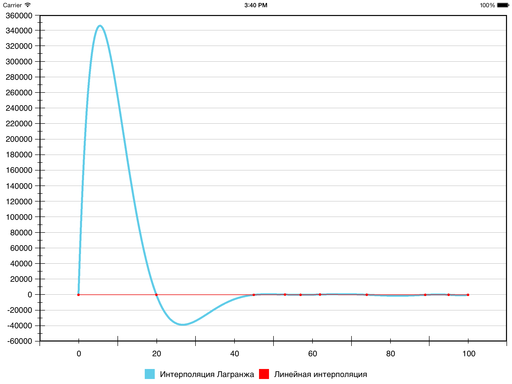
Coreplot, самая популярная библиотека построения графиков для iOS и OS X

Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.

aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n&nbsp–&nbsp1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.

Источник