Как сделать карту шухарта
InLean
Методики бережливого производства и оптимизации бизнес процессов
Контрольные карты Шухарта
Контрольная карта Шухарта показывает, когда ваш процесс выходит из-под контроля и помогает определить наличие специальных причин вариации. Когда мы сталкиваемся с особыми причинами вариации, наш процесс начинает быть нестабильным и нам необходимо принимать меры, чтобы выровнять процесс. Также на контрольной карте можно увидеть тренды и предсказать дальнейшее развитие процесса. Поэтому контрольные карты используются для определения зон фокуса.
Контрольная карта – это график, на котором отображены данные, упорядоченные по времени. Большинство контрольных карт включает центральную линию и верхний и нижний контрольный лимит. Центральная линия – это среднее значение процесса. Контрольные лимиты – это вариабельность процесса. По умолчанию, контрольные лимиты рисуются на расстоянии 3-х стандартных отклонений от центральной линии.
Когда использовать контрольные карты
Контрольные карты могут быть полезным инструментом вне зависимости контролируете ли вы текущий процесс или пытаетесь лучше понять новый процесс.
Вы можете использовать карты Шухарта для:
Структура контрольных карт
Как я уже говорил ранее, обычная контрольная карта состоит из графика переменных процесса, центральной линии и верхних и нижних контрольных лимитов. Также некоторые карты могут содержать спецификационные лимиты. Давайте разберем каждый из этих элементов более подробно.
Центральная линия представляет собой фактическое среднее значение процесса и это не обязательно требуемое среднее значение процесса.
Центральная линия представляет собой горизонтальную линию на графике и отражает среднее значение измеряемого параметра качества. Центральная линия нужна, чтобы видеть, как ведет себя процесс по сравнению со средним значением. Если наш процесс контролируется, точки будут случайным образом распределены по обе стороны от центральной линии.
Не путайте центральную линию с целевым значением процесса. Целевое значение – это желаемый результат, а не фактический.
Контрольные лимиты отражают вариабельность процесса и помогают понять, когда ваш процесс находится не под контролем.
Контрольные лимиты – это горизонтальные линии выше и ниже центральной линии, которые используются для оценки стабильности процесса. Верхний и нижний контрольные лимиты рассчитываются на основе случайной вариабельности процесса. По умолчанию, контрольные лимиты отражают 3 стандартных отклонения выше и ниже центральной линии.
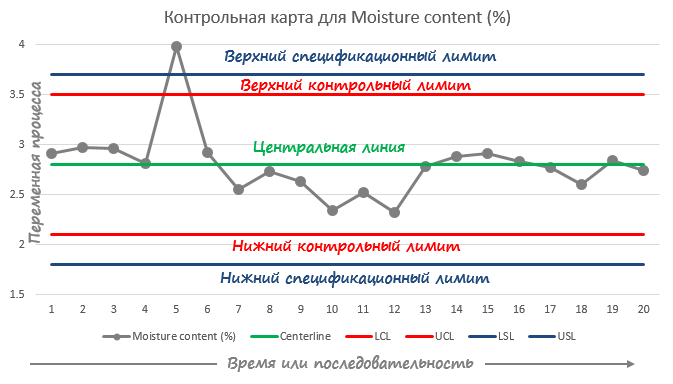
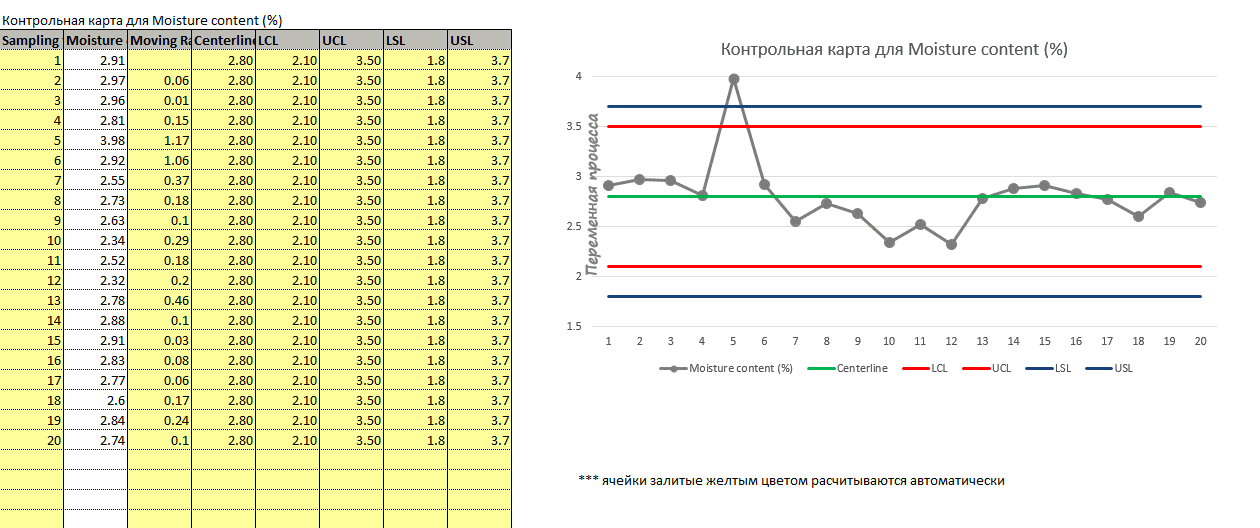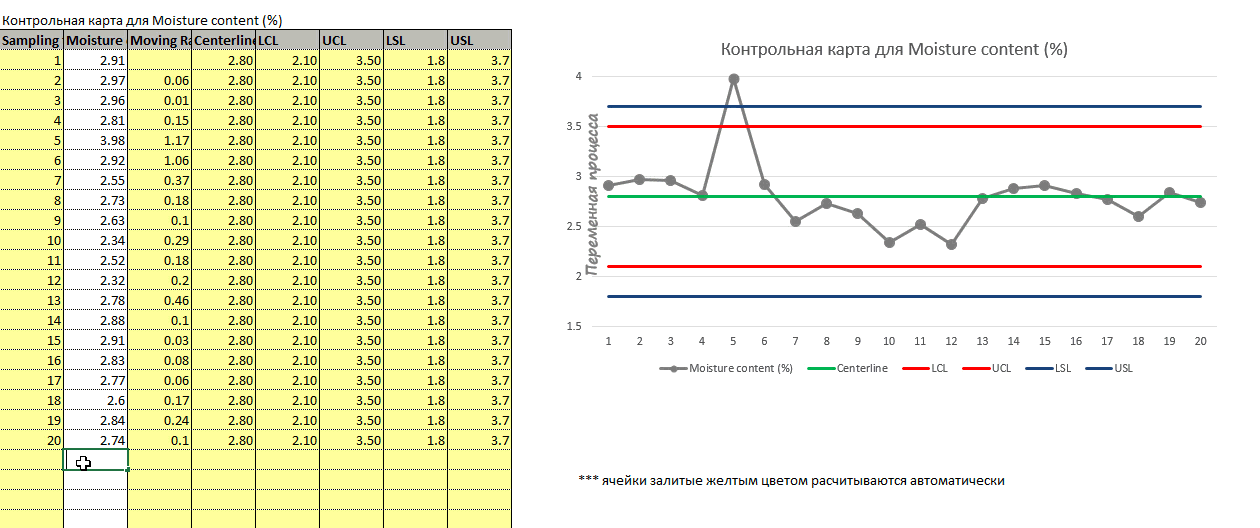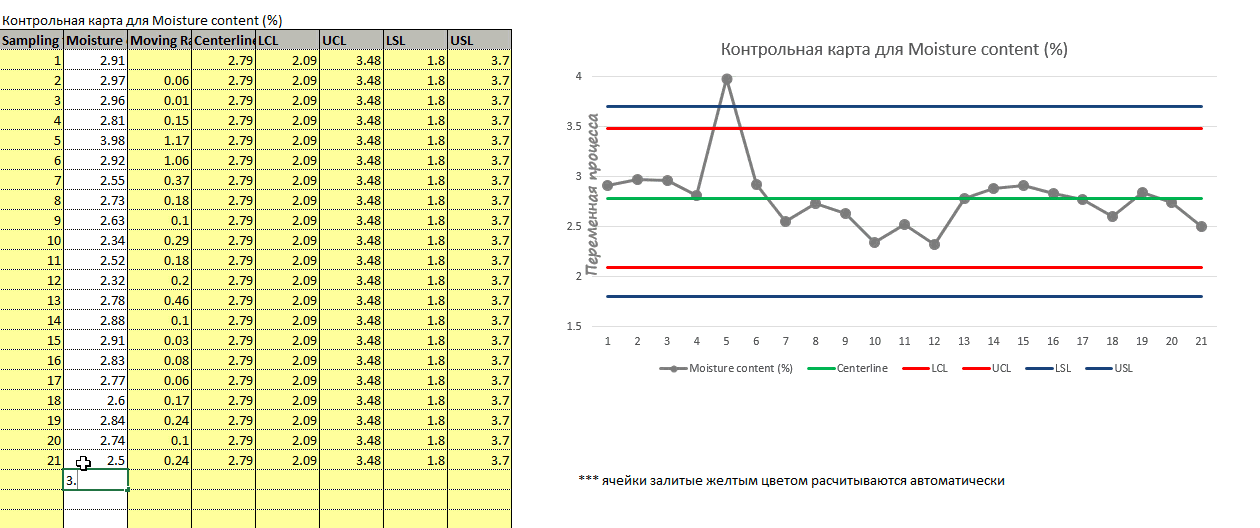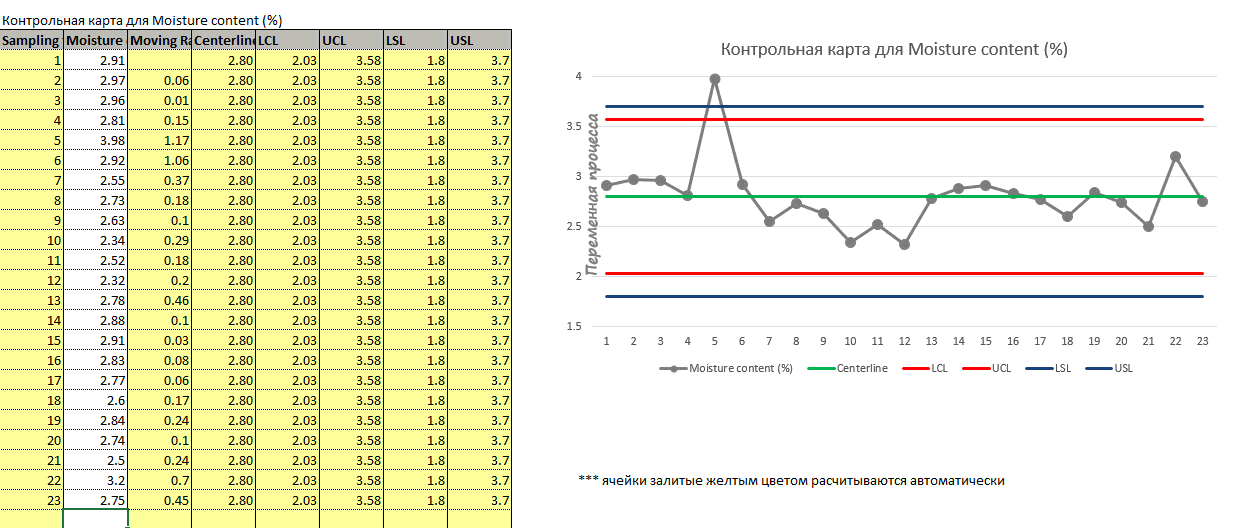
На примере выше график отражает измерения влажности продукта. Видно, что пятая точка измерения находится выше верхнего контрольного лимита. Эта точка показывает, что влажность продукта в этот момент времени была выше ожидаемого.
Не путайте контрольные лимиты со спецификационными лимитами. Контрольные лимиты рассчитываются исходя из вариабельности процесса, спецификационные лимиты основаны на ожиданиях клиента. Процесс может быть под контролем и, тем не менее, не отвечать требованиям спецификации.
Спецификационные лимиты — это значения, внутри которых должен находится процесс. На графике это горизонтальные линии ниже и выше центральной линии. Эти границы обычно определяются требованиями потребителя. На примере влажности продукта выше. Если влажность будет выше спецификационного лимита, продукт испортится раньше, указанного на упаковке, срока годности. И наоборот, если влажность будет ниже, продукт будет очень твердым и его никто не будет покупать.
Построение контрольных карт
Контрольные карты строятся достаточно просто, при наличие Minitab. Достаточно иметь данные для построения и знать, какой график вы хотите построить (об этом мы поговорим в следующих статьях). Но даже если Minitab’a нету под рукой, в Excel контрольные карты тоже можно построить.
Давайте с вами рассмотрим пример построения самого популярного графика для контрольных карт I-MR. I-MR расшифровывается как Individual – Moving Range и используется, если в одном тесте у нас всего одно измерение.
В появившемся диалоговом окне Individuals-Moving Range Chart в поле Variables указываем набор переменных для нашего графика.
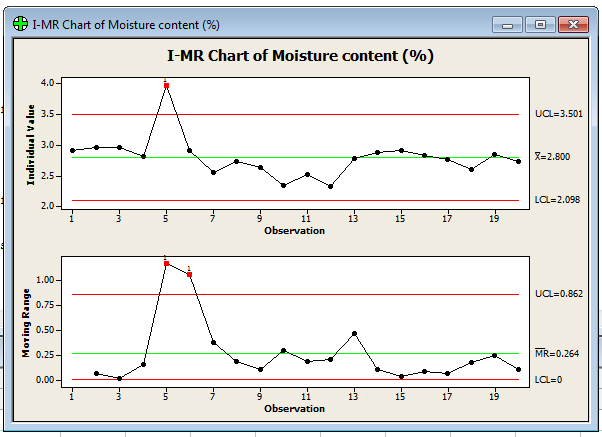
Щелкаем кнопку OK, и программа выдает окно, которое состоит из двух графиков. Первый, верхний график выстроен по индивидуальным значениям каждого измерения. Второй, нижний график отражает размер смещения каждого последующего измерения от предыдущего, т.е. насколько изменилось значение по сравнению с предыдущим. По сути, это разница измерений, например, между вторым и первым, третьим и вторым и т.д. Поэтому для первой точки измерения на графике Individual отсутствует точка на графике Moving Range, так как она первая и сравниваться ей не с чем.
Если у вас не установлен Minitab не расстраивайтесь. Excel также прекрасно справляется с построением графиков временного ряда, только нужно будет добавить функционал позволяющий рассчитывать контрольные лимиты. Да и это тоже не проблема. Я создал для вас файл-шаблон, который выстраивает контрольную карту по тому набору данный, который у вас имеется.
Для более простого понимания вы можете скачать файлы, которые я использовал при создании этой статьи.
Сегодня мы с вами поговорили о контрольных картах – основном инструменте статистического управления процессами. Контрольные карты помогают понять, является ли процесс под контролем и предсказать изменения в процессах в будущем. В следующей статье мы с вами поговорим о типах контрольных карт, встречающихся в SPC
Один комментарий
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Построение x-R карты Шухарта
Оценка индекса работоспособности процесса термомеханического упрочнения
И.А. Гунькин
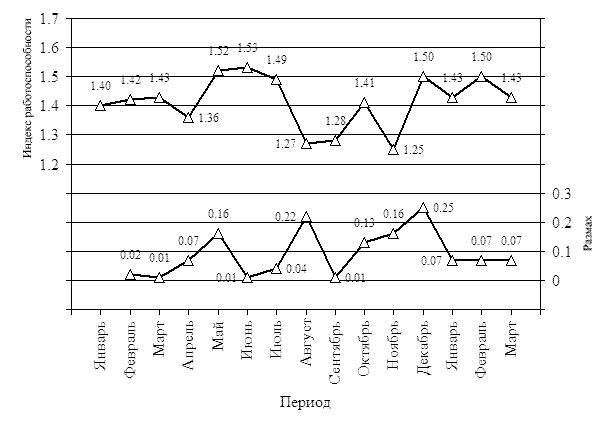
На предприятии ведется мониторинг индекса работоспособности процесса термомеханического упрочнения арматурного проката диаметром 12 мм класса А500С по ДСТУ 3760. Данные о величине индекса работоспособности за 15 последних месяцев приведены в Таблице 1. Необходимо построить карту Шухарта индивидуальных значений и текущего размаха для наблюдаемого процесса.
Мониторинг индекса работоспособности процесса термомеханического упрочнения арматурного проката диаметром 12 мм класса А500С по ДСТУ 3760
Строим расчетную таблицу:
Расчетная таблица для построения контрольной x-R карты
Первый шаг построения контрольной карты Шухарта
Строим две диаграммы:
● верхняя диаграмма: x-карта (текущие значения xi),
● нижняя диаграмма: R-карта (текущий размах Ri).
Рис. 1. Первый шаг построения x-R карты. Нанесение на диаграмму исходных данных.
На первом шаге построения можно провести два теста:
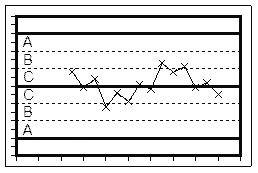
Таким образом, Тест “6” и Тест “14” не выявили особых точек на строящейся диаграмме Шухарта.
Второй шаг построения контрольной карты Шухарта
Определяем параметры диаграммы, для чего рассчитываем оценки статистического распределения:
● среднее значение параметра 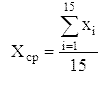
● среднее значение текущего размаха 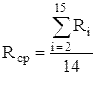
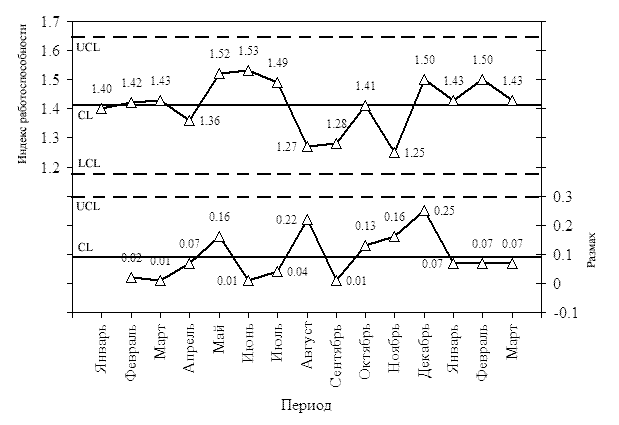
Принимаем для x-карты значение центральной линии CL=1.41 (см. Таблицу 3). Для R-карты значение центральной линии принимаем равной CL=0.09.
Линии контрольных карт
Примечания:
1. Нижняя контрольная граница LCL для R-карты отсутствует, так как она меньше нуля.
2. Границы для контрольных карт необходимо принимать таким образом, чтобы наносимые значения не могли принадлежать какой-либо контрольной линии. Если, например, точность измерения обеспечивает 0.01 единицу, то для границы значение надо принимать в виде x.xx5. В этом случае, к примеру, параметр может принять значение 1.32 или 1.33, но никак не 1.325. Искомая точка при этом будет обязательно лежать ниже или выше границы.
Наносим контрольные пределы на диаграмму.
Рис. 2. Второй шаг построения x-R карты. Нанесение на диаграмму центральных линий и контрольных пределов.
На втором шаге построения также можно провести два теста:
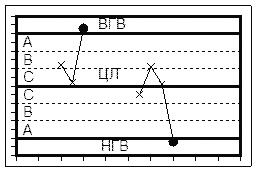
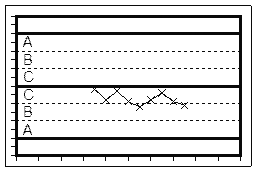
Тест одной точки: Точка выходит за контрольные пределы
Ни одна из исследуемых точек не выходит за контрольные пределы, т.е. не лежит выше UCL или ниже LCL.
Таким образом, Тест одной точки и Тест “9” не выявили особых точек на строящейся диаграмме Шухарта.
Третий шаг построения контрольной карты Шухарта
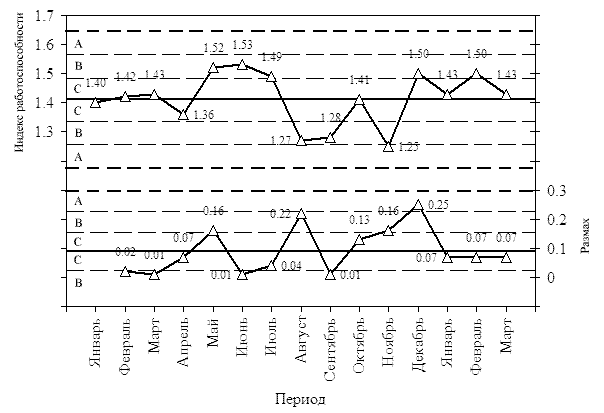
Определяем зоны A, B и C на контрольных картах.
Рис. 3. Третий шаг построения x-R карты. Выделение зон A, B и C.
На третьем (завершающем) шаге построения проводят еще четыре теста:
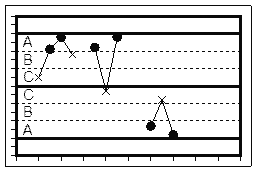
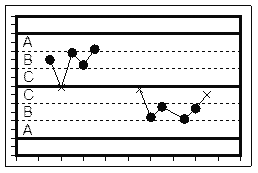
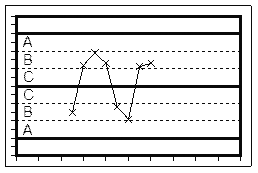
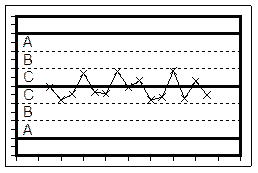
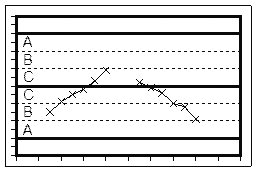
Тест “3”: Две из трех последовательных точек находятся с одной стороны от центральной линии в зоне A или дальше
На R-карте в зоне A находятся только одна точка: декабрь 2007 г. На x-карте в зоне A нет ни одной точки. Тест “3” для карты Шухарта отрицательный.
Тест “5”: Четыре из пяти последовательных точек находятся с одной стороны от центральной линии в зоне B или дальше
Для R-карты составим таблицу:
Таким образом, все 8 тестов дали отрицательный результат. Особых точек на карте Шухарта не обнаружено. Причин отклонить предположение о том, что рассматриваемая последовательность подчинена нормальному закону со средним 1.41 и средним размахом 0.09 нет.
Окончательный вид контрольной карты Шухарта индивидуальных значений и текущего размаха (x-R карты) показан на рис. 3.
Материал подготовлен на основании ДСТУ ISO 8258-2001 Статистический контроль. Контрольные карты Шухарта.
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди «Не укради»
Основы 6-сигм и контрольных карт Шухарта (слайдкаст)
Недавно дошли руки до превращения записи моего доклада на AgileKitchen в полноценный слайдкаст.
По моему опыту, в Agile-командах процент собираемых метрик, использующихся для принятия управленческих решений, заметно выше, чем в командах, следующих более консервативным моделям разработки. Однако нужно понимать, что каждое измерение неизбежно содержит в себе ошибку. Перед тем, как принять то или иное решение на основе «аномалий» в наблюдаемых значениях, было бы не плохо понять, что стоит за этой «аномалией»: некоторая особая причина, требующая реакции со стороны руководства, или такое поведение является нормальным для рассматриваемой системы?
В слайдкасте дается намек на то, как в результатах измерений отделить свойства системы от особых причин отклонений, и рассказывается об основных ошибках при использовании данных измерений при принятии управленческих решений.
Ой, у вас баннер убежал!
Читают сейчас
Редакторский дайджест
Присылаем лучшие статьи раз в месяц
Скоро на этот адрес придет письмо. Подтвердите подписку, если всё в силе.
Похожие публикации
Six Towers. История успеха?
Практикум использования контрольных карт Шухарта
Ubisoft выпускает патчем к новой «Rainbow Six» крек от RELOADED!
Курсы
AdBlock похитил этот баннер, но баннеры не зубы — отрастут
Минуточку внимания
Комментарии 34
Да, в наших кругах это уже становится мемом.
А на самом деле откровенных снежинок в нашей индустрии не так уж и много. Как правило, за внешними проявлениями качеств человека-снежинки лежит более глубокая системная проблема.
В свое время меня очень утомило гнусное бухтелово под отвратительные слайды в PowerPoint, с тех пор я стараюсь доказать (прежде всего самому себе), что практически любую тему можно передать аудитории более эффективно и интересно.
Подготовка к такому докладу занимает на много больше времени, но результат того стоит.
Менеджеры любят цифры. Да это проще, чем работать с людьми, узнавать их ценности и потребности, понимать их и изучать их, учиться узнавать, что их мотивирует на самом деле.
В фильме Невидимая сторна, есть классный эпизод с основной мыслью — Знай свою команду. Просто вспомнилось.
Тайная мечта большинства менеджеров — иметь абсолютно объективный способ принимать любые решения да и еще таким образом, что бы все с этим были согласны.
Но с цифрами отнюдь не проще. Иллюзия простоты есть, но по сути это так же сложно как разбираться с ценностями людей.
Тема статистического обоснования не раскрыта. Если мы (как написано в русской википедии) рассматриваем σ как среднеквадратичное отклонение, то хотя бы понятно, что при нормальном распределении мы с p=0.95 должны попадать шесть сигм, и это легко доказать.
Что можно говорить о «вообще любом» распределении, да и ещё считая размах, я не понимаю. Есть какие-то доказательства на этот счет?
Очень хороший вопрос.
Строго математического доказательства нет. В книге Д. Уилера и Д. Чамберса Статистическое управление процессами есть отдельная глава, посвященная результатам численного моделирования. Авторы моделировали случайные величины, распределенные по пяти разным законам и показывали, что критерий Шухарта (отклонение больше, чем на 3 сигма от центральной линии) достаточно хорош для каждого из распределений.
К сожалению, в википедии написана не вся правда. Изначально Шухарт, а затем Деминг разработали эту модель, и на практике показали ее экономическую целесообразность (а не математическую справедливость) без каких-то априорных предположений о конкретном виде распределения. Единственным требованием на этот счет было лишь существование этого распределения и достаточная его стабильность во времени.
В той же книге Уилера и Чамберса есть отдельная глава про мифы и распространенные заблуждения насчет контрольных карт. Заблуждениям насчет нормального распределения и центральной предельной теоремы посвящены как раз первые два раздела этой главы.
Если сделать чуть более глубокий шаг в сторону теоретизации то тут мы имеем задачу, сходную с байесовским детектором. В далеких 20-х годах прошлого века, когда Шухарт и Деминг работали в Bell Laboratories, перед ними стоял простой вопрос: «как из данных измерений производства, понять, когда стоит идти в цех и искать особые причины сбоев системы, а когда можно в цех не ходить и списать все на ее свойства?». В итоге получалась простая, конечная игра с матрицей выигрышей 2х2 (цена правильного детектирования, цена правильного пропуска, цена ложной тревоги и цена ложного пропуска особой причины). В их время, в их компании, в их экономической ситуации, в их производственной системе критерий Шухарта оказался наиболее экономически оправданным.
Вот, собственно, и все. Никаких чудес и никакой математической строгости.
Я хоть и в статистике и не очень, но есть вот такая штука, называется Central Limit Theorem. Не буду кривляться, не знаю как она в РФ правильно называется терминологически. Так вот, она говорит:
Какое бы дикое не было наше распределение, но если мы будем брать достаточное количество проб, высчитывать их среднюю, и смотреть распределение средних, то мы все равно придем к (сюрприз) нормальному распределению.
Вот тут, есть симулятор. Можно взять, нарисовать любой дикий процесс и получить Гаусса.
В РФ это называется Центральная Предельная Теорема.
Но контрольные карты Шухарта работают и при небольших размерах подгрупп (даже 2 точки). Двух точек не достаточно, что бы превратить какое угодно распределение в нормальное.
Да, конечно. Я написал это лишь к тому чтобы «засигнализировать» что статистически даже в мейнстриме науки не нужно знать распределения чтобы делать выводы.
Тот же тест «студента» изначально выводился синтетически just to obtain better real life estimations. Несколько подобный принцип, как я понял, и с этой таблицой Шухарта. Эмпирически вывели параметры/коэффиценты для получения положительных (с точки зрения эфф.) результатов.
Спасибо за хорошее замечание. Log-normal так и называется — логнормальное распределение.
Фактически вы правы, если заранее известен вид распределения, то можно более точно вычислять контрольные пределы, однако полученная прибавка к точности может не оправдать возросшей математической сложности задачи. Плюс ко всему в реальном производстве достоверно судить о конкретном виде распределения практически никогда нельзя.
Согласен, это достаточно интересное направление. Но этого мы не исследовали, так как вариацию команды саму по себе в наших обстоятельствах мы считаем негативным явлением, проявление которого лучше избегать.
На вопрос «Делать самим или отдать компании-подрядчику?» универсального ответа нет и все будет зависеть от многих условий. И, самое главное, все определяется ответом на вопрос «Зачем?». Как ни странно, при определенных условиях, имея целью увеличение прибыли компании, иногда будет правильным отдать проект на аутсорс даже если это дольше, дороже и с сомнительным качеством. Но это уже другая история, идущая в сторону теории ограничений…
На этом слайде у манагера руки не оттуда нарисованы:
Только полноправные пользователи могут оставлять комментарии. Войдите, пожалуйста.