Как сделать кинематический анализ

Примеры кинематического анализа

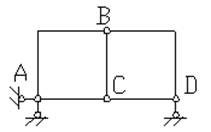
Пример 1.1. Произвести кинематический анализ системы (рис.1.14).

Определяем степень свободы системы по формуле П.Л.Чебышева:

где Д – число дисков, Ш – число простых шарниров, С₀ – количество стержней.

Рис.1.14

Отсюда W = 3∙5 – 2∙6 – 3 = 0, то есть система может быть геометрически неизменяемой и статически неопределимой. Чтобы убедиться, что это так, выполним анализ структуры системы. Так как диски АВ, ВС и АС связаны тремя шарнирами А, В и С, не лежащими на одной прямой, то они образуют диск, к которому жестко присоединен диск ВД с помощью шарнира В и стержня СД, ось которого не проходит через центр шарнира. Эта неизменяемая фигура жестко присоединена к земле с помощью трех стержней, не пересекающихся в одной точке. Таким образом, система (рис.1.14) геометрически неизменяема и не является мгновенно изменяемой.

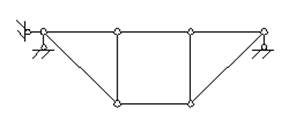
Пример 1.2. Выполнить кинематический анализ системы (рис.1.15).

Рис.1.15

Так как система является шарнирно-стержневой, то для определения ее степени свободы используем формулу (1.2):

где У – число узлов фермы; С – число внутренних стержней; С₀ – число опорных стержней.

Здесь У = 6, С = 8, С₀ = 3, следовательно, W = 2∙6 – 8 – 3 = 1.

Таким образом, система имеет одну степень свободы, и не может использоваться как строительная конструкция.

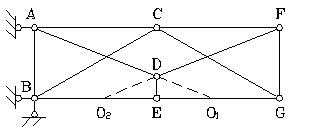
Пример 1.3.Исследовать ферму (рис.1.16).

Рис.1.16

По формуле (1.2) определяем степень свободы фермы: W = 2∙7 – 11 – 3 = 0, следовательно, система может быть геометрически изменяемой и статически определимой.

Проанализируем систему. Она состоит из трех дисков – треугольники АВС, CFG и стержень DЕ, связанных между собой стержнями ВЕ, АD, ЕG, DF, которые можно заменить фиктивными шарнирами О₁, О₂ и шарниром С. Следовательно, можно сделать вывод: все стержни соединены между собой жестко и прикрепляются к земле так же жестко с помощью трех стержней, не пересекающихся в одной точке.

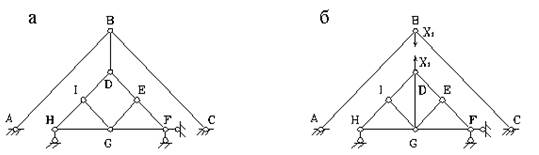
Пример 1.4. Выполнить кинематический анализ системы (рис.1.17,а).

Рис.1.17

По формуле (1.2) определяем степень свободы: W = 2∙9 – 11 – 7 = 0, то есть система обладает необходимым минимумом связей, чтобы быть геометрически неизменяемой. Для проверки того, является ли система действительно неизменяемой, используем метод замены стержней. Выберем заменяющую систему (рис.1.17,б). Здесь отброшен стержень ВD, а его действие заменено силами Х₁, и добавлен заменяющий стержень DG. Выбранная заменяющая система неизменяема: стержни АВ, ВС и земля жестко соединены тремя шарнирами, не лежащими на одной прямой. А нижняя часть системы неизменяема, поскольку состоит из треугольника (например, GHI), к которому жестко прикреплены все остальные узлы с помощью диад, и все это прикреплено к земле тремя опорными стержнями.

Пример 1.5. Произвести анализ образования системы, показанной на рис.1.18.

Рис.1.18

Пример 1.6. Произвести анализ образования системы, показанной на рис.1.19, а.

Рис.1.19

1. Пользуясь формулой W = 2У – С – С₀ для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У=6, число стержней системы С=9, число опорных стержней С₀=3, следовательно, W = 2∙6 – 9 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы быть неизменяемой и статически определимой.

2. Проводим анализ структуры системы. Рассмотрим треугольник 123, который в соответствии с третьим признаком является неизменяемой системой. Считая его жестким диском (заштрихован на рис. 1.19, б), присоединим к нему двумя стержнями (3-4 и 2-4) узел 4. Эти стержни не лежат на одной прямой, следовательно, на основании первого принципа узел 4 неподвижно прикреплен к диску 123. Полученная система также является жестким диском (заштрихован на рис.1.19, в). Прикрепив к нему двумя стержнями (4-5 и 2-5) узел 5 снова получим жесткий диск, заштрихованный на рис.1.19, г). К этому диску присоединим двумя стержнями (3-6 и 5-6) не лежащими на одной прямой последний узел 6.

Поскольку система образована в соответствии с принципами образования структурно неизменяемых систем, она неизменяема и не является мгновенно изменяемой. К земле система прикреплена так же жестко, с помощью трех опорных стержней, не пересекающихся в одной точке.

Пример 1.7. Произвести кинематический анализ системы, показанной на рис. 1.20.

Рис.1.20

1. Пользуясь формулой W = 2У – С – С₀ для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У=9, число стержней системы С=15, число опорных стержней С₀=3, следовательно, W = 2∙9 – 15 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы быть геометрически неизменяемой.

2. Проводим анализ структуры системы. Вначале найдем заведомо неизменяемые части системы – два диска, образованные треугольниками (заштрихованы на рис. 1.21, б). Они соединены тремя стержнями. Однако эти стержни пересекаются в одной точке (т. k на рис. 1.21, б). Следовательно, система мгновенно изменяемая.

Пример 1.8. Проанализировать систему, изображенную на рис. 1.21.

Система состоит из четырех дисков (AС, СE, EF и FH) т.е. Д=4. Число шарниров Ш=3 (все шарниры простые). Число опорных стержней С₀=2+1∙4=6. Степень свободы системы по формуле W = 3Д – 2Ш – С₀ = 3∙4-2∙3-6=0.

Рис.1.21

Необходимое условие неизменяемости системы удовлетворено. Производим анализ структуры. Диск АС присоединен к земле тремя опорными стержнями, не пересекающимися в одной точке. Такое прикрепление обеспечивает неподвижность диска АС. К нему шарниром С и к земле опорным стержнем в точке D прикреплен диск СЕ. При этом ось стержня D не проходит через шарнир С. К полученной неизменяемой системе стержнем EF и двумя опорными стержнями в точках G и H присоединен диск FH. Эти три стержня не пересекаются в одной точке.

Таким образом, рассматриваемая система неизменяема и не является мгновенно изменяемой.

Пример 1.9.Проверить геометрическую неизменяемость системы, приведенной на рис. 1.22.

Рис.1.22

Следовательно, система имеет необходимое количество связей, чтобы неизменяемой. Проанализируем ее структуру.

Вместе с землей система состоит из трех дисков, соединенных между собой шарниром Ш_{1 – 2} и четырьмя стержнями, эквивалентными условным шарнирам Ш_{1 – 3} и Ш_{2– 3}.

Так как три шарнира, соединяющие три диска, лежат на одной прямой, система мгновенно изменяема.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Порядок выполнения кинематического анализа

1. Производим подсчет числа степеней свободы по формуле (1.1),

либо (1.2). «Земля» при этом не является диском.

2. Если W>0, система геометрически изменяема (ГН). Кинемати- ческий анализ окончен.

Г. Комбинированные системы. Это сложные системы, представ- ляющие собой комбинацию элементов разного вида.

Примеры кинематического анализа плоских стержневых систем

А. Системы балочного типа

а) б)

в)

Рис. 1.20

Пример 1.1. Выполним кинематический анализ балки и рамы, изображен- ных на рис. 1.20, а, б.

1. Подсчитываем число степеней свободы по формуле (1.1). При этом число дисков Д =1; шарниров нет; количество опорных связей С ₀ =3. Подставив в формулу (1.1), получим: W =3·1–3=0. Отсюда вы- вод: возможно, что система СО и ГН.

Рис. 1.21

2. Анализ по образованию.

«Земля» здесь также является дис- ком. Необходимо доказать, что диск самой конструкции (Диск 1) и «зем- ля» (Диск 2) соединены опорными связями в ГН-систему (рис. 1.21).

Каждый элемент опоры можно считать связью 1-го вида. Тогда мы прихо- дим к стандартному случаю соединения двух дисков в ГН-систему: диски связаны при помощи трех стержней, не пересекающихся в одной точке и не параллельных между собой.

3. Делаем окончательный вывод: система ГН и СО.

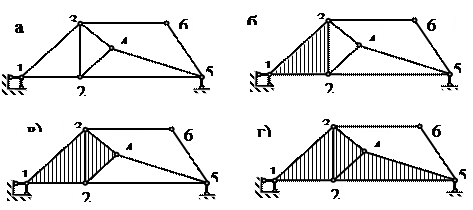
Пример 1.2. Выполним кинематический анализ фермы (рис. 1.20, в):

1. Подсчитываем число степеней свободы по формуле (1.2). Здесь количество стержней С = 25 ; узлов У = 14; связей С ₀ = 3 .

Вывод: возможно система ГН и СО.

2. Кинематический анализ фермы по ее образованию. Сначала не- обходимо доказать, что сама ферма является диском. А затем рассмотреть, как этот диск соединяется с «землей» (рис. 1.22). Здесь каждый элемент (стержень) фермы является диском. Анализ удобнее производить по сле- дующей схеме: принимаем любой стержень фермы за базовый диск (на- пример, левая стойка – диск 1). Далее считаем, что к этому диску присое- динена диада (стержни, помеченные штрихом), следовательно, образовал- ся новый диск из трех стержней. К этому диску присоединяется новая диа- да (стержни, помеченные двумя штрихами) – образуется новый диск из пя- ти стержней и т. д. Для левой полуфермы диады обозначены соответст- вующими значками. Таким образом, анализ по образованию фермы можно сформулировать так: ферма образована последовательным присоединени- ем диад к диску 1, следовательно, она ГН и представляет собой диск.

Этот диск связан с «землей» тремя

Рис. 1.22

связями, не пересекающимися в од- ной точке и не параллельными меж- ду собой.

3. Делаем окончательный вы- вод: система ГН и СО.

Подчеркнем общие положения, связанные с кинематическим анали- зом систем балочного типа. Если доказано, что сама система является дис- ком, она должна иметь как минимум три связи с «землей». Эти связи не должны быть параллельны друг другу и не должны пересекаться в одной точке.

Б. Составные системы

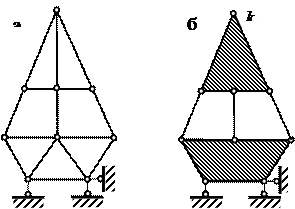
Примеры составных систем показаны на рис. 1.23.

a) б) Главный

Главный диск

Второстеп. диск

Диск

Диск

в) Главный диск

Второстеп. диск

Рис. 1.23

Это могут быть составные балки, рамы, фермы, арки. Все системы, показанные на рис. 1.24, образованы по одному принципу. Главный диск связан с «землей» тремя связями. Второстепенный диск присоединен к главному при помощи шарнира (рис. 1.24, а), либо при помощи двух стержней (рис. 1.24, б). Он обязательно имеет одну связь с «землей». На рис. 1.24 схематично показаны системы, имеющие один или несколько второстепенных дисков, присоединенных последовательно один через дру- гой (рис. 1.24, в), либо только к главному диску (рис. 1.24, г).

а)

г)

Рис. 1.24

Число степеней свободы W для всех схем, показанных на рис. 1.23, 1.24, равно нулю. Например, для системы, показанной на рис. 1.24, г, число

дисков Д = 3, число шарниров Ш = 2, число опорных связей С ₀ = 5. То-

гда получаем W =3·3–2·2–5=0.

Аналогично можно подсчитать W для всех остальных схем.

Кинематический анализ по образованию таких систем выполняется по следующей схеме:

1. Сначала доказывается, что главный диск и «земля» образуют об- щий диск (они связаны тремя связями).

2. Второстепенный диск присоединяется к этому вновь образован- ному диску при помощи шарнира и стержня (либо при помощи трех стержней). Если имеется несколько второстепенных частей, рассматрива- ется присоединение каждой второстепенной части по той же схеме.

Вывод: Система в целом является диском.

Подчеркнем общие положения, связанные с кинематическим анали- зом составных систем. Главный диск должен иметь три связи с «землей» (не параллельные друг другу и пересекающиеся в одной точке). Если вто- ростепенный диск связан с главным шарниром, то ось стержня, соеди- няющего второстепенный диск с «землей» не должна пересекать этот шарнир. В противном случае система мгновенно изменяема (рис. 1.25, а).

б) Второстеп.

Главный диск

Диск

Рис. 1.25. Примеры мгновенно изменяемых систем

Если второстепенный диск связан с главным двумя стержнями, то оси этих стержней, и ось опорного стержня, соединяющего второсте- пенный диск с «землей», не должны пересекаться в одной точке. В про- тивном случае система мгновенно изменяема (рис. 1.25, б).

В. Трехшарнирные системы

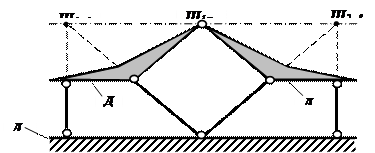
Примеры трехшарнирных систем показаны на рис. 1.26.

Рис. 1.26

Трехшарнирные системы состоят из двух дисков, которые связаны шарниром. К «земле» каждый диск присоединяется шарнирно неподвижной опорой.

Рис. 1.27

Схематично такая система показана на рис. 1.27, а. Вместо шарнира соединение дисков может производиться двумя стержнями (рис. 1.27, б).

Кинематический анализ систем, где диски связаны шарниром (рис.

1. Определяется число степеней свободы по формуле (1.1). Здесь число дисков Д =2, число шарниров Ш =1 , опорных связей С ₀ =4. Под- ставив в формулу, получим: W=3·2– 2 ·1 –4 =0 .

Вывод: возможно, что система СО и ГН.

2. Анализ по образованию:

Рис. 1.28

Включаем «землю» как дополнитель- ный диск (рис. 1.28). Опоры А и В мож- но показать в виде шарниров, присое- диненных к «земле». Тогда мы получа- ем 3 диска, связанных при помощи трех шарниров (А, В, С). Система в целом является СО и ГН. При этом опорные шарниры А, В и шарнир С не должны лежать на одной прямой.

Трехшарнирные системы с затяжкой

В этом случае одна опора становится шарнирно-подвижной. Недос- тающая связь устанавливается как внутренняя и соединяет диски. Приме- ры трехшарнирных систем с затяжкой показаны на рис.1.29

Рис. 1.29

Кинематический анализ производится по следующей схеме.

Вывод: возможно, что система СО и ГН.

2. Анализ по образованию системы:

Включаем «землю» как диск (рис. 1.30). Диск 1 и диск 2 связаны шарниром С и стержнем А-В (ось стержня не пересе- кает шарнир). Следовательно, они обра- зуют общий диск. Этот диск связан с

«землей» тремя связями, которые не пе- ресекаются в одной точке и не парал- лельны друг другу.

Рис. 1.30

Вывод: система СО и ГН.

Пример 1.3. Дана составная балка, показанная на рис. 1.31. Требуется вы- полнить ее кинематический анализ.

A B C D E F

Рис. 1.31

1. Подсчитываем число степеней свободы по выражению (1.1). Чис- ло дисков Д =5; число шарниров Ш =4; число опорных связей С ₀ =7.

Отсюда вывод: возможно, что система СО и ГН.

2. Выполняем анализ балки по ее образованию. При этом «землю»

принимаем за дополнительный диск (рис. 1.32).

E

Ди Земля

Рис. 1.32

Обозначим диски, на которые делится балка (A-B, C-D, D-E, E-F). Соединения этих дисков должны быть четко выделены: это опорные связи G,H,K,F и шарнир D. Диск B-C можно принять за связь 1-го вида, так как он шарнирно присоединен к дискам A-B и C-D и не связан с «землей».

Начнем с того, что диск А-В и диск «земля» связаны жестко, следо- вательно, образуют один общий диск. Обозначим его Д1 и обведем пунк- тиром.

Далее рассмотрим соединения трех дисков: Д1, C-D и D-E. Диски C-D и D-E соединены шарниром D, диски Д1 и C-D – двумя стержнями (B-C и G), и наконец, диски D-E и «земля» соединены двумя стержнями H и K. В целом получается соединение трех дисков при помощи шарнира и четырех стержней. Такой стандартный способ соединения трех дисков су- ществует. Однако необходимо доказать, что система не является мгновенно изменяемой. Для этого определим положение эквивалентных шарниров, которые находятся на пересечении стержней. Это шарнир Ш1 (на пересе- чении стержней B-C и G) и шарнир, положение которого уходит в беско- нечность, т. к. стержни H и K параллельны. Шарниры, соединяющие диски Д1, C-D и D-E, не лежат на одной прямой. Таким образом, мы доказали, что эти 3 диска образуют общий диск. Обозначим его Д2 и обведем точеч- ной линией.

Диск Д2 связан c диском E-F шарниром E и стержнем F (стержень не пересекает шарнир). Таким образом, они образуют общий диск.

3. Окончательный вывод: система в целом является диском, следова- тельно, она геометрически неизменяема. При этом она статически опреде- лима, т. к. W =0 (см. п. 1).

Вопросы и задачи для закрепления темы

1. Какие системы называются геометрически неизменяемыми? Приведите пример.

2. Запишите порядок кинематического анализа плоских стержневых систем? Дайте количественную оценку геометрической неизменяемости системы.

3. Покажите на примерах простейшие способы образования гео- метрически неизменяемых стержневых систем, состоящих из двух дис- ков. То же для систем, состоящих из трех дисков.

4. Какие системы называются мгновенно изменяемыми? Приве- дите пример.

5. Покажите пример системы близкой к мгновенно изменяемой.

6. Перечислите основные типы опорных устройств, имеющихся в раме на рис. 1.34, дайте их статические и кинематические характери- стики.

7. Подсчитайте число степеней сво- боды рамы, показанной на рис. 1.33, и вы- явите ее кинематический статус.

8. Выполните анализ этой рамы по

ее образованию. Рис. 1.33

9. Сколько связей нужно удалить в раме (рис. 1.34), чтобы она стала статиче- ски определимой? Приведите пример та- кой статически определимой рамы.

Рис. 1.34

10. Определите число степеней свободы фермы, изображенной на рис. 1.35, и сделайте вывод о ее кинематиче- ском статусе.

11.Сколько шарниров нужно добавить, чтобы балка, показанная на рис. 1.36, стала статически определимой?

Источник