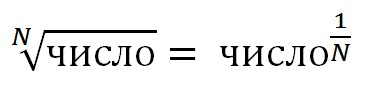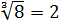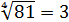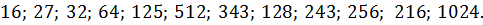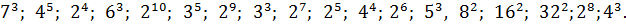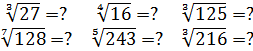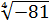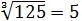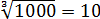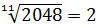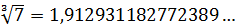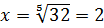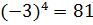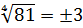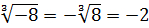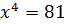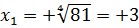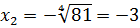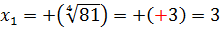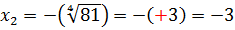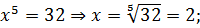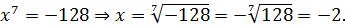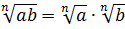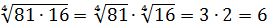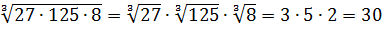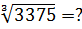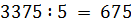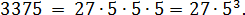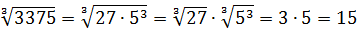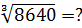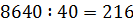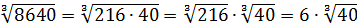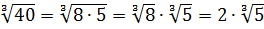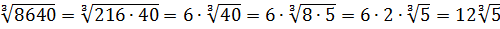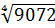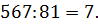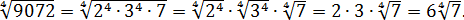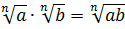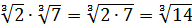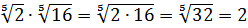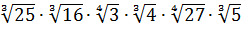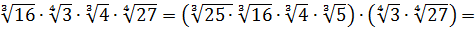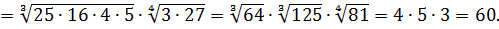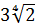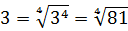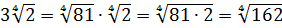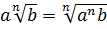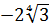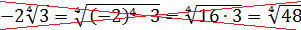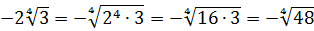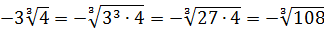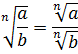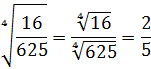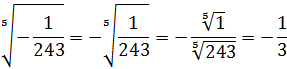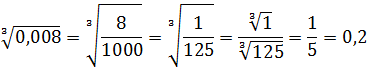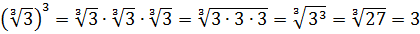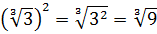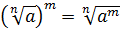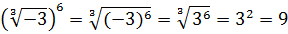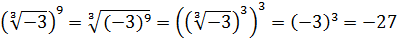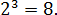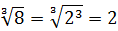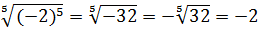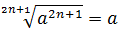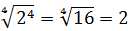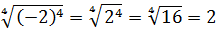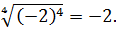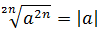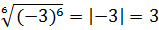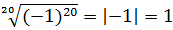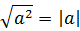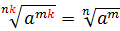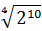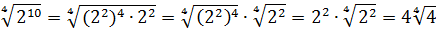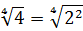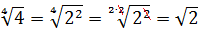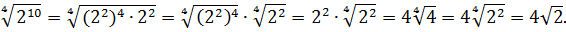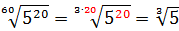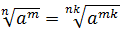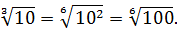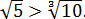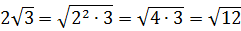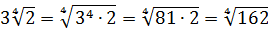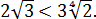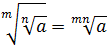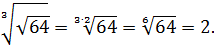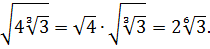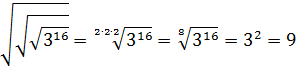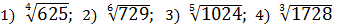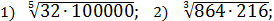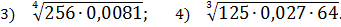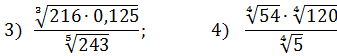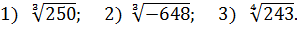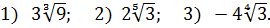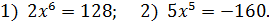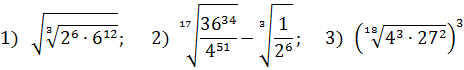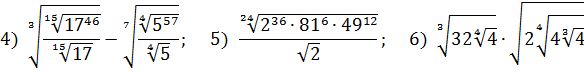Как сделать корень степенью
Квадратный, кубический и другие корни в Excel с примерами
На клавиатуре нет кнопок с написанием квадратного или другого корня, поэтому в Excel создана специальная функция, вводит и вычисляет квадратный корень. Как ей воспользоваться, а также как извлечь корни разных степеней в Excel? Рассмотрим несколько примеров.
Важно! Функции в Excel вводятся в ячейках русскими буквами без пробелов, перед названием функции ставится знак равно =
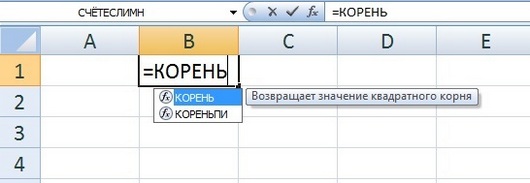
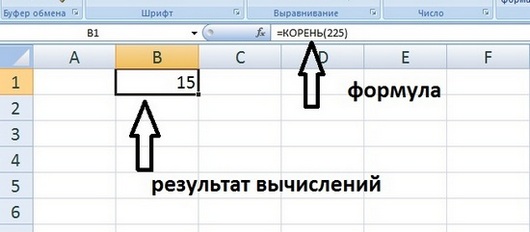
За квадратный корень отвечает функция КОРЕНЬ(значение). Чтобы воспользоваться ей, нужно в ячейке написать =КОРЕНЬ и без пробелов внутри скобки написать значение, от которого нужно найти квадратный корень.
Как извлечь в Excel корень третьей, четвертой и иной степеней?
Для квадратного корня есть своя функция — КОРЕНЬ — а как быть с другими с другими корнями?
Этой формулой и нужно пользоваться для вычисления корней разных степеней в Excel. Для возведения степени использовать функцию СТЕПЕНЬ(аргумент) или галочку ^ (на английской раскладке SHIFT + 6). Саму дробную степень писать в скобках.
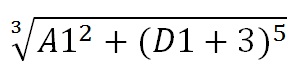
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст
Ошибка в тексте? Мы очень сожалеем,
что допустили ее. Пожалуйста, выделите ее
и нажмите на клавиатуре CTRL + ENTER.
Кстати, такая возможность есть
на всех страницах нашего сайта
2007-2021 «Педагогическое сообщество Екатерины Пашковой — PEDSOVET.SU».
12+ Свидетельство о регистрации СМИ: Эл №ФС77-41726 от 20.08.2010 г. Выдано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций.
Адрес редакции: 603111, г. Нижний Новгород, ул. Раевского 15-45
Адрес учредителя: 603111, г. Нижний Новгород, ул. Раевского 15-45
Учредитель, главный редактор: Пашкова Екатерина Ивановна
Контакты: +7-920-0-777-397, info@pedsovet.su
Домен: https://pedsovet.su/
Копирование материалов сайта строго запрещено, регулярно отслеживается и преследуется по закону.
Отправляя материал на сайт, автор безвозмездно, без требования авторского вознаграждения, передает редакции права на использование материалов в коммерческих или некоммерческих целях, в частности, право на воспроизведение, публичный показ, перевод и переработку произведения, доведение до всеобщего сведения — в соотв. с ГК РФ. (ст. 1270 и др.). См. также Правила публикации конкретного типа материала. Мнение редакции может не совпадать с точкой зрения авторов.
Для подтверждения подлинности выданных сайтом документов сделайте запрос в редакцию.
Мы используем cookie.
Публикуя материалы на сайте (комментарии, статьи, разработки и др.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьми лицами.
При этом редакция сайта готова оказывать всяческую поддержку как в публикации, так и других вопросах.
Если вы обнаружили, что на нашем сайте незаконно используются материалы, сообщите администратору — материалы будут удалены.
Формулы степеней и корней.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n-ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
5. Возводя степень в степень, показатели степеней перемножают:
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n-ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n-ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n, необходимо извлечь корень n–ой степени из m-ой степени этого числа а:
Формулы степеней.
6. a — n = 
7. 
8. a 1/n = 
Корень n-й степени и его свойства
Корень n-й степени и его свойства
Что такое корень n-й степени? Как извлечь корень?
В восьмом классе вы уже успели познакомиться с квадратным корнем. Решали типовые примеры с корнями, применяя те или иные свойства корней. Также решали квадратные уравнения, где без извлечения квадратного корня — никак. Но квадратный корень — это лишь частный случай более широкого понятия — корня n-й степени. Помимо квадратного, бывает, например, кубический корень, корень четвёртой, пятой и более высоких степеней. И для успешной работы с такими корнями неплохо бы всё-таки для начала быть на «ты» с корнями квадратными.) Поэтому у кого проблемы с ними — настоятельно рекомендую повторить.
Извлечение корня — это одна из операций, обратных возведению в степень.) Почему «одна из»? Потому, что, извлекая корень, мы ищем основание по известным степени и показателю. А есть ещё одна обратная операция — нахождение показателя по известным степени и основанию. Такая операция называется нахождением логарифма. Она более сложная, чем извлечение корня и изучается в старших классах.)
Во-первых, обозначение. Квадратный корень, как мы уже знаем, обозначается вот так: 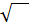
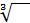
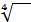
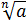
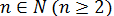
Как, например, извлечь кубический корень из 8? То есть 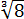
Или 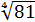
А корень десятой степени из 1? Ну, ежу понятно, что единица в любой степени (в том числе и в десятой) равна единице. ) То есть:
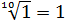
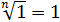
С нулём та же история: ноль в любой натуральной степени равен нулю. Стало быть, 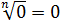
Ответы (в беспорядке):
Потренировались? Тогда считаем примерчики:
Ответы (тоже в беспорядке): 6; 2; 3; 2; 3; 5.
Получилось? Великолепно! Движемся дальше.)
Ограничения в корнях. Арифметический корень n-й степени.
В корнях n-й степени, как и в квадратных, тоже есть свои ограничения и свои фишки. По своей сути, они ничем не отличаются от таковых ограничений для квадратных корней.
Например, попробуем посчитать вот такой корень:
Зато корни нечётной степени из отрицательных чисел — пожалуйста!
Например, 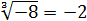
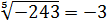
А из положительных чисел можно со спокойной душой извлекать любые корни, любых степеней:
В общем, понятно, думаю. ) И, кстати, корень совершенно не обязан извлекаться ровно. Это просто примеры такие, чисто для понимания.) Бывает, что в процессе решения (например, уравнений) выплывают и довольно скверные корни. Что-нибудь типа 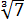
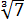
Причём, это число никогда не кончается и не имеет периода: цифры следуют совершенно беспорядочно. Иррациональное оно… В таких случаях ответ так и оставляют в виде корня.) А вот если корень извлекается чисто (к примеру, 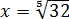
Снова берём наше подопытное число 81 и извлекаем из него корень четвёртой степени:
Потому, что три в четвёртой будет 81. Ну, хорошо! Но ведь и минус три в четвёртой тоже будет 81!
И, чтобы её устранить, так же, как и в квадратных корнях, ввели специальный термин: арифметический корень n-й степени из числа a – это такое неотрицательное число, n-я степень которого равна a .
А ответ с плюсом-минусом называется по-другому — алгебраический корень n-й степени. У любой чётной степени алгебраическим корнем будет два противоположных числа. В школе же работают только с арифметическими корнями. Поэтому отрицательные числа в арифметических корнях попросту отбрасываются. Например, пишут: 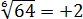
Всё, казалось бы, просто, но… А как же быть с корнями нечётной степени из отрицательных чисел? Ведь там-то всегда при извлечении получается отрицательное число! Так как любое отрицательное число в нечётной степени также даёт отрицательное число. А арифметический корень работает только с неотрицательными числами! На то он и арифметический.)
В таких корнях делают вот что: выносят минус из-под корня и ставят перед корнем. Вот так:
В таких случаях говорят, что 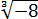
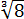
Но есть один пунктик, который может вносить путаницу, — это решение простеньких уравнений со степенями. Например, вот такое уравнение:
Пишем ответ: 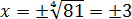
Непонятка здесь заключается в том, что чуть выше я уже написал, что в школе рассматриваются только неотрицательные (т.е. арифметические) корни. А тут один из ответов с минусом… Как быть? Да никак! Знаки здесь — это результат решения уравнения. А сам корень — величина всё равно неотрицательная! Смотрите сами:
Ну как, теперь понятнее? Со скобочками?)
С нечётной степенью всё гораздо проще — там всегда получается один корень. С плюсом или с минусом. Например:
Итак, если мы просто извлекаем корень (чётной степени) из числа, то мы всегда получаем один неотрицательный результат. Потому что это — арифметический корень. А вот, если мы решаем уравнение с чётной степенью, то мы получаем два противоположных корня, поскольку это — решение уравнения.
С корнями нечётных степеней (кубическими, пятой степени и т.д.) проблем никаких. Извлекаем себе и не паримся со знаками. Плюс под корнем — значит, и результат извлечения с плюсом. Минус — значит, минус.)
А теперь настал черёд познакомиться со свойствами корней. Некоторые уже будут нам знакомы по квадратным корням, но добавится и несколько новых. Поехали!
Свойства корней. Корень из произведения.
Это свойство уже знакомо нам из квадратных корней. Для корней других степеней всё аналогично:
То есть, корень из произведения равен произведению корней из каждого множителя отдельно.
Если показатель n чётный, то оба подкоренных числа a и b должны быть, естественно, неотрицательными, иначе формула смысла не имеет. В случае нечётного показателя ограничений никаких нет: выносим минусы из-под корней вперёд и дальше работаем с арифметическими корнями.)
Как и в квадратных корнях, здесь эта формула одинаково полезна как слева направо, так и справа налево. Применение формулы слева направо позволяет извлекать корни из произведения. Например:
Эта формула, кстати говоря, справедлива не только для двух, а для любого числа множителей. Например:
Также по этой формуле можно извлекать корни из больших чисел: для этого число под корнем раскладывается на множители поменьше, а дальше извлекаются корни отдельно из каждого множителя.
Например, такое задание:
Число достаточно большое. Извлекается ли из него корень ровно — тоже без калькулятора непонятно. Хорошо бы его разложить на множители. На что точно делится число 3375? На 5, похоже: последняя цифра — пятёрка.) Делим:
Ой, снова на 5 делится! 675:5 = 135. И 135 опять на пятёрку делится. Да когда ж это кончится!)
135:5 = 27. С числом 27 всё уже ясно — это тройка в кубе. Значит,
Извлекли корень по кусочкам, ну и ладно.)
Снова раскладываем на множители по признакам делимости. Каким? На 4, т.к. последняя парочка цифр 40 — делится на 4. И на 10, т.к. последняя цифра — ноль. Значит, можно поделить одним махом сразу на 40:
Про число 216 мы уже знаем, что это шестёрка в кубе. Стало быть,
А 40, в свою очередь, можно разложить как 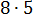
И тогда окончательно получим:
Как вынести множитель за знак корня?
Вынести множитель (или множители) за знак корня очень просто. Раскладываем подкоренное выражение на множители и извлекаем то, что извлекается.) А что не извлекается — так и оставляем под корнем. Смотрите:
Раскладываем число 9072 на множители. Так как у нас корень четвёртой степени, в первую очередь пробуем разложить на множители, являющиеся четвёртыми степенями натуральных чисел — 16, 81 и т.д.
Попробуем поделить 9072 на 16:
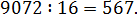
А вот 567, похоже, делится на 81:
Значит, 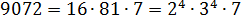
Тогда
Свойства корней. Умножение корней.
Рассмотрим теперь обратное применение формулы — справа налево:
На первый взгляд, ничего нового, но внешность обманчива. ) Обратное применение формулы значительно расширяет наши возможности. Например:
Хм, ну и что тут такого? Умножили и всё. Здесь и впрямь ничего особенного. Обычное умножение корней. А вот такой пример!
Отдельно из множителей корни чисто не извлекаются. Зато из результата — отлично. )
Опять же формула справедлива для любого числа множителей. Например, надо посчитать вот такое выражение:
Здесь главное — внимание. В примере присутствуют разные корни — кубические и четвёртой степени. И ни один из них точно не извлекается…
А формула произведения корней применима только к корням с одинаковыми показателями. Поэтому сгруппируем в отдельную кучку кубические корни и в отдельную — четвёртой степени. А там, глядишь, всё и срастётся.))
И калькулятора не понадобилось.)
Как внести множитель под знак корня?
Следующая полезная вещь — внесение числа под корень. Например:
Можно ли убрать тройку внутрь корня? Элементарно! Если тройку превратить в корень, то сработает формула произведения корней. Итак, превращаем тройку в корень. Раз у нас корень четвёртой степени, то и превращать будем тоже в корень четвёртой степени.) Вот так:
Корень, между прочим, можно сделать из любого неотрицательного числа. Причём той степени, какой хотим (всё от конкретного примера зависит). Это будет корень из n-й степени этого самого числа:
А теперь — внимание! Источник очень грубых ошибок! Я не зря здесь сказал про неотрицательные числа. Арифметический корень работает только с такими. Если у нас в задании где-то затесалось отрицательное число, то либо минус так и оставляем, перед корнем (если он снаружи), либо избавляемся от минуса под корнем, если он внутри. Напоминаю, если под корнем чётной степени получается отрицательное число, то выражение не имеет смысла.
Например, такое задание. Внести множитель под знак корня:
Если мы сейчас внесём под корень минус два, то жестоко ошибёмся:
В чём здесь ошибка? А в том, что четвёртая степень, в силу своей чётности, благополучно «съела» этот минус, в результате чего заведомо отрицательное число 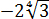
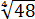
В корнях нечётных степеней минус хоть и не «съедается», но его тоже лучше оставлять снаружи:
Здесь корень нечётной степени — кубический, и мы имеем полное право минус тоже загнать под корень. Но предпочтительнее в таких примерах минус также оставлять снаружи и писать ответ выраженным через арифметический (неотрицательный) корень 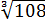
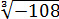
Итак, с внесением числа под корень тоже всё ясно, я надеюсь.) Переходим к следующему свойству.
Свойства корней. Корень из дроби. Деление корней.
Это свойство также полностью повторяет таковое для квадратных корней. Только теперь мы его распространяем на корни любой степени:
Корень из дроби равен корню из числителя, делённому на корень из знаменателя.
Если n чётно, то число a должно быть неотрицательным, а число b – строго положительным (на ноль делить нельзя). В случае нечётного показателя единственным ограничением будет 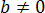
Это свойство позволяет легко и быстро извлекать корни из дробей:
Идея понятна, думаю. Вместо работы с дробью целиком мы переходим к работе отдельно с числителем и отдельно со знаменателем.) Если дробь десятичная или, о ужас, смешанное число, то предварительно переходим к обыкновенным дробям:
А теперь посмотрим, как эта формула работает справа налево. Здесь тоже выявляются очень полезные возможности. Например, такой примерчик:
Из числителя и знаменателя корни ровно не извлекаются, зато из всей дроби — прекрасно.) Можно решить этот пример и по-другому — вынести в числителе множитель из-под корня с последующим сокращением:
Как вам будет угодно. Ответ всегда получится один — правильный. Если ошибок не наляпать по дороге.)
Итак, с умножением/делением корней разобрались. Поднимаемся на следующую ступеньку и рассматриваем третье свойство — корень в степени и корень из степени.
Корень в степени. Корень из степени.
Как возвести корень в степень? Например, пусть у нас есть число 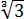
Здесь корень и степень как бы взаимоуничтожились или скомпенсировались. Действительно, если мы число, которое при возведении в куб даст нам тройку, возведём в этот самый куб, то что получим? Тройку и получим, разумеется! И так будет для любого неотрицательного числа. В общем виде:
Если показатели степени и корня разные, то тоже никаких проблем. Если знать свойства степеней.)
Если показатель степени меньше показателя корня, то просто загоняем степень под корень:
В общем виде будет:
Идея понятна: возводим в степень подкоренное выражение, а дальше упрощаем, вынося множители из-под корня, если это возможно. Если n чётно, то a должно быть неотрицательным. Почему — понятно, думаю.) А если n нечётно, то никаких ограничений на a уже нету:
Разберёмся теперь с корнем из степени. То есть, в степень будет возводиться уже не сам корень, а подкоренное выражение. Здесь тоже ничего сложного, но простора для ошибок значительно больше. Почему? Потому, что в игру вступают отрицательные числа, которые могут вносить путаницу в знаках. Пока начнём с корней нечётных степеней — они гораздо проще.
Пусть у нас есть число 2. Можно его возвести в куб? Конечно!
А теперь — обратно извлечём из восьмёрки кубический корень:
С двойки начали, к двойке же и вернулись.) Ничего удивительного: возведение в куб скомпенсировалось обратной операцией — извлечением кубического корня.
Здесь тоже всё путём. Степень и корень друг друга скомпенсировали. В общем виде для корней нечётных степеней можно записать такую формулку:
То есть, нечётная степень и корень этой же степени всегда друг друга компенсируют и получается подкоренное выражение. 🙂
А вот с чётной степенью этот фокус может уже не пройти. Смотрите сами:
Здесь пока ничего особенного. Четвёртая степень и корень четвёртой же степени тоже друг друга уравновесили и получилась просто двойка, т.е. подкоренное выражение. И для любого неотрицательного числа будет то же самое. А теперь всего лишь заменим в этом корне два на минус два. То есть, посчитаем вот такой корень:
Минус у двойки благополучно «сгорел» из-за четвёртой степени. И в результате извлечения корня (арифметического!) мы получили положительное число. Было минус два, стало плюс два.) А вот если бы мы просто бездумно «сократили» степень и корень (одинаковые же!), то получили бы
Что является грубейшей ошибкой, да.
Поэтому для чётного показателя формула корня из степени выглядит вот так:
Здесь добавился нелюбимый многими знак модуля, но в нём страшного ничего нет: благодаря ему, формула также работает для любого действительного числа a. И модуль просто отсекает минусы:
И так далее.) Эта формула — аналог формулы корня квадратного из квадрата:
Только в корнях n-й степени появилось дополнительное разграничение на чётные и нечётные степени. Чётные степени, как мы видим, более капризные, да.)
А теперь рассмотрим новое полезное и весьма интересное свойство, уже характерное именно для корней n-й степени: если показатель корня и показатель степени подкоренного выражения умножить (разделить) на одно и то же натуральное число, то значение корня не изменится.
Чем-то напоминает основное свойство дроби, не правда ли? В дробях мы тоже числитель и знаменатель можем умножать (делить) на одно и то же число (кроме нуля). На самом деле, это свойство корней — тоже следствие основного свойства дроби. Когда мы познакомимся со степенью с рациональным показателем, то всё станет ясно. Что, как и откуда. )
Прямое применение этой формулы позволяет нам упрощать уже совершенно любые корни из любых степеней. В том числе, если показатели степени подкоренного выражения и самого корня разные. Например, надо упростить вот такое выражение:
Поступаем просто. Выделяем для начала под корнем четвёртую степень из десятой и — вперёд! Как? По свойствам степеней, разумеется! Выносим множитель из-под корня или работаем по формуле корня из степени.
А вот 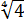
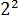
И теперь — самое интересное — сокращаем мысленно показатель под корнем (двойку) с показателем корня (четвёркой)! И получаем:
Вся цепочка преобразований выглядит так:
Это было прямое применение формулы. А вот обратное применение ещё сильнее повышает наш математический уровень. Сомневаетесь? Напрасно! Дело в том, что обратное применение этой формулы справа налево 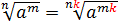
Как сравнивать корни?
Допустим, надо (без калькулятора!) сравнить два числа:
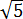
Берём 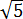
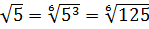
С числом 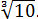
Теперь дело за малым — сравнить два числа 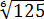
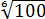
Ясно, что 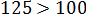
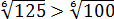
Если перед корнями тусуются какие-то множители, то убираем их внутрь корней и — по накатанной колее. Например, такое задание:
Сравнить 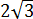
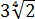
Первым делом вносим множители под корни:
А теперь — приводим оба корня к одному показателю. К четвёрке.)
Ну, число 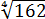
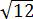
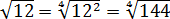
Вот теперь всё и прояснилось: 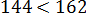
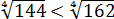
А это значит, что
Этот принцип сравнения одинаковых корней по подкоренным выражениям, строго говоря, основывается на монотонном возрастании функции 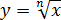
Что ж, осталось последнее усилие. Собираем волю в кулак и знакомимся с последним (и тоже новым для нас) свойством корней — корень под корнем.
Как извлечь корень из корня?
Это свойство на самом деле очень простое и по своей сути очень похоже на возведение степени в степень. Так как является обратным к этой операции.) Вот как оно выглядит:
Чтобы извлечь корень из корня, надо перемножить показатели корней.
Это свойство позволяет несколько вложенных корней заменить одним корнем. Например:
Причём вложений может быть сколько угодно — формула всё равно сработает:
Как видим, никаких хитростей. Просто перемножаем показатели и считаем (если считается).
Вот, собственно, всё что я пока хотел рассказать.)) Следующим этапом нашей работы с корнями будет преобразование иррациональных выражений. Но это — в следующий раз.
А теперь, как всегда, делаем задания.
Задание 1
Задание 2
Задание 3
Найти значение выражения:
Задание 4
Вынести множитель из-под знака корня:
Внести множитель под знака корня:
Задание 5
Задание 6
Всё решилось? Одной левой? Великолепно! Корни — не ваш камень преткновения.) Не всё получилось? Не беда! Не ошибается тот, кто ничего не делает.)