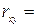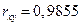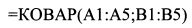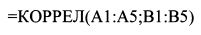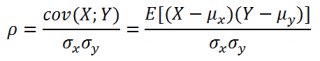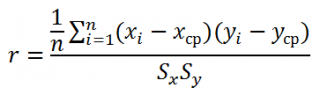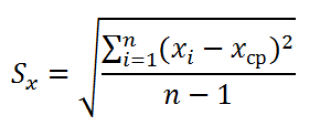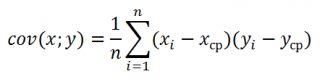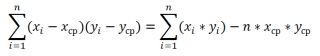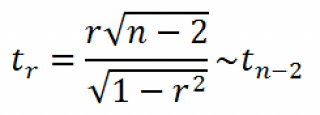Как сделать ковариацию в экселе
Примеры расчетов функций КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г в Excel
Функция КОВАРИАЦИЯ.В в Excel предназначена для расчета коэффициента ковариации двух наборов данных (массивов или диапазонов ячеек, хранящих числовые значения), являющихся выборками соответствующих диапазонов данных, и возвращает соответствующее числовое значение.
Функция КОВАРИАЦИЯ.Г в Excel используется для расчета коэффициента ковариации всей совокупности двух диапазонов данных (генеральной совокупности) и возвращает соответствующее значение.
Функция КОВАР в Excel предназначена для расчета коэффициента ковариации двух любых наборов числовых данных, являющихся генеральными совокупностями.
Использование функций КОВАР, КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г в Excel
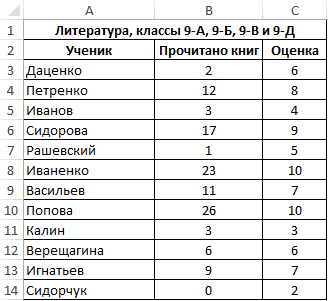
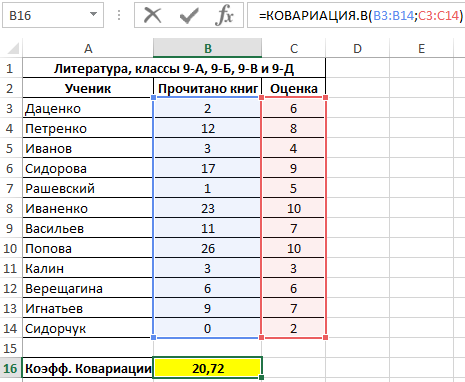
Пример 1. В таблице Excel содержится два диапазона данных, значения первого из которых характеризуют количество прочитанных книг за год каждым учеником, отобранным из нескольких классов школы, а второй – итоговую оценку по литературе по 10-бальной шкале. Определить коэффициент ковариации двух диапазонов данных.
Вид исходной таблицы:
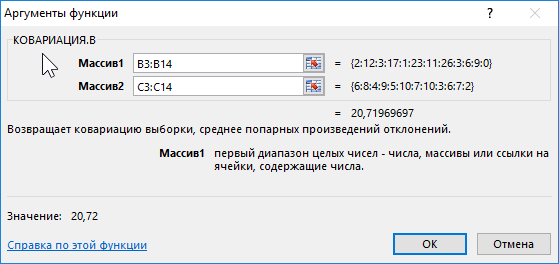
Поскольку для анализа были отобраны по несколько учеников различных классов, оба диапазона можно считать выборками из генеральной совокупности, которой являются все ученики 9-го класса данной школы. Используем следующую функцию:
Полученное значение свидетельствует о наличии прямой связи между значениями из двух диапазонов. То есть, можно полагать, что ученик, прочитавший большее количество книг, получит более высокую оценку за предмет.
Расчет ковариации роста и падения цен двух видов акций в Excel
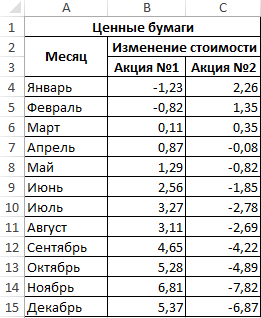
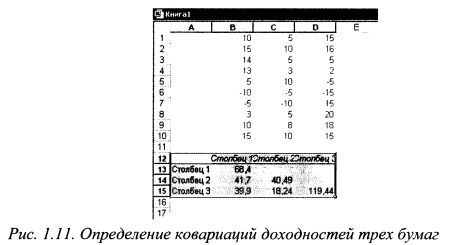
Пример 2. В таблице Excel внесены данные роста (положительное число) или падения цены (отрицательное) двух различных ценных бумаг на протяжении 12 месяцев года относительно некоторой начальной величины. Определить ковариацию двух диапазонов данных и сделать выводы. Сделать отчет доступным для пользователей Excel 2007.
Вид исходной таблицы:
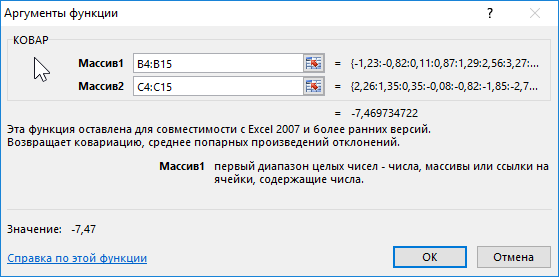
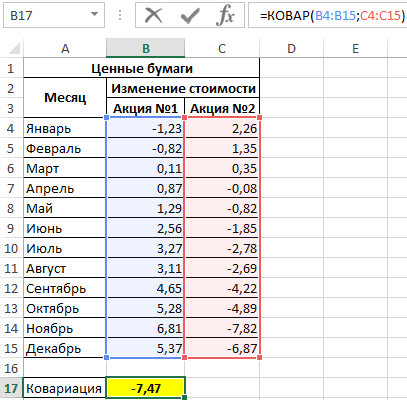
В данном примере исследуется вся генеральная выборка. Для расчета можно использовать функцию КОВАРИАЦИЯ.Г, однако результаты не будут доступны для пользователей более старых версий Excel. Применим следующую формулу:
В результате получим:
Это значение свидетельствует о достаточно большой взаимосвязи между исследуемыми значениями. Поскольку число отрицательное, данная взаимосвязь является обратной. То есть, с ростом цены одной акции наблюдается падение цены второй и наоборот. Можно предположить, что эти акции принадлежат двум конкурирующим компаниям.
Статистический анализ ковариации показателей в Excel
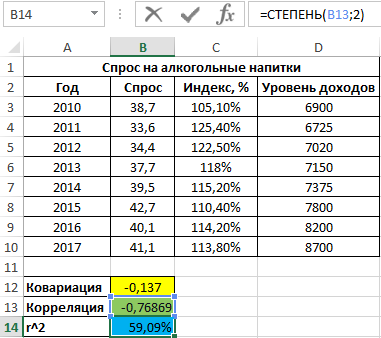
Пример 3. В таблице Excel введены данные о спросе на алкогольные напитки, индексе цен и уровне дохода населения государства. Проанализировать взаимосвязи между имеющимися данными.
Вид исходной таблицы данных:
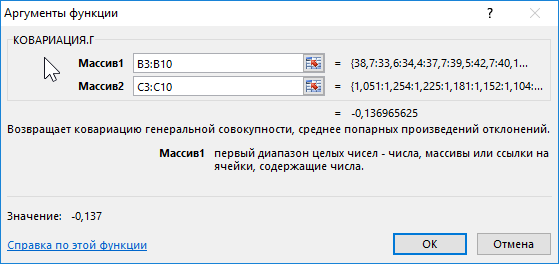
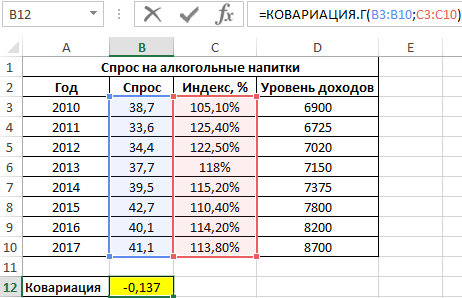
Вначале рассчитаем ковариацию между спросом и индексом цен по формуле:
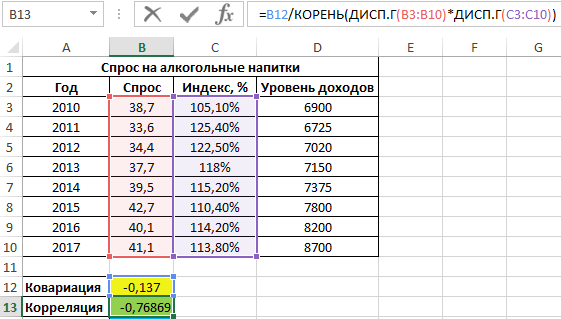
Для оценки степени взаимосвязи двух диапазонов данных удобнее использовать коэффициент корреляции, который можно рассчитать без использования функции КОРРЕЛ следующим способом:
Функция ДИСП.Г используется для расчета дисперсии генеральной совокупности. Приведенная выше формула наглядно демонстрирует взаимосвязь между коэффициентами ковариации и корреляции.
Как видно, между ценами и спросом существует довольно сильная обратная связь. Однако для определения степени влияния спроса определим коэффициент детерминации r2 по формуле:
Полученное значение, выраженное в процентах:
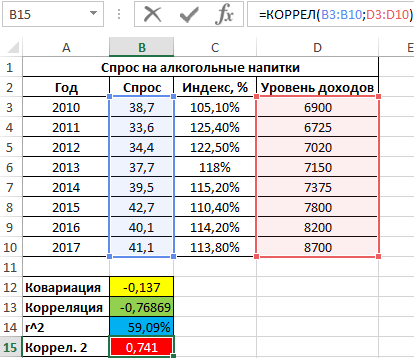
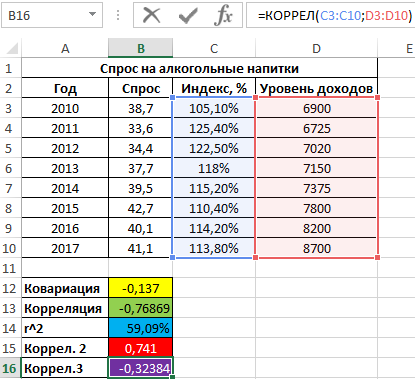
Положительное значение 0,741 соответствует о наличии довольно сильной зависимости между ростом уровня доходов и спросом. Чтобы определить общий коэффициент корреляции и сделать выводы, найдем коэффициент корреляции между индексом цен и уровнем доходов:
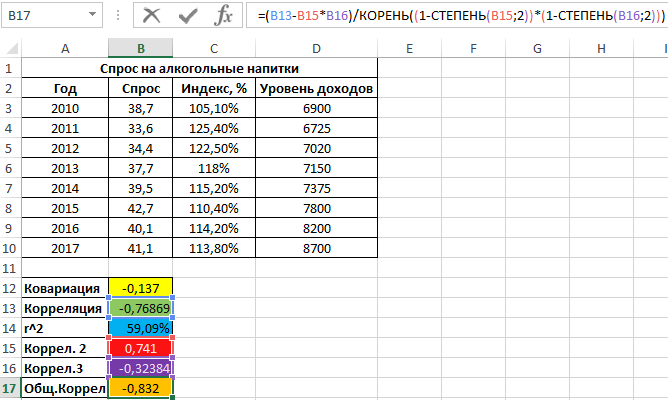
Имеем не сильно выраженную обратную взаимосвязь. Теперь выполним расчет общего коэффициента корреляции по формуле:
Расчеты показывают, что влияние роста цен на уровень спроса «сглаживается» благодаря росту уровня дохода населения. Корень квадратный из последнего значения, взятого по модулю, равен примерно 91%, показывая, насколько вариация цен определяла вариация спроса на алкогольные напитки, если не брать в учет параллельное изменение уровня дохода.
Особенности использования функций КОВАР, КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г в Excel
Функция КОВАР имеет следующий синтаксис:
Функция КОВАРИАЦИЯ.В имеет следующую синтаксическую запись:
Синтаксис функции КОВАРИАЦИЯ.Г:
Все рассматриваемые функции принимают на вход следующие аргументы:
1.2.4. Использование программы Excel для расчета ковариации и коэффициента корреляции доходностей ценных бумаг
Рассмотрим технику расчета ковариации и корреляции доходностей бумаг на примере.
Доходность бумаги X за пять лет составила соответственно 20%, 25%, 22%, 28%, 24%. Доходность бумаги F: 24%, 28%, 25%, 27%, 23%. Определить ковариацию доходностей бумаг.
Приведем решение задачи двумя способами.
Определить коэффициент корреляции доходностей бумаг для условий примера 1. Решение. Приведем решение задачи двумя способами.
б) Корреляцию можно рассчитать с помощью программы «Мастер функций». Для этого выбираем курсором на панели инструментов значок л» и щелкаем мышью. Появилось окно «Мастер функций». В левом поле («Категория») выбираем курсором строку «Статистические» и щелкаем мышью. В правом поле окна («Функция») появился перечень статистических функций. Выбираем курсором строку «КОРРЕЛ» и щелкаем мышью. Строка высветилась синим цветом. Наводим курсор на кнопку ОК и щелкаем мышью. Появилось окно «КОРРЕЛ». В окне две строки, которые называются «Массив 1» и «Массив 2». В первую строку заносим номера ячеек с Al no A5. Для этого наводим курсор на знак ЗР справа от первой строки и щелкаем мышью. Окно «КОРРЕЛ» превратилось в поле первой строки. Наводим курсор на ячейку А1, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, проводим курсор вниз до ячейки А5 и отпускаем клавишу. В поле строки появилась запись А1:А5. Вновь наводим курсор на знак Щ и щелкаем мышью. Появилось развернутое окно «КОРРЕЛ». Заносим номера ячеек с Bl no B5 во вторую строку. Для этого наводим курсор на знак Ш во второй строке и щелкаем мышью. Наводим курсор на ячейку В1, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, доводим курсор вниз до ячейки В5, отпускаем клавишу. В поле строки появилась запись В1:В5. Наводим курсор на кнопку Щ и щелкаем мы шью. Появилось развернутое окно «КОРРЕЛ». Наводим курсор на кнопку ОК и щелкаем мышью. В ячейке С1 появилась цифра 0,612114.
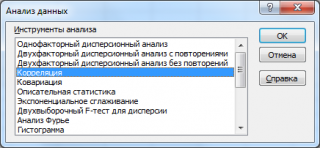
В примерах 1 и 2 мы рассчитали ковариацию и корреляцию доходностей двух бумаг в портфеле. Если в портфель входит большее количество бумаг, то ковариации и корреляции их доходностей можно рассчитывать попарно изложенным выше способом, однако это трудоемкий вариант решения задачи. В Excel имеется специальный пакет «Анализ данных», который позволяет быстро решить такую задачу для большого количества бумаг. Рассмотрим расчет ковариации и корреляций с его помощью.
Знаете ли Вы, что: один из лучших современных Форекс-брокеров – компания HYCM является частью корпорации «Henyep Group», которая успешно предоставляет финансовые услуги уже более 40 лет. Корпорация была основана в 1977 году.
«Пакет анализа» может быть не установлен. Тогда его необходимо установить. Для этого наводим курсор на меню «Сервис» и щелкаем левой клавишей мыши. Появилось выпадающее меню. Курсором выбираем в нем команду «Надстройки» и щелкаем левой клавишей мыши. Появилось окно диалога «Надстройки». Наводим курсор на окошко слева от строки «Пакет анализа» и щелкаем левой клавишей мыши. В окошке появился флажок (галочка). Наводим курсор на кнопку ОК и щелкаем мышью. «Пакет анализа» установлен. Рассмотрим определение ковариации и корреляций для нескольких бумаг на примере.
Пример 3. Расчет ковариации
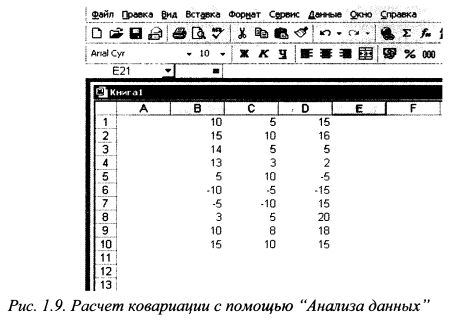
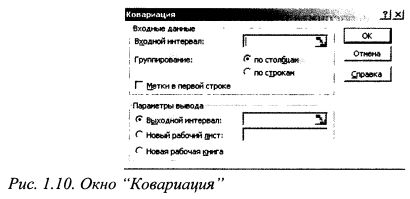
Имеется выборка данных по доходностям бумаг В, С и D за десять периодов. Печатаем значения доходности для бумаги В в ячейки от В1 до В10, бумаги С от С1 до СЮ и бумаги D от D1 до D10, как показано на рис. 1.8. Наводим курсор на меню «Сервис» и щелкаем левой клавишей мыши. Появилось выпадающее меню. Наводим курсор на строку «Анализ данных» и щелкаем левой клавишей мыши. Появилось окно» Анализ данных». Наводим курсор на строку «Ковариация» и щелкаем левой клавишей мыши. Строка высвечивается синим цветом. Наводим курсор на кнопку ОК и щелкаем мышью. Появилось окно Ковариация». (см. рис. 1.10).
Пример 4. Расчет корреляций
Корреляция и ковариация в EXCEL
Вычислим коэффициент корреляции и ковариацию для разных типов взаимосвязей случайных величин.
Коэффициент корреляции ( критерий корреляции Пирсона, англ. Pearson Product Moment correlation coefficient) определяет степень линейной взаимосвязи между случайными величинами.
Как следует из определения, для вычисления коэффициента корреляции требуется знать распределение случайных величин Х и Y. Если распределения неизвестны, то для оценки коэффициента корреляции используется выборочный коэффициент корреляции r ( еще он обозначается как R xy или r xy ) :
где S x – стандартное отклонение выборки случайной величины х, вычисляемое по формуле:
Теоретическое отступление
Таким образом, например, при исследовании зависимости среднегодовой температуры нельзя говорить о корреляции температуры и года наблюдения и, соответственно, применять показатели корреляции с соответствующей их интерпретацией.
Корреляционная связь между переменными может возникнуть несколькими путями:
Таким образом, показатель корреляции показывает, насколько сильна линейная взаимосвязь между двумя факторами (если она есть), а регрессия позволяет прогнозировать один фактор на основе другого.
Для вычисления коэффициента корреляции требуется, чтобы сопоставляемые переменные удовлетворяли следующим условиям:
Двумерные данные могут иметь различную структуру. Для работы с некоторыми из них требуются определенные подходы:
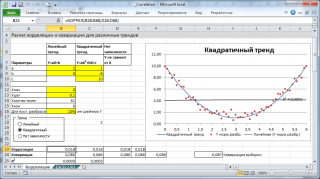
Использование MS EXCEL для расчета корреляции
Примечание : В файле примера можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.
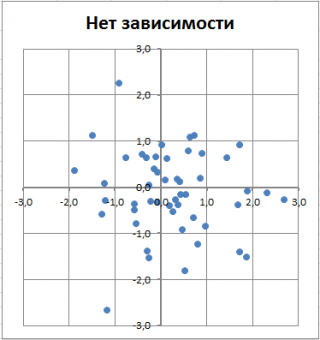
В файле примера для построения диаграммы рассеяния в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.
Примечание : Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми.
Для того, чтобы удостовериться, что вычисления корреляции производятся функцией КОРРЕЛ() по вышеуказанным формулам, в файле примера приведено вычисление корреляции с помощью более подробных формул:
Использование MS EXCEL для расчета ковариации
Примечание : Функции КОРРЕЛ() и КОВАР() в английской версии представлены как CORREL и COVAR. Функции КОВАРИАЦИЯ.Г() и КОВАРИАЦИЯ.В() как COVARIANCE.P и COVARIANCE.S.
Дополнительные формулы для расчета ковариации :
Эти формулы используют свойство ковариации :
Если переменные x и y независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:
VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)
А дисперсия их разности равна
VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)
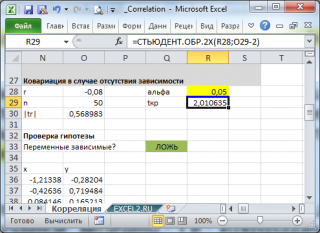
Оценка статистической значимости коэффициента корреляции
Для того чтобы проверить гипотезу, мы должны знать распределение случайной величины, т.е. коэффициента корреляции r. Обычно, проверку гипотезы осуществляют не для r, а для случайной величины t r :
которая имеет распределение Стьюдента с n-2 степенями свободы.
Если вычисленное значение случайной величины |t r | больше, чем критическое значение t α,n-2 (α- заданный уровень значимости ), то нулевую гипотезу отклоняют (взаимосвязь величин является статистически значимой).
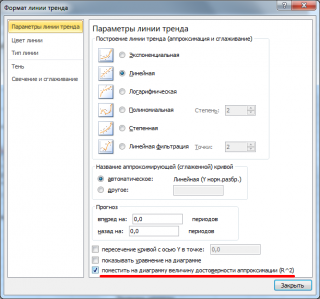
Надстройка Пакет анализа
После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:
Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).
Расчет коэффициентов ковариации и корреляции в табличном процессоре Microsoft Excel
Дата добавления: 2014-04-26 ; просмотров: 2749 ; Нарушение авторских прав
Режим работы «Ковариация» служит для расчета генеральной ковариации на основе выборочных данных.
Режим работы «Корреляция» предназначен для расчета генерального и выборочного коэффициентов корреляции соответственно на основе генеральных и выборочных данных.
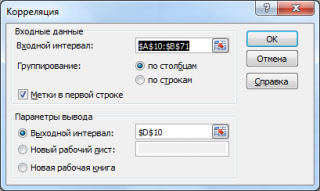
В диалоговых окнах данных режимов задаются следующие параметры:
1. Входной интервал.
3. Метки в первой строке/ Метки в первом столбце.
4. Выходной интервал/ Новый рабочий лист/ Новая рабочая книга.
Пример 1. Показатели уровня образования, уровня преступности, а также отношение числа безработных к числу вакансий в некоторых центральных областях России в 1995 году (по данным Госкомстата РФ) приведены в таблице, сформированной на рабочем листе Excel
| B | C | D | E |
| Область | Уровень образования | Отношение числа безработных к числу вакансий | Уровень преступности |
| Брянская | 22,3 | ||
| Владимирская | 10,8 | ||
| Ивановская | 52,9 | ||
| Калужская | 2,2 | ||
| Костромская | 10,4 | ||
| г. Москва | 0,4 | ||
| Московская | 2,4 | ||
| Нижегородская | 5,4 | ||
| Орловская | 4,1 | ||
| Рязанская | 4,1 | ||
| Смоленская | 1,0 | ||
| Тверская | 4,2 | ||
| Тульская | 2,1 | ||
| Ярославская | 25,1 |
По выборочным данным, представленным в таблице, требуется установить наличие взаимосвязи между указанными показателями в центральном регионе России.
Для решения задачи используем режим работы «Ковариация» и «Корреляция». Значения параметров, установленных в одноименных диалоговых окнах следующие:
1. Входной интервал: С4:E18.
2. Группирование: по столбцам.
3. Метки в первой строке: устанавливаем флажок.
4. Выходной интервал: G4 для «Ковариации» и G9 для «Корреляции».
Рассчитанные в данных режимах показатели представлены в таблицах.
| Уровень образования | Отношение числа безработных к числу вакансий | Уровень преступности | |
| Уровень образования | 1750,245 | ||
| Отношение числа безработных к числу вакансий | -149,859 | 192,5135 | |
| Уровень преступности | -4159,28 | 498,4541 | 22905,66 |
| Уровень образования | Отношение числа безработных к числу вакансий | Уровень преступности |
| Уровень образования | ||
| Отношение числа безработных к числу вакансий | -0,25817 | |
| Уровень преступности | -0,6569 | 0,237369 |
Как видно из таблиц, между парами всех исследуемых показателей существуют стохастические связи. Причем характер всех выявленных связей различен и состоит в следующем:
– связь «отношение числа безработных к числу вакансий» – «уровень преступности» является слабой и прямой (rxy = 0,237369), т.е. с увеличением отношения числа безработных к числу вакансий увеличивается и уровень преступности.
Ковариация (корреляционный момент) вычисляется в Excel с помощью стандартной статистической функции КОВАР. Аргументом этой функции являются диапазоны ячеек, содержащие значения наблюдаемых величин Х и Y.
Коэффициент корреляции вычисляется в Excel одной из двух функций: КОРРЕЛ или ПИРСОН. Эти функции выдают одинаковый результат, если значения наблюдаемых величин записаны в виде чисел.
Пример 2.Получены данные о числе работников магазинов (Х) и объем розничного товарооборота в млн. руб. (Y):
| Х | ||||||||
| Y | 0,5 | 0,7 | 0,9 | 1,1 | 1,4 | 1,4 | 1,7 | 1,9 |
Предполагается, что в исследуемой группе магазинов значения факторов, влияющих на объем товарооборота, примерно одинаковы. Поэтому влияние различия их значений на изменение объема розничного товарооборота сказывается незначительно.
Исследовать связь объема розничного товарооборота магазинов и числа работников в них, т.е. найти ковариацию, коэффициент корреляции.
Для выполнения этого задания необходимо проделать следующие пункты.
1. Наберите исходные данные в два столбца, в заголовке которых наберите буквы Х и Y, соответственно, в ячейки А1 и В1. Тогда данные Х займут диапазон А2:А9, а данные Y займут диапазон В2:В9.
2. Вычислите ковариацию. Для этого в ячейку А10 наберите «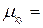
3. Вычислите коэффициент корреляции. Наберите в ячейку А11 «