Как сделать куб в разрезе
Как построить куб в перспективе: пошаговый метод
Здравствуйте, подписчики моего блога!
Многие сталкивались со сложностью в рисовании, когда хотели изобразить сложный по форме объект. Дело в том, что в основе всех сложных структур скрываются простые формы. И куб – одна из таких форм. Сегодня мы подробно разберем, как построить куб.
Перспектива
Куб – это геометрическое тело, состоящее из 6 плоскостей. Знаете, чем отличается куб от квадрата? Куб – это объемная фигура. А при рисовании любых объемных фигур нужно помнить о перспективе.
Из-за законов перспективы стороны куба будут сокращаться, иными словами становиться меньше.
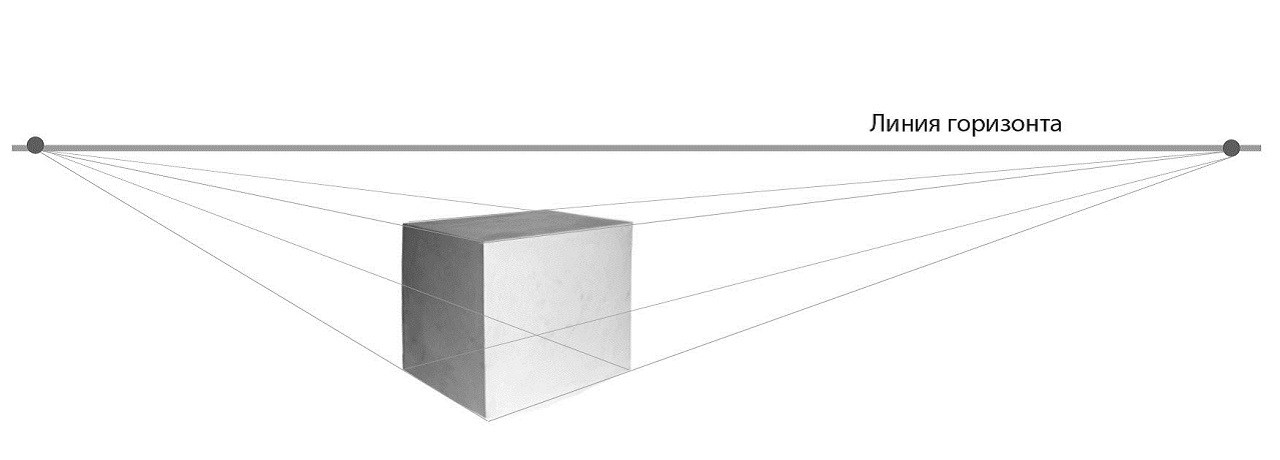
Для начала нужно определить линию горизонта. Это необходимо для того, чтобы правильно построить куб в перспективе.
Линия горизонта – это уровень глаз художника. На ней будут располагаться две точки схода. В каждую из этих точек придёт по 4 линии. Наглядно такой рисунок будет выглядеть следующим образом: 
Рисуем пошагово
Чтобы было проще воспринять последовательность действий, давайте нарисуем куб пошагово.
Прежде чем заниматься перспективой куба, нужно наметить верные размеры предмета и определить его положение в листе. Куб не должен быть слишком маленьким или, наоборот, слишком большим.
Шаг 1 — Композиция
Композиция – это начало любой работы. От точного нахождения композиции зависит 50% успеха работы.
Следует оставить чуть больше расстояния сверху, чем снизу. Это придаст ощущение весомости.
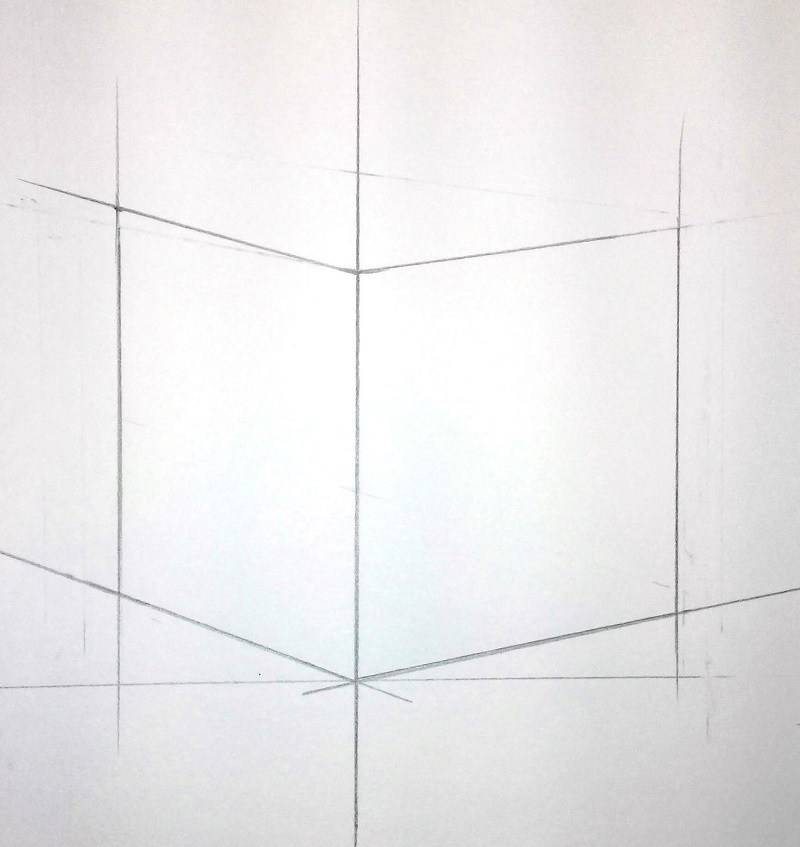
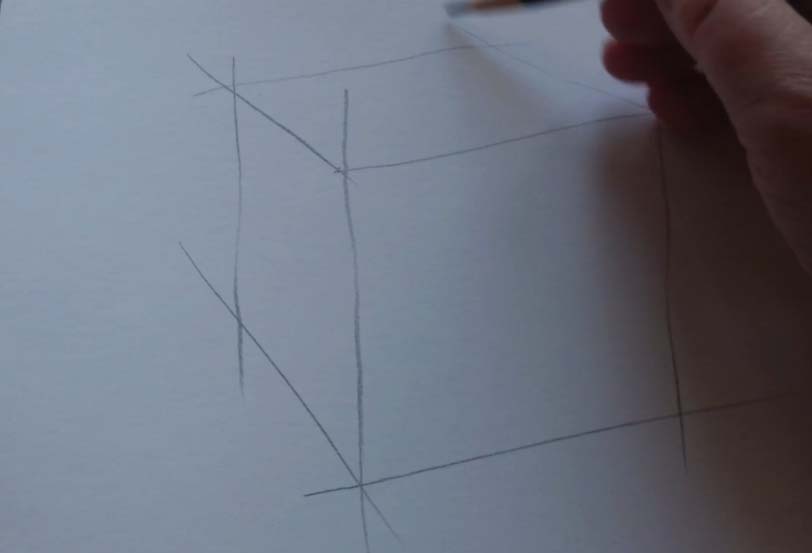
Начинаем рисунок с самого ближнего к нам ребра куба. Наметьте его так, чтобы оно не совпадало с центром листа. Легкими засечками определяем высоту этого ребра. Так как оно находится ближе всего, его высота будет больше остальных ребер. 
Шаг 2 — Сокращение
Плоскости в кубе заметно удаляются в силу перспективного сокращения. Чтобы верно определить это сокращение на листе, необходимо определить углы наклона ребер.
Проводим горизонтальную линию, параллельную листу бумаги, она поможет определить какой угол меньше, а какой больше. Тренируйте свой глаз, переводите взгляд с куба на рисунок, таким образом, перепроверяя себя. 
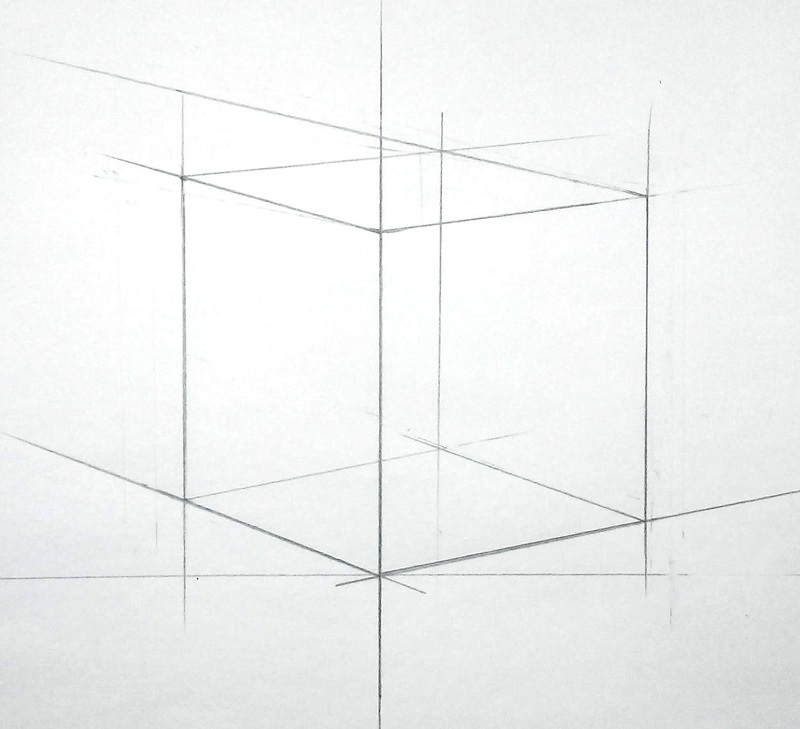
Шаг — 3 — Линейная перспектива
Чтобы куб «лег» в пространство, ребра, удаленные от нас, мы рисуем выше и меньше. Этот прием лежит в основе линейной перспективы. Найдите, где заканчиваются эти ребра и обозначьте их точками. Сечение куба по трем точкам – это верных способ при построении.
Соединяем горизонтальными линиями пересечения плоскостей в кубе. Помните о том, что они сокращаются, и, если, мы их продлим, то они сойдутся в точке схода. 
Невидимые грани мы также должны нарисовать. При правильном построении нужно проверить все сокращения, чтобы не было обратной перспективы.
Шаг 4 — Проверка пропорций
Также можно использовать метод визирования. Вы наверняка замечали, как художники вытягивают руку и измеряют пропорции? Это и есть метод визирования.
Для того, чтобы проверить пропорции, закройте один глаз, возьмите карандаш и на вытянутой руке сопоставьте его кончик с верхом переднего ребра куба. Большой палец передвиньте в то место, где ребро заканчивается.
Высота ребра найдена. Теперь, не переставляя палец, наклоните кисть руки на 90 градусов и уже по горизонтали сопоставьте величину одного ребра с другим. Таким образом вы можете проверять и другие величины.
С опытом художники измеряют пропорции «на глаз», это значит, что они обходятся без метода визирования. Их глаз настолько натренирован, что видит размеры без измерений.
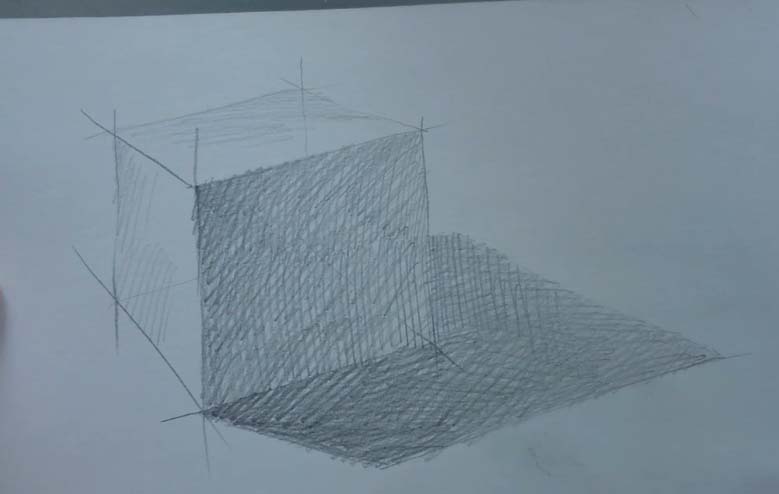
Итак, линейное построение подошло к концу, а значит, мы переходим к воздушной перспективе или, проще говоря, к штрихованию.
Штрихование
Основная задача рисунка – это передать объем. Внимательно посмотрите на предмет, определите для себя тональность каждой из сторон.
Штриховать следует по форме куба. Внимательно подходите к штриховке, не стоит излишне чернить, все-таки мы рисуем гипсовый куб.
Набирайте тон постепенно, не старайтесь все сделать за один подход. Штрихи можно накладывать и в диагональном направлении. 
Используйте карандаши разной мягкости. Для освещённой стороны отлично подойдет твердый карандаш – H, для полутона – HB, а для теневой стороны – B.
В некоторых случаях карандаши стоит выбирать индивидуально: некоторые люди имеют «легкую» руки и штрихуют еле заметно, а есть те, кто с помощью HB может довести рисунок до черноты.
Падающая тень
Как построить тень от куба? Чтобы падающая тень была убедительной, давайте рассмотрим основные принципы построения тени на поверхности листа.
Падающая тень всегда темнее, чем собственная тень на предмете. Чем ближе она подходит к объекту, тем темнее она становится.
На самом кубе тон становится также активнее на границе двух плоскостей – освещенной и теневой. Теневая сторона, по мере удаления в пространство, высветляется за счет отраженного света от поверхности. Рефлексы помогают передать световоздушное пространство.
Заключение
Мы поговорили о сечении куба плоскостью, о том, как правильно построить куб с натуры в перспективе. Рисование простых геометрических тел весьма полезно для начинающих и тех, кто хочет овладеть академическим рисунком.
Геометрия и расположение плоскостей в пространстве очень хорошо тренирует зрительное восприятие.
Если у вас нет гипсового куба, не беда, смастерите куб из бумаги. Для первых упражнений главное – это понять основные принципы при построении. А затем, можно будет перейти к гипсовым фигурам.
Удачи в творчестве! Рисуйте то, что любите!
Если вам понравилась статья, поделитесь ей с друзьями!
Узнать ещё
Знание — сила. Познавательная информация
Сечение куба плоскостью
Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
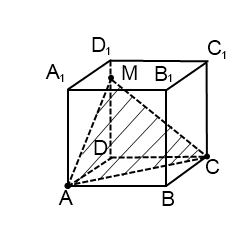
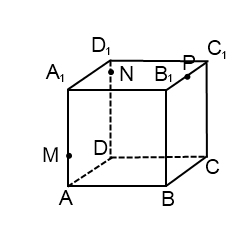
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
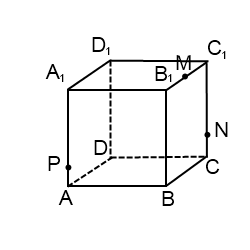
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
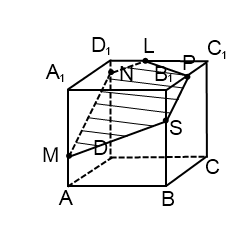
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
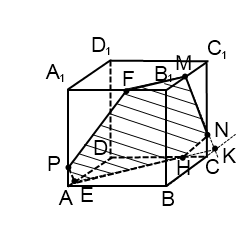
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
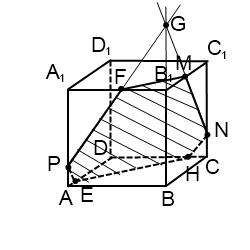
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.
Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
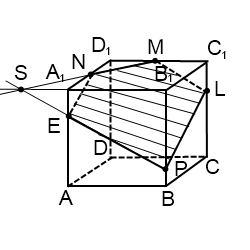
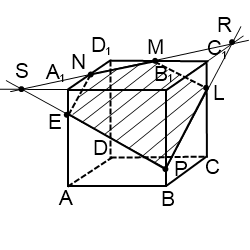
ВРЕЗКА КУБА И ЧЕТЫРЕХГРАННОЙ ПРИЗМЫ. ОСНОВНОЙ ПРИНЦИП ПОСТРОЕНИЯ ВРЕЗОК
ЦЕЛЬ ЗАДАНИЯ. Получить начальные навыки в рисунке врезок геометрических тел. Понять основной принцип построения врезок на примере связки двух кубов. Научиться строить врезку куба и четырехгранной призмы. Оценить многообразие возможных связок куба и четырехгранника, отработать приемы построения их врезок, научиться создавать на листе связки с гармоничными пропорциями.
ПОСТАНОВКА ЗАДАНИЯ. Нарисуйте связки куба и четырехгранной призмы сначала по заданным ортогональным проекциям, а затем в произвольном положении по отношению друг к другу. Найдите наиболее красивые, гармоничные пропорции связок, изменяя положение линии пересечения геометрических тел.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ
Врезки геометрических тел с плоскими гранями, таких как кубы и четырехгранные призмы, самые простые из огромного разнообразия всех возможных врезок геометрических тел. Именно на примере таких врезок проще всего понять основной принцип их построения. Сначала рассмотрим построение линии пересечения двух кубов. Положение кубов в пространстве по отношению друг к другу задано в
Такими иррациональными отношениями являются:
1) отношение диагонали квадрата к его стороне;
2) отношение высоты равностороннего треугольника к половине его основания;
3) отношение золотого сечения, выражаемое дробным числом 1:1,618…».
Есть и другое правило, которым вы легко можете пользоваться на первых порах при создании врезок. Выбирая линию врезки одного геометрического тела в другое, ориентируйтесь на линии и членения, заложенные в самих телах, в данном случае речь идет о высотах и осях симметрии, т. е. о тех элементах геометрических тел, которые составляют и определяют их структуру. Как правило, врезки, сделанные по этим линиям, естественны и гармоничны.
Ортогональных проекциях – плане и фасаде на рис. 5.1. Заметьте, что ребра обоих кубов параллельны или перпендикулярны друг другу, иными словами, кубы находятся в некой пространственной сетке, состоящей из прямых линий, идущих в трех взаимно перпендикулярных направлениях. Представьте взаимное расположение кубов и их положение относительно зрителя, линию горизонта задайте самостоятельно (в нашем примере она проходит выше кубов). Стрелка на плане показывает направление луча зрения, определяющего поворот геометрического тела по отношению к зрителю, – ближнее к нам вертикальное ребро куба совпадает на рисунке с центром дальней от нас грани.
Изобразите кубы в перспективе. Для этого сначала нарисуйте один куб (рис. 5.2). Если вам трудно сразу определить, какое место на рисунке займет второй куб, найдите место любой грани, ребра или точки второго куба относительно первого куба. В нашем примере одно из вертикальных ребер второго куба совпадает с вертикальной осью первого куба. Точка 1, лежащая в центре верхней грани первого куба, делит это вертикальное ребро пополам. Найдите размер этого ребра и нарисуйте любую грань, которая ограничена этим ребром – например, грань а (рис. 5.3). На основании этой грани нарисуйте второй куб (рис. 5.4).
Теперь постройте линию врезки этих кубов. Проведите из точки 1 прямую линию, являющуюся пересечением двух граней (а и Ь). Эта прямая будет параллельна горизонтальным ребрам, ограничивающим пересекающиеся грани а и б. Продолжите прямую до точки 2, где одна из двух пересекающихся граней заканчивается (рис. 5.5). В этой точке линия врезки кубов меняет свое направление. Далее необходимо рассматривать пересечение продолжающейся грани а с гранью с и строить линию их пересечения до точки 3, где грань а заканчивается (рис. 5.6). Построенные подобным образом линии объединятся в замкнутую ломаную 1 – 2 – 3 – 4 – 5 – 6, которая и будет линией врезки двух кубов (рис. 5.7). Запомните основной принцип, знание которого поможет вам в создании врезок любой сложности: построение любой врезки можно рассматривать как последовательное построение пересечений пар поверхностей. Теперь сделайте объем двух пересекающихся кубов более понятным для восприятия при помощи легкого тона, так как это сделано на рис. 5.8.
Рассмотрите ортогональные проекции двух геометрических тел – куба и четырехгранной призмы – на рис. 5.9. Представьте взаимное положение тел.
Изобразите в перспективе заданную связку геометрических тел с различным положением относительно линии горизонта (выше линии горизонта на рис. 5.10 и ниже линии горизонта на рис. 5.11).
При усложнении задачи, когда необходимо пересечь три тела и более, сначала изобразите связку двух тел, построив линию их пересечения. Представьте эту связку как монолит, иначе говоря – одно геометрическое тело сложной структуры. Теперь постройте линию врезки этого нового сложного тела со следующим геометрическим телом. Так, на рис. 5.12 и 5.13 показаны стадии построения врезки трех тел – двух кубов и четырехгранной призмы. Тонируйте полученные связки трех геометрических тел так, как это показано на рис. 5.14 и 5.15.
Создавая свои первые связки, ориентируйтесь на те гармоничные отношения, о которых говорилось в самом начале этой части пособия. Упражняясь далее, вы постепенно научитесь чувствовать эти гармоничные отношения и создавать красивые связки геометрических тел, руководствуясь не измерениями, а собственными ощущениями. На достижение этой цели направлены задания, в которых вы можете изменять линию врезки двух и более геометрических тел, не меняя их положения на листе. Рассмотрите простой пример изменения линии врезки двух геометрических тел (куба и четырехгранной призмы), изображенных на рис. 5.16. Рассмотрите последовательно рис. 5.17; 5.18 и 5.19.
На всех этих рисунках общий абрис геометрических тел сохраняется, мы лишь изменяем линию их пересечения, меняя таким образом положение тел в пространстве по отношению друг к другу и пропорции врезки. Если предположить, что четырехгранная призма неподвижна, то куб на каждом следующем рисунке перемещается ближе к зрителю. Следует отметить, что пользоваться этим приемом можно лишь в том случае, когда перспективные сокращения незначительны. Тогда мы можем пренебречь небольшим изменением в размерах геометрических тел при перемещении их в пространстве относительно друг друга.
Куб карандашом
Построение куба – это один из базовых этапов академического рисунка для начинающих. На примере этой геометрической фигуры хорошо изучать законы линейной перспективы, правильность наложение штриха (светотень) и объем.
Куб – это равносторонняя призма, имеющая 6 граней. Противоположные всегда будут параллельны друг другу. Ребра куба – точки, где пересекаются грани.
В школе-студии «Мастер рисунка» опытный преподаватель подробно расскажет о правильном построении куба, обо всех тонкостях и распространенных ошибках. Умение строить геометрические фигуры при помощи простого карандаша – это основа основ для будущего профессионального художника или архитектора. Ведь все, что изображает на листе рисовальщик состоит из них. А это значит, что без базовых знаний вы не сможете продвинуться дальше и начать создавать более сложные работы.
В этой статье мы подробно расскажем обо всех нюансах построения при помощи карандаша, а также сделаем акценты на важных моментах при создании рисунка куба.
Для начала нам понадобиться наглядная модель куба. Это могут быть гипсовый или картонный макет. Также желательно, чтобы куб был белого цвета, т.к. на нем будет лучше видно светотень, а она тоже важна при построении фигуры, т.к. именно светотень создает объем на нашем рисунке.
Еще как один из вариантов – модель куба, выполненная из проволоки. Так мы сможем увидеть все грани нашей фигуры, включая невидимые. Но в данном случае, не будет светотени, которая должна ложиться на грани.
Расположение на листе
На начальном этапе очень важно правильно расположить куб, с которого мы будем рисовать. Модель должна стоять на ровной поверхности. Куб должен быть расположен так, чтобы с той точки, с которой вы будете рисовать, вам хорошо было видно три его стороны: верхнюю и две боковые.
Далее на листе бумаги нужно определить линию горизонта. По ней мы будем ориентироваться, где будет расположена фигура. Куб должен быть немного выше центра листа. Но в процессе рисования помните, что оно должно быть достаточно крупным, чтобы вы смогли отобразить все нюансы. Поэтому не располагайте куб слишком высоко к верхней границе поверхности бумаги.
Определяем высоту
Начнем мы с вертикальной линии, то есть с ближней к нам грани. Очень важно сразу задать правильную высоту линии, т.к. в дальнейшем она будет служить нам ориентиром. При неправильном расположении нам может не хватить места на листе бумаги, чтобы построить верхнюю видимую сторону.
Рисование основания
Ориентиром для основания куба служит нижняя точка вертикальной черты. В ней будут сходиться две нижние грани. Тут важно определить углы, т.е. как будут расположены линии относительно вертикальной.
Чтобы это определить, поднесите карандаш к ближнему углу модели куба, который расположен внизу. Модель должна быть повернута так, чтобы на кубе вам были видны две вертикальные стороны. Внимательно посмотрите, какая из них больше развернута. Если сторона больше направлена к вам, то угол получится меньше. Старайтесь развивать зрительную память, и запомнить расположение углов, чтобы перенести их на бумагу в процессе рисования.
Куб. Верхнее основание
Куб – объемная фигура. Поэтому нам важно передать ее объем на плоскости листа. В этом нам помогут законы линейной перспективы. Основной принцип таков – то, что находится от нас дальше, визуально становится меньше. И все параллельные линии, которые удаляются от смотрящего, в конечном итоге сходятся в одной точке.
У куба, как мы уже выяснили, группы линий параллельны друг другу. Но по законам перспективы, по мере удаления этих линий, они будут сходиться. То есть, если мы продолжим проводить прямые через грани куба, то в конечном итоге они сойдутся в одной точке.
Наша цель — нарисовать верхние грани так, чтобы в перспективе они сошлись с нижними в одной точке, если бы мы их продолжили.
Достраиваем куб
После того, как мы провели верхние линии от первоначальной вертикальной грани, мы достраиваем фигуру. Помните, что вертикальные линии остаются параллельны между собой.
Мы изображаем все грани на рисунке куба, включая невидимые. Прежде чем приступить к построению дальнего невидимого ребра, нужно убедиться в том, что точки пересечения задних граней оказались друг над другом. Иначе у нас получится заваленный куб, а это означает, что с самого начала были допущены ошибки.
Чтобы это исправить, проверьте еще раз все этапы построения в той последовательности, как вы это создавали. Если расхождение незначительное, то их можно быстро исправить, просто уточнив линии при помощи карандаша.
Добавляем светотень
После того, как вы провели все линии построения и проверили, что вертикальные грани остались параллельны друг другу, а уходящие горизонтальные линии стремятся в одну точку, можно приступать к прорисовке куба.
Выделяем передние грани при помощи карандаша, чтобы сделать на них акцент.
Наша основная цель не просто скопировать куб, а передать его объем на плоскости. У нас три видимых поверхности куба: две боковые стороны и верхнее основание. Каждая грань уходит в пространство, что мы уже изобразили при построении.
От куба с левой стороны падает тень. Ее мы рисуем в первую очередь. Для этого мы обозначаем границы нашей тени. Но накладывать штрих мы начнем с передней ближней грани, которая оказалась в тени. Штриховку делаем вертикальной, т.к. сама сторона стоит перпендикулярно относительно линии горизонта. Усиливаем штриховку возле грани, которая ближе всего к нам, и ослабеваем нажим по мере удаления от этой вертикальной линии. Таким образом, при помощи светотени мы показываем, какая грань находится к нам ближе, а какая дальше.
Продолжаем наносить штрих и на отбрасываемую кубом тень. Это будет самым темным, то есть неосвещенным местом. Поэтому наносим штриховку более плотно, чтобы рисунок получился реалистичным.
На освещенные стороны куба также можно нанести штрих, чтобы подчеркнуть объем. Но у этой видимой вертикальной грани все будет наоборот: чем ближе к ближней передней линии, тем тон светлее. Точнее, пространство возле самого ближнего ребра мы вообще не закрашиваем, оставляя белым. Штрих должен быть диагональным и легким.
Также мы можем нанести полутон на верхнее основание куба. Участок, который расположен ближе всего к горизонтальной верхней грани оставляем нетронутым.
На заключительном этапе делаем акценты при помощи тона, которые подчеркнут объем нашей фигуры. Не забывайте, что падающая тень, которую отбрасывает куб, должна быть темнее собственной.
Наше построение закончено. Нам не нужно рисовать фон за кубом, т.к. главная задача заключается не в полном срисовывании изображения, а в правильном построении по законам перспективы и в передаче объемности трехмерного предмета на плоскости.
Чтобы добиться автоматизма в рисовании фигур, нужно постоянно тренироваться. Пробовать рисовать геометрическое тело в разных ракурсах и с разной освещенностью. Только доведя базовые фигуры до автоматизма, вы сможете приступить к выполнению более сложных художественных задач.
В нашей школе-студии вы сможете пройти все этапы построения куба и других тел, начиная с элементарных фигур и их ракурсов. Вы научитесь выполнять задания различной сложности, определять на глаз пропорции и расположение предмета, а также правильно наносить штрих. Опытный педагог поможет подготовиться к вступительным экзаменам и развить наши художественные способности. Ведь академический рисунок очень важен для тех, кто собирается поступать в высшие художественные или архитектурные заведения.