Как сделать макеты по геометрии
Как сделать объемные геометрические фигуры из бумаги (схемы, шаблоны)?
Вот несколько схем, по которым можно изготовить объёмные геометрические фигуры.
Чуть сложнее будет изготовить октаэдр.
Более подробно об изготовлении объёмных фигур можно посмотреть здесь.
Вот так выглядят объёмные фигуры не в собранном виде:
А вот так выглядят уже готовые:
Из объёмных геометрических фигур можно сделать много оригинальных поделок, в том числе и упаковки для подарка.
Чтобы дети лучше запомнили, какие бывают геометрические фигуры, и знали, как они называются, можно из плотной бумаги или картона сделать объемные геометрические фигуры. Кстати, на основе их можно изготовить красивую подарочную упаковку.
Чтобы линия сгиба была ровной и острой, можно воспользоваться тупой иглой и металлической линейкой. При проведении линии иголку нужно сильно нагнуть в направлении движения, практически положив её набок.
Это развертка трехгранной пирамиды
Это развертка куба
Это развертка октаэдра (четырехгранной пирамиды)
Это развертка додекаэдра
Это развертка икосаэдра
Вот здесь можно найти шаблоны более сложных фигур (Платоновы Тела, Архимедовы тела, многогранники, полиэдры, разные виды пирамид и призм, простые и косые бумажные модели).
Кстати, чтобы рассчитать параметры пирамиды, можно воспользоваться вот этой программой.
Прежде чем начать делать объемные геометрические фигуры, нужно представить (или знать как выглядит) фигуру в 3D измерении: сколько граней имеет та или иная фигура.
Сначала необходимо правильно начертить на бумаге фигуру по граням, которые должны быть соединены между собой. У каждой фигуры грани имеют определенную форму: квадрат, треугольник, прямоугольник, ромб, шестиугольник, круг и т.д.
Очень важно, чтобы длина ребер фигуры, которые будут соединены друг с другом имели одинаковую длину, чтобы во время соединения не возникло проблем. Если фигура состоит из одинаковых граней, я бы предложила сделать шаблон во время черчения использовать этот шаблон. Так же можно скачать из интернета готовые шаблоны, распечатать их, согнуть по линиям и соединить (склеить).
Моделирование на уроках геометрии
Разделы: Математика
Учитель призван быть творцом своих уроков. Новый стандарт, обозначив требования к образовательным результатам, предоставляет почву для новых идей и новых творческих находок. Но, если учитель знает, прежние методы работы помогают реализовать требования нового стандарта, не стоит отбрасывать их совсем. Необходимо найти им применение наряду с новыми педагогическими технологиями в новой образовательной среде.
И я хочу рассказать вам об одном из таких «прежних» методов, используемом на уроках геометрии. Речь пойдёт о моделях, сделанных из картона и ниток.
В большинстве случаев на уроках геометрии средством наглядности является рисунок.
Однако, учащиеся часто забывают, что стереометрический рисунок отличается от планиметрического и не вспоминают, что он должен быть объёмным. На чертеже величины углов сильно искажаются, пересекаются линии, в действительности, не имеющие общих точек. Часто, по чертежу, сделанному обучающимися, трудно получить нужную информацию, так как многие элементы изображаются не правильно.
Сделанные нами модели просты, удобны и наглядны и поэтому дают возможность учащимся правильно изображать фигуры и их элементы на плоскости.
Демонстрация моделей:
1. Призма: учащиеся сами формулируют определение, называют и показывают основные элементы и так далее. Сразу наглядно виден параллельный перенос, какая часть ребра видимая, с помощью этой модели можно демонстрировать свойства параллельных плоскостей и т.д.
2. Тетраэдр: иллюстрация угла между прямой и плоскостью, построение линейного угла двугранного угла и т.д.
3. Пирамида, у которой боковой ребро перпендикулярно основанию (в основании прямоугольник): иллюстрация теоремы о трёх перпендикулярах и её применение и т. д. (Приложение 1).
Применение сделанных моделей даёт возможность ученикам рассматривать их с разных сторон, помогает им представить элементы, необходимые для решения задач и доказательства теорем, и вместе, значительно упрощает процесс решения задач.
Ещё одна методическая находка, которая помогает развить пространственные представления, пространственное воображение, мышления и навыки моделирования учащихся, это комплект, состоящий из модели плоскости, спиц и пластилина.
Перед вами фрагмент урока в 10 классе, тема: «Перпендикулярность в пространстве». Форма проведения — групповая. Групповая деятельность лучше всего помогает развитию коммуникативных способностей обучающихся. Эпиграфом к уроку служат слова китайской мудрости (Приложение 1).
На одном из этапов урока предлагались задачи на моделирование и исследование.
Задание участникам групп: сделать модель из спиц и пластилина и провести обоснование.
Обучающиеся должны проанализировать в задачах конфигурацию, увидеть связь между различными прямыми и плоскостями, выделить те свойства, которые им необходимы при обосновании своего ответа. Участники групп включаются в исследовательскую деятельность, выдвигают свои идеи, предложения по проблеме, приходят к компромиссу. На этом этапе урока ребята в группе разделяются на Конструкторов и Аналитиков. Результаты этой работы: 1 группа – модель: тетраэдр в основании которого прямоугольный треугольник, а ребро, выходящее из вершины острого угла, перпендикулярно основанию. 2 группа – точки должны быть вершинами пирамиды, в основании которой – прямоугольник, а боковое ребро перпендикулярно основанию. Затем заслушиваются ответы учащихся (аналитиков): почему у 1 группы всего 4 прямоугольных треугольника, а у 2 группы 9 прямоугольных треугольников.
Это знакомство привело к написанию учебно-исследовательской работы «Звёздчатые многогранники». За эту работу обучающаяся 11 класса Иванова Полина была награждена дипломом III степени районного этапа городского конкурса учебно-исследовательских работ старшеклассников «Я и Земля» им. В.И. Вернадского.
Полиной были изготовлены модели: звёздчатый октаэдр и малый звёздчатый додекаэдр (Приложение 1).
В кабинетах математики многих школ имеется стандартный набор тел вращения, среди них и модель шара. Но не у всех есть, наверное, модели частей шара. В моём кабинете они есть. Перед вами одна из таких моделей — шаровой сектор. Данная модель — это совместная творческая работа ученика и его родителей (демонстрация модели).
В учебнике геометрии Л.С. Атанасяна даётся определение сектора как тела вращения. (Приложение 1).
С помощью этой модели можно продемонстрировать как из шара получить шаровой сектор.
Профессия учителя творческая и нельзя весь учебный процесс заложить в инструкцию. Каждый шаг учителя, каждый его урок индивидуален.
Макет модель Моделирование конструирование Модели для уроков по стереометрии Трубочки коктейльные
Моей супруге Татьяне очень сильно были нужны модели для проведения уроков. Много думал, пробовал. Вот такие модели у меня получились
Слишком они жесткие были. То есть, имея всего одну модель можно было показывать только ее. Следовательно, на каждый случай надо делать свою модель.
То есть модели должны были быть с подвижными элементами: ребрами и узлами. Ребра подвижными можно сделать на манер телескопических антенн. Наиболее оптимальным будет ребро из 3 секций. Нашел подходящий материал: палочки от шариков, трубочки из детского набора и стержни
Выдул чернила из стержней.
Чтобы секции не выскакивали друг из друга на концах сделал внутри утолщение, а снаружи, нагревая зажигалкой, завальцевал
Чтобы соединить ребра между собой, их концы выполнил из пластмассовых спиц диаметром 5 мм, наделал острые кончики по 15 мм длиной, а в концы вплавил колечки, сделанные из скоб для степлера
Для крепления стоек цилиндра соединения сделал из трубочки, разрезав ее
Крепление получилось примерно таким, как я и ожидал
Кольца, лучше сказать круги, для цилиндра и конуса сделал, нагревая и аккуратно сворачивая, из двух палочек для шариков
Треугольная пирамида может трансформироваться как угодно
Также из треугольной пирамиды благодаря гибким узлам можно сделать плоские четырехугольные фигуры и треугольники
Из четырехугольной пирамиды также можно сделать треугольную с высотами, медианами..
Поменяв верхний круг из цилиндра, получаем усеченный конус
Для большей наглядности сделал еще желтые элементы, стало красивее
Пользуясь резинками можно показать сечения
Всем спасибо за внимание!
Браво!Завидую Вашей жене в хорошем смысле слова.Великолепное наглядное пособие.К сожалению,пространственное мышление современных десятиклассников развито плохо.Так что такой набор-замечательный наглядный материал.А главное,что модели трансформируются,можно показать и пирамиды различного вида, и наличие мнимых точек пересечения рёбер.
Пожалуй,добавлю себе в «избранное».Вдруг мне кто-то сможет сделать подобное.
Как сделать геометрические фигуры из бумаги? Схемы и советы
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Создание геометрии модели в COMSOL Multiphysics®
Создание геометрии является одним из первых шагов при настройке модели. Для отрисовки геометрии в программном обеспечении COMSOL Multiphysics® доступно множество геометрических операций, инструментов и различных функций, включая геометрические примитивы; логические операции, операции разделения и преобразования; возможность использования рабочих (секущих) плоскостей и другие CAD-операции. В данной статье мы разберём весь данный функционал. В процессе изложения мы укажем ссылки на учебные видео, в которых демонстрируется процесс создания геометрических последовательностей с использованием доступного в пакете функционала.
Создание геометрии в COMSOL Multiphysics®
Существует четыре основных способа создания геометрии для последующего моделирования в COMSOL Multiphysics:
У каждого из них есть свои преимущества и предпочтительные варианты использования. Самый первый подход позволяет вам создавать геометрию, используя встроенные в COMSOL Multiphysics CAD-инструменты. Он является основной темой этой статьи, поскольку мы подробно разберём связанный с ним рабочий процесс.
Отметим основные этапы создания геометрии:
Иногда более эффективным подходом может стать создание геометрических примитивов меньшей размерности с использованием рабочих плоскостей (work planes), с последующим их преобразованием в объекты большей размерности. Рабочие плоскости также можно использовать для создания поперечного сечения трёхмерного объекта.
Давайте подробнее рассмотрим использование геометрических примитивов, геометрических операций и рабочих плоскостей. Обратите внимание, что эти операции можно применять как к геометрии, созданной непосредственно в COMSOL Multiphysics, так и к геометрии, импортированной из стороннего CAD-пакета.
Использование геометрических примитивов
В COMSOL Multiphysics доступно несколько вариантов создания объектов для построения геометрии. Одним из вариантов является выбор объекта из набора встроенных в программное обеспечение типовых фигур и добавление геометрического примитива в геометрическую последовательность с последующим редактированием в окне Settings (настройки). Такой способ позволяет вам указать точное положение, угол и размеры объекта, а также быстро внести изменения в любой из этих параметров при необходимости. После добавления объектов в последовательность, их можно комбинировать и преобразовывать для создания окончательной геометрии.
Создание и изменение прямоугольника с использованием окна настроек в COMSOL Multiphysics.
Типы доступных объектов зависят от размерности модели. Это касается как совсем классических геометрических примитивов, так и более редких и специфичных их вариаций. Для трёхмерных моделей доступны такие геометрические фигуры, как блоки, сферы, торы, спиралевидные объекты и т.д.
Аналогично, для двухмерных моделей вы можете добавлять прямоугольники, круги, полигоны Бизье, параметрические кривые и т.д. Отметим, что в двухмерных и одномерных моделях вы можете отрисовывать геометрические примитивы при помощи мыши.
Это можно сделать следующим образом:
Сразу после этого нарисованный объект появится в геометрической последовательности.
Создание и изменение прямоугольника с помощью встроенных графических инструментов.
Для трёхмерных моделей отрисовка геометрических примитивов с использованием мыши недоступна. Однако, вы можете нарисовать поперечное сечение в рабочей плоскости, а затем вытянуть его, превратив в трёхмерный объект. Демонстрация вышеупомянутых вариантов доступна в серии с учебных видео на тему построения двухмерных геометрий. Кроме того, там мы обсуждаем преимущества использования параметров при построении геометрии и показываем, как с их помощью можно оптимизировать настройку геометрии.
Логические операции, операции разделения и преобразования
После добавления нескольких объектов в геометрическую последовательность, вы можете приступать к их осмысленному комбинированию с помощью различных геометрических операций. В серии учебных видео о построении двухмерных и трёхмерных геометрий мы показываем, как создать прямоугольную пластину с решеткой овальных отверстий. Для этого была использована комбинация нескольких логических (Boolean) операций и операций преобразования (transformation).
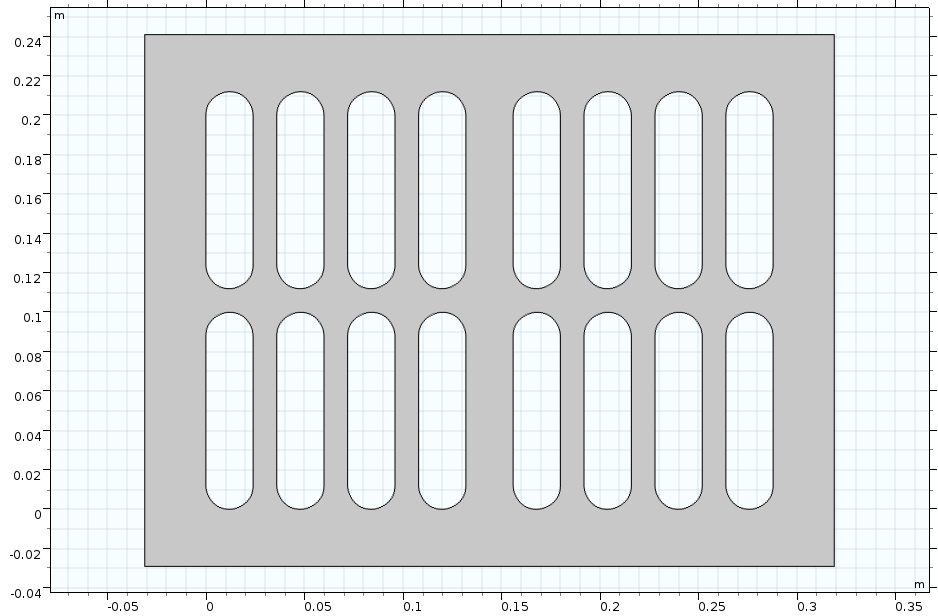
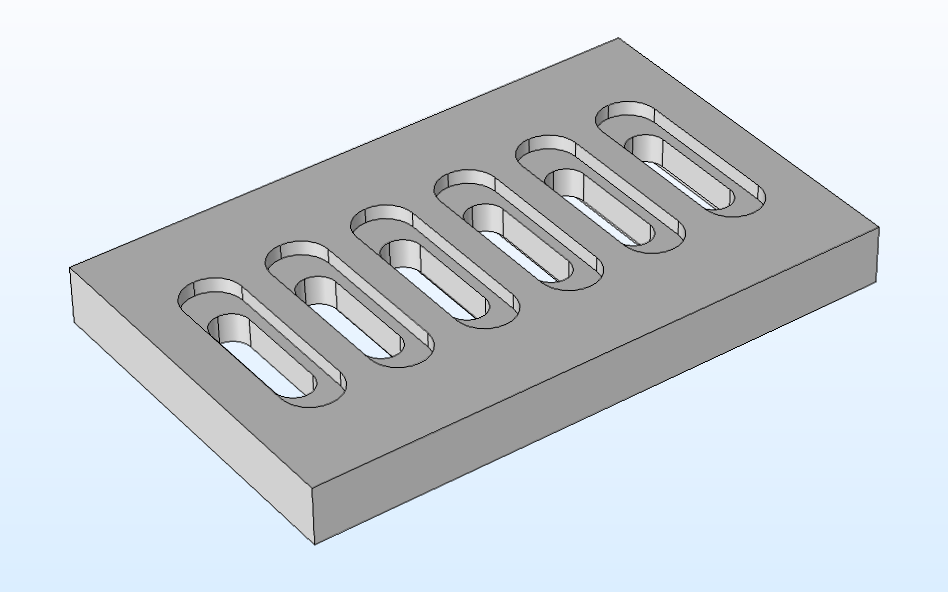
Прямоугольная пластина с овальными отверстиями в 2D (слева) и в 3D (справа).
Для создания геометрии, как на изображении выше, использовались такие логические операции, как Union (Объединение), Intersection (Пересечение), Difference (Разность), с помощью которых можно объединять объекты, создавать новые объекты при пересечении других объектов и вычитать объекты друг из друга, соответственно. Также использовались некоторые операции преобразования — Move (Переместить), Copy (Копировать), Mirror (Отобразить) и Array (Массив). Они позволяют изменять положение объектов, копировать объекты, отображать и отзеркаливать объекты относительно плоскости, линии или точки и создавать массивы из копий объектов.
Помимо стандартных геометрических операций, указанных выше, также есть специализированные геометрические инструменты, с помощью которых можно создавать сложные геометрии. С помощью операций разбиения (partition) можно разделять объекты, домены, границы и рёбра для дальнейшего разделения, удаления или упрощения геометрии вашей модели. В учебном видео на тему использования операций разбиения геометрии мы демонстрируем их применение на спиралевидном объекте и модели кожухотрубного теплообменника.
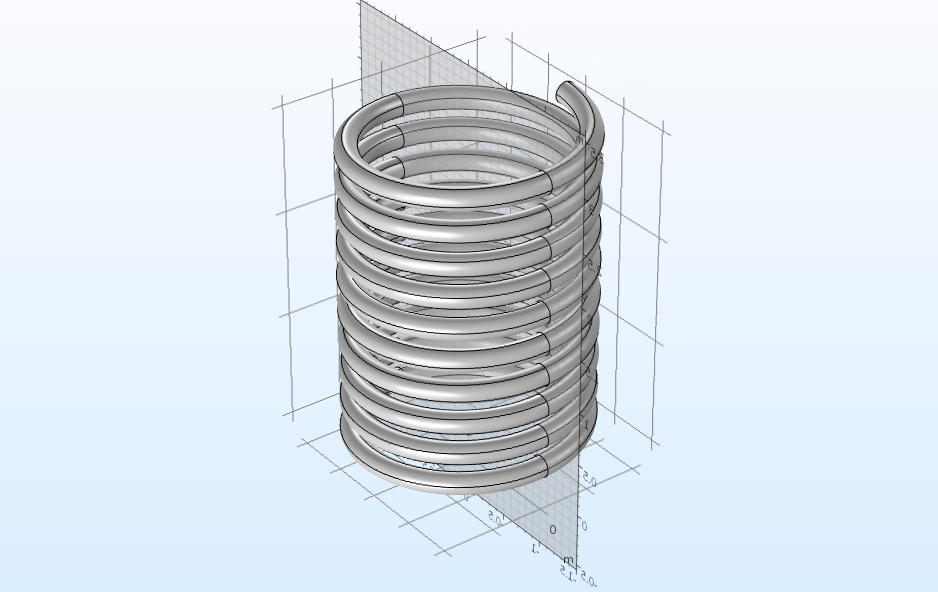
Геометрия спирали разделена посередине. Изображение взято из учебного видео на тему разделения геометрии.
По мере усложнения геометрии и добавления различных операций и преобразований вы можете заметить, что геометрическая последовательность стала довольно сложной и любые последующие изменения могут привести к ещё большему её усложнению. Изменение размера одного из элементов может потребовать и изменение размеров других объектов для корректной модификации всей геометрии. По этим и другим причинам мы рекомендуем параметризовывать геометрические операции. В серии учебных видео мы подробно рассказываем о преимуществах такого подхода и демонстрируем несколько примеров построения геометрии.
Операции с рабочими плоскостями
В COMSOL Multiphysics есть несколько инструментов для выполнения операций с рабочими плоскостями, которые позволяют преобразовывать двухмерную геометрию на рабочей плоскости в трёхмерный объект. В серии видео мы демонстрируем применение операций Extrude (Выдавливание), Revolve (Вращение) и Sweep (Протяжка).
С помощью операции Extrude можно выдавливать объекты с рабочей плоскости или плоской грани для создания трёхмерных элементов.
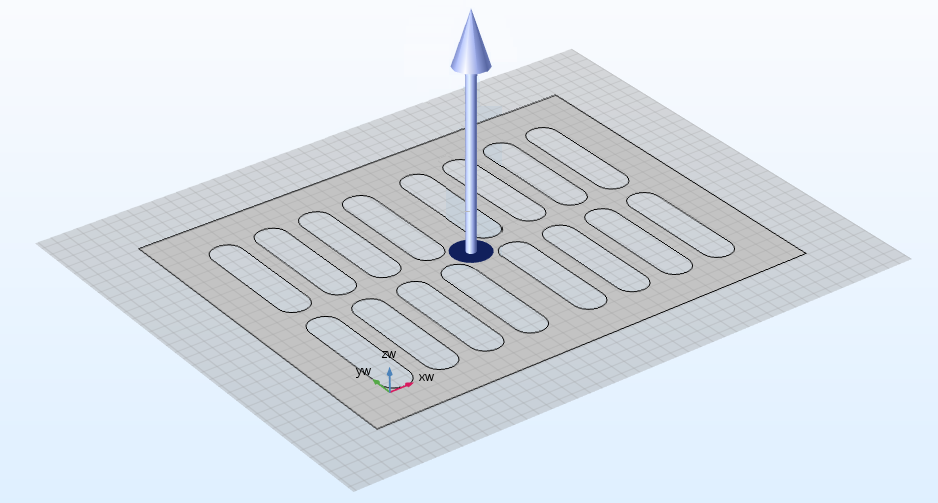
Операция Extrude используется для преобразования прямоугольной пластины с отверстиями в трёхмерный параллелепипед с решёткой. Синей стрелкой по центру показано направление выдавливания, которое перпендикулярно рабочей плоскости.
С помощью операции Revolve можно поворачивать объекты, нарисованные на рабочей плоскости или плоской грани, вокруг оси для создания трёхмерных элементов.
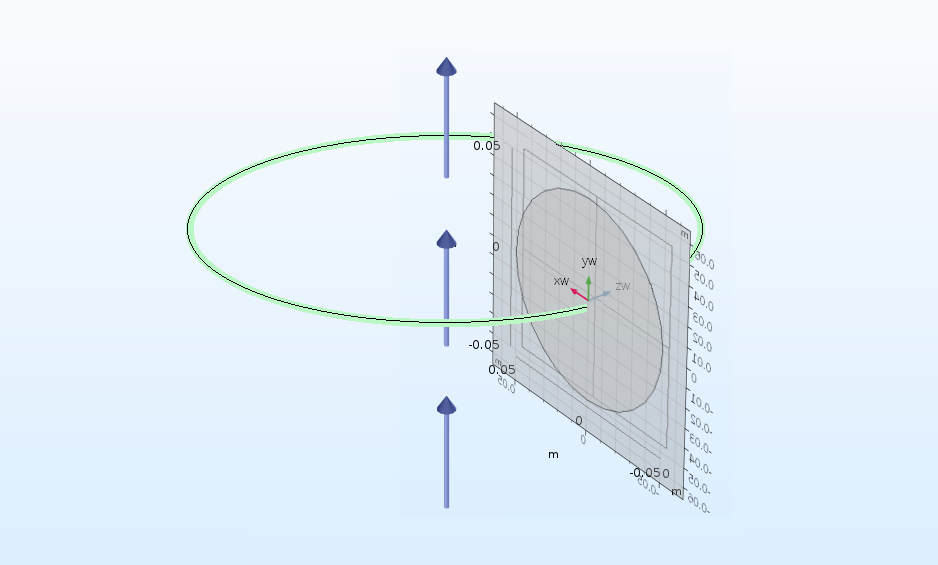
Операция Revolve преобразует круг в тор. Синими стрелками показана ось вращения.
Наконец, используя операцию Sweep, можно протягивать объекты, нарисованные на рабочей плоскости или плоской грани, по заданной траектории для создания трёхмерного элемента.
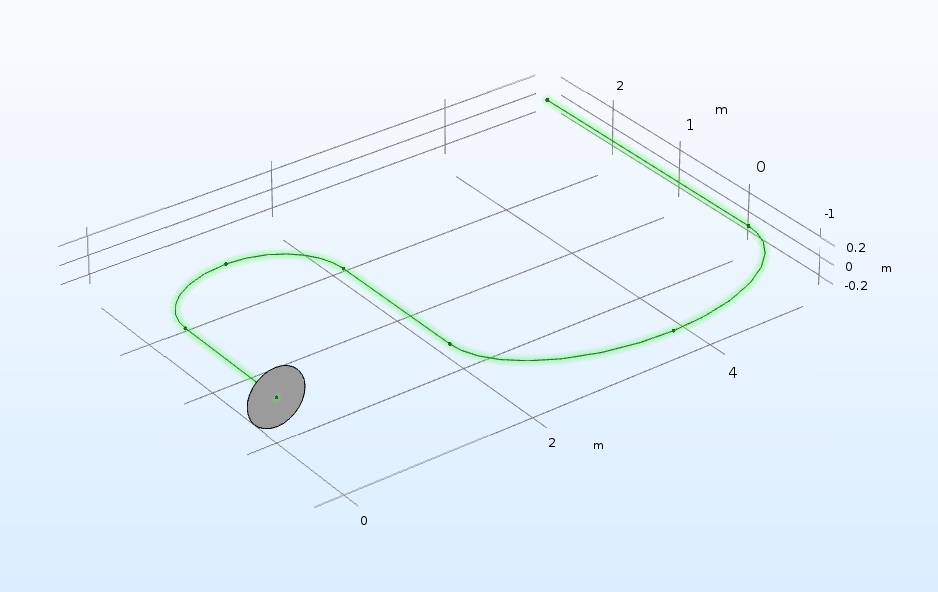
Операция Sweep, преобразующая круг и заданную двухмерную траекторию в трубу. Две перпендикулярные рабочие плоскости используются для определения формы и траектории протяжки.
Использование этих операций (позволяющих начать с 2d модели, а затем превратить её в трёхмерную) может значительно ускорить процесс создания трёхмерной геометрии, в отличие от её изначального создания исключительно из трёхмерных объектов.
Геометрическая операция Поперечное сечение
В программном обеспечении COMSOL Multiphysics также есть инструмент, позволяющий преобразовывать трёхмерную геометрию в двухмерную. Для его использования необходимо выбрать рабочую плоскость и использовать в ней операцию Cross Section (Поперечное сечение). Данный функционал можно использовать для упрощения вашей модели, о чём мы также подробно рассказываем в серии видеоуроков.
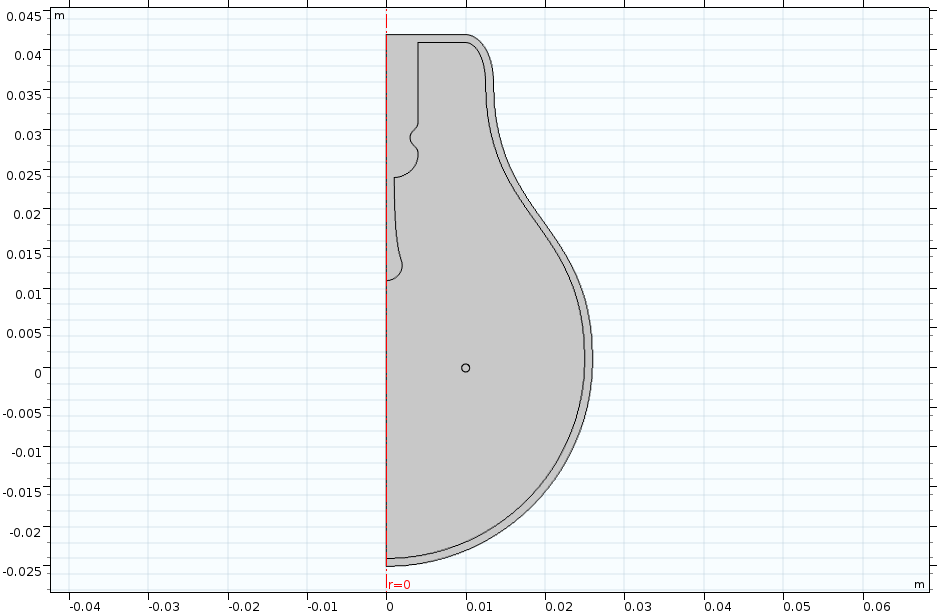
Поперечное сечение лампочки для осесимметричной постановки, которое мы построили в видео на тему создания двухмерных моделей из трёхмерной геометрии.
Геометрия, созданная при помощи операции Cross Section, основана на пересечении трёхмерной геометрии с рабочей плоскостью. Таким образом, полученная двухмерная геометрия является результатом пересечения рабочей плоскости с трёхмерным полнотельным объектом. В настройках операции можно выбрать трёхмерные объекты, которые будет пересекать рабочая плоскость.
Обратите внимание что, для того чтобы получить подходящее поперечное сечение для дальнейшего моделирования может потребоваться дополнительная подготовка исходной трёхмерной геометрии. Иногда это может быть разделение отдельных частей геометрии с их последующим удалением. В таком случае будут полезны операции разбиения (partition). Мы подробно рассказываем эти аспекты в соответствующей части видеоурока.
Дальнейшие шаги: Посмотрите серию видеоуроков об использовании инструментов для создания геометрии
Независимо от того, создаёте ли вы геометрию с использованием встроенных в COMSOL Multiphysics CAD-инструментов или работаете с импортированным файлом, вы можете пользоваться функционалом, о котором мы рассказали в данной заметке, для полной кастомизации и настройки всех геометрических объектов. Чтобы наглядно увидеть все указанные инструменты в действии, ознакомьтесь с анонсированной серией видеоуроков на тему построения геометрии: