Как сделать стандартизацию данных
Как нормализовать и стандартизировать данные временных рядов в Python
Дата публикации 2016-12-12
Некоторые алгоритмы машинного обучения будут обеспечивать лучшую производительность, если ваши данные временных рядов будут иметь постоянный масштаб или распределение.
Двумя методами, которые вы можете использовать для последовательного масштабирования данных временных рядов, являются нормализация и стандартизация.
В этом руководстве вы узнаете, как применить нормализацию и масштабирование стандартизации к данным временных рядов в Python.
После завершения этого урока вы узнаете:
Набор данных минимальных суточных температур
Этот набор данных описывает минимальные дневные температуры за 10 лет (1981-1990) в городе Мельбурн, Австралия.
Ниже приведен пример первых 5 строк данных, включая строку заголовка.
Ниже приведен график всего набора данных, взятого из Data Market.
Набор данных показывает сильную сезонную составляющую и имеет приятные мелкозернистые детали для работы.
В этом руководстве предполагается, что набор данных находится в вашем текущем рабочем каталоге с именем файла «ежедневно минимальная температура-в-me.csv«.
Заметка: Загруженный файл содержит несколько знаков вопроса («?»), Которые необходимо удалить, прежде чем вы сможете использовать набор данных. Откройте файл в текстовом редакторе и удалите символы «?». Также удалите любую информацию нижнего колонтитула в файле.
Нормализуйте данные временного ряда
Нормализация может быть полезной и даже необходимой в некоторых алгоритмах машинного обучения, когда данные временных рядов имеют входные значения с различными масштабами. Это может потребоваться для алгоритмов, таких как k-Nearest соседей, которые используют вычисления расстояний и линейную регрессию и искусственные нейронные сети, которые весовые значения ввода.
Нормализация требует, чтобы вы знали или могли точно оценить минимальные и максимальные наблюдаемые значения. Возможно, вы сможете оценить эти значения по вашим доступным данным. Если ваш временной ряд имеет тенденцию к повышению или понижению, оценка этих ожидаемых значений может быть затруднена, и нормализация может оказаться не лучшим методом для решения вашей проблемы.
Значение нормализуется следующим образом:
Где минимальные и максимальные значения относятся к значениюИкснормализуется.
Вы можете увидеть, что еслиИкспредоставляется значение, которое находится за пределами минимального и максимального значений, что результирующее значение не будет находиться в диапазоне от 0 до 1. Вы можете проверить эти наблюдения перед выполнением прогнозов и либо удалить их из набора данных, либо ограничить их до предопределенных максимальных или минимальных значений.
Вы можете нормализовать свой набор данных, используя объект scikit-learn.MinMaxScaler,
Хорошая практика использования сMinMaxScalerи другие методы масштабирования следующие:
При необходимости преобразование может быть инвертировано. Это полезно для преобразования прогнозов в исходную шкалу для составления отчетов или построения графиков. Это можно сделать, позвонивinverse_transform ()функция.
Ниже приведен пример нормализации набора данных «Минимальные суточные температуры».
Скейлер требует, чтобы данные были представлены в виде матрицы строк и столбцов. Загруженные данные временного ряда загружаются как пандыСерии, Затем он должен быть преобразован в матрицу из одного столбца с 3650 строками.
Затем измененный набор данных используется для подгонки скейлера, набор данных нормализуется, затем преобразование нормализации инвертируется, чтобы снова показать исходные значения.
При выполнении примера печатаются первые 5 строк из загруженного набора данных, отображаются те же 5 значений в их нормализованной форме, а затем значения возвращаются в исходный масштаб с использованием обратного преобразования.
Мы также видим, что минимальное и максимальное значения набора данных равны 0 и 26,3 соответственно.
Существует другой тип масштабирования, который более устойчив к новым значениям, находящимся вне диапазона ожидаемых значений; это называется стандартизацией. Мы посмотрим на это дальше.
Стандартизировать данные временных рядов
Это можно рассматривать как вычитание среднего значения или центрирование данных.
Как и нормализация, стандартизация может быть полезной и даже необходимой в некоторых алгоритмах машинного обучения, когда ваши данные временного ряда имеют входные значения с различными масштабами.
Стандартизация предполагает, что ваши наблюдения соответствуют гауссовскому распределению (кривая колокола) со средним значением и стандартным отклонением. Вы все еще можете стандартизировать данные временных рядов, если это ожидание не будет выполнено, но вы можете не получить надежных результатов.
Это включает в себя алгоритмы, такие как машины опорных векторов, линейная и логистическая регрессия, и другие алгоритмы, которые предполагают или имеют улучшенную производительность с гауссовыми данными.
Стандартизация требует, чтобы вы знали или были в состоянии точно оценить среднее и стандартное отклонение наблюдаемых значений. Возможно, вы сможете оценить эти значения по вашим данным обучения.
Значение стандартизировано следующим образом:
Гдеимею в видурассчитывается как:
Истандартное отклонениерассчитывается как:
Например, мы можем построить гистограмму набора данных «Минимальные суточные температуры» следующим образом:
Выполнение кода дает следующий график, который показывает гауссово распределение набора данных, как предполагается стандартизацией.
Мы можем угадать среднюю температуру 10 и стандартное отклонение около 5. Используя эти значения, мы можем стандартизировать первое значение в наборе данных 20,7 следующим образом:
Оценки среднего и стандартного отклонения набора данных могут быть более устойчивыми к новым данным, чем минимальное и максимальное.
Вы можете стандартизировать свой набор данных, используя объект scikit-learn.StandardScaler,
Ниже приведен пример стандартизации набора данных «Минимальные суточные температуры».
При выполнении примера печатаются первые 5 строк набора данных, печатаются те же стандартизированные значения, а затем печатаются значения обратно в их исходном масштабе.
Мы можем видеть, что расчетное среднее значение и стандартное отклонение составляли 11,1 и 4,0 соответственно.
Резюме
В этом руководстве вы узнали, как нормализовать и стандартизировать данные временных рядов в Python.
В частности, вы узнали:
У вас есть вопросы о масштабировании данных временных рядов или об этом посте?
Задайте свои вопросы в комментариях, и я сделаю все возможное, чтобы ответить.
Как стандартизировать данные семантики с помощью логарифмов
Сбор, кластеризация и анализ полученных данных по семантическому ядру – один из наиболее важных этапов продвижения сайтов в поисковых системах.
Так как процесс сбора ядра имеет примерно одинаковый алгоритм во многих компаниях, в данной статье мы поговорим не о самом процессе формирования кластеров, а о способе быстрой оценки данных при выборе наиболее значимых кластеров для работы. Это позволит сделать быстрый старт именно с тех позиций, которые имеют наиболее весомые показатели как по коммерческой оценке, так и по частотности.
Проблема
При работе с большим объемом запросов в коммерческой тематике и при необходимости быстрого запуска наиболее весомых кластеров часто возникает ситуация, когда выборка по частотности показывает запросы некоммерческого характера. После сортировки ключей по коммерческим оценкам мы можем увидеть вверху низкочастотные запросы, которые не интересны для нас на этапе старта работ.
На скриншоте видно, что, фильтруя по частотности, мы получаем вверху запросы с низкими коммерческими показателями
Если представить ситуацию, при которой мы работаем с готовой чистой информационной семантикой, то тогда мы можем отбирать
Данный способ не подходит, когда при сортировке по частотности мы получаем запросы, не отсортированные по коммерческой оценке.
Стандартизация данных
Суммировать сумму запросов кластера и смотреть на ее отношение к сумме по процентам коммерческой оценки некорректно. Во-первых, это две разные сущности. Во-вторых, большой кластер с низкими коммерческими оценками запросов за счет их суммы может оказаться выше кластера из меньшего количества запросов, которые обладают 100% коммерческим интентом.
В результате в числе приоритетных ключей мы увидим ключевые фразы, не соответствующие нашим требованиям.
Чтобы решить этот вопрос мы должны:
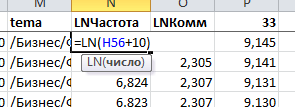
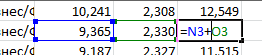
1. Стандартизировать данные, для чего мы вводим функцию натурального логарифмирования. Прежде, чем объединять данные, нам нужно их нормировать и сжать. Функция логарифма для Excel «=LN(в скобках указываем нужное число)».
На скриншоте показано, как выглядит формула
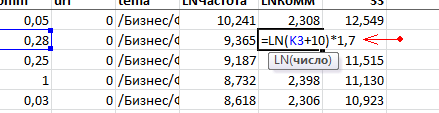
2. Прибавить условное число для каждого показателя частотности и коммерческости, чтобы избежать ошибок, если данные равны 0 или 1.
3. Логарифм обезличивает наши данные и дает возможность сопоставить их для сравнения.
Далее мы складываем полученные числа, чтобы получить показатель, по которому можно сделать сортировку запросов и увидеть наиболее приоритетные в семантическом ядре по соотношению коммерческой оценки запроса и его частотности.
Также мы можем сдвинуть веса, изменив приоритет суммируемых данных. Это можно сделать через коэффициент, который добавляем к тем данным, которые для нас важнее.
После того как сделана сортировка и выбраны запросы для работы, остальные ключи кластера можно подтянуть по номеру группы.
Заключение
Предлагая данный метод, мы бы хотели, в первую очередь, услышать обратную связь. Возможно, есть способ повысить точность итоговых данных или ускорить процесс.
Данный подход встречается в прогнозной аналитике Дмитрия Иванова, но при этом метод не распространен среди SEO-специалистов. Часто на различных курсах по SEO вопрос выбора кластеров сводится только к частотности или коммерческой оценке. Однако проблема отсутствия возможности увидеть сбалансированные данные по этим двум характеристикам остается. На наш взгляд это некорректно, поэтому мы попробовали систематизировать работу в этом направлении.
Представленный метод позволяет:
Стандартизация данных
Перед началом проведения кластерного анализа необходимо провести стандартизацию данных по формуле:
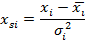 | (5.1) |
где 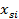
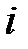
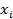
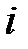
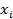
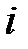
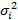
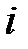
Расчеты можно провести в Microsoft Office Excel, используя встроенные статистические функции СРЗНАЧ () и СТАНДОТКЛОН (). Полученный результат представлен в таблице 5.2.
Таблица 5.2. Стандартизованные данные по уровню жизни населения
| REGION | ID BIRTH (S) | ID EDUCATION (S) | ID POVERTY (S) | ID_UNEMP LAYMENT (S) | ID_VVP (S) | ID_DEVE LOPMENT (S) |
| Российская Федерация | 0,2527 | 0,2071 | 0,4753 | 0,2035 | 0,0677 | 0,4357 |
| Тюменская область | 0,7159 | 1,5634 | 1,9933 | -0,1463 | 5,549 | 4,9334 |
| Самарская область | 0,7159 | 0,7496 | 1,4873 | 1,6026 | 0,7211 | 1,9077 |
| Мурманская область | 1,6424 | 1,8346 | 1,4873 | -2,5947 | 0,9212 | 1,5397 |
| Республика Татарстан | 1,6424 | -0,0641 | 1,15 | 0,9031 | 0,241 | 1,1717 |
| Республика Коми | -0,2106 | 1,2921 | 0,9813 | -1,5454 | 1,0279 | 1,0899 |
| Республика Якутия | -1,1371 | 1,5634 | -0,874 | -0,1463 | 2,0948 | 1,0899 |
| Магаданская область | -0,2106 | 2,9196 | -1,2113 | -1,5454 | 1,4147 | 0,7628 |
| Хабаровский край | -1,6003 | 1,5634 | 0,3067 | 0,5533 | 0,4411 | 0,7219 |
| Пермская область | -0,2106 | -0,3354 | 0,9813 | 0,2035 | 0,3344 | 0,5992 |
| Белгородская область | 2,1057 | -1,1491 | 1,15 | 0,9031 | -0,3191 | 0,5992 |
| Липецкая область | 1,1792 | -1,1491 | 1,3187 | 0,9031 | -0,2658 | 0,5583 |
| Московская область | 0,2527 | 0,7496 | -0,0307 | 1,2528 | -0,0657 | 0,5174 |
| Камчатская область | -1,6003 | 2,3771 | -1,0427 | -1,5454 | 1,4813 | 0,4765 |
| Нижегородская область | 0,2527 | -0,8779 | 0,9813 | 1,6026 | -0,1857 | 0,5174 |
| Ульяновская область | 1,1792 | -0,8779 | 1,3187 | 0,9031 | -0,5592 | 0,4357 |
| Красноярский край | -2,0635 | 0,2071 | 0,644 | -0,8458 | 0,8812 | 0,3539 |
| Ярославская область | 0,2527 | -0,6066 | 0,4753 | 0,9031 | -0,0257 | 0,2721 |
| Томская область | -0,2106 | 0,2071 | -0,0307 | -0,496 | 0,4678 | 0,1903 |
| Иркутская область | -2,0635 | 0,7496 | -0,0307 | -0,1463 | 0,3744 | 0,0268 |
| Вологодская область | -0,2106 | -0,8779 | 0,3067 | 0,2035 | 0,2677 | 0,0677 |
| Кемеровская область | -1,6003 | -0,3354 | 0,644 | 0,5533 | -0,0124 | 0,0677 |
| Ростовская область | 0,7159 | 0,2071 | 0,9813 | -0,8458 | -0,8126 | -0,0141 |
| Тульская область | -0,6738 | -0,6066 | 0,9813 | 0,5533 | -0,6125 | -0,055 |
| Респ.Башкортостан | 0,7159 | -0,3354 | -0,1993 | 0,2035 | -0,0257 | -0,055 |
| Воронежская область | 1,6424 | -1,1491 | 0,3067 | 1,6026 | -0,7459 | 0,0268 |
| Челябинская область | 0,7159 | -0,0641 | -0,0307 | 0,5533 | -0,3591 | -0,0141 |
| Свердловская область | -0,2106 | 0,2071 | -1,0427 | 1,2528 | 0,1743 | -0,0959 |
| Курская область | 0,2527 | -1,1491 | 0,138 | 1,2528 | -0,3858 | -0,1777 |
| Калужская область | -0,2106 | -0,0641 | 0,138 | 1,2528 | -0,6925 | -0,1368 |
| Омская область | 1,1792 | -0,6066 | 0,3067 | -0,496 | -0,2791 | -0,0959 |
| Республика Карелия | -0,6738 | -0,0641 | 0,644 | -1,1956 | -0,1457 | -0,1777 |
| Орловская область | 0,7159 | -0,6066 | 0,138 | 0,2035 | -0,5458 | -0,2595 |
| Оренбургская область | 0,2527 | -0,3354 | -0,0307 | 0,2035 | -0,3458 | -0,2186 |
| Новгородская область | -1,1371 | -1,4204 | 1,3187 | -0,496 | -0,3725 | -0,3412 |
| Рязанская область | 0,2527 | -0,8779 | -0,5367 | 2,3022 | -0,5858 | -0,3003 |
| Краснодарский край | 0,7159 | -0,3354 | 0,3067 | -0,8458 | -0,6259 | -0,423 |
| Удмуртская Республика | 0,7159 | 0,2071 | -0,874 | 0,2035 | -0,4258 | -0,4639 |
| Владимирская область | -0,2106 | -0,3354 | -0,1993 | 0,5533 | -0,7192 | -0,5457 |
| Волгоградская область | 0,7159 | 0,2071 | -0,7053 | -0,496 | -0,5192 | -0,5866 |
| Саратовская область | 0,7159 | 0,2071 | -0,5367 | -0,8458 | -0,6392 | -0,6683 |
| Приморский край | -0,6738 | 1,0209 | -1,2113 | -0,496 | -0,1857 | -0,6275 |
| Сахалинская область | -2,0635 | 1,5634 | -1,886 | -1,1956 | 0,6545 | -0,6683 |
| Костромская область | -0,6738 | -1,4204 | -0,0307 | 0,9031 | -0,5592 | -0,7092 |
| Смоленская область | -0,6738 | -0,8779 | 0,644 | -0,8458 | -0,6259 | -0,6683 |
| Тамбовская область | 0,7159 | -1,6916 | 0,138 | 0,2035 | -0,9193 | -0,8319 |
| Тверская область | -1,1371 | -0,6066 | -0,7053 | 0,9031 | -0,5858 | -0,8728 |
| Калининградская область | -0,6738 | 0,7496 | -0,5367 | -1,1956 | -0,7992 | -0,9137 |
| Амурская область | -1,1371 | 0,4784 | -1,0427 | -1,1956 | -0,1724 | -0,9546 |
| Архангельская область | -0,6738 | 0,4784 | -1,886 | -0,496 | -0,0657 | -1,0363 |
| Ленинградская область | -0,2106 | -0,3354 | -1,38 | -0,496 | -0,3858 | -1,159 |
| Брянская область | 0,2527 | -1,4204 | -0,0307 | -0,8458 | -0,9193 | -1,159 |
| Астраханская область | -0,2106 | -0,0641 | -1,2113 | -0,8458 | -0,6392 | -1,2408 |
| Новосибирская область | 0,7159 | -0,3354 | -2,5607 | -0,1463 | -0,3591 | -1,4861 |
| Ставропольский край | 1,1792 | -0,3354 | -1,886 | -0,8458 | -0,6259 | -1,4044 |
Дата добавления: 2015-01-13 ; просмотров: 1171 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ