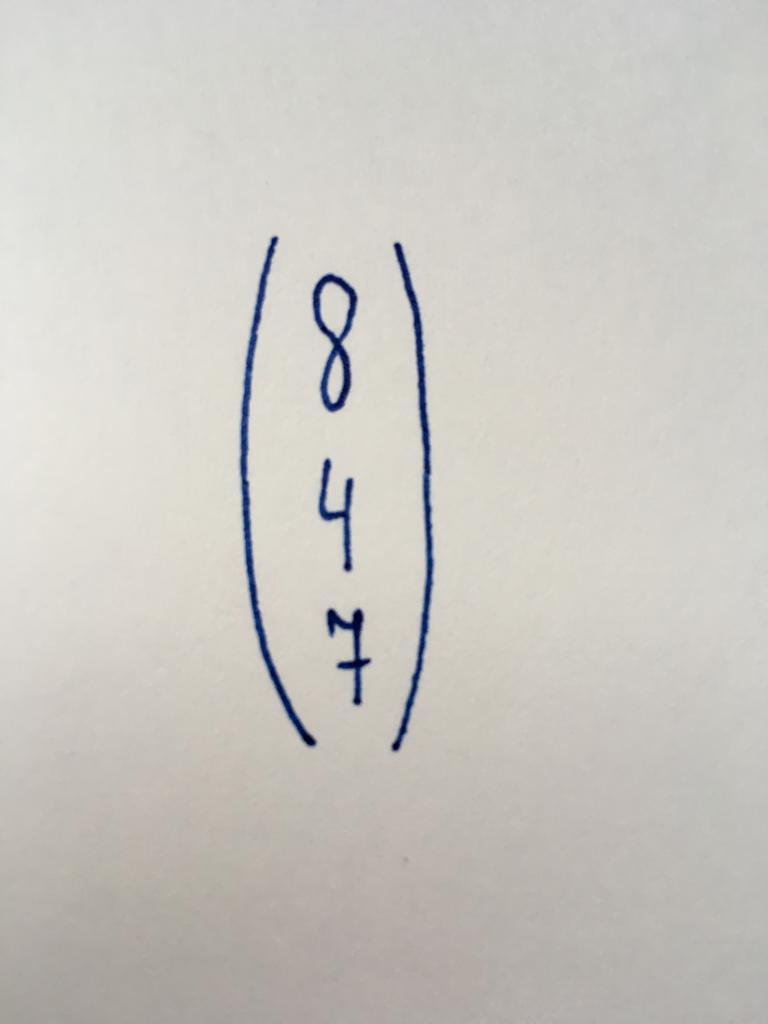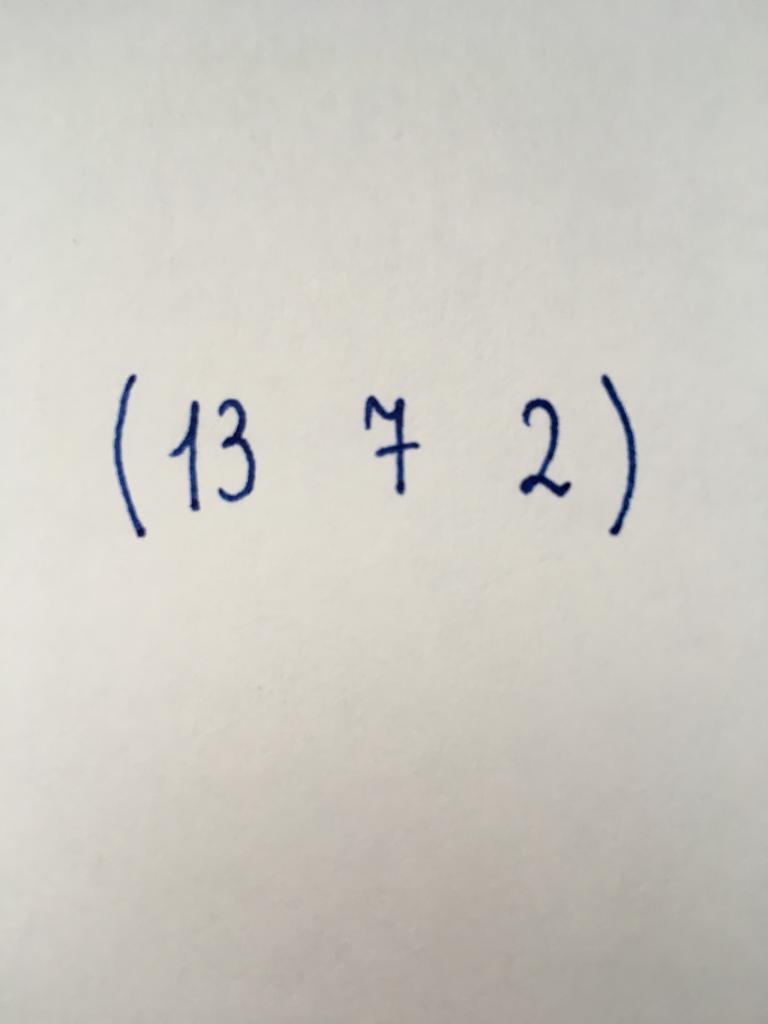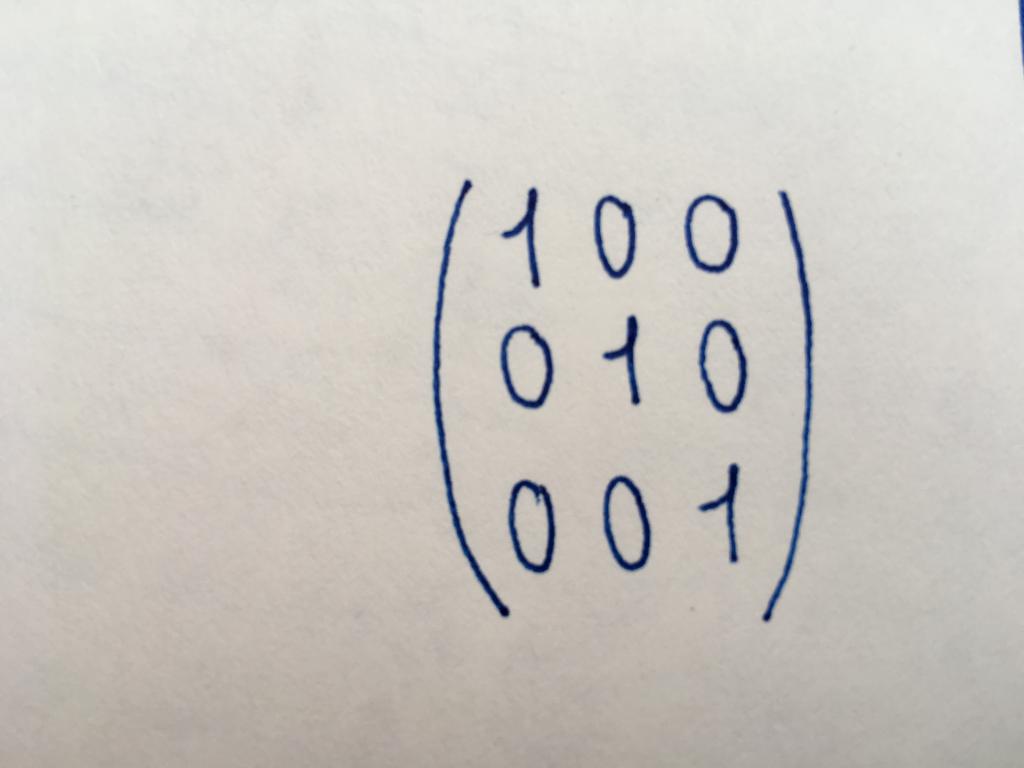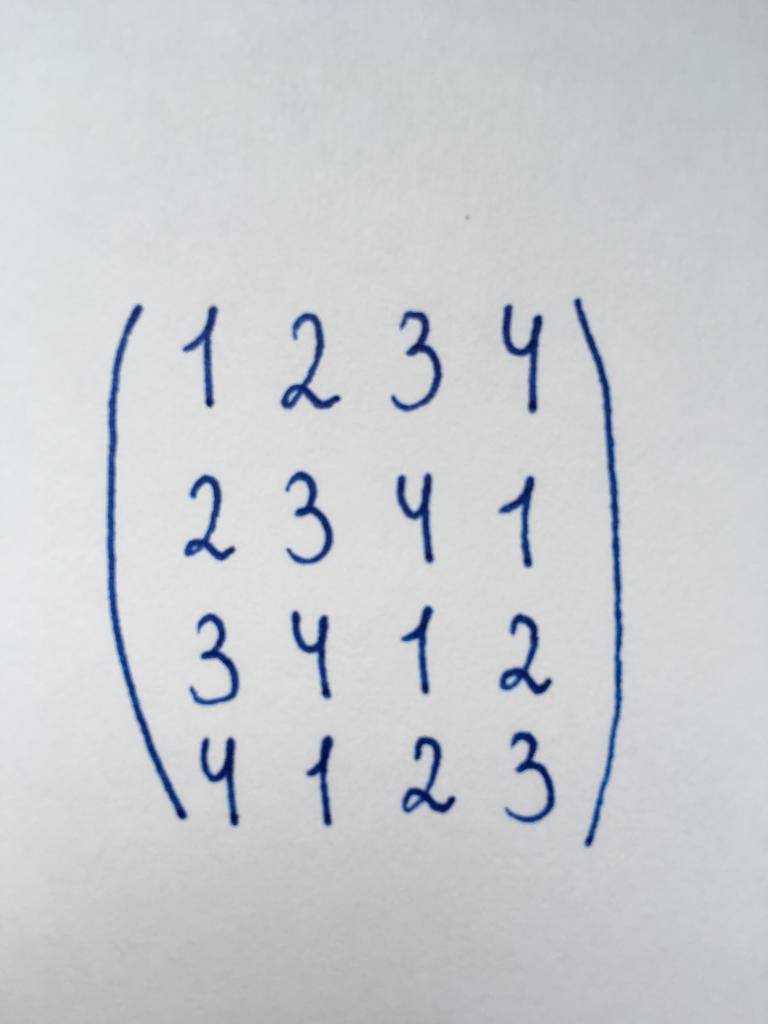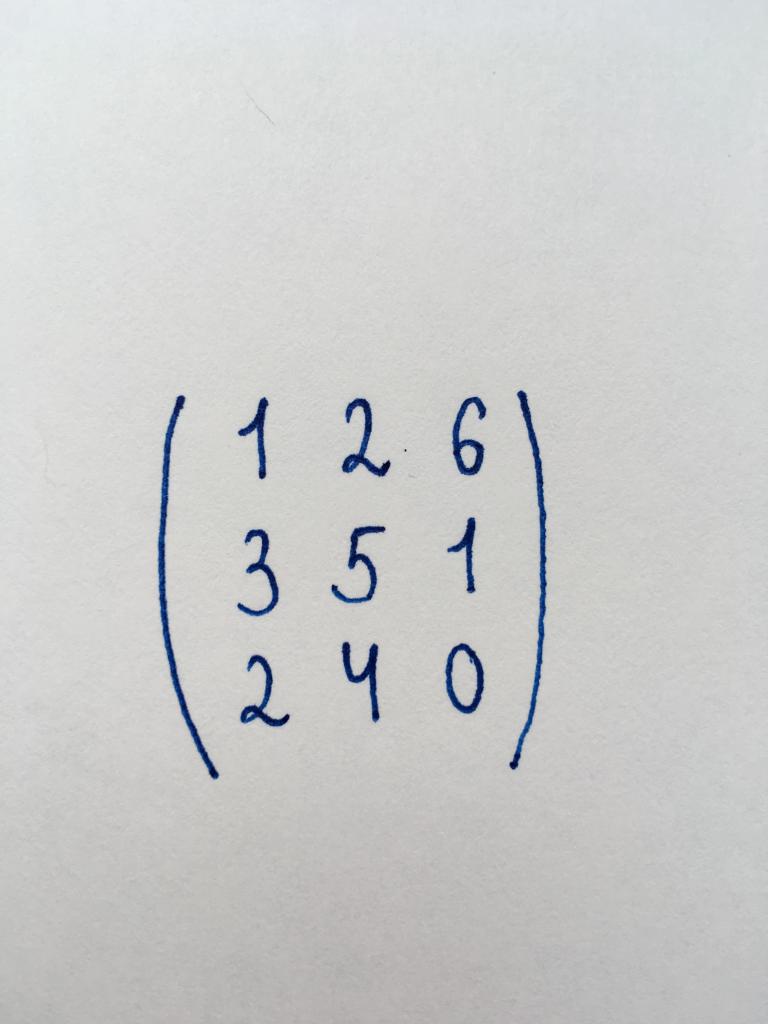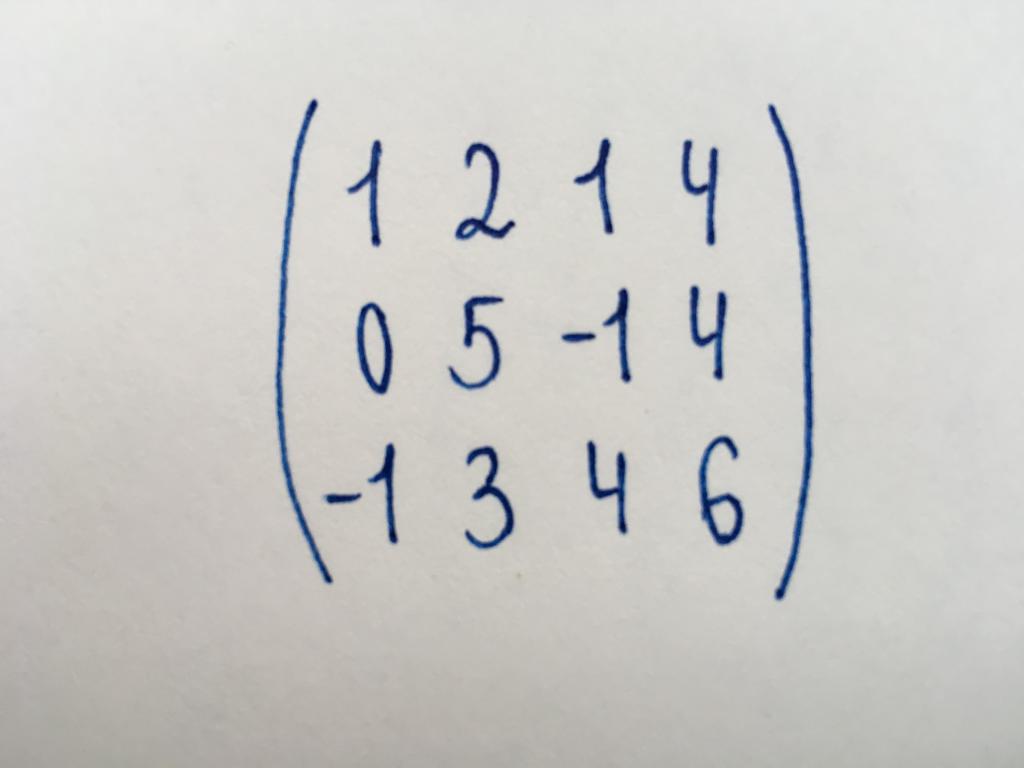Как сделать ступенчатый вид матрицы

Приведение матрицы к ступенчатому виду

Матрица — математический объект, представленный в форме квадратной или прямоугольной таблицы, содержащей определенное число строк и столбцов, именуемых порядками. Матрицы могут различаться размерами и содержанием. Матрицы позволяют упорядочить записи систем линейных уравнений, что ведет к удобному поиску их результатов. Работа с матрицами предполагает приведение их к стандартному виду.
В математике множество разнообразных видов матриц. Все элементы нулевой матрицы равны нулю, а число строк и столбцов может быть совершенно разным.
Матрица квадратного типа имеет одинаковое количество строк и столбцов. Матрица простейшего вида вектор-столбец имеет три численных значений, расположенных в столбец. Вектор-строка содержит три численных элементов, размещенных в одну строку. В диагональной матрице числовые значения имеют лишь элементы главной диагонали, остальные равны нулю. Начинается диагональ с элемента в правом верхнем углу и заканчивается в последнем столбце последней строки. Диагональный тип может иметь лишь квадратная матрица. Подвид диагональной матрицы — единичная, все числовые значения которой равны единицам. В канонической матрице не все компоненты основной диагонали равны единице, число строк и столбцов может быть разное, но, как и в единичной матрице, элементы, расположенные не на основной диагонали, равны нулю. Матрица треугольного типа является квадратной. Матрица, элементы которой, расположенные ниже главной диагонали, равны нулю, называется нижнетреугольной. В верхнетреугольной матрице числовые значения имеют элементы, расположенные на основной диагонали и под ней. Над диагональю элементы имеют нулевое значение.

Матрица, имеющая «ступени» из нулей, называется ступенчатой. В данном типе матриц диагональ из нулей не обязательно должна быть основной. Элементы под диагональю, как и на диагонали, должны иметь нулевые значения. Элемент в углу каждой ступеньки — ненулевой. Первый ненулевой элемент строки обязательно располагается правее первого ненулевого элемента строки предыдущей. Все элементы под 1-м ненулевым элементом строки имеют нулевые значения. Если ступенчатая матрица имеет нулевую строку, строки ниже нее тоже не имеют числовых значений. Т.е нулевые строки — последние. Для приведения матрицы к ступенчатому виду следует определить ее детерминант. Задание выполнимо, если детерминант больше или меньше нуля, в противном случае (равен нулю) привести матрицу к ступенчатому виду нельзя.

Любую матрицу несложно привести к ступенчатой форме, используя следующие элементарные преобразования:
— перестановка двух строк (столбцов);
— умножение строки (столбца) на любое, кроме нуля, число;
— сложение строки (столбца) с другой (другим), умноженной (умноженным) на любое, произвольно взятое (кроме нуля) число.

Приводим матрицу к ступенчатому виду:
1. Выбираем элемент, отличный от нуля в 1-м столбце. Если выбранный элемент (ведущий) расположен не в 1-й строке, переставляем строку с ведущим элементом на первую (ведущую) строку. Если элементы 1-го столбца равны нулю, исключаем его и переходим к следующему.
2. Делим элементы ведущей строки на ведущий элемент. Преобразования закончены при условии, что ведущая строка последняя.
3. К строке, расположенной под ведущей, добавляем ведущую, предварительно умноженную на число, чтобы элементы стоящей ниже строки стали равняться нулю.
4. Исключаем строку и столбец с ведущим элементом на пересечении.
Повторяем те же действия с оставшейся частью матрицы.

Привести матрицу к ступенчатому виду вам поможет онлайн калькулятор. Выберите размерность и введите значение ее элементов.

Источник

Виды матриц. Ступенчатый вид матрицы. Приведение матрицы к ступенчатому и треугольному виду

Нулевой тип

Квадратный тип

Количество столбцов и строк этого вида матрицы совпадает. Иначе говоря, она представляет собой таблицу формы «квадрат». Число ее столбцов (или строк) именуются порядком. Частными случаями считается существование матрицы второго порядка (матрица 2×2), четвертого порядка (4×4), десятого (10×10), семнадцатого (17×17) и так далее.

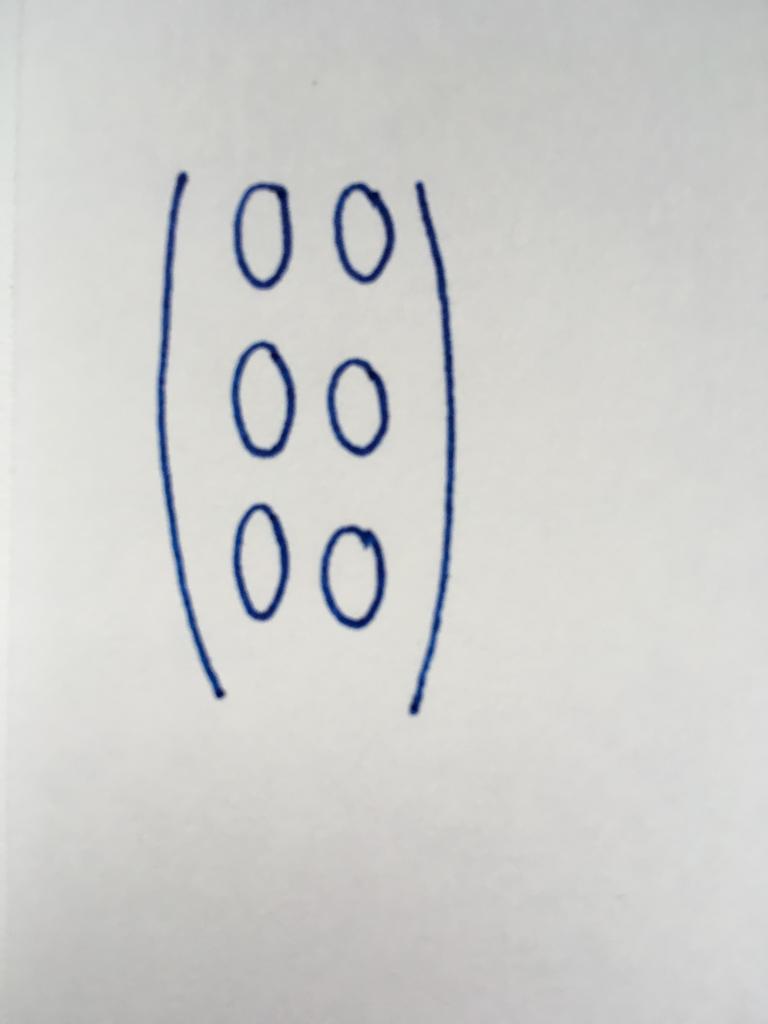
Вектор-стобец

Это один из простейших видов матриц, содержащий только один столбец, который включает в себя три численных значения. Она представляет ряд свободных членов (чисел, независимых от переменных) в системах линейных уравнений.

Вектор-строка

Вид, аналогичный предыдущему. Состоит из трех численных элементов, в свою очередь организованных в одну строку.

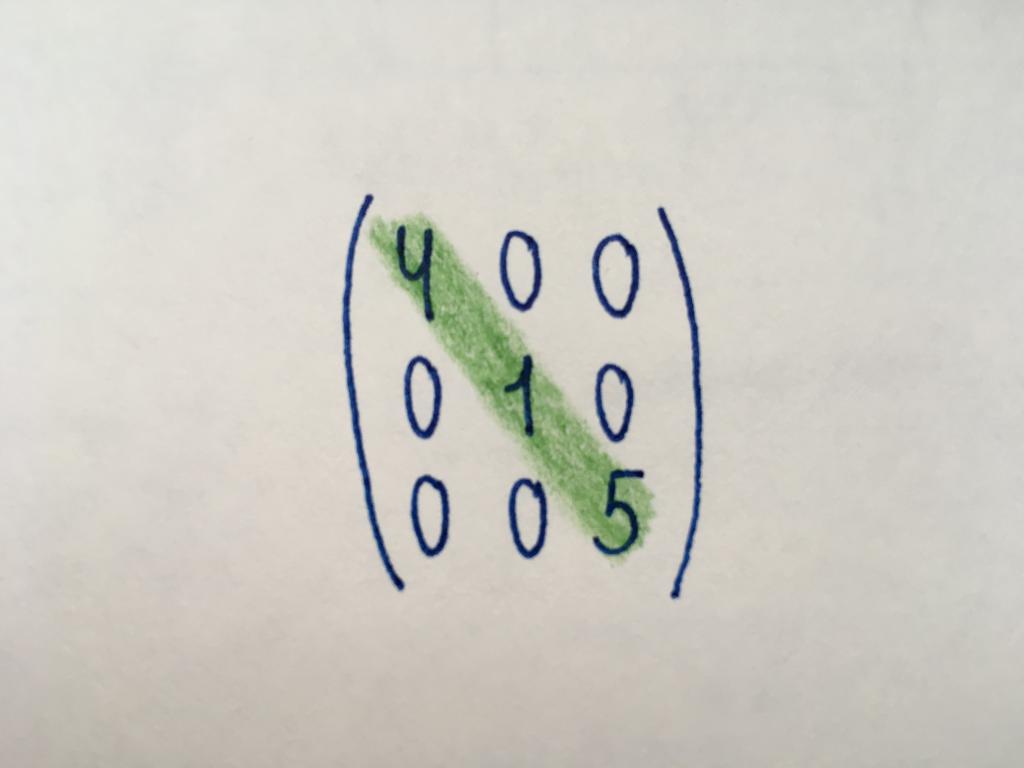
Диагональный тип

Числовые значения в диагональном виде матрицы принимают только компоненты главной диагонали (выделена зеленым цветом). Основная диагональ начинается с элемента, находящегося в левом верхнем углу, а заканчивается элементом в правом нижнем соответственно. Остальные компоненты равны нулю. Диагональный тип представляет собой только квадратную матрицу какого-либо порядка. Среди матриц диагонального вида можно выделить скалярную. Все ее компоненты принимают одинаковые значения.

Единичная матрица

Подвид диагональной матрицы. Все ее числовые значения являются единицами. Используя единичный тип матричных таблиц, выполняют ее базовые преобразования или находят матрицу, обратную исходной.

Канонический тип

Канонический вид матрицы считается одним из основных; приведение к нему часто необходимо для работы. Число строк и столбцов в канонической матрице различно, она необязательно принадлежит к квадратному типу. Она несколько похожа на единичную матрицу, однако в ее случае не все компоненты основной диагонали принимают значение, равное единице. Главнодиагональных единиц может быть две, четыре (все зависит от длины и ширины матрицы). Или единицы могут не иметься вовсе (тогда она считается нулевой). Остальные компоненты канонического типа, как и элементы диагонального и единичного, равны нулю.

Треугольный тип

Один из важнейших видов матрицы, применяемый при поиске ее детерминанта и при выполнении простейших операций. Треугольный тип происходит от диагонального, поэтому матрица также является квадратной. Треугольный вид матрицы подразделяют на верхнетреугольный и нижнетреугольный.

В верхнетреугольной матрице (рис. 1) только элементы, которые находятся над главной диагональю, принимают значение, равное нулю. Компоненты же самой диагонали и части матрицы, располагающейся под ней, содержат числовые значения.

В нижнетреугольной (рис. 2), наоборот, элементы, располагающиеся в нижней части матрицы, равны нулю.

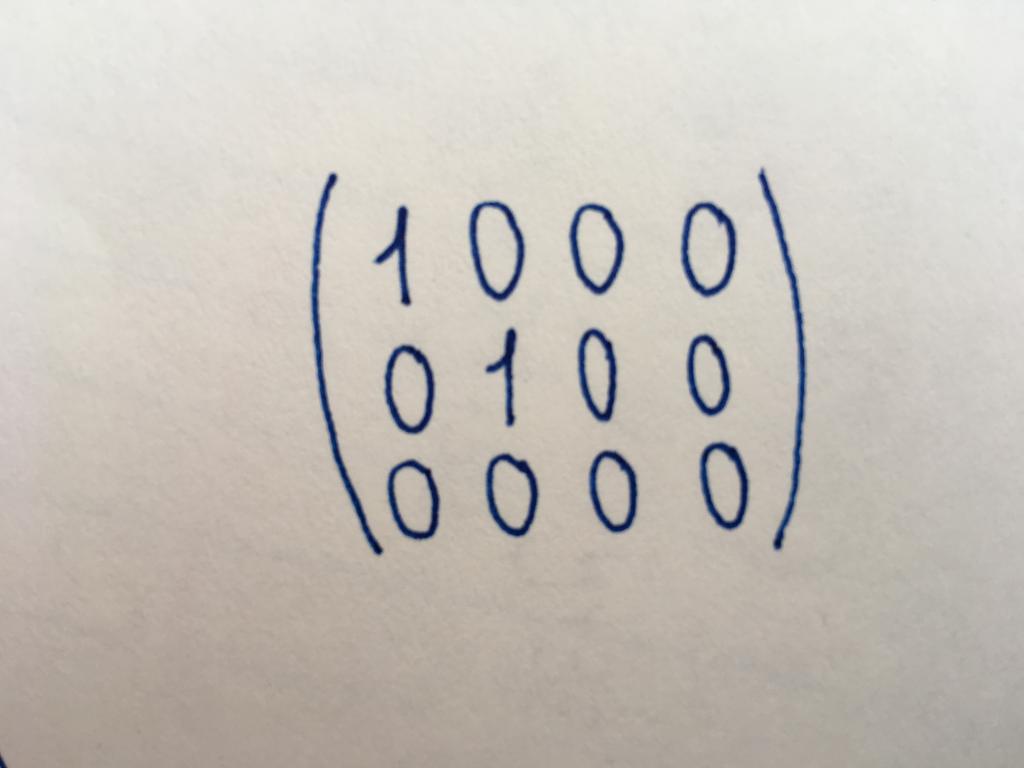
Ступенчатая матрица

Вид необходим для нахождения ранга матрицы, а также для элементарных действий над ними (наряду с треугольным типом). Ступенчатая матрица названа так, потому что в ней содержатся характерные «ступени» из нулей (как показано на рисунке). В ступенчатом типе образуется диагональ из нулей (необязательно главная), и все элементы под данной диагональю тоже имеют значения, равные нулю. Обязательным условием является следующее: если в ступенчатой матрице присутствует нулевая строка, то остальные строки, находящиеся ниже нее, также не содержат числовых значений.

Таким образом, мы рассмотрели важнейшие типы матриц, необходимые для работы с ними. Теперь разберемся с задачей преобразования матрицы в требуемую форму.

Приведение к треугольному виду

Как же привести матрицу к треугольному виду? Чаще всего в заданиях нужно преобразовать матрицу в треугольный вид, чтобы найти ее детерминант, по-другому называемый определителем. Выполняя данную процедуру, крайне важно «сохранить» главную диагональ матрицы, потому что детерминант треугольной матрицы равен именно произведению компонентов ее главной диагонали. Напомню также альтернативные методы нахождения определителя. Детерминант квадратного типа находится при помощи специальных формул. Например, можно воспользоваться методом треугольника. Для других матриц используют метод разложения по строке, столбцу или их элементам. Также можно применять метод миноров и алгебраических дополнений матрицы.

Подробно разберем процесс приведения матрицы к треугольному виду на примерах некоторых заданий.

Задание 1

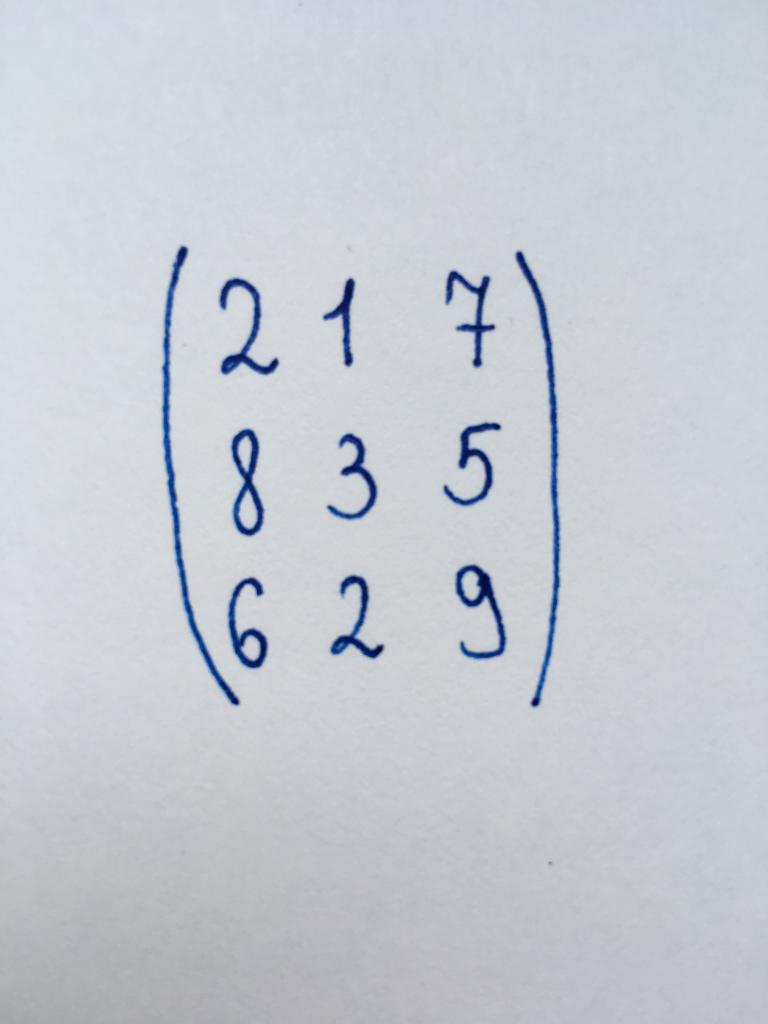
Необходимо найти детерминант представленной матрицы, используя метод приведения его к треугольному виду.

Данная нам матрица представляет собой квадратную матрицу третьего порядка. Следовательно, для ее преобразования в треугольную форму нам понадобится обратить в нуль два компонента первого столбца и один компонент второго.

Важно! Верхняя строка не изменяется, а остается такой же, как и в исходной матрице. Записывать строку, в четыре раза большую исходной, не нужно. Но значения строк, компоненты которых нужно обратить в нуль, постоянно меняются.

Задание 2

Нужно найти детерминант матрицы методом приведения его к треугольному виду.

Представленная матрица принадлежит к квадратному типу и является матрицей четвертого порядка. Значит, необходимо обратить в нуль три компонента первого столбца, два компонента второго столбца и один компонент третьего.

Итак, компонент четвертой строки обращен в нуль. Перейдем к первому элементу третьей строки, к числу 3. Выполняем аналогичную операцию. Умножаем на три первую строку, вычитаем ее из третьей строки и записываем результат.

Далее видим число 2 во второй строке. Повторяем операцию: умножаем верхнюю строку на два и вычитаем ее из второй.

После всех произведенных преобразований мы привели предложенную матрицу к треугольному виду. Теперь, чтобы найти ее детерминант, нужно только произвести умножение получившихся элементов главной диагонали. Получаем: detA = 1 x (-1) x (-4) x 40 = 160. Следовательно, решением является число 160.

Итак, теперь вопрос приведения матрицы к треугольному виду вас не затруднит.

Приведение к ступенчатому виду

При элементарных операциях над матрицами ступенчатый вид является менее «востребованным», чем треугольный. Чаще всего он используется для нахождения ранга матрицы (т. е. количества ее ненулевых строк) или для определения линейно зависимых и независимых строк. Однако ступенчатый вид матрицы является более универсальным, так как подходит не только для квадратного типа, но и для всех остальных.

Чтобы привести матрицу к ступенчатому виду, сначала нужно найти ее детерминант. Для этого подойдут вышеназванные методы. Цель нахождения детерминанта такова: выяснить, можно ли преобразовать ее в ступенчатый вид матрицы. Если детерминант больше или меньше нуля, то можно спокойно приступать к заданию. Если же он равен нулю, выполнить приведение матрицы к ступенчатому виду не получится. В таком случае нужно проверить, нет ли ошибок в записи или в преобразованиях матрицы. Если подобных неточностей нет, задание решить невозможно.

Рассмотрим, как привести матрицу к ступенчатому виду на примерах нескольких заданий.

Задание 1. Найти ранг данной матричной таблицы.

Детерминант = 12. Он больше нуля, значит, матрицу можно привести к ступенчатому виду. Приступим к ее преобразованиям.

Мы видим, что в результате приведения образовалась треугольная матрица. В нашем случае продолжить преобразование нельзя, так как остальные компоненты не удастся обратить в нуль.

Задание 2. Определить количество линейно независимых строк данной матрицы.

Нам требуется найти такие строки, которые нельзя какими-либо преобразованиями обратить в нуль. Фактически нам нужно найти количество ненулевых строк, или ранг представленной матрицы. Для этого выполним ее упрощение.

Прибавляем первую строку к третьей. Далее вычитаем из нее вторую, чтобы обратить число 5 в нуль.

Теперь приведение матрицы к ступенчатому виду не является для вас невыполнимым заданием.

На примерах данных заданий мы разобрали приведение матрицы к треугольному виду и ступенчатому виду. Чтобы обратить в нуль нужные значения матричных таблиц, в отдельных случаях требуется проявить фантазию и правильно преобразовать их столбцы или строки. Успехов вам в математике и в работе с матрицами!

Источник

Метод Гаусса приведения матрицы к ступенчатому виду

Элементарными преобразованиями матрицы называются следующие ее преобразования:

I. Перестановка двух столбцов (строк) матрицы.

II. Умножение всех элементов одного столбца (строки) матрицы на одно и то же число, отличное от нуля.

III. Прибавление к элементам одного столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и то же число.

Элементарные преобразования применяются для упрощения матриц, что будет в дальнейшем использоваться для решения разных задач.

Алгоритм приведения матрицы к ступенчатому виду

Чтобы привести матрицу к ступенчатому виду (рис. 1.4), нужно выполнить следующие действия.

1. В первом столбце выбрать элемент, отличный от нуля ( ведущий элемент ). Строку с ведущим элементом ( ведущая строка ), если она не первая, переставить на место первой строки (преобразование I типа). Если в первом столбце нет ведущего (все элементы равны нулю), то исключаем этот столбец, и продолжаем поиск ведущего элемента в оставшейся части матрицы. Преобразования заканчиваются, если исключены все столбцы или в оставшейся части матрицы все элементы нулевые.

2. Разделить все элементы ведущей строки на ведущий элемент (преобразование II типа). Если ведущая строка последняя, то на этом преобразования следует закончить.

3. К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную соответственно на такое число, чтобы элементы, стоящие под ведущим оказались равными нулю (преобразование III типа).

4. Исключив из рассмотрения строку и столбец, на пересечении которых стоит ведущий элемент, перейти к пункту 1, в котором все описанные действия применяются к оставшейся части матрицы.

Пример 1.29. Привести к ступенчатому виду матрицы

Прибавим ко второй строке первую, умноженную на (-2):

Первый столбец и первую строку исключаем из рассмотрения. В оставшейся части матрицы имеется один элемент (-2), который выбираем в качестве ведущего. Разделив последнюю строку на ведущий элемент, получаем матрицу ступенчатого вида

Преобразования закончены, так как ведущая строка последняя. Заметим, что получившаяся матрица является верхней треугольной.

Пункт 3 алгоритма делать не надо, так как под ведущим элементом стоит нуль. Исключаем из рассмотрения первую строку и первый столбец. В оставшейся части ведущий элемент — число 2. Разделив ведущую строку (вторую) на 2, получаем ступенчатый вид:

Преобразования закончены, так как ведущая строка последняя.

Ко второй и третьей строкам прибавим первую, умноженную на (-3) и на (-6) соответственно:

Обратим внимание на то, что полученная матрица еще не является матрицей ступенчатого вида, так как вторую ступеньку образуют две строки (2-я и 3-я) матрицы. Исключив 1-ю строку и 1-й столбец, ищем в оставшейся части ведущий элемент. Это элемент (-1). Делим вторую строку на (-1), а затем к третьей строке прибавляем ведущую (вторую), умноженную на 5:

Исключим из рассмотрения вторую строку и второй столбец. Поскольку исключены все столбцы, дальнейшие преобразования невозможны. Полученный вид — ступенчатый.

1. Говорят, что матрица имеет ступенчатый вид также и в случае, когда на месте ведущих элементов (обозначенных на рис. 1.4 единицей) стоят любые отличные от нуля числа.

2. Считается, что нулевая матрица имеет ступенчатый вид.

Пример 1.30. Привести к ступенчатому виду матрицу

Решение. Первый столбец матрицы — нулевой. Исключаем его из рассмотрения и исследуем оставшуюся часть (последние 5 столбцов):

Вторую строку и четвертый столбец исключаем из рассмотрения. Берем элемент в качестве ведущего. Делим третью строку на число 2 (умножаем на 0,5):

К четвертой строке прибавляем третью, умноженную на (-2):

Третью строку и четвертый столбец исключаем из рассмотрения. Поскольку в оставшейся части матрицы все элементы (один) нулевые, преобразования закончены. Матрица приведена к ступенчатому виду (см. рис. 1.4).

Замечание 1.9. Продолжая выполнять элементарные преобразования над строками матрицы, можно упростить ступенчатый вид, а именно привести матрицу к упрощенному виду (рис. 1.5).

Здесь символом 1 обозначены элементы матрицы, равные единице, символом * — обозначены элементы с произвольными значениями, остальные элементы матрицы нулевые. Заметим, что в каждом столбце с единицей остальные элементы равны нулю.

Пример 1.31. Привести к упрощенному виду матрицу

Решение. Матрица имеет ступенчатый вид. Прибавим к первой строке третью, умноженную на (-1), а ко второй строке третью, умноженную на (-2):

Теперь к первой строке прибавим вторую, умноженную на (-1). Получим матрицу упрощенного вида (см. рис. 1.5):

Замечание 1.10. При помощи элементарных преобразований (строк и столбцов) любую матрицу можно привести к простейшему виду (рис. 1.6).

Пример 1.32. Привести матрицу к простейшему виду.

Умножим все элементы последнего столбца на (-1) и переставим его на место второго:

Таким образом, исходная матрица при помощи элементарных преобразований приведена к простейшему виду (см. рис. 1.6).

Свойства элементарных преобразований матриц

Следствие (о приведении матрицы к простейшему виду). Любую матрицу при помощи элементарных преобразований ее строк и столбцов можно привести к простейшему виду.

2. В теореме 1.1 говорится о приведении матрицы к ступенчатому (упрощенному) виду при помощи элементарных преобразований только ее строк, не используя преобразования ее столбцов. Чтобы привести произвольную матрицу к простейшему виду (следствие теоремы 1.1), нужно использовать преобразования и строк, и столбцов матрицы.

3. Рассмотрим следующую модификацию пункта 3 метода Гаусса. Ведущий элемент, выбранный в п. 1 метода Гаусса, определяет ведущую строку и ведущий столбец матрицы (он находится на их пересечении). Делим все элементы ведущей строки на ведущий элемент (см. п.2 метода Гаусса). Прибавляя ведущую строку, умноженную на соответствующие числа, к остальным строкам матрицы (аналогично п.3 метода Гаусса), делаем равными нулю все элементы ведущего столбца, за исключением ведущего элемента. Затем, прибавляя полученный ведущий столбец, умноженный на соответствующие числа, к остальным столбцам матрицы, делаем равными нулю все элементы ведущей строки, за исключением ведущего элемента. При этом получаем ведущие строку и столбец, все элементы которых равны нулю, за исключением ведущего элемента, равного единице.

Источник

03. Ступенчатая матрица

Определение 6. Матрицей размерности называется прямоугольная таблица

Определение 7. Матрицей ступенчатого вида называется такая матрица, которая обладает свойствами:

1) в каждой строке матрицы имеется неравный нулю элемент;

2) в каждой строке матрицы, начиная со второй, первый слева неравный нулю элемент расположен правее первого слева неравного нулю элемента предыдущей строки матрицы.

Матрицу ступенчатого вида называют также Трапециидальной матрицей, а квадратную матрицу ступенчатого вида называют Треугольной матрицей. Ниже показаны две не ступенчатые матрицы и три ступенчатые матрицы (последняя матрица треугольная).

, , , , .

Определение 8. Элементарными преобразованиями строк матрицы называются следующие ее преобразования:

1) перестановка любых двух строк матрицы местами;

2) умножение одной строки матрицы на любое число ;

3) прибавление к одной строке матрицы другой ее строки умноженной на любое число k ;

(при этом все остальные строки матрицы остаются неизменными).

Аналогично можно рассматривать элементарные преобразования столбцов матрицы.

Теорема 2. Любую ненулевую матрицу конечным числом элементарных преобразований и преобразований вычеркивания нулевой строки можно привести к матрице ступенчатого вида.

Доказательство. Доказательство проводим методом математической индукции по числу M строк матрицы. Для m=1 утверждение теоремы справедливо, так как ненулевая однострочная матрица по определению имеет ступенчатый вид.

.

. (9)

Рассмотрим матрицу, состоящую из последних M-1 строк матрицы (9):

. 10)

Если матрица (10) нулевая, то все строки в матрице (9) кроме первой нулевые. Вычеркивая их, приходим к матрице ступенчатого вида. Если матрица (10) ненулевая, то по индуктивному предположению конечным число элементарных преобразований и преобразований вычеркивания нулевой строки может быть приведена к матрице ступенчатого вида: ,

Где элементы и не равны нулю. Тогда соответствующими преобразованиями строк матрица (9) преобразуется в матрицу ступенчатого вида:

; (11)

Элементы , . не равны нулю. Теорема доказана.

Источник