Как сделать сумму в маткаде

Как сделать сумму в маткаде

Некоторые команды из меню Символика позволяют выполнять алгебраические действия. Можно упрощать выражения, разлагать их на члены и сомножители, объединять подобные члены выражения, находить коэффициенты полиномаhigh, разлагать выражение в ряд, или изменять все вхождения переменной на содержимое буфера обмена.

При преобразовании выражений, содержащих комплексные числа, можно выбрать команду Вычислить В комплексном виде из меню Символика. Это предпишет Mathcad выражать результаты в форме a + ib. Рисунок 8 показывает соответствующий пример.

Обычно символьный процессор возвращает результаты, перестраивая переменные. Таким образом, когда Mathcad преобразует выражение, содержащее p или e, он будет обычно возвращать другое выражение, содержащее p или exp(x). Чтобы предписать Mathcad возвратить числовые значения p или e, выберите Вычислить N плавающей запятой из меню Символика.

Появится диалоговое окно, в котором можно определить число цифр справа от десятичной точки. По умолчанию это число равно 20.

Рисунок 8: Символьное преобразование выражений, использующее подкоманды, доступные из пункта меню Вычислить в Mathcad PLUS.

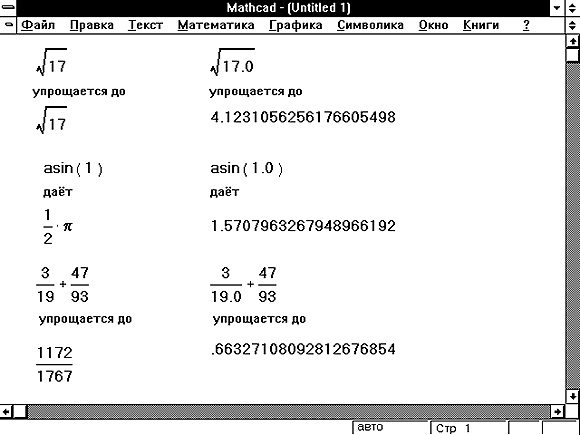
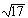
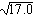
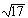
Рисунок 9 показывает некоторые примеры того, как наличие десятичной точки влияет на ответы, получаемые от символьного процессора. В этом примере обратите внимание, что возвращается неизменённым, так как это число не является рациональным. Но возвращается как десятичная аппроксимация к иррациональному числу .

Когда символьная операция дает приближенный ответ в виде десятичной дроби, этот ответ всегда отображается с 20 значащими цифрами. На это отображение не воздействует ни локальный, ни глобальный числовой формат Mathcad.

Рисунок 9: Численные ответы в символьных вычислениях.

Команда Упростить выполняет основные алгебраическое и тригонометрическое упрощения выбранного выражения. Упростить выполняет арифметические преобразования, сокращает общие множители, использует основные тождества для тригонометрических и обратных функций, и упрощает квадратные корни и степени.

Можно упрощать как части выражений (например, знаменатель дроби, или один член суммы), так и всё выражение целиком. Можно также упрощать выражения, содержащие массивы, например, суммы или произведения матриц. Для этого заключите требуемую часть выражения в выделяющую рамку прежде, чем выберете Упростить.

Mathcad иногда может упростить части выражения, даже если он не может упростить выражение целиком. Если преобразование всего выражения не дает желаемый ответ, попытайтесь выделить и упростить часть выражения. Рисунок 10 иллюстрирует некоторые результаты применения команды Упростить.

Рисунок 10: Некоторые результаты упрощения.

Команда Разложить по степеням из меню Символика разлагает все степени и произведения сумм в выделенном выражении. Если выражение — дробь, числитель будет разложен, и выражение будет представлено как сумма дробей. Синусы, косинусы и тангенсы сумм переменных, или целого числа, умноженного на аргумент, будут разложены, насколько возможно, в выражения, включающие только синусы и косинусы одиночных переменных. См. Рисунок 12.

Разложения выражений в ряды

Рисунок 11 показывает некоторые примеры разложений, полученных с использованием этой команды меню. Относительно альтернативного метода выполнения разложений в ряды см. о ключевом слове series в разделе “Символьные преобразования” ранее в этой главе.

Рисунок 11: Разложение в ряд.

Разложение выражения на множители

Команда Разложить на множители. из меню Символика разлагает на множители выбранное выражение. Если выражение представляет целое число, Mathcad разложит его на множители по степеням простых чисел. В остальных случаях Mathcad будет пытаться преобразовывать выражение в произведение. Эта команда будет объединять сумму дробей в одну дробь и будет упрощать многоэтажную дробь с несколькими дробными чертами.

Обратите внимание, что при использовании этой команды Mathcad разлагает на множители “только то, что выделено”. Например, если выделить всё выражение

ab + ac + x

a(b + c) + x

Разлагая на множители, всегда можно немного упростить выражение, выбирая и разлагая на множители подвыражения, даже если выражение в целом не факторизуемо. Команду Разложить на множители. следует использовать также, чтобы объединить сумму дробей в одну дробь или упростить сложную дробь. См. примеры на Рисунке 12.

Поскольку выделяющая рамка следует структуре выражения, может понадобиться прежде вставить скобки, чтобы удалось выделить требуемое подвыражение. Например, чтобы выделить ac + x в выражении, приведенном выше, необходимо вставить левую скобку перед вторым a и правую скобку — после x.

Приведение подобных членов

Команда меню Разложить по подвыражению. объединяет члены, содержащие одинаковые степени выделенного подвыражения. Результатом является полином от подвыражения. Выбираемое подвыражение должно быть либо простой переменной, либо встроенной функцией вместе с аргументом. См. пример на Рисунке 12.

Рисунок 12: Разложение по степеням, разложение на множители и приведение подобных членов.

Разложение на элементарные дроби

Символьный процессор будет пытаться разлагать знаменатель выражения на линейные или квадратичные множители, имеющие целочисленные коэффициенты. Если это удастся, он будет разлагать выражение в сумму дробей с этими множителями в качестве знаменателя. Все константы в выделенном выражении должны быть целыми числами или дробями: Mathcad не будет разлагать выражение, которое содержит десятичные точки. См. некоторые примеры на Рисунке 13.

Рисунок 13: Разложение на элементарные дроби.

Нахождение коэффициентов полинома

Mathcad возвращает вектор, содержащий коэффициенты требуемого полинома в порядке возрастания степеней. Первое выражение на Рисунке 14 показывает пример такой операции.

Если нужно, чтобы символьнай процессор рассматривал выражение как полином относительно функции, заключите в выделяющую рамку функцию. Второе выражение на Рисунке 14 показывает пример разложения по степеням sin(x).

Mathcad подставит выражение из буфера обмена вместо выделенной переменной. Если переменная появляется более чем один раз в преобразуемом выражении, Mathcad заменит все её вхождения на содержимое буфера обмена. Рисунок 15 показывает некоторые примеры.

Обратите внимание, что команда Заменить переменную не может подставлять векторы или матрицы. Чтобы подставить скалярное выражение вместо переменной, которая находится в матрице, поместите выражение в буфер обмена, используя команду Копировать. Затем щёлкните кнопкой мыши на каждом элементе матрицы, который содержит заменяемую переменную, и выберите Заменить переменную.

Рисунок 15: Замена переменной выражением.

Вычисление произведения по индексу производится аналогично, за исключением того, что требуется напечатать [Ctrl][Shift]3, чтобы получить оператор произведения. Если при суммировании или вычислении произведения используются числовые пределы, убедитесь, чтобы верхний предел был больше или равен нижнему.

Вычисление других функций и операторов

Как правило, можно символьно преобразовать любую комбинацию встроенных функций Mathcad. Если результат может быть вычислен точно — sin( p ), например, — появится точный ответ. В противном случае Mathcad будет возвращать в качестве ответа первоначальное выражение. Рисунок 16 иллюстрирует различные результаты символьного вычисления.

Рисунок 16: Символьное вычисление сумм, произведений и функций.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

MathCAD является интегрированной системой, ориентированной на проведение математических и инженерно-технических расчетов. Он объединяет понятность, ясность, простоту в обращении при вычислениях и т.п. с простотой в обращении, свойственной электронным таблицам.

Использоваться как калькулятор для простых вычислений.

Определять значения выражений, заданных в символьном виде.

Производить матричные и векторные преобразования.

Решать линейные, нелинейные уравнения и системы уравнений.

Заменять справочные таблицы.

Производить дифференцирование, интегрирование, статистические расчеты и анализ данных.

Строить двумерные и трехмерные графики и т.п.

Документ MathCAD, на котором могут быть совмещены текст, графика и формулы, выглядит как страница научной статьи или учебника, при этом формулы являются «живыми» – стоит внести изменения в одну из них, как MathCAD пересчитает результаты, перерисует графики и т.д.

После запуска приложения MathCAD открывается окно, как это показано на рис. 1.1.

Главное окно оформлено стандартным для Windows-приложений образом: заголовок, главное меню, панель инструментов, окно редактирования, строка состояния.

Рис. 1.1. Рабочее окно системы MathCAD

1.1. Основные команда MathCad

Главное меню системы MathCAD представлено набором команд, общим для большинства приложений операционной системы MS Windows, а также командами, представляющими специфические возможности:

Меню File (Файл) — работа с файлами.

Меню Edit (Правка) — редактирование документов.

Меню View (Вид) — настройка элементов окна. Команды меню View представлены на рис. 1.2.

ToolBars – содержит кнопки панелей инструментовStandard, Formatting, Math. Если отсутствует какая-либо из панелей, то следует включить соответствующую опцию, например, командой ViewToolbarsMath.

Status Bar – позволяет включать и отключать отображение строки состояния.

Ruler – позволяет включать и отключать отображение горизонтальной линейки для точного позиционирования документов на листе.

Regions – делает видимыми/невидимыми границы областей.

Zoom – изменение масштаба.

Refresh – обновить содержимое экрана.

Animate – анимация.

PlayBack – воспроизведение.

Preferences – настройки.

Рис. 1.2. Команды меню View (Вид) – редактирование документов

Меню Insert (Вставка) — позволяет помещать в MathCAD – документ графики, функции, матрицы, гиперссылки, компоненты и настраивать объекты.

Меню Format (Формат) — содержит команды, предназначенные для задания различных параметров, определяющих внешнее представление чисел, формул, текста, абзацев, колонтитулов и т.д.

Меню Math (Математика) — позволяет установить режимы и параметры вычислений.

Меню Symbolics (Символы) — реализует символьные вычисления.

Меню Window (Окно) — содержит команды для упорядочения взаимного расположения нескольких окон и позволяет активизировать одно из них.

Меню Help (Помощь) — информационный центр и справочники. Команда Help открывает окно, представленное на рис. 5.3. На вкладке «Содержание» справочные сведения распределены по темам. На вкладке «Указатель» темы представлены в алфавитном порядке. Вкладка «Поиск» позволяет находить конкретное понятие.

Рис. 1.3. Окно меню справки

1.2. Кнопки панели Math

Одна из сильных сторон MathCAD – это представление и ввод математических символов и выражений в привычной для человека форме. Это обеспечивается развитым графическим интерфейсом и инструментами, располагающимися на панелях инструментов приложения MathCAD (Math, Graph …). Открыть соответствующую панель инструментов можно с помощью команды главного меню ViewToolbars. Для удобства работы ссылки на них объединены на панели Math.

На панели Math расположены 9 кнопок. Каждая из кнопок, в свою очередь, открывает панели инструментов специального назначения. Это следующие кнопки (в развернутом виде эти панели представлены на рис. 5.4):

Calculator (Калькулятор). На этой панели находятся кнопки для задания математических операций, а также некоторых часто используемых функций. Эту кнопку можно использовать как калькулятор.

Boolean (Булева) – для ввода операторов сравнения и логических операций.

Evaluation (Вычисление) – содержит кнопки для ввода операторов присвоения значений переменных и функций.

Graph (Графика) – инструменты для построения графика.

Vector and Matrix (Векторы и Матрицы) – инструменты для работы с векторами и матрицами.

Calculus (Исчисление) – представляет математические выражения с элементами интегрирования, дифференцирования в привычном виде. Кнопки этой панели позволяют вычислять значения пределов, сумм, произведений.

Programming (Программирование) – инструменты для написания программ.

Greak Symbol (Греческий алфавит).

Symbolic (Символы) – для символьных вычислений.

Рис. 1.4. Рабочее окно системы MathCAD с развернутыми панелями инструментов панели Math

1.3. Запись команд в рабочем документе системы MathCad

Запись команд в системе MathCAD на языке очень близка к стандартному языку математических расчетов выполняемых на бумаге, что значительно упрощает постановку и решение задач. В результате главные аспекты решения математических задач смещаются с их программирования на алгоритмическое и математическое описание.

MathCAD реализует вычисления в строго определенном порядке, как это делает человек: читая страницу книги, т.е. слева направо и сверху вниз. Правильный порядок выполнения блоков — основа правильного функционирования системы при обработке документа. Например, если в некотором блоке содержатся операции, требующие данных из другого блока, то этот «другой» блок обязательно должен выполняться первым и располагаться перед использующим его блоком. Иначе ошибка. Сигнал ошибки в системе имеет вид всплывающей надписи, заключенной в прямоугольник.

1.4. Используемые типы констант

В системе MathCAD предусмотрены следующие типы данных:

Вещественные (1.876, –375.08).

Комплексные (2.5+3i). Следует иметь в виду, что при записи мнимой единицы следует использовать специальную кнопку панели Calculator.

Строковые. Обычно это комментарий «Вычисление суммы».

Системные. Системная константа – это предварительно определенная переменная, значение которой задается в начале загрузки системы. Примерами таких констант являются числа e или .

1.5. Простые вычисления

Результат арифметического выражения отображается, если после него стоит знак «=» или знак «». В первом случае результат представляется в численном виде, а во втором – в символьном. Например, если записать арифметическое выражение в виде:

то в результате будем иметь: 123 + 256 = 379.

Пример символьного вычисления:

При выполнении вычислительной системой арифметического выражения используются знаки арифметических операций с приоритетами, принятыми в обычной математике. Для изменения порядка используются круглые скобки. Выражение может содержать также другие операции:

возведения в степень;

интегрирования и дифференцирования;

знаков факториала и суммирования и т.д.

Часть из этих операций можно «взять» на панели Calculator (Калькулятор). Примером записи выражения может быть:

В качестве операндов выражение может использовать любые константы, в том числе, системные константы и функции.

Если набрать выражение=, то в окне документа будет отображено значение этой константы в виде: =3.141592.

Количество значащих цифр, отображаемых при вычислении, можно регулировать с помощью команды главного меню Format→Result. В этом случае команда предоставит диалоговое окно, как это показано на рис. 5.5, в котором следует переустановить параметры для вывода результата.

Рис. 1.5. Рабочее окно команды главного меню Format (формат Result )

Ниже приведен результат символьного вычисления арифметического выражения:

После знака «» отображен результат символьного вычисления. Для замены результата символьного вычисления численным значением применена команда float, расположенная на панели Symbolic. Эта команда предоставляет шаблон, в котором пользователю предлагается задать количество знаков (цифр) для отображения результата.

1.6. Использование встроенных функций

Важным понятием в математике является функция, т.е. некоторая зависимость одной переменной от другой или ряда других переменных и констант. В системе MathCAD имеется множество встроенных функций. Для избегания возможных ошибок не рекомендуется имя функции вводить с клавиатуры. Наиболее часто используемые функции, такие как: sin,cos, ln,… можно задать, используя их обозначение на панели инструментов Calculator. К другим функциям можно обратиться с помощью команды главного меню Insert (вставка функции), либо с помощью команды (кнопки) f(x). В окне, которое предоставляет команда (рис. 5.6), пользователь может установить категорию функции, познакомиться с примером ее записи и спецификацией (описанием), а затем произвести нужный выбор. После этого система предоставляет пользователю шаблон, в который требуется вписать необходимые параметры.

Рис. 1.6. Рабочее окно команды вставка функции: Insert → Function

Особенностью функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием её аргументов должна возвратить свое значение. Например, если где-то используется функция sin(0.452·), то вместо нее будет подставлено число, равное значению синуса с аргументом, равным значению выражения 0.452·.

1.7. Определение переменных и пользовательских функций

1.8. Локальные и глобальные переменные

Как и в других языках программирования в MathCAD различают локальные и глобальные переменные. Присваивание локальным переменным своего значения в системе MathCAD реализуют с помощью знака «:=». Для этого достаточно ввести знак двоеточие. Если ввести «X:5» то на экране появится «X:=5» (т.е. переменной X присваивается значение 5).

X := 1

sin(X) = 0.841

X := 1

Y := sin(X)

Y= 0.841

Глобальная переменная вводится следующим образом: “переменная

выражение”. Вид, который принимает в документе введенное таким образом присваивание: “переменнаявыражение”. Отличие глобальных переменных от локальных переменных в том, что глобальные переменные могут использоваться в любом месте документа (в том числе, слева от их определения и над ним).

Пример введение глобальной переменной.

1.9. Определение и использование пользовательских функций

Важным инструментом в математических вычислениях являются пользовательские функции. Функции особенно целесообразно использовать, когда приходится производить многократные вычисления по одним и тем же формулам, но с разными исходными данными.

Чтобы воспользоваться собственной функцией, нужно:

Вызвать описанную функцию для выполнения.

Очевидно, что описание/определение функции должно быть расположено выше, чем ее использование. Для определения функции используются идентификаторы: имя функции и имена формальных параметров функции. Формальный параметр – это идентификатор, конкретное значение которого определяется путем замены его на соответствующее емузначение фактического параметра при обращении к функции. Функции однозначно ставят в соответствие значениям аргументов (формальным параметрам) значения фактических параметров функции.

Формат определения функции:

Имя_функции(список формальных параметров) := выражение

Вызов пользовательской функции производится подобно тому, как и в случае вызова любой стандартной функции.

Можно поместить результат в отдельную переменную:

Имя_переменной_результата:=Имя_функции(список_фактических параметров)

Имя_функции(список_фактических параметров)=

Пример 1. Требуется определить функцию Dist, которая будет возвращать расстояние заданной точки от начала координат. Использовать эту функцию для вычисления расстояний от точек А(1.96; –3.8) и В(6; 42.5) до начала координат.

Решение. Из курса линейной алгебры известно, что расстояние от начала координат до некоторой точки A(x, y) определяется по формуле . Здесь (x, y) – координаты заданной точки. Эта формула и будет составлять основу функцию Dist. При описании функции следует предусмотреть два формальных параметра — координаты точки. На место этих параметров должны будут вписаны фактические координаты заданных точек.

В соответствии с формулой определения расстояния от точки на плоскости до начала координат функция Dist может быть записана в виде: . А обращение к функцииDist для вычислений расстояний от заданных точек может быть представлено в виде:

Во втором случае результат помещается во вспомогательную переменную.

Пример 2. Дана функция вида: . Требуется найти ее максимальное и минимальные значения.

Рис. 1.7. Поиск максимального и минимального значений заданной функции

1.10. Определение переменных, принимающих значения из заданного промежутка

В системе MathCAD предоставлена возможность определения переменных, принимающих значения из заданного промежутка, причем соседние значения удалены на равные расстояния друг от друга. При этом задается только начальное значение, следующее значение (второе значение, неявно задающее шаг изменения значения переменной) и конечное значение.

Строго говоря, переменные, принимающие значения из промежутка, представляют собой векторы с равноудаленными значениями компонент.

В качестве переменных, принимающих значения из промежутка, можно использовать только идентификаторы без индексов.

Формат определения переменной:

Если конечное значение при данном значении шага не достигается точно, последним значением переменной будет наибольшее значение из заданного промежутка, не превышающее конечное значение.

Кроме этого MathCAD предоставляет возможность не задавать следующее значение, если шаг по величине совпадает со значением 1 или –1.

В этом случае формат определения переменной можно представить в виде:

Имя_переменной := начальное_значение .. конечное_значение

Пример 3. Требуется определить переменную р, принимающую значения на интервале [0, 1] с шагом 0,1.

Решение. На рис. 5.8 представлены два фрагмента с решением поставленной задачи. На рис. 5.8, а представлено решение в соответствии с форматом, принятым для определения заданной переменной. А на рис. 5.8, b – такое же определение, но с введением вспомогательных переменных для обозначения и задания границ интервала, и величины шага, необходимых для определения переменной.

Рис. 1.8. Определение переменной, принимающей значения на интервале

Пример 4. Требуется получить таблицу значений функции на интервале [a, b] с шагом h.

Решение. Решение задачи можно свести к выполнению следующих шагов:

Определить функцию .

Задать переменную (например, t), принимающую значения из промежутка [a, b] с шагом h.

Получить таблицу значений функции для переменной t.

На рис. 5.9 представлен фрагмент документа с решением задачи 4.

Рис. 1.9. Получение таблицы значений функции на заданном интервале с постоянным шагом

1.11. Построение графиков в декартовой системе координат

Все основные типы графиков и инструменты работы с ними расположены на рабочей панели Graph (График) семействаMath (Математические). На этой панели вы можете найти ссылки на семь типов графиков. В данном разделе остановимся на декартовой системе координат.

В MathCAD существует несколько способов построения графиков, однако, первый шаг для всех способов будет один и тот же. Этим первым шагом является введение специальной заготовки для будущего графика – так называемой графической области. Ввести графическую область, как для декартового, так и для любого другого графика можно либо с панели Graph (Графические), либо командой одноименного подменю меню Insert (Вставка).

Графическая область представляет собой две вложенные рамки, как это показано на рис. 5.10, а. Во внутренней области отображаются непосредственно кривые зависимостей. Пространство между рамками служит для визуализации разного рода служебной информации. Графическую область можно увеличивать и уменьшать с помощью специальных маркеров, расположенных на ее внешней рамке. Перемещать по документу и удалять графические области можно точно так же, как простые формулы.

Рис. 1.10. Графическая область в декартовой системе координат

После того как графическая область будет введена, в общем случае требуется задать два соразмерных вектора, определяющих значения координат точек. Сделать это можно различными способами. Наиболее простым и часто используемым методом задания координатной сетки является так называемый быстрый метод. При его применении пользователь задает только имя переменной и вид функции, а шкалы осей и величину шага между узловыми точками автоматически определяет система.

Для построения графика функции по быстрому методу, необходимо выполнить следующую последовательность действий:

Введите графическую область.

В специальном маркере, расположенном в центре под внутренней рамкой графической области, задайте имя независимой переменной.

В центральный маркер, расположенный слева от внутренней рамки, введите функцию или имя функции (если функцию определить раньше переменной, то работа даже упрощается, так как независимая переменная будет задана автоматически).

На рис. 1.10, b показан график функции y=sin(t), построенный по быстрому методу.

К недостаткам рассматриваемого метода относится, прежде всего, то, что область изменения переменной для всех функций определяется одна и та же: от –10 до +10. В большинстве же случаев такие пределы будут неприемлемы по целому ряду причин. Например, если амплитуда экстремумов мала по сравнению с изменением величины функции на промежутке, что они становятся просто незаметными.

Чтобы справиться с возникшими трудностями, нужно просто уменьшить интервал изменения либо переменной, либо функции. Для этого выделите графическую область щелчком левой кнопкой мыши. При этом визуализируются все элементы, которые до этого были скрыты (рис. 1.11, а).

Рис. 1.11. Графическая область в декартовой системе координат

Непосредственно под крайними значениями (для оси X) или слева от них (для оси Y) появятся цифры, отражающие максимальные и минимальные величины координат узловых точек графика. Чтобы изменить их значения, просто удалите (точно так же, как при редактировании формул) старые величины и введите новые. Изменения пределов по осиX вызывает автоматический пересчет крайних значений по Y. Однако если вы переопределите область по оси Y, то область изменения переменной останется старой.

Графическую область можно отформатировать – изменить внешний вид и цветовую гамму. Для этого можно воспользоваться командой Properties (Свойства) из контекстного меню графика (вызывается щелчком правой кнопкой мыши на графической области), как это показано на рис. 1.11, b.

В окне Properties (Свойства) для подавляющего большинства пользователей объективно могут быть полезны два параметра, расположенных на вкладке Display (см. рис. 1.11, b):

Highlight Region (Цветная область). Установив этот флажок, вы сможете на палитре Choose Color (Выбор цвета) определить наиболее подходящий цвет заливки для вашей графической области.

Show Border (Показать границу). Параметр отвечает за отображение внешней границы графической области. По умолчанию она не визуализируется.

При исследовании функции большое применение находит команда Trace (След) из контекстного меню графика. Эта команда позволяет считать с графика текущее значение аргумента и соответствующего ему значение функции. В результате выполнения этой команды открывается окно «X—Y Trace», как это показано на рис. 1.12. Чтобы активизировать трассировку, нужно мышью щелкнуть по графику. В результате на графике появляются две линии – вертикальная и горизонтальная, которые легко с помощью мыши перемещаются по графической области, а координаты точки пересечения линий отражается в окне трассировки.

Рис. 1.12. Считывание координат точки на графике

Источник