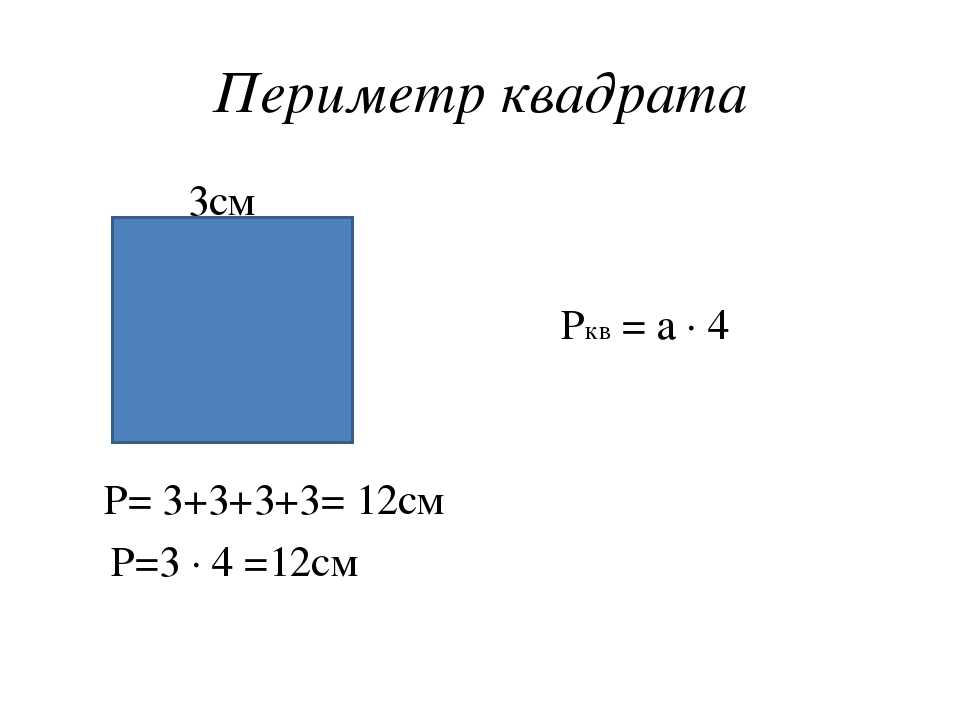
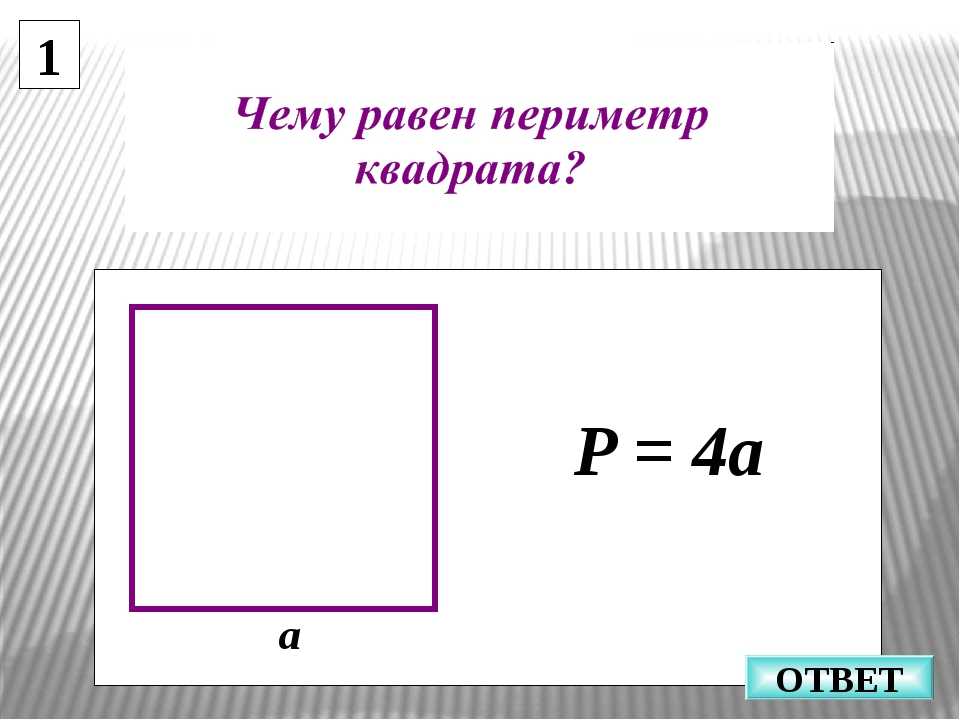
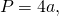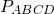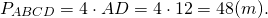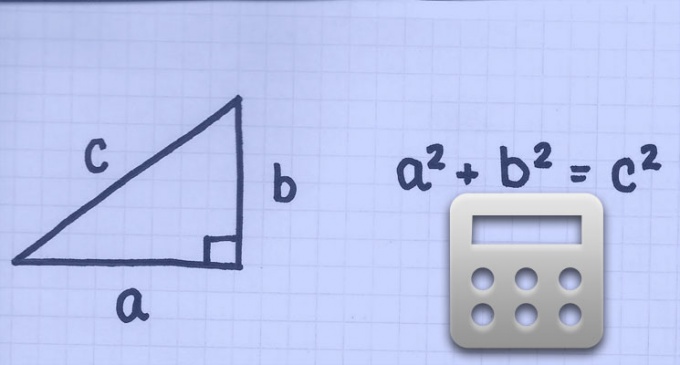Как узнать периметр квадрата

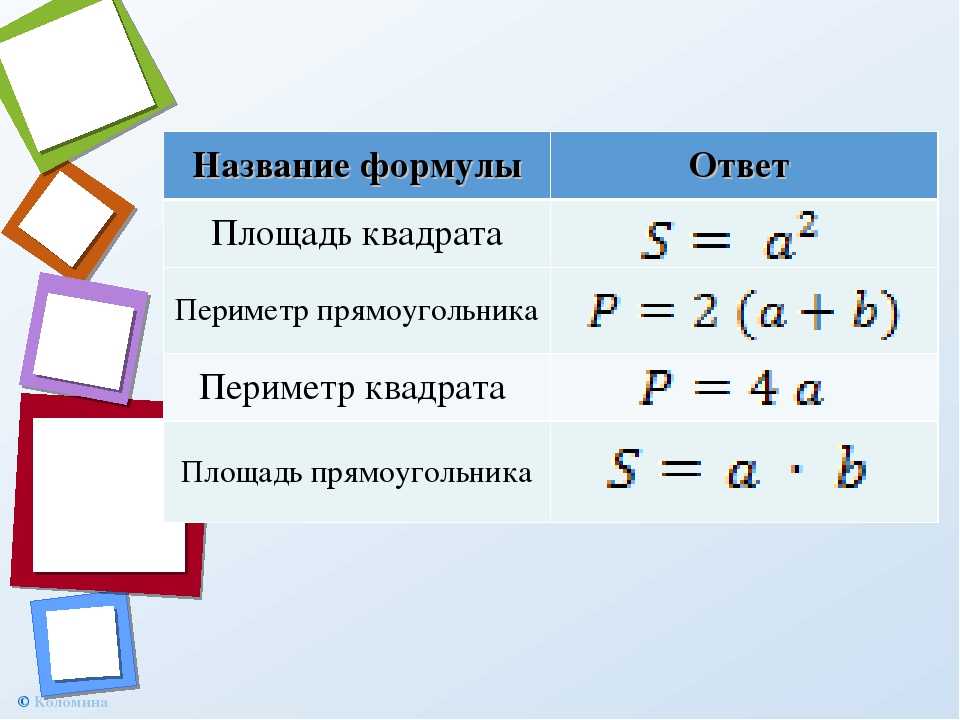
Периметры фигур. Периметр квадрата.

Периметр квадрата, да и любой геометрической фигуры, равен сумме длин всех сторон.

четыре прямых угла.

Квадрат является боковой гранью куба.

Найти периметр квадрата крайне просто. Для этого просто следуйте этим шагам.

Метод 1 из 3: Найдите периметр квадрата, если известна длина одной стороны

Умножьте длину стороны на 4. Квадрат имеет четыре стороны одинаковой длины, значит для нахождения

периметра квадрата нужно просто умножить длину любой из сторон на 4.

Следуйте простой формуле:

где P = периметр и S = длина стороны.

Пример: Если одна из сторон квадрата 5, то P = 4 * 5 или 20.

Метод 2 из 3: Найдите периметр квадрата, если известна его площадь

Для этого нужно понимать формулу нахождения площади квадрата

или длина умноженная на ширину.

Так как все стороны квадрата равны, то формулу можно упростить до:

или квадрат длины стороны.

Метод 3 из 3: Найдите периметр квадрата, если известна его диагональ

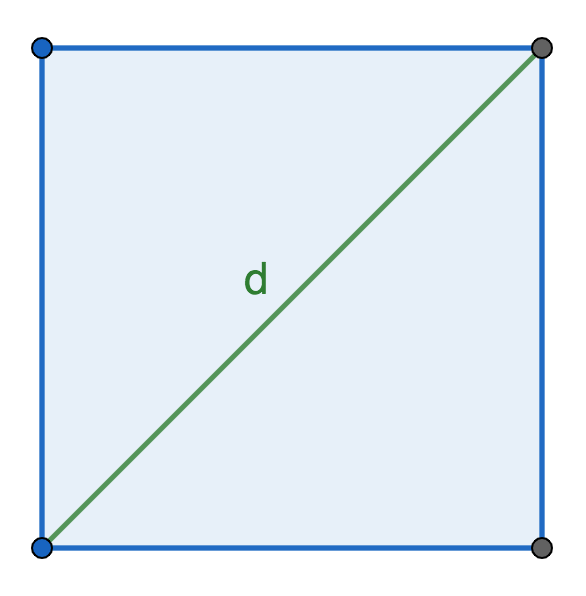
Периметр квадрата равен произведению длины его диагонали на два корня из двух.

Источник

Как найти периметр квадрата

Что такое периметр квадрата

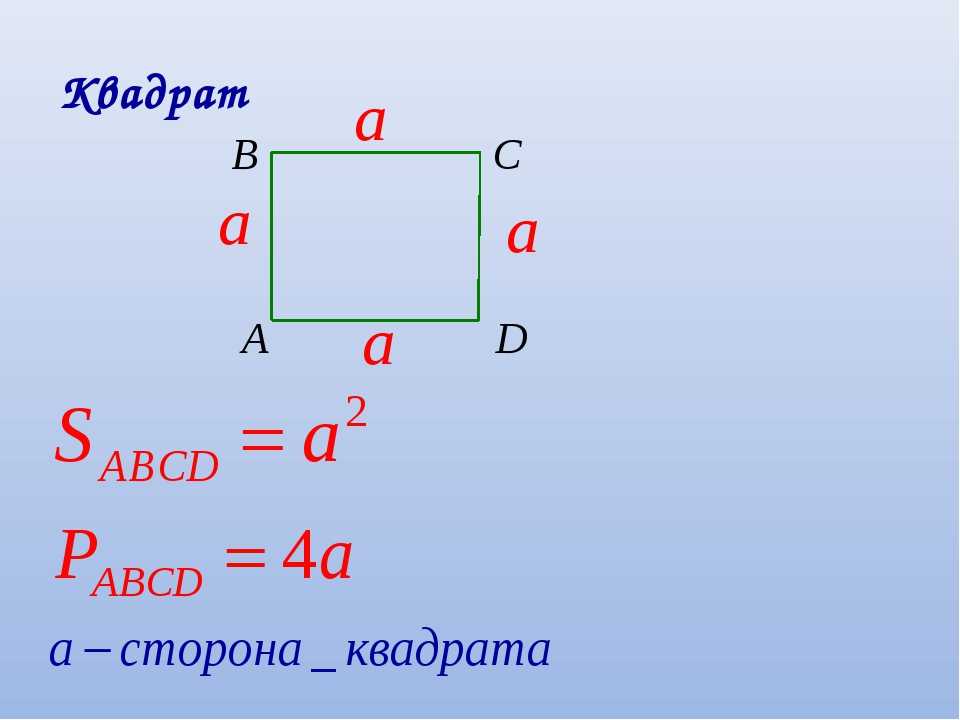
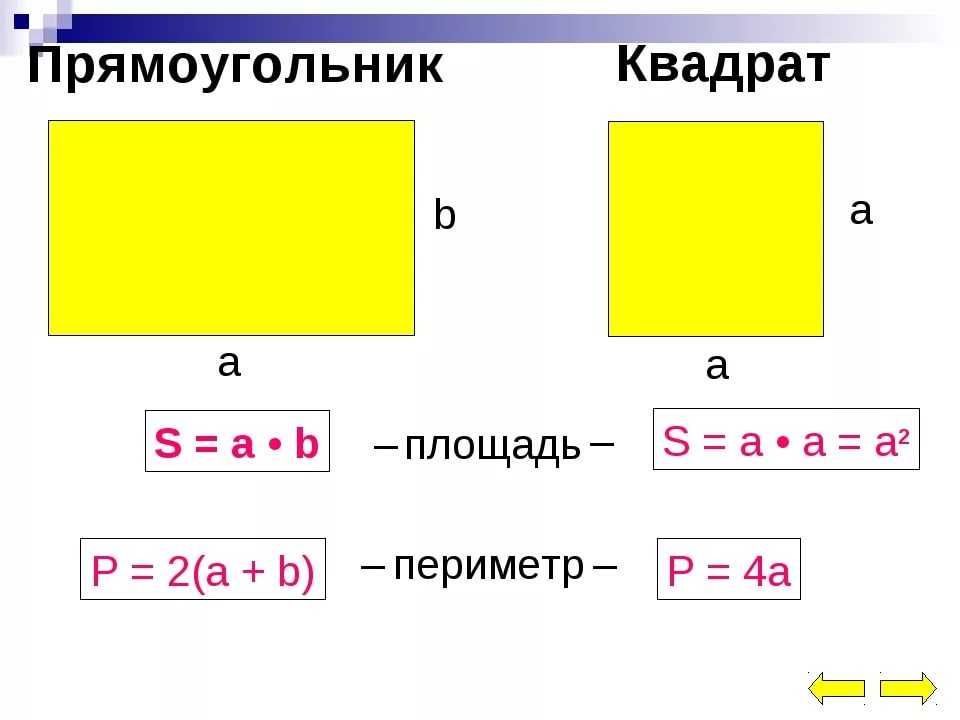
Квадрат — это правильный четырехугольник, все его стороны и углы равны.

Про него также говорят, что это частный случай прямоугольника или ромба.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Способы вычисления

Для вычисления периметра квадрата применяется несколько видов несложных формул.

По длине стороны

Самый простой способ, если известна величина одной из его сторон. Сразу вспоминаем, что мы имеем дело с правильным четырехугольником, и подставляем значение в уравнение:

где \(a\) — это сторона фигуры.

По длине диагонали

Если известна только диагональ правильного прямоугольника, формула для нахождения суммы всех его ребер будет выглядеть так:

что следует из соотношения длин стороны и диагонали \(d=a\sqrt2\)

По площади

Зная площадь фигуры, найти ее периметр можно так:

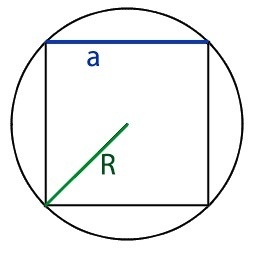
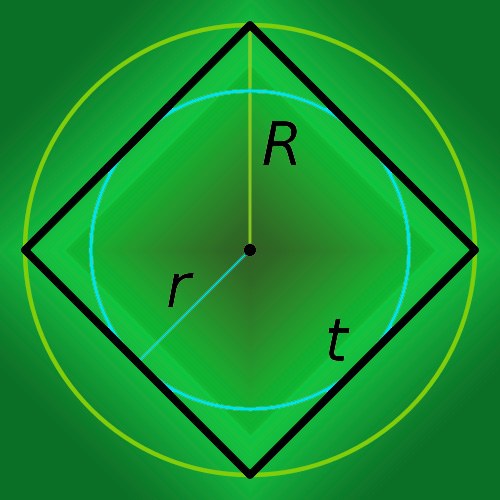
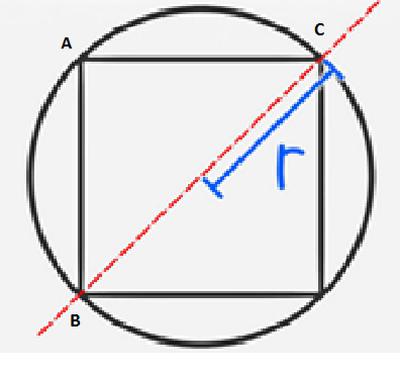
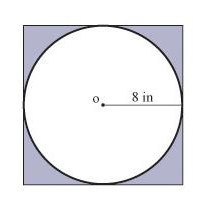
По радиусу описанной окружности

Радиус описанной вокруг квадрата окружности — это половина его диагонали. Формула для нахождения P в данном случае:

где R — радиус данной окружности.

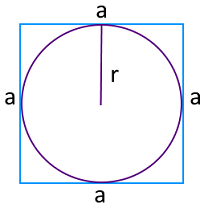
По радиусу вписанной окружности

Радиус вписанной окружности — это половина величины ребра правильного прямоугольника. Таким образом, уравнение для нахождения P выглядит так:

где r — радиус вписанной окружности.

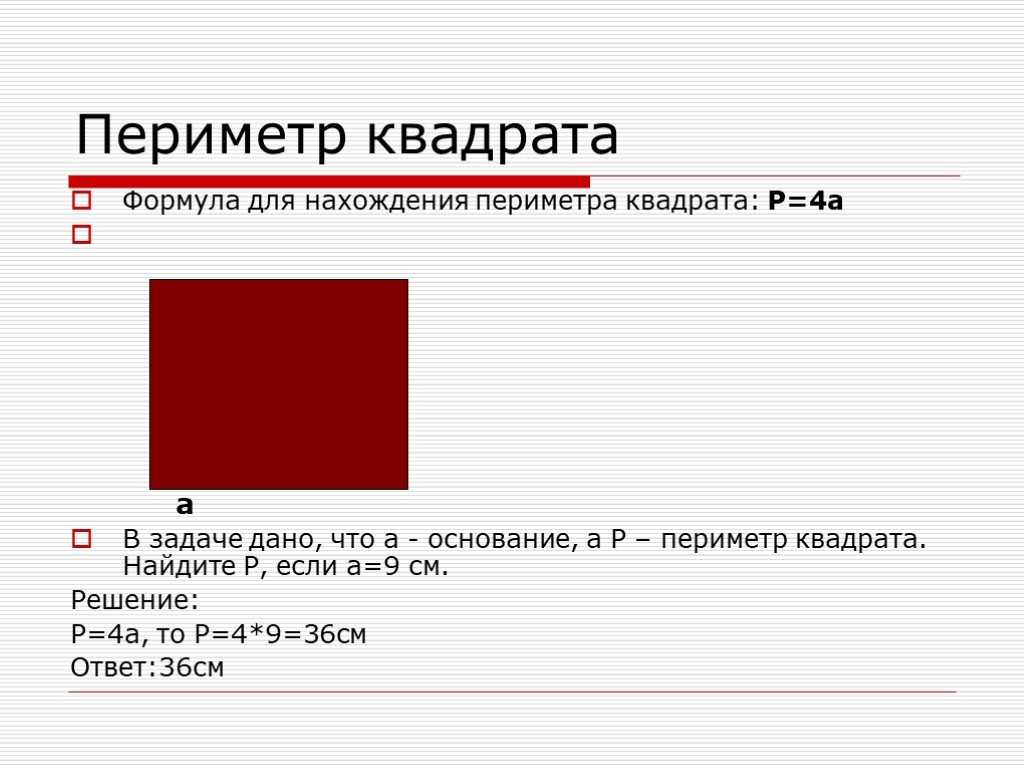
Найти P квадрата, если его ребро a равно 5 см.

Так как P = 4a, подставляем сюда известное значение, и получается \(P = 4\times5= 20\ см.\)

Узнать P правильного четырехугольника, если его диагональ d равна 6 см.

Используем формулу \(P\;=\;2d\sqrt2\) и подставляем известное значение. Получается: \(P = 2 * 6\sqrt2\ = 12\sqrt2\ см.\)

Ответ: \(12\sqrt2\ см.\)

Площадь квадрата равна 16 см². Каков периметр?

Известно, что 1/2 диагонали правильного прямоугольника составляет \(9\sqrt2\\ \) см. Вычислить P.

Дан квадрат и вписанная в него окружность. Половина стороны a фигуры равна 7 см, посчитать P.

Источник

Как найти периметр квадрата

Формула

Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.

Примеры вычисления периметра квадрата

Решение. Для нахождения периметра квадрата воспользуемся формулой

Подставляя в неё значение 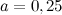, получим:

Решение. Сделаем рисунок.

Диаметр описанной окружности является диагональю вписанного в неё квадрата, то есть

$DB=d=2r=2 \cdot 2=4$ (дм)

Откуда получаем, что

А тогда искомый периметр:

Источник

Нахождение периметра квадрата: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.

Формула вычисления периметра

По длине стороны

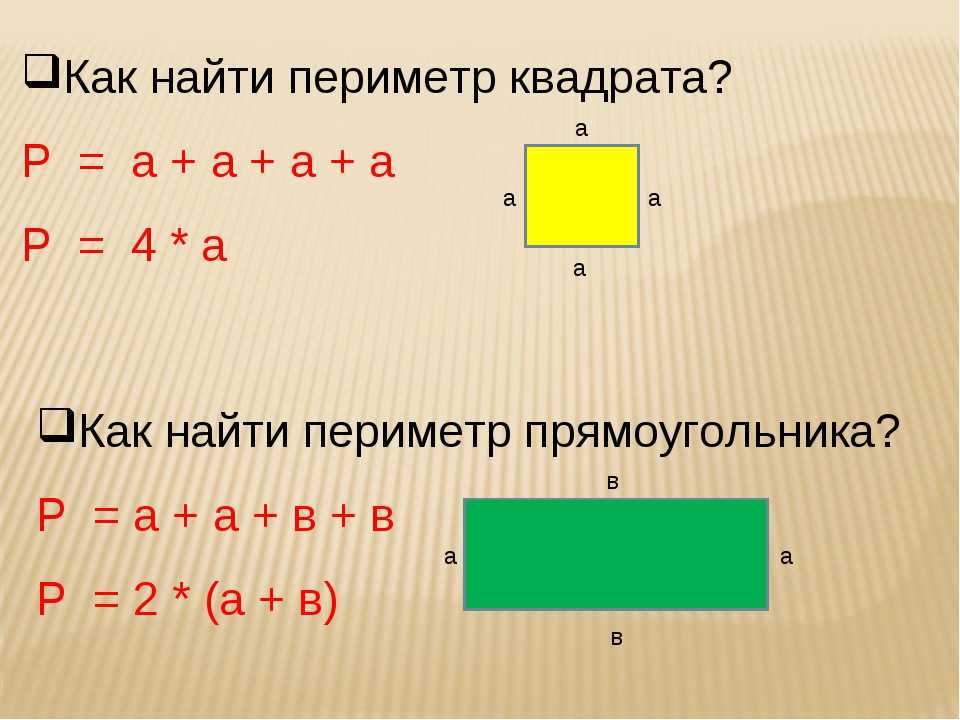
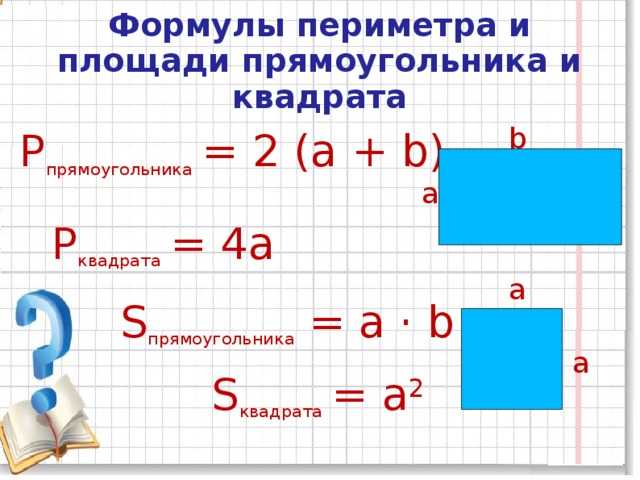
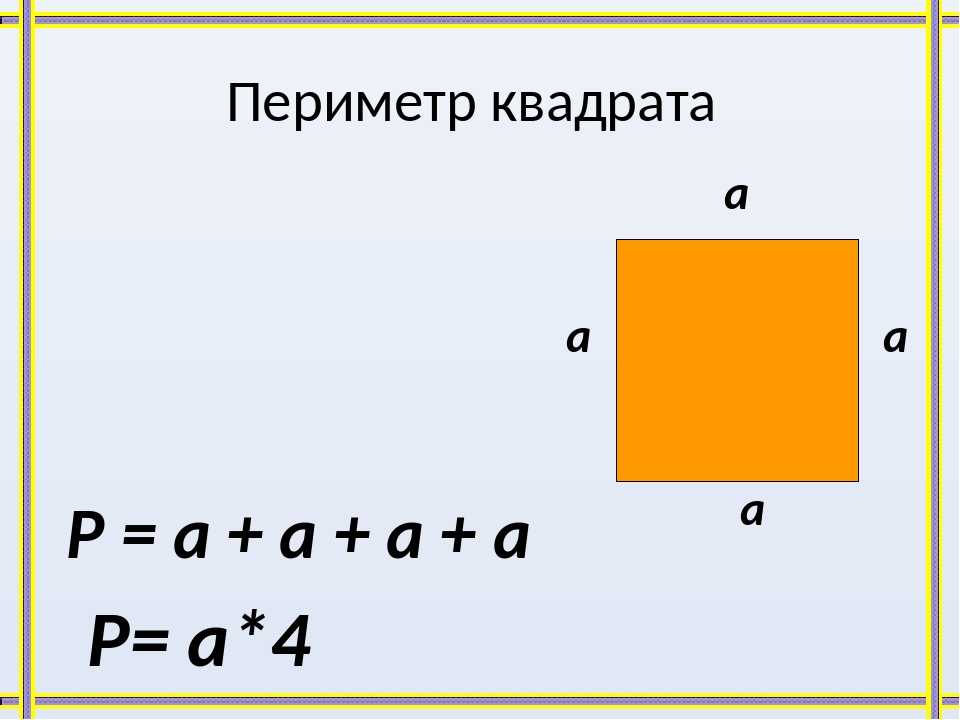
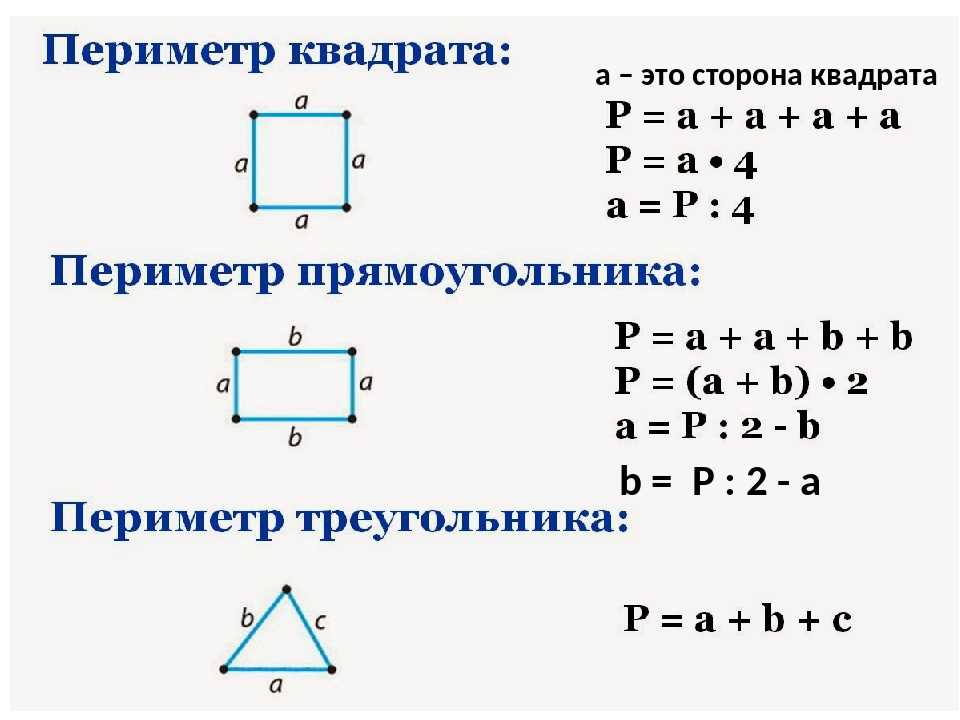
Периметр (P) квадрата равняется сумме длин его сторон.

P = a + a + a + a

Так как все стороны квадрата равны, формулу можно представить в виде произведения:

P = 4 ⋅ a

По длине диагонали

Периметр (P) квадрата равен произведению длины его диагонали на число 2√ 2 :

P = d ⋅ 2√ 2

Примеры задач

Задание 1
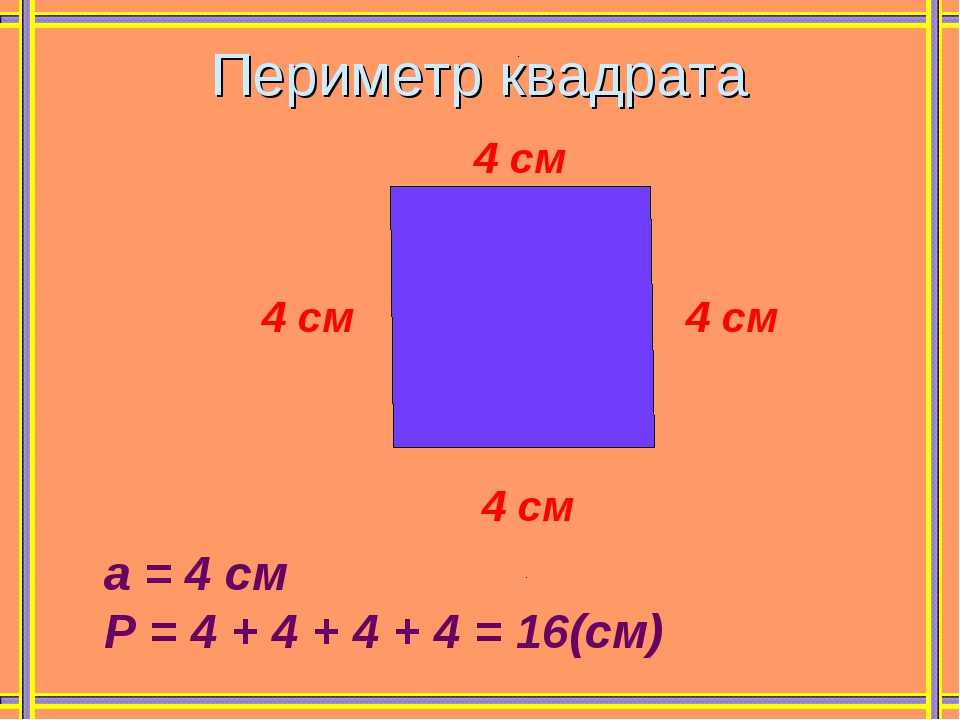
Найдите периметр квадрата, если его сторона равна 6 см.

Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.

Задание 2
Найдите периметр квадрата, диагональ которого равняется √ 2 см.

Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √ 2 см ⋅ 2√ 2 = 4 см.

Решение 2:
Выразим длину стороны через диагональ:
a = d / √ 2 = √ 2 см / √ 2 = 1 см.

Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.

Источник

Формула периметра квадрата

Квадрат — правильный четырёхугольник, у которого все стороны и углы равны между собой. Может быть определён как прямоугольник, у которого две смежные стороны равны между собой, или как ромб, у которого все углы прямые. У квадрата есть две диагонали, соединяющие несмежные вершины.

Первый способ вычисления периметра квадрата

Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).

\[ \LARGE P = 4 \cdot a \]

Второй способ вычисления периметра квадрата

Периметр квадрата равен произведению длины его диагонали на два корня из двух.

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

О сайте

На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.

Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.

calcsbox.com

На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.

© 2022 Все калькуляторы online

Копирование материалов запрещено

Источник

Как найти периметр квадрата?

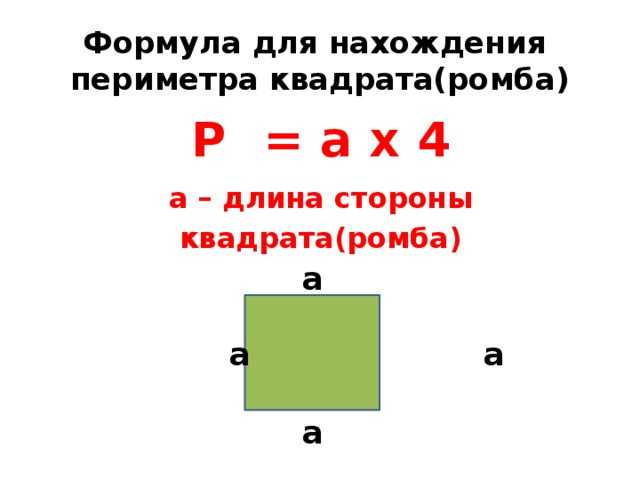
Периметр квадрата равен его стороне умноженной на четыре: Р=4а.

Формула соответствует определениям периметра и квадрата: периметр – это сумма всех сторон, а квадрат – это четырёхугольник с равными сторонами и прямыми углами.

Для самых ленивых Яндекс даже предлагает онлайн калькулятор, где вводишь длину стороны квадрата (значение а) и получаешь готовое значение периметра (Р).

Увидев этот вопрос, мы с сыном, который перешёл в пятый класс, улыбнулись, и начали вспоминать, когда же нахождение периметра проходили в школе. После небольшой, но оживлённой дискуссии, я решил этот вопрос, пробежав программу по математике в начальной школе на сайте Министерства образования и науки Украины. Как оказалось, мой мальчик был прав, что ещё во 2-ом классе, а не в 3-ем, как запомнилось мне, детям уже даются основы геометрический знаний.

Для того же, чтобы узнать периметр (сумму всех сторон), достаточно измерить длину одного из отрезков и полученную величину умножить на 4.

Для наглядности проиллюстрирую ниже.

Источник

Периметр квадрата

Как найти периметр квадрата, зная его сторону? Как найти сторону квадрата, если известен его периметр?

Периметр квадрата равен сумме длин его сторон.

Так как все стороны квадрата равны, периметр квадрата равен произведению 4 на длину стороны квадрата.

Формула для нахождения периметра квадрата:

где a — длина стороны квадрата.

Найти периметр квадрата со стороной 12 м.

Делаем чертеж и записываем условие:

Дано:

По формуле P=4a, где a — сторона квадрата,

Найти сторону квадрата, если его периметр равен 20 см.

Дано : ABCD — квадрат,

Так как периметр квадрата P=4a, где a — сторона квадрата, чтобы найти сторону квадрата через его периметр, надо периметр разделить на 4:

Источник

Онлайн калькулятор. Периметр квадрата

Используя этот онлайн калькулятор, вы сможете найти периметр квадрата.

Воспользовавшись онлайн калькулятором для вычисления периметра квадрата, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

Найти периметр квадрата

Выберите известную величину

Ввод данных в калькулятор для вычисления периметра квадрата

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!

Если у вас возниели трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины.

Теория. Периметр квадрата

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Научитесь вычислять периметр квадрата.

Глядя вокруг себя, мы наблюдаем множество правильных и неправильных геометрических фигур. От основных принципов евклидовой геометрии (точка, прямая, плоскость и т. д.) и до наших дней мы можем наблюдать великие преобразования, которые произошли в геометрии объектов, домов, искусства, появляются новые и смелые архитектуры, бросающие вызов всем. формы классической геометрии. Периметр плоской геометрической фигуры широко применяется математикой во многих случаях. Среди этих фигур квадрат имеет большое значение и постоянно появляется в гражданском строительстве, машиностроении, искусстве и других приложениях. В связи с этим сегодня мы поговорим о фигуре квадрата и научим вас, как найти периметр этой геометрической фигуры. Еще больше информации можно узнать на https://skysmart.ru/courses/matematika.

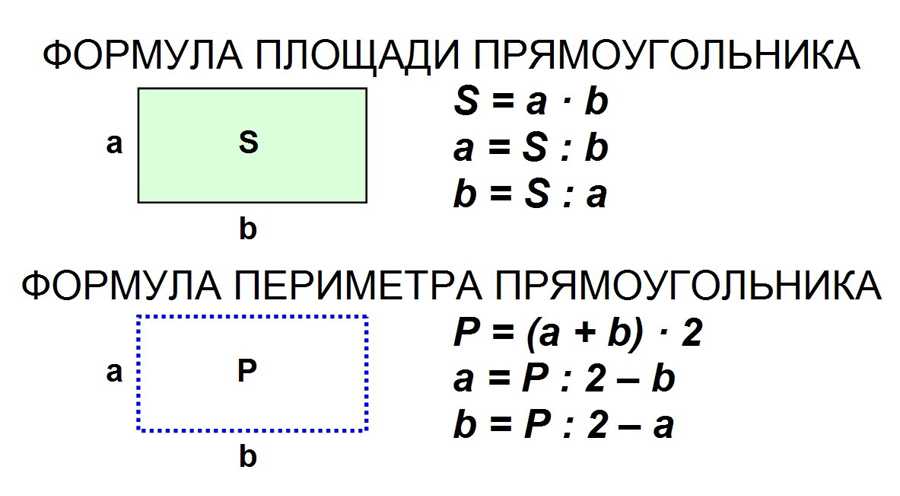
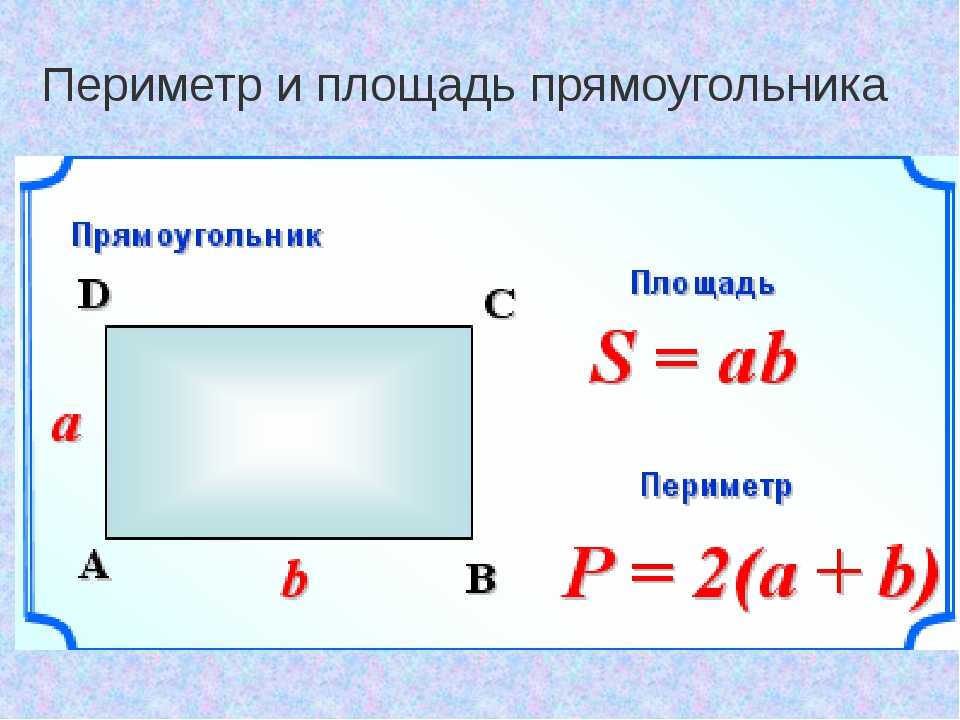
Площадь и периметр

Площадь и периметр — величины, имеющие большое значение для изучения плоских фигур в планиметрии. Существуют специальные формулы для расчета площади и периметра.

Площадь и периметр являются важными расчетами при изучении плоских фигур. Мы знаем площадь как меру поверхности фигуры, периметр — это длина контура фигуры, и его значение находится при вычислении суммы всех сторон фигуры. При изучении многоугольников, являющихся частными случаями плоских фигур, для нахождения их периметра достаточно выполнить сумму длин всех сторон, при этом площадь вычисляется по конкретным формулам для каждого многоугольника.

Площадь и периметр фигуры очень полезны в гражданском строительстве, на плантациях, а также для того, чтобы иметь представление о размерах поверхностей в быту, с несколькими приложениями этих понятий.

Что такое площадь?

Площадь является важной величиной геометрии. Для данной геометрической фигуры площадь является измерением поверхности этой фигуры. Для вычисления площади плоских фигур используем специфические формулы для каждой из них, при необходимости делим плоскую фигуру на известные плоские фигуры и складываем площади. Вот основные плоские фигуры и формула для расчета площади каждой из них.

Что такое периметр?

Периметр плоской фигуры равен сумме длин всех сторон фигуры. Таким образом, хотя и существует формула для некоторых плоских фигур, просто помните, что сумма их сторон дает их периметр.

Как рассчитать периметр?

Периметр всегда равен сумме всех сторон плоской фигуры, поэтому для некоторых плоских фигур можно использовать соответствующую формулу. Посмотрим на периметр основных плоских фигур.

Определение квадрата

Квадрат – это плоская геометрическая фигура, имеющая четыре стороны одинаковой длины, называемая правильным квадратом. Углы, образуемые этими сторонами квадрата, равны 90° (прямой угол). Также квадрат можно разделить по диагонали, соединив две диагонально противоположные вершины. То есть мы можем провести линию, которая соединит его углы (вершины) по диагонали.

Вычисление периметра квадрата

Вычислить периметр квадрата несложно и можно сделать в уме. Ввиду того, что все его стороны имеют одинаковую меру, то мы можем определить периметр квадрата, только зная меру одной из сторон. Самое большое определение периметра – это измерение контура двумерной геометрической фигуры.

Итак, исходя из этой концепции, мы можем определить периметр квадрата, сложив каждую сторону этого квадрата. Формула выглядит следующим образом:

P = L + L + L + L или P = L x 4

Где «L» — сторона квадрата.

Собственник участка выделил участок площадью 25 м под огороженное место с экраном. Он намерен посадить листья и немного овощей на этом небольшом пространстве. Однако он хочет использовать в этой ручке как можно меньше экрана. Какая плоская геометрическая фигура будет использовать как можно меньший экран, чтобы окружить эту область?

В этом случае это было бы возможно только с фигурой четырехугольника.

Начнем с прямоугольника:

Возможные измерения для прямоугольника площадью 25 м будут иметь ширину 4 метра и длину 6,25 метра, откуда мы можем получить периметр:

Р = 4 + 4 + 6,25 + 6,25 = 20,5

Итак, мы знаем, что периметр прямоугольника площадью 25 м эквивалентен 20,5 метрам в длину. В этом случае это будет размер экрана, используемый в данной конфигурации.

Теперь вычислим периметр этой самой площади в 25 м, используя фигуру квадрата.

Единственная возможная мерка для площади 25 м от обычного квадрата – по 5 метров с каждой стороны.

Итак, мы знаем, что используя угольник, длина периметра забора составит 20 метров. В этом случае владелец участка будет использовать меньше холста с конфигурацией квадрата в своем ограждении.

Эта важная особенность квадрата может остаться незамеченной при проектировании комнаты или любой другой среды. Квадрат всегда будет иметь меньший периметр той же площади по сравнению с другими четырехугольниками.

Источник

Как найти площадь и периметр квадрата? Какие есть формулы?

Периметр квадрата в этом случае равен длине четырех сторон или учетверенной длине одной стороны:

Всё так, но ведь на практике может сложиться такая ситуация, когда мы уже будем знать значение площади квадрата, а необходимо будет посчитать его периметр. Или, наоборот, потребуется вычислить значение площади, исходя из сведений о периметре. Стало быть для каждого из (P) и (S) нам потребуется определиться не с двумя, а с тремя формулами. Что же, давайте приступим. Только одно маленькое замечание: очень неудобно рисовать буквами знак «квадратный корень» и я предлагаю использовать функцию «Корень()», как это делается в электронной таблице Excel, если вы не против. Тогда мы можем получить следующие записи формул:

Периметр (P)

Площадь (S)

Вроде бы всё готово и можно было бы на этом остановиться. Но, друзья мои, как в таком деле обойтись без проверки? Я предлагаю подставить в качестве длины число 12, как в нашем квадрате на картинке. Тогда значение диагонали для него составит = Корень(2*a²) = 16,97. Тогда мы можем подставить эти данные в найденные формулы и получим следующие результаты:

Вычисление через длину стороны:

Вычисление через длину диагонали:

Вычисление через площадь или периметр, соответственно:

Вот, теперь с чистой совестью можно отправляться на заслуженный отдых.

Источник

Расчет периметра квадрата

Способы вычисления

Для вычисления периметра квадрата применяется несколько видов несложных формул.

По длине стороны

Самый простой способ, если известна величина одной из его сторон. Сразу вспоминаем, что мы имеем дело с правильным четырехугольником, и подставляем значение в уравнение:

где \(a\) — это сторона фигуры.

По длине диагонали

Если известна только диагональ правильного прямоугольника, формула для нахождения суммы всех его ребер будет выглядеть так:

что следует из соотношения длин стороны и диагонали \(d=a\sqrt2\)

Зная площадь фигуры, найти ее периметр можно так:

По радиусу описанной окружности

Радиус описанной вокруг квадрата окружности — это половина его диагонали. Формула для нахождения P в данном случае:

где R — радиус данной окружности.

По радиусу вписанной окружности

Радиус вписанной окружности — это половина величины ребра правильного прямоугольника. Таким образом, уравнение для нахождения P выглядит так:

где r — радиус вписанной окружности.

Найти P квадрата, если его ребро a равно 5 см.

Так как P = 4a, подставляем сюда известное значение, и получается \(P = 4\times5= 20\ см.\)

Узнать P правильного четырехугольника, если его диагональ d равна 6 см.

Используем формулу \(P\;=\;2d\sqrt2\) и подставляем известное значение. Получается: \(P = 2 * 6\sqrt2\ = 12\sqrt2\ см.\)

Ответ: \(12\sqrt2\ см.\)

Площадь квадрата равна 16 см². Каков периметр?

Мы знаем, что \(P\;=\;4\sqrt S\\\). Значит, подставляя значение в формулу \(P\;=\;4\sqrt S\\\), мы имеем: \(P\;=\;4\sqrt 16\ = 4\times4\ = 16\) см.

Известно, что 1/2 диагонали правильного прямоугольника составляет \(9\sqrt2\\ \)см. Вычислить P.

1/2 диагонали имеющейся фигуры — это как раз радиус описанной окружности. Подставляем значение в уравнение \(P\;=\;4R\sqrt2\\\). Получается: \(P\;=\;4R\sqrt2\ = 4\times9\sqrt2\times\sqrt2\ = 72\) см.

Дан квадрат и вписанная в него окружность. Половина стороны a фигуры равна 7 см, посчитать P.

Так как половина стороны данной фигуры — это радиус вписанной в нее окружности. Используем метод нахождения по радиусу вписанной окружности: \(P\;=\;8r\\\). Подставляем известное значение: \(P\;=\;8r\ = 8\times7\ = 56\ см.\)

Чему равно отношение стороны квадрата к его периметру?

1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).

Часто на просторах интернета можно найти насмешки по поводу того, как знания по математике — интегралы, дифференциалы, тригонометрические функции и прочие разделы предмета — не помогают облегчить жизнь человека. Такие шутки напрасны, ведь как выручает умение правильно рассчитывать периметр квадрата, прямоугольника и других геометрических фигур в строительных работах. Расход материала: плитки, обоев, напольного покрытия — не определить без понимания элементарных математических формул и геометрических фигур.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Что такое форма?

Если кто-то спросит вас, что такое форма, вы, вероятно, сможете назвать довольно много из них. Но у «формы» тоже есть особое значение.- это не просто названия кругов, квадратов и треугольников.

Форма — это форма объекта, а не то, сколько места он занимает или где находится физически, а реальная форма, которую он принимает. Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее реальной круглой формой, которую он принимает.

Форма может быть любого размера и появляться где угодно; они ничем не ограничены, потому что фактически не занимают места. Трудно осознать это, но не думайте о них как о физических объектах — форма может быть трехмерной и занимать физическое пространство, например подставку для книг в форме пирамиды, цилиндрическую банку с овсянкой или он может быть двухмерным и не занимать физического места, например треугольник, нарисованный на листе бумаги.

Тот факт, что он имеет форму, отличает форму от точки или линии.

Точка — это просто позиция; у него нет ни размера, ни ширины, ни длины, ни вообще никаких размеров.

Линия же одномерная. Он бесконечно тянется в любом направлении и не имеет толщины. Это не форма, потому что у нее нет формы.

Хотя мы можем представлять точки или линии как фигуры, потому что нам действительно нужно их видеть, на самом деле они не имеют никакой формы. Вот что отличает форму от других геометрических фигур — она ​​двух- или трехмерная, потому что имеет форму.

Кубики, подобные тем, что мы видим здесь, представляют собой трехмерные квадраты — обе формы!

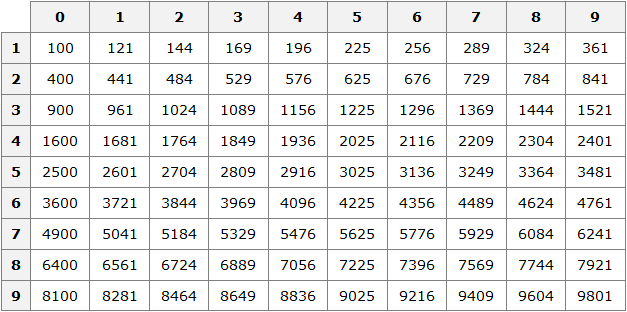
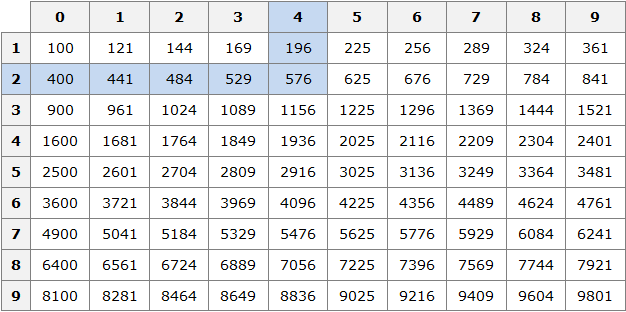
Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов
.

Первая строка данной таблицы (цифры от 0 до 9) это исходного числа, а первый столбец (цифры от 1 до 9) это исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

А как насчет трехмерных геометрических фигур?

Существуют также трехмерные формы, которые имеют не только длину и ширину, но также глубину или объем. Это формы, которые вы видите в реальном мире, такие как сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.

Трехмерные формы, естественно, более сложные, чем двухмерные, с дополнительное измерение — количество места, которое они занимают, а не только форма, — которое необходимо учитывать при расчете площади и периметра.

Математика, включающая двумерные фигуры, подобные приведенным выше, называется плоская геометрия, потому что она имеет дело с плоскостями или плоскими формами. Математика, включающая трехмерные формы, такие как сферы и кубы, называется сплошная геометрия, потому что она имеет дело с твердыми телами, другим словом для трехмерных форм.

2D-формы составляют 3D-фигуры, которые мы видим каждый день!

Прямоугольник и тригонометрические функции

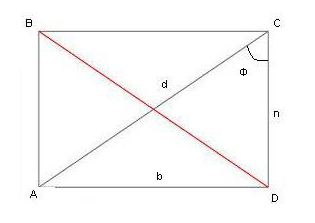
Для наглядности приведен пример решения задачи. Дано: прямоугольник АВСД; длина диагонали (d) 20 см; угол ф – 30°. Найти периметр фигуры.

Из тригонометрии необходимо вспомнить следующее: синус угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе. Синус 30° (существуют таблицы, по которым можно определить значения тригонометрических функций для правильных углов) равен 1/2. Получается 1/2 = отношению в к d. Неизвестная величина в будет равна d/2=20/2=10 см.

Для расчета периметра следует найти вторую сторону фигуры. Можно через теорему Пифагора, так как известны длины гипотенузы и одного из катетов или опять через отношение сторон для косинуса угла.

Косинус угла ф выражается как отношение прилежащего катета к гипотенузе и равен √3/2.

√3/2=n/d, n=(d*√3)/2 или 10*√3. После извлечения корня из 3, получаем длину стороны треугольника: 10*1,73=17,3 см.

Периметр равен 2(17,3+10)=2*27,3=54,6 см.

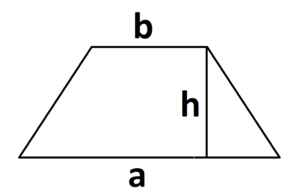
Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 1003 = 1 000 000 см3

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м3 = 1 000 000 см3

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.

Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»

300 000 000 см3 : 1 000 000 см3 = 300 м3

Пример 2. Выразить 3 м3 в кубических сантиметрах.

Умножим 3 м3 на 1 000 000

3 м3 × 1 000 000 = 3 000 000 см3

Пример 3. Выразить 60 000 000 см3 в кубических метрах.

Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3

60 000 000 см3 : 1 000 000 см3 = 60 м3

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм3

Теперь переведём эти 6000 дм3 в кубические метры.

Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1000 дм3

V = 103= 1000 дм3

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3

6 000 дм3 : 1 000 дм3 = 6 м3

Значит, 6000 л = 6 м3.

Площадь прямоугольника

Площадь прямоугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.

Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь прямоугольника с помощью различных формул или проверить уже выполненные вычисления.

Площадь прямоугольника через две стороны

a (или b) — сторона

a (или b) — сторона

α° — угол между диагоналями

a (или b) — сторона

R — радиус описанной окружности

a (или b) — сторона

D — диаметр описанной окружности

Прямоугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.

Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.

Окружность — это граница круга.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Как найти периметр квадрата?

Зная, что все стороны данного прямоугольника равны, необходимо сделать следующие манипуляции, чтобы вычислить его периметр:

Все формулы и исчисления, приведенные в рамках данной статьи, применимы для любого прямоугольника

Важно помнить, что когда речь идет о других прямоугольниках, которые не являются правильными, значение сторон будет разным, например 4 и 8 метров. Это означает, что для нахождения площади такого прямоугольника необходимо будет умножать разные по значению стороны фигуры, а не одинаковые

Необходимо помнить и то, что площадь измеряется в квадратных, а периметр в простых метрах. Если периметр нарисовать в виде одной длинной линии, то его значение не изменится, что говорит о том, что исчисления проводятся в одномерном пространстве.

Площадь измеряется в двухмерном пространстве, о чем говорят квадратные метры, которые мы получаем, умножив метры на метры. Площадь является индикатором наполненности геометрической фигуры, и говорит нам о том, сколько воображаемого покрытия необходимо для того чтобы заполнить квадрат или другой прямоугольник.

Простые объяснения видео урока позволят быстро вычислить площадь и периметр не только квадрата, но и любого прямоугольника. Данные знания школьного курса будут полезны во время ремонта дома или на садовом участке.

Как найти периметр, зная площадь квадрата | Сделай все сам

Квадрат – положительный четырехугольник, у которого все стороны равны, и все углы прямые. Периметромквадрата именуется сумма длин всех его сторон, а площадью – произведение 2-х сторон либо квадрат одной стороны. Исходя из знаменитых соотношений, через один параметр дозволено вычислить иной.

Инструкция

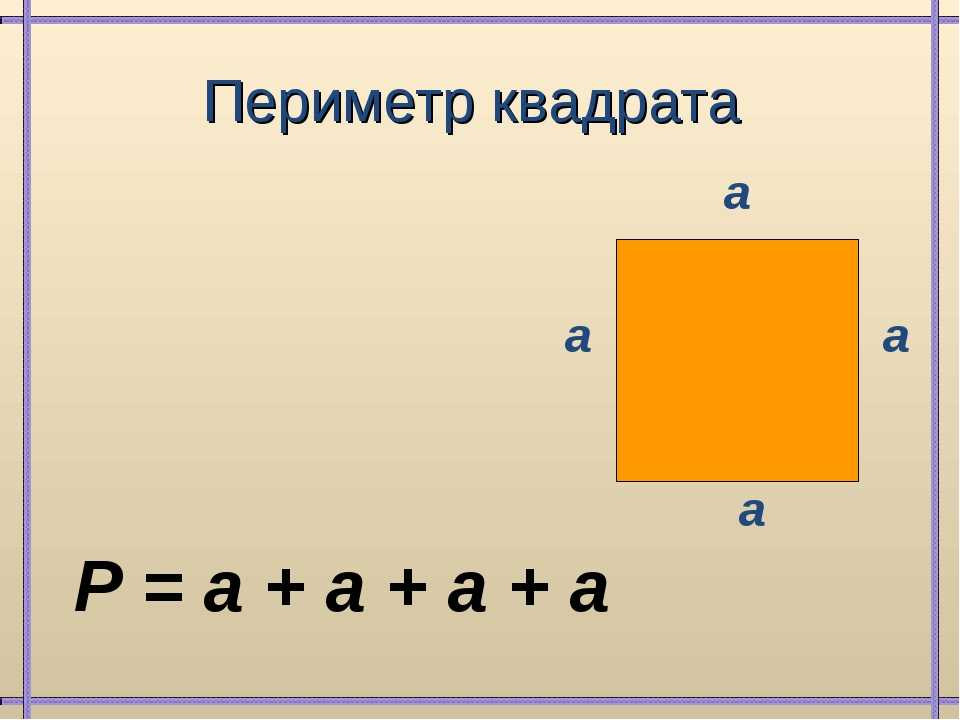
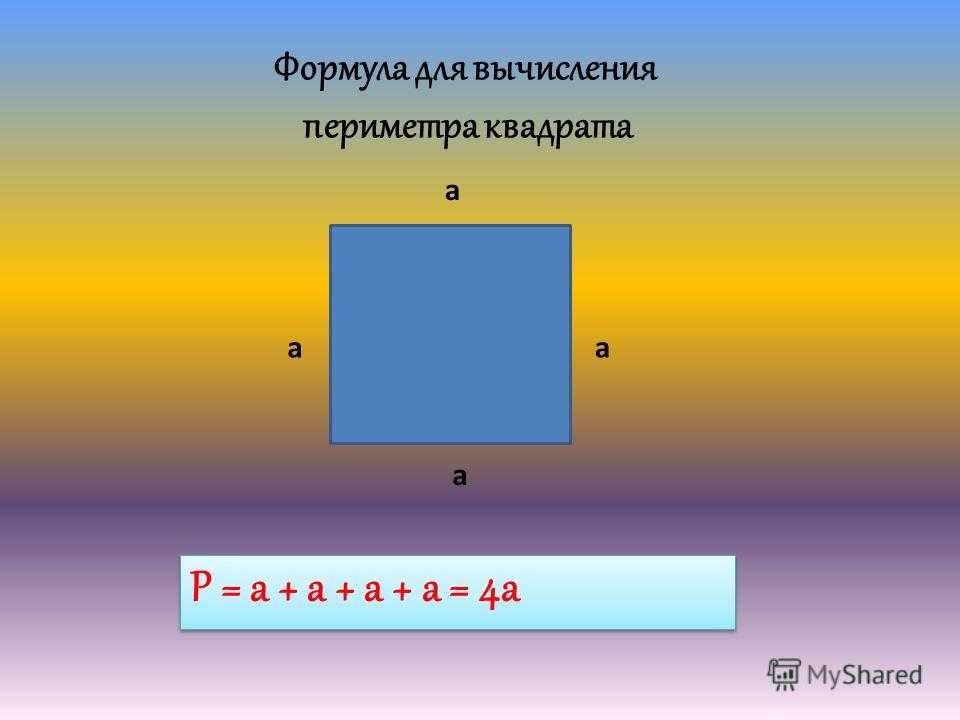
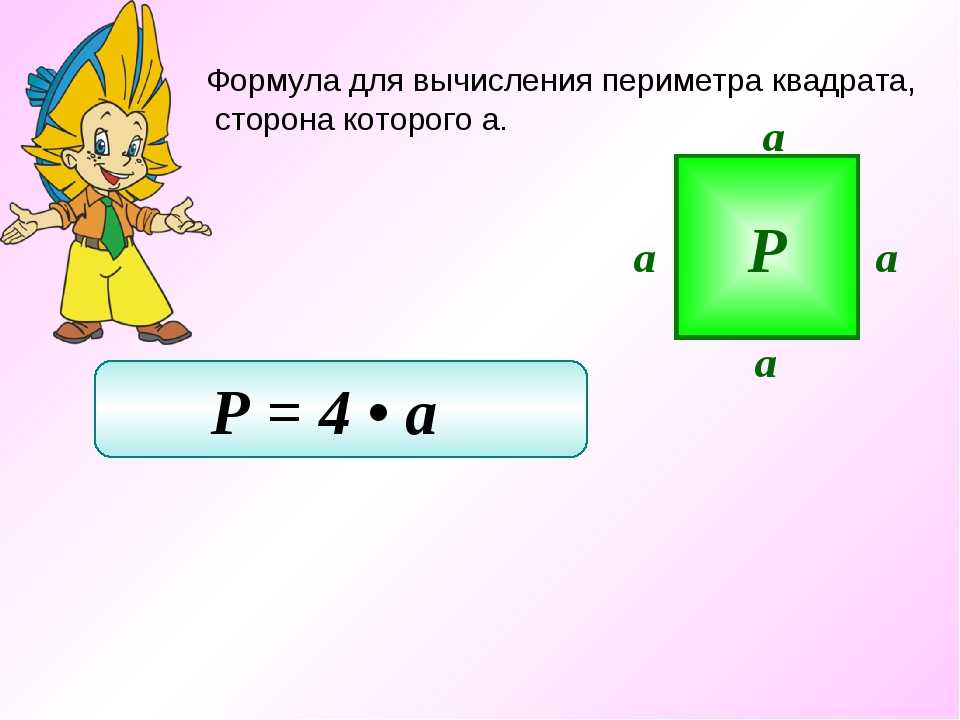
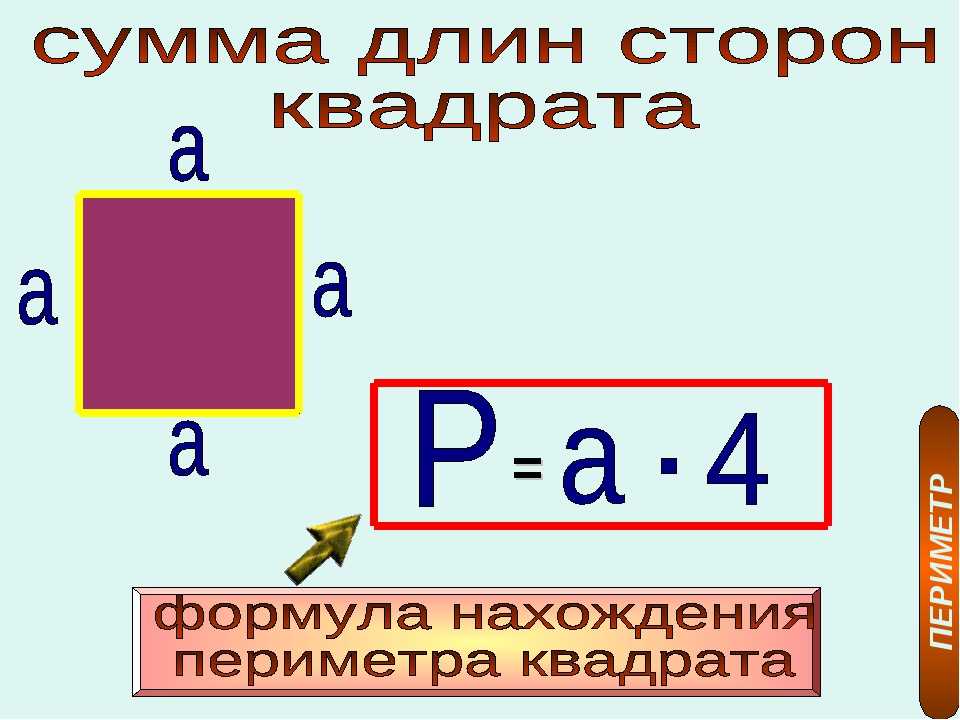
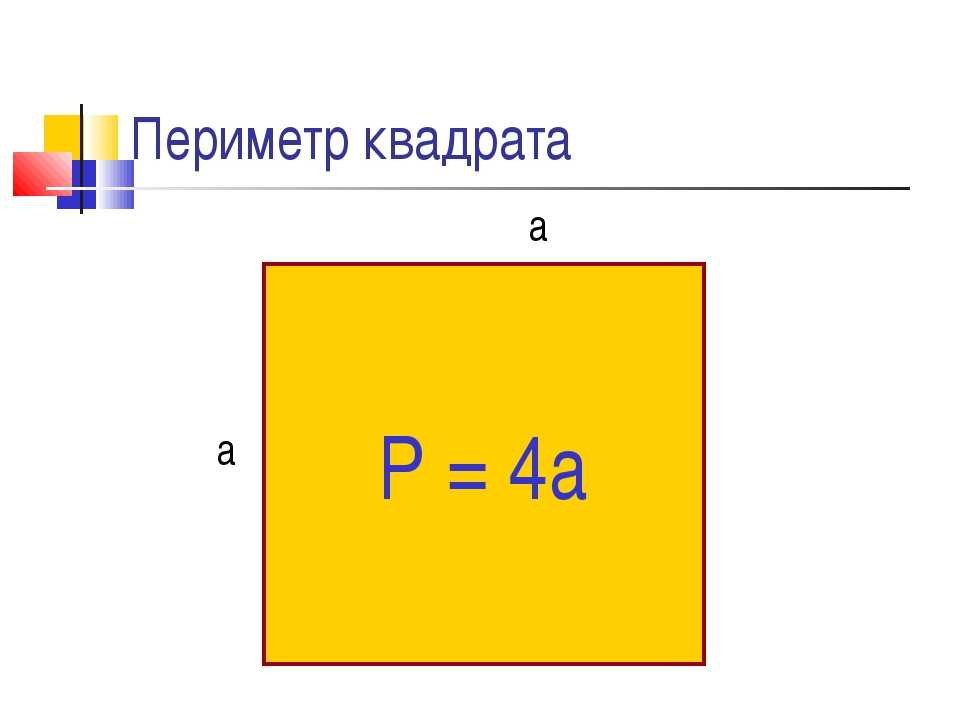
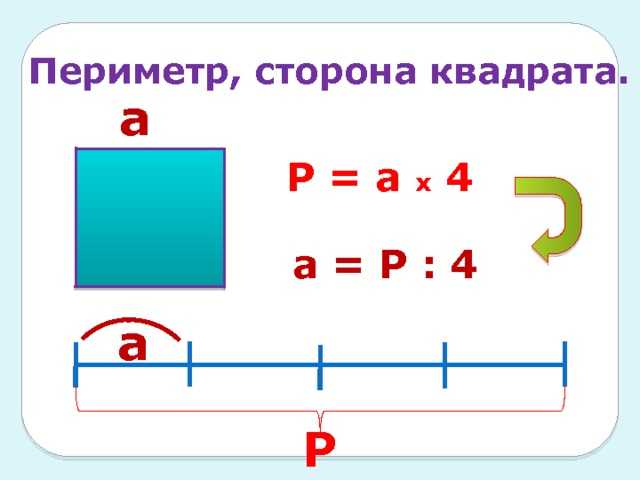
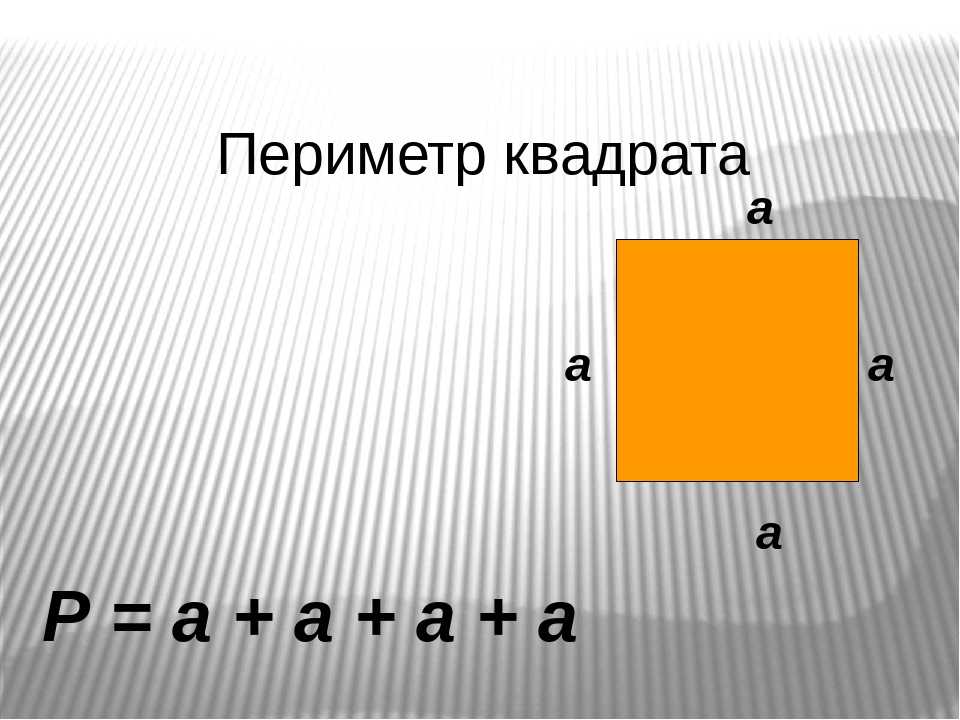
1. Для квадрата периметр (P) равен четырехкратному значению одной его стороны (b). P = 4*b либо сумме значений длин всех его сторон P = b + b + b + b.

3. Обнаружить периметр квадрата через площадь дозволено, не прибегая к лишнему действию (вычислению стороны). Для этого воспользуйтесь формулой вычисления периметра, объективной только для квадрата P = 4*?S.

4. Решение 2. Обнаружьте периметр квадрата : P = 4*?S, P = 4*?36см?, P = 24 см.Результат: периметр квадрата равен 24 см.

5. Многие параметры этой геометрической фигуры связаны между собой. Зная один из них, вы сумеете обнаружить всякий иной.

Совет 2: Как обнаружить периметр в математике

Периметр – это суммарная длина сторон геометрической фигуры. Но если возникнет надобность стремительно рассчитать периметр чего-либо (скажем, во время ремонта либо строительства), не всякий сумеет это сделать с легкостью. Припомним основные правила для вычисления периметра.

геометриеская фигура, линейка, ручка

Совет 3: Как обнаружить сторону квадрата, если вестима его диагональ

Квадрат является одной из особенно примитивных геометрических фигур в плане вычисления его параметров – длин сторон и диагоналей, площади и периметра.

Это определяется тем, что в различие от других многоугольников, неизменно вестимы величины всех его углов, а также довольно знать длину каждого одной стороны.

Нахождение длины стороны квадрата по вестимой длине диагонали, как в всеобщем виде, так и с фактическими расчетами не представляет трудности.

Совет 4: Как обнаружить площадь, зная диаметр

Задачи на вычисление площади круга зачастую встречаются в школьном курсе геометрии. Дабы обнаружить площадь круга, нужно знать длину диаметра либо радиуса окружности, в которую он заключен.

– длина диаметра окружности.

Совет 5: Как обнаружить площадь и периметр квадрата

Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон идентичной длины и четырех прямых углов, всякий из которых равен 90°.

Определение площади либо периметра четырехугольника, причем всякого, требуется не только при решении задач по геометрии, но и в повседневной жизни.

Эти знания могут стать пригодными, скажем, во время ремонта при расчете необходимого числа материалов – покрытий для пола, стен либо потолка, а также для разбивки газонов и грядок и т.д.

Перевод единиц измерения площади

Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.

1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100

S = 1002 = 10 000 см2

Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.

1 м2 = 10 000 см2

Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.

Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.

А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.

Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»

100 000 см2 : 10 000 см2 = 10 м2

Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.

Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000

S = 10002 = 1 000 000 м2

Получается, что на один квадратный километр приходится один миллион квадратных метров:

1 км2 = 1 000 000 м2

Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.

Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.

Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000

2 км2 × 1 000 000 = 2 000 000 м2

А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.

Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»

3 500 000 м2 : 1 000 000 м2 = 3,5 км2

Пример 2. Выразить 7 м2 в квадратных сантиметрах.

Умножим 7 м2 на 10 000

7 м2 = 7 м2 × 10 000 = 70 000 см2

Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.

5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2

Пример 4. Выразить 550 000 см2 в квадратных метрах.

Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2

550 000 см2 : 10 000 см2 = 55 м2

Пример 5. Выразить 7 км2 в квадратных метрах.

Умножим 7 км2 на 1 000 000

7 км2 × 1 000 000 = 7 000 000 м2

Пример 6. Выразить 8 500 000 м2 в квадратных километрах.

Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2

8 500 000 м2 × 1 000 000 м2 = 8,5 км2

Как найти площадь зная периметр квадрата, прямоугольника, многоугольника, треугольника

Затеяв ремонт, необходимо в первую очередь иметь план действий и рассчитать свой бюджет. Только при грамотной планировке можно добиться качественной работы в короткие сроки. Если вы собираетесь сделать ремонт своего потолка, то необходимо сделать необходимые замеры.

встает вопрос можно ли узнать периметр, зная при этом площадь? Рассмотрим этот вопрос повнимательнее, и постараемся найти периметр прямоугольника.

Данные необходимые для того чтобы найти периметр

Сумма всех сторон прямоугольника называется периметром – это еще мы уяснили из курса арифметики начальных классов. Как видно из условия необходимо знать длину сторон. Площадь же – результат умножения двух сторон, в этом случае так же необходимо знать длину сторон. И в первом и во втором случае обязательным условием является знание длин сторон А и В.

Как же через показатель площади найти у прямоугольника периметр? Тут может быть два варианта: первый, если наш прямоугольник с равными сторонами, то есть квадрат, а второй, если длина сторон разная.

При условии, что потолок квадратный то найти периметр очень просто. Зная формулу нахождения площади квадрата, можно выяснить найти длину всех сторон, ведь они у квадрата одинаковые.

Довольно простой способ, который позволит посчитать периметр квадратного потолка. Квадратный потолок будет отличаться тем что, при большом показателе периметра будет относительно не большие площади. Однако квадратные потолки – это довольно редкий случай. Как правило, такие помещения не очень смотрятся, поэтому наиболее распространенные являются прямоугольные потолки.

Можно ли также найти периметр не квадратного прямоугольника?

Данный способ для прямоугольника с разными сторонами не подходит. Ведь вариантов разности сторон может быть до бесконечности много. И тут для определения периметра обязательным условием является знание хотя бы одной из сторон и площади.

Площадь = длина первой стороны умножается на длину второй стороны

Исходя из этой формулы, зная площадь найти две неизвестные стороны прямоугольника невозможно, но возможно выяснить длину одной стороны, если есть длина первой. Так если площадь прямоугольника 10 квадратных метров, а длина одной из сторон 2 метра, то можно посчитать

10 = 2 умножить на длину неизвестной стороны, следовательно, неизвестная сторона = 10 разделить на 2. Получаем ответ 5 метров.

Периметр = ( 5 + 2 ) * 2. Периметр такого прямоугольника будет 14 метров.

Использование подобных услуг – это очень простой способ решения нудной проблемы ремонта потолков. Вы получаете компетентную помощь от высококвалифицированной бригады мастеров, которые имеют большой опыт работы. А подписывая с ними контракт, вы страхуете себя от ненужных проблем, которые порою бывают из-за недопонимания.

Договоры о сотрудничестве содержат все нюансы работы, и выполняются в соответствии с законом.

При планировании бюджета на ремонт потолка, после проведенных расчетов необходимо закупить расходные материалы. Рекомендуется покупать немного больше требуемого объема материалов, так как бывают случаи с неожиданным результатом.

Так хорошо будет брать запас в 15 процентов – это оптимальный объем. Но еще более приемлемым будет заказать ремонт потолков под ключ, ведь в этом случае нет надобности беспокоиться о закупках.

Мастера сами предложат выбрать материалы для ремонта, после того как выбор был сделан они привезут и сделают ремонт. Как правило, у них налажена система логистики, поэтому с доставкой не возникает проблем.

Нахождение сторон прямоугольника при известных периметре и площади

Рассмотрим первую задачу:

Так как периметр прямоугольника – это удвоенное произведение суммы двух сторон прямоугольника, то мы можем найти эту сумму, разделив значение периметра на 2:

А дальше мы рассуждаем так.

Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – четное число, то очевидно, что прямоугольник с максимально возможным значением площади при сумме его двух сторон, равной 12, – это квадрат со стороной \( <\color12 : 2 = 6>\) см.

Тогда площадь этого квадрата равна

По условию нашей задачи площадь прямоугольника составляет 32 см2. Находим разницу между полученной площадью квадрата и заданной площадью прямоугольника.

Это значит, что нам нужно изменить стороны рассматриваемого квадрата со стороной 6 см так, чтобы уменьшилась его площадь, но не изменился периметр.

Так как квадрат имеет самую большую площадь среди прямоугольников с одинаковым периметром, то для уменьшения площади нам нужно увеличить разницу между его длиной и шириной. То есть, ширину уменьшить, а длину увеличить на одно и то же число.

Площадь 4 см2 – это квадрат со стороной 2 см. Это и есть нужное нам число.

Тогда, ширина искомого прямоугольника будет равна:

Проверим найденные длины сторон, определив периметр и площадь полученного прямоугольника:

Теперь рассмотрим вторую задачу.

Находим полупериметр, то есть, сумму двух сторон прямоугольника.

Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – нечетное число, значит, нам нужен такой прямоугольник, разница между значениями ширины и длины которого в натуральных числах минимальна, то есть, единица. Это прямоугольник со сторонами 11 и 12, т.к. \( <\color23=11+12>\).

Разница между полученной площадью и заданной по условию задачи составляет:

6 см2 – это площадь прямоугольника со сторонами 2 и 3 см. Чтобы уменьшить площадь нашего прямоугольника со сторонами 11 см и 12 см, нужно увеличить разницу между значениями этих сторон, а именно, уменьшить его короткую сторону, то есть, ширину. При этом длину также нужно увеличить на это же число, чтобы сохранить значение периметра.

Для этого ширину 11 мы уменьшаем на одноименное значение, то есть, тоже на ширину прямоугольника с площадью 6 см2, а именно, на 2.

Кстати, подумайте и напишите в комментарии к этой статье, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью (например, в этой задаче как прямоугольник 2 на 3, а не 1 на 6, а в первой – как квадрат 2 на 2, а не прямоугольник 1 на 4), и почему ширину уменьшаем именно на ширину (в этой задаче 11 – 2, а не 11 – 3).

Находим ширину искомого прямоугольника:

Длину нужно увеличить также на это число, чтобы не изменился периметр прямоугольника:

И эта задача решена тоже верно.

На этом все. Не забудьте написать в комментарии ответы на вопросы, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью, и почему ширину уменьшаем именно на ширину.

Вам также пригодится:

Текстовые задачи в начальной школе – так ли трудно научиться их решать?

Как научить ребенка преодолевать трудности?

6 правил, которые научат ребенка собранности

Источник

Как найти площадь и периметр квадрата

О том, что такое квадрат, многие помнят из школьного курса. Этот четырехугольник, который является правильным, имеет абсолютно равные углы и стороны. Оглянувшись вокруг, можно заметить, что нас окружает множество квадратов. Каждый день мы сталкиваемся с ними, и порой возникает необходимость найти площадь и периметр этой геометрической фигуры. Вычисление этих значений не принесет труда, если уделить несколько минут времени для просмотра данного видео урока, объясняющего простые правила проведения расчетов.

Обучающее видео “Как найти площадь и периметр квадрата”

Что необходимо знать о квадрате?

Прежде чем приступать к проведению вычислений, необходимо знать некоторые важные сведения об этой фигуре, среди которых:

Как найти площадь квадрата?

Вычисление площади данной фигуры можно просто и легко объяснить на примере:

Как найти периметр квадрата?

Зная, что все стороны данного прямоугольника равны, необходимо сделать следующие манипуляции, чтобы вычислить его периметр:

Все формулы и исчисления, приведенные в рамках данной статьи, применимы для любого прямоугольника. Важно помнить, что когда речь идет о других прямоугольниках, которые не являются правильными, значение сторон будет разным, например 4 и 8 метров. Это означает, что для нахождения площади такого прямоугольника необходимо будет умножать разные по значению стороны фигуры, а не одинаковые.

Необходимо помнить и то, что площадь измеряется в квадратных, а периметр в простых метрах. Если периметр нарисовать в виде одной длинной линии, то его значение не изменится, что говорит о том, что исчисления проводятся в одномерном пространстве.

Площадь измеряется в двухмерном пространстве, о чем говорят квадратные метры, которые мы получаем, умножив метры на метры. Площадь является индикатором наполненности геометрической фигуры, и говорит нам о том, сколько воображаемого покрытия необходимо для того чтобы заполнить квадрат или другой прямоугольник.

Простые объяснения видео урока позволят быстро вычислить площадь и периметр не только квадрата, но и любого прямоугольника. Данные знания школьного курса будут полезны во время ремонта дома или на садовом участке.

Источник

«Периметр квадрата». 2-й класс

Класс: 2

Цели урока:

Формирование универсальных учебных действий:

Технологии: Технология проблемного диалога.

Оборудование:

Ход урока

Деятельность учителя

Деятельность ученика

Ресурсы

Модули

Мотивационный этап.

Проверить ранее изученное, выйти на тему урока, создать мотивацию у учащихся, пробудить интерес.

1. Организационный момент: Приветствие (диагностика эмоционального настроения)

– Ребята повернитесь друг к другу и пожелайте всего хорошего, пожмите друг другу руки, поменяйтесь местами и повторите тоже самое.

Выполняют задание обмениваются пожеланиями

Видеоролик (у автора).

Новые подходы в преподавании и обучении

2. «Логическая разминка »

Быстро дают ответы на вопросы

Делятся на отвечают на вопросы

3. «Идеальный опрос»

– Кто прочитает наизусть 4 столбик Таблицы умножения?

4. «Математический диктант»

5. Разделение на группы по загадкам.

Отгадывают загадки и садятся в группу по соответствующей фигуре.

Прикатилось колесо,
Ведь похожее оно,
Как наглядная натура
Лишь на круглую фигуру.
Догадался, милый друг?
Ну, конечно, это … (круг).

Я фигура – хоть куда,
Очень ровная всегда,
Все углы во мне равны
И четыре стороны.
Кубик – мой любимый брат,
Потому что …. (квадрат)

Он похожий на яйцо
Или на твое лицо.
Вот такая есть окружность –
Очень странная наружность:
Круг приплюснутым стал.
Получился вдруг…. (овал).

Под линейку я рисую
Очень ровную, простую
Всем заметную черту.
Как фигуру назову?
Не спеши, а рассуждай
И ответ скорее дай. (Линия)

делятся на группы

Отвечают высказывают мнение

6. Повторение правил работы в группах. Выбор спикера и контролера

называют правила работы в группе

7. «Вопросы из бочонка»

Вытаскивают вопросы, обсуждают в группе. Один отвечает.

8. «Отсроченная отгадка»

Чтобы определить тему урока решите данные примеры, ответьте какое слово получилось?

Сегодня мы научимся находить периметр прямоугольника и квадрата?

– А что такое периметр?

– Как находить периметр? Попробуем разобраться вместе.

Новые подходы в преподавании и обученииНовый материал.

9. «Лаборатория открытий»

1. Дается задание в карточке, группа обсуждает приходит к выводу записывают формулу на плакате. Представитель из группы защищает.

Итак еще раз сделаем вывод как найти Р квадрата, прямоугольника?

Работают в группеСовершенствование критического мышления

2. Работа по учебнику с 132 (отработка умений)

№2,4,6 (самопроверка по ключу)

10. Работа с доски на повторение

В магазине продаются детские игрушки. Кукла стоит 30 рублей, а машинка на 6 рублей дороже. Сколько стоит машинка?

Новые подходы в преподавании и обучении

Рефлексивный этап.

Закрепление изученного материала, систематизация знаний, контроль знаний

12. Рефлексия

Тест-игра «Да – нет»

(если «Да» – хлопаем в ладоши, если «нет» – топаем ногами.)

13. Подведение итогов работы на уроке.

Отвечают на вопросы

Оценивание в обучении

14. Самооценка «Светофор»

Напишите на листочках свое имя и прикрепите к цвету светофора

15. Дома: Печатная тетрадь.с.55 №1, №2

Источник

Как найти периметр квадрата, если известна его площадь

Квадрат представляет собой положительный четырехугольник (либо ромб), в котором все углы являются прямыми, а стороны равны между собой. Как и у всякого другого верного многоугольника, у квадрата дозволено высчитать периметр и площадь. Если площадь квадрата теснее знаменита, то обнаружить его стороны, а после этого и периметр не составит труда.

Инструкция

Совет 2: Как обнаружить сторону квадрата

Зачастую в геометрических задачах требуется обнаружить длину стороны квадрата, если вестимы другие его параметры – такие, как площадь, диагональ либо периметр.

Вам понадобится

Инструкция

1. Если вестима площадь квадрата, то для того, дабы обнаружить сторону квадрата, нужно извлечь квадратный корень из числового значения площади (потому что площадь квадрата равняется квадрату его стороны):a=?S, гдеa – длина стороны квадрата;S – площадь квадрата.Единицей измерения стороны квадрата будет являться линейная единица измерения длины, соответствующая единице измерения площади. Скажем, если площадь квадрата дана в сантиметрах квадратных, то длина его стороны получится примитивно в сантиметрах.Пример:Площадь квадрата составляет 9 квадратных метров.Обнаружить длину стороны квадрата.Решение:a=?9=3Ответ:Сторона квадрата равняется 3 метрам.

2. В том случае, когда знаменит периметр квадрата, для определения длины стороны необходимо числовое значение периметра поделить на четыре (потому что квадрат имеет четыре стороны идентичной длины):a=P/4, где:a – длина стороны квадрата;P – периметр квадрата.Единицей измерения стороны квадрата будет являться та же самая линейная единица измерения длины как и у периметра. Скажем, если периметр квадрата задан в сантиметрах, то длина его стороны также получится в сантиметрах.Пример:Периметр квадрата составляет 20 метров.Обнаружить длину стороны квадрата.Решение:a=20/4=5Ответ:Длина стороны квадрата равняется 5 метрам.

3. Если знаменита длина диагонали квадрата, до длина его стороны будет равняться длине его диагонали, поделенной на корень квадратный из 2 (по теореме Пифагора, потому что смежные стороны квадрата и диагональ составляют прямоугольный равнобедренный треугольник):a=d/?2(т.к. a^2+a^2=d^2), где:a – длина стороны квадрата;d – длина диагонали квадрата.Единицей измерения стороны квадрата будет являться единица измерения длины та же самая, что и у диагонали. Скажем, если диагональ квадрата измерена в сантиметрах, то и длина его стороны получится в сантиметрах.Пример:Диагональ квадрата равняется 10 метров.Обнаружить длину стороны квадрата.Решение:a=10/?2, либо примерно: 7,071Ответ:Длина стороны квадрата равняется 10/?2, либо приблизительно 1,071 метра.

Совет 3: Как находить периметр квадрата

Инструкция

Видео по теме

Совет 4: Как обнаружить длину квадрата

Периметром называют всеобщую длину границы фигуры почаще каждого на плоскости. Квадрат — положительный четырехугольник либо ромб, у которого все углы прямые, либо параллелограмм, у которого все стороны и углы равны.

Вам понадобится

Инструкция

1. Периметр квадрата равен сумме длин его сторон. Потому что квадрат, по своей сути, есть четырехугольник, то и сторон у него четыре, а значит периметр равен сумме длин четырех сторон либо P = a+b+c+d.

2. Квадрат, как видно из определения, верная геометрическая фигура, а это значит, что все его стороны равны. Значит a=b=c=d. Следственно P = a+a+a+a либо P = 4*a.

Видео по теме

Обратите внимание!
Периметр квадрата величина неизменно правильная, как и любая иная длина.

Полезный совет
Аналогичным образом дозволено обнаружить и периметр ромба, потому что квадрат является частным случаем ромба с прямыми углами.

Совет 5: Как высчитывать периметр

Периметр характеризует длину замкнутого силуэта. Как и площадь, он может быть обнаружен по иным величинам, приведенным в условии задачи. Задачи на нахождении периметра крайне зачастую встречаются в школьном курсе математики.

Инструкция

1. Зная периметр и сторону фигуры, дозволено обнаружить иную ее сторону, а также площадь. Сам же периметр, в свою очередь, может быть обнаружен по нескольким заданным сторонам либо по углу и сторонам, в зависимости от условий задачи. Также в ряде случаев его выражают через площадь. Особенно примитивно находится периметр прямоугольника. Начертите прямоугольник с одной из сторон, равной а, и диагональю, равной d. Зная эти две величины, обнаружьте по теореме Пифагора иную его сторону, которая является шириной прямоугольника. Обнаружив ширину прямоугольника, вычислите его периметр дальнейшим образом: p=2(a+b). Эта формула объективна для всех прямоугольников, от того что у всякого из них четыре стороны.

2. Обратите внимание на тот факт, что периметр треугольника в большинстве задач находят при наличии информации правда бы об одном его угле. Впрочем, имеются и задачи, в которых все стороны треугольник знамениты, и тогда периметр может быть вычислен простым суммированием, без применения тригонометрических вычислений: p=a+b+c, где a, b и c – стороны. Но такие задачи встречаются в учебниках редко, от того что метод их решения явствен. Больше трудные задачи по нахождению периметра треугольника решайте поэтапно. Скажем, начертите равнобедренный треугольник, у которого знамениты основание и угол при нем. Для того дабы обнаружить его периметр, сначала обнаружьте стороны a и b дальнейшим образом: b=c/2cos?. От того что a=b (треугольник равнобедренный), сделайте дальнейший итог: a=b=c/2cos?.

3. Периметр многоугольника вычисляйте аналогичным образом, складывая длины всех его сторон: p=a+b+c+d+e+f и так дальше. Если многоугольник положительный и вписан в окружность либо описан около нее, вычислите длину одной из его сторон, а после этого умножьте на их число. Скажем, дабы обнаружить стороны шестиугольника, вписанного в окружность, действуйте дальнейшим образом: a=R, где a – сторона шестиугольника, равная радиусу описанной окружности. Соответственно, если шестиугольник верный, то его периметр равен: p=6a=6R. Если окружность вписана в шестиугольник, то сторона последнего равна: a=2r?3/3. Соответственно, периметр такой фигуры обнаружьте дальнейшим образом: p=12r?3/3.

Совет 6: Как вычислить периметр квадрата

Хоть слово «периметр» и случилось от греческого обозначения окружности, им принято называть суммарную длину границ всякий плоской геометрической фигуры, включая квадрат. Вычисление этого параметра, как водится, трудности не представляет и может быть осуществлено несколькими методами, в зависимости от знаменитых начальных данных.

Инструкция

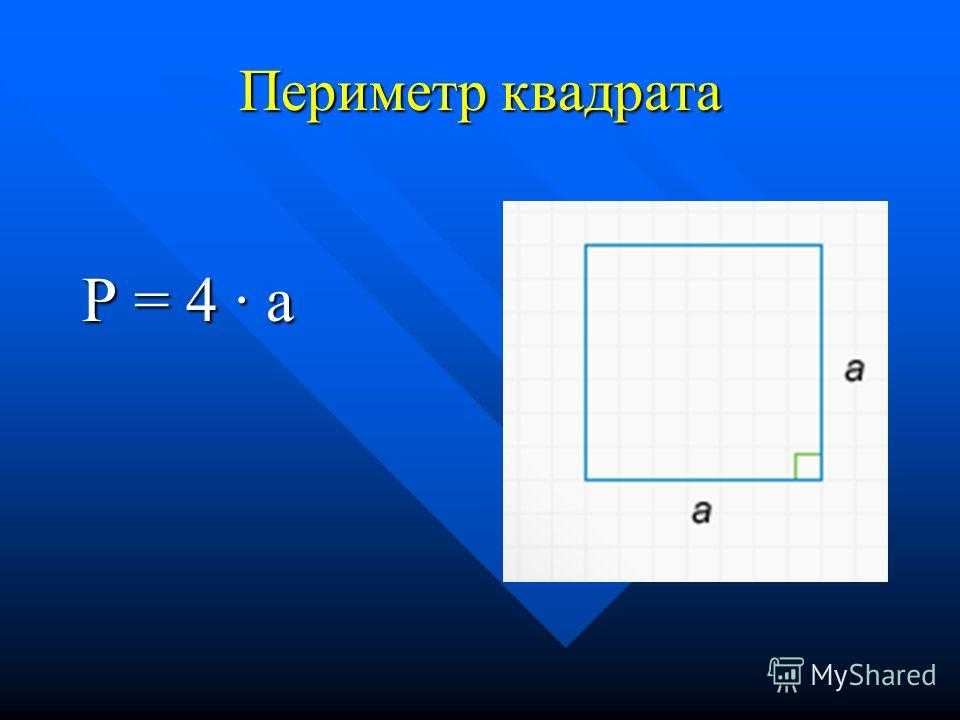
1. Если вестима длина стороны квадрата (t), то для нахождения его периметра (p) примитивно увеличьте эту величину в четыре раза: p=4*t.

2. Если длина стороны незнакома, но в условиях задачи дана длина диагонали (c), то этого довольно для вычисления длины сторон, а следственно и периметра (p) многоугольника. Используйте теорему Пифагора, которая заявляет, что квадрат длины длинной стороны прямоугольного треугольника (гипотенузы) равен сумме квадратов длин коротких сторон (катетов). В прямоугольном треугольнике, составленном из 2-х смежных сторон квадрата и соединяющего их крайние точки отрезка, гипотенуза совпадает с диагональю четырехугольника. Из этого вытекает, что длина стороны квадрата равна отношению длины диагонали к квадратному корню из двойки. Используйте это выражение в формуле для вычисления периметра из предыдущего шага: p=4*c/?2.

3. Если дана лишь площадь (S) ограниченного периметром квадрата участка плоскости, то и этого будет довольно, дабы определить длину одной стороны. Потому что площадь всякого прямоугольника равна произведению длин его смежных сторон, то для нахождения периметра (p) извлеките квадратный корень из площади, а итог увеличьте в четыре раза: p=4*?S.

4. Если знаменит радиус описанной вблизи квадрата окружности (R), то для нахождения периметра многоугольника (p) умножьте его на восемь и поделите полученный итог на квадратный корень из двойки: p=8*R/?2.

5. Если окружность, радиус которой вестим, вписана в квадрат, то вычисляйте его периметр (p) простым умножением радиуса (r) на восьмерку: P=8*r.

6. Если рассматриваемый квадрат в условиях задачи описан координатами своих вершин, то для вычисления периметра вам потребуются данные лишь о 2-х вершинах, принадлежащих к одной из сторон фигуры. Определите длину этой стороны, исходя из все той-же теоремы Пифагора для треугольника, составленного из нее самой и ее проекций на оси координат, а полученный итог увеличьте в четыре раза. Потому что длины проекций на координатные оси равны модулю разностей соответствующих координат 2-х точек (X?;Y? и X?;Y?), то формулу дозволено записать так: p=4*?((X?-X?)?+(Y?-Y?)?).

Совет 7: Что такое периметр

Периметром в всеобщем случае называют длину линии, которая ограничивает замкнутую фигуру. Для многоугольников периметром является сумма всех длин сторон. Эту величину дозволено измерить, а для многих фигур и легко рассчитать, если вестимы длины соответствующих элементов.

Вам понадобится

Инструкция

1. Дабы измерить периметр произвольного многоугольника, измерьте при помощи линейки либо иным измерительным прибором все его стороны, а после этого обнаружьте их сумму. Если дан четырехугольник со сторонами 5, 3, 7 и 4 см, которые измерены линейкой, обнаружьте периметр, сложив их совместно Р=5+3+7+4=19 см.

2. Если же фигура произвольная и включает в себя не только прямые линии, то измерьте ее периметр традиционной веревкой либо ниткой. Для этого расположите ее так, дабы она верно повторяла все линии, ограничивающие фигуру, и сделайте на ней отметку, если дозволено, примитивно обрежьте ее дабы избежать путаницы. После этого при помощи рулетки либо линейки, измерьте длину нитки, она и будет равна периметру данной фигуры. Непременно следите за тем, дабы нить максимально верно повторяла линию для большей точности итога.

3. Периметр трудной геометрической фигуры измеряйте роликовым дальномером (курвиметром). Для этого не линии намечается точка, в которую устанавливается ролик дальномера и прокатывается по ней, до возвращения в начальную точку. Дистанция, измеренная роликовым дальномером, и будет равна периметру фигуры.

4. Периметр некоторых геометрических фигур вычисляйте. Скажем, дабы обнаружить периметр всякого положительного многоугольника (выпуклого многоугольника, стороны которого равны), длину стороны умножьте на число углов либо сторон (они равны). Дабы обнаружить периметр верного треугольника со стороной 4 см умножьте это число на 3 (Р=4?3=12 см).

Совет 8: Как обнаружить периметр верного многоугольника

Периметром многоугольника называют замкнутую ломаную линию, составленную из всех его сторон. Нахождение длины этого параметра сводится к суммированию длин сторон. Если все отрезки, образующие периметр такой двухмерной геометрической фигуры, имеют идентичные размеры, многоугольник именуется верным. В этом случае вычисление периметра гораздо упрощается.

Инструкция

1. В самом простом случае, когда вестимы длина стороны (а) верного многоугольника и число вершин (n) в нем, для вычисления длины периметра (Р) примитивно перемножьте эти две величины: Р = а*n. Скажем, длина периметра верного шестиугольника со стороной в 15 см должна быть равна 15*6=90 см.

2. Вычислить периметр такого многоугольника по вестимому радиусу (R) описанной около него окружности тоже допустимо. Для этого придется вначале выразить длину стороны с применением радиуса и числа вершин (n), а после этого умножить полученную величину на число сторон. Дабы рассчитать длину стороны умножьте радиус на синус числа Пи, поделенного на число вершин, а итог удвойте: R*sin(?/n)*2. Если вам комфортнее вычислять тригонометрическую функцию в градусах, замените число Пи на 180°: R*sin(180°/n)*2. Периметр вычислите умножением полученной величины на число вершин: Р = R*sin(?/n)*2*n = R*sin(180°/n)*2*n. Скажем, если шестиугольник вписан в круг с радиусом 50 см, его периметр будет иметь длину 50*sin(180°/6)*2*6 = 50*0,5*12 = 300 см.

Совет 9: Как обнаружить площадь и периметр квадрата

Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон идентичной длины и четырех прямых углов, всякий из которых равен 90°. Определение площади либо периметра четырехугольника, причем всякого, требуется не только при решении задач по геометрии, но и в повседневной жизни. Эти знания могут стать пригодными, скажем, во время ремонта при расчете необходимого числа материалов – покрытий для пола, стен либо потолка, а также для разбивки газонов и грядок и т.д.

Инструкция

1. Для определения площади квадрата умножьте величину длины на величину ширины. Потому что в квадрате длина и ширина идентичны, то значение одной стороны довольно построить в квадрат. Таким образом, площадь квадрата равна длине его стороны, возведенной в квадрат. Единицей измерения площади могут быть квадратные миллиметры, сантиметры, дециметры, метры, километры.Дабы определить площадь квадрата, дозволено воспользоваться формулойS = aa, где S – площадь квадрата,а – сторона квадрата.

2. Пример № 1. Комната имеет форму квадрата. Сколько ламината (в кв.м) понадобится для того, дабы всецело покрыть пол, если длина одной стороны комнаты составляет 5 метров.Запишите формулу: S = aa. Подставьте в нее указанные в условии данные.Потому что а = 5 м, следственно, площадь будет равнаS (комнаты) = 5х5= 25 кв.м, значит, и S (ламината) = 25 кв.м.

3. Периметр представляет собой всеобщую длину границы фигуры. В квадрате периметр – это длина всех четырех, причем идентичных, сторон. То есть, периметр квадрата представляет собой сумму всех его четырех сторон. Дабы вычислить периметр квадрата, довольно знать длину одной его стороны. Измеряется периметр в миллиметрах, сантиметрах, дециметрах, метрах, километрах.Для определения периметра имеется формула:P = a + а + а + а илиP = 4a, гдеР – периметр,а – длина стороны.

4. Пример № 2. Для отделочных работ помещения в форме квадрата требуются потолочные плинтуса. Вычислите всеобщую длину (периметр) плинтусов, если величина одной стороны комнаты равна 6 метров. Запишите формулу P = 4a.Подставьте в нее указанные в условии данные:Р (комнаты) = 4 х 6 = 24 метра.Следственно, длина потолочных плинтусов тоже будет равна 24 метров.

Видео по теме

Обратите внимание!
Для квадрата объективны следующие определения:Квадрат – это прямоугольник, тот, что владеет равными между собой сторонами.Квадрат – это специальная разновидность ромба, у которого весь из углов равен 90 градусам.Являясь положительным четырехугольником, вокруг квадрата дозволено описать либо вписать окружность. Радиус вписанной в квадрат окружность дозволено обнаружить по формуле:R = t/2, где t – сторона квадрата.Если же окружность описана вокруг него, то ее радиус находится так:R = (?2*t)/2Исходя из данных формул, дозволено вывести новые для нахождения периметра квадрата:P = 8*R, где R – радиус вписанной окружности;P = 4*?2*R, где R – радиус описанной окружности.Квадрат является уникальной геометрической фигурой, от того что он безусловно симметричен, самостоятельно от того, как и где провести ось симметрии.

Источник

Квадрат. Периметр и площадь квадрата.

Рассмотрим фигуру она называеться квадрат.

Стороны AB, BC, CD, DA другое название они имеют ребра; углы A, B, C, D; второе название вершины, зеленим цветом обозначаются диагонали AD, BC. Диагонали в квадрате равны и точкой пересечения делятся пополам.

Периметр P=4•a, Площадь S=a·а

Свойства квадрата

1. Длины сторон квадрата равны.

2. Все углы квадрата прямые.

3. Противолежащие стороны квадрата параллельны друг другу AB∥CD,BC∥AD

4. Сумма всех углов квадрата равна 360 градусов ∠ABC+∠BCD+∠CDA+∠DAB=360​∘​​

5. Величина угла между диагональю и стороной равна 45 градусов ∠BAC=∠BCA=∠CAD=∠ACD=45​∘​​

6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.

7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.

8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.

Поделись с друзьями в социальных сетях:

Источник

Периметр квадрата и прямоугольника. Способы определения и примеры решения.

Свойства квадрата

Для подсчета плинтусов для завершения ремонта в квадратном помещении, необходимо знать длину комнаты. Для этого необходимо посчитать ее периметр.

Периметр

В переводе с греческого языка слово означает «измерять вокруг». Термин применим ко всем замкнутым фигурам: квадрату, окружности, прямоугольнику, треугольнику, трапеции и прочим. Знания по определению периметра элементарных фигур необходимы для решения сложных геометрических задач с объектами неправильной формы. Например, для расчета плинтусов в комнату планировкой типа «Г», или как еще называют, «сапожком», потребуется определить периметр квадрата и прямоугольника. Ведь форма помещения состоит из этих элементарных фигур.

Общепринятое обозначение такой величины – буква Р. Каждой фигуре с учетом ее свойств присуща своя формула для определения периметра.

Свойства прямоугольника

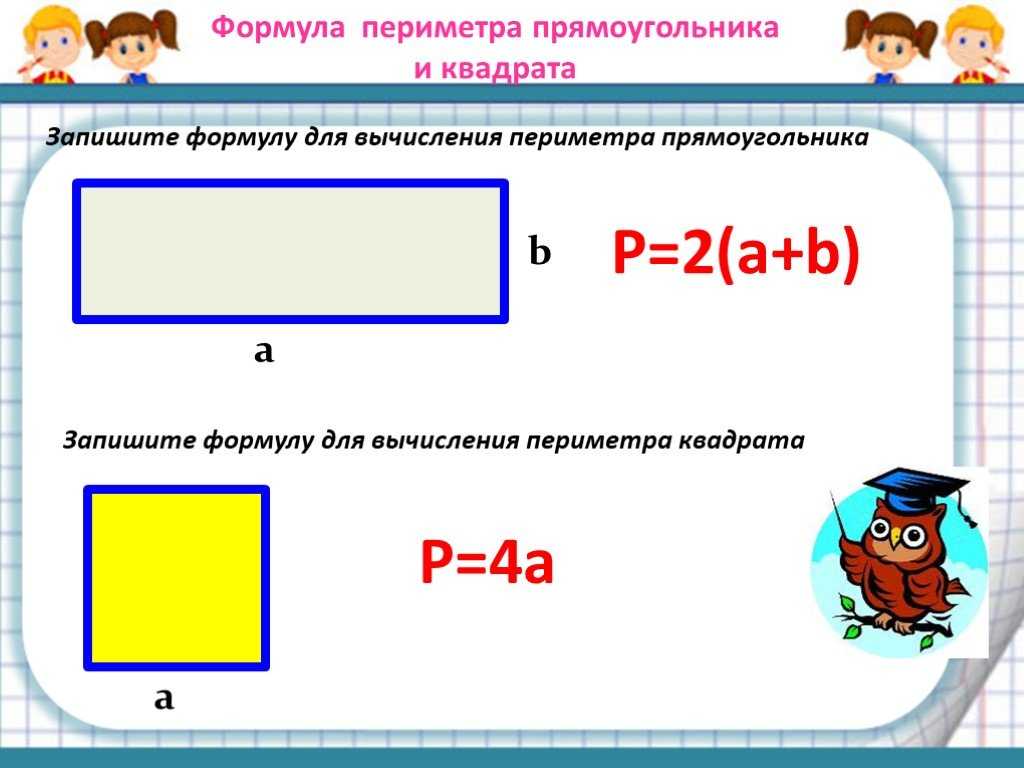
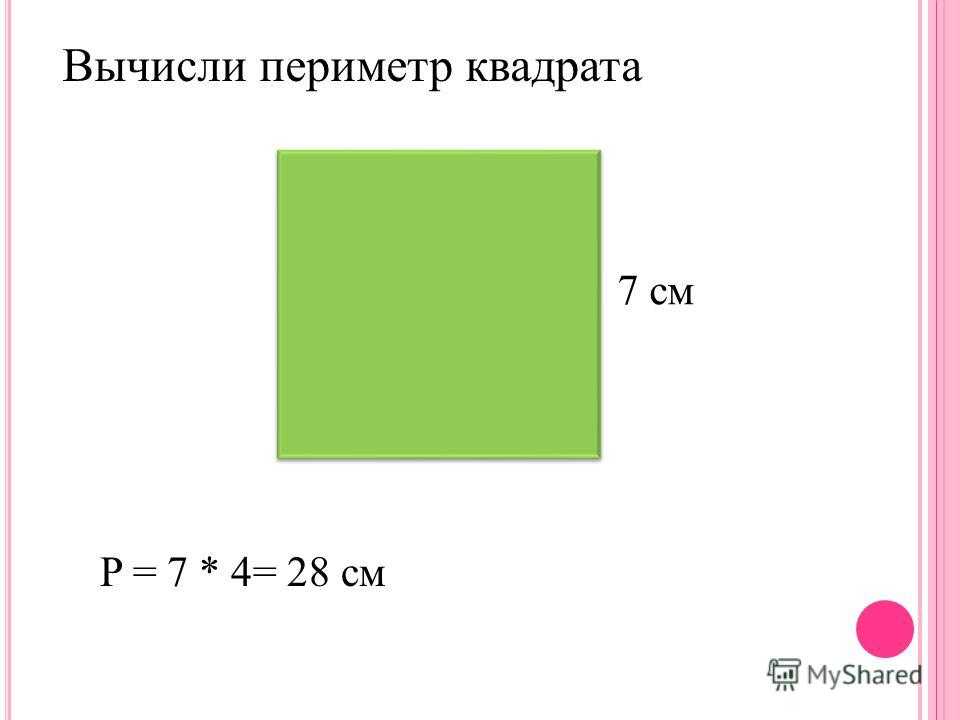
Периметр квадрата

В зависимости от установленных (известных) параметров квадрата, существуют разные формулы для определения его периметра. Простой задачей является расчет периметра при установленной длине его стороны (с). В этом случае Р=с+с+с+с или 4*с. Например, длина стороны квадрата 7 см, тогда периметр фигуры буде 28 см (4*7).

Квадрат и окружность

Из свойств рассматриваемой фигуры выплывает, что в квадрат можно вписать окружность и также ее описать вокруг фигуры.

Особенностью вписанной окружности является деление сторон квадрата пополам. Поэтому радиус равняется половине длины стороны квадрата. Тогда сторона с=2*радиус. Периметр квадрата в этом случае равен 4*2*радиус или 8 радиусам окружности.

Периметр прямоугольника

Если неизвестна ни одна из сторон, тогда в дело вступают знания тригонометрии: синусы, косинусы и другие функции.

Нахождение периметра по описанной окружности и известному диаметру сводится к тому, что диаметр равен длине диагонали фигуры. Дальше решение задачи определяется по наличию известных величин. Если даны углы, тогда через тригонометрические функции. Если дана сторона, ответ будет найден через теорему Пифагора.

Прямоугольник и тригонометрические функции

Для наглядности приведен пример решения задачи. Дано: прямоугольник АВСД; длина диагонали (d) 20 см; угол ф – 30°. Найти периметр фигуры.

Из тригонометрии необходимо вспомнить следующее: синус угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе. Синус 30° (существуют таблицы, по которым можно определить значения тригонометрических функций для правильных углов) равен 1/2. Получается 1/2 = отношению в к d. Неизвестная величина в будет равна d/2=20/2=10 см.

Для расчета периметра следует найти вторую сторону фигуры. Можно через теорему Пифагора, так как известны длины гипотенузы и одного из катетов или опять через отношение сторон для косинуса угла.

Косинус угла ф выражается как отношение прилежащего катета к гипотенузе и равен √3/2.

√3/2=n/d, n=(d*√3)/2 или 10*√3. После извлечения корня из 3, получаем длину стороны треугольника: 10*1,73=17,3 см.

Периметр равен 2(17,3+10)=2*27,3=54,6 см.

Периметр и отношение сторон

В школьной программе встречаются задачи по геометрии, когда длины сторон прямоугольника выражены их отношением друг к другу. Рассмотрение решения подобной задачи представлено ниже.

Известно, что сумма длин всех сторон прямоугольника, то есть его периметр, равен 84 см. Отношение длины (д) к ширине (ш) – 3:2. Найти стороны фигуры.

Решение: пусть длина будет 3х, а ширина 2х, согласно соотношению из условия задачи. Формула периметра прямоугольника с полученными данными длин сторон будет следующей: 3х+3х+2х+2х = 84. Далее, 10х = 84, х=8,4 см. Подставив х в выражение длины и ширины прямоугольника, можно найти искомые величины. Длина будет: 3*8,4 = 25,2 см; ширина: 2*8,4 = 16,8 см.

Статья посвящена решению наиболее часто встречаемых задач в школьной программе. И это далеко не все способы нахождения периметра квадрата и прямоугольника.

Источник

Как найти периметр, зная площадь квадрата

Квадрат – положительный четырехугольник, у которого все стороны равны, и все углы прямые. Периметром квадрата именуется сумма длин всех его сторон, а площадью – произведение 2-х сторон либо квадрат одной стороны. Исходя из знаменитых соотношений, через один параметр дозволено вычислить иной.

Инструкция

3. Обнаружить периметр квадрата через площадь дозволено, не прибегая к лишнему действию (вычислению стороны). Для этого воспользуйтесь формулой вычисления периметра, объективной только для квадрата P = 4*?S.

4. Решение 2. Обнаружьте периметр квадрата : P = 4*?S, P = 4*?36см?, P = 24 см.Результат: периметр квадрата равен 24 см.

Совет 2: Как обнаружить периметр в математике

Периметр – это суммарная длина сторон геометрической фигуры. Но если возникнет надобность стремительно рассчитать периметр чего-либо (скажем, во время ремонта либо строительства), не всякий сумеет это сделать с легкостью. Припомним основные правила для вычисления периметра.

Вам понадобится

Инструкция

1. Периметр для квадратов и ромбов рассчитывается по формуле Р=4а, где а – это длина одной стороны фигуры. От того что все ее стороны равны, измерьте одну сторону и полученное число умножьте на число сторон, т.е. на четыре.

2. Для прямоугольников и параллелограммов, т.к. у них равны не все стороны, а только противоположные, существует иная формула: Р=2(а+b). Под а и b подразумеваются смежные стороны. Их всеобщую длину умножьте на два.

3. Дабы получить периметр трапеции суммируйте длины всех ее сторон (у трапеции они не идентичны), т.е. в данном случае воспользуйтесь формулой P=а+b+с+d.

4. Всеобщая формула для расчета периметра треугольника выглядит как Р=а+b+с, т.е. вы обязаны будете сложить длины сторон треугольника. Но от того что треугольники бывают различных видов, то вычисления могут производиться напротив. Скажем, если вам вестимо, что измеряемый треугольник – равносторонний, то умножьте длину его стороны на три.

5. Больше трудно вычислить периметр круга (длина окружности, р). Вестимо, что длина окружности составляет 317 от длины диаметра круга (d). В математике это соотношение принято обозначать буквой “Пи” (?) и усреднено считать как 3,14. Получается, что рd=?. Отсель p=?d=2?r, где r – это радиус имеющейся окружности. Следственно, дабы вычислить периметр круга, вам нужно вначале обнаружить радиус окружности, а после этого умножить это число на 2 и на 3,14.

6. Если же у вас появилась надобность узнать периметр дуги, то для начала вам необходимо замерить две величины – длину радиуса дуги и центральный, т.е. образованный двумя радиусами (в градусах, n). Подставьте полученные величины в формулу p=Пrn180°.

Видео по теме

Совет 3: Как обнаружить сторону квадрата, если вестима его диагональ

Квадрат является одной из особенно примитивных геометрических фигур в плане вычисления его параметров – длин сторон и диагоналей, площади и периметра. Это определяется тем, что в различие от других многоугольников, неизменно вестимы величины всех его углов, а также довольно знать длину каждого одной стороны. Нахождение длины стороны квадрата по вестимой длине диагонали, как в всеобщем виде, так и с фактическими расчетами не представляет трудности.

Инструкция

4. Введите вестимую длину стороны, после этого нажмите клавишу со звездочкой и Enter – так вы исполните операцию возведения в квадрат. После этого нажмите клавишу с косой чертой, введите двойку и нажмите Enter. Позже этого щелкните кнопку с надписью sqrt и увидите желанную длину стороны квадрата – 10,606601717798212866012665431573 сантиметров.

Совет 4: Как обнаружить площадь, зная диаметр

Задачи на вычисление площади круга зачастую встречаются в школьном курсе геометрии. Дабы обнаружить площадь круга, нужно знать длину диаметра либо радиуса окружности, в которую он заключен.

Вам понадобится

Инструкция

2. Площадь круга равна произведению квадрата радиуса на число и вычисляется по формуле: S=?R^2, где S — площадь круга, R — длина радиуса окружности.

4. Площадь круга измеряется в единицах площади — мм2, см2, м2 и т.п. В каких единицах выражается полученная вами площадь круга, зависит от того, в каких единицах был дан диаметр окружности.

5. Если вам нужно вычислить площадь кольца, воспользуйтесь формулой: S=?(R-r)^2, где R, r – радиусы внешней и внутренней окружностей кольца соответственно.

Полезный совет
Существует Интернациональный день числа «пи», тот, что отмечается 14 марта. Точное время наступления триумфальной даты — 1 час 59 минут 26 секунд, согласно цифрам числа — 3,1415926…

Совет 5: Как обнаружить площадь и периметр квадрата

Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон идентичной длины и четырех прямых углов, всякий из которых равен 90°. Определение площади либо периметра четырехугольника, причем всякого, требуется не только при решении задач по геометрии, но и в повседневной жизни. Эти знания могут стать пригодными, скажем, во время ремонта при расчете необходимого числа материалов – покрытий для пола, стен либо потолка, а также для разбивки газонов и грядок и т.д.

Инструкция

1. Для определения площади квадрата умножьте величину длины на величину ширины. Потому что в квадрате длина и ширина идентичны, то значение одной стороны довольно построить в квадрат. Таким образом, площадь квадрата равна длине его стороны, возведенной в квадрат. Единицей измерения площади могут быть квадратные миллиметры, сантиметры, дециметры, метры, километры.Дабы определить площадь квадрата, дозволено воспользоваться формулойS = aa, где S – площадь квадрата,а – сторона квадрата.

2. Пример № 1. Комната имеет форму квадрата. Сколько ламината (в кв.м) понадобится для того, дабы всецело покрыть пол, если длина одной стороны комнаты составляет 5 метров.Запишите формулу: S = aa. Подставьте в нее указанные в условии данные.Потому что а = 5 м, следственно, площадь будет равнаS (комнаты) = 5х5= 25 кв.м, значит, и S (ламината) = 25 кв.м.

3. Периметр представляет собой всеобщую длину границы фигуры. В квадрате периметр – это длина всех четырех, причем идентичных, сторон. То есть, периметр квадрата представляет собой сумму всех его четырех сторон. Дабы вычислить периметр квадрата, довольно знать длину одной его стороны. Измеряется периметр в миллиметрах, сантиметрах, дециметрах, метрах, километрах.Для определения периметра имеется формула:P = a + а + а + а илиP = 4a, гдеР – периметр,а – длина стороны.

4. Пример № 2. Для отделочных работ помещения в форме квадрата требуются потолочные плинтуса. Вычислите всеобщую длину (периметр) плинтусов, если величина одной стороны комнаты равна 6 метров. Запишите формулу P = 4a.Подставьте в нее указанные в условии данные:Р (комнаты) = 4 х 6 = 24 метра.Следственно, длина потолочных плинтусов тоже будет равна 24 метров.

Видео по теме

Обратите внимание!
Пригодные свойства квадрата:Квадрат – верный четырехугольник, владеющий свойствами прямоугольника и ромба.Квадрат – прямоугольник, у которого все стороны равны.Квадрат – ромб, у которого все углы по 90 градусов.Квадрат – грань куба.Диагонали квадрата равны и пересекаются под прямым углом.Диагональ квадрата разбивает его на два равных прямоугольных треугольника и является гипотенузой к всем из этих треугольников.Диагональ квадрата – это диаметр описанной в фигуру окружности.

Источник

Три способа периметра квадрата

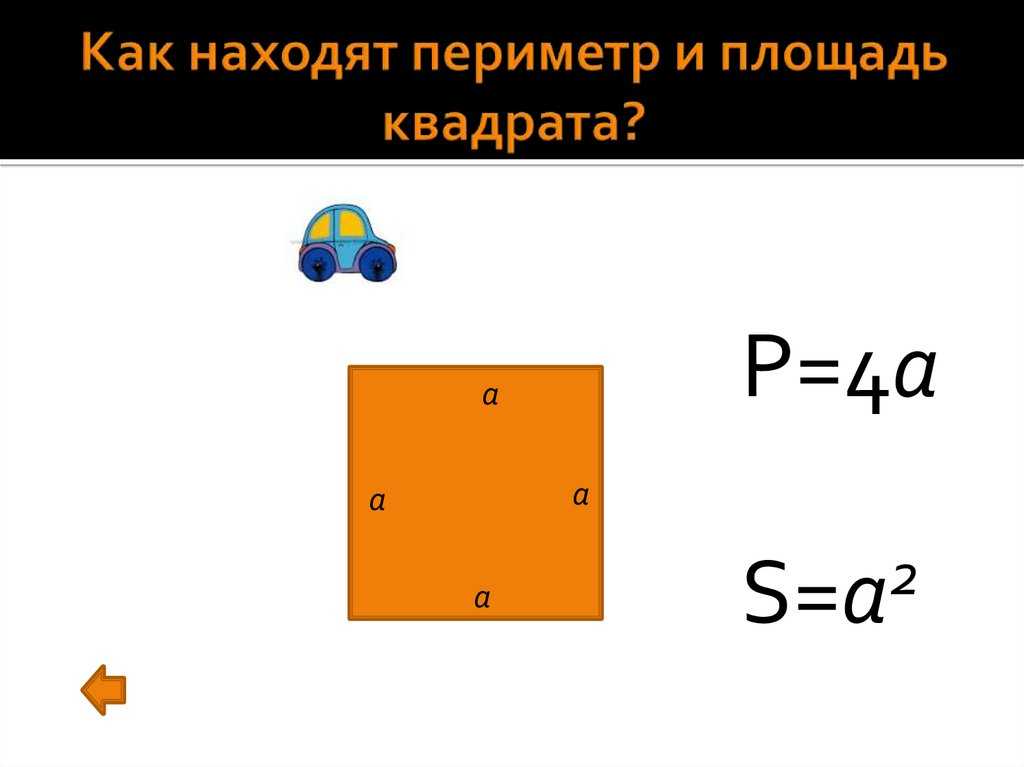
Как найти периметр квадрата

Что такое периметр квадрата

Квадрат — это правильный четырехугольник, все его стороны и углы равны.

Про него также говорят, что это частный случай прямоугольника или ромба.

Периметр квадрата — это сумма длин всех его сторон или произведение одной его стороны на 4.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Способы вычисления

Для вычисления периметра квадрата применяется несколько видов несложных формул.

По длине стороны

Самый простой способ, если известна величина одной из его сторон. Сразу вспоминаем, что мы имеем дело с правильным четырехугольником, и подставляем значение в уравнение:

где \(a\) — это сторона фигуры.

По длине диагонали

Если известна только диагональ правильного прямоугольника, формула для нахождения суммы всех его ребер будет выглядеть так:

что следует из соотношения длин стороны и диагонали \(d=a\sqrt2\)

По площади

Зная площадь фигуры, найти ее периметр можно так:

По радиусу описанной окружности

Радиус описанной вокруг квадрата окружности — это половина его диагонали. Формула для нахождения P в данном случае:

где R — радиус данной окружности.

По радиусу вписанной окружности

Радиус вписанной окружности — это половина величины ребра правильного прямоугольника. Таким образом, уравнение для нахождения P выглядит так:

где r — радиус вписанной окружности.

Найти P квадрата, если его ребро a равно 5 см.

Так как P = 4a, подставляем сюда известное значение, и получается \(P = 4\times5= 20\ см.\)

Узнать P правильного четырехугольника, если его диагональ d равна 6 см.

Используем формулу \(P\;=\;2d\sqrt2\) и подставляем известное значение. Получается: \(P = 2 * 6\sqrt2\ = 12\sqrt2\ см.\)

Ответ: \(12\sqrt2\ см.\)

Площадь квадрата равна 16 см². Каков периметр?

Известно, что 1/2 диагонали правильного прямоугольника составляет \(9\sqrt2\\ \) см. Вычислить P.

Дан квадрат и вписанная в него окружность. Половина стороны a фигуры равна 7 см, посчитать P.

Как найти периметр квадрата

О чем эта статья:

2 класс, 3 класс

Основные определения

Квадратом принято называть правильный четырёхугольник, у которого равны все углы и стороны. Это частный случай прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов.

Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра квадрата

Как находится периметр квадрата, всегда зависит от исходных данных. Рассмотрим две формулы, которые проходят 2 и 3 класс.

Если известна длина стороны

P = a + a + a + a, где a — сторона.

Так как все стороны фигуры равны, можно использовать формулу в таком виде: P = 4 * a

Если известна длина диагонали

P = d * 2 * √2, где d — диагональ.

Диагональ — это отрезок, который соединяет противоположные стороны фигуры.

Математика, как и любой другой предмет не сразу дается легко. Сложности могут возникать из-за неумения быстро делать простые арифметические действия — именно поэтому полезно практиковаться в решении примеров, как можно чаще. Давайте сделаем это прямо сейчас!

Занимайся изучением математики онлайн! Курсы по математике для учеников с 1 по 11 классы!

Решение задач

1. Найти периметр квадрата, диагональ которого равняется √4 см.

2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах

3. Периметр квадрата 48 см. Чему равна его сторона?

4. Периметр квадрата 20 см. Как найти его площадь?

Как найти периметр фигуры

О чем эта статья:

Определение периметра

Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра

Рассмотрим пять фигур.

Треугольник

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.

P = 3 * a, где a — длина стороны.

Квадрат и ромб

Периметр квадрата — это произведение длины стороны на четыре. Формула ромба выглядит идентично.

P = 4 * a, где a — длина стороны.

Прямоугольник и параллелограмм

Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно.

P = 2 * (a + b), где a — ширина, b — высота.

Записывайтесь на онлайн уроки по математике к лучшим преподавателям! Уроки для учеников с 1 по 11 классы!

Равнобедренная трапеция

Формула для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.

P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

Ответ: две другие стороны равны 17см.

Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга.

Нахождение периметра квадрата: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.

Формула вычисления периметра

По длине стороны

Периметр (P) квадрата равняется сумме длин его сторон.

P = a + a + a + a

Так как все стороны квадрата равны, формулу можно представить в виде произведения:

P = 4 ⋅ a

По длине диагонали

Периметр (P) квадрата равен произведению длины его диагонали на число 2√ 2 :

P = d ⋅ 2√ 2

Примеры задач

Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.

Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.

Задание 2
Найдите периметр квадрата, диагональ которого равняется √ 2 см.

Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √ 2 см ⋅ 2√ 2 = 4 см.

Решение 2:
Выразим длину стороны через диагональ:
a = d / √ 2 = √ 2 см / √ 2 = 1 см.

Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.

Периметр

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.

Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».

KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Разные способы © 2022
Внимание! Информация, опубликованная на сайте, носит исключительно ознакомительный характер и не является рекомендацией к применению.

Источник