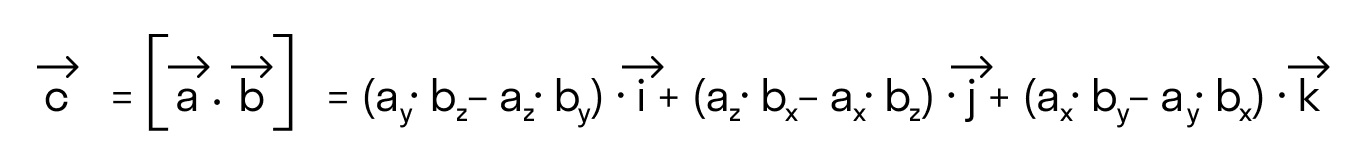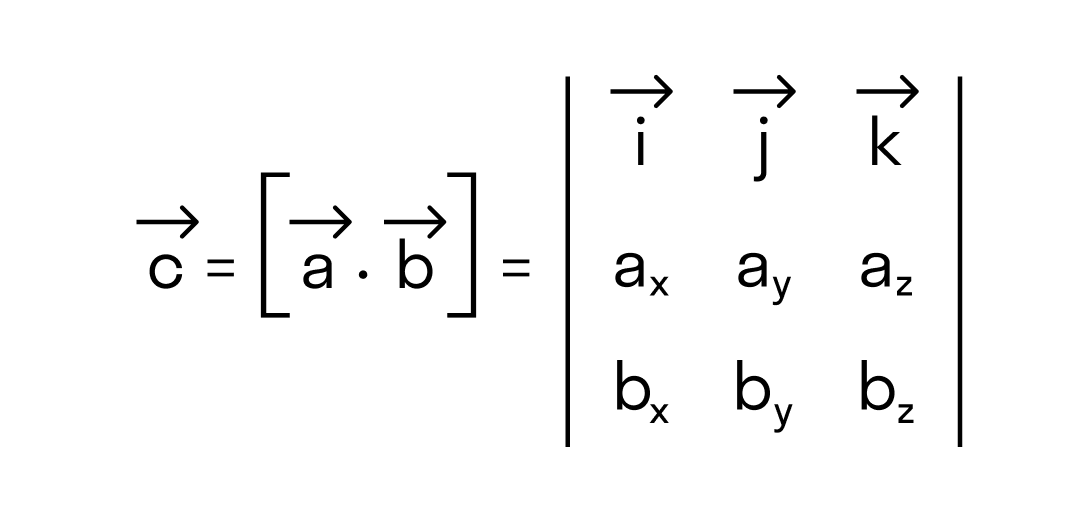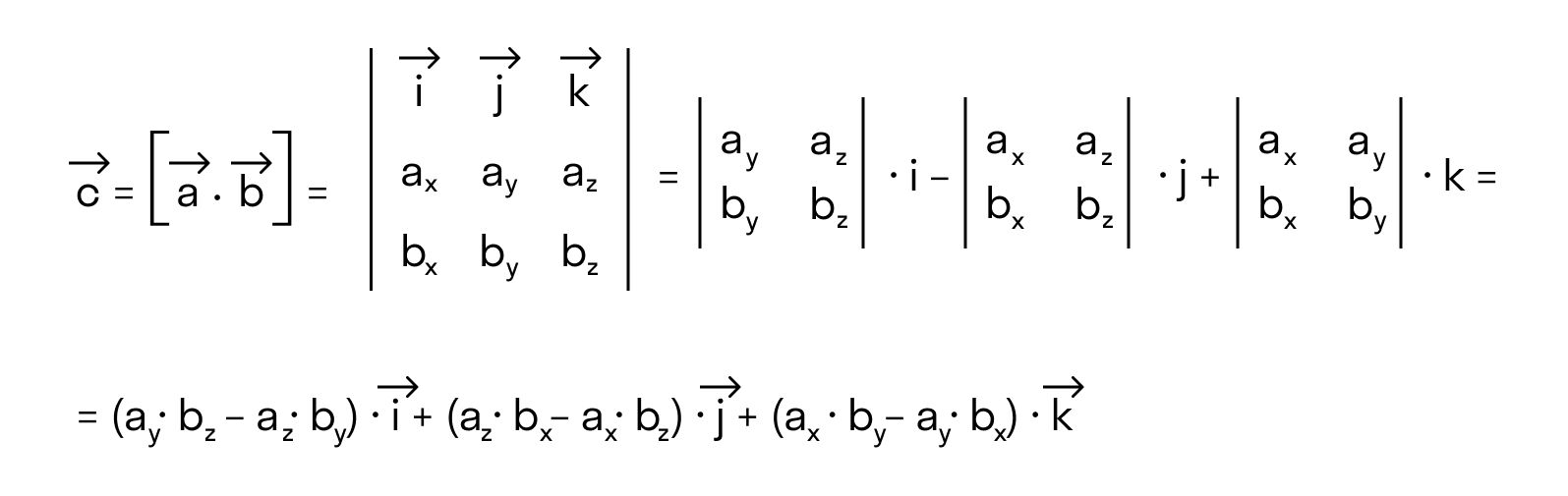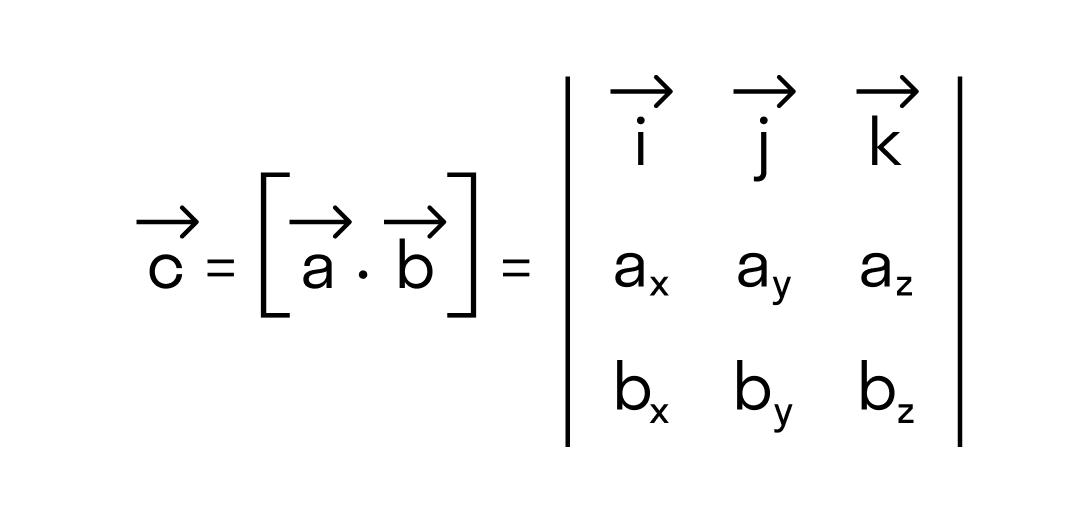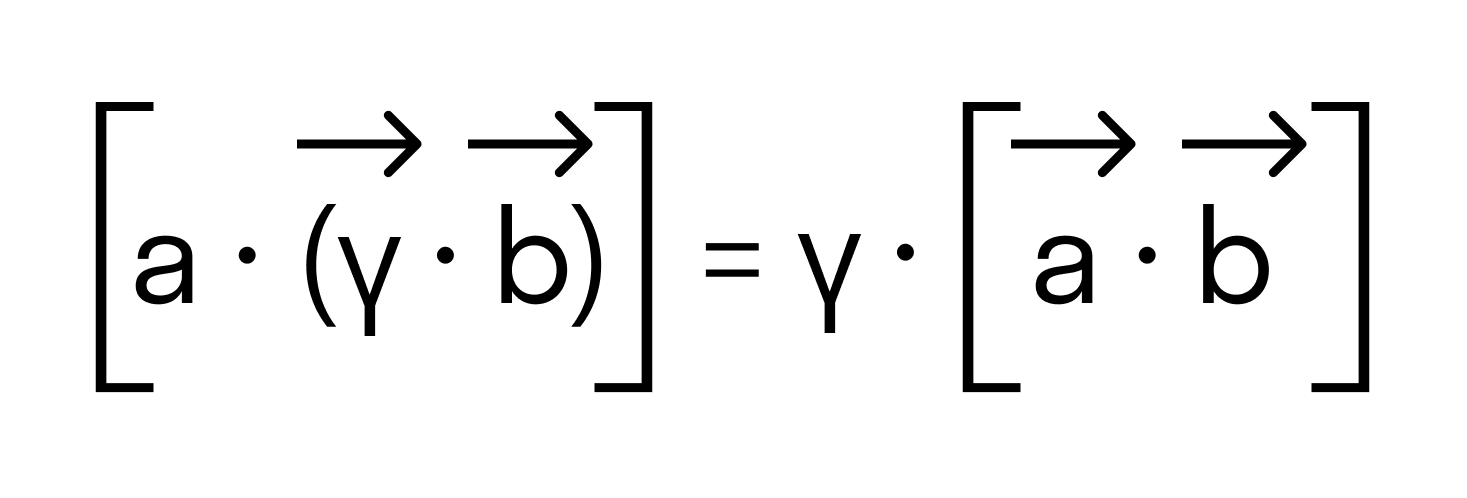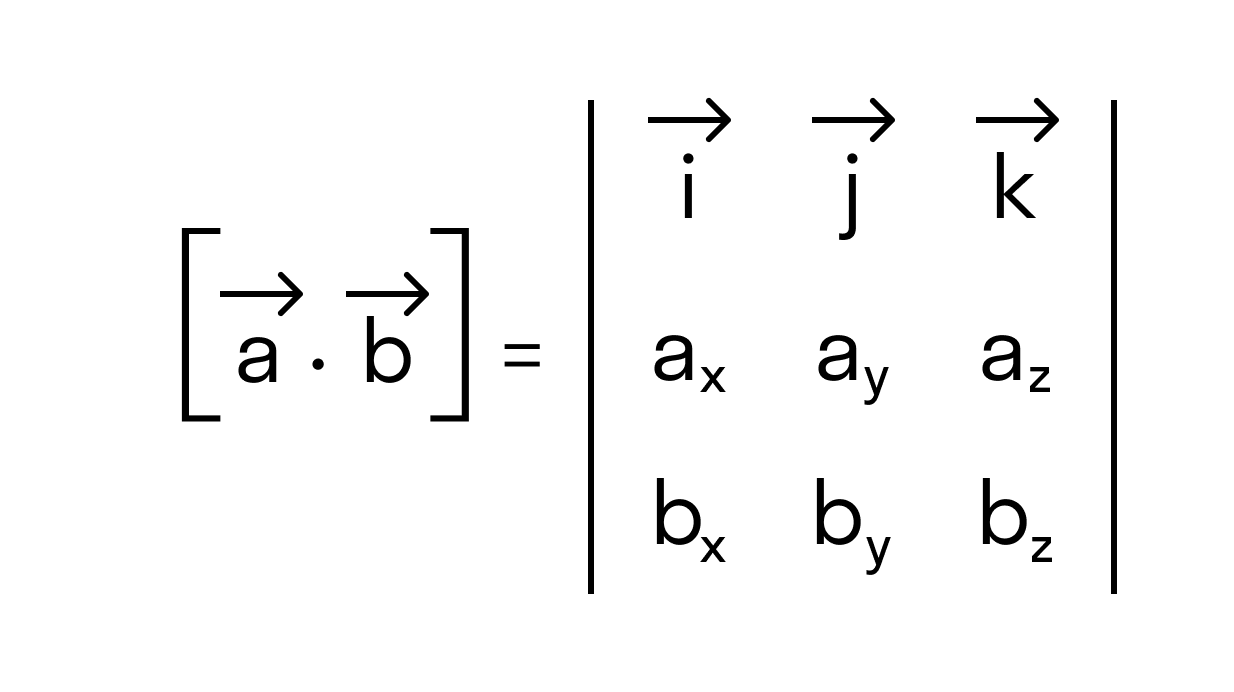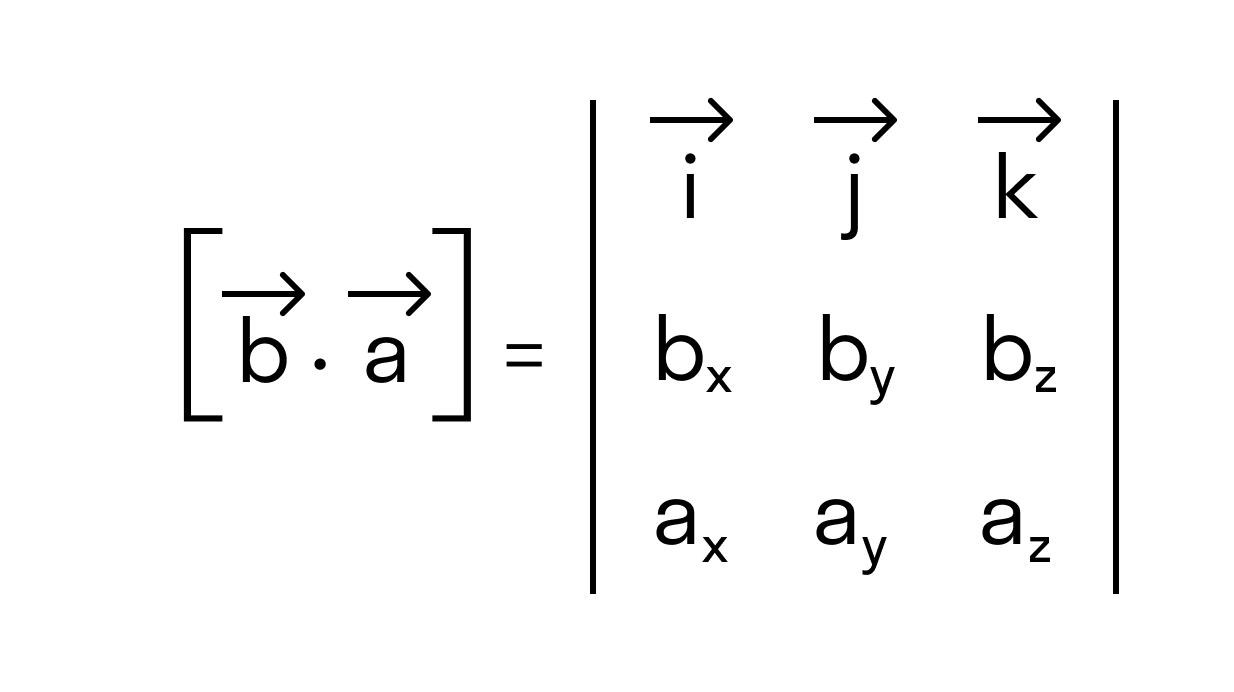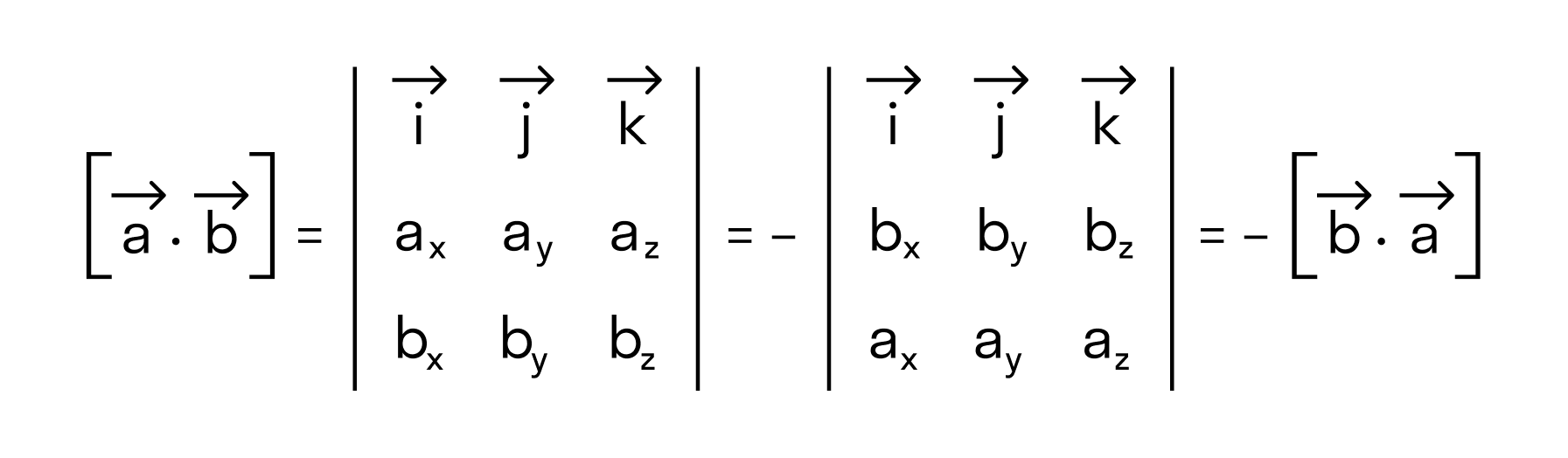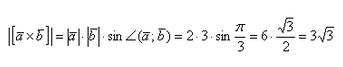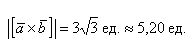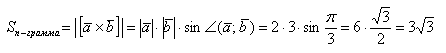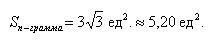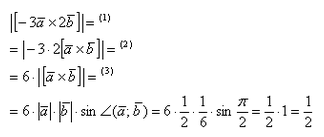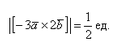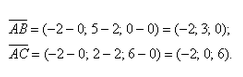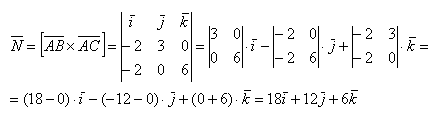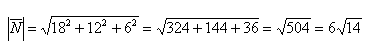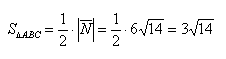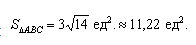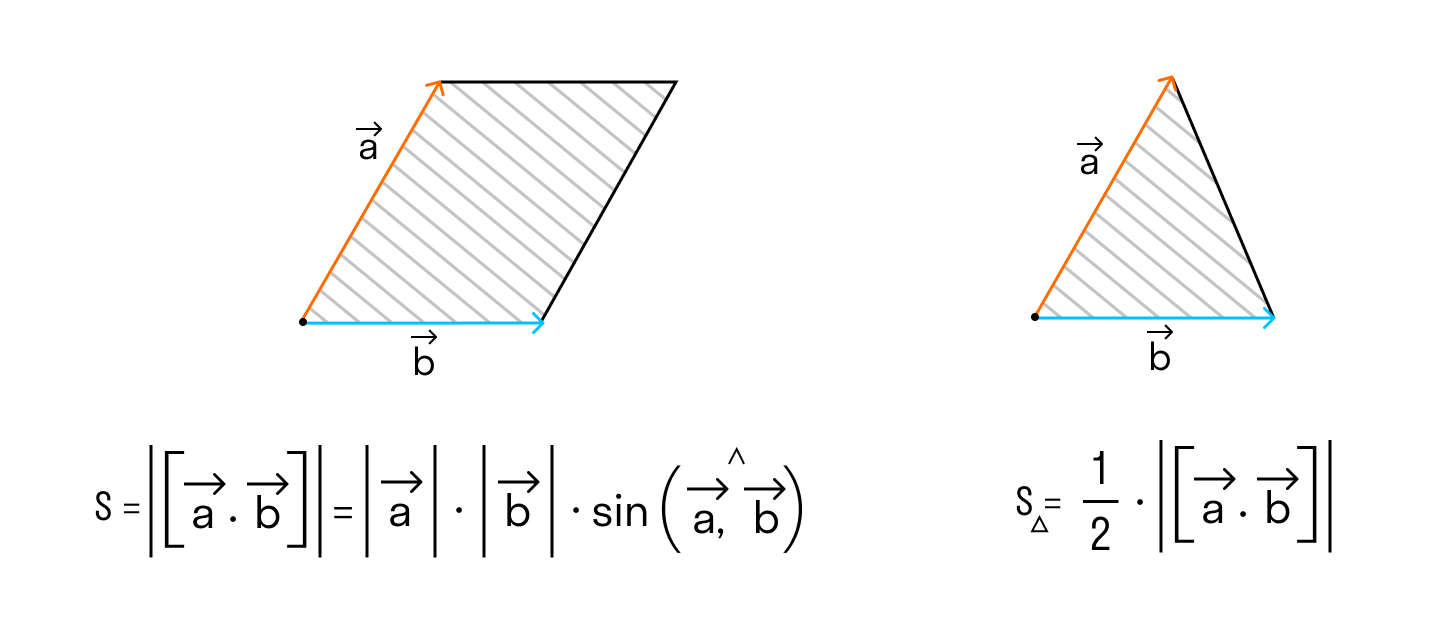как узнать тройка векторов правая или левая

Определение правой и левой тройки векторов

Вы будете перенаправлены на Автор24

Понятие тройки векторов

Определение правой и левой тройки векторов

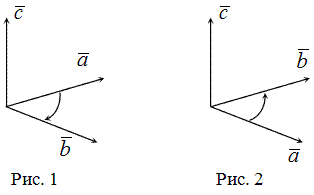
Приведём чертёж правой связки.

Рисунок 1. Чертёж правой связки. Автор24 — интернет-биржа студенческих работ

Если большой палец и указательный пальцы левой руки вытянуть, а средний согнуть под углом ладони, то три пальца в порядке большой-указательный-средний составят правую связку. Те же пальцы на левой руке составят левую связку.

На чертеже левой связки то же вращение идёт по часовой стрелке.

Рисунок 2. Чертеж левой связки. Автор24 — интернет-биржа студенческих работ

Готовые работы на аналогичную тему

Способы преобразования правой связки в левую и обратно:

Правая и левая системы координат

Рисунок 3. Чертёж ортогональной системы координат в пространстве. Автор24 — интернет-биржа студенческих работ

$i, j, k$ образуют правую связку. Система координат в данном случае называется правой.

Система координат называется левой, когда орты образуют левую связку. То есть:

Рисунок 4. Левая система координат. Автор24 — интернет-биржа студенческих работ

Подведём итог. В статье мы дали определение связки тройки векторов, описали правую и левую тройку векторов, а также правую и левую систему координат, как вытекающую тему из определения правой и левой тройки векторов. Стоит сказать, что на практике определение правой и левой тройки векторов со временем происходит интуитивно или «на автомате». Самое важное, это один раз понять, как это делается. Также стоит заметить, что чаще в задачах используется всё-таки правая тройка векторов и соответственно правая система координат.

Источник

Как узнать тройка векторов правая или левая

Для дальнейшего изучения свойств пространства необходимо ввести определение ориентации пространства. Строгая теория, касающаяся этого понятия не очень сложна, но достаточно суха. В связи с этим ограничимся лишь некоторыми “качественными” пояснениями.

Итак, все упорядоченные некомпланарные тройки векторов могут быть разбиты на два непересекающихся класса: правые тройки и левые тройки.

Есть и ещё один способ разделить эти два класса:

Правило правой руки: Совместите начала всех векторов тройки в одной точке. Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая.

Выбрав один из двух классов и назвав все входящие в него базисы “положительными” мы зададим ориентацию пространства.

Далее будем считать положительными правые тройки векторов. Все дальнейшие определения будем давать с учетом этого

Свойства скалярного произведения:

Пример 1. Найти угол между векторами.

Свойства векторного произведения:

=

Пример 2. Вычислить площадь параллелограмма, построенного на векторах a и b.

Пример 3. Проверка компланарности векторов.

Пример 4. Принадлежность 4 точек одной плоскости.

Пример 5. Вычислить объем тетраэдра и его высоту.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Хелпа по матану 2

06 Oct 2015 в 18:03

06 Oct 2015 в 18:03 #1

06 Oct 2015 в 18:14 #2

06 Oct 2015 в 18:14 #3

Омг, неужели в доту играют только шк

06 Oct 2015 в 18:16 #4

А ты думал здесь только люди знающие математику сидят? Иди на математические форумы

06 Oct 2015 в 18:16 #5

Тем что она правая?

06 Oct 2015 в 18:16 #6

06 Oct 2015 в 18:17 #7

чёт не понял ничего, рисунок векторов где?

06 Oct 2015 в 18:21 #8

06 Oct 2015 в 18:22 #9

06 Oct 2015 в 18:35 #10

Для левой руки левая.

06 Oct 2015 в 18:41 #11

еще дауны, не сильно далеко ушедшие от шк по развитию и не умеющие в гугл

06 Oct 2015 в 18:45 #12

06 Oct 2015 в 18:46 #13

Научным языком: Упорядоченная тройка некомпланарных векторов a, b, c в трёхмерном пространстве называется правой, если с конца вектора c кратчайший поворот от вектора a к вектору b виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой. (спасибо Википедии за это)

06 Oct 2015 в 18:52 #14

Научным языком: Упорядоченная тройка некомпланарных векторов a, b, c в трёхмерном пространстве называется правой, если с конца вектора c кратчайший поворот от вектора a к вектору b виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой. (спасибо Википедии за это)

Источник

Векторное произведение векторов

Определение векторного произведения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

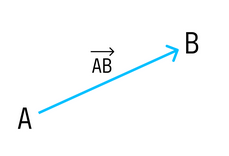
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.

Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

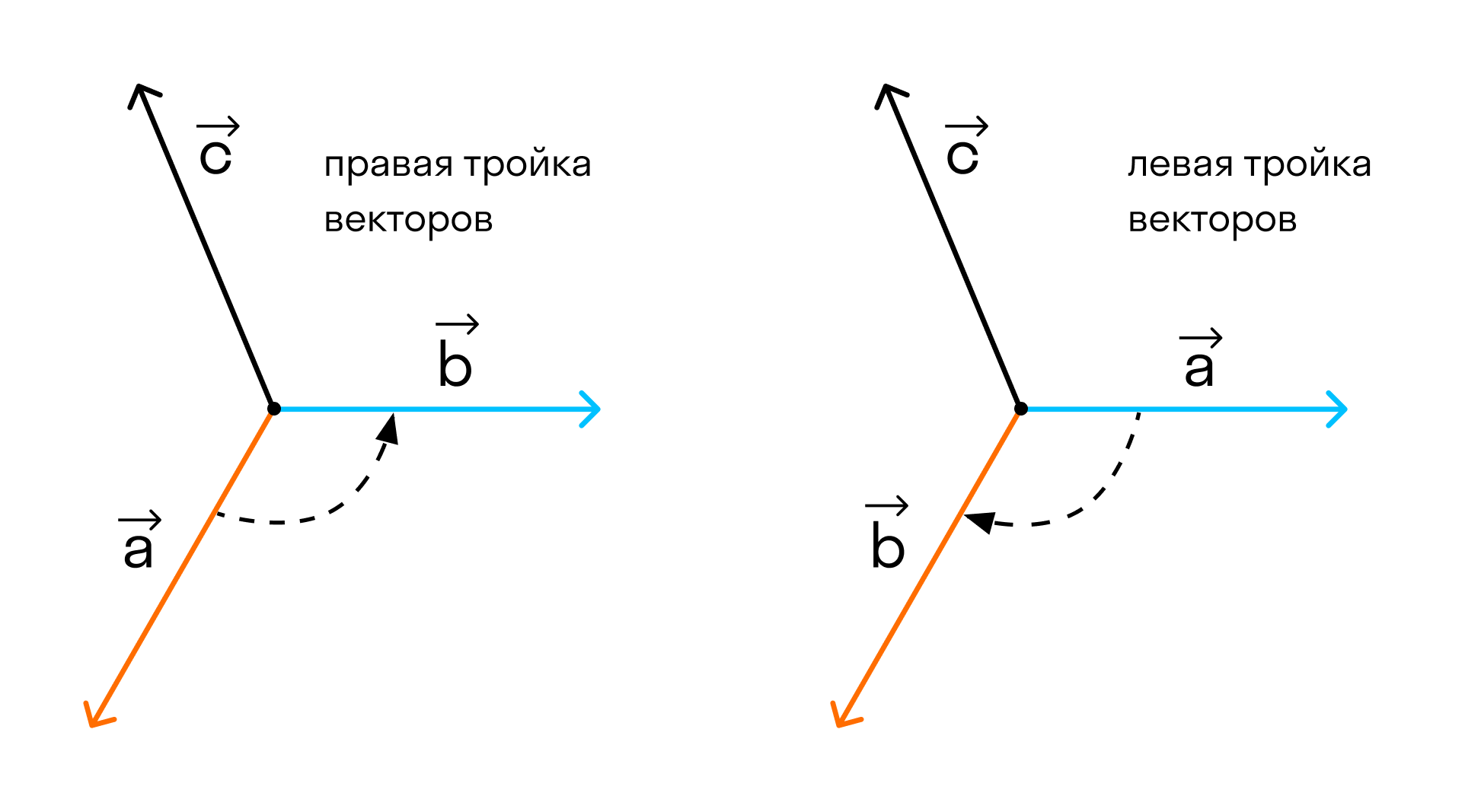
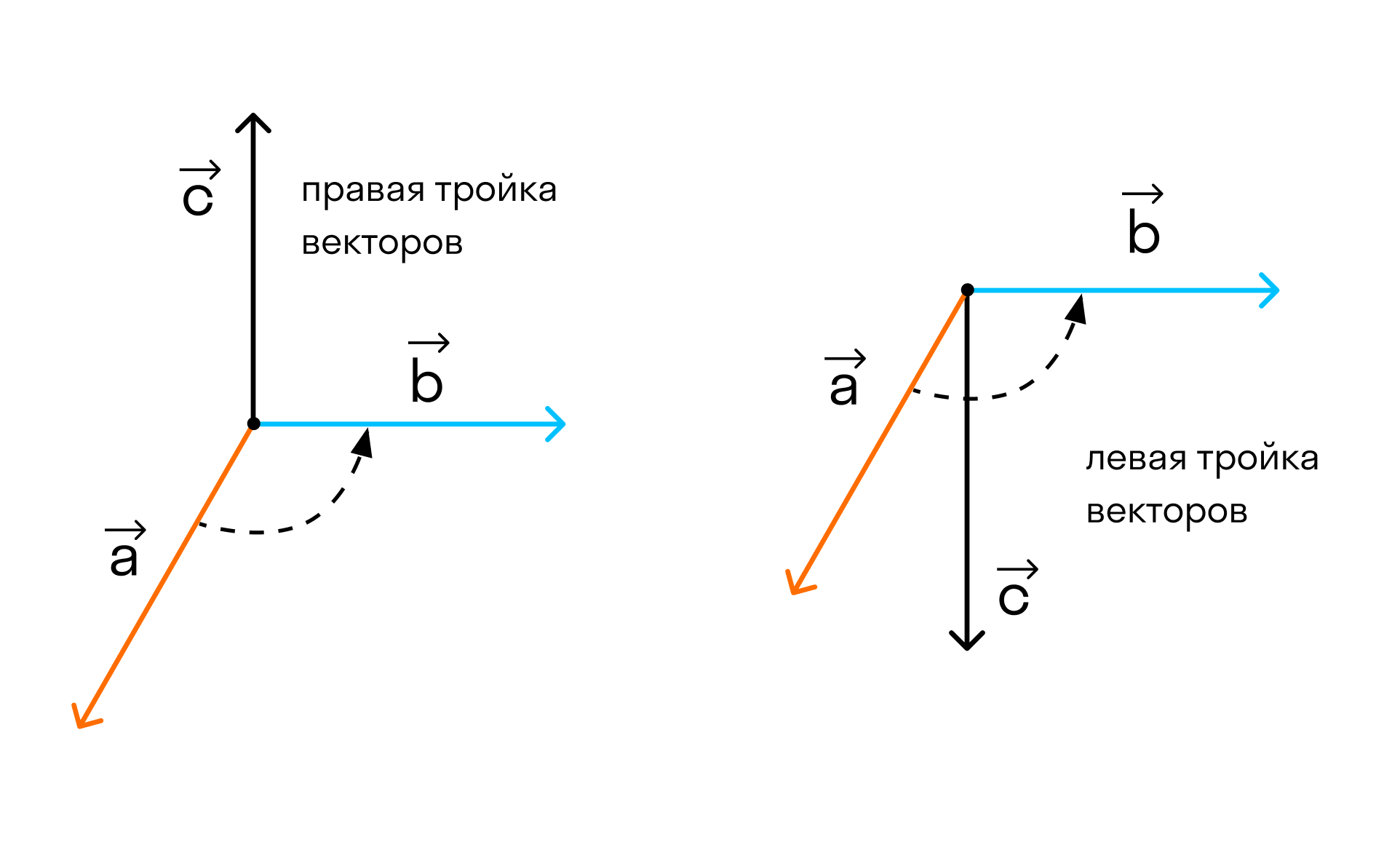
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

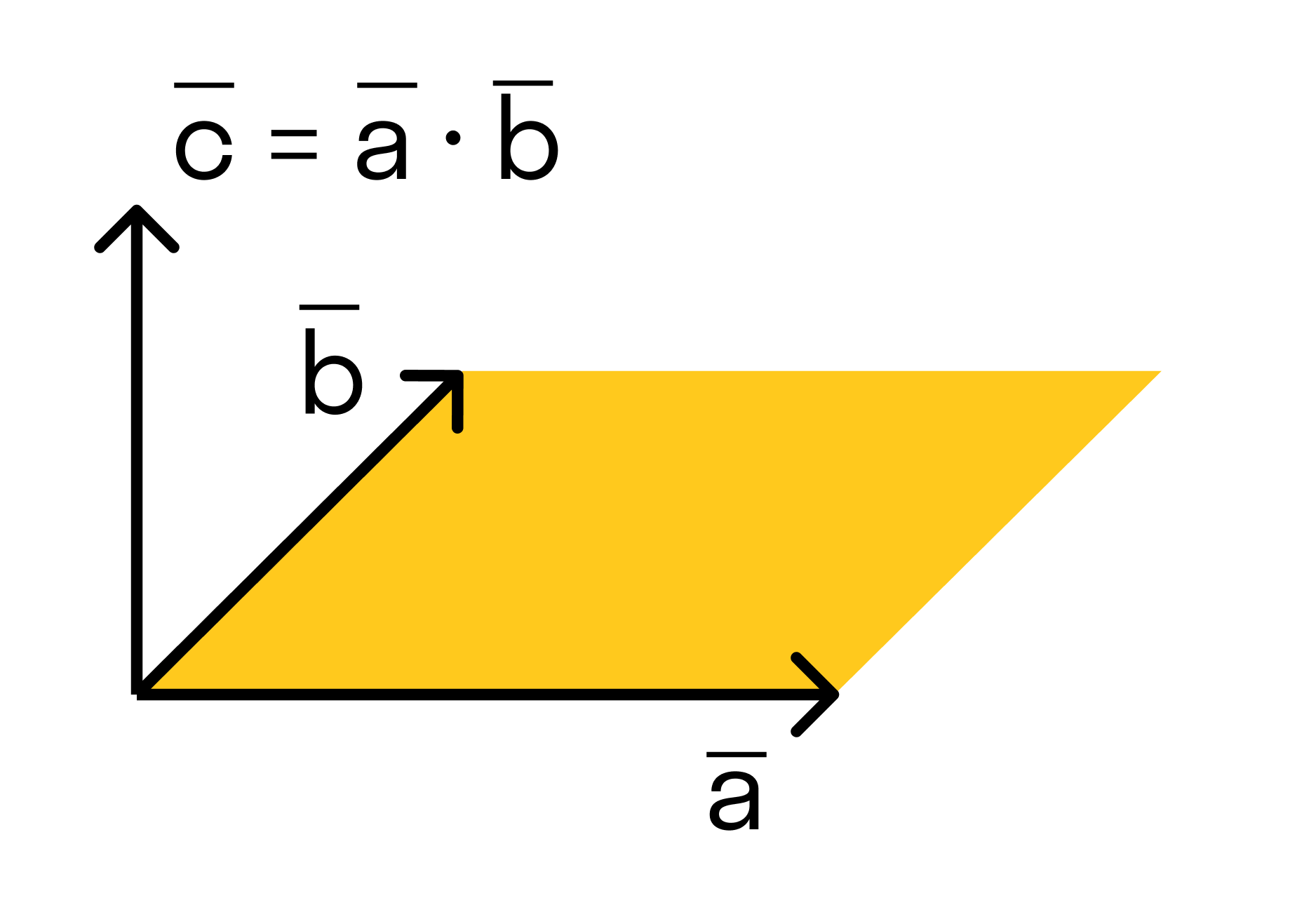
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Векторное произведение векторов →a и →b обозначается как [→a • →b].

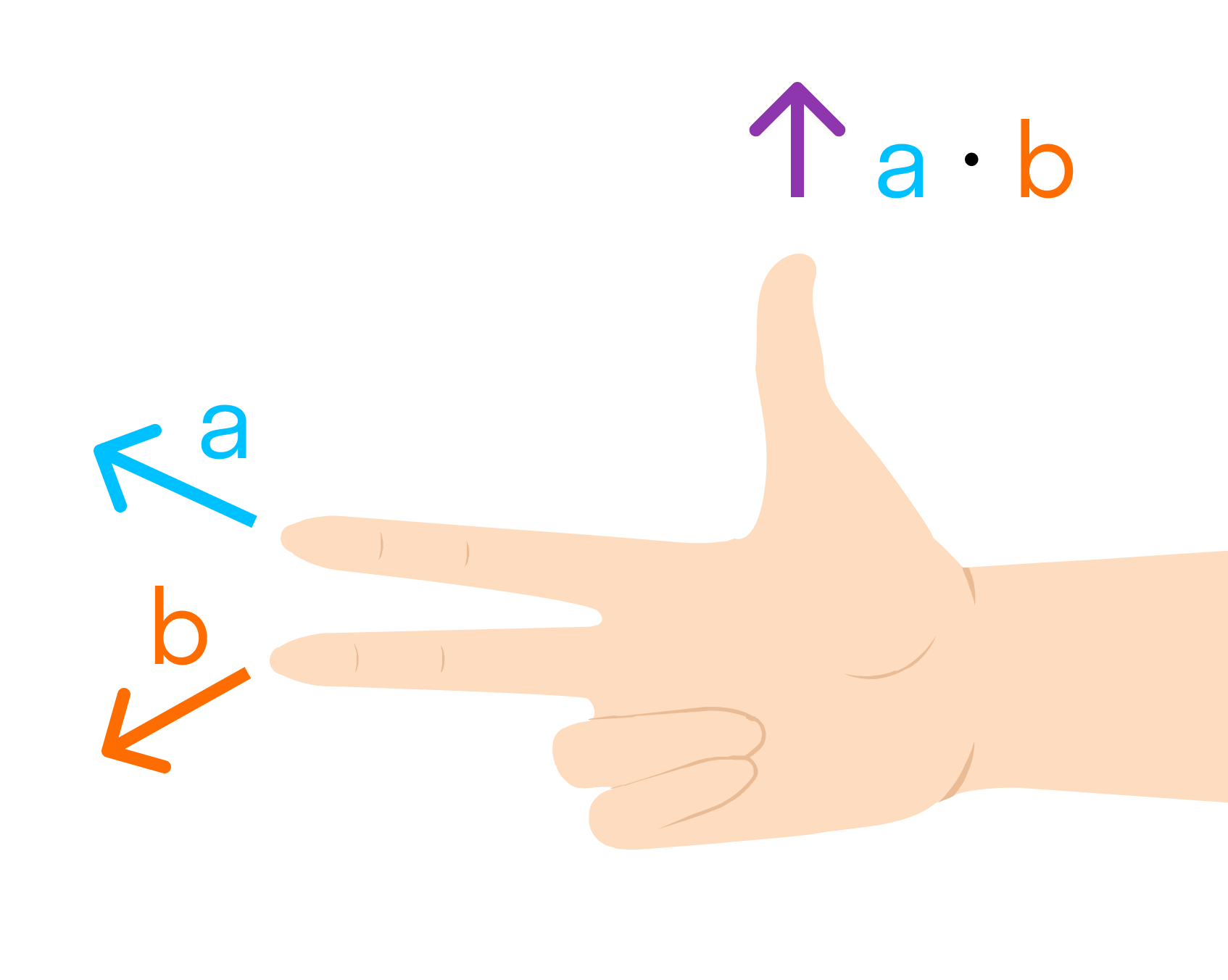
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

Координаты векторного произведения

Рассмотрим векторное произведение векторов в координатах.

Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.

В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

→i, →j, →k — координатные векторы.

Это определение показывает нам векторное произведение в координатной форме.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:

Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

, где λ произвольное действительное число.

Для большей ясности докажем свойство антикоммутативности векторного произведения.

Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому

что доказывает свойство антикоммутативности векторного произведения.

Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.

Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Примеры решения задач

Пример 1

а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:

Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.

б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:

Пример 2

Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.

По условию снова нужно найти длину векторного произведения. Используем нашу формулу:

Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.

Пример 3

Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.

Сначала найдём векторы:

Затем векторное произведение:

Вычислим его длину:

Подставим данные в формулы площадей параллелограмма и треугольника:

Геометрический смысл векторного произведения

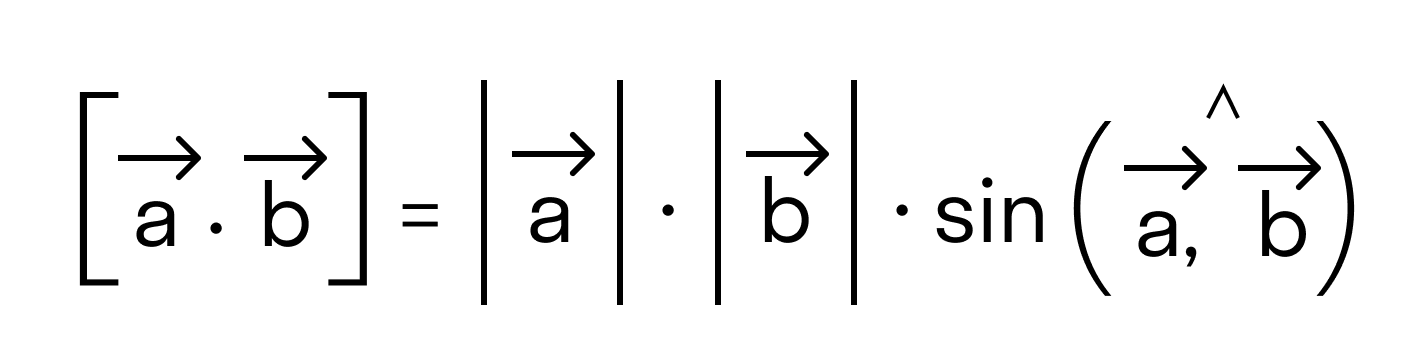
По определению длина векторного произведения векторов равна

А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

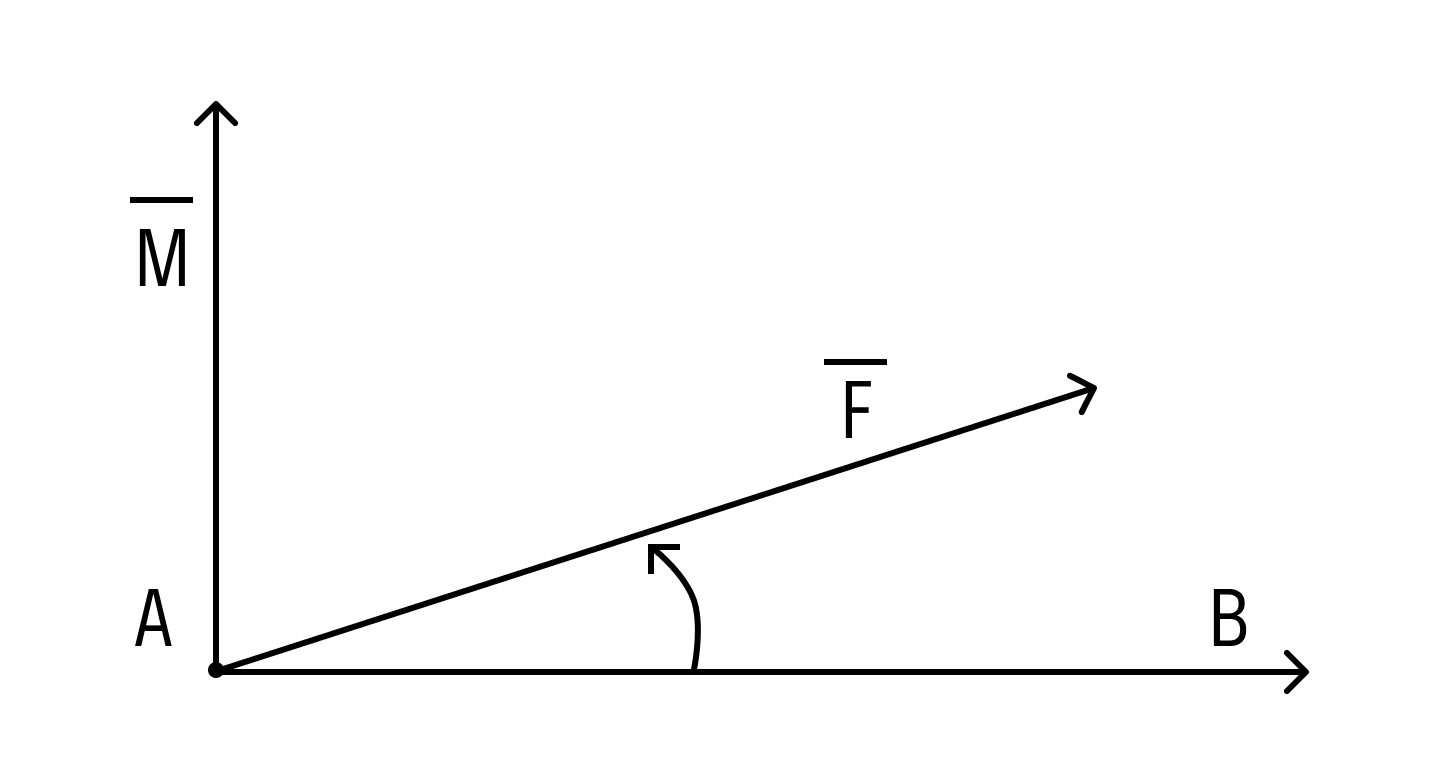
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].

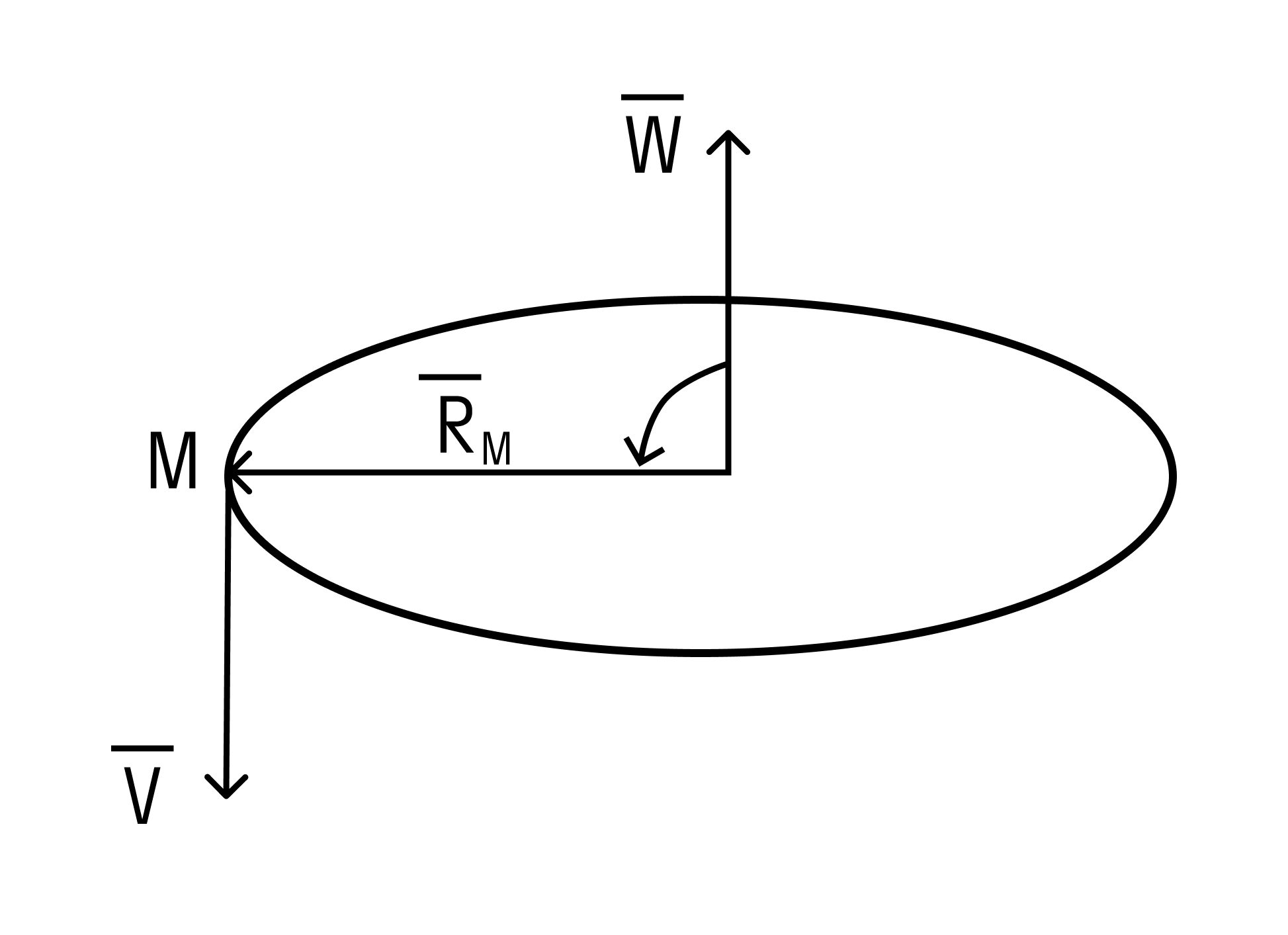
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Понятие тройки векторов. Левая, правая тройка, Определение векторного произведения. Геометрический смысл. Свойства. Векторное произведение в декартовых координатах.

Тройка некомпланарных векторов abc называется правой (левой), если после приведения к общему началу вектор с располагается по ту сторону от плоскости, определяемой векторами а и b, откуда кратчайший поворот от а к b кажется совершающимся против часовой стрелки (по часовой стрелке).

abc – правая тройка abc – левая тройка

Замечание. В дальнейшем будем рассматривать только правые системы координат, т.е. системы, базисные векторы которых образуют правую тройку.

Векторное произведение векторов.

Вектор с называется векторным произведениемвекторов аи b, если:

1) |c| = |a||b|sinφ, где φ – угол между а и b.

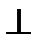
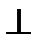
2) c a, c b.

3) Тройка векторов abc является правой.

Обозначения векторного произведения: c =[ab],c = a 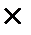b.

Свойства векторного произведения.

Доказательство. Вектор —с удовлетворяет первым двум условиям определения векторного произведения и образует с векторами b и аправую тройку векторов.

2) [ab] = 0 a ║ b.

Доказательство. Из первого пункта определения 6.2 следует, что модуль векторного произведения ненулевых векторов равен нулю только при sinφ = 0, что соответствует коллинеарности векторов аи b.

3) Модуль векторного произведения |[ab]| равняется площади S параллелограмма, построенного на приведенных к общему началу векторах аи b.

Доказательство следует из первого пункта определения 6.2.

Орт е_а произвольного вектора а – это вектор единичной длины, коллинеарный аи одинаково с ним направленный ( |е_а| =1, е_а || a).

Cледствие из свойства 3. [ab] = Se, где е – орт вектора [ab].

4) [(ka)b] = k[ab].

5) [(a + b)c] = [ac] + [bc].

6) Если в декартовой системе координат a = a, Y_a, Z_a>, b = b, Y_b, Z_b>, то

7) [ab] =

Представим векторы а и bв виде: a = X_ai+ Y_aj +Z_ak, b = X_bi + Y_bj +Z_bk. Отметим, что [ij] = k, [jk] = i, [ki] = j, [ii] = [jj] = [kk] = 0. Тогда с использованием свойств 4 и 5 получим:

17) Смешанное произведение векторов. Свойства и геометрический смысл. Компланарные векторы.

Векторы называютсякомпланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях.

Смешанным произведением векторов а, bи сназывается результат скалярного умножения векторного произведения [ab] на вектор с.

Обозначение: abc= [ab]c.

Свойства смешанного произведения.

1) Смешанное произведение [ab]c равно объему параллелепипеда, построенного на приведенных к общему началу векторах a,b,c, если они образуют правую тройку, или числу, противоположному этому объему, если abc – левая тройка. Если a,bи скомпланарны, то [ab]c = 0.

а) Если a,b и с компланарны, то вектор [ab] ортогонален плоскости векторов аи b, и, следовательно, [ab] 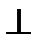c. Поэтому [ab]c = 0.

в) Если a,b,cне компланарны, [ab]c = |[ab]||c| = S·|c|cosφ, где φ – угол между с и [ab]. Тогда |c|cosφ – высота рассматриваемого параллелепипеда. Таким образом, [ab]c = V, где выбор знака зависит от величины угла между с и [ab]. Утверждение доказано.

Следствие. [ab]c = a[bc].

Действительно, обе части равенства представляют объем одного и того же переллелепипеда. Поэтому положение векторных скобок в смешанном произведении не важно, и в его обозначении скобки не ставятся : abc.

abc = .

Доказательство. Используя координатную запись скалярного и векторного произведения, запишем:

[ab]c = (Y_aZ_b – Y_bZ_a)X_c + (X_bZ_a – X_aZ_b)Y_c + (X_aY_b – X_bY_a)Z_c = .

следовательно, векторы компланарны.

Полярная система координат

Последнее изменение этой страницы: 2017-03-14; Просмотров: 832; Нарушение авторского права страницы

Источник