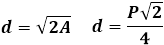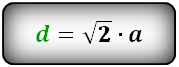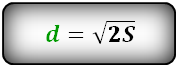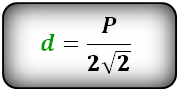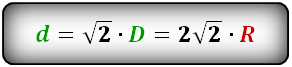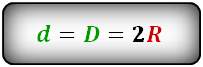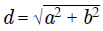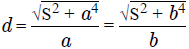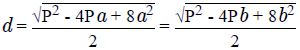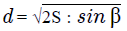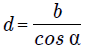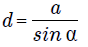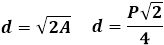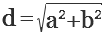Как вычислить диагональ квадрата

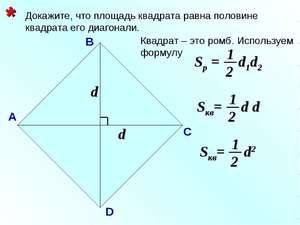
Диагональ квадрата формула и расчет

Из школьного курса математики мы знаем, что квадрат — это четырёхугольник у которого все углы прямые, а все стороны равны.

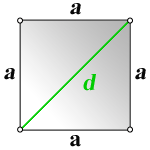
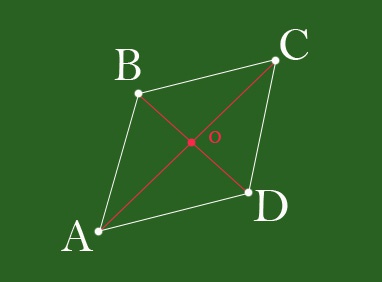
Диагональ — отрезок, соединяющий две противоположные вершины квадрата. Задача нахождения диагонали квадрата может встретиться и после окончания школы. К примеру, при постройке дома у которого фундамент должен быть квадратным. Когда размечается фундамент, мало убедиться, что все 4 стороны равны. Ведь у ромба тоже все стороны равны. И получить ромбовидный фундамент вряд ли кто захочет.

В этом случае, чтобы убедиться в том, что фундамент действительно представляет собой квадрат, вычисляют диагональ квадрата и измеряют обе диагонали фундамента. Если все 4 стороны равны между собой и две диагонали также имеют одинаковую длину — фундамент точно будет квадратным. Для вычисления длины диагонали квадрата достаточно знать длину его стороны и простую формулу.

Как найти диагональ квадрата

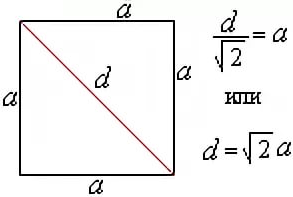
d — диагональ квадрата

a — сторона квадрата

Достаточно подставить в формулу длину стороны квадрата вместо a.

А можно воспользоваться нашим калькулятором. Просто введите длину стороны и тут же получите длину диагонали квадрата. У нас также можно найти диагональ прямоугольника.

Источник

Диагональ квадрата

Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.

Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
— Все стороны квадрата равны (от ромба)
— Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)

a 2 +b 2 =c 2
a 2 +b 2 =d 2
2a 2 =d 2

Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:

Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.

Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.

Формулы диагонали квадрата через площадь, периметр

Источник

Все формулы длины диагонали квадрата

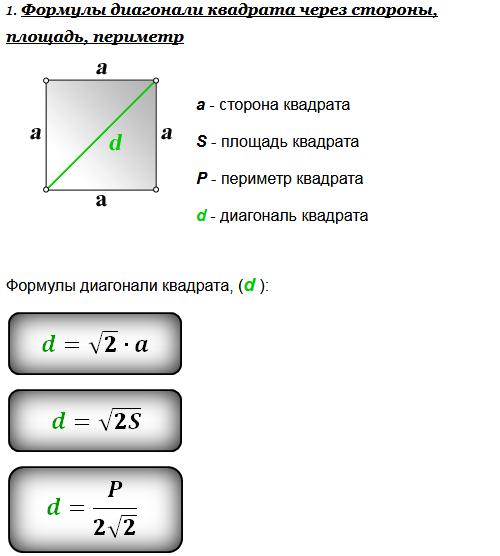
1. Формулы диагонали квадрата через стороны, площадь, периметр

Формулы диагонали квадрата, ( d ):

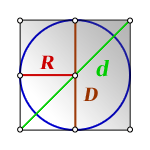
2. Формула диагонали квадрата через радиус вписанной окружности

Формула диагонали квадрата, ( d ):

3. Формула диагонали квадрата через радиус описанной окружности

Формула диагонали квадрата, ( d ):

4. Формула диагонали квадрата через линию выходящую из угла на середину стороны квадрата

Формула диагонали квадрата, ( d ):

Источник

Формулы и способы как находить диагональ квадрата

При решении задач по школьной математике часто требуется определить, чему равняется диагональ заданного квадрата. При кажущейся некоторой сложности, эта задача является весьма простой и имеет несколько несложных способов решения. Рассмотрим их, для начала введём некоторые понятия и определения.

Определения и соглашения

Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.

Вычисление диагонали квадрата по известной стороне

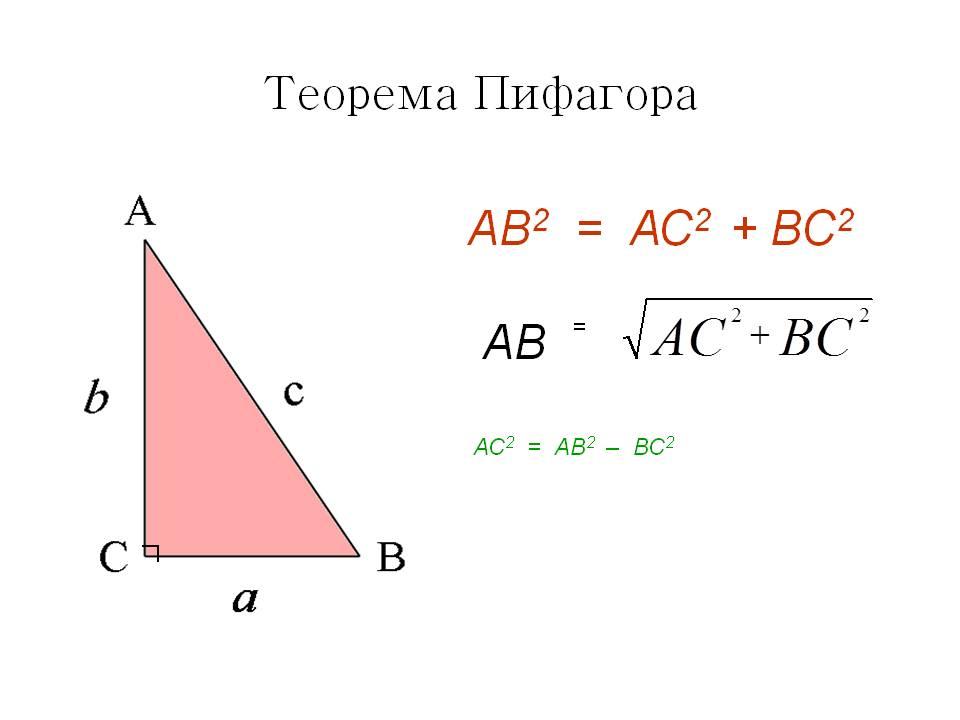
Самым простым способом является вычисление диагонали, если известна сторона квадрата. Здесь действует широко известная теорема Пифагора для прямоугольных треугольников. Запишем эту формулу: c^2 = a^2+b^2.

Отметим, что в нашем случае диагональ квадрата есть гипотенуза треугольника с равными катетами. Перепишем формулу исходя из наших условий: d^2 = a^2+a^2. Преобразуем, получим: d^2 = 2*a^2. Следующим шагом извлечём квадратный корень, получится: d = rad2*a. Это и есть наша конечная формула.

Рассмотрим вычисление на примере. Пусть a = 64. Подставим наше значение в формулу. Получим d = 64*rad2. Это и есть ответ.

Вычисление диагонали квадрата по известной площади

Пусть нам дана площадь квадрата, её обозначают латинской буквой S, найдём его диагональ.

Используем свойства прямоугольника и запишем формулу его площади.

S = a*b. Перепишем для b = a. Получим: s = a^2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS.

Пример: допустим, площадь равна 32 квадратных метра. Подставим это число. Получим rad2*rad32 = rad2*4*rad2 = 4*2 = 8 метров.

Вычисление диагонали по известному периметру

Пусть нам известен периметр. В дальнейшем его будем записывать латинской буквой P, найдём его d. Воспользуемся свойствами прямоугольника и запишем формулу его периметра.

P = два*(a + b). Перепишем для b = a. У нас получится: P = два*(a + a) = 2*2a = 4*a. Выразим из последней формулы сторону. Имеем: a = P/4. Воспользуемся тем, что: d = rad2*a. Выразим сторону через периметр. Наша формула примет видd = rad2*P/4.

Примере: пусть периметр равен 128 метров. Проведём несложный расчёт. Имеем, rad =d2*128/4 = 32*rad2 метров.

Вычисление по радиусу описанной и вписанной окружности

Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.

Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.

И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.

Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.

Заключение

Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.

Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.

Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.

Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.

Видео

Из видео вы узнаете, как найти диагональ квадрата, если известна его площадь.

Источник

Диагональ квадрата

Свойства

Зная диагональ квадрата, можно легко вычислить его сторону. Для этого нужно диагональ поделить на корень из двух, полученный в ходе вычислений по теореме Пифагора. a=d/√2

При вычислении периметра и площади, подставляя данное выражение вместо стороны квадрата, корень из двух претерпевает изменения, сокращаясь с другими коэффициентами, или подвергаясь возведению в степень. P=4a=4d/√2=2√2 d S=a^2=(d/√2)^2=d^2/2

Диагонали при пересечении со сторонами квадрата и между собой образуют конгруэнтные углы по 45 градусов. (рис. 69.1) m(

Радиус вписанной в квадрат окружности зависит от стороны квадрата, тем не менее, подставив вместо нее формулу через диагональ, можно сразу вычислить радиус. r=a/2=d/(2√2)

Радиус окружности описанной вокруг квадрата изначально зависит от его диагонали, поэтому никаких преобразований можно не проводить, нужно всего лишь разделить диагональ на два. (рис. 69.3) R=d/2

Источник

Как посчитать диагональ квадрата? Формула длины диагонали квадрата.

Как посчитать диагональ квадрата?

Безусловно, лучше всего просто запомнить формулу длины диагонали квадрата и пользоваться ею всегда, ведь это гораздо быстрее и удобнее. Особенно это чувствуется при решении задач в буквенном виде, где вместо целых больших подкорневых выражений можно обойтись лишь одним произведением.

Пример

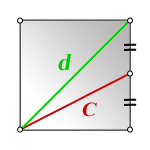
Возьмем, к примеру, квадрат 6 на 6, то есть со стороной, равной шести сантиметрам.

Тогда получим, что С=√А^2+А^2 или С=√2А^2.

Запишем в числовом виде: С =√36 + 36. Получили √72, а это 3√8 или 6√2.

А теперь найдем ту же диагональ, но уже по второму способу: С = А√2 или в числовом виде: 6√2

Другие свойства диагоналей квадрата

Помимо знания того, как найти диагонали квадрата, нужно также знать и их свойства. Основные из них:

Вывод

Вопросом, как посчитать диагонали квадрата, обычно задаются ученики, пропустившие эту тему в школе. Однако такие фундаментальные правила математики должен знать каждый! Желательно решать как можно быстрее, и для этого необходимы знания сокращенных формул. Все это предельно просто и легко, но вместе с тем является базой, необходимой для решения в дальнейшем гораздо более сложных задач. И важную часть этой базы занимает квадрат.

Источник

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Перечислим свойства квадрата:

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Очевидно, радиус окружности равен половине диагонали квадрата.

Диаметр окружности равен стороне квадрата.

Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.

Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Источник

Формулы квадрата

Для расчёта всех основных параметров квадрата воспользуйтесь калькулятором.

Свойства квадрата

Сторона квадрата

Стороны квадрата через диагональ

Стороны квадрата через радиус вписанной окружности

Стороны квадрата через радиус описанной окружности

Стороны квадрата через площадь, S

Стороны квадрата через периметр, P

Стороны квадрата через линию выходящую из угла на середину стороны квадрата, AA₁

Площадь квадрата

Где:	AB – сторона квадрата
AC(BD) – диагональ квадрата

Площадь квадрата через сторону

Площадь квадрата через диагональ

Периметр квадрата

Диагональ квадрата

Где:	AB – сторона квадрата
AC(BD) – диагональ квадрата
S – площадь квадрата
P – периметр квадрата

Диагональ квадрата через сторону

Диагональ квадрата через площадь

Диагональ квадрата через периметр

Вписанная окружность

Радиус вписанной окружности

Длина окружности, L

Площадь окружности, S

Описанная окружность

Где:	AB – сторона квадрата
AC(BD) – диагональ квадрата

Радиус описанной окружности через сторону

Радиус описанной окружности через диагональ

Источник

Диагональ квадрата. Формула. Как найти диагональ квадрата?

Длину диагонали квадрата можно найти зная длину его стороны или длину его периметра, или его площадь.

1.Если известна сторона квадрата а, диагональ d будет равна:

2.Если известен периметр (сумма четырёх сторон) P, диагональ будет равна:

3.Если известна площадь квадрата S, диагональ будет равна:

Источник

Как найти диагональ квадрата

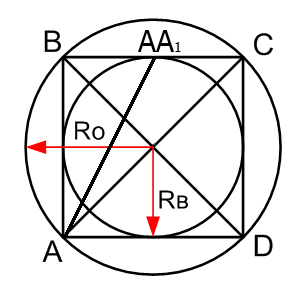
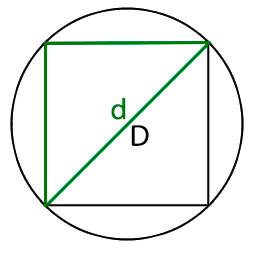
Итак, стоит начать с того, что вокруг квадрата можно описать окружность, диагональ которой в точности равна диагонали квадрата. Для того, чтобы подсчитать радиус описанной окружности, надо воспользоваться формулой:

Также в квадрат можно и вписать окружность. При этом окружность в точках касания ее со сторонами квадрата делит их пополам. Формула, с помощью которой можно вычислить радиус вписанной окружности, выглядит так:

Если, при решении задачи, известен радиус окружности, который вписан в данный квадрат, то возможно таким образом выразить и сторону квадрата, величина которой необходима для нахождения диагонали квадрата:

Длина радиуса окружности равна половине длины ее диагонали. Таким образом, длина диагонали описанной окружности, а, значит, и длина диагонали квадрата может быть рассчитана по формуле:

Для большей ясности, можно рассмотреть небольшой пример:

Дан квадрат с длиной стороны 9 см, требуется найти длину ее диагонали.

Решение: для того, чтобы подсчитать ее длину, потребуется воспользоваться формулой выше:

Ответ: длина диагонали квадрата со стороной 9 см равна √162 см или, приблизительно, 14.73 см

Источник

Формулы и способы как находить диагональ квадрата

3Онлайн-калькулятор

Теперь, зная несколько способов для решения задачи на данную тематику, вы не будете листать книгу по математике в поисках нужной формулы, а просто воспользуетесь онлайн-калькулятором или примерами, которые приведены выше.

2Как найти диагональ квадрата через прямоугольный треугольник

Пример 3: Найти диагональ квадрата, если его сторона равна 3.

Несмотря на то, что последний способ более длинный и в конечном итоге мы выходи на формулу из первого примера, знать его необходимо. По сути, этот способ является доказательством формулу диагонали квадрата. Именно это доказательство может прийти на экзамене или олимпиаде. Хорошо выучите ее, ведь она может помочь вам на вышеупомянутых мероприятиях.

Вычисление по радиусу описанной и вписанной окружности

Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.

Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.

И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.

Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.

Нахождение третьего и четвертого углов

При расчете используется теорема Пифагора

Соответствие частей в треугольнике, по которому размечается прямой угол на участке, можно проверить теоремой Пифагора. Она выражается формулой a² + b² = c²: квадрат гипотенузы равняется сумме квадратов катетов.

Чтобы высчитать длину соединяющей гипотенузы, нужно высчитать квадрат одного расстояния на шнуре с квадратом другой стороны угла и сложить полученные значения. Из результата следует высчитать квадратный корень, чтобы получить длину гипотенузы. Так можно выровнять диагональ прямоугольника, чтобы получить идеальный прямой угол.

Третий и четвертый углы находятся аналогичным способом по отправной вершине и существующей стороне. После выставления последнего угла проверяется противоположные диагонали и стороны в фигуре для сравнения. Используется шнур, который не растягивается по длине, чтобы не искажать измерения.

Выравнивание величины прямоугольника

В прямоугольнике все углы должны равняться 90°, иначе получится неравнобедренная фигура с перекосами стен. Абрис фундамента имеет наружную и внутреннюю сторону, поэтому требование к прямоугольности касается обоих контуров. Легче всего выровнять величину для дома простой прямоугольной формы, который имеет четыре стены.

Иногда фундаменты в плане имеют сложное строение, например, делаются дополнительные монолитные ленты под пристройку или веранду, а каминный зал рассматривается как вынесенное помещение. В таком случае разметка усложняется тем, что площадь дома будет складываться из отдельных прямоугольников, которые размечаются отдельно.

Каждая фигура после распланировки поверяется на соответствие с другими частями и между составными элементами также устанавливаются прямые углы. Первоначальная сторона привязывается к какой-нибудь основе на местности, которая выглядит прямолинейно. Это может быть ограда, забор, трамвайные пути или бордюр асфальтированной трассы. От этой линии откладывается одинаковое расстояние для обозначения первой стороны искомого плана фундамента.

После окончательной разметки нужно правильно рассчитать диагональ и сравнить расстояние между первой-третьей и второй-четвертой вершиной прямоугольника на местности. Должны получиться идеально одинаковые расстояния. Проверяют и длину противоположных сторон, которые также должны быть равны.

Необходимость расчета диагонали фундамента

При неверном расчете диагонали все дальнейшее строительство будет расходиться с планом

Проект предполагает подбор конструктивных элементов точно в размер, чтобы при строительстве не возникало перекосов. Длина балки или плиты перекрытия берется с требуемой глубиной опирания, которая принимается по конструктивному расчету. Во время разметки фундамента нужна предельная точность, т.к. отклонение в размерах повлечет расхождение вертикальных конструкций.

Горизонтальные элементы могут не влезть в проектное положение или вываливаться из монтажного пространства, поэтому потребуется перерасчет длины, а также других показателей.

Правильная разметка основания ведет к приятным бонусам при возведении здания:

Перед тем как вымерить диагональ фундамента, нужно выровнять строительную площадку, чтобы удобно было размечать линии на местности. Почти всегда строительные конструкции и материалы от утеплительных матов до досок и стеновых щитов имеют прямые углы, поэтому фундамент также размечают с учетом этих требований.

Сложности при неправильной разметке

Нарушение геометрии фундамента снижает прочность стен

Неправильная переноска размеров на местность и пренебрежение сравнением диагоналей приведет к тому, что на поверхности земли появится ромб или трапеция. При устройстве самого фундамента это может и не станет заметно, но первая укладка плит над подвалом выявит несоответствия и приведет к потерям времени для перерасчета сборных элементов или переделке основания.

Если плита опирается меньше требуемой глубины, после получения нагрузки от оборудования или людей она может обломить опорную часть стены и упасть. Такая неприятность коснется горизонтальных элементов перекрытия на всех этажах высотного строения и будет повторяться вплоть до кровли.

Выполнить устройство крыши трудно, если не соответствуют размеры между балками, фермы приходится ставить большего размера, а в других местах уменьшать габариты. Увеличивается трудоемкость работ, т.к. исполнитель выступает в несвойственной для него роли конструктора и проектировщика.

Усложнится установка кровельного покрытия, т.к. листы профнастила или шифера выпускаются с прямыми углами. Сборные угловые элементы водоотлива также рассчитаны на установку под 90°, желоб будет отходить от края кровли, а вода попадет на вертикальные ограждения, стены будут отсыревать.

1Как найти диагональ квадрата – формула

Существует довольно простая формула для нахождения диагонали квадрата. Она выглядит следующим образом: a√2. a – сторона квадрата. Вспомним, что все стороны квадрата равны. Таким образом, если вы знаете величину одной стороны, вы знаете и величину остальных трех сторон. Чтобы узнать диагональ квадрата необходимо ее сторону умножить на корень из двух.

Пример 1: Найти диагональ квадрата, если известно, что его сторона равна 5.

Решение: Подставив значение в вышеупомянутую формулу, нетрудно догадаться, что диагональ будет равна 5√2.

Пример 2: Найти сторону квадрата, если известно, что его диагональ составляет 5√2.

Решение: Диагональ обозначается маленькой латинской буквой d. d = a√2. Следовательно, чтобы найти сторону зная диагональ необходимо значение диагонали разделить на корень из двух. Проделав это действие, мы узнаем сторону квадрата, которая, в данном случае, равна 5.

Необходимые инструменты для работы

Инструменты для разметки фундамента

Во время рытья траншей экскаватором убирают шнуры, которые натянуты с выносом от углов, а места сторон отмечают на грунте посыпкой контрастным веществом, например, светлым песком или мелом. Элементы обноски красят яркой краской, чтобы экскаваторщик мог их увидеть и не наехать на разметочные части. После рытья траншеи шнуры натягивают на старое место и проверяют расположение ям или котлованов.

Расчет диагонали фундамента ведется с применением инструментов и приспособлений:

Геодезисты используют теодолит, чтобы размечать углы и давать отметки по высоте. У частников нет такого инструмента, для работы с ним требуется навык. Правильно измерить диагональ дома можно с помощью простых приспособлений.

На угольник закрепляют лазерные указки и строительный уровень — такое приспособление покажет высокую точность при разметке. Продаются транспортиры и угольники большого размера, лучше взять такие, чтобы было удобнее переносить линии плана на местность. Первоначальная разметка очень важна для начала строительства, поэтому желательно высчитать диагональ несколько раз, чтобы быть уверенным в правильности работы.

Прямоугольник

Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.

Диагональ прямоугольника или квадрата всегда:

Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.

При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.

Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.

Заключение

Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.

Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.

Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.

Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.

Источник

Как рассчитать диагональ в квадрате?

Как правильно рассчитать диагональ?

Если известны длины сторон прямоугольника, несложно определить его диагональ, используя теореме Пифагора. Согласно теоремы квадрат гипотенузы равен сумме квадратов катетов.

Как рассчитать диагональ если известна длина и ширина?

Как найти диагональ квадрата по его площади?

Диагональ квадрата равна кв. корню из произведения 2*S. В данном случае она равна арифметическому корню суммы 2-ух площадей квадрата, или арифметический корень площади умножить на арифметический корень 2-ух.

Как найти сторону квадрата по диагонали?

d2 = а2 + а2 = 2а2. Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.

Как найти длину диагонали?

Площадь прямоугольника равна произведению длины стороны a на длину стороны b. Периметр прямоугольника равен удвоенной сумме сторон a и b. Диагональ прямоугольника равна квадратному корню из суммы квадратов сторон a и b.

Как найти длину диагонали прямоугольника?

Как найти длину диагонали ромба?

Как рассчитать диагональ прямоугольного треугольника?

Как найти сторону квадрата по его площади?

Чтобы найти сторону квадрата, если известна его площадь, извлеките из числового значения площади квадратный корень. То есть найдите такое число, квадрат (вторая степень) которого равняется площади квадрата.

Как найти формулу площади квадрата?

Формула вычисления площади

е. S = a*a = a2. Соотношение стороны и диагонали квадрата: d=a√2.

Чему равен квадрат биссектрисы?

Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Источник

Как посчитать диагональ квадрата

Здравствуйте!
Как посчитать диагональ квадрата. Можно на примерах, так даже лучше.
Спасибо!

Решая задачи на расчет диагонали квадрата, необходимо учитывать те наборы исходных данных, которые известны из условия.
Рассмотрим наиболее часто встречающиеся варианты заданий.

Задача 1.
Как посчитать диагональ квадрата по его стороне, равной 18 см?

Решение.
Формула для расчета диагонали квадрата имеет следующий вид:

Известная сторона подставляется в формулу и в результате получается готовый ответ.
Итак,
(см).
При необходимости может быть вычислено приближенное значение полученного числа:
(см).

Ответ. 25,5 см.

Задача 2.
Найти диагональ квадрата с периметром 28 см.

Решение.
Запишем формулу для периметра квадрата, согласно которой:

Поскольку периметр из условия известен, то можно рассчитать длину стороны:
(см).
Далее применим формулу для диагонали квадрата, выраженную через его сторону:
(см).
Или приближенное значение:
(см).

Ответ. 9,9 см.

Задача 3.
Рассчитать диагональ квадрата при площади 25 кв. см.

Решение.
Запишем формулу для расчета площади квадрата:

Сторону квадрата, выраженная из этой формулы:
(см).
Теперь подставим полученное значение в формулу диагонали, выраженную через сторону:
(см)
Приближенное значение:
(см)

Источник

Как вычислить диагональ квадрата

Здравствуйте!
Как можно вычислить диагональ квадрата. Нужны формулы!
Спасибо!

Диагональ квадрата соединяет противолежащие углы квадрата. Обе диагонали квадрата пересекаются в его центре.
Для вычисления диагонали квадрата существует множество методов, выбор одного из которых зависит от тех исходных данных, которые известны по условию.
Разберем самые распространенные из вариантов как вычислить диагональ квадрата.

Для вычисления диагонали квадрата по его стороне существует формула, которая выводится с помощью теоремы Пифагора и выглядит следующим образом:

Если в условии задана длина стороны, то стоит только подставить ее значение в формулу и диагональ найдена.

Периметр квадрата равен сумме всех его сторон, то есть четырем сторонам квадрата:

Поскольку периметр известен, то из этой формулы можно вычислить сторону квадрата, которая будет равна:

А далее можно использовать формулу диагонали через сторону квадрата. В общем виде формула диагонали квадрата через периметр будет выглядеть так:

Запишем формулу для вычисления площади квадрата:

Поступаем таким же образом, как и в предыдущем случае — выразим сторону квадрата из данной формулы:

Теперь подставим полученное выражение в формулу диагонали через сторону:

Источник

Диагональ прямоугольника

Прямоугольник — четырёхугольник, у которого все углы равны 90 градусов, т. е. прямые.

Диагональ прямоугольника — прямая проложенная из противоположных вершин прямоугольника.

Диагонали прямоугольника равны и они делят прямоугольник на два равных прямоугольных треугольника.

Чтобы найти диагональ прямоугольника необходимо вспомнить теорему Пифагора, ведь диагональ — это гипотенуза прямоугольного треугольника, а стороны (длина и ширина) прямоугольника являются катетами треугольника.

Как найти диагональ прямоугольника

Воспользуемся теоремой Пифагора и формулой

d — диагональ квадрата

a — длина прямоугольника

b — ширина прямоугольника

Подставив в формулу вместо a длину прямоугольника, а вместо b — ширину прямоугольника и произведя расчет мы получим диагональ прямоугольника. Следует помнить, что у прямоугольника две диагонали и они равны между собой.

Диагональ прямоугольника онлайн калькулятор

Чтобы найти диагональ с помощью калькулятора введите длину и ширину прямоугольника и нажмите кнопку Рассчитать. В результате вы получите ответ и подробное решение.

Нахождение диагонали прямоугольника используется в различных жизненных ситуациях. К примеру, при проектировании фундамента дома необходимо проверить его диагонали — они должны быть равны между собой. Также на сайте можно рассчитать диагональ квадрата.

Источник

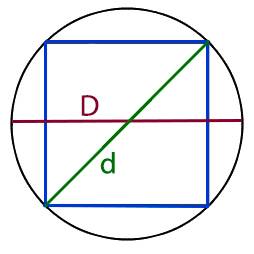
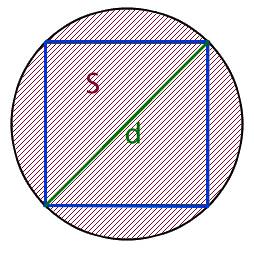
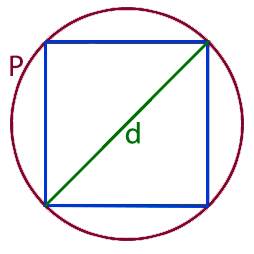
Онлайн калькулятор диагонали вписанного в круг квадрата. Как узнать длину диагонали вписанного в круг квадрата.

Вычислить диагональ вписанного квадрата через:Радиус круга R:

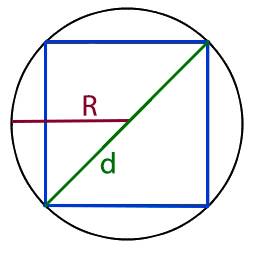
Для того что бы найти диагональ вписанного в круг квадрата, нам необходимо узнать диаметр круга в который вписан квадрат при этом диагональ квадрата (d) и диаметр круга (D) равны.

Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:

Теперь для того что бы найти диагональ треугольника (которая равна диаметру) нам необходимо перейти к следующему шагу

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

Соответственно если мы знаем диаметр круга мы знаем и длину диагонали квадрата,

Источник

Найти диагональ прямоугольника разными способами онлайн

Одна из основных фигур курса математики – прямоугольник. Впервые о нем заговорили еще в Древнем Египте, а позже и в Древней Греции. Именно свойства его диагоналей помогают решить многие задания учебного курса. Подход, который сейчас используется в геометрии разработал Евклид. Формулы, представленные в данной статье, пригодятся как при решении домашних упражнений, так и на ЕГЭ. Именно такие задачки помогают набрать недостающие баллы, поэтому ими не стоит пренебрегать.

Диагональ прямоугольника через его стороны

Если заданы хотя бы 2 стороны, то вычислить линию, соединяющую противоположные вершины, будет довольно просто. Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:

Где a, b – это стороны, а d – прямая, которую мы ищем.

Диагональ прямоугольника через площадь и известную сторону

Когда в дано есть S и одна сторона, то узнать искомое значение можно используя следующее равенство:

Где D – это прямая, которую необходимо найти, a и b – любая заданная сторона, а S – площадь.

Диагональ прямоугольника через периметр и сторону

Когда задан периметр (сумма сторон) и, хотя бы одна сторона, отрезок, соединяющий несмежные точки высчитывают так:

Где P – сумма сторон, a и b – любая заданная сторона.

Рассчитать искомый отрезок можно и через соотношение сторон и площадь.

Диагональ прямоугольника через диаметр описанной окружности

Поиск отрезка через описанную окружность еще более прост, здесь даже не придется проводить расчеты: D = d

Где d – это обозначенный диаметр.

Различить вписанную/описанную окружность легко. Когда геометрическое тело вписано куда-то, то оно всегда будет находиться в другой фигуре. Когда окружность описана, то она находится снаружи, она как бы описывает другое геометрическое тело. Описанные фигуры задевают собой точки, а вписанные – касаются сторон.

Диагональ прямоугольника через радиус описанной окружности

Для расчета искомого отрезка через описанную окружность нужно провести вычисления, где: D = 2R

Где R – это заданный радиус.

Диагональ прямоугольника через площадь и острый угол между диагоналями

Если необходимо узнать прямую, соединяющую вершины 4-хугольника, это можно осуществить с помощью двух диагоналей. Для получения ответа к задаче понадобится sin β между ними и S (произведение длины и ширины). Расчет проводится с равенством:

Где соответственно S – это площадь, а sin β – это острый угол, расположенный внутри фигуры (меж пересекающимися прямыми).

Если в 4-хугольнике расчертить 2 отрезка, объединяющие несмежные вершины, то они будут равны меж собой (все 4 отрезка), а точка пересечения разделит их пополам.

Пересечение всегда происходит в геометрическом центре самой фигурки. Этот же центр является центром описанной окружности.

Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу

Когда одна из сторон 4-хугольника прилегает к углу, то просчитать отрезок, соединяющий вершины тоже возможно:

Где b – это сторона, прилегающая к углу, а cos a – это тот самый угол.

Косинус угла в треугольнике с прямым углом рассчитывается по формуле – длина соседней стороны, разделенная на гипотенузу. Синус – это противолежащий катет, разделенный на гипотенузу. Либо можно поступить еще проще, подсмотрев в таблицу Брадиса.

Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу

Чтобы найти нужный отрезок внутри четырехугольника, должен быть задан угол, прилегающий к искомому отрезку и сторона, противоположная углу:

Где a – это сторона четырехугольника, а sin a – это прилегающий угол.

Длинная сторона 4-хугольника– это длина, а короткая – его ширина. Помните, что каждая сторона одновременно является высотой.

Что такое диагональ прямоугольника, когда требуется ее вычисление

Прямоугольник – это частный случай параллелограмма. Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.

Диагональ разделяет фигуру на два новых элемента – треугольники с прямым углом. Это прямая, объединяющая противоположные вершины. Имея 2 прямоугольных треугольника, отрезок уже можно рассчитать по теореме Пифагора. По теореме гипотенуза – это квадрат из суммы катетов (обозначенных сторон треугольника), возведенных в квадрат.

Линии, соединяющие противоположные точки в четырехугольнике всегда пересекаются друг с другом.

Отрезок обозначают как d или D. Если названы все точки, то его можно называть в соответствии с ними – AC или BD.

Знания о линии, проходящей через несмежные точки 4-хугольника может понадобиться в легких геометрических упражнениях, так и в более сложных многоуровневых задачках, которые появляются на ЕГЭ. Свойства данного отрезка помогают находить важные параметры прямоугольника. Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.

Перед решением любой геометрической задачки рекомендуется сделать чертеж и обозначить всю заданную информацию. Так будет значительно проще сосредоточиться на искомом значении.

Если регулярно решать тесты по геометрии, то формулы легче запомнятся, а их применение будет доведено до автоматизма.

Источник

Как найти диагональ квадрата если известна сторона

Здравствуйте!
Как найти диагональ квадрата, если известна сторона? Объясните, пожалуйста.
Спасибо!

Разберем Ваш вопрос: «Как найти диагональ квадрата, если известна сторона».
Рассмотрим квадрат ABCD.
Проведем в нем одну диагональ АС. Напомню, что диагональ квадрата соединяет два противолежащих угла.
Квадрат — это фигура, у которой равны все стороны. Следовательно, стороны АВ, ВС, CD и AD равны:
АВ = ВС = CD = AD.
А также у квадрата все углы прямые, то есть равны по 90 градусов.
Рассмотрим фигуру, которая образовалась диагональю и двумя сторонами квадрата. Мы получили треугольник АВС, у которого прямой угол между двумя сторонами, которые к тому же равны.
Следовательно, полученный треугольник — прямоугольный.
Исходя из сути вопроса стороны квадрата известны. Обозначим их равными какому-то числу а.
В прямоугольном треугольнике, таким образом, известны две стороны АВ и ВС, которые являются катетами, а нужно найти третью — АС, которая является гипотенузой.
К прямоугольному треугольнику можно применить теорему Пифагора. Запишем ее для нашего треугольника:

Так как стороны АВ и ВС известны и равны а, подставим их значения в формулу:

Источник

Квадрат, свойства и формулы, площадь и периметр

Квадрат, свойства и формулы, площадь и периметр.

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат (понятие, определение), диагональ квадрата:

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат – это четырехугольник, имеющий равные стороны и углы.

Все углы квадрата прямые. Каждый из них прямой и равен 90°.

Таким образом, все квадраты отличаются друг от друга только длиной стороны.

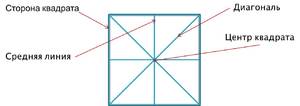
Рис. 2. Квадрат и диагонали квадрата

Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.

Квадрат – это равносторонний прямоугольник.

Квадрат – это ромб с прямыми углами.

Свойства квадрата:

1. Длины всех сторон равны.

2. Противоположные стороны квадрата параллельны.

3. Все углы квадрата прямые. Каждый из них равен 90°.

4. Сумма углов квадрата равна 360 градусам.

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.

5. Диагонали квадрата равны между собой.

6. Диагонали квадрата взаимно перпендикулярны.

7. Диагонали квадрата точкой пересечения делятся пополам.

8. Угол между диагональю и стороной квадрата равен 45 градусам.

9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.

10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.

11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.

Формулы квадрата. Площадь квадрата. Периметр квадрата:

Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.

Формула диагонали квадрата:

, , , , .

Формула радиуса вписанной окружности квадрата:

Радиус вписанной окружности квадрата равен половине его стороны.

.

Формула радиуса описанной окружности квадрата:

.

Формула периметра квадрата:

, , .

Формула площади квадрата:

, , , , .

Источник

Диагональ квадрата

Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.

Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
— Все стороны квадрата равны (от ромба)
— Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)

a 2 +b 2 =c 2
a 2 +b 2 =d 2
2a 2 =d 2

Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:

Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.

Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.

Формулы диагонали квадрата через площадь, периметр

Предложения и пожелания пишите на [email protected]

Поделитесь этим калькулятором на форуме или в сети!

Это помогает делать новые калькуляторы.

Источник

Узнаем как посчитать диагональ квадрата? Формула длины диагонали квадрата.

Как посчитать диагональ квадрата?

Безусловно, лучше всего просто запомнить формулу длины диагонали квадрата и пользоваться ею всегда, ведь это гораздо быстрее и удобнее. Особенно это чувствуется при решении задач в буквенном виде, где вместо целых больших подкорневых выражений можно обойтись лишь одним произведением.

Пример

Возьмем, к примеру, квадрат 6 на 6, то есть со стороной, равной шести сантиметрам.

Тогда получим, что С=√А^2+А^2 или С=√2А^2.

Запишем в числовом виде: С =√36 + 36. Получили √72, а это 3√8 или 6√2.

А теперь найдем ту же диагональ, но уже по второму способу: С = А√2 или в числовом виде: 6√2

Другие свойства диагоналей квадрата

Помимо знания того, как найти диагонали квадрата, нужно также знать и их свойства. Основные из них:

Вывод

Вопросом, как посчитать диагонали квадрата, обычно задаются ученики, пропустившие эту тему в школе. Однако такие фундаментальные правила математики должен знать каждый! Желательно решать как можно быстрее, и для этого необходимы знания сокращенных формул. Все это предельно просто и легко, но вместе с тем является базой, необходимой для решения в дальнейшем гораздо более сложных задач. И важную часть этой базы занимает квадрат.

Источник

Диагонали квадрата

Свойства диагоналей квадрата

Свойство 1

Диагонали квадрата равны.

Свойство равенства диагоналей следует из свойств прямоугольника:

Свойство равенства диагоналей квадрата

Свойство 2

Диагонали квадрата точкой пересечения делятся пополам.

Свойство пересечения диагоналей квадрата следует из свойств прямоугольника:

Пересечение диагоналей квадрата

Свойство 3

Диагонали квадрата пересекаются под прямым углом:

Свойство пересечения диагоналей квадрата под прямым углом следует из свойств ромба.

Пересечение диагоналей квадрата

Свойство 4

Точка пересечения диагоналей квадрата – это центр квадрата, а также центр описанной и вписанной окружностей.

Точка пересечения диагоналей квадрата

Свойство 5

Диагонали квадрата и являются биссектрисами его углов:

Данное свойство диагоналей квадрата следует из свойств ромба.

Диагонали и биссектрисы углов квадрата

Свойство 6

Диагональ квадрата через его сторону

Диагональ квадрата равна произведению его стороны на квадратный корень из двух:

Данное свойство следует из теоремы Пифагора:

Диагональ квадрата через его площадь

Диагональ квадрата через его сторону и площадь

Свойство 7

Диагональ квадрата делит его на два равных прямоугольных равнобедренных треугольника, которые являются симметричными фигурами.

Свойство диагонали квадрата

Свойство 8

Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника.

Свойства диагоналей квадрата

Свойство 9

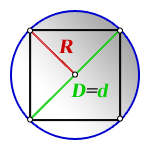
Диагональ квадрата и описанная окружность

Диагональ квадрата равна диаметру описанной окружности.

Диагональ квадрата в два раза больше радиуса описанной окружности вокруг квадрата:

Диагональ квадрата через радиус вписанной окружности:

Диагональ квадрата и описанная окружность

Свойство 10

Диагональ квадрата через отрезок, который соединяет вершину квадрата с серединой противоположной стороны:

a – сторона квадрата;

d – диагональ квадрата;

P – периметр квадрата;

S – площадь квадрата;

R – радиус окружности, описанной около квадрата;

r – радиус окружности, вписанной в квадрат;

l – отрезок, соединяющий вершину квадрата с серединой противоположной стороны.

Источник

как найти диагональ квадрата,стороны у которого равны 4

Второй способ (по теореме Пифагора):
диагональ d1 квадрата является гипотенузой прямоугольного треугольника, катетами которого являются стороны квадрата.
d1² = 4² + 4²
d1² = 16 + 16 = 32
d1 = √32 = 4√2

Третий способ (через вписанную и описанную в\около квадрата окружности) :
Радиус вписанной окружности квадрата равен:
r = a / 2
Радиус описанной окружности квадрата равен:
R = (√2 / 2) · a
площадь квадрата равна:
S = a² = 2R² = 4r²
Радиус описанной окружности равен половине диагонали:
R = d1 / 2
S = 4² = 16
2R² = 16
R² = 8
R = 2√2
d1 = R · 2 = 2√2 · 2 = 4√2

вспомнить, что квадрат состоит из двух прямоугольных треугольников и, по теореме Пифагора
диагональ можно рассчитать из соотношения
c^2 = 4^2 + 4^2 = 32

Источник

Диагональ прямоугольника

Четырехугольник, противоположные стороны которого параллельны друг другу, а все углы прямые, называется прямоугольником. Отрезок, который соединяет две противоположные вершины прямоугольника, будет его диагональю d. В прямоугольнике обе диагонали равны. Если провести в прямоугольнике диагональ, то она поделит его на 2 одинаковых прямоугольных треугольника, у которых диагональ d будет гипотенузой, а стороны прямоугольника a, b — катетами. Если известны длины сторон прямоугольника, несложно определить его диагональ, используя теореме Пифагора. Согласно теоремы квадрат гипотенузы равен сумме квадратов катетов.

d 2 = a 2 + b 2

Исходя из этого, гипотенуза равна корню квадратному из суммы квадратов катетов. Как было отмечено выше, гипотенуза является диагональю прямоугольника, соответственно она вычисляется по формуле:

Источник

О диагонали квадрата

Введение в оборот комплексных чисел было далеко не первой революцией в понимании человеком природы числа. За две тысячи лет до этого мощнейшее потрясение испытал мир древнегреческой математики.

Неприятности у пифагорейцев начались далеко не сразу. Основанная Пифагором научная школа в итоге кончила плохо, но сегодняшний рассказ не о том бодром погроме, который был учинен над пифагорейцами благодарным за просвещение народом, а в большей степени о духовных перипетиях.

Термин «научная школа» по отношению к организации, основанной Пифагором, является эдаким эвфемизмом. Здраво взглянув на ее структуру и применяемые технологии, пифагореизм следует смело отнести к тоталитарным культам, что было вполне в духе времени (впрочем, это всегда в духе времени, вечная классика). Наличествовало и разделение на степени посвящения, и сложная система ритуалов с запретами (например, общеизвестные, вроде «не есть бобов» или «не откусывать от целой булки»), и сложное философское вероучение. Привет Рону Хаббарду сотоварищи. Ничто не ново под Луной.

В целом, при жизни Пифагора его «школа» была солидным предприятием, к тому же обладающим значительным и все время растущим политическим влиянием.

Вообще, философия Пифагора оказала значительное влияние на западную культуру (и на нас в том числе). Многие идеи нашли свое развитие в классической греческой философии, а уже про теорему Пифагора знают вообще все. Выражение «гармония сфер», кстати, также восходит к пифагорейцам.

Одним из существенных элементов их философии была идея, что любое число можно представить как отношение двух целых чисел, то бишь в виде простой дроби. В этом они, в том числе, видели совершенство природы числа. Больше того, это представлялось вполне очевидным. В современной математике такие числа называются рациональными, а их множество обозначается знаком 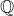. Сделайте теперь паузу на несколько секунд, задумайтесь, откуда вообще следует, что это не так? Можете ли вы привести аргумент, который был бы достаточно убедителен для древнего грека? Ну или, хотя бы, достаточно убедителен для себя, лично?

В общем, мир чисел был прост, изящен, и все были довольны. Источником возникших неприятностей, неожиданно, стала уже помянутая теорема, носящая имя Пифагора: одно из важнейших, дошедших до нас, его достижений. К сожалению, доказательство самого Пифагора нам неизвестно. Самое старое из дошедших до нас — приведено в «Началах» Евклида и датируется 3 в. д.н.э. Напомню, сам Пифагор жил в 6 в. д.н.э.

Фрагмент из Vatican Manuscript Number 190, датируемого 10 в. н.э. (целиком здесь):

Доказательство Евклида далеко не самое простое. Есть основания считать, что он знал путь и попроще, но из методических соображений привел именно этот вариант, демонстрирующий, помимо собственно теоремы Пифагора, и некоторые другие интересные идеи.

Однако, вернемся к пифагорейцам.

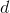
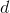
Вот представьте себе простейшую вещь: квадрат со сторонами единичной длины. Если обозначить длину его диагонали , то по теореме Пифагора получим:

и, соответственно: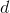

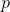
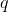
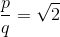
Само-то по себе это еще не проблема. С точки зрения пифагорейцев, дальше просто нужно было найти целые числа и , такие что

Вот на этом-то «простом» моменте все и застопорилось. Причем наглухо. Стопор сей продолжался до тех пор, пока один умник (как утверждают, Гиппас из Метапонта, тоже пифагореец), не доказал, внезапно, что таких чисел не существует. Все зло от шибко умных идет, как известно. По легенде, это научное достижение столь потрясло коллег, что, в ознаменование признания научных заслуг, Гиппаса не медля вышвырнули за борт корабля, на котором он в момент своего математического озарения плыл. А вот нечего было гадить уважаемым людям, подрывать основы столь любовно выпестованной и весьма доходной философской системы.

Ныне, числа не представимые в виде отношения двух целых, называются иррациональными.

Некоторое время пифагорейцы даже держали факт иррациональности в секрете. Однако, шила в мешке не утаишь, и правда довольно быстро (по историческим меркам) нашла путь наружу.

Доказать иррациональность совсем не сложно.
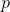
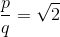
Пусть существуют такие , что

Более того, будем считать, что хотя бы одно из чисел 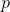— нечетно. Если это не так, числитель и знаменатель дроби всегда можно сократить на 2 (нужное количество раз).
Тогда получим: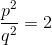

отсюда: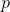

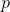
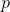
Таким образом, — четное число. Но тогда и — четное.

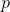
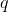
По условию нечетности хотя бы одного из чисел , получим, что — нечетно.
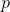
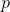
В силу четности , можно записать
,
где 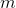— некоторое целое.
Но тогда:

отсюда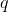

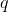
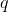
Но это означает, что — четно, а значит четно и . Противоречие.

Число невозможно представить в виде отношения двух целых чисел.

Остается добавить, что — это вовсе не какой-то странный уродец. Можно показать, что иррациональных чисел больше, чем рациональных, принципиально больше. Кстати, отношение больше-меньше в мире бесконечных множеств само бывает весьма контритуитивным. Но это уже другая история.

PS. Пользуясь случаем, поздравляю хабровчан с наступающими. Удачи в новом году!

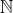
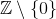
UPD. В связи с разгоревшейся в комментариях дискуссией хочу заметить следующее: если по-честному, то рациональные числа вводятся как поле частных кольца целых чисел. Использовать ли в качестве мультипликативной системы множество или множество — сугубо дело вкуса, никак не влияющее на результат. Вопрос же, какое из школьных псевдоопределений «верно», решается министерством образования, и к математике этот процесс имеет весьма отдаленное отношение.

Источник

Как сделать диагональ квадрата?

Напоминание: диагонали d’un квадрат иметь одинаковую длину et перпендикулярны в своей середине. Чтобы построить квадрат ABCD из диагональный 6 см: рисуем отрезок [ас] 6 см et ставим его середину о; проведем прямую, перпендикулярную в O к [AC], на которой поместим D et B такой, что OD = OB = 3 см.

Как рассчитать диагональ? Как рассчитать длина диагональный прямоугольника

Для диагональный [AC], изучите один из прямоугольных треугольников ABC или ADC и y вычисление AC с теоремой Пифагора: AC 2 = АВ 2 + БК 2 = л 2 + л 2 для прямоугольника длины AB = L и ширины BC = l.

Как построить диагональ? Напоминание: диагонали прямоугольника имеют одинаковую длину и пересекаются посередине. За строить прямоугольник, чей диагонали отмерьте 6 см: начертите круг радиусом 3 см, затем два диаметра; их концы являются вершинами прямоугольника.

Диагональ квадрата равна стороне?

Elle равно длина боковая сторона.

Итак, как сделать квадрат 10 см?

Как нарисовать квадрат?

Как нарисовать четырехугольник см2?

Чему равны диагонали прямоугольника?

– Если четырехугольник прямоугольник так что это два диагонали одинаковой длины. – Если четырехугольник прямоугольник тогда у него есть две оси симметрии, перпендикулярная к его сторонам посередине.

Чему равны диагонали прямоугольника? Mesures

Чему равны диагонали ромба?

этот четырехугольник является un алмаз ; у этого четырехугольника четыре стороны одинаковой длины и четыре различные вершины; в диагонали этого четырехугольника пересекаются посередине (другими словами: c’является параллелограмм) и они находятся перпендикуляр.

Как вычислить сторону квадрата по его диагонали?

Таким образом, формула для расчета l’aire d’un квадрат с диагоналями это: площадь квадрат = диагональ² / 2.

Как найти длину стороны квадрата с его диагональю?

Как сделать в Ворде квадрат со стороной 8 см? Выбирать вставить > Формы.
.
Советы:

Как нарисовать квадрат со стороной 5 см? Используя линейку, трассирующие отрезок, размер которого соответствует размеру одной из сторон квадрат (5 см). 2. Поместите квадрат на один конец начального сегмента и трассирующие перпендикулярная линия, выступающая 5 см. 3.

Как нарисовать квадрат на белом листе?

Как сделать квадрат на белом листе?

Как найти квадратную линию?

Из точки (A) вы проводите линию, проходящую через две именованные точки (C), как на изображении. Горизонтальная и вертикальная линии образуют угол 90°. В некоторых профессиях это называется ( квадратная линия). Эта калька будет отправной точкой для выполнения рабочего чертежа фермы, полуфермы или др.

Как нарисовать квадрат ce2?

Как нарисовать четырехугольник?

Шаги, которые нужно выполнить: Шаг 1: С помощью градуированной линейки мы прослеживать отрезок длины АВ = 6 см. Шаг 2: Используя квадрат, мы помещаем прямой угол в точку B и прослеживать отрезок длины ВС = 4 см. Шаг 3: Все еще с квадратом, мы прослеживать перпендикуляр к (BC), проходящий через точку C.

Как классифицировать четырехугольники?

Как определить четырехугольник?

многоугольник четырехсторонняя замкнутая фигура, имеющая в геометрии четыре стороны. Пример: Параллелограмм уподобляется четырехугольник, имеющая противоположные стороны параллельны два на два, при этом трапеция также параллельна, при этом параллельны только ее основания, противоположные.

Источник

Как найти диагональ квадрата

Итак, стоит начать с того, что вокруг квадрата можно описать окружность, диагональ которой в точности равна диагонали квадрата. Для того, чтобы подсчитать радиус описанной окружности, надо воспользоваться формулой:

Также в квадрат можно и вписать окружность. При этом окружность в точках касания ее со сторонами квадрата делит их пополам. Формула, с помощью которой можно вычислить радиус вписанной окружности, выглядит так:

Если, при решении задачи, известен радиус окружности, который вписан в данный квадрат, то возможно таким образом выразить и сторону квадрата, величина которой необходима для нахождения диагонали квадрата:

Длина радиуса окружности равна половине длины ее диагонали. Таким образом, длина диагонали описанной окружности, а, значит, и длина диагонали квадрата может быть рассчитана по формуле:

Для большей ясности, можно рассмотреть небольшой пример:

Дан квадрат с длиной стороны 9 см, требуется найти длину ее диагонали.

Решение: для того, чтобы подсчитать ее длину, потребуется воспользоваться формулой выше:

Ответ: длина диагонали квадрата со стороной 9 см равна √162 см или, приблизительно, 14.73 см

Источник

Как найти диагональ квадрата

Квадрат представляет собой верный четырехугольник либо ромб, у которого все стороны равны и образуют между собой углы в 90 градусов. Диагональ квадрата – отрезок, тот, что соединяет между собой два противоположных угла квадрата.Обнаружить диагональ квадрата довольно легко

Инструкция

1. Выходит, стоит начать с того, что вокруг квадрата дозволено описать окружность, диагональ которой в точности равна диагонали квадрата. Для того, дабы подсчитать радиус описанной окружности, нужно воспользоваться формулой:R = (?2*a)/2, где a – это сторона квадрата.Также в квадрат дозволено и вписать окружность. При этом окружность в точках касания ее со сторонами квадрата делит их напополам. Формула, по средствам которой дозволено вычислить радиус вписанной окружности, выглядит так:r = a/2Если, при решении задачи, знаменит радиус окружности, тот, что вписан в данный квадрат, то допустимо таким образом выразить и сторону квадрата, величина которой нужна для нахождения диагонали квадрата:a = 2*r

Совет 2: Как обнаружить диагональ ромба

У ромба стороны равны и попарно параллельны. Его диагонали пересекаются под прямым углом и делятся точкой пересечения на равные части. Эти свойства легко дозволяют обнаружить величину диагоналей ромба.

Инструкция

1. Обозначим вершины ромба буквами латинского алфавита A, B, C и D для комфорта обсуждения. Точку пересечения диагоналей обычно обозначают буквой O. Длину ребра ромба обозначим буквой a. Величину угла BCD, тот, что равен углу BAD, обозначим α.

2. Обнаружим величину короткой диагонали. Потому что диагонали пересекаются под прямым углом, то треугольник COD является прямоугольным. Половина короткой диагонали OD является катетом этого треугольника и может быть обнаружена через гипотенузу CD, а также угол OCD.Диагонали ромба являются также биссектрисами его углов, следственно угол OCD равен α/2.Таким образом, OD = BD/2 = CD*sin(α/2). То есть, короткая диагональ BD = 2a*sin(α/2).

3. Аналогичным образом, из того, что треугольник COD прямоугольный, можем выразить величину OC (а это половина длинной диагонали).OC = AC/2 = CD*cos(α/2)Величина длинной диагонали выражается дальнейшим образом: AC =2a*cos(α/2)

Обратите внимание!
Ромб с прямыми углами именуется квадратом.Из прямоугольности треугольника COD, как и остальных 3 треугольников, образованных диагоналями и сторонами ромба, вытекает еще такое качество ромба: AC²+BD²=4a²

Полезный совет
Зная диагонали, легко обнаружить площадь ромба. Обыкновенно для этого их и вычисляют. Площадь ромба равна половине произведения его диагоналей.

Совет 3: Как обнаружить диагональ у квадрата

Инструкция

1. Диагональ квадрата обнаружить довольно легко, воспользовавшись теоремой Пифагора.Поделим квадрат диагональ ю на два равных треугольника. В этом случае диагональ будет являться гипотенузой одного из треугольников. А, как вестимо, квадрат гипотенузы равен сумме квадратов катетов.Рассматривая. что катеты – стороны квадрата и они равны, формула для расчета диагонали квадрата по его стороне дюже примитивна:длина диагонали квадрата равна длине его стороны умноженной на корень из 2-х.

Видео по теме

Полезный совет
Если точность математического итога не дюже значима, то взамен корня из 2-х дозволено применять его примерное значение 1,41.

Совет 4: Как вписать квадрат в окружность

Вписать квадрат в окружность легко дозволено с поддержкой чертежных инструментов. Но эта задача решается даже при полном их отсутствии. Нужно только помнить некоторые свойства квадрата.

Вам понадобится

Инструкция

1. Нарисуйте эскиз к задаче. Видимо, что диаметр окружности является диагональю вписанного в эту окружность квадрата. Припомните вестимое качество квадрата: его диагонали взаимно перпендикулярны. Используйте эту связь диагоналей при построении заданного квадрата.

2. Начертите в окружности диаметр. Из центра с поддержкой угольника проведите 2-й диаметр под углом 90 градусов к первому. Объедините точки пересечения перпендикулярных диаметров с окружностью и получите вписанный в эту окружность квадрат.

3. Если из чертежных инструментов у вас имеется только циркуль, начертите окружность. Подметьте на окружности произвольную точку и проведите через нее диаметр с поддержкой всякого предмета с ровным краем. Сейчас надобно с подмогой циркуля поделить половину окружности между концами диаметра на две равные части. Из точек пересечения диаметра с окружностью сделайте две засечки, сберегая постоянным раствор циркуля. Через точку пересечения этих засечек и центр окружности проведите 2-й диаметр. Видимо, что он будет перпендикулярен первому.

4. Если чертежных инструментов у вас нет, дозволено ножницами вырезать из бумаги круг, ограниченный заданной окружностью. Сложите вырезанную фигуру верно напополам. Повторите операцию. Надобно совместить концы линии сгиба, тогда криволинейные участки совпадут без дополнительных усилий. Зафиксируйте линии сложения. Сейчас разверните круг. Линии сгибов ясно видны. Загните секции круга между точками пересечения линий сгибов с окружностью и отрежьте эти секции. Линии отреза являются сторонами желанного квадрата. Разместите вырезанный квадрат в заданную окружность, совместив ее центр с точкой пересечения линий сгиба круга. Вершины квадрата окажутся лежащими на окружности, что и требовалось исполнить.

Видео по теме

Полезный совет
Невозможно забывать, что квадрат является уникальной геометрической фигурой. Квадрат владеет пятью осями симметрии, четыре из которых являются отражательными осями, а одна – вращательной.

Источник

Чему равна диагональ квадрата? Как найти диагональ квадрата?

Два способа решения.

Диагональ квадрата представляет собой отрезок, соединяющий две противоположные вершины.

В то же время диагональ разбивает квадрат на 2 равных прямоугольных треугольника.

Таким образом, чтобы найти диагональ квадрата, следует воспользоваться теоремой Пифагора.

Перепишем формулу в виде:

Выразим диагональ c:

Таким образом, диагональ квадрата равна произведению его стороны на квадратный корень из числа 2.

Пример

Сторона квадрата равна 10 см.

Диагональ будет равна 10 * √2 см ≈ 14 см.

Если поделить квадрат диагональю, то мы увидим перед собой два одинаковых прямоугольных треугольника, а диагональ квадрата будет для любого из этих треугольников гипотенузой. А как рассчитывать длину гипотенузы, зная длину катетов, мы все знаем. Для этого у нас имеется теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Катеты у нас равны друг другу (потому что у нас квадрат), значит, обозначив длину катета латинской буквой «а», а длину гипотенузы латинской буквой «с», получаем формулу:

Ответ: диагональ квадрата равна квадратному корню из суммы квадратов его сторон.

Под диагональю квадрата понимается отрезок, соединяющий противоположные углы квадрата. Для того, чтобы найти диагональ квадрата, можно воспользоваться следующими формулами, для которых нужно знать, чему равна сторона квадрата, площадь или периметр:

К примеру, если у нас есть квадрат со сторонами 100 см, то его диагональ будет по формуле

√2*a = √2*100 = 1,4142*100 = 141,42 см.

Например, если длина стороны квадрата 5 сантиметров, то, согласно нашей формуле, длина диагонали будет: d=5√2, или d=5*1,414=7,07.

Длину диагонали можно узнать, если известны, например, площадь или периметр квадрата. В этом случае придется использовать сразу несколько формул.

То есть вот так:

Это можно вычислить так же по теореме Пифагора, при которой сторона a*a+a*a=2a*a, из этого извлекаем корень и получаем √2а.

Так же как и найти гипотенузу у равнобедренного треугольника.

Квадрат это правильная геометрическая фигура, имеющая четыре равных стороны.

Имея в условии слово «квадрат» можно вообще найти его диагональ по одной стороне, ибо все остальные будут равные ёй.

Длину одной из сторон, умножить её на два и возвести в квадрат. Результатом и будет квадрат диагонали.

Диагональ квадрата принято рассчитывать, оперируя понятиями сторона, площадь и периметр. Имея эти данные легко воспользоваться формулами для расчета диагонали квадрата.

По данной тематике очень много нюансов и я бы посоветовал Вам сайт,по которому сам лично готовился к экзаменам для поступления.Расписыв­ ать очень много ибо поэтому заходите сюда и читайте,я посмотрел всё что нужнои даже больше о данной теме смотрите тут

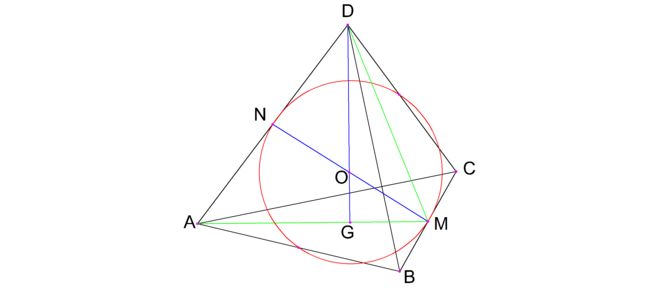
Как найти ребро тетраэдра, в который вписан шар так, что он касается всех его ребер?

Шар радиусом R=3,98 и с центром О касается всех рёбер тетраэдра ABCD. Точки касания шара приходятся на середины рёбер, так как вершины тетраэдра равноудалены от центра О.

Плоскость, проведённая через ребро AD и высоту тетраэдра DG, пересечёт ребро ВС в его середине М. В полученном равнобедренном треугольнике AMD (MD = AM) его медиана MN является также высотой, т. е. треугольник MNA будет прямоугольным. В треугольнике сторона MN пересекает DG посередине и совпадает с центром О, так как она равноудалёна от точек А и D. Следовательно, MN равна диаметру шара — 2R

Апофема равностороннего треугольника ABC с ребром а

Чтобы решать подобные задачи, нужно помнить, что в них существуют 4 скорости: скорость течения реки, скорость катера, скорость катера ПО течению(сумма 2 предыдущих скоростей), скорость катера ПРОТИВ течения( разность 2 предыдущих скоростей).

Если сложение дробей определено таким правилом (a/b + c/d = (a + c)/(b + d)), то умножение тоже может быть определено таким же «придуманным» правилом. То есть варианты могут быть разные, все зависит от фантазии автора.

Евклидово расстояние есть длина отрезка прямой, проведённой через две точки, между которыми измеряется расстояние, причём отрезок вот этими двумя точками определяется. Правило, по которому вычисляется расстояние, называется метрикой пространства. В частности, для евклидова пространства это расстояние вычисляется по обычной теореме Пифагора, как корень из суммы квадратов координат вектора, соответствующего отрезку.

Для неевклидовых пространств правило может быть другим, в частности вообще может быть невозможно однозначно измерить расстояние (в пространстве, рассматриваемом в Общей теории относительности).

Источник

Как вычислить длину диагонали

Диагональ – отрезок, соединяющий две вершины какой-нибудь фигуры, не лежащие на одной стороне. Для вычисления ее длины почаще каждого применяется теорема Пифагора либо теорема косинусов.

Инструкция

3. В некоторых случаях для вычисления диагонали нужно делать добавочные построения.Пример 3: равносторонний многоугольник со стороной, равной 6 см, угол BCD прямой. Обнаружьте длину диагонали AB.Решение: объедините точки B и D. Получился прямоугольный треугольник BCD, в котором сторона BD является гипотенузой. Вычислите гипотенузу BD: BD?=BC+CD?; BD?=6?+6?=72; Гипотенуза BD из треугольника BCD является катетом в треугольнике ABD. А диагональ AB – гипотенуза в нем. Вычислите диагональ AB: AB?=BD?+AD?=72+36=108; AB=?108=10,4 см.Результат: длина диагонали AB=10,4 см.

4. Диагональ куба дозволено обнаружить через диагональ одной из его граней.Пример 4: куб со стороной 5 см. Обнаружьте диагональ куба.Решение: достройте и вычислите диагональ грани куба. AC?=5?+5?=50. Диагональ AC перпендикулярна ребру CB, следственно, угол ACB – прямой. Диагональ куба AB – гипотенуза в треугольнике ACB. Обнаружьте длину диагонали куба: AB?=AC?+CB?=50+25=75; извлеките квадратный корень. AB=?75=8,7 см.Результат: длина диагонали куба – 8,7 см.

Совет 2: Как вычислить площадь куба

Куб представляет собой частный случай параллелепипеда, в котором вся из граней образована положительным многоугольником – квадратом. Каждого куб владеет шестью гранями. Вычислить площадь не представляет сложностей.

Инструкция

1. Изначально нужно вычислить площадь всякого из квадратов, тот, что является гранью данного куба. Площадь квадрата дозволено вычислить, перемножив друг на друга пару из его сторон. Формулой это дозволено выразить так:S = a*a = a?

2. Сейчас, зная площадь одной из грани квадрата, дозволено узнать площадь каждой поверхности куба. Это дозволено осуществить, если модифицировать формулу, указанную выше:S = 6*a?Напротив говоря, зная, что таких квадратов (граней) у куба даже шесть штук, то площадь поверхности куба составляет площадей одной из граней куба.

3. Для наглядности и комфорта дозволено привести пример:Возможен, дан куб, у которого длина ребра равна 6 см, требуется обнаружить площадь поверхности данного куба. Изначально понадобится обнаружить площадь грани:S = 6*6 = 36 см?Таким образом, узнав площадь грани, дозволено обнаружить и всю площади поверхности куба:S = 36*6 = 216 см?Результат: площадь поверхности куба с ребром, равным 6 см, составляет 216 см?

Обратите внимание!
Куб является частным случаем не только параллелепипеда, но и призмы.Параллелепипедом именуется призма, у которого основанием является параллелограмм. Спецификой параллелепипеда является то, что 4 из 6 его граней – прямоугольники.Призмой считается многогранник, в основании которого находятся равные многоугольники. Одной из основных особенностей призмы дозволено назвать то, что боковые грани ее является параллелограммами. Помимо куба, существуют и иные виды многогранников: пирамиды, призмы, параллелепипеды и т.д., всему из них соответствуют разные методы нахождения площадей их поверхностей.

Полезный совет
Если дан не куб, а другой верный многогранник, то в любом случае, площадь его поверхности будет находиться подобно. Это обозначает, что площадь поверхности верного многогранника находится путем суммирования всех площадей его граней – положительных многоугольников.

Совет 3: Как вычислить длину

Длина характеризует расстояние между исходной и финальной точками отрезка. Различают длину прямой, ломаной и замкнутой линий. Ее находят экспериментальным либо аналитическим методом.

Инструкция

1. Термин «длина» у большинства людей ассоциируется с соответствующей колляцией прямой линии. Впрочем на самом деле, данный параметр имеется у линии всякий формы. Так, скажем, она имеется у окружности.

2. Окружность представляет собой замкнутый отрезок, тот, что является образующей круга. Если верно следовать определению, то окружностью именуется геометрическое место точек плоскости, равноудаленных от ее центра. Все окружности имеют определенный радиус, обозначаемый как r, а также диаметр, равный D=2r. Длина этой линии равна значению выражения:C=2?r=?D, где r – радиус окружности, D – диаметр окружности.

3. Если речь идет о прямой линии, то имеется в виду либо обыкновенный отрезок, либо замкнутая фигура, такая как треугольник либо прямоугольник. Для последнего длина является стержневой колляцией. Примитивный отрезок дозволено измерить экспериментально, а длину стороны у фигуры комфортнее каждого вычислить. Особенно легко осуществить эту операцию в отношении прямоугольника.

5. Длина стороны треугольника находится несколько другим методом. Для определения этой величины нужно знать не только длины остальных сторон, но и значения углов. Если дан прямоугольный треугольник с углом 60° и стороной с, которая является его гипотенузой, длину катета обнаружьте по дальнейшей формуле:a=c*cos?.Помимо того, если в задаче дана площадь треугольника и высота, длину основания дозволено обнаружить по иной формуле:a=2?S/??3.

6. Длину сторон всякий фигуры проще каждого обнаружить, если она равносторонняя. Скажем, если вокруг равностороннего треугольника описана окружность, длину стороны этого треугольника вычислите дальнейшим образом:a3=R?3.Для произвольного верного n-угольника сторону обнаружьте дальнейшим образом:an=2R*sin(?/2)=2r*tg(?/2), где R – радиус описанной окружности, r – радиус вписанной окружности.

Видео по теме

Совет 4: Как вычислить диагональ прямоугольника

Прямоугольник – одна из простейших геометрических фигур, которая, имея все углы идентичными и равными 90°, является частным случаем параллелограмма. Отрезок, соединяющий две вершины прямоугольника, не имеющие всеобщей стороны, именуется диагональю этого многоугольника. Вычислить длину диагонали дозволено несколькими методами в зависимости от вестимых начальных данных.

Инструкция

1. Если вестимы длины обеих сторон (A и B) прямоугольника, то длину диагонали (C) дозволено определить как квадратный корень из суммы квадратов длин сторон. Это вытекает из теоремы Пифагора, потому что диагональ в этой геометрической фигуре образует прямоугольный треугольник, двумя другими сторонами которого являются стороны прямоугольника. Диагональ в этом треугольнике является гипотенузой, а стороны прямоугольника – катетами. То есть: C=√(A²+B²).

2. Если длина одной из сторон незнакома, но вестима длина иной (A) и площадь (S) прямоугольника, то длину диагонали тоже дозволено вычислить. Потому что площадь прямоугольника находится умножением длин его сторон, то незнакомую сторону дозволено выразить как частное от деления площади на длину иной стороны. Подставьте это выражение в полученную на первом шаге формулу: C=√(A²+S²/A²)=√(A?+S²)/A.

3. Если вестима длина одной из сторон прямоугольника (A), а также длина его периметра (P), то длину 2-й стороны тоже дозволено определить. Потому что периметр в прямоугольнике – это удвоенная сумма 2-х сторон, то всякую сторону дозволено определить как разность между полупериметром и длиной иной стороны. Подставьте это выражение во все ту же формулу из первого шага: C=√(A²+(P/2-A)²=√(A²+P²/4-P×A+A²)=√(2×A²+P²/4-P×A).

4. Если знаменит радиус окружности (R), в которую вписан прямоугольник, то диагональ его будет равна удвоенному радиусу, потому что центр прямоугольника и круга в этом случае совпадают. Прямая, соединяющая две точки круга и проходящая через его центр равна его диаметру, то есть двум радиусам. А потому что вершины этого прямоугольника лежат на окружности, а соединяющая их диагональ проходит через центр, то она тоже соответствует определению диаметра круга: C=2×R.

5. Если знаменит радиус вписанной в прямоугольник окружности (r), то длины его сторон идентичны. Данный частный случай прямоугольника именуется квадратом. Определить длину сторон в этом случае дозволено как удвоенную длину радиуса окружности, а подставив это выражение в формулу из первого шага, вы получите: C=√(4×r²+4×r²)=r×√8.

Совет 5: Как вычислить площадь параллелограмма

Параллелограмм – это выпуклая четырехугольная геометрическая фигура, в которой пары противоположных сторон имеют идентичную длину. Также и пары углов в противоположных вершинах имеют идентичные величины. Всякий отрезок, соединяющий две противоположные стороны и перпендикулярный всякой из них, дозволено назвать высотой этого четырехугольника. Умение длин сторон, величин углов и высот в различных сочетаниях этих параметров разрешает рассчитать площадь параллелограмма.

Инструкция

1. Если знаменита величина угла в всякий вершине параллелограмма (?) и длины прилегающих к нему сторон (a и b), то рассчитать площадь фигуры (S) дозволено с применением тригонометрической функции – синуса. Перемножьте знаменитые длины сторон на синус знаменитого угла: S=a*b*sin(?). Скажем, если угол составляет 30°, а длины сторон 15,5 и 8,25 сантиметров, то площадь фигуры будет равна 63,9375 см?, потому что 15,5*8,25*sin(30°)=127,875*0,5=63,9375.

2. Если знамениты длины (a) 2-х параллельных сторон (они идентичны по определению) и высота (h), опущенная на всякую из этих сторон (они тоже идентичны), то этих данных довольно для расчета площади (S) такого четырехугольника. Умножьте вестимую длину стороны на высоту: S=a*h. Скажем, если длина противоположных сторон составляет 12,25 сантиметров, а высота – 5,75 сантиметров, то площадь параллелограмма будет равна 70,07 см?, потому что 12,25*5,75=70,07.

3. Если длины сторон незнакомы, но есть данные о длинах диагоналей параллелограмма (e и f) и величина угла между ними (?), то этих параметров довольно для вычисления площади (S) фигуры. Обнаружьте половину от произведения вестимых длин диагоналей на синус угла между ними: S=?*e*f*sin(?). Скажем, если длины диагоналей равны 20,25 и 15,75 сантиметрам, а угол между ними равен 25°, то площадь многоугольника составляет примерно 134,7888 см?, потому что 20,25*15,75*sin(25°)?318,9375*0,42261?134,7888.

4. Используйте при расчетах, скажем, калькулятор, совмещенный с функцией поиска в поисковой системе Nigma. Он комфортен тем, что разрешает рассчитывать площадь параллелограмма, вводя всю последовательности математических действий одной строкой. Скажем, для вычисления площади с данными, приведенными в последнем шаге, введите в строку поискового запроса 20,25*15,75*sin(25) и нажмите кнопку отправки данных на сервер. Сервер вернет рассчитанное значение площади с точностью до 12 знаков позже запятой (134,788811853924).

Видео по теме

Совет 6: Как вычислить похитителя в коллективе

К сожалению, изредка даже в самых сплоченных и дружных коллективах возникают похитители. Сотрудники начинают скрупулезно присматриваться друг к другу, пытаясь осознать, кто же ворует вещи и деньги. И зачастую получается, что и подумать не на кого, впрочем пропажи продолжаются.

Вам понадобится

Инструкция

2. Наблюдательно приглядитесь к коллегам. Посмотрите на поведение всего работника. Глаза у вора зачастую «бегают» в поисках наживы, а если он встретится взором с вами, он здесь же отведет глаза.

3. Побеседуете с всяким работником. Тет-а-тет скажите своему коллеге, что вы верно знаете, что похититель – это он, и посмотрите на его реакцию и поведение. Улики и доказательства вы вряд ли сумеете обнаружить, но такие беседы помогут вам осознать, кто же ворует дорогие вещи.

4. Приобретите особый порошок и фонарь. Таким порошком обрабатывают деньги. И когда человек дотрагивается до них, у него на руках останутся следы, которые дозволено будет увидеть при помощи ультрафиолетового света. Дабы вычислить вора необходимо оставить меченые купюры на видном месте, а когда они пропадут, посветить на руки работников.

5. Установите спрятанную камеру. О планируемом действии значимо не рассказывать своим коллегам – оно должно протекать в тайне, напротив похититель узнает о подготавливающейся западне. Установите камеру в том месте, из которого чудесно просматривается все помещение. Так вы сумеете получить неопровержимые доказательства вины определенного работника.

Совет 7: Как вычислить прямой угол

«Прямым» называют угол, имеющий размер в 90°, что соответствует половине числа Пи в радианах. Это составляет половину величины развернутого угла, тот, что совпадает с прямой линией – данный факт применяется для определения перпендикулярности 2-х прямых. С применением прямых углов строятся многие верные геометрические фигуры, форму которых имеет множество создаваемых человеком предметов и сооружений.

Вам понадобится

Инструкция

1. Если линии, образующие угол, начерчены на бумаге, то определить, что угол является прямым дозволено, скажем, с подмогой транспортира. Приложите его параллельно всякий из сторон таким образом, дабы нулевая отметка совпала с вершиной угла. Если иная сторона угла соответствует девяностоградусному делению транспортира, то вас дозволено поздравить – вы определили, что именно данный угол и является прямым. Это же самое дозволено проделать и с подмогой угольника, а если безусловной точности не требуется, то даже с применением других имеющихся под рукой предметов – спичечного коробка, дискеты, пластиковой коробки CD/DVD-диска и всякого иного прямоугольного предмета.

3. Если вам надобно рассчитать построение прямого угла, то проделайте операцию, обратную описанной в предыдущем шаге. Вначале определите длины 2-х сторон, которые будут данный угол образовывать. Проще трудиться с верным равнобедренным треугольником, следственно отличнее взять идентичные длины катетов. Если итог нужно отобразить на бумаге, то отложите на циркуле необходимую длину, поставьте точку в вершине грядущего угла и обозначьте ее буквой А. Начертите круг с центром в этой точке и проведите радиус, обозначив точку его касания с окружностью буквой В. После этого рассчитайте длину гипотенузы – умножьте длину катета на квадратный корень из двойки. Полученное значение отложите на циркуле и начертите 2-й круг с центром в точке В. После этого объедините точку пересечения 2-х окружностей (точка С) с центром первого круга (точка А). Это и будет прямой угол ВАС.

Совет 8: Как вычислить корень пятой степени

Математическая операция извлечения корня N-ой степени из числа (подкоренного выражения) обозначает подбор такого значения, которое при умножении на само себя (N-1) раз даст подкоренное выражение. Если при степени, равной двойке, подобрать такое значение в уме еще дозволено, то для пятой степени это будет достаточно затруднительно. Один из особенно примитивных методов решить задачу – воспользоваться встроенным в ОС программным калькулятором.

Вам понадобится

Инструкция

1. Запустите типовой калькулятор, входящий в состав базового программного обеспечения операционной системы. В любой применяющейся сегодня версии Windows это дозволено сделать через диалог запуска программ — вызовите его одновременным нажатием клавиш Win и R. В единственное поле диалога введите calc, щелкните по кнопке OK и калькулятор будет запущен. В ОС Windows 7 это же дозволено сделать, раскрыв основное меню (скажем, нажатием клавиши Win), введя в поле с надписью «Обнаружить программы и файлы» буквы «кальк», а затем кликнув по ссылке «Калькулятор» в списке с результатами поиска. В других версиях Windows такую же ссылку нужно искать в секции «Типовые» раздела «Все программы» основного меню системы.

2. Нажмите сочетание клавиш Alt и 2 — так интерфейс этого приложения переключается в свой «инженерный» вариант, содержащий надобную вам функцию извлечения корня. Дозволено это сделать и через меню программы — соответствующий пункт размещен в раздел «Вид».

3. Введите число, из которого нужно извлечь корень. Это дозволено сделать как с использованием клавиатуры, так и кликая мышкой соответствующие кнопки в интерфейсе на экране.

4. Нажмите кнопку, на которой помещен символ извлечения корня степени y из подкоренного значения x (??x). После этого введите пятерку и кликните знак равенства в интерфейсе приложения либо нажмите Enter на клавиатуре. Программа произведет вычисление и отобразит итог.

5. Взамен примененной на предыдущем шаге функции дозволено воспользоваться другой — возведением в степень. Возведение всякого числа в дробную степень обозначает, в частности, извлечение из него корня с показателем, стоящим в знаменателе дроби. Следственно, если вы возведете число в степень 1/5 либо 0,2, то тоже получите надобный итог. Кликните в интерфейсе кнопку, отвечающую за запуск операции возведения числа x в степень y (x?), введите 0,2 и нажмите клавишу Enter. Программа рассчитает и отобразит тот же итог, что и в предыдущем шаге.

Видео по теме

Совет 9: Как узнать диагональ телевизора

Диагональ телевизора благотворно знать. О ней спросят в ремонтном центре, если агрегату понадобится реанимация. С учетом диагонали нужно выбирать и расстояние, на котором дозволено сидеть перед экраном.

Вам понадобится

Инструкция

1. Дабы узнать диагональ телевизора, можете воспользоваться несколькими методами. 1-й и самый элементарный – посмотреть в инструкции к агрегату либо даже на его коробке. Прямо на обложке начальства пользователя указана марка телевизора, модель и его диагональ.

2. Бывает, что ни коробки, ни инструкции теснее не обнаружить. В таком случае верно определите, какой телевизор представлен для измерения: кинескопный (телевизор с ЭЛТ), ЖК (жидкокристаллический) либо плазменный.

3. Если у вас кинескопный телевизор, то измерять диагональ нужно по стеклу колбы. Легко протяните сантиметр из одного угла экрана наискосок к иному. Запишите полученный итог в сантиметрах.

4. Жидкокристаллический/плазменный телевизор перед измерением нужно включить. Отойдите от него на метр–полтора, взором зафиксируйте крайние светящиеся пиксели в углах. Дело в том, что в ЖК и плазменных телевизорах изображение заключено в небольшую черную рамочку по периметру телевизора. Следственно измерения нужно проводить по максимально далеким друг от друга пикселям.

5. Не выключая телевизор, подойдите к нему впритирку. Приложите сантиметр от одного крайнего светящегося пиксела наискосок, через экран, к иному. Запишите итог.

6. Произведите расчеты. Диагональ у телевизора либо монитора неизменно указывается в дюймах. Дабы узнать верный размер, поделите полученные в сантиметрах данные на 2,54 см. Полученный итог и будет диагональю вашего телевизора.

Обратите внимание!
Если вы измеряете диагональ телевизора с подмогой рулетки, не прикладывайте ее впритирку к экрану. Металл может оставить царапины на покрытии.

Полезный совет
Верно измерить диагональ телевизора довольно трудно, следственно не изумляйтесь, если у вас получилось необычное число. Для достоверности итога, округлите его в крупную либо меньшую сторону.

Совет 10: Как вычислить длину стороны треугольника

Для вычисления длин сторон в произвольном треугольнике почаще каждого доводится использовать теоремы синусов и косинусов. Но среди каждого множества произвольных многоугольников этого рода существуют их «больше верные» вариации – равносторонние, равнобедренные, прямоугольные. Если о треугольнике знаменито, что он принадлежит к одной из этих разновидностей, методы вычисления его параметров гораздо упрощаются. При вычислении длин их сторон зачастую дозволено обойтись без тригонометрических функций.

Инструкция

1. Длину стороны (А) равностороннего треугольника дозволено обнаружить по радиусу вписанной в него окружности (r). Для этого увеличьте ее в шесть раз и поделите на квадратный корень из тройки: А = r*6/?3.

2. Зная радиус описанной окружности (R), тоже дозволено вычислить длину стороны (А) положительного треугольника. Данный радиус вдвое огромнее использованного в предыдущей формуле, следственно утройте его и тоже поделите на квадратный корень из тройки: А = R*3/?3.

3. По периметру (Р) равностороннего треугольника вычислить длину его стороны (А) еще проще, потому что длины сторон в этой фигуре идентичны. Легко поделите периметр натрое: А = Р/3.

4. В равнобедренном треугольнике вычисление длины стороны по знаменитому периметру немножко труднее – необходимо знать еще и длину правда бы одной из сторон. Если знаменита длина стороны А, лежащей в основании фигуры, длину всякий из боковых (В) находите делением напополам разности между периметром (Р) и размером основания: В = (Р-А)/2. А если знаменита боковая сторона, то длину основания определяйте вычитанием из периметра удвоенной длины боковой: А = Р-2*В.

5. Познания площади (S), занимаемой на плоскости положительным треугольником, тоже довольно для нахождения длины его стороны (А). Извлеките квадратный корень из соотношения площади и квадратного корня из тройки, а полученный итог удвойте: А = 2*?(S/?3).

Совет 11: Как вычислить длину гипотенузы

Гипотенуза – математический термин, встречающийся при рассмотрении прямоугольных треугольников. Это наибольшая из его сторон, противолежащая прямому углу. Вычислить длину гипотенузы дозволено различными методами, в том числе по теореме Пифагора.

Инструкция

1. Треугольник является примитивной замкнутой геометрической фигурой, состоящей из 3 вершин, углов и сторон, всякая из которых имеет свое наименование. Гипотенуза и два катета – стороны прямоугольного треугольника, длины которых связаны между собой и с другими величинами разными формулами.

8. Перейдите к иному прямоугольному треугольнику BHC и обнаружьте его гипотенузу, которая равна b, т.е. второму катету треугольника ABC:b? = 16 + x?.

10. Подставьте х и обнаружьте гипотенузу:AC = 16/3 + 3 = 25/3.

Совет 12: Как вычислить диагональ квадрата

Вам понадобится

Инструкция

1. Для решения задачи из курса геометрии начертите квадрат с заданной длиной стороны. Обозначьте его, скажем, как ABCD. Припомните свойства данной геометрической фигуры. У квадрата стороны попарно параллельны. Помимо того, все они равны, а углы между смежными сторонами составляют 90°. Для решения математической задачи начерченный на листе квадрат совсем не неукоснительно имеет ту же длину стороны, что и в условии. Дозволено принять воображаемый размер либо же вычертить фигуру в масштабе.

3. Дабы составить формулу, обозначьте вестимые и незнакомые величины буквами. Скажем, сторона пускай будет а, а диагональ – d. Припомните теорему Пифагора. Квадрат гипотенузы равен сумме квадратов катетов, то есть в данном случае d2=a2+a2=2*a2.

4. Обнаружьте значение d. Длина диагонали равна квадратному корню из 2*а2, то есть d=??2*a2=a*?2.

Видео по теме

Обратите внимание!
?Для решения фактической задачи нужно заблаговременно замерить сторону реально присутствующего квадрата либо сделать чертеж в масштабе.

Полезный совет
?Длину диагонали дозволено обнаружить и через радиусы вписанной и описанной окружностей, если в условиях задачи даны именно эти параметры. В первом случае обнаружьте диаметр вписанной окружности, тот, что равен стороне квадрата, а дальше считайте так же, как в описанном методе. Вторая задача скорее на находчивость, нежели на вычисления. Припомните, чему равен радиус описанной около квадрата окружности. Он представляет собой половину диагонали, так что довольно данный вам радиус примитивно умножить на 2.

Совет 13: Как вычислить диагонали ромба

Ромб – стандартная геометрическая фигура, состоящая из четырех вершин, углов, сторон, а также 2-х диагоналей, которые перпендикулярны друг другу. Исходя из этого свойства, дозволено вычислить их длины по формуле для четырехугольника.

Инструкция

2. Облегчить решение геометрических задач с этой фигурой поможет познание некоторых свойств, присущих ромбу и связанных с длинами его диагоналей:• Ромб является частным случаем параллелограмма, следственно, противолежащие стороны у него также попарно параллельны и равны;• Диагонали точкой пересечения делятся напополам, а угол между ними – прямой;• Каждая диагональ делит напополам углы, вершины которых соединяет, являясь их биссектрисами и единовременно медианами треугольников, образованных двумя смежными сторонами ромба и иной диагональю.

5. Решение.Выразите длины диагоналей через сторону, которая в данном случае незнакома. Обозначьте ее за x, тогда: d1=x+3; d2=1,5•x.

6. Запишите формулу для диагоналей ромба :d1? + d2? = 4•a?

7. Подставьте полученные выражения и составьте уравнение с одной переменной:(x + 3)? + 9/4•x? = 4•x?

Источник