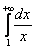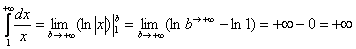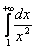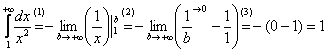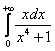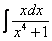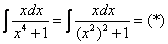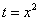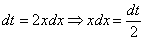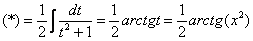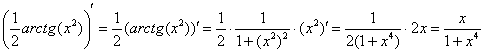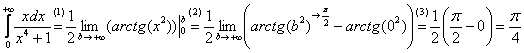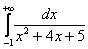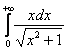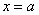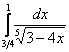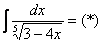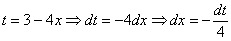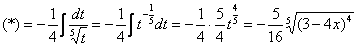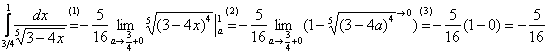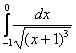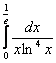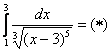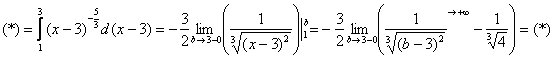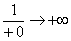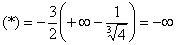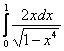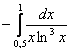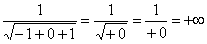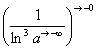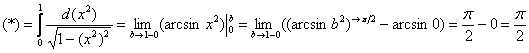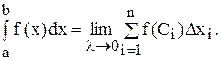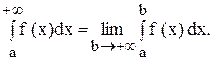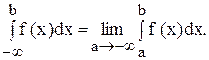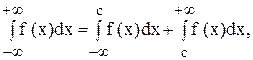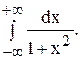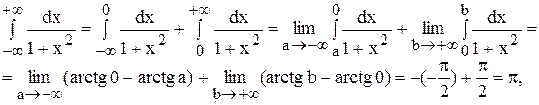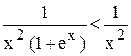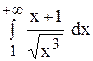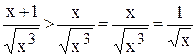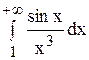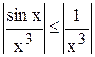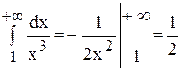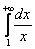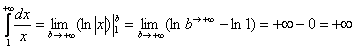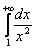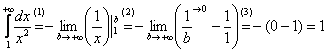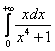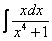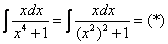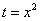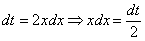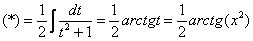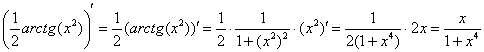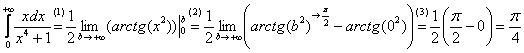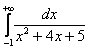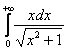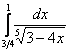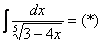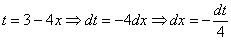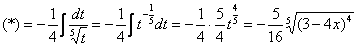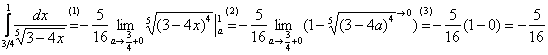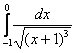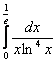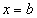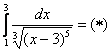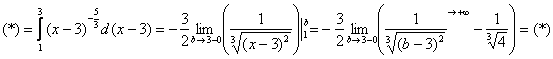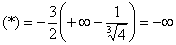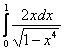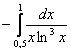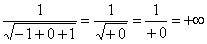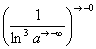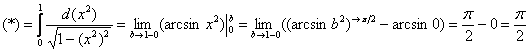Как вычислить несобственный интеграл
Как вычислить несобственный интеграл
Несобственные интегралы. Примеры решений
К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Читатель данного урока должен быть хорошо подкован в неопределенных интегралах, определенных интегралах, уметь находить площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются знания простейших пределов и графиков элементарных функций. По логике изложения материала эта статья является продолжением урока Определенный интеграл. Как вычислить площадь фигуры.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрирования
Иногда такой несобственный интеграл называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: 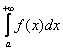
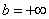
Реже встречаются интегралы с бесконечным нижним пределом 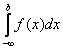
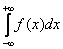
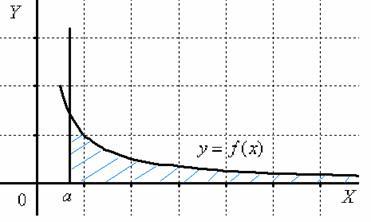
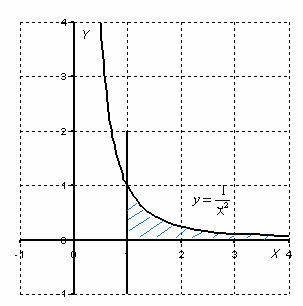
Ну а сейчас разберём самый популярный случай 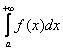
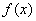
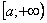
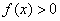
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл 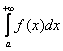
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то 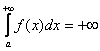
2) Но. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: 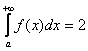
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции 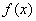
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл 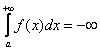
Таким образом, несобственный интеграл может быть отрицательным.
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно. Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: 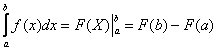
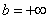
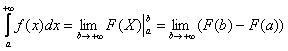
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию 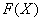
Рассмотрим два классических примера:
Вычислить несобственный интеграл или установить его расходимость.
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно.
Подынтегральная функция 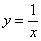
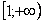
Применение нашей формулы 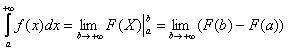
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применяется эта формула под знаком предела. Вместо привычной буквы 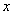
Если Вам не понятно почему 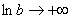
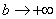
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“ 
Подынтегральная функция непрерывна на 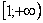
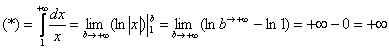
Несобственный интеграл расходится.
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция 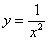
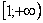
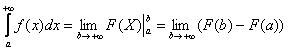
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что 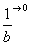
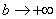
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“ 
Подынтегральная функция непрерывна на 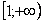
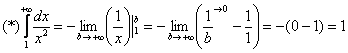
“
Что делать, если вам встретится интеграл наподобие 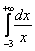
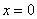
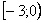
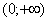
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать, так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: 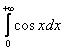
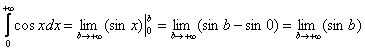
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на 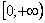
Интеграл не так прост, особенно для чайника. Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать? В этом случае целесообразно применить алгоритм, о котором я уже рассказал в статье Определенный интеграл. Примеры решений.
Сначала попытаемся найти первообразную функцию 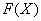
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: 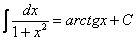
Проведем замену:
Неопределенный интеграл найден, константу 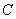
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой 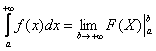
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему 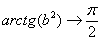
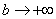
(3) Получаем окончательный ответ. Тот факт, что 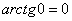
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“ 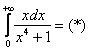
Подынтегральная функция непрерывна на 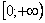
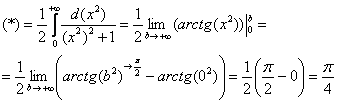
“
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей.
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов. Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функций
Или несобственные интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: 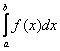
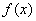
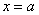
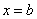
Если подынтегральной функции не существует в точке
Сразу пример, чтобы было понятно: 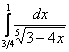
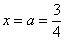
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел: 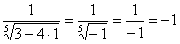
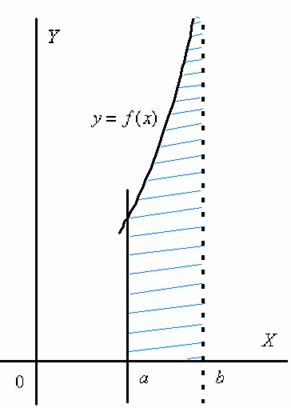
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению 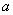
Посмотрим, как это реализуется на практике.
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке 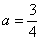
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле.
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: 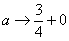
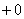
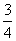
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с 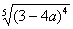
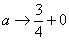
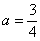
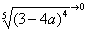
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью 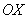
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению 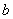
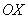
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке 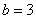
Для разнообразия я решу этот интеграл сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.
Добавка 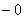
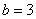
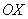
Разбираемся, почему дробь 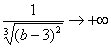
Подставляем под корень предельное значение 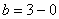
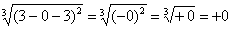
Окончательно:
Несобственный интеграл расходится.
Будьте очень внимательны в знаках. Да, конечно, несобственный интеграл расходится, но 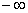
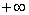
И заключительные два примера для самостоятельного рассмотрения:
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Разбор ситуации, когда оба предела интегрирования «плохие», или точка разрыва содержится прямо на отрезке интегрирования, можно найти в статье Эффективные методы решения несобственных интегралов.
Решения и ответы:
Пример 4: Решение:
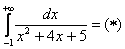
Подынтегральная функция непрерывна на 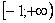

Пример 5: Решение: 
Подынтегральная функция непрерывна на 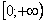
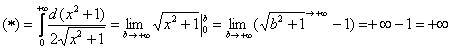
Несобственный интеграл расходится.
Пример 7: Решение: 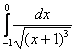
Подынтегральная функция терпит бесконечный разрыв в точке 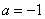
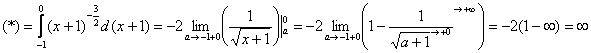
Несобственный интеграл расходится.
Примечание: с пределом выражения 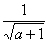
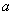
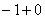
Пример 8: Решение: 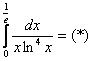
Подынтегральная функция терпит бесконечный разрыв в точке 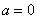
Примечание: Разбираемся в пределе выражения 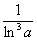
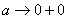
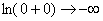
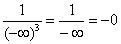
Пример 10: Решение: 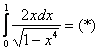
Подынтегральная функция терпит бесконечный разрыв в точке 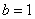
Пример 11: Решение: 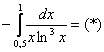
Подынтегральная функция терпит бесконечный разрыв в точке 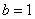
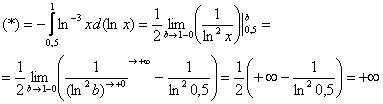
Несобственный интеграл расходится
Примечание: Разбираемся в пределе выражения 
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Несобственные интегралы
Определение несобственных интегралов.
Интеграл Римана был введен для ограниченных на отрезке функций. Естественно поставить вопрос о распространении понятия интеграла на случай бесконечного промежутка, а также на случай, когда подынтегральная функция является неограниченной.
Интеграл на бесконечном промежутке.
Рассмотрим функцию \(\displaystyle\frac<1><1+x^<2>>\). Эта функция непрерывна на отрезке \([0,\xi]\) при любом \(\xi \geq 0\), и поэтому существует интеграл \(J(\xi) = \displaystyle\int\limits_0^ <\xi>\frac
Число \(\displaystyle\frac<\pi><2>\) — можно интерпретировать как площадь фигуры, ограниченной графиком функции \(y = \displaystyle\frac<1><1+x^<2>>,\ x \geq 0\), и координатными осями (рис. 38.1).
Рис. 38.1
Рассмотрим несобственный интеграл на бесконечном промежутке от функции \(f\).
Пусть функция \(f(x)\) определена при \(x \geq a\), где \(a\) — заданное число, и интегрируема на отрезке \([a,\xi]\) при любом \(\xi \geq a\). Тогда символ \(\displaystyle\int\limits_a^ <+\infty>f(x)\ dx\) будем называть несобственным интегралом от функции \(f\) на промежутке \([0, +\infty)\). Если существует конечный \(\displaystyle\lim_ <\xi \rightarrow +\infty>\int\limits_a^ <+\infty>f(x)\ dx = A\), то говорят, что несобственный интеграл \(\displaystyle\int\limits_a^ <+\infty>f(x)\ dx\) сходится и равен \(A\), а функцию \(f\) называют интегрируемой в несобственном смысле на промежутке \([a, +\infty)\). Таким образом, сходящийся несобственный интеграл от функции \(f\) на промежутке \([a, +\infty)\) определяется равенством
$$
\int\limits_a^ <+\infty>f(x)\ dx = \lim_ <\xi \rightarrow +\infty>\int\limits_a^ <\xi>f(x)\ dx.\label
$$
Если функция \(\displaystyle\int\limits_a^ <\xi>f(x)\ dx\) не имеет конечного предела при \(\xi \rightarrow +\infty\), то говорят, что несобственный интеграл \(\displaystyle\int\limits_a^ <+\infty>f(x)\ dx\) расходится.
Сходимость интеграла \eqref
$$
\int\limits_a^ <\xi>f(x)\ dx = \int\limits_a^c f(x)\ dx+\int\limits_c^ <\xi>f(x)\ dx.\nonumber
$$
Показать, что интеграл \(J = \displaystyle\int\limits_<-\infty>^0 xe^<-x^<2>>\ dx\) сходится, и вычислить этот интеграл.
Показать, что интеграл \(J = \int\limits_<-\infty>^ <+\infty>\frac
Исследовать на сходимость интеграл
$$
J(\alpha) = \int\limits_1^ <+\infty>\frac
$$
Интеграл на конечном промежутке.
Рис. 38.2
Обратимся к несобственному интегралу на конечном промежутке.
Пусть функция \(f(x)\) определена на конечном промежутке \([a, b)\), интегрируема на отрезке \([a, \xi]\) при любом \(\xi \in [a, b)\).
Если существует конечный \(\displaystyle\lim_ <\xi \rightarrow b-0>\int\limits_a^ <\xi>f(x)\ dx = A\), то говорят, что несобственный интеграл от функции \(f(x)\) на промежутке \([a, b)\) равен \(A\). Его обозначают символом \(\displaystyle\int\limits_a^b f(x)\ dx\). Таким образом, по определению
$$
\int\limits_a^b f(x)\ dx = \lim_ <\xi \rightarrow b-0>\int\limits_a^ <\xi>f(x)\ dx.\label
$$
В случае существования конечного предела \eqref
Аналогично, если функция \(f(x)\) определена на конечном промежутке \((a, b]\), интегрируема на отрезке \([\xi, b]\) при любом \(\xi \in (a, b]\), то символ \(\displaystyle\int\limits_a^b f(x)\ dx\) называют несобственным интегралом от функции \(f\) на промежутке \((a, b]\).
Если существует конечный \(\displaystyle\lim_ <\xi \rightarrow a+0>\int\limits_<\xi>^b f(x)\ dx = A\), то говорят, что несобственный интеграл сходится и равен \(A\), то есть
$$
\int\limits_a^b f(x)\ dx = \lim_ <\xi \rightarrow a+0>\int\limits_<\xi>^b f(x)\ dx.\label
$$
Если функция \(\displaystyle\int\limits_<\xi>^b f(x)\ dx\) не имеет конечного предела при \(\xi \rightarrow a+0\), то несобственный интеграл называют расходящимся.
Определение \eqref
Поэтому в дальнейшем, рассматривая несобственный интеграл \eqref
Аналогично, рассматривая несобственный интеграл \eqref
Исследовать на сходимость интеграл
$$
J = \int\limits_0^1 \frac
$$
\(\vartriangle\) Обозначим \(F(\xi) = \displaystyle\int\limits_<\xi>^ <1>\frac
$$
F(\xi) = \left\<\begin
\frac<1><1-\alpha>(1-\xi^<1-\alpha>),\ \mbox<если>\ \alpha \neq 1 \\
-\ln \xi,\ \mbox<если>\ \alpha = 1.
\end
$$
Поэтому при \(\alpha Замечание 3.
Сходимость несобственного интеграла \eqref
Другие типы несобственных интегралов.
Если функция \(f\) определена на конечном интервале \((a, b)\), интегрируема по Риману на отрезке \([\xi, \eta]\) при любых \(\xi,\ \eta\) таких, что \(a
Свойства и вычисление несобственных интегралов.
Будем рассматривать несобственные интегралы вида \(\displaystyle\int\limits_a^b f(x)\ dx\) предполагая, что:
Согласно определению сходящегося несобственного интеграла
$$
\int\limits_a^b f(x)\ dx = \lim_ <\xi \rightarrow b-0>\int\limits_a^ <\xi>f(x)\ dx,\ \mbox<если>\ b \neq +\infty,\nonumber
$$
$$
\int\limits_a^ <+\infty>f(x)\ dx = \lim_ <\xi \rightarrow +\infty>\int\limits_a^ <\xi>f(x)\ dx\ \mbox<если>\ b = +\infty.\nonumber
$$
Линейность интеграла.
Если сходятся несобственные интегралы от функций \(f(x)\) и \(g(x)\) на промежутке \([a, b)\), то при любых \(\lambda, \mu \in \mathbb
$$
\int\limits_a^ <\xi>(\lambda f(x)+\mu g(x))\ dx = \lambda \int\limits_a^ <\xi>f(x)\ dx+\mu \int\limits_a^ <\xi>f(x)\ dx,\label
$$
\(\circ\) Для любого \(\xi \in [a, b)\) в силу свойств интеграла Римана справедливо равенство
$$
\int\limits_a^ <\xi>(\lambda f(x)+\mu g(x))\ dx = \lambda \int\limits_a^ <\xi>f(x)\ dx+\mu \int\limits_a^ <\xi>f(x)\ dx,\nonumber
$$
правая часть которого имеет по условию конечный предел при \(\xi \rightarrow b-0\), откуда следует существование предела при \(\xi \rightarrow b-0\) в левой части и справедливость формулы \eqref
Формула Ньютона-Лейбница.
Если функция \(f(x)\) непрерывна на промежутке \([a, b)\) и если \(F(x)\) — первообразная для функции \(f(x)\), то несобственный интеграл \(\displaystyle\int\limits_a^b f(x)\ dx\) сходится тогда и только тогда, когда существует конечный
$$
\lim_ <\xi \rightarrow b-0>F(\xi) = F(b-0),\label
$$
причем
$$
\int\limits_a^b f(x)\ dx = F(b-0)-F(a).\label
$$
\(\circ\) Так как функция \(f\) непрерывна на отрезке \([a, \xi]\) при любом \(\xi \in [a, b)\), то справедлива формула Ньютона-Лейбница
$$
\int\limits_a^ <\xi>f(x)\ dx = F(\xi)-F(a),\nonumber
$$
откуда, переходя к пределу при \(\xi \rightarrow b-0\) и используя соотношение \eqref
Правую часть формулы \eqref
Интегрирование по частям.
Пусть функции \(u(x)\), \(v(x)\) определены на промежутке \([a, b)\), имеют непрерывные производные на отрезке \([a, \xi]\) для любого \(\xi \in (a, b)\). Если существует конечный предел
$$
\lim_ <\xi \rightarrow b-0>[u(\xi)v(\xi)] = u(b-0)v(b-0) = uv|_<\xi = b-0>,\label
$$
и интеграл \(\displaystyle\int\limits_a^b vu’\ dx\) сходится, то и интеграл \(\displaystyle\int\limits_a^b uv’\ dx\) сходится и справедлива формула интегрирования по частям
$$
\int\limits_a^b uv’\ dx = uv|_^
$$
\(\circ\)Так как функции \(u'(x)\), \(v'(x)\) непрерывны на отрезке \([a, \xi]\) при любом \(\xi \in (a, b)\), то справедлива формула интегрирования по частям
$$
\int\limits_a^ <\xi>uv’\ dx = u(\xi)v(\xi)-u(a)v(a)-\int\limits_a^ <\xi>vu’\ dx.\label
$$
Правая часть равенства \eqref
Отметим, что при наличии конечного предела \eqref
Вычислить несобственный интеграл \(J = \displaystyle\int\limits_0^ <+\infty>xe^<-x>\ dx\).
Замена переменного.
Если функция \(f(x)\) непрерывна на промежутке \([a, b)\), а функция \(x = \varphi(t)\) непрерывно дифференцируема на промежутке \([\alpha, \beta)\), строго возрастает и удовлетворяет условиям \(\displaystyle\varphi(\alpha) = a,\ \lim_
$$
\int\limits_a^b f(x)\ dx = \int\limits_<\alpha>^ <\beta>f(\varphi(t))\varphi'(t)\ dt.\label
$$
при условии, что хотя бы один из интегралов в \eqref
\(\circ\) Пусть \(\tau \in [\alpha, \beta),\ \varphi(\tau) = \xi\). Тогда \(\varphi(\tau) \rightarrow b\) при \(\tau \rightarrow \beta-0\). Применяя формулу замены переменного для интеграла Римана, получаем
$$
\int\limits_a^ <\xi>f(x)\ dx = \int\limits_<\alpha>^ <\tau>f(\varphi(t))\varphi'(t)\ dt.\label
$$
Так как функция \(x = \varphi(t)\) строго возрастает и непрерывна на \([\alpha, \beta)\), то обратная функция строго возрастает и непрерывна на \([a, b)\). Поэтому если существует конечный предел при \(\tau \rightarrow \beta-0\) правой части равенства \eqref
Вычислить интеграл \(J = \displaystyle\int\limits_0^ <+\infty>\frac
\(\vartriangle\) Положим \(x = \operatorname
Вычислить интеграл \(J = \displaystyle\int\limits_0^ <+\infty>\frac
\(\vartriangle\) Преобразуем интеграл \(J = \displaystyle\int\limits_0^ <+\infty>\frac<(1+1/x^<2>)dx><(x-1/x)^<2>+2>\ dx\) и положим \(\displaystyle x-\frac<1>
$$
J = \int\limits_<-\infty>^<+\infty>\frac
$$
Вычислить интеграл \(J = \displaystyle\int\limits_0^ <+\infty>\frac
Таким образом, \(J_ <1>= \displaystyle\int\limits_0^ <+\infty>\frac
Интегрирование неравенств.
Если сходятся интегралы \(\displaystyle\int\limits_a^b f(x)\ dx\) и \(\displaystyle\int\limits_a^b g(x)\ dx\) и для всех \(x \in [a, b)\) выполняется неравенство
$$
f(x) \leq g(x),\nonumber
$$
то
$$
\int\limits_a^b f(x)\ dx \leq \int\limits_a^b g(x)\ dx.\label
$$
\(\circ\) Неравенство \eqref
$$
\int\limits_a^ <\xi>f(x)\ dx \leq \int\limits_a^ <\xi>g(x)\ dx,\quad a \leq \xi \leq b,\nonumber
$$
с помощью перехода к пределу при \(\xi \rightarrow b-0\). \(\bullet\)
Несобственные интегралы от неотрицательных функций.
Будем рассматривать несобственные интегралы вида \(\displaystyle\int\limits_a^b f(x)\ dx\) предполагая, что:
Согласно определению сходящегося несобственного интеграла
$$
\int\limits_a^b f(x)\ dx = \lim_ <\xi \rightarrow b-0>\int\limits_a^ <\xi>f(x)\ dx,\ \mbox<если>\ b \neq +\infty,\nonumber
$$
$$
\int\limits_a^ <+\infty>f(x)\ dx = \lim_ <\xi \rightarrow +\infty>\int\limits_a^ <\xi>f(x)\ dx\ \mbox<если>\ b = +\infty.\nonumber
$$
Если для всех \(x \in [a, b)\) выполняется неравенство
$$
f(x) \geq 0,\label
$$
то для сходимости несобственного интеграла \(\displaystyle\int\limits_a^b f(x)\ dx\) необходимо и достаточно, чтобы функция \(\int\limits_a^ <\xi>f(x)\ dx\) была ограничена сверху, то есть
$$
\exists\ C: \forall \xi \in [a,b) \rightarrow \int\limits_a^ <\xi>f(x)\ dx \leq C.\label
$$
\(\circ\) Заметим, что \(F(\xi) = \displaystyle\int\limits_a^ <\xi>f(x)\ dx\) — возрастающая функция. В самом деле, из условия \eqref
$$
\forall\ \xi_<1>,\ \xi_ <2>\in [a, b): \xi_ <2>> \xi_ <1>\rightarrow F(\xi_<2>)-F(\xi_<1>) = \int\limits_<\xi_<1>>^<\xi_<2>> f(x)\ dx \geq 0.\nonumber
$$
Если интеграл \(\displaystyle\int\limits_a^b f(x)\ dx\) сходится, то есть существует конечный \(\displaystyle\lim_ <\xi \rightarrow b-0>F(\xi) = \int\limits_a^b f(x)\ dx = J\), то по теореме о пределе монотонной функции \(J = \sup_ F(\xi)\), откуда согласно определению точной верхней грани следует, что для всех \(\xi \in [a, b)\) справедливо неравенство
$$
\int\limits_a^ <\xi>f(x)\ dx \leq \int\limits_a^b f(x)\ dx,\nonumber
$$
то есть выполняется условие \eqref
Обратно: если выполняется условие \eqref
$$
\lim_ <\xi \rightarrow b-0>F(\xi) = F(b-0) = \sup_ F(\xi),\nonumber
$$
то есть интеграл \(\displaystyle\int\limits_a^b f(x)\ dx\) сходится. \(\bullet\)
Если для всех \(x \in [a, b)\) выполняется условие
$$
0 \leq f(x) \leq g(x),\label
$$
то:
Исследовать на сходимость интеграл
$$
\int\limits_1^ <+\infty>\frac <\cos^<4>3x><\sqrt[5]<1+x^<6>>>dx.\nonumber
$$
\(\vartriangle\) Так как \(\displaystyle0 \leq \frac <\cos^<4>3x><\sqrt[5]<1+x^<6>>> \leq \frac<1>
Если для всех \(x \in [a, b)\) выполняются условия
$$
f(x) > 0,\qquad g(x) > 0,\label
$$
и, кроме того,
$$
f(x)
g(x)\ \mbox<при>\ x \rightarrow b-0,\label
$$
то интегралы \(J_ <1>= \displaystyle\int\limits_a^b f(x)\ dx\) и \(J_ <2>= \displaystyle\int\limits_a^b g(x)\ dx\) сходятся или расходятся одновременно.
\(\circ\) Если выполнены условия \eqref
$$
\forall \varepsilon > 0\ \exists \delta (\varepsilon) \in [a, b): \forall x \in [\delta (\varepsilon), b) \rightarrow \left|\frac
$$
\frac<1><2>g(x) 1\) и расходится при \(\alpha \leq 1\).
Исследовать на сходимость интеграл
$$
J = \int\limits_
$$
\(\vartriangle\) Подынтегральная функция \(f(x) = \displaystyle\frac<\ln (e^
Таким образом, интеграл \(J\) сходится в том и только том случае, когда выполняются условия \(\alpha 2\), то есть при \(2 Пример 13.
\(\vartriangle\) Подынтегральная функция \(f(x)\) положительна и непрерывна на интервале (0,1). Интеграл \(J\) сходится тогда и только тогда, когда сходятся интегралы от \(f(x)\) по промежуткам (0,1) и (1, \(+\infty\)). Обозначим эти интегралы \(J_<1>\) и \(J_<2>\) соответственно.
Для сходимости несобственного интеграла
$$
J = \int\limits_a^b f(x)\ dx\nonumber
$$
необходимо и достаточно, чтобы выполнялось условие Коши
$$
\forall \varepsilon > 0\ \exists \delta_ <\varepsilon>\in (a, b): \forall \xi’, \xi″ \in (\delta_<\varepsilon>, b) \rightarrow \left|\int\limits_<\xi’>^ <\xi″>f(x)\ dx\right| Доказательство.
\(\circ\) Обозначим
$$
F(\xi) = \int\limits_a^ <\xi>f(x)\ dx,\ a \leq \xi 0\ \exists \tilde<\delta>_ <\varepsilon>\in (a, b): \forall \xi’, \xi″ \in (\tilde<\delta>_<\varepsilon>, b) \rightarrow \left|F(\xi″)-F(\xi’)\right| Замечание 5.
Если условие Коши \eqref
$$
\exists \varepsilon_ <0>> 0\ \forall \delta_ <\varepsilon>\in (a, b): \exists \xi_<\delta>’, \xi_<\delta>″ \in (\delta_<\varepsilon>, b) \rightarrow \left|\int\limits_<\xi_<\delta>’>^<\xi_<\delta>″> f(x)\ dx\right| \geq \varepsilon_<0>,\label
$$
то интеграл \(\displaystyle\int\limits_a^b f(x)\ dx\) расходится.
Исследовать на сходимость интеграл
$$
J(\alpha) = \int\limits_1^ <+\infty>\frac <\sin^<2>x>
$$
Так как \(|\sin x| \geq \sin^ <2>x\), то по теореме сравнения из расходимости интеграла \eqref
Абсолютно и условно сходящиеся интегралы.
Несобственный интеграл \(J = \displaystyle\int\limits_a^b f(x)\ dx\) называется:
Если несобственный интеграл \(\tilde
$$
\left|\int\limits_a^b f(x)\ dx\right| \leq \int\limits_a^b |f(x)|\ dx.\label
$$
\(\circ\) Из сходимости интеграла \(\tilde
$$
\forall \varepsilon > 0\ \exists \delta_ <\varepsilon>\in (a, b): \forall \xi’, \xi″ \in (\delta_<\varepsilon>, b) \rightarrow \left|\int\limits_<\xi’>^ <\xi″>|f(x)|\ dx\right| Пример 15.
Исследовать на сходимость и абсолютную сходимость интеграл
$$
J(\alpha) = \int\limits_1^ <+\infty>\frac<\sin x>
$$
Итак, интеграл \eqref
Аналогично можно показать, что интеграл
$$
\int\limits_1^ <+\infty>\frac<\cos x>
$$
абсолютно сходится при \(\alpha > 1\), условно сходится при \(\alpha \in \) (0,1] и расходится при \(\alpha \leq 0\).
При исследовании сходимости интегралов часто может оказаться полезным следующее утверждение.
Если функция \(g(x)\) абсолютно интегрируема на промежутке \([a, b)\), то есть несобственный интеграл \(\tilde
\(\circ\) Обозначим \(J = \displaystyle\int\limits_a^b g(x)\ dx\), \(\tilde
Теорему 5 коротко можно сформулировать так: прибавление (вычитание) под знаком интеграла абсолютно интегрируемой функции не влияет ни на сходимость интеграла, ни на характер сходимости (абсолютная, условная сходимость).
Признаки Дирихле и Абеля сходимости интегралов.
Пусть функция \(f\) непрерывна, а функция \(g\) имеет непрерывную производную на промежутке \([a, +\infty)\) и выполняются следующие условия:
Тогда интеграл
$$
J = \int\limits_a^ <+\infty>f(x)g(x)\ dx\label
$$
сходится.
Условия \eqref
Следствие (признак Абеля).
Если функция \(f\) непрерывна на промежутке \(\Delta = [a, +\infty)\), интеграл \(J = \displaystyle\int\limits_a^ <+\infty>f(x)\ dx\) сходится, а функция \(g(x)\) ограничена на \(\Delta\) и ее производная \(g'(x)\) не меняет знака на \(\Delta\) (удовлетворяет условию \eqref
\(\circ\) По теореме о пределе монотонной функции существует конечный \(\displaystyle\lim_<\substack
Исследовать на сходимость и абсолютную сходимость интеграл
$$
J = \int\limits_0^ <+\infty>(e^
$$
\(\vartriangle\) Положим \(e^ <2x>= t\). Тогда \(x = \displaystyle\frac<1> <2>\ln t\), \(dx = \displaystyle\frac
$$
J = \frac<1> <2>\int\limits_1^ <+\infty>\frac<\cos t><\sqrt
$$
Оба интеграла в формуле \eqref
Исследовать на сходимость интеграл
$$
J = \int\limits_4^ <+\infty>\frac<\sin x><\sqrt
$$
\(\vartriangle\) Признак Дирихле применить нельзя, так как \(g(x) = \displaystyle\frac<1><\sqrt
$$
\varphi(t) = 1+t+\frac<\varphi″(\xi)><2!>t^<2>,\nonumber
$$
Отсюда следует, что если \(x \geq 4\), то
$$
\left(1-\frac<\sin x><\sqrt
$$
где \(|h(x)| \leq 2^ <3>\displaystyle\left|\frac<\sin x><\sqrt
2.1. Понятие несобственного интеграла
Это «родственник» определённого интеграла. …Нормальное такое определение :). И сразу возникает вопрос: чем отличается несобственный интеграл от «собрата»? Он может отличаться пределами интегрирования:
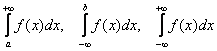
Такие интегралы получили название несобственные интегралы первого рода.
Кроме того, несобственный интеграл может быть «внешне похож» на определённый интеграл и иметь вид 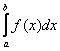



Это так называемые несобственные интегралы второго рода.
Что значит решить несобственный интеграл? В отличие от определённого интеграла, тут есть три варианта. Решить несобственный интеграл – это значит найти конечное число, либо получить бесконечность, либо выяснить, что несобственного интеграла не существует.
1) Если несобственный интеграл равен конечному числу, то говорят, что он сходится. Число может быть как положительным, так и отрицательным. Или нулём.
2) Если несобственный интеграл равен бесконечности (со знаком «плюс» или «минус»), то говорят, он расходится.
3) И в ряде случаев несобственного интеграла может вовсе не существовать. Даже если подынтегральная функция непрерывна на промежутке интегрирования! (вспоминаем, что определённый интеграл при этом условии существует всегда).
Как решить несобственный интеграл? С помощью той же формулы Ньютона-Лейбница. С некоторыми особенностями.
И здесь вы должны понимать и уметь решать несложные пределы функций.
В чём смысл несобственного интеграла? Геометрически – это тоже площадь (если интеграл существует). Но площадь своеобразная. И с этим своеобразием мы познакомимся прямо на следующей странице:
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Несобственные интегралы



1. Несобственные интегралы с бесконечными пределами
Вспомним определение интеграла 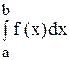
В определении предполагается, что интервал интегрирования конечен, а функция f (x) непрерывна в нем. Нарушение этих предположений приводит к несобственным интегралам.
Определение. Если интеграл 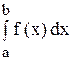
В этом случае говорят, что несобственный интеграл 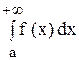
Если указанный предел не существует или существует, но бесконечен, то говорят, что интеграл не существует или расходится.
Аналогично определяется несобственный интеграл с бесконечной нижней границей:
Несобственный интеграл с двумя бесконечными границами определяется формулой:
Итак, несобственные интегралы могут быть с бесконечно нижней границей, с бесконечно верхней границей, а также с двумя бесконечными границами.
Признаки сходимости. Абсолютная и условная сходимость
Интеграл 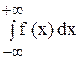
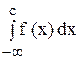
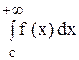
Пример. Исследовать на сходимость интеграл
Полагая с = 0, получим:
т.е. интеграл сходится.
Иногда нет необходимости вычислять несобственный интеграл, а достаточно лишь знать, сходится он или расходится, сравнив его с другим интегралом.
Теорема сравнения несобственных интегралов.
Пусть в интервале [a; +¥) функции f (x) и j (х) непрерывны и удовлетворяют неравенству 0 £ j (x) £ f (x). Тогда:
а) если интеграл 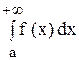
б) если интеграл 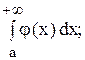
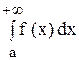
Пример.1. Исследовать, сходится ли интеграл:
Решение. Заметим, что при 1 £ x :

Следовательно, 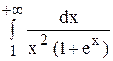
Пример. 2. Исследовать, сходится ли интеграл
Замечаем, что
Но, 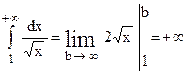
Следовательно, расходится и данный интервал.
Теорема. Если интеграл 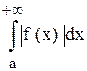
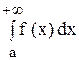
В этом случае последний интеграл называется абсолютно сходящимся.
Если интеграл от 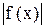
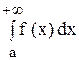
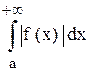
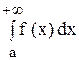
Пример. Исследовать сходимость интеграла
Здесь подынтегральная функция – знакопеременная.
Замечаем, что
Но
Следовательно, интеграл 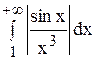
Отсюда следует, что сходится и данный интеграл.
Итак, для определения сходимости несобственного интеграла можно его сравнивать с другим интегралом, который заведомо сходится или расходится.
Несобственные интегралы от разрывных функций
Если на отрезке [a; b] функция f (x) имеет несколько (конечное число) точек разрыва первого рода, это “препятствие” легко устранить, разбив отрезок точками разрыва на несколько отрезков, вычислить определенные интегралы на каждом отдельном участке и результаты сложить.
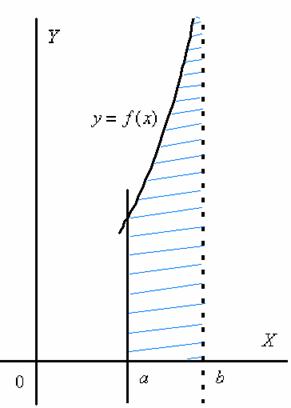
Рассмотрим определенный интеграл от функции, неограниченной при приближении к одному из концов отрезка [a; b], например, 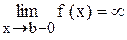
(В таких случаях обычно говорят : ’’Функция имеет бесконечный разрыв на правом конце отрезка интегрирования’’.)
Ясно, что обычное определение интеграла здесь теряет свой смысл.
Определение. Несобственным интегралом от функции f(x), непрерывной при а £ х
Несобственные интегралы. Примеры решений
К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Читатель данного урока должен быть хорошо подкован в неопределенных интегралах, определенных интегралах, уметь находить площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются знания простейших пределов и графиков элементарных функций. По логике изложения материала эта статья является продолжением урока Определенный интеграл. Как вычислить площадь фигуры.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрирования
Иногда такой несобственный интеграл называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: 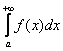
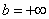
Реже встречаются интегралы с бесконечным нижним пределом 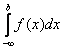
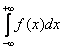
Ну а сейчас разберём самый популярный случай 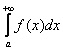

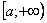
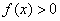
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл 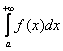
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то 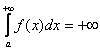
2) Но. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: 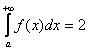
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции 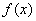
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл 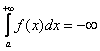
Таким образом, несобственный интеграл может быть отрицательным.
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно. Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: 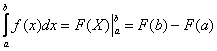
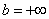
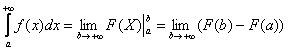
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию 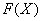
Рассмотрим два классических примера:
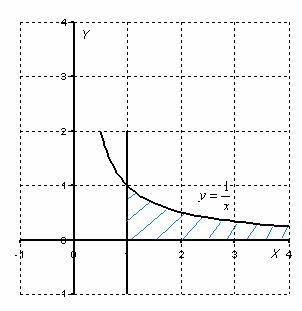
Вычислить несобственный интеграл или установить его расходимость.
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно.
Подынтегральная функция 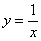
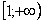
Применение нашей формулы 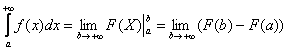
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применяется эта формула под знаком предела. Вместо привычной буквы 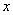
Если Вам не понятно почему 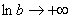
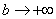
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“ 
Подынтегральная функция непрерывна на 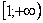
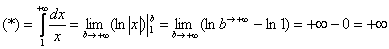
Несобственный интеграл расходится.
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
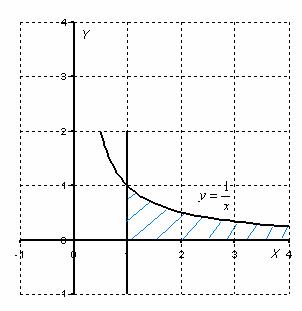
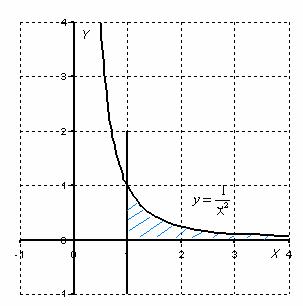
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция 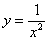
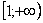
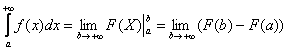
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что 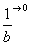
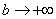
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“ 
Подынтегральная функция непрерывна на 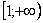
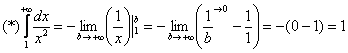
“
Что делать, если вам встретится интеграл наподобие 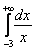
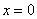
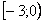
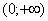
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать, так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: 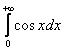
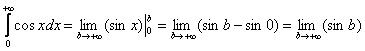
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на 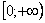
Интеграл не так прост, особенно для чайника. Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать? В этом случае целесообразно применить алгоритм, о котором я уже рассказал в статье Определенный интеграл. Примеры решений.
Сначала попытаемся найти первообразную функцию 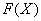
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: 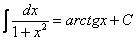
Проведем замену:
Неопределенный интеграл найден, константу 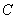
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой 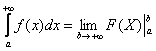
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему 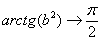
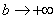
(3) Получаем окончательный ответ. Тот факт, что 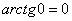
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“ 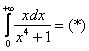
Подынтегральная функция непрерывна на 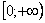
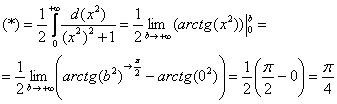
“
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей.
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов. Там же разобран случай, когда оба предела интегрирования бесконечны.
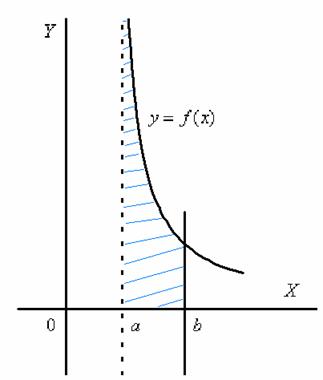
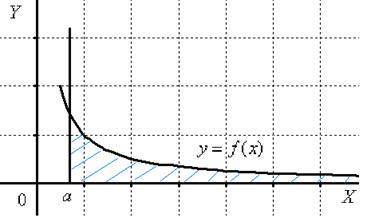
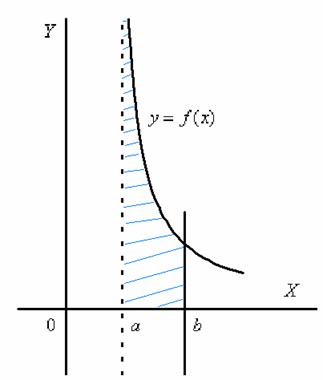
Несобственные интегралы от неограниченных функций
Или несобственные интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: 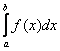
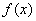
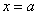
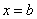
Если подынтегральной функции не существует в точке
Сразу пример, чтобы было понятно: 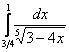
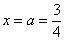
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел: 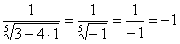
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению 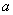
Посмотрим, как это реализуется на практике.
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке 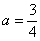
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле.
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: 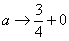
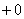
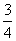
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с 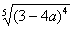
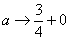
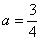
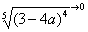
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью 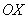
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению 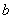
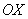
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке 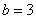
Для разнообразия я решу этот интеграл сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.
Добавка 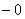
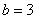
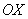
Разбираемся, почему дробь 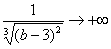
Подставляем под корень предельное значение 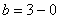
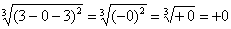
Окончательно:
Несобственный интеграл расходится.
Будьте очень внимательны в знаках. Да, конечно, несобственный интеграл расходится, но 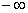
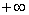
И заключительные два примера для самостоятельного рассмотрения:
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Разбор ситуации, когда оба предела интегрирования «плохие», или точка разрыва содержится прямо на отрезке интегрирования, можно найти в статье Эффективные методы решения несобственных интегралов.
Решения и ответы:
Пример 4: Решение:
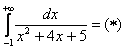
Подынтегральная функция непрерывна на 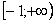

Пример 5: Решение: 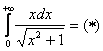
Подынтегральная функция непрерывна на 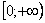
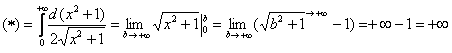
Несобственный интеграл расходится.
Пример 7: Решение: 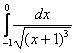
Подынтегральная функция терпит бесконечный разрыв в точке 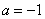
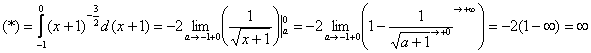
Несобственный интеграл расходится.
Примечание: с пределом выражения 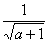
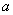
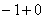
Пример 8: Решение: 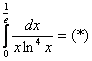
Подынтегральная функция терпит бесконечный разрыв в точке 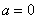
Примечание: Разбираемся в пределе выражения 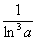
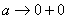
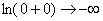
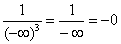
Пример 10: Решение: 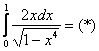
Подынтегральная функция терпит бесконечный разрыв в точке 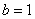
Пример 11: Решение: 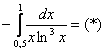
Подынтегральная функция терпит бесконечный разрыв в точке 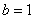
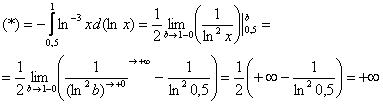
Несобственный интеграл расходится
Примечание: Разбираемся в пределе выражения 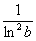
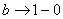
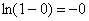
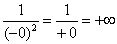
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys